the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Leaf-scale quantification of the effect of photosynthetic gas exchange on Δ17O of atmospheric CO2
Thijs L. Pons
Gerbrand Koren
Wouter Peters
Thomas Röckmann
Understanding the processes that affect the triple oxygen isotope composition of atmospheric CO2 during gas exchange can help constrain the interaction and fluxes between the atmosphere and the biosphere. We conducted leaf cuvette experiments under controlled conditions using three plant species. The experiments were conducted at two different light intensities and using CO2 with different Δ17O. We directly quantify the effect of photosynthesis on Δ17O of atmospheric CO2 for the first time. Our results demonstrate the established theory for δ18O is applicable to Δ17O(CO2) at leaf level, and we confirm that the following two key factors determine the effect of photosynthetic gas exchange on the Δ17O of atmospheric CO2. The relative difference between Δ17O of the CO2 entering the leaf and the CO2 in equilibrium with leaf water and the back-diffusion flux of CO2 from the leaf to the atmosphere, which can be quantified by the cm∕ca ratio, where ca is the CO2 mole fraction in the surrounding air and cm is the one at the site of oxygen isotope exchange between CO2 and H2O. At low cm∕ca ratios the discrimination is governed mainly by diffusion into the leaf, and at high cm∕ca ratios it is governed by back-diffusion of CO2 that has equilibrated with the leaf water. Plants with a higher cm∕ca ratio modify the Δ17O of atmospheric CO2 more strongly than plants with a lower cm∕ca ratio. Based on the leaf cuvette experiments, the global value for discrimination against Δ17O of atmospheric CO2 during photosynthetic gas exchange is estimated to be ‰ using cm∕ca values of 0.3 and 0.7 for C4 and C3 plants, respectively. The main uncertainties in this global estimate arise from variation in cm∕ca ratios among plants and growth conditions.
- Article
(2022 KB) - Full-text XML
-
Supplement
(2012 KB) - BibTeX
- EndNote
Stable isotope measurements of CO2 provide important information about the magnitude of the CO2 fluxes between atmosphere and biosphere, which are the largest components of the global carbon cycle (Farquhar et al., 1989, 1993; Ciais et al., 1997a, b; Flanagan and Ehleringer, 1998; Yakir and Sternberg, 2000; Gillon and Yakir, 2001; Cuntz et al., 2003a, b). A better understanding of the terrestrial carbon cycle is essential for predicting future climate and atmospheric CO2 mole fractions (Booth et al., 2012). Gross primary productivity (GPP), the total carbon dioxide uptake by vegetation during photosynthesis, can only be determined indirectly and remains poorly constrained (Cuntz, 2011; Welp et al., 2011). For example, Beer et al. (2010) estimated global GPP to be 102–135 PgC yr−1 (85 % confidence interval, CI) using machine learning techniques by extrapolating from a database of eddy covariance measurements of CO2. This estimate has since then been widely used as target for terrestrial vegetation models (Sitch et al., 2015) and replicated based on cross-consistency checks with atmospheric inversions, sun-induced fluorescence (SIF), and global vegetation models (Jung et al., 2020). As an alternative, Welp et al. (2011) estimated global GPP to be 150–175 PgC yr−1 using variations in δ18O of atmospheric CO2 after the 1997/98 El Niño event; see Eq. (1) for definition of the δ value.
The concept behind the latter study was that atmospheric CO2 exchanges oxygen isotopes with leaf and soil water, and this isotope exchange mostly determines the observed variations in δ18O of CO2 (Francey and Tans, 1987; Yakir, 1998). Following the 97/98 El Niño–Southern Oscillation (ENSO) event, the anomalous δ18O signature imposed on tropical leaf and soil waters was transferred to atmospheric CO2, before slowly disappearing as a function of the lifetime of atmospheric CO2. This in turn is governed by the land vegetation uptake of CO2 during photosynthesis, as well as soil invasion of CO2 (Miller et al., 1999; Wingate et al., 2009). For the photosynthesis term, the equilibration of CO2 with water is an uncertain parameter in this calculation, partly because the δ18O of water at the site of isotope exchange in the leaf is not well defined. Importantly, a significant δ18O variation can occur in leaves due to the preferential evaporation of relative to (Gan et al., 2002, 2003; Farquhar and Gan, 2003; Cernusak et al., 2016), which induces a considerable uncertainty in estimating δ18O of CO2. Similar considerations for the transfer of the δ18O signature of precipitation into the soils, and then up through the roots, stems, and leaves makes 18O of CO2 a challenging measurement to interpret (Peylin et al., 1999; Cuntz et al., 2003a, b).
Classical isotope theory posits that oxygen isotope distributions are modified in a mass-dependent way. This means that the 17O∕16O ratio changes by approximately half of the corresponding change in 18O∕16O (Eq. 2), and it applies to the processes involved in gas exchange between atmosphere and plants. However, in 1983 Thiemens and co-workers (Heidenreich and Thiemens, 1983, 1986; Thiemens and Heidenreich, 1983) reported a deviation from mass-dependent isotope fractionation in ozone (O3) formation called mass-independent isotope fractionation (Δ17O, Eq. 3). In the stratosphere, the Δ17O of O3 is transferred to CO2 via isotope exchange of CO2 with O(1D) produced from O3 photolysis (Yung et al., 1991, 1997; Shaheen et al., 2007), which results in a large amount of Δ17O in stratospheric CO2 (Thiemens et al., 1991, 1995; Lyons, 2001; Lämmerzahl et al., 2002; Thiemens, 2006; Kawagucci et al., 2008; Wiegel et al., 2013).
Once Δ17O has been created in stratospheric CO2, the only process that modify its signal is isotope exchange with leaf water, soil water and ocean water at the Earth's surface, after CO2 has reentered the troposphere (Boering, 2004; Thiemens et al., 2014; Liang and Mahata, 2015; Hofmann et al., 2017). Isotope exchange with leaf water is more efficient relative to ocean water due to the presence of the enzyme carbonic anhydrase (CA), which effectively catalyzes the conversion of CO2 and H2O to and H+ and vice versa (Francey and Tans, 1987; Friedli et al., 1987; Badger and Price, 1994; Gillon and Yakir, 2001). The isotope exchange in the atmosphere is negligible due to lower liquid water content, lower residence time, and the absence of carbonic anhydrase (Mills and Urey, 1940; Miller et al., 1971; Johnson, 1982; Silverman, 1982; Francey and Tans, 1987).
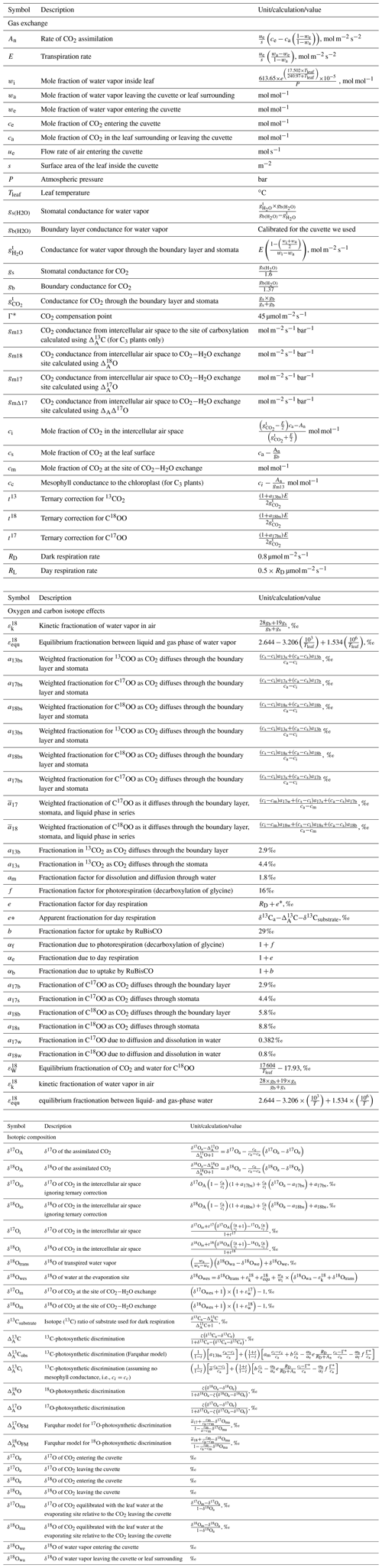
Δ17O of CO2 has been suggested as an additional independent tracer for constraining global GPP (Hoag et al., 2005; Thiemens et al., 2013; Hofmann et al., 2017; Liang et al., 2017b; Koren et al., 2019) because the processes involved in plant–atmosphere gas exchange are all mass dependent. Therefore, Δ17O at the CO2−H2O exchange site in the leaf will vary much less than δ18O. Nevertheless, mass-dependent isotope fractionation processes with slightly different three-isotope fractionation slopes are involved, which have been precisely established in the past years. Figure 1 shows how the different processes affect Δ17O of the H2O and CO2 reservoirs involved. The triple isotope slope of oxygen in meteoric waters is taken as reference slope, λRef=0.528 (Meijer and Li, 1998; Barkan and Luz, 2007; Landais et al., 2008; Luz and Barkan, 2010; Uemura et al., 2010), and we assume that soil water is similar to meteoric water. Due to transpiration and diffusion in the leaf, Δ17O of leaf water gets modified following a humidity-dependent three-isotope slope (Landais et al., 2006). Exchange of oxygen isotopes between leaf water and CO2 follows (Barkan and Luz, 2012), which determines the Δ17O of CO2 inside the leaf at the CO2−H2O exchange site. Finally, the Δ17O of the CO2 is modified when CO2 diffuses into and out of the leaf with λdiff=0.509 (Young et al., 2002).
Figure 1Schematic for mass-dependent isotope fractionation process that affects the Δ17O of the CO2 and H2O during the photosynthetic gas exchange (not to scale). The triple oxygen isotope relationships for the individual isotope fractionation processes (both kinetic and equilibrium fractionation) are assigned with θ. , where h is relative humidity (Landais et al., 2006). In this study the humidity is 75 %, θtrans=0.516, (Barkan and Luz, 2012), (Young et al., 2002), (Barkan and Luz, 2005), and (Barkan and Luz, 2007), where v and l are vapor and liquid water, respectively. ε18O is enrichment or depletion in 18O isotope composition due to the corresponding isotope fractionation process, and diff and trans stand for diffusion and transpiration, respectively.
In the first box model study of Hoag et al. (2005), the small deviations in Δ17O of CO2 due to differences in three-isotope slopes were neglected and exchange with water was assumed to reset Δ17O to 0. Hofmann et al. (2017) included the different isotope effects shown in Fig. 1 in their box model. Koren et al. (2019) incorporated all the physicochemical processes affecting Δ17O of CO2 in a 3D atmospheric model and investigated the spatiotemporal variability of Δ17O and its use as tracer for GPP. Using these and other similar models, numerous measurements of Δ17O in atmospheric CO2 from different locations have been performed and used to estimate GPP (Liang et al., 2006; Barkan and Luz, 2012; Thiemens et al., 2014; Liang and Mahata, 2015; Laskar et al., 2016; Hofmann et al., 2017). The three-isotope slopes of the processes involved in the gas exchange (Fig. 1) have been precisely determined in idealized experiments. In the advanced models mentioned above it is assumed that when all the pieces are put together they result in a realistic overall modification of Δ17O of CO2 in the atmosphere surrounding the leaf. However, this has not been confirmed by measurements previously.
In this study we report the effect of photosynthesis on Δ17O of CO2 in the surrounding air at the leaf scale. We measured Δ17O of CO2 entering and leaving a leaf cuvette to calculate the isotopic fractionation associated with photosynthesis for three species that are representative for three different biomes. The fast-growing annual herbaceous C3 species Helianthus annuus (sunflower) has a high photosynthetic capacity (An) and high stomatal conductance (gs) and is representative for temperate and tropical crops (Fredeen et al., 1991). The slower-growing perennial evergreen C3 species Hedera hibernica (ivy) is representative of forests and other woody vegetation and stress-subjected habitats (Pons et al., 2009). The fast-growing, agronomically important crop Zea mays (maize) is an herbaceous annual C4 species with a high An and a low gs, typical for savanna type vegetation (van der Weijde et al., 2013). The mole fraction of CO2 at the CO2−H2O exchange site (cm) is an important parameter to determine the effect of photosynthesis on Δ17O of CO2. In C3 plants, the CO2−H2O exchange can occur anywhere between the plasma membrane and the chloroplast since the catalyzing enzyme CA has been found in the chloroplast, cytosol, mitochondria, and plasma membrane (Fabre et al., 2007; DiMario et al., 2016). For C4 plants, CA is mainly found in the cytosol, and the CO2−H2O exchange occurs there (Badger and Price, 1994). In our experiments, sunflower and ivy are used to cover the wide cm∕ca ratio range among C3 plants and maize represents the cm∕ca ratio for the C4 plants. Using our results from the leaf-scale experiments, we estimated the effect of terrestrial vegetation on Δ17O of CO2 in the global atmosphere.
2.1 Notation and definition of δ values
Isotopic composition is expressed as the deviation of the heavy-to-light isotope ratio in a sample relative to a reference ratio and is denoted as δ, expressed in per mill (‰). In the case of oxygen isotopes, the isotope ratios are and and the reference material is Vienna Standard Mean Ocean Water (VSMOW):
For most processes, isotope fractionation depends on mass, and therefore the fractionation against 17O is approximately half of the fractionation against 18O (Eq. 3).
The mass-dependent isotope fractionation factor λ ranges from 0.5 to 0.5305 for different molecules and processes (Matsuhisa et al., 1978; Thiemens, 1999; Young et al., 2002; Cao and Liu, 2011). Δ17O is used to quantify the degree of deviation from Eq. (2) (see Eq. 3). Note that Δ17O changes not only by mass-independent isotope fractionation processes but also by mass-dependent isotope fractionation processes with a different λ value from the one used in the definition of Δ17O (Barkan and Luz, 2005, 2011; Landais et al., 2006, 2008; Luz and Barkan, 2010; Pack and Herwartz, 2014).
The choice of λ is in principle arbitrary, and in this study we use λ=0.528, which was established for meteoric waters (Meijer and Li, 1998; Landais et al., 2008; Brand et al., 2010; Luz and Barkan, 2010; Barkan and Luz, 2012; Sharp et al., 2018). Equation (3) can be linearized to (Miller, 2002), but this approximation causes an error that increases with δ18O (Miller, 2002; Bao et al., 2016).
2.2 Discrimination against Δ17O of CO2
The overall isotope fractionation associated with the photosynthesis of CO2 is commonly quantified using the term discrimination, as described in Farquhar and Richards (1984), Farquhar et al. (1989), and Farquhar and Lloyd (1993). We use the symbol ΔA for discrimination due to assimilation in this paper since the commonly used Δ is already used for the definition of Δ17O (see Eq. 3). ΔA quantifies the enrichment or depletion of carbon and oxygen isotopes of CO2 in the surrounding atmosphere relative to the CO2 that is assimilated (Farquhar and Richards, 1984). It can be calculated from the isotopic composition of the CO2 entering and leaving the leaf cuvette (Evans et al., 1986; Gillon and Yakir, 2000a; Barbour et al., 2016) as follows:
where the indices e, a and A refer to CO2 entering and leaving the cuvette and being assimilated, respectively. , where ce and ca are the mole fractions of CO2 entering and leaving the cuvette. For quantifying the effect of photosynthesis on Δ17O in our experiments, the ΔAΔ17O is calculated from and using the three-isotope slope λRL=0.528, similar to Eq. (3). In previous studies slightly different formulations have been used to define the effect of photosynthesis on Δ17O, and a comparison of the different definitions is provided in the Supplement (Eqs. S37–S40).
It is important to note that when the logarithmic definition of Δ17O or ΔAΔ17O is used, values are not additive (Kaiser et al., 2004). In linear calculations, the error gets larger when the relative difference in δ18O between the two CO2 gases increases regardless of the Δ17O of the individual CO2 gases (Fig. S1 in the Supplement). Therefore, ΔAΔ17O values have to be calculated from the individual and values and not by linear combinations of the Δ17O of air entering and leaving a plant chamber.
3.1 Plant material and growth conditions
Sunflower (Helianthus annuus L. cv “sunny”) was grown from seeds in 0.6 L pots with potting soil (Primasta, the Netherlands) for about 4 weeks. All leaves appearing above the first leaf pair were removed to avoid shading. Established juvenile ivy (Hedera hibernica L.) plants were pruned and planted in 6 L pots for 6 weeks. Ivy leaves that had developed and matured were used for the experiments. Maize (Z. mays L. cv “saccharate”) was grown from seed in 1.6 L pots for at least 7 weeks. For maize, the fourth or higher leaf number was used for the experiments when it was mature. A section of the leaf at about one-third from the tip was inserted into the leaf cuvette. They were placed on a sub-irrigation system that provided water during the growth period in a controlled-environment growth chamber, with an air temperature of 20 ∘C, relative humidity of 70 %, and CO2 mole fraction of about 400 ppm. The photosynthetic photon flux density (PPFD) was about 300 during a daily photoperiod of 16 h measured with a PPFD meter (Li-Cor LI-250A, Li-Cor Inc, NE, USA).
3.2 Gas exchange experiments
Gas exchange experiments were performed in an open system where a controlled flow of air enters and leaves the leaf cuvette, similar to the setup used by Pons and Welschen (2002). A schematic for the gas exchange experimental setup is shown in Fig. 2. The leaf cuvette had dimensions of cm3 () and the top part of the cuvette was transparent. The temperature of the leaf was measured with a K type thermocouple. The leaf chamber temperature was controlled by a temperature-controlled water bath kept at 20 ∘C (Tamson TLC 3, The Netherlands). A halogen lamp (Pradovit 253, Ernst Leitz Wetzlar GmbH, Germany) in a slide projector was used as a light source. Infrared was excluded by reflection from a cold mirror. The light intensity was varied with spectrally neutral filters (Pradovit 253, Ernst Leitz Wetzlar GmbH, Germany).
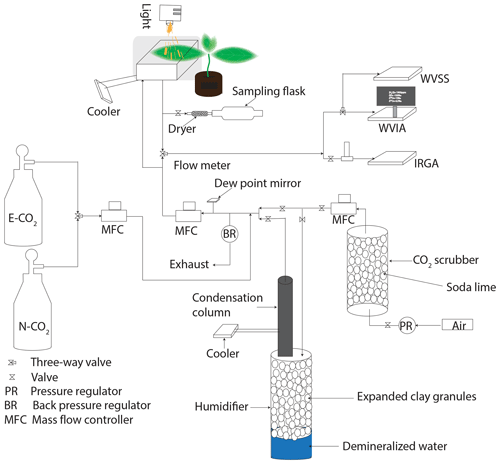
Figure 2Schematic diagram of the leaf cuvette experimental setup. IRGA stands for the infrared gas analyzer, WVSS is the water vapor standard source, WVIA is the water vapor isotope analyzer, N-CO2 is normal CO2, and E-CO2 is 17O-enriched CO2.
The CO2 mole fraction of the incoming and outgoing air was measured with an infrared gas analyzer (IRGA, model LI-6262, Li-Cor Inc., NE, USA). The isotopic composition and mole fraction of the incoming and outgoing water vapor were measured with a triple water vapor isotope analyzer (WVIA, model 911-0034, Los Gatos Research, USA). Compressed air (ambient outside air without drying) was passed through soda lime to scrub the CO2. The CO2-free air could be humidified depending on the experiment conditions (see Fig. 2). The humidity of the inlet air was monitored continuously with a dew point meter (HYGRO-M1, General Eastern, Watertown, MA, USA). Pure CO2 (either normal CO2 or isotopically enriched CO2) was mixed with the incoming air to produce a CO2 mole fraction of 500 ppm. The isotopically enriched CO2 was prepared by photochemical isotope exchange between CO2 and O2 under UV irradiation (Adnew et al., 2019).
An attached leaf or part of it was inserted into the cuvette, the composition of the inlet air was measured, and both IRGA and WVIA were switched to measure the outlet air. Based on the CO2 mole fraction of the outgoing air the flow rate of the incoming air to the cuvette was adjusted to establish a drawdown of 100 ppm CO2 due to photosynthesis in the plant chamber. The water vapor content entering the cuvette was adjusted depending on the transpiration rate relative to CO2 uptake to avoid condensation (Fig. 2). The outgoing air was measured continuously until a steady state was reached for CO2 and H2O mole fractions and δD and δ18O of the water vapor. After a steady state was established, the air was directed to the sampling flask while the IRGA and WVIA were switched back to measure the inlet air. The air passed through a Mg(ClO4)2 dryer before entering the sampling flask.
After sampling, the leaf area inside the cuvette was measured with a LI-3100C area meter (Li-Cor Inc., USA). Immediately afterward, the leaf was placed in a leak-tight 9 mL glass vial and kept in a freezer at −20 ∘C until leaf water extraction.
3.3 Calibration of the water vapor isotope analyzer (WVIA) and leaf water analysis
The WVIA was calibrated using five water standards provided by IAEA (Wassenaar et al., 2018) for both δ18O and δD (Fig. S2). We did not calibrate the WVIA for δ17O, so the δ17O data are not used in the quantitative evaluation. The isotopic composition of the water standards ranged from −50.93 ‰ to 3.64 ‰ and −396.98 ‰ to 25.44 ‰ for δ18O and δD, respectively. The detailed characterization and calibration of the WVIA is provided in the Supplement (Figs. S2 to S4).
Leaf water was extracted by cryogenic vacuum distillation for 4 h at 60 ∘C following a well-established procedure as shown in Fig. S5 (Wang and Yakir, 2000; Landais et al., 2006; West et al., 2006). Details are provided in the Supplement. The δ17O and δ18O of leaf water were determined at the Laboratoire des Sciences du Climat et de l'Environnement laboratory using a fluorination technique as described in Barkan and Luz (2005) and Landais et al. (2006, 2008).
3.4 Carbon dioxide extraction and isotope analysis
CO2 was extracted from the air samples in a system made from electropolished stainless steel (Fig. S6). Our system used four commercial traps (MassTech, Bremen, Germany). The first two traps were operated at dry ice temperature (−78 ∘C) to remove moisture and some organics. The other two traps were operated at liquid nitrogen temperature (−196 ∘C) to trap CO2. The flow rate during extraction was 55 mL min−1 controlled by a mass flow controller (Brooks Instruments, the Netherlands). The reproducibility of the extraction system was 0.030 ‰ for δ18O and 0.007 ‰ for δ13C determined on 14 extractions (1σ standard deviation, Table S1 in the Supplement).
The Δ17O of CO2 was determined using the CO2−O2 exchange method (Mahata et al., 2013; Barkan et al., 2015; Adnew et al., 2019). The CO2−O2 exchange system used at Utrecht University is described in Adnew et al. (2019). In short, equal amounts of CO2 and O2 were mixed in a quartz reactor containing a platinum sponge catalyst and heated at 750 ∘C for 2 h. After isotope equilibration, the CO2 was trapped at liquid nitrogen temperature, while the O2 was collected with 1 pellet of a 5Å molecular sieve (1.6 mm, Sigma Aldrich, USA) at liquid nitrogen temperature. The isotopic composition of the isotopically equilibrated O2 was measured with a DeltaPlusXL isotope ratio mass spectrometer in dual-inlet mode with reference to a pure O2 calibration gas that has been assigned values of δ17O=9.254 ‰ and δ18O=18.542 ‰ by Eugeni Barkan at the Hebrew University of Jerusalem. The reproducibility of the Δ17O measurement was better than 0.01 ‰ (Table S1).
3.5 Leaf cuvette model
We used a simple leaf cuvette model to evaluate the dependence of ΔAΔ17O on key parameters. In this model, the leaf is partitioned into three different compartments: the intercellular air space, the mesophyll cell, and the chloroplast. In the leaf cuvette model, we used a 100 ppm down-draw of CO2, similar to the leaf exchange experiments, i.e., the CO2 mole fraction decreases from 500 ppm in the entering air (ce) to 400 ppm in the outgoing air (co), which is identical to the air surrounding the leaf (ca) as a result of thorough mixing in the cuvette. The assimilation rate is set to 20.0 . The leaf area and flow rate of air are set to 30 cm2 and 0.7 L min−1, respectively. The isotope composition of leaf water at the site where the H2O−CO2 exchange occurs is δ17O=5.39 ‰ and δ18O=10.648 ‰, which is the mean of the measured δ17O and δ18O values of bulk leaf water in our experiments. The leaf water temperature is set to 22 ∘C (similar to the experiment). In the model, the δ18O of the CO2 entering the cuvette is set to 30.47 ‰ for all the simulations, as in the normal CO2 experiments, but the assigned Δ17O values range from −0.5 ‰ to 0.5 ‰, which encompasses both the stratospheric intrusion and combustion components. The corresponding δ17O of the CO2 entering the cuvette is calculated from the assigned δ18O value (30.47 ‰) and Δ17O values (−0.5 ‰ to 0.5 ‰). For the calculations with this model, we assumed an infinite boundary layer conductance. The leaf cuvette model is illustrated in the Supplement (Fig. S7), and the detailed code and description is available at https://git.wur.nl/leaf_model (last access: 23 March 2020, Koren et al., 2020).
4.1 Gas exchange parameters
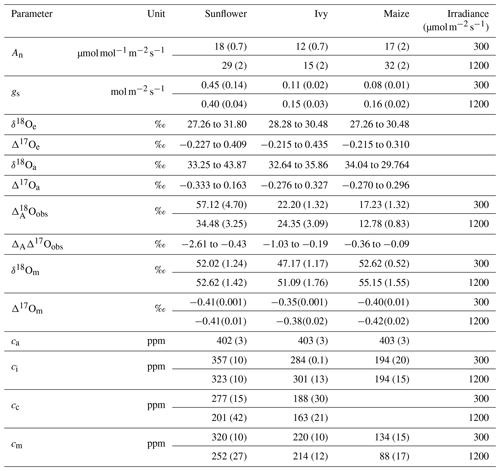
Table 1 summarizes the isotopic composition and mole fraction of the CO2 used in this study for sunflower, ivy and maize. The Δ17O of CO2 used in this study varies from −0.215 ‰ to 0.44 ‰, while the δ18O value is close to 30 ‰ for all the experiments. For all the experiments, the mole fraction of CO2 entering the leaf (ca) is 400 ppm, whereas the mole fraction of the CO2 in the intercellular air space (ci), at the CO2−H2O exchange site (cm), and in the chloroplast (cc) varies depending on the assimilation rate and metabolism type of the plants. Estimating the mesophyll conductance is described in the companion paper. A detailed description for estimating cm and cc is provided in the Supplement. A list of variables and parameters used in this study are summarized in Table 2.
Table 1Summary of gas exchange parameters and isotopic compositions of maize, sunflower, and ivy. Mole fraction at the site of exchange (cm) is calculated assuming complete isotopic equilibrium with the water at the CO2−H2O exchange site. The water at the CO2−H2O exchange site is assumed to be the same as the isotopic composition at the site of evaporation. Numbers in parentheses are the standard deviations of the mean (1σ).
4.2 Discrimination against 18O of CO2
Figure 3a shows discrimination against 18O associated with photosynthesis () for sunflower, ivy, and maize as a function of the cm∕ca ratio. varies with cm∕ca, as found in previous studies (Gillon and Yakir, 2000a; Barbour et al., 2016) . For sunflower, we observe values between 29 ‰ and 64 ‰ for cm∕ca between 0.54 and 0.86. Ivy shows relatively little variation in around a mean of 22 ‰ for cm∕ca between 0.48 and 0.58. For maize, is lower than for the C3 plants measured in this study, with values between 10 ‰ and 20 ‰ for cm∕ca between 0.15 and 0.37.
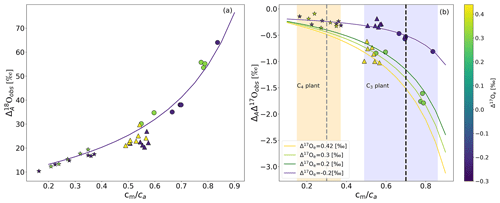
Figure 3(a) during photosynthesis for two C3 plants, sunflower (circles) and ivy (triangles), and C4 plant maize (stars), as a function of cm∕ca. The solid lines show results from the leaf cuvette model, where δ18O of the CO2 entering the cuvette is 30.47 ‰. (b) ΔAΔ17O of CO2 as a function of cm∕ca for isotopically different CO2 gases entering the cuvette (color bar shows Δ17Oe) for sunflower (circles), ivy (triangles), and maize (stars). ΔAΔ17O values calculated using the leaf cuvette model are shown as solid lines in corresponding colors (Δ17Oe values are given in the legend). The shaded areas indicate the cm∕ca ranges for C4 and C3 plants, and the vertical dashed lines indicate the mean cm∕ca ratio used for extrapolating from the leaf scale to the global scale. The solid line is the leaf cuvette model results for the corresponding cm∕ca ratio.
For sunflower, changing the irradiance from 300 (low light, hereafter LL) to 1200 (high light, hereafter HL) leads to a clear decrease in (average 22 ‰). For maize, the change is only 4.4 ‰ on average. For ivy, changing the light intensity does not significantly change the observed . The solid lines in Fig. 3a show the results of leaf cuvette model calculations, where the dependence of on cm∕ca is explored for a set of calculations with otherwise fixed parameters. The model agrees well with the experimental results, except for ivy, where the model overestimates the discrimination.
4.3 Discrimination against Δ17O of CO2
The discrimination of photosynthesis against Δ17O of CO2 (ΔAΔ17O) is shown in Fig. 3b. ΔAΔ17O is negative for all experiments, it depends strongly on the cm∕ca ratio, and |ΔAΔ17O| increases with cm∕ca ratio. For instance, for Δ17O of CO2 entering the cuvette of −0.215 ‰, ΔAΔ17O is −0.25 ‰ for maize with cm∕ca ratio of 0.3, −0.3 ‰ for ivy with cm∕ca ratio of 0.5 ‰, and −0.5 ‰ for sunflower with cm∕ca ratio of 0.7 (Fig. 3b). For sunflower and ivy, ΔAΔ17O is also strongly dependent on the Δ17O of CO2 supplied to the cuvette, whereas no significant dependence is found for maize. For an increase in Δ17O of CO2 entering the cuvette from −0.215 ‰ to 0.435 ‰, ΔAΔ17O increases from −0.3 ‰ to −0.9 ‰ at cm∕ca ratio of 0.5 for ivy. For sunflower, an increases Δ17O of CO2 entering the cuvette from −0.215 ‰ to 0.31 ‰ increases ΔAΔ17O from −0.8 ‰ to −1.7 ‰ at cm∕ca ratio of 0.8. The leaf cuvette model results illustrate the shape of the dependence on the cm∕ca ratio and agree well with the experiments. For the leaf cuvette model, the Δ17O value of the water is assigned a constant value of −0.122 ‰ (average Δ17O value for the bulk leaf water).
Figure 4b shows the same values of ΔAΔ17O as a function of the difference between Δ17O of CO2 entering the leaf and the calculated Δ17O of leaf water at the evaporation site where CO2−H2O exchange takes place (Δ17Oa−Δ17Owes) for different cm∕ca ratios. The leaf cuvette model results (solid lines in Fig. 4b) suggest a linear dependence between ΔAΔ17O and (Δ17Oa−Δ17Owes). The experimental results agree with the hypothesis that ΔAΔ17O is linearly dependent on Δ17Oa−Δ17Owes at a certain cm∕ca ratio. Figure 4a shows the corresponding relation where ΔAΔ17O is divided by Δ17Oa−Δ17Om. All the values follow the same relationship as a function of the cm∕ca ratio, which can be approximated quite well by an exponential function (Eq. 5). This function quantifies the dependence of ΔAΔ17O on cm∕ca and thus the effect of the diffusion of isotopically exchanged CO2 back to the atmosphere, which increases with increasing cm∕ca ratio.
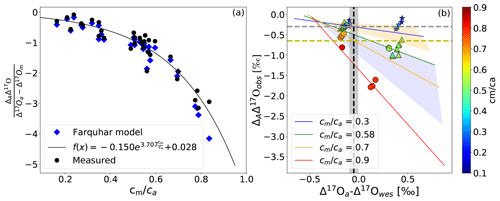
Figure 4(a) Dependency of ΔAΔ17O on the relative difference of the Δ17O(CO2) entering the leaf and the Δ17O of CO2 in equilibrium with leaf water against the cm∕ca ratio. (b) Dependency of ΔAΔ17O on the difference between the Δ17O of CO2 entering the cuvette and the Δ17O of leaf water at the evaporation site color coded for different cm∕ca ratios. The solid lines are the results of the leaf cuvette model for different cm∕ca ratios as stated in the legend. The vertical dashed black line indicates the difference between the global average Δ17O value for CO2 (−0.168 ‰) and leaf water (−0.067 ‰) (Koren et al., 2019). The gray and yellow horizontal dashed lines indicate global ΔAΔ17O of C4 and C3 plants for a cm∕ca ratio of 0.3 and 0.7, respectively.
Figure 5a and c show results from the leaf cuvette model that illustrates in more detail how Δ17Oe and Δ17Owes affect Δ17Oa and ΔAΔ17O and their dependence on cm∕ca. At lower cm∕ca, only a very small fraction of CO2 that has undergone isotopic equilibration in the mesophyll diffuses back to the atmosphere, and therefore Δ17Oa stays close to the incoming Δ17Oe, modified by the fractionation during CO2 diffusion through the stomata (Fig. 5a). Figure 5c confirms that at low cm∕ca, ΔAΔ17O approaches the fractionation constant expected for diffusion, −0.170 ‰. This diffusional fractionation is independent of the isotopic composition of the CO2 entering the leaf, and therefore at low cm∕ca, the ΔAΔ17O curves for the different values of the anomaly of the CO2 entering the leaf converge. For a high cm∕ca ratio, the back-diffusion flux of CO2 that has equilibrated with water becomes the dominant factor, and, in this case, the isotopic composition of the outgoing CO2 converges towards this isotope value, independent of the isotopic composition of the incoming CO2 (Fig. 5a). This can lead to a very wide range of values for the discrimination against Δ17O because now the effect on Δ17O of the ambient CO2 depends strongly on the difference in isotopic composition between incoming CO2 and CO2 in isotopic equilibrium with the leaf water.
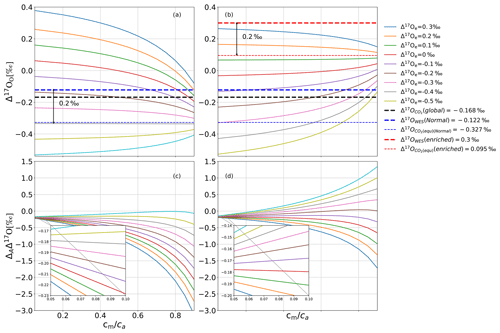
Figure 5(a, b) Δ17Oa as a function of cm∕ca for various values of Δ17Oe (see legend) for ‰ in (a) and Δ17Owes=0.300 ‰ in (b). Panels (c, d) show the corresponding values for ΔAΔ17O. Δ17Oglobal is the global average Δ17O value for atmospheric CO2 (Koren et al., 2019). When Δ17O of CO2 entering the cuvette is approximately 0.2 ‰ lower than the Δ17O of leaf water at the CO2−H2O exchange site, Δ17O of the CO2 leaving the cuvette does not change when the cm∕ca ratio varies.
In the model calculations shown in Fig. 5b and d, the isotopic composition of the water was changed from ‰ to 0.300 ‰, whereas all other parameters were kept the same. The value of Δ17Oe for which Δ17Oa does not depend on cm∕ca is shifted accordingly, again being similar to Δ17Om. At low converges to the same value as in Fig. 5c, confirming the role of diffusion into the stomata as discussed above.
Figure 6 shows how δ18O and Δ17O vary in key compartments of the leaf cuvette system that determine the oxygen isotope effects associated with photosynthesis, based on the previously established three-isotope slopes of the various processes (Fig. 1). The irrigation water has a Δ17O value of 0.017 ‰. The measured bulk leaf water is 6 ‰ to 16 ‰ enriched in 18O and its Δ17O value is lower by −0.075 ‰ to −0.200 ‰ (mean value −0.121 ‰) than the irrigation water, calculated using a three-isotope slope of θtrans=0.516 % at 80 % humidity (Landais et al., 2006). Δ17O of leaf water at the evaporation site, calculated from the transpired water, has slightly lower Δ17O, with values between −0.119 ‰ and −0.237 (average −0.184 ‰). Note that the bulk leaf water was not measured for all the experiments. For the experiments where the bulk leaf water is measured, Δ17O of leaf water at the evaporation site ranges from −0.160 ‰ to −0.231 ‰ with an average value of ‰. The calculated isotopic composition of water at the exchange site was thus similar but slightly lower in Δ17O than the values measured for bulk leaf water. CO2 exchanges with the water in the leaf with a well-established fractionation constant (see Eq. S17) and a three-isotope slope of (Barkan and Luz, 2012), leading to the lower Δ17O values of the equilibrated CO2. In our experiments, the Δ17O value of CO2 in equilibrium with leaf water is lower than the Δ17O value of CO2 entering the leaf. The Δ17O of the CO2 in the intercellular air space is a mixture between two end-members, the Δ17O of the CO2 entering the leaf and Δ17O of the CO2 in equilibrium with leaf water. This explains why the observed values of ΔAΔ17O are negative for the experiments performed in this study.
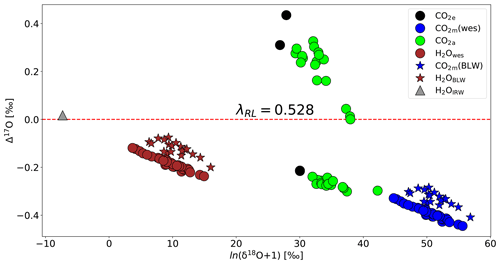
Figure 6Isotopic composition of various relevant oxygen reservoirs that affect the Δ17O of atmospheric CO2 during photosynthesis: irrigation water (gray triangle), calculated leaf water at the evaporation site (brown circles), measured bulk leaf water (brown star), CO2 entering the cuvette (black circles), CO2 leaving the leaf cuvette (green circles), CO2 equilibrated with leaf water at the evaporation site (blue circles), and CO2 equilibrated with bulk leaf water (blue stars). Δ17O is calculated with λ=0.528.
5.1 Discrimination against δ18O of CO2
The higher values for sunflower compared to maize and ivy (Fig. 3a) are mainly due to a higher back-diffusion flux (). The back-diffusion flux is higher for the C3 plants sunflower and ivy than for the C4 plant maize, a consequence of the lower stomatal conductance and higher assimilation rate of C4 plants (Gillon and Yakir, 2000a; Barbour et al., 2016). In C4 plants most of the CO2 entering the stomata is carboxylated by phosphoenolpyruvate carboxylase (PEPC), resulting in a lower CO2 mixing ratio in the mesophyll, which results in a lower back-diffusion flux. The increase in assimilation rate with higher light intensity decreases the cm∕ca ratio and thus leads to a lower back-diffusion flux, which explains the decreases in for maize and most clearly for sunflower. A similar trend of increase in with an increase in cm∕ca ratio has been reported in previous studies (Gillon and Yakir, 2000b, a; Osborn et al., 2017). For ivy, and do not decrease with an increase in irradiance because the change in assimilation rate with irradiance is small. Thus, cm will not decrease strongly and the effect on the back diffusion is smaller than the variability in of different leaves of the same plant.
In our experiments, photosynthesis causes an enrichment in the δ18O of atmospheric CO2 for both C3 and C4 plants, i.e., positive value of . In principle, can also be negative if the δ18Om is depleted relative to the ambient CO2. This is in contrast to , which will always be positive since it is determined by the fractionation due to the PEPC and RuBisCO enzyme activity (Figs. S8 and S9). In general, in our experiments the values are about 5 times larger than δ18Oa−δ18Oe, the δ18O difference between CO2 entering and leaving the cuvette (Figs. S10 to S12). This is easy to understand from the definition of ΔA. Taking as an example, , and in our experiments .
5.2 Discrimination against the Δ17O of CO2
The leaf cuvette model includes the isotope fractionations of all the individual processes that have been quantified in dedicated experiments previously (Fig. 1). The good agreement of the model results with the measurements (Fig. 3a) demonstrates that when all these processes are combined in the quantitative description of a gas exchange experiment, they actually result in a correct quantification of the isotope effects associated with photosynthesis. This has already been demonstrated before for but has now been confirmed for ΔAΔ17O.
Unlike ivy and sunflower, maize does not show a significant change in ΔAΔ17O when CO2 gases with different Δ17O are supplied to the plant. The C4 plant maize has a small back-diffusion flux due to its high assimilation rate and low stomatal conductance, leading to a low cm∕ca ratio. At low cm∕ca ratios, ΔAΔ17O is expected to be close to the weighted fractionation due to diffusion through boundary layer and stomata. In general, the effect of diffusion on Δ17O of atmospheric CO2 can be expressed as follows:
where Δ17Oa is the Δ17O of the CO2 surrounding the leaf; Δ17Omodified is the Δ17O of the CO2 modified due to diffusional fractionation; and , λRL, and αdiffusion are the oxygen three-isotope relationships during diffusion from the CO2−H2O exchange site to the atmosphere, the reference slope used, and the fractionation against 18O for CO2 during diffusion through the stomata. Using the values λRL=0.528, (Young et al., 2002), and αdiffusion=0.9912 (Farquhar and Lloyd, 1993), the effect of diffusional fractionation on the Δ17O of atmospheric CO2 is −0.168 ‰ regardless of the anomaly of the CO2 entering the leaf, and the model results confirm this at low cm∕ca ratios (Fig. 5c and d, inset).
At a high cm∕ca ratio, Δ17Oa is dominated by the back-diffusion flux of CO2 that has equilibrated with water. As a consequence, Δ17Oa converges to a common value that is independent of the anomaly of the CO2 entering the cuvette and is determined by the isotopic composition of leaf water. Figure 5 confirms that the end-member is equal to the Δ17O of CO2 in equilibrium with leaf water, Δ17Om. In fact, when Δ17Oa=Δ17Om, Δ17Oa does not change with cm∕ca, indicating that in this case the Δ17O of the CO2 diffusing back from the leaf is the same as the Δ17O(CO2) entering the leaf.
is the overall discrimination occurring during the diffusion of 12C18O16O from the ambient air surrounding the leaf to the CO2−H2O exchange site (see Table 2 for the list of variables). In our study ranges from 5 ‰ to 7.2 ‰, lower than the literature estimate of 7.4 ‰ (Farquhar et al., 1993). depends on the ratio of stomatal conductance, which is associated with a strong fractionation of 8.8 ‰, to mesophyll conductance with an associated fractionation of only 0.8 ‰. Therefore, the higher the ratio (gs∕gm18) the lower the (Table S2). The difference in of 2.4 ‰ between the literature value of 7.4 ‰ and the lowest estimate in this study will introduce an error of only 0.046 ‰ in the Δ17O value (see Eq. 6). The uncertainty has lower influence on the ΔAΔ17O of C3 plants compared to C4 plants since the diffusional fractionation is less important at the higher cm∕ca ratio where C3 plants operate.
5.3 Global average value of ΔAΔ17O and Δ17O isoflux
We can use the established relationship between ΔAΔ17O and Δ17Oa−Δ17Owes for a certain cm∕ca ratio to provide a bottom-up estimate for the global effect of photosynthesis on Δ17O in atmospheric CO2, based on data obtained in real gas exchange experiments. For this, we use results from a recent modeling study, which provides global average values for CO2 and leaf water ( ‰, ‰; Koren et al., 2019; Figs. S13 and 14). The Δ17O(CO2) values agree well with the limited amount of available measurements (Table 3).
Table 3Summary of the parameters used for the extrapolation of leaf-scale experiments to the global scale and the results obtained, as well as an overview of available Δ17O measurements.
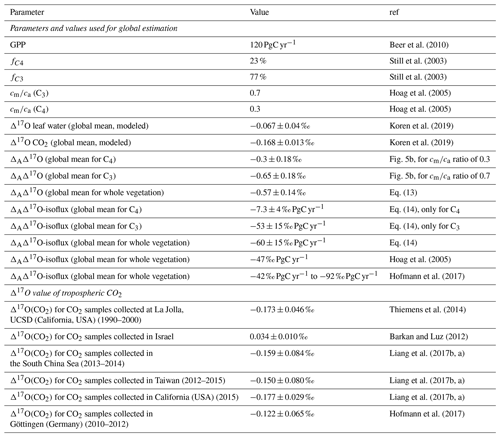
To extrapolate ΔAΔ17O determined in the leaf-scale experiments to the global scale, global average cm∕ca ratios of 0.7 and 0.3 are used for C3 and C4 plants, respectively, similar to previous studies (Hoag et al., 2005; Liang et al., 2017b). From the SIBCASA model results we obtained an annual variability of ci∕ca values with a standard deviation of 0.12 and 0.17 for C4 and C3 plants, respectively (Fig. S15) (Schaefer et al., 2008; Koren et al., 2019). We use this variability as the upper limit of the error estimate for cm∕ca, as shown in the light orange and light pink shaded areas in Fig. 4b. This error is converted to an error in ΔAΔ17O using the relation with cm∕ca. Based on the linear dependency of ΔAΔ17O and Δ17Oa−Δ17Owes, we estimate the ΔAΔ17O for tropospheric CO2 based on the Δ17O of leaf water and cm∕ca ratio. In Fig. 4b, the vertical dashed black line indicates Δ17Oa−Δ17Owes obtained from the 3D global model (Koren et al., 2019). The results of the global estimate and parameters used for the extrapolation of a leaf-scale study to the global scale are summarized in Table 3.
The δ17O value of atmospheric CO2 (21.53 ‰) is calculated from the global δ18O and Δ17O values (41.5 ‰ and −0.168 ‰, respectively) (Koren et al., 2019). The δ17O and δ18O values of global mean leaf water are calculated from the soil water. A global mean δ18O value of soil water is −8.4 ‰ assuming soil water to be similar to precipitation (Bowen and Revenaugh, 2003; Koren et al., 2019). The δ17O value of soil water is −4.4 ‰, calculated using Eq. (7) (Luz and Barkan, 2010).
δ17O and δ18O of leaf water are calculated from δ17O and δ18O of soil water with fractionation factors of 1.0043 and 1.0084, respectively (Hofmann et al., 2017; Koren et al., 2019). The fractionation factor for δ17O is calculated using with λtrans=0.516, assuming relative humidity to be 75 % (Landais et al., 2006). The δ17O and δ18O values of global mean leaf water are then −0.136 ‰ and −0.131 ‰, respectively. Thus, the difference between global atmospheric CO2 and leaf water is ‰ and ‰. This yields ‰, and this value is indicated as a dashed black line in Fig. 4. The gray shaded area indicates the propagated error using the standard deviation of the relevant parameters in 180×360 grid boxes for 12 months of leaf water and 45×60 grid boxes for 24 months for CO2 (Koren et al., 2019). In Fig. 4b, the intersection between the vertical dashed black line and the discrimination lines for the representative cm∕ca ratios of C3 and C4 plants corresponds to the ΔAΔ17O value of C3 and C4 plants. For C4 plants () this yields ‰ (dashed gray line in Fig. 4b), and for C3 plants it yields () ‰ (dashed black line in Fig. 4b).
Three main factors contribute to the uncertainty of the extrapolated ΔAΔ17O value. The first is the measurement error, which contributes 0.25 ‰ (standard error for individual experiments). The second factor is the uncertainty in the difference between Δ17O of atmospheric CO2 and leaf water, and we use results from the global model to estimate an error. For Δ17O of atmospheric CO2, statistics for all 45×60 grid boxes for 24 months (2012–2013) show a range of −0.218 ‰ to −0.151 ‰, with a mean of −0.168 ‰ and a standard deviation of 0.013 ‰ (Fig. S13). For Δ17O of the leaf water statistics for all 180×360 grid boxes for 12 months show a range of −0.236 ‰ and −0.027 ‰ (Fig. S14). The mean is −0.067 ‰ with a standard deviation of 0.041 ‰. From the combined errors we estimate the error in (Δ17Oa−Δ17Owes) to be 0.043 ‰. The third uncertainty in the extrapolation of Δ17O comes from the uncertainty in the cm∕ca ratio. For C3 and C4 plants, these errors are indicated by the light orange and light blue shadings in Fig. 4b.
Taking these uncertainties into account leads to a mean value of ‰ for C4 plants and ‰ for C3 plants. The leaf-scale discrimination against Δ17O is then extrapolated to global vegetation using these representative values of ΔAΔ17O and the relative fractions of photosynthesis by C4 and C3 plants, respectively, as follows:
where and are the photosynthesis-weighted global coverage of C4 and C3 vegetation. and quantify the discrimination against Δ17O by C4 and C3 plants, which are calculated using estimated values of cm∕ca from a model. Using assimilation-weighted fractions of 23 % for C4 and 77 % for C3 vegetation (Still et al., 2003), the global mean value of ΔAΔ17O obtained from Eq. (8) is ‰.
Isoflux is the product of isotope composition and gross mass flux of the molecule. In the case of assimilation, the net flux is multiplied with the discrimination associated with assimilation (Ciais et al., 1997a). FLA and FAL are total CO2 fluxes from leaf to the atmosphere and from atmosphere to leaf, respectively. The global-scale Δ17OA isoflux is calculated by multiplying the discrimination with the assimilation flux as follows:
where is the terrestrial assimilation rate. The factor 0.88 accounts for the fraction of CO2 released due to autotrophic respiration (Ciais et al., 1997a). The ΔAΔ17O isoflux due to photosynthesis is calculated using a GPP value of 120 PgC yr−1 (Beer et al., 2010) and , resulting in an isoflux of ‰ PgC yr−1 globally. This is the first global estimate of ΔAΔ17O based on direct measurements of the discrimination during assimilation. Our value is in good agreement with previous model estimates. Hofmann et al. (2017) estimated an isoflux ranging from −42 ‰ PgC yr−1 to −92 ‰ PgC yr−1 (converted to a reference line with λ=0.528) using an average cm∕ca ratio of 0.7 for both C4 and C3 plants and Δ17O of −0.147 ‰ for atmospheric CO2. A model-estimated value from Hoag et al. (2005) is −47 ‰ PgC yr−1 (converted to our reference slope of λ=0.528), derived with a more simple model and using Δ17O of −0.146 ‰ with cm∕ca ratio of 0.33 and 0.66 for C4 and C3 plants, respectively.
The main uncertainty in the extrapolation of ΔAΔ17O from the leaf experiments to the global scale is the uncertainty in the cm∕ca ratio. The error from the uncertainty in cm∕ca ratio increases when the relative difference in Δ17O between CO2 and leaf water increases (Fig. 5b). It is difficult to determine a single representative cm value for different plants because this value would need to be properly weighted with temperature, irradiance, CO2 mole fraction, and other environmental factors (Flexas et al., 2008, 2012; Shrestha et al., 2019). Recent developments in laser spectroscopy techniques (McManus et al., 2005; Nelson et al., 2008; Tuzson et al., 2008; Kammer et al., 2011) might enable more and easier measurements of cm∕ca both in the laboratory and under field conditions. This could lead to a better understanding of variations in the cm∕ca ratio among plant species temporally, spatially, and environmentally.
In order to directly quantify the effect of photosynthetic gas exchange on the Δ17O of atmospheric CO2, gas exchange experiments were carried out in leaf cuvettes using two C3 plants (sunflower and ivy) and one C4 plant (maize) with isotopically normal and slightly anomalous (17O-enriched) CO2. Results for 18O agree with results reported in the literature previously. Our results for Δ17O confirm that the formalism developed by Farquhar and others for δ18O is also applicable to the evaluation of Δ17O. In particular, our experiments confirm that two parameters determine the effect of photosynthesis on CO2: (1) the Δ17O difference between the incoming CO2 and CO2 in equilibrium with leaf water and (2) the cm∕ca ratio, which determines the degree of back-flux of isotopically exchanged CO2 from the mesophyll to the atmosphere. At low cm∕ca ratios, ΔAΔ17O is mainly influenced by the diffusional fractionation. Under our experimental conditions, the isotopic effect increased with cm∕ca, e.g., ΔAΔ17O was −0.3 ‰ and −0.65 ‰ for maize and sunflower with cm∕ca ratios of 0.3 and 0.7, respectively. However, experiments with mass independently fractionated CO2 demonstrate that the results depend strongly on the Δ17O difference between the incoming CO2 and CO2 in equilibrium with leaf water. This is supported by calculations with a leaf cuvette model.
δ18O is largely affected by kinetic and equilibrium processes between CO2 and leaf water, and also leaf water isotopic inhomogeneity and dynamics. The Δ17O variation is much smaller compared to δ18O and is better defined since conventional biogeochemical processes that modify δ17O and δ18O follow a well-defined three-isotope fractionation slope. Results from the leaf exchange experiments were upscaled to the global atmosphere using modeled values for Δ17O of leaf water and CO2, which results in ‰ and a value for the Δ17O isoflux of ‰ PgC yr−1. This is the first study that provides such an estimate based on direct leaf chamber measurements, and the results agree with previous Δ17O calculations. The largest contribution to the uncertainty originates from uncertainty in the cm∕ca ratio and the largest contributions to the isoflux come from C3 plants, which have both a higher share of the total assimilation and higher discrimination. ΔAΔ17O is less sensitive to cm∕ca ratios at lower values of cm∕ca, for instance for C4 plants such as maize.
Δ17O of tropospheric CO2 is controlled by photosynthetic gas exchange, respiration, soil invasion, and stratospheric influx. The stratospheric flux is well established and the effect of photosynthetic gas exchange can now be quantified more precisely. To untangle the contribution of each component to the Δ17O atmospheric CO2, we recommend measuring the effects of foliage respiration and soil invasion both in the laboratory and at the ecosystem scale.
The data used in this study are included in the paper either with figures or tables. The python code for the cuvette model is available at https://git.wur.nl/leaf_model (last access: 23 March 2020, Koren et al., 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-3903-2020-supplement.
GAA and TR designed the main idea of the study. GAA and TP designed the leaf cuvette setup. TP monitors plant growth. GAA and TR designed the CO2 extraction and CO2−O2 exchange system. GAA conducted all the measurements. GK provided the leaf cuvette model. WP enabled the work within the ASICA project. All authors discussed the results at different steps of the project. GAA and TR prepared the manuscript with contributions from all the co-authors.
The authors declare that they have no conflict of interest.
The authors thank Leonard I. Wassenaar and Stefan Terzer-Wassmuth from the International Atomic and Energy Agency, Vienna, for supplying water standards. The authors thank Eugeni Barkan and Rolf Vieten from the Hebrew University of Jerusalem for calibration of our O2 and CO2 working gases. We are grateful to Amaelle Landais from Laboratoire des Sciences Du Climat et de l'Environnement Université Paris-Saclay for measuring the Δ17O of leaf water samples for our study. The authors thank Amzad Laskar for the useful discussion during the design of the experiment. This work is funded by the EU ERC project ASICA.
This research has been supported by the European Research Council (ASICA (grant no. 649087)).
This paper was edited by Aninda Mazumdar and reviewed by two anonymous referees.
Adnew, G. A., Hofmann, M. E. G., Paul, D., Laskar, A., Surma, J., Albrecht, N., Pack, A., Schwieters, J., Koren, G., Peters, W., and Röckmann, T.: Determination of the triple oxygen and carbon isotopic composition of CO2 from atomic ion fragments formed in the ion source of the 253 Ultra High-Resolution Isotope Ratio Mass Spectrometer, Rapid Commun. Mass. Sp., 33, 17 pp., 2019.
Badger, M. R. and Price, G. D.: The role of carbonic anhydrase in photosynthesis, Annu. Rev. Plant Biol., 45, 23 pp., 1994.
Bao, H., Cao, X., and Hayles, J. A.: Triple oxygen isotopes: fundamental relationships and applications, Annu. Rev. Earth Planet. Sci., 44, 29 pp., 2016.
Barbour, M. M., Evans, J. R., Simonin, K. A., and von Caemmerer, S.: Online CO2 and H2O oxygen isotope fractionation allows estimation of mesophyll conductance in C4 plants, and reveals that mesophyll conductance decreases as leaves age in both C4 and C3 plants, New Phytol., 210, 875–889, https://doi.org/10.1111/nph.13830, 2016.
Barkan, E. and Luz, B.: High precision measurements of 17O∕16O and 18O∕16O ratios in H2O, Rapid Commun. Mass. Sp., 19, 3737–3742, https://doi.org/10.1002/rcm.2250, 2005.
Barkan, E. and Luz, B.: Diffusivity fractionations of and in air and their implications for isotope hydrology, Rapid Commun. Mass. Sp., 21, 6 pp., 2007.
Barkan, E. and Luz, B.: The relationships among the three stable isotopes of oxygen in air, seawater and marine photosynthesis, Rapid Commun. Mass. Sp., 25, 2 pp., 2011.
Barkan, E. and Luz, B.: High-precision measurements of 17O∕16O and 18O∕16O ratios in CO2, Rapid Commun. Mass. Sp., 26, 2733–2738, https://doi.org/10.1002/rcm.6400, 2012.
Barkan, E., Musan, I., and Luz, B.: High-precision measurements of δ17O and 17O-excess of NBS19 and NBS18, Rapid Commun. Mass. Sp., 29, 2219–2224, https://doi.org/10.1002/rcm.7378, 2015.
Beer, C., Reichstein, M., Tomelleri, E., Ciais, P., Jung, M., Carvalhais, N., Rodenbeck, C., Arain, M. A., Baldocchi, D., Bonan, G. B., Bondeau, A., Cescatti, A., Lasslop, G., Lindroth, A., Lomas, M., Luyssaert, S., Margolis, H., Oleson, K. W., Roupsard, O., Veenendaal, E., Viovy, N., Williams, C., Woodward, F. I., and Papale, D.: Terrestrial gross carbon dioxide uptake: global distribution and covariation with climate, Science, 329, 834–838, https://doi.org/10.1126/science.1184984, 2010.
Boering, K. A.: Observations of the anomalous oxygen isotopic composition of carbon dioxide in the lower stratosphere and the flux of the anomaly to the troposphere, Geophys. Res. Lett., 31, L03109, https://doi.org/10.1029/2003GL018451, 2004.
Booth, B. B. B., Jones, C. D., Collins, M., Totterdell, I. J., Cox, P. M., Sitch, S., Huntingford, C., Betts, R. A., Harris, G. R., and Lloyd, J.: High sensitivity of future global warming to land carbon cycle processes, Environ. Res. Lett., 7, 024002, https://doi.org/10.1088/1748-9326/7/2/024002, 2012.
Bowen, G. J. and Revenaugh, J.: Interpolating the isotopic composition of modern meteoric precipitation, Water Resour. Res., 39, 1299, https://doi.org/10.1029/2003WR002086, 2003.
Brand, W. A., Assonov, S. S., and Coplen, T. B.: Correction for the 17O interference in δ13C measurements when analyzing CO2 with stable isotope mass spectrometry (IUPAC Technical Report), Pure Appl. Chem., 82, 1719–1733, https://doi.org/10.1351/pac-rep-09-01-05, 2010.
Cao, X. and Liu, Y.: Equilibrium mass-dependent fractionation relationships for triple oxygen isotopes, Geochim. Cosmochim. Ac., 75, 7435–7445, https://doi.org/10.1016/j.gca.2011.09.048, 2011.
Cernusak, L. A., Barbour, M. M., Arndt, S. K., Cheesman, A. K., English, N. B., Feild, T. S., Helliker, B. R., Holloway-Phillips, M. M., Holtum, J. A., Kahmen, A., McInerney, F. A., Munksgaard, N. C., Simonin, K. A., Song, X., Stuart-Williams, H., West, J. B., and Farquhar, G. D.: Stable isotopes in leaf water of terrestrial plants, Plant Cell Environ., 39, 1087–1102, https://doi.org/10.1111/pce.12703, 2016.
Ciais, P., Denning, A. S., Tans, P. P., Berry, J. A., Randall, D. A., Collatz, G. J., Sellers, P. J., White, J. W. C., Trolier, M., Meijer, H. A. J., Francey, R. J., Monfray, P., and Heimann, M.: A three-dimensional synthesis study of δ18O in atmospheric CO2: 1. Surface fluxes, J. Geophys. Res., 102, 5857–5872, https://doi.org/10.1029/96jd02360, 1997a.
Ciais, P., Tans, P. P., Denning, A. S., Francey, R. J., Trolier, M., Meijer, H. A. J., White, J. W. C., Berry, J. A., Randall, D. A., and Collatz, G. J.: A three-dimensional synthesis study of δ18O in atmospheric CO2: 2. Simulations with the TM2 transport model, J. Geophys. Res., 102, 5873–5883, https://doi.org/10.1029/96JD02361, 1997b.
Cuntz, M.: A dent in carbon's gold standard, Nature, 477, 547–548, 2011.
Cuntz, M., Ciais, P., Hoffmann, G., Allison, C. E., Francey, R. J., Knorr, W., Tans, P. P., White, J. W. C., and Levin, I.: A comprehensive global three-dimensional model of δ18O in atmospheric CO2: 2. Mapping the atmospheric signal J. Geophys. Res., 108, 4528, https://doi.org/10.1029/2002JD003154, 2003a.
Cuntz, M., Ciais, P., Hoffmann, G., and Knorr, W.: A comprehensive global three-dimensional model of δ18O in atmospheric CO2: 1. Validation of surface processes, J. Geophys. Res.-Atmos., 108, 24 pp., 2003b.
DiMario, R. J., Quebedeaux, J. C., Longstreth, D. J., Dassanayake, M., Hartman, M. M., and Moroney, J. V.: The cytoplasmic carbonic anhydrases βCA2 and βCA4 are required for optimal plant growth at low CO2, Plant Physiol., 171, 13 pp., 2016.
Evans, J. R., Sharkey, T. D., Berry, J. A., and Farquhar, G. D.: Carbon isotope discrimination measured concurrently with gas exchange to investigate CO2 diffusion in leaves of higher plants, Funct. Plant. Biol., 13, 11 pp., 1986.
Fabre, N., Reiter, I. M., Becuwe-Linka, N., Genty, B., and Rumeau, D.: Characterization and expression analysis of genes encoding alpha and beta carbonic anhydrases in Arabidopsis, Plant Cell Environ., 30, 617–629, https://doi.org/10.1111/j.1365-3040.2007.01651.x, 2007.
Farquhar, G. D. and Gan, K. S.: On the progressive enrichment of the oxygen isotopic composition of water along a leaf, Plant Cell Environ., 26, 18 pp., 2003.
Farquhar, G. D. and Lloyd, J.: Carbon and oxygen isotope effects in the exchange of carbon dioxide between terrestrial plants and the atmosphere, Stable isotopes and plant carbon-water relations, Acadamic Press Inc., London, 47 pp., 1993.
Farquhar, G. D. and Richards, R. A.: Isotopic composition of plant carbon correlates with water-use efficiency of wheat genotypes, Funct. Plant Biol., 11, 11 pp., 1984.
Farquhar, G. D., Ehleringer, J. R., and Hubic, K. T.: Carbon isotope discrimination and photosynthesis, Annu. Rev. Plant Phys., 40, 34 pp., 1989.
Farquhar, G. D., Lloyd, J., Taylor, J. A., Flanagan, L. B., Syvertsen, J. P., Hubick, K. T., Wong, S. C., and Ehleringer, J. R.: Vegetation effects on the isotope composition of oxygen in atmospheric CO2, Nature, 363, 4 pp., 1993.
Flanagan, L. B. and Ehleringer, J. R.: Ecosystem-atmosphere CO2 exchange: interpreting signals of change using stable isotope ratios, Trends Ecol. Evol., 13, 4 pp., 1998.
Flexas, J., Ribas-Carbo, M., Diaz-Espejo, A., Galmes, J., and Medrano, H.: Mesophyll conductance to CO2: current knowledge and future prospects, Plant Cell Environ., 31, 19 pp., 2008.
Flexas, J., Barbour, M. M., Brendel, O., Cabrera, H. M., Carriquí, M., Díaz-Espejo, A., Douthe, C., Dreyer, E., Ferrio, J. P., and Gago, J.: Mesophyll diffusion conductance to CO2: an unappreciated central player in photosynthesis, Plant Sci., 193, 14 pp., 2012.
Francey, R. J. and Tans, P. P.: Latitudinal variation in oxygen-18 of atmospheric CO2, Nature, 327, 2 pp., 1987.
Fredeen, A. L., Gamon, J. A., and Field, C. B.: Responses of photosynthesis and carbohydrate-partitioning to limitations in nitrogen and water availability in field-grown sunflower, Plant Cell Environ., 14, 7 pp., 1991.
Friedli, H., Siegenthaler, U., Rauber, D., and Oeschger, H.: Measurements of concentration, 13C∕12C and 18O∕16O ratios of tropospheric carbon dioxide over Switzerland, Tellus B, 39, 8 pp., 1987.
Gan, K. S., Wong, S. C., Yong, J. W. H., and Farquhar, G. D.: 18O spatial patterns of vein xylem water, leaf water, and dry matter in cotton leaves, Plant Physiol., 130, 13 pp., 2002.
Gan, K. S., Wong, S. C., Yong, J. W. H., and Farquhar, G. D.: Evaluation of models of leaf water 18O enrichment using measurements of spatial patterns of vein xylem water, leaf water and dry matter in maize leaves, Plant Cell Environ., 26, 16 pp., 2003.
Gillon, J. and Yakir, D.: Influence of carbonic anhydrase activity in terrestrial vegetation on the 18O content of atmospheric CO2, Science, 291, 3 pp., 2001.
Gillon, J. S. and Yakir, D.: Internal conductance to CO2 diffusion and C18OO discrimination in C3 leaves, Plant Physiol., 123, 13 pp., 2000a.
Gillon, J. S. and Yakir, D.: Naturally low carbonic anhydrase activity in C4 and C3 plants limits discrimination against C18OO during photosynthesis, Plant Cell Environ., 23, 12 pp., 2000b.
Heidenreich, J. E. and Thiemens, M. H.: A non-mass-dependent isotope effect in the production of ozone from molecular oxygen J. Chem. Phys., 78, 3 pp., 1983.
Heidenreich, J. E. and Thiemens, M. H.: A non-mass-dependent oxygen isotope effect in the production of ozone from molecular oxygen: The role of molecular symmetry in isotope chemistry J. Chem. Phys., 84, 5 pp., 1986.
Hoag, K. J., Still, C. J., Fung, I. Y., and Boering, K. A.: Triple oxygen isotope composition of tropospheric carbon dioxide as a tracer of terrestrial gross carbon fluxes, Geophys. Res. Lett., 32, L02802, https://doi.org/10.1029/2004gl021011, 2005.
Hofmann, M. E. G., Horváth, B., Schneider, L., Peters, W., Schützenmeister, K., and Pack, A.: Atmospheric measurements of Δ17O in CO2 in Göttingen, Germany reveal a seasonal cycle driven by biospheric uptake, Geochim. Cosmochim. Ac., 199, 143–163, https://doi.org/10.1016/j.gca.2016.11.019, 2017.
Johnson, K. S.: Carbon dioxide hydration and dehydration kinetics in seawater 1, Limnol. Oceanogr., 27, 6 pp., 1982.
Jung, M., Schwalm, C., Migliavacca, M., Walther, S., Camps-Valls, G., Koirala, S., Anthoni, P., Besnard, S., Bodesheim, P., Carvalhais, N., Chevallier, F., Gans, F., Goll, D. S., Haverd, V., Köhler, P., Ichii, K., Jain, A. K., Liu, J., Lombardozzi, D., Nabel, J. E. M. S., Nelson, J. A., O'Sullivan, M., Pallandt, M., Papale, D., Peters, W., Pongratz, J., Rödenbeck, C., Sitch, S., Tramontana, G., Walker, A., Weber, U., and Reichstein, M.: Scaling carbon fluxes from eddy covariance sites to globe: synthesis and evaluation of the FLUXCOM approach, Biogeosciences, 17, 1343–1365, https://doi.org/10.5194/bg-17-1343-2020, 2020.
Kaiser, J., Röckmann, T., and Brenninkmeijer, C. A. M.: Contribution of mass-dependent fractionation to the oxygen isotope anomaly of atmospheric nitrous oxide, J. Geophys. Res., 109, D03305, https://doi.org/10.1029/2003JD004088, 2004.
Kammer, A., Tuzson, B., Emmenegger, L., Knohl, A., Mohn, J., and Hagedorn, F.: Application of a quantum cascade laser-based spectrometer in a closed chamber system for real-time δ13C and δ18O measurements of soil-respired CO2, Agr. Forest Meteorol., 151, 9 pp., 2011.
Kawagucci, S., Tsunogai, U., Kudo, S., Nakagawa, F., Honda, H., Aoki, S., Nakazawa, T., Tsutsumi, M., and Gamo, T.: Long-term observation of mass-independent oxygen isotope anomaly in stratospheric CO2, Atmos. Chem. Phys., 8, 6189–6197, https://doi.org/10.5194/acp-8-6189-2008, 2008.
Koren, G., Adnew, G. A., Röckmann, T., and Peters, W.: Leaf conductance model for Δ17O in CO2, Git@WUR, available at: https://git.wur.nl/leaf_model, last access: 23 March 2020.
Koren, G., Schneider, L., van der Velde, I. R., van Schaik, E., Gromov, S. S., Adnew, G. A., Mrozek Martino, D. J., Hofmann, M. E. D., Liang, M.-C., Mahata, S., Bergamaschi, P., van der Laan-Luijkx, I. T., Krol, M. C., Röckmann, T., and Peters, W.: Global 3-D Simulations of the Triple Oxygen Isotope Signature Δ17O in Atmospheric CO2, J. Geophys. Res.-Atmos., 124, 28 pp., 2019.
Lämmerzahl, P., Röckmann, T., and Brenninkmeijer, C. A. M.: Oxygen isotope composition of stratospheric carbon dioxide, Geophys. Res. Lett., 29, 23-1–23-4, https://doi.org/10.1029/2001gl014343, 2002.
Landais, A., Barkan, E., Yakir, D., and Luz, B.: The triple isotopic composition of oxygen in leaf water, Geochim. Cosmochim. Ac., 70, 4105–4115, , 2006.
Landais, A., Barkan, E., and Luz, B.: Record of δ18O and 17O-excess in ice from Vostok Antarctica during the last 150,000 years, Geophys. Res. Lett., 35, L02709, https://doi.org/10.1029/2007gl032096, 2008.
Laskar, A. H., Mahata, S., and Liang, M.-C.: Identification of anthropogenic CO2 using triple oxygen and clumped isotopes, Environ. Sci. Technol., 50, 18 pp., https://doi.org/10.1021/acs.est.6b02989, 2016.
Liang, M.-C. and Mahata, S.: Oxygen anomaly in near surface carbon dioxide reveals deep stratospheric intrusion, Scientific Reports, 5, 11352, https://doi.org/10.1038/srep11352, 2015.
Liang, M.-C., Blake, G. A., Lewis, B. R., and Yung, Y. L.: Oxygen isotopic composition of carbon dioxide in the middle atmosphere, P. Natl. Acad. Sci. USA, 104, 4 pp., 2006.
Liang, M.-C., Mahata, S., Laskar, A. H., and Bhattacharya, S. K.: Spatiotemporal variability of oxygen isotope anomaly in near surface air CO2 over urban, semi-urban and ocean areas in and around Taiwan, Aerosol Air Qual. Res., 17, 24 pp., 2017a.
Liang, M.-C., Mahata, S., Laskar, A. H., Thiemens, M. H., and Newman, S.: Oxygen isotope anomaly in tropospheric CO2 and implications for CO2 residence time in the atmosphere and gross primary productivity, Scientific Reports, 7, 13180, https://doi.org/10.1038/s41598-017-12774-w, 2017b.
Luz, B. and Barkan, E.: Variations of 17O∕16O and 18O∕16O in meteoric waters, Geochim. Cosmochim. Ac., 74, 10 pp., 2010.
Lyons, J. R.: Transfer of mass-independent fractionation in ozone to other oxygen-containing radicals in the atmosphere, Geophys. Res. Lett., 28, 3231–3234, https://doi.org/10.1029/2000gl012791, 2001.
Mahata, S., Bhattacharya, S. K., Wang, C. H., and Liang, M.-C.: Oxygen isotope exchange between O2 and CO2 over hot platinum: an innovative technique for measuring Δ17O in CO2, Anal. Chem., 85, 6894–6901, 10.1021∕ac4011777, 2013.
Matsuhisa, Y., Goldsmitrh, J. R., and Clayton, R. N.: Mechanisms of hydrothermal crystallization of quartz at 250 ∘C and 15 kbar, Geochim. Cosmochim. Ac., 42, 9 pp., 1978.
McManus, J. B., Nelson, D. D., Shorter, J. H., Jimenez, R., Herndon, S., Saleska, S., and Zahniser, M.: A high precision pulsed quantum cascade laser spectrometer for measurements of stable isotopes of carbon dioxide, J. Mod. Optic., 52, 12 pp., 2005.
Meijer, H. and Li, W.: The use of electrolysis for accurate 17O and 18O isotope measurements in water isotopes, Isot. Environ. Health S., 34, 20 pp., 1998.
Miller, J. B., Yakir, D., White, J. W. C., and Tans, P. P.: Measurement of 18O∕16O in the soil-atmosphere CO2 flux, Global Biogeochem. Cy., 13, 13 pp., 1999.
Miller, M. F.: Isotopic fractionation and the quantification of 17O anomalies in the oxygen three-isotope system: an appraisal and geochemical significance, Geochim. Cosmochim. Ac., 66, 8 pp., 2002.
Miller, R. F., Berkshire, D. C., Kelley, J. J., and Hood, D. W.: Method for determination of reaction rates of carbon dioxide with water and hydroxyl ion in seawater, Environ. Sci. Technol., 5, 6 pp., 1971.
Mills, G. A. and Urey, H. C.: The kinetics of isotopic exchange between carbon dioxide, bicarbonate ion, carbonate ion and water, J. Am. Chem. Soc., 62, 7 pp., 1940.
Nelson, D. D., McManus, J. B., Herndon, S., Zahniser, M. S., Tuzson, B., and Emmenegger, L.: New method for isotopic ratio measurements of atmospheric carbon dioxide using a 4.3 µm pulsed quantum cascade laser, Appl. Phys. B-Lasers O., 90, 8 pp., 2008.
Osborn, H. L., Alonso-Cantabrana, H., Sharwood, R. E., Covshoff, S., Evans, J. R., Furbank, R. T., and von Caemmerer, S.: Effects of reduced carbonic anhydrase activity on CO2 assimilation rates in Setaria viridis: a transgenic analysis, J. Exp. Bot., 68, 11 pp., 2017.
Pack, A. and Herwartz, D.: The triple oxygen isotope composition of the Earth mantle and understanding Δ17O variations in terrestrial rocks and minerals, Earth. Planet. Sc. Lett., 390, 7 pp., 2014.
Peylin, P., Ciais, P., Denning, A. S., Tans, P. P., Berry, J. A., and White, J. W.: A 3-dimensional study of δ18O in atmospheric CO2: contribution of different land ecosystems, Tellus B, 51, 25 pp., 1999.
Pons, T. L. and Welschen, R. A. M.: Overestimation of respiration rates in commercially available clamp-on leaf chambers. Complications with measurement of net photosynthesis, Plant Cell Environ., 25, 5 pp., 2002.
Pons, T. L., Flexas, J., von Caemmerer, S., Evans, J. R., Genty, B., Ribas-Carbo, M., and Brugnoli, E.: Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations J. Exp. Bot., 60, 7 pp., 2009.
Schaefer, K., Collatz, G. J., Tans, P., Denning, A. S., Baker, I., Berry, J., Prihodko, L., Suits, N., and Philpott, A.: Combined simple biosphere/Carnegie-Ames-Stanford approach terrestrial carbon cycle model, J. Geophys. Res., 113, G03034, https://doi.org/10.1029/2007JG000603, 2008.
Shaheen, R., Janssen, C., and Röckmann, T.: Investigations of the photochemical isotope equilibrium between O2, CO2 and O3, Atmos. Chem. Phys., 7, 495–509, https://doi.org/10.5194/acp-7-495-2007, 2007.
Sharp, Z. D., Wostbrock, J. A. G., and Pack, A.: Mass-dependent triple oxygen isotope variations in terrestrial materials, Geochemical Perspectives Letters, 7, 27–31, https://doi.org/10.7185/geochemlet.1815, 2018.
Shrestha, A., Song, X., and Barbour, M. M.: The temperature response of mesophyll conductance, and its component conductances, varies between species and genotypes, Photosynth. Res., 141, 65–82, 2019.
Silverman, D. N.: Carbonic anhydrase: Oxygen-18 exchange catalyzed by an enzyme with rate-contributing Proton-transfer steps, Method. Enzymol., 87, 732–752, 1982.
Sitch, S., Friedlingstein, P., Gruber, N., Jones, S. D., Murray-Tortarolo, G., Ahlström, A., Doney, S. C., Graven, H., Heinze, C., Huntingford, C., Levis, S., Levy, P. E., Lomas, M., Poulter, B., Viovy, N., Zaehle, S., Zeng, N., Arneth, A., Bonan, G., Bopp, L., Canadell, J. G., Chevallier, F., Ciais, P., Ellis, R., Gloor, M., Peylin, P., Piao, S. L., Le Quéré, C., Smith, B., Zhu, Z., and Myneni, R.: Recent trends and drivers of regional sources and sinks of carbon dioxide, Biogeosciences, 12, 653–679, https://doi.org/10.5194/bg-12-653-2015, 2015.
Still, C. J., Berry, J. A., Collatz, G. J., and DeFries, R. S.: Global distribution of C3 and C4 vegetation: Carbon cycle implications, Global Biogeochem. Cy., 17, 1006, https://doi.org/10.1029/2001gb001807, 2003.
Thiemens, M. H.: Mass-independent isotope effects in planetary atmospheres and the early solar system, Science, 283, 4 pp., 1999.
Thiemens, M. H.: History and Applications of Mass-Independent Isotope Effects, Annu. Rev. Earth Pl. Sc., 34, 62 pp., https://doi.org/10.1146/annurev.earth.34.031405.125026, 2006.
Thiemens, M. H. and Heidenreich III, J. E.: Mass-independent fractionation of oxygen: a novel isotope effect and its possible cosmochemical implications, Science, 219, 1073–1075, https://doi.org/10.1126/science.219.4588.1073, 1983.
Thiemens, M. H., Jackson, T., Mauersberger, K., Schüler, B., and Morton, J.: Oxygen isotope fractionation in stratospheric CO2, Geophys. Res. Lett., 18, 669–672, 1991.
Thiemens, M. H., Jackson, T., Zipf, E. C., Erdman, P. W., and van Egmond, C.: Carbon dioxide and oxygen isotope anomalies in the mesosphere and stratosphere, Science, 270, 3 pp., 1995.
Thiemens, M. H., Chakraborty, S., and Jackson, T. L.: Decadal Δ17O record of tropospheric CO2: Verification of a stratospheric componentin the troposphere, J. Geophys. Res.-Atmos., 119, 8 pp., https://doi.org/10.1002/2013JD020317, 2013.
Thiemens, M. K., Chakraborty, S., and Jackson, T. L.: Decadal Δ17O record of tropospheric CO2: Verification of a stratospheric component in the troposphere, J. Geophys. Res.-Atmos., 119, 8 pp., 2014.
Tuzson, B., Mohn, J., Zeeman, M. J., Werner, R. A., Eugster, W., Zahniser, M. S., Nelson, D. D., McManus, J. B., and Emmenegger, L.: High precision and continuous field measurements of δ13C and δ18O in carbon dioxide with a cryogen-free QCLAS, Appl. Phys. B-Lasers O., 92, 7 pp., 2008.
Uemura, R., Barkan, E., Abe, O., and Luz, B.: Triple isotope composition of oxygen in atmospheric water vapor, Geophys. Res. Lett., 37, L04402, https://doi.org/10.1029/2009GL041960, 2010.
van der Weijde, T., Kamei, C. L. A., Torres, A. F., Vermerris, W., Dolstra, O., Visser, R. G. F., and Trindade, L. M.: The potential of C4 grasses for cellulosic biofuel production, Front. Plant. Sci., 4, 107, https://doi.org/10.3389/fpls.2013.00107, 2013.
Wang, X.-F. and Yakir, D.: Using stable isotopes of water in evapotranspiration studies, Hydrol. Process., 14, 14 pp., 2000.
Wassenaar, L. I., Terzer-Wassmuth, S., Douence, C., Araguas-Araguas, L., Aggarwal, P. K., and Coplen, T. B.: Seeking excellence: An evaluation of 235 international laboratories conducting water isotope analyses by isotope-ratio and laser-absorption spectrometry, Rapid Commun. Mass Sp., 32, 393–406, https://doi.org/10.1002/rcm.8052, 2018.
Welp, L. R., Keeling, R. F., Meijer, H. A. J., Bollenbacher, A. F., Piper, S. C., Yoshimura, K., Francey, R. J., Allison, C. A., and Wahlen, M.: Interannual variability in the oxygen isotopes of atmospheric CO2 driven by El Niño, Nature, 477, 579–582, https://doi.org/10.1038/nature10421, 2011.
West, A. G., Patrickson, S. J., and Ehleringer, J. R.: Water extraction times for plant and soil materials used in stable isotope analysis, Rapid Commun. Mass Sp., 20, 1317–1321, https://doi.org/10.1002/rcm.2456, 2006.
Wiegel, A. A., Cole, A. S., Hoag, K. J., Atlas, E. L., Schauffler, S. M., and Boering, K. A.: Unexpected variations in the triple oxygen isotope composition of stratospheric carbon dioxide, P. Natl. Acad. Sci. USA, 110, 17680–17685, https://doi.org/10.1073/pnas.1213082110, 2013.
Wingate, L., Ogée, J., Cuntz, M., Genty, B., Reiter, I., Seibt, U., Yakir, D., Maseyk, K., Pendall, E. G., Barbour, M. M., Mortazavi, B., Burlett, R., Peylin, P., Miller, J., Mencuccini, M., Shim, J. H., Hunt, J., and Grace, J.: The impact of soil microorganisms on the global budget of δ18O in atmospheric CO2, P. Natl. Acad. Sci. USA, 106, 4 pp., 2009.
Yakir, D.: Oxygen-18 of leaf water: a crossroad for plant-associated isotopic signals, in: Stable isotopes: integration of biological, ecological and geochemical processes, edited by: Griffiths, H., BIOS Scientific Publishers, Oxford, 147–188, 1998.
Yakir, D. and Sternberg, L. S. L.: The use of stable isotopes to study ecosystem gas exchange, Oecologia, 123, 4 pp., 2000.
Young, E. D., Galy, A., and Nagahara, H.: Kinetic and equilibrium mass-dependent isotope fractionation laws in nature and their geochemical and cosmochemical significance, Geochim. Cosmochim. Ac., 66, 9 pp., 2002.
Yung, Y. L., DoMore, W. B., and Pinto, J. P.: Isotopic exhange between carbon dioxide and ozone via O(1D) in the stratosphere, Geophys. Res. Lett., 18, 3 pp., 1991.
Yung, Y. L., Lee, A. Y. T., Irion, F. W., DeMore, W. B., and Wen, J.: Carbon dioxide in the atmosphere: Isotopic exchange with ozone and its use as a tracer in the middle atmosphere, J. Geophys. Res., 102, 9 pp., 1997.