the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Ecosystem physio-phenology revealed using circular statistics
Daniel E. Pabon-Moreno
Talie Musavi
Mirco Migliavacca
Markus Reichstein
Christine Römermann
Miguel D. Mahecha
Quantifying how vegetation phenology responds to climate variability is a key prerequisite to predicting how ecosystem dynamics will shift with climate change. So far, many studies have focused on responses of classical phenological events (e.g., budburst or flowering) to climatic variability for individual species. Comparatively little is known on the dynamics of physio-phenological events such as the timing of maximum gross primary production (DOYGPPmax), i.e., quantities that are relevant for understanding terrestrial carbon cycle responses to climate variability and change. In this study, we aim to understand how DOYGPPmax depends on climate drivers across 52 eddy covariance (EC) sites in the FLUXNET network for different regions of the world. Most phenological studies rely on linear methods that cannot be generalized across both hemispheres and therefore do not allow for deriving general rules that can be applied for future predictions. One solution could be a new class of circular–linear (here called circular) regression approaches. Circular regression allows circular variables (in our case phenological events) to be related to linear predictor variables as climate conditions. As a proof of concept, we compare the performance of linear and circular regression to recover original coefficients of a predefined circular model for artificial data. We then quantify the sensitivity of DOYGPPmax across FLUXNET sites to air temperature, shortwave incoming radiation, precipitation, and vapor pressure deficit. Finally, we evaluate the predictive power of the circular regression model for different vegetation types. Our results show that the joint effects of radiation, temperature, and vapor pressure deficit are the most relevant controlling factor of DOYGPPmax across sites. Woody savannas are an exception, where the most important factor is precipitation. Although the sensitivity of the DOYGPPmax to climate drivers is site-specific, it is possible to generalize the circular regression models across specific vegetation types. From a methodological point of view, our results reveal that circular regression is a robust alternative to conventional phenological analytic frameworks. The analysis of phenological events at the global scale can benefit from the use of circular statistics. Such an approach yields substantially more robust results for analyzing phenological dynamics in regions characterized by two growing seasons per year or when the phenological event under scrutiny occurs between 2 years (i.e., DOYGPPmax in the Southern Hemisphere).
- Article
(2368 KB) - Full-text XML
-
Supplement
(1125 KB) - BibTeX
- EndNote
Phenology is the study of the timing of biological events that can be observed at either the organismic level or the ecosystem scale (Lieth, 1974). For the latter, phenology is the study of some integral behavior across phenological states of the integrated canopy reflectance captured by remote sensing (Richardson et al., 2009; Zhang et al., 2003) or vegetation-driven ecosystem–atmosphere CO2 exchange fluxes (Richardson et al., 2010). Ecosystem-scale physio-phenological processes of this kind are relevant quantities in global biogeochemical cycles and integrate both the seasonal dynamics of biophysical states (e.g., reflected in the canopy development) and the observed photosynthesis at the stand level (i.e., gross primary production). Here we are particularly interested in the timing when ecosystems reach their maximum CO2 uptake within a growing season. Ecosystem physio-phenology is influenced by climate conditions but simultaneously contributes to the regulation of different micro- and macrometeorological patterns. Physio-phenological cycles determine the temporal dynamics of land–atmosphere water and energy exchange fluxes. Likewise, the terrestrial carbon cycle is affected by phenological controls on CO2 uptake and release (Peñuelas et al., 2009).
The eddy covariance (EC) technique allows us to continuously measure the exchange of energy and matter between ecosystems and the atmosphere (Aubinet et al., 2012). The FLUXNET network collects EC data for most ecosystems of the world along with other meteorological variables, i.e., radiation, temperature, precipitation, atmospheric humidity, and often soil moisture (Baldocchi et al., 2001; Baldocchi, 2020). Particularly relevant to phenological studies is the seasonal trajectory of gross primary production (GPP), which allows us to derive phenological transition dates such as start and end of the growing season (e.g., Luo et al., 2018) as well as the timing of the maximum gross primary production, hereafter as referred to as DOYGPPmax (Zhou et al., 2016; Peichl et al., 2018; Wang and Wu, 2019).
In this study we focus on understanding how climate variability affects the time when ecosystems reach their maximum potential for CO2 absorption. In order to reach this “optimum state”, several preconditions must be met during the preceding part of the growing season. So far several studies have focused on studying the variability of maximum GPP during the growing season (GPPmax). For instance, Zhou et al. (2017) studied how the variability of annual GPP is influenced by GPPmax and the start and the end of the growing season. The authors found that GPPmax is a better explanatory parameter for the interannual variability of annual GPP than the start and end days of the growing season. Bauerle et al. (2012) studied how photoperiod and temperature influence plants' photosynthetic capacity for 23 tree species in temperate deciduous hardwoods, reporting that the photoperiod explains the variability of photosynthetic capacity better than temperature. So far, to the best of our knowledge, only one study has focused on understanding the temporal variability of GPPmax; Wang and Wu (2019) used a combination of satellite remote-sensing and eddy covariance data to explore how DOYGPPmax is controlled by climatic conditions. The authors reported that higher temperatures advance DOYGPPmax, while the influence of precipitation and radiation were biome-dependent. This study had a geographical focus on China; a global approach considering several ecosystems across the whole latitudinal gradient is still lacking.
The challenge of understanding phenology is generally to characterize a discrete event that repeats periodically. Classically, phenological analyses have been performed using linear regression models (Morente-López et al., 2018; Zhou et al., 2016). Most of these studies analyze ecosystems characterized by one growing season (e.g., temperate or boreal forests) and when the summer is centered around the middle of the calendar year. The existing methods are, however, not sufficiently generic to describe (i) ecosystems in the Southern Hemisphere and (ii) ecosystems with multiple growing seasons per year as is often observed in, for example, semiarid regions.
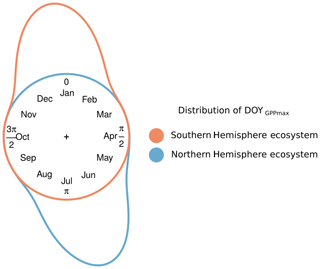
Figure 1Conceptual distribution of GPPmax timing (DOYGPPmax) for two hypothetical ecosystems: one in the Northern (blue) and one in the Southern Hemisphere (red). The distance between the color line and the circle represents the frequency of the DOYGPPmax observations. The distance between the end and the beginning of the distribution represents the DOYGPPmax interannual variability.
Figure 1 illustrates the problem of northern vs. southern hemispheric summers from a conceptual point of view, assuming that some discrete event recurs annually, but the timing varies according to some external drivers. We would then need to find a predictive model explaining the interannual variability of phenology, i.e., the probability of this recurrent event in the course of the annual cycle. Figure 1 shows that linear regression models would be inappropriate to predict the day of the year (DOY) of some phenological event in the Southern Hemisphere as the actual target values to predict may alternate between and .
In recent years, circular statistics have gained some attention as they offer a solution to problems of this kind (Morellato et al., 2010; Beyene et al., 2018). Unlike classical statistics, the predicted variables are expressed in terms of angular directions (degrees or radians) across a circumference (Fisher, 1995), allowing us to perform statistical analysis where the data space is not Euclidean. In this framework, point events can be described as a von Mises distribution (Von Mises, 1918), the equivalent to the normal distribution in circular statistics. The von Mises distribution is described by two parameters: the mean angular direction (μ) and the concentration parameter (κ). Circular–linear regressions (in the following simply named circular regression) allow us to predict circular responses (e.g., the timing of phenological events) from other linear variables (Morellato et al., 2010). Given that any phenological event can be interpreted as an angular direction and should be modeled as such, we assume that these circular regressions are well suited in this context. Despite this evident suitability, circular statistics have not yet been extensively applied in the study of phenology and will therefore be presented here as an alternative to conventional linear techniques.
In this paper, we aim to identify the factors controlling the timing of the maximal seasonal GPP (DOYGPPmax). The questions we want to answer are as follows: first, can circular statistics describe and predict DOYGPPmax per vegetation type? This aspect requires testing the methodological advantages and caveats of circular statistics across hemispheres in comparison with linear methods. Second, can DOYGPPmax be explained using cumulative climate conditions? This question needs to consider different possibilities for generating temporally integrating features. And third, how is DOYGPPmax affected by the climatic conditions during the growing season? The last question requires a global cross-site analysis. Based on the findings of these three questions, we then discuss the potential of circular regressions beyond this specific application case in related phenological problems and outline future applications.
2.1 Data
We use 52 EC sites (with at least 7 years of data) located throughout the latitudinal gradient of the globe from the FLUXNET2015 database (Table A1; http://fluxnet.fluxdata.org/, last access: 11 July 2019 Pastorello et al., 2020). Each FLUXNET site is identified with an abbreviation of the country and the name of the place, e.g., the EC tower AU-How, means that it is located in Howard Springs, Australia. From the dataset we use the GPP data that were derived using the nighttime partitioning method and considering the threshold of the variable u∗ to discriminate values of insufficient turbulence (Reichstein et al., 2005). In order to identify maximum daily GPP, we compute the quantile 0.9 for each day based on the half-hourly flux observations. As potential explanatory variables for DOYGPPmax we use the daily air temperature (Tair), shortwave incoming radiation (SWin), precipitation (Precip), and vapor pressure deficit (VPD).
Given that the past climate conditions affect the CO2 exchange between the atmosphere and the ecosystems (ecological memory; Liu et al., 2019; Ryan et al., 2015), we assume that an aggregated form of these climatic variables needs to be considered in the prediction of the phenological responses. We aggregate the original time series of the Tair, SWin, Precip, and VPD for each DOYGPPmax using a half-life decay function (Eq. 1),
for estimating an exponentially weighted mean of the observation vector at time step t. The symbol 〈…〉 denotes the weighted average; i indicates the number of days before t, going back to τ=365 days. The weight decay is represented by
The decay function gives the instantaneous value a weight of 1 (w0=1), and all preceding values receive an exponentially reduced weight as determined by the half-time parameter t1∕2. Finally, we make these variables comparable via centering standardization to unit variance. We perform a sensitivity analysis, evaluating the effect of the half-time parameter, and identify the optimum as the value when the variance explained by the circular regression model is at a maximum. The results are presented in Supplement 1.
Due to the high colinearity between the exponential weighted variables of Tair, SWin, and VPD, we perform a principal component analysis (PCA) on the matrix of variables and FLUXNET sites and retain the leading principal component of these variables as well as precipitation as input for the circular statistics model (Hastie et al., 2009). The results of the PCA are presented in Supplement 2.
2.2 Circular statistics
Since units of the circular response variable must be in radians or degrees, we transform the days of the year to radians using Eq. (3). For leap years we remove the last day.
where DOY means day of the year.
A basic circular regression model was proposed by Fisher and Lee (1992) as follows:
where y is the target variable (i.e., DOYGPPmax) in radians, μ is the mean angular direction of the target variable, xi represents the values for the variable i, and βi is the regression coefficient. The parameters μ and β are fitted via the maximum likelihood method using the reweighted least squares algorithm as proposed by Green (1984).
Relevant interpretations of fitted circular regression models are (1) the sign of the β coefficients, (2) the statistical significance of the coefficients, and (3) the accuracy of the prediction. Regarding the first point, a negative sign of the coefficient would mean that an increasing value of the predictor would lead to an earlier DOYGPPmax compared to the mean angular direction. The inverse would happen when the coefficient is positive. Figure 2 conceptually illustrates how the coefficients affect the predictions. Regarding the second aspect, we can state that if a coefficient is not significant, then its contribution would not be relevant to explaining the phenological observation. In our case we define the coefficient to be significant if the median of the distribution of p values is less than 0.05. Finally, we can estimate the accuracy of the prediction using the Jammalamadaka–Sarma (JS) correlation coefficient (Jammalamadaka and Sarma, 1988). As in any other regression framework, this approach helps us to quantify the effect of each climate variable on the interannual variability of DOYGPPmax.
To estimate the relative sensitivity of DOYGPPmax to the leading principal component representing Tair, SWin, and VPD as well as to Precip, we use the implementation of Eq. (4) in the R package “circular” (Agostinelli and Lund, 2017). To increase the robustness of the method we implemented a block bootstrapping per growing season, generating a model parameter average based on 1000 iterations. In each analysis, we estimate the accuracy of the model using the JS correlation coefficient.
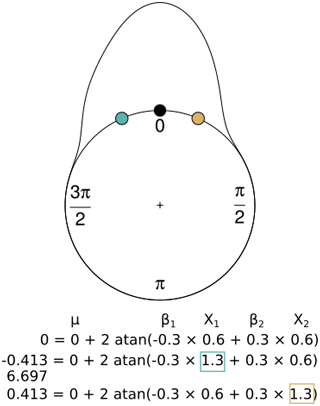
Figure 2Interpretation of the coefficients in the circular regression considering a reference point (black) generated with a circular–linear model with mean angular direction (μ=0), two coefficients (β1, β2) and two variables (x1, x2), where one of the coefficients is negative (β1), and the other one is positive (β2). When the coefficient is negative and the value of the parameter increases (blue), the result is an earlier observation compared with the reference point (the equivalent of −0.413 rad is 6.697 rad, as is shown below the equation). On the other hand, when the coefficient is positive and the variable increases (yellow), the observation is later.
2.3 Circular vs. linear regression
To assess the performance of linear versus circular regressions we perform an experiment with simulated data in which we evaluate the accuracy and precision of both approaches to recover original regression coefficients in a circular setting (Eq. 4). We add noise generated with a random von Mises distribution with the parameters n=100 and κ=30 to the model to ensure that the result follows a normal distribution. We predefined a range of values for two regression coefficients (, ). We simulate the variables x1 and x2 as normal distributions with n=100; a mean of 10 and 15, respectively; and standard deviations (SDs) of 1 and 2. We evaluate all possible combinations for the regression coefficients 100 times, simulating different x1 and x2. In each iteration we generate y using the setup previously described, and we recover the original regression coefficients using y as a response variable and x1 and x2 as predictors. Finally, we analyze two scenarios: (1) when the target timing occurs at the beginning of the year (μ=0) and (2) when the target timing happens midyear (μ=π). The parameters for the entire setup generate realistic data, where the standard deviation of y is not higher than 0.3 rad. An SD of 0.5 rad would be equivalent to having phenological observations across half a year, which would not be realistic.
To quantify the accuracy of each model per coefficient we estimate the mean absolute error per model and coefficient (Eq. 5). To compare the accuracy between models by coefficient we test the mean absolute errors between models (Eq. 6). To generate a single measure that allows us to compare both coefficients and models we estimate the mean difference accuracy (Eq. 7). The results can be understood as follows: if the difference is higher than 0, the circular model has a higher mean accuracy compared to the linear model and vice versa. To quantify which model has higher precision we estimate the difference between the SD of the mean absolute errors per model for each coefficient (Eq. 8). Finally, we estimate the mean differences of precision between the regression coefficients (Eq. 9), where again if the value is higher than 0, the circular model has a higher mean accuracy than the linear model; the inverse is true if the value is lower than 0.
We estimate regression coefficients for the bootstrap sample (m=100) for the regression coefficient βj, , and the model (denoted as ). The model accuracy can then be estimated as the mean absolute error of the estimated regression parameter , for the linear model M=l and the circular model M=c:
The difference in accuracy for the coefficient j between the circular and the linear model is shown in
Finally, the mean difference in accuracy between the linear and the circular model is given by
The difference in precision for the coefficient j between the linear (l) and the circular model (c) is shown in
The mean difference in precision between the linear and the circular model is given by
where sM,j is the sample SD of the vector , .
2.4 Analysis setup
The target variable DOYGPPmax is the day of the year when GPP reaches its maximum during the growing season. Given that different ecosystems present more than one growing season per year (e.g., semiarid ecosystems), it is necessary to identify the number of growing seasons per year. To identify the number of growing seasons we apply a fast Fourier transformation (FFT; Cooley and Tukey, 1965) to the mean seasonal cycle of the GPP time series. The number of growing seasons is equal to the maximum absolute value of the first four FFT coefficients (excluding the first one). For each FLUXNET site, we reconstruct the GPP time series, taking the real numbers of the inverse FFT. We use these reconstructed time series to calculate the expected mean timing of DOYGPPmax and use this value as a template. To recover the real DOYGPPmax from the original time series, we define a window around the template of length inversely proportional to the number of cycles (180 d∕number of growing seasons). To increase the robustness of the analysis we identify the days with the 10 highest GPP values. These days are used in the block bootstrapping mentioned above. Finally, since most of the sites are located in the Northern Hemisphere we expect that, in most cases, DOYGPPmax will be reached by the middle of the calendar year.
To quantify the contribution of each climate variable, we count the number of sites per vegetation type where the regression coefficient is statistically significant. We perform a leave-one-out cross-validation per vegetation type to evaluate the predictive power of the circular regression using climate conditions. We only consider vegetation types with more than five sites. In this case the standardization of the climate variables is not applied. Finally, we use the mean of the optimum half-time parameter per vegetation type to weigh the climate conditions.
Here, we first report results from simulated data to describe the performance of the circular regression approach compared to a linear model. Second, we compare the performance of circular and linear regression using empirical data. Third, we analyze the sensitivity of DOYGPPmax across vegetation types and climate classes. Finally, we show the results of the predictive power of circular regression per vegetation type.
3.1 Circular vs. linear regression
Figure 3a and c show that for μ=0 (DOYGPPmax at the beginning of the year), circular regression has a higher accuracy and precision compared to the linear regression for the entire space of regression coefficient values, with a maximum difference of the order of 0.1 in terms of accuracy and of the order of 1 for precision. For μ=π (DOYGPPmax midyear) the linear model has a higher accuracy in most of the evaluated space, with a maximum difference of the order of 0.001 compared with the circular regression, while circular regression has a higher precision for most of the regression coefficients of the order of 0.001. These results show that circular regression has a higher precision in recovering the original regression coefficients than linear regression no matter the moment of the year. On the other hand, circular regression has a higher accuracy than the linear model at the beginning of the year. While linear is better midyear, the differences are of the order of 0.001.
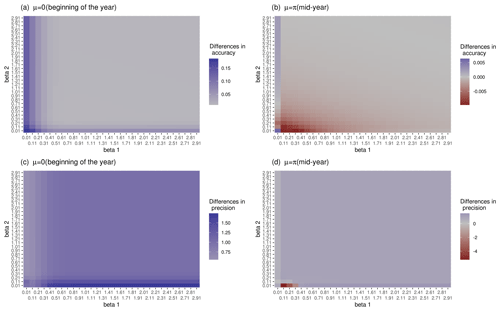
Figure 3Accuracy and precision of linear and circular regression models by recovering the original regression coefficients of a circular regression. (a, c) μ=0 (maximum at the beginning of the year). (b, d) μ=pi (maximum midyear). Panels (a) and (b) correspond to the differences in accuracy between the models. Panels (c) and (d) correspond to the differences in the precision between the models. Blue means better performance of the circular model compared with the linear model, and red means higher performance of the linear model.
To illustrate the method in practice, we compare the circular and linear models using data from two sites: US-Ha1 (Northern Hemisphere, deciduous broadleaf forest) and AU-How (Southern Hemisphere, woody savanna). We relate the climate variables with DOYGPPmax (see Methods) and reconstruct the DOYGPPmax using the linear and circular regression models. We compare observed and predicted DOYGPPmax using JS correlation for the circular model and the Pearson product moment for the linear model. For US-Ha1 both methods show similar performance in predicting DOYGPPmax (Fig. 4), while for AU-How, the circular model retrieves the original data better than the linear model, explaining 30 % more of the variance. In the event that the DOYGPPmax is reached at the beginning of the year, linear methods produce a strong bias that predicts the timing across the entire year (Fig. 4b).
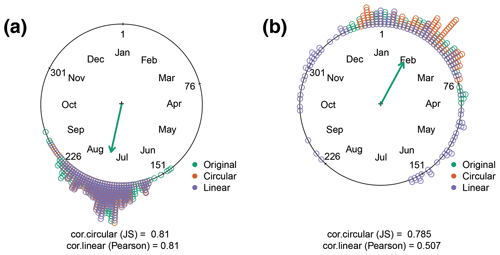
Figure 4Correlation coefficient between the observed and predicted DOYGPPmax using climatic variables. Two sites are presented: (a) US-Ha1 and (b) AU-How. The observed DOYGPPmax (green) is compared with the data retrieved using circular (orange) and linear (purple) regressions. Two correlation coefficients are used: Jammalamadaka–Sarma (JS) and the Pearson product moment (Pearson). In the circular plot the months and the day of the year (DOY) are also plotted every 75 d. The green arrow indicates the mean angular direction of the original data distribution.
3.2 Sensitivity of DOYGPPmax to climate variables
From the 52 sites analyzed in this study, only one site (ES-LJu) shows bimodal growing seasons (see Supplement 1.2). As expected, in most cases DOYGPPmax occurs in the middle of the calendar year (Fig. S6 in the Supplement), reflecting the uneven site distribution in FLUXNET (Schimel et al., 2015). However, some ecosystems in the Northern Hemisphere do reach DOYGPPmax at the beginning of the year; these are Mediterranean sites such as US-Var and ES-LJu. In general terms, most of the sites have an SD between 10 d and 40 d. The maximal SD is 46.9 d for the AU-Tum site. A detailed table with the mean angular direction and SD of DOYGPPmax of each site is presented in Sect. S1.2.
For half of the sites, the JS correlation coefficients are between 0.70 and 0.97 (Supplement 1, Fig. S5), showing that the interannual variability of DOYGPPmax is mainly explained by the cumulative effect of the climate variables. Nineteen sites have a JS coefficient of less than 0.7 (DK-Sor, FI-Hyy, US-MMS, DK-ZaH, FR-Pue, US-UMB, AU-Tum, US-Ton, FR-LBr, US-Me2, IT-Lav, AT-Neu, DE-Gri, IT-MBo, IT-Ro2, US-Wkg, BR-Sa1, FR-Fon, CZ-wet). For ES-LJu the JS coefficient is 0.77 for the first growing season and 0.78 for the second one (Table S2 in the Supplement).
We find that air temperature, shortwave incoming radiation, and vapor pressure deficit appear as the dominant drivers worldwide at 43 of the total sites (84 %; Supplement 3). Precipitation is the main driver for five sites (AU-How US-Ton ZA-Kru US-SRM US-Wkg; Supplement 3). Interestingly, precipitation was the most important factor for all the woody savanna sites (Supplement 3). For three sites (DE-Gri, IT-Ro2, BRSa1), any climatic variable is significant. In terms of the sign of the coefficients, all the variables are predominantly negative (Table 1). This means that higher values of radiation, air temperature, VPD, and precipitation lead to an earlier DOYGPPmax. Individual sensitivities per site are shown in Supplement 3.
Table 1Number of FLUXNET sites where each regression coefficient is statistically significant to explain the physio-phenology of GPPmax (DOYGPPmax). The table is divided by the sign of the coefficient. The first column is the coefficient for the dimensionality reduction between air temperature (Tair), shortwave incoming radiation (SWin), and vapor pressure deficit (VPD); the second column is the coefficient for precipitation (Precip).

The PCA between shortwave incoming radiation, air temperature, and vapor pressure deficit has the highest frequency of significant correlation coefficients by number of sites for all the vegetation types with the exception of woody savannas (WSAs), where precipitation is shown to be more important for most sites than the dimensionality reduction between Tair, SWin, and VPD (Fig. 5). For closed shrublands (CSHs) and savannas (SAVs), both drivers have the same number of sites where the coefficients are statistically significant.
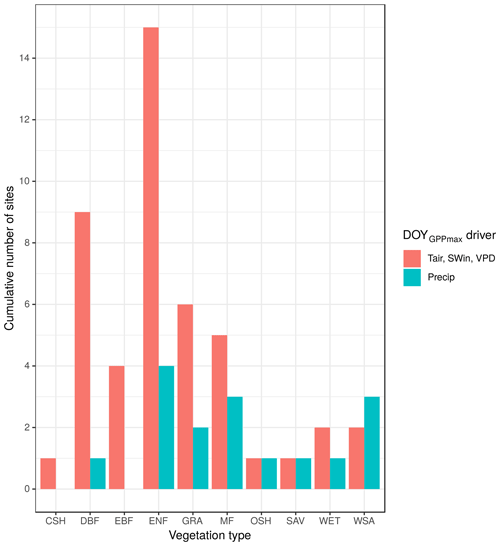
Figure 5Contribution of each climate variable to explain the interannual variation in DOYGPPmax per vegetation type. CSHs: closed shrublands (n=1); DBF: deciduous broadleaf forest (n=10); EBF: evergreen broadleaf forest (n=5); ENF: evergreen needleleaf forest (n=15); GRA: grassland (n=8); MF: mixed forest (n=5); OSHs: open shrublands (n=1); SAV: savannas (n=1); WET: permanent wetlands (n=2); WSAs: woody savannas (n=3). Each bar shows the cumulative number of sites where each climate variable is statistically significant.
A special case for understanding the sensitivity of DOYGPPmax to climate variables is the site “Llano de los Juanes” (ES-LJu), an open shrubland ecosystem in Spain. It is the only clearly bimodal ecosystem in our study (Fig. 6). In this case precipitation is not statistically significant, while the combination of Tair, SWin, and VPD is significant for both seasons. Furthermore, in both growing seasons Tair, SWin, and VPD have a negative coefficient.
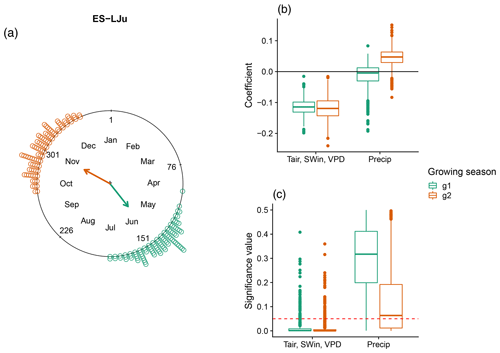
Figure 6DOYGPPmax sensitivity to different climate drivers in a Mediterranean ecosystem: Llano de los Juanes (ES-LJu), Spain, with two growing seasons (green and orange). (a) DOYGPPmax distribution across the year. The arrows indicate the mean angular direction of the growing season. (b) Regression coefficients for each growing season and (c) the significance values for each variable. The red line in panel (c) represents a p value of 0.05.
The leave-one-out cross-validation for several vegetation types shows that the predictive power of the model for grassland (GRA) and evergreen broadleaf forest (EBF) is −0.3 and −0.31, respectively. For deciduous broadleaf forest (DBF) it is 0.46, and for evergreen needleleaf forest (ENF) it is 0.4, while for mixed forest (MF) the predictive power of the model is 0.88 (Fig. 7).
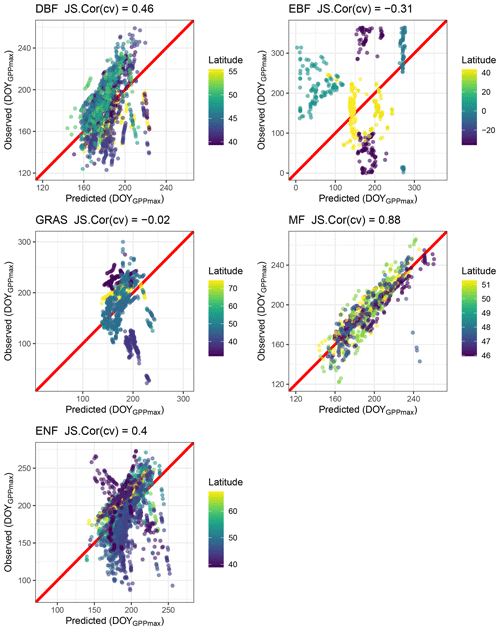
Figure 7Cross-validation of the circular regression model to predict DOYGPPmax for different vegetation types using air temperature, shortwave incoming radiation, precipitation and vapor pressure deficit (see Methods). Deciduous broadleaf forest (DBF), evergreen broadleaf forest (EBF), grassland (GRA), mixed forest (MF), and evergreen needleleaf forest (ENF). For each vegetation type the Jammalamadaka–Sarma (JS) correlation coefficient is shown in the title of each plot. The red line represents the perfect fit.
4.1 Circular vs. linear regression
We explored whether circular regression is a suitable tool for analyzing phenological events. Our results suggest that circular regressions can recover predefined coefficients in a set of simulations with higher accuracy and precision than linear regressions. Hence, we would generally suggest that circular regressions may be advantageous when the aim is analyzing the effect of climatic variables on phenological events. We also found cases where the classical linear regression may be either more robust or equally suitable, e.g., when phenological events are reached close to midyear. In the overall view, however, we consider that circular regressions are to be preferred over linear regression for their conceptual capacity to analyze the physio-phenology of ecosystems regardless of the day of the year when an event of interest occurs. This allows us to analyze phenological studies at the global scale regardless of geographic location or the distribution of the observations during the year.
Different phenological models have been developed, ranging from empirical approaches (Richardson et al., 2013) to process models (Asse et al., 2020) over the last decades. As we demonstrate here, circular statistics open new opportunities to increase the robustness of phenological models, allowing us to analyze ecosystems across hemispheres within the same consistent framework. In fact, the results of the phenological sensitivity of DOYGPPmax indicate the complexity of ecosystem responses to climate variability. Our approach provides motivation to integrate circular regressions into more complex statistical techniques like regression trees, Gaussian processes, or artificial neural networks, targeting a circular response variable.
4.2 Sensitivity of DOYGPPmax to climate variables
The geographical location of the FLUXNET2015 sites represents an advantage when capturing the DOYGPPmax variability at the global scale (Supplement 1, Fig. S6). Most of the analyzed sites (47) are located in the Northern Hemisphere. Two sites (GF-Guy and BR-Sa1) are located in the tropical region, and three sites (ZA-Kru, AU-How, AU-Tum) are in the Southern Hemisphere. However, because of the low number of sites reported in the tropical and southern region with more than 7 years of data, our understanding of the DOYGPPmax variability in these regions is still limited. Increasing the number of tropical and Southern Hemisphere sites should be considered a high priority in the near future to complement our knowledge about the physio-phenological ecosystem state.
The high values of the JS correlation coefficients for most of the sites demonstrate that the interannual variability of DOYGPPmax can be explained as the cumulative effect of the climate variables during the growing season. Sites where it was not possible to explain the variations in DOYGPPmax with enough confidence (JS correlation <0.7) might require the incorporation of biotic variables (e.g., species composition; Peichl et al., 2018) or soil property information that can improve the predictive power of the model.
Our results suggest that there is no pattern between the DOYGPPmax sensitivity across vegetation types and climate classes (Sect. Fig. S1.7). In other words, the DOYGPPmax sensitivity is site-specific, probably produced by the unique combination of biotic (e.g., species composition, species phenology, species interaction, and phenotypic plasticity) factors that are not evaluated in our study. Several studies that focused on ecosystem phenology suggest that species composition plays a fundamental role in ecosystem physio-phenology of the CO2 uptake (Gonsamo et al., 2017; Peichl et al., 2018).
While there is no clear relationship between the DOYGPPmax sensitivity and the vegetation type, we find a predominant role of the combined effects of shortwave incoming radiation (SWin), air temperature (Tair), and vapor pressure deficit (VPD) at the global scale on the DOYGPPmax interannual variability, where for most of the sites these variables have a negative regression coefficient. This means that if the SWin, Tair, and VPD increase during the growing season, the DOYGPPmax will be reached earlier. This effect can be a consequence of DOYGPPmax being reached when SWin and Tair are at a maximum.
On a global scale, our analysis shows that the combination of air temperature, shortwave incoming radiation, and vapor pressure deficit as well as precipitation has a negative sign. This means that if these variables increase during the growing season, the GPPmax will be reached earlier. Our results are similar to those obtained by Wang and Wu (2019), who were the authors to conclude that an increase in the temperature produces an earlier DOYGPPmax. This phenomenon is likely explained by the leaf-out advancing during spring. Nevertheless, there is still no consensus on whether the increase in temperature will produce an earlier end of the growing season. Several studies have demonstrated for different vegetation types that when temperature increases, spring onset is earlier, and autumn senescence is later (Stocker et al., 2013; Linkosalo et al., 2009; Migliavacca et al., 2012; Morin et al., 2010; Post and Forchhammer, 2008), increasing the length of the growing season and the amount of CO2 that is taken up by ecosystems (Richardson et al., 2013).
Ecosystems with two growing seasons per year represent a very interesting case of the effect of climate drivers on DOYGPPmax across different growing seasons. In Llano de los Juanes, Spain (ES-LJu; Fig. 6), DOYGPPmax is reached in the first growing season, when the rainy season is finishing, while in the second growing season DOYGPPmax is reached in the middle of the rainy season (data not shown). The effect of shortwave incoming radiation, temperature, and vapor pressure deficit for both growing seasons is negative, suggesting that if we increase these variables during the period before, the DOYGPPmax will happen earlier.
Phenology in Mediterranean ecosystems is mainly controlled by water availability (Kramer et al., 2000; Luo et al., 2018; Peñuelas et al., 2009). However, our results suggest that DOYGPPmax is mainly sensitive to SWin, Tair, and VPD. These results agree with the analysis performed by Gordo and Sanz (2005), who were the authors to evaluate the phenological sensitivity of Mediterranean ecosystems to temperature and precipitation. They concluded that temperature was the most important driver. Although water is a limiting factor in Mediterranean ecosystems, its influence on plant physiology and plant phenology can be completely different. In terms of physiology, the GPPmax value can decrease, but in terms of phenology, DOYGPPmax can still be the same.
Complex interactions between climate variables and phenological response and the interspecificity of the sensitivity at the site level explain in part the poor predictive power of the model for grasslands, evergreen broadleaf forest, evergreen needleleaf forest, and deciduous broadleaf forests in the cross-validation analysis (Fig. 7). However, the predictive power for mixed forest is high, even when the distribution of the latitudinal gradient is not the same for all the sites. These results reflect the fact that the circular regression model can be extrapolated from different sites to predict the DOYGPPmax interannual variability. This advantage could be a way to solve the common criticism that phenological models cannot be extrapolated by only generating ad hoc hypotheses (Richardson et al., 2013).
In this study we explored the potential of “circular regressions” to explain the physio-phenology of maximal CO2 uptake rates. We conclude that (1) shortwave incoming radiation, temperature, and vapor pressure deficit are the main drivers of the timing of maximal CO2 uptake at the global scale (precipitation only plays a secondary role, with the exception of woody savannas, where the most important variable is precipitation), and (2) although the sensitivity of the DOYGPPmax to the climate drivers is site-specific, it is possible to extrapolate the circular regression model for different sites with the same vegetation type and similar latitudes. Finally, we used simulated and empirical data to demonstrate that circular regression produces more accurate results than linear regression, in particular in cases when data need to be explored across hemispheres.
Table A1FLUXNET sites used in our study. We report the name of the sites, the time period used for the analysis, and the climate class of each site following Köppen–Geiger classification: tropical monsoon climate (Am), tropical savanna climate (Aw), cold semiarid climate (BSk), humid subtropical climate (Cfa), oceanic climate (Cfb), hot summer Mediterranean climate (Csa), warm summer Mediterranean climate (Csb), humid subtropical climate (Cwa), humid continental climate (Dfb), subarctic climate (Dfc, Dsc), and tundra climate (ET). We also report the vegetation type of the sites: closed shrubland (CSH), deciduous broadleaf forest (DBF), evergreen broadleaf forest (EBF), evergreen needleleaf forest (ENF), grassland (GRA), mixed forest (MF), open shrubland (OSH), savanna (SAV), permanent wetland (WET), and woody savanna (WSA).
Code is available under GPL-3 license at https://github.com/dpabon/ecosystem-physio-phenology-repo, last access: 29 July 2020 (https://doi.org/10.5281/zenodo.3921892 Pabon-Moreno et al., 2020).
FLUXNET database is available online at https://fluxnet.fluxdata.org/, last access: 11 July 2019 (https://doi.org/10.1038/s41597-020-0534-3 Pastorello et al., 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-3991-2020-supplement.
DEPM, TM, MM, and MDM designed the study in collaboration with MR and CR. DEPM conducted the analysis and wrote the manuscript, with substantial contributions from all coauthors.
The authors declare that they have no conflict of interest.
We thank the reviewers for their helpful suggestions and Guido Kraemer for his help with the mathematical notation. This project has received funding from the European Union's Horizon 2020 research and innovation program via the TRuStEE project under the Marie Skłodowska-Curie grant agreement no. 721995. This work used eddy covariance data acquired and shared by the FLUXNET community, including these networks: AmeriFlux, AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet-Canada, GreenGrass, ICOS, KoFlux, LBA, NECC, OzFlux-TERN, TCOS-Siberia, and USCCC. The ERA-Interim reanalysis data are provided by ECMWF and processed by LSCE. The FLUXNET eddy covariance data processing and harmonization were carried out by the European Fluxes Database Cluster, AmeriFlux Management Project, and the Fluxdata project of FLUXNET, with the support of CDIAC and ICOS Ecosystem Thematic Center, as well as the OzFlux, ChinaFlux, and AsiaFlux offices.
This research has been supported by the H2020 Marie Skłodowska-Curie Actions (TRuStEE grant no. 721995).
The article processing charges for this open-access
publication were covered by the Max Planck Society.
This paper was edited by David Bowling and reviewed by two anonymous referees.
Agostinelli, C. and Lund, U.: R package circular: Circular Statistics (version 0.4-93), CA: Department of Environmental Sciences, Informatics and Statistics, Ca' Foscari University, Venice, Italys UL: Department of Statistics, California Polytechnic State University, San Luis Obispo, California, USA, available at: https://r-forge.r-project.org/projects/circular/, last access: 29 June 2017. a
Archibald, S. A., Kirton, A., van der Merwe, M. R., Scholes, R. J., Williams, C. A., and Hanan, N.: Drivers of inter-annual variability in Net Ecosystem Exchange in a semi-arid savanna ecosystem, South Africa, Biogeosciences, 6, 251–266, https://doi.org/10.5194/bg-6-251-2009, 2009. a
Asse, D., Randin, C. F., Bonhomme, M., Delestrade, A., and Chuine, I.: Process-based models outcompete correlative models in projecting spring phenology of trees in a future warmer climate, Agr. Forest Meteorol., 285–286, 107931, https://doi.org/10.1016/j.agrformet.2020.107931, 2020. a
Aubinet, M., Chermanne, B., Vandenhaute, M., Longdoz, B., Yernaux, M., and Laitat, E.: Long term carbon dioxide exchange above a mixed forest in the Belgian Ardennes, Agr. Forest Meteorol., 108, 293–315, https://doi.org/10.1016/S0168-1923(01)00244-1, 2001. a
Aubinet, M., Vesala, T., and Papale, D. (Eds.): Eddy Covariance: A Practical Guide to Measurement and Data Analysis, Springer Atmospheric Sciences, Springer Netherlands, 2012. a
Baker, B., Guenther, A., Greenberg, J., Goldstein, A., and Fall, R.: Canopy fluxes of 2-methyl-3-buten-2-ol over a ponderosa pine forest by relaxed eddy accumulation: Field data and model comparison, J. Geophys. Res.-Atmos., 104, 26107–26114, https://doi.org/10.1029/1999JD900749, 1999. a
Baldocchi, D., Falge, E., Gu, L., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X., Malhi, Y., Meyers, T., Munger, W., Oechel, W., Paw U, K. T., Pilegaard, K., Schmid, H. P., Valentini, R., Verma, S., Vesala, T., Wilson, K., and Wofsy, S.: FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities, B. Am. Meteorol. Soc., 82, 2415–2434, https://doi.org/10.1175/1520-0477(2001)082<2415:FANTTS>2.3.CO;2, 2001. a
Baldocchi, D. D.: How eddy covariance flux measurements have contributed to our understanding of Global Change Biology, Glob. Change Biol., 26, 242–260, https://doi.org/10.1111/gcb.14807, 2020. a
Bauerle, W. L., Oren, R., Way, D. A., Qian, S. S., Stoy, P. C., Thornton, P. E., Bowden, J. D., Hoffman, F. M., and Reynolds, R. F.: Photoperiodic regulation of the seasonal pattern of photosynthetic capacity and the implications for carbon cycling, P. Natl. Acad. Sci. USA, 109, 8612–8617, https://doi.org/10.1073/pnas.1119131109, 2012. a
Berbigier, P., Bonnefond, J.-M., and Mellmann, P.: CO2 and water vapour fluxes for 2 years above Euroflux forest site, Agr. Forest Meteorol., 108, 183–197, https://doi.org/10.1016/S0168-1923(01)00240-4, 2001. a
Berger, B. W., Davis, K. J., Yi, C., Bakwin, P. S., and Zhao, C. L.: Long-Term Carbon Dioxide Fluxes from a Very Tall Tower in a Northern Forest: Flux Measurement Methodology, J. Atmos. Ocean. Technol., 18, 529–542, https://doi.org/10.1175/1520-0426(2001)018<0529:LTCDFF>2.0.CO;2, 2001. a
Beringer, J., Hutley, L. B., Tapper, N. J., and Cernusak, L. A.: Savanna fires and their impact on net ecosystem productivity in North Australia, Glob. Change Biol., 13, 990–1004, https://doi.org/10.1111/j.1365-2486.2007.01334.x, 2007. a
Beyene, M. T., Jain, S., and Gupta, R. C.: Linear-Circular Statistical Modeling of Lake Ice-Out Dates, Water Resour. Res., 54, 7841–7858, https://doi.org/10.1029/2017WR021731, 2018. a
Bonal, D., Bosc, A., Ponton, S., Goret, J.-Y., Burban, B., Gross, P., Bonnefond, J.-M., Elbers, J., Longdoz, B., Epron, D., Guehl, J.-M., and Granier, A.: Impact of severe dry season on net ecosystem exchange in the Neotropical rainforest of French Guiana, Glob. Change Biol., 14, 1917–1933, https://doi.org/10.1111/j.1365-2486.2008.01610.x, 2008. a
Brooks, J. R., Flanagan, L. B., Varney, G. T., and Ehleringer, J. R.: Vertical gradients in photosynthetic gas exchange characteristics and refixation of respired CO2 within boreal forest canopies, Tree Physiol., 17, 1–12, https://doi.org/10.1093/treephys/17.1.1, 1997. a
Carrara, A., Janssens, I. A., Curiel Yuste, J., and Ceulemans, R.: Seasonal changes in photosynthesis, respiration and NEE of a mixed temperate forest, Agr. Forest Meteorol., 126, 15–31, https://doi.org/10.1016/j.agrformet.2004.05.002, 2004. a
Chiesi, M., Maselli, F., Bindi, M., Fibbi, L., Cherubini, P., Arlotta, E., Tirone, G., Matteucci, G., and Seufert, G.: Modelling carbon budget of Mediterranean forests using ground and remote sensing measurements, Agr. Forest Meteorol., 135, 22–34, https://doi.org/10.1016/j.agrformet.2005.09.011, 2005. a
Cooley, J. W. and Tukey, J. W.: An Algorithm for the Machine Calculation of Complex Fourier Series, Math. Comput., 19, 297–301, https://doi.org/10.2307/2003354, 1965. a
Curtis, P. S., Hanson, P. J., Bolstad, P., Barford, C., Randolph, J. C., Schmid, H. P., and Wilson, K. B.: Biometric and eddy-covariance based estimates of annual carbon storage in five eastern North American deciduous forests, Agr. Forest Meteorol., 113, 3–19, https://doi.org/10.1016/S0168-1923(02)00099-0, 2002. a, b
Davis, K. J., Bakwin, P. S., Yi, C., Berger, B. W., Zhao, C., Teclaw, R. M., and Isebrands, J. G.: The annual cycles of CO2 and H2O exchange over a northern mixed forest as observed from a very tall tower, Glob. Change Biol., 9, 1278–1293, https://doi.org/10.1046/j.1365-2486.2003.00672.x, 2003. a
Delpierre, N., Berveiller, D., Granda, E., and Dufrêne, E.: Wood phenology, not carbon input, controls the interannual variability of wood growth in a temperate oak forest, New Phytol., 210, 459–470, https://doi.org/10.1111/nph.13771, 2016. a
Desai, A. R., Bolstad, P. V., Cook, B. D., Davis, K. J., and Carey, E. V.: Comparing net ecosystem exchange of carbon dioxide between an old-growth and mature forest in the upper Midwest, USA, Agr. Forest Meteorol., 128, 33–55, https://doi.org/10.1016/j.agrformet.2004.09.005, 2005. a
Dušek, J., Čížková, H., Stellner, S., Czerný, R., and Květ, J.: Fluctuating water table affects gross ecosystem production and gross radiation use efficiency in a sedge-grass marsh, Hydrobiologia, 692, 57–66, https://doi.org/10.1007/s10750-012-0998-z, 2012. a
Emmerich, W. E.: Carbon dioxide fluxes in a semiarid environment with high carbonate soils, Agr. Forest Meteorol., 116, 91–102, https://doi.org/10.1016/S0168-1923(02)00231-9, 2003. a
Etzold, S., Ruehr, N. K., Zweifel, R., Dobbertin, M., Zingg, A., Pluess, P., Häsler, R., Eugster, W., and Buchmann, N.: The Carbon Balance of Two Contrasting Mountain Forest Ecosystems in Switzerland: Similar Annual Trends, but Seasonal Differences, Ecosystems, 14, 1289–1309, https://doi.org/10.1007/s10021-011-9481-3, 2011. a
Fisher, N. I.: Statistical Analysis of Circular Data, Cambridge University Press, Cambridge, 1995. a
Fisher, N. I. and Lee, A. J.: Regression Models for an Angular Response, Biometrics, 48, 665–677, https://doi.org/10.2307/2532334, 1992. a
Garbulsky, M. F., Peñuelas, J., Papale, D., and Filella, I.: Remote estimation of carbon dioxide uptake by a Mediterranean forest, Glob. Change Biol., 14, 2860–2867, https://doi.org/10.1111/j.1365-2486.2008.01684.x, 2008. a
Gonsamo, A., D'Odorico, P., Chen, J. M., Wu, C., and Buchmann, N.: Changes in vegetation phenology are not reflected in atmospheric CO2 and 13C/12C seasonality, Glob. Change Biol., 23, 4029–4044, https://doi.org/10.1111/gcb.13646, 2017. a
Gordo, O. and Sanz, J. J.: Phenology and climate change: a long-term study in a Mediterranean locality, Oecologia, 146, 484–495, https://doi.org/10.1007/s00442-005-0240-z, 2005. a
Green, P. J.: Iteratively Reweighted Least Squares for Maximum Likelihood Estimation, and some Robust and Resistant Alternatives, J. Roy. Stat. Soc. B, 46, 149–192, 1984. a
Grünwald, T. and Bernhofer, C.: A decade of carbon, water and energy flux measurements of an old spruce forest at the Anchor Station Tharandt, Tellus B, 59, 387–396, https://doi.org/10.1111/j.1600-0889.2007.00259.x, 2007. a
Hastie, T., Tibshirani, R., and Friedman, J. H.: The elements of statistical learning: data mining, inference, and prediction, Springer Series in Statistics, 2nd Edn., Springer, New York, NY, 2009. a
Imer, D., Merbold, L., Eugster, W., and Buchmann, N.: Temporal and spatial variations of soil CO2, CH4 and N2O fluxes at three differently managed grasslands, Biogeosciences, 10, 5931–5945, https://doi.org/10.5194/bg-10-5931-2013, 2013. a
Jammalamadaka, S. R. and Sarma, Y.: A correlation coefficient for angular variables, Statistical theory and data analysis II, North-Holland, Amsterdam, 349–364, 1988. a
Knohl, A., Schulze, E.-D., Kolle, O., and Buchmann, N.: Large carbon uptake by an unmanaged 250-year-old deciduous forest in Central Germany, Agr. Forest Meteorol., 118, 151–167, https://doi.org/10.1016/S0168-1923(03)00115-1, 2003. a
Kramer, K., Leinonen, I., and Loustau, D.: The importance of phenology for the evaluation of impact of climate change on growth of boreal, temperate and Mediterranean forests ecosystems: an overview, Int. J. Biometeorol., 44, 67–75, https://doi.org/10.1007/s004840000066, 2000. a
Kurbatova, J., Li, C., Varlagin, A., Xiao, X., and Vygodskaya, N.: Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia, Biogeosciences, 5, 969–980, https://doi.org/10.5194/bg-5-969-2008, 2008. a
Leuning, R., Cleugh, H. A., Zegelin, S. J., and Hughes, D.: Carbon and water fluxes over a temperate Eucalyptus forest and a tropical wet/dry savanna in Australia: measurements and comparison with MODIS remote sensing estimates, Agr. Forest Meteorol., 129, 151–173, https://doi.org/10.1016/j.agrformet.2004.12.004, 2005. a
Lieth, H. (Ed.): Phenology and Seasonality Modeling, Ecological Studies, Springer-Verlag, Berlin Heidelberg, 1974. a
Linkosalo, T., Häkkinen, R., Terhivuo, J., Tuomenvirta, H., and Hari, P.: The time series of flowering and leaf bud burst of boreal trees (1846–2005) support the direct temperature observations of climatic warming, Agr. Forest Meteorol., 149, 453–461, https://doi.org/10.1016/j.agrformet.2008.09.006, 2009. a
Liu, Y., Schwalm, C. R., Samuels-Crow, K. E., and Ogle, K.: Ecological memory of daily carbon exchange across the globe and its importance in drylands, Ecol. Lett., 22, 1806–1816, https://doi.org/10.1111/ele.13363, 2019. a
Lund, M., Falk, J. M., Friborg, T., Mbufong, H. N., Sigsgaard, C., Soegaard, H., and Tamstorf, M. P.: Trends in CO2 exchange in a high Arctic tundra heath, 2000–2010, J. Geophys. Res.-Biogeo., 117, G02001, https://doi.org/10.1029/2011JG001901, 2012. a
Luo, Y., El-Madany, T. S., Filippa, G., Ma, X., Ahrens, B., Carrara, A., Gonzalez-Cascon, R., Cremonese, E., Galvagno, M., Hammer, T. W., Pacheco-Labrador, J., Martín, M. P., Moreno, G., Perez-Priego, O., Reichstein, M., Richardson, A. D., Römermann, C., and Migliavacca, M.: Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems, Remote Sens., 10, 1293, https://doi.org/10.3390/rs10081293, 2018. a, b
Marcolla, B., Pitacco, A., and Cescatti, A.: Canopy Architecture and Turbulence Structure in a Coniferous Forest, Bound.-Layer Meteorol., 108, 39–59, https://doi.org/10.1023/A:1023027709805, 2003. a
Marcolla, B., Cescatti, A., Manca, G., Zorer, R., Cavagna, M., Fiora, A., Gianelle, D., Rodeghiero, M., Sottocornola, M., and Zampedri, R.: Climatic controls and ecosystem responses drive the inter-annual variability of the net ecosystem exchange of an alpine meadow, Agr. Forest Meteorol., 151, 1233–1243, https://doi.org/10.1016/j.agrformet.2011.04.015, 2011. a
Marras, S., Pyles, R. D., Sirca, C., Paw U, K. T., Snyder, R. L., Duce, P., and Spano, D.: Evaluation of the Advanced Canopy–Atmosphere–Soil Algorithm (ACASA) model performance over Mediterranean maquis ecosystem, Agr. Forest Meteorol., 151, 730–745, https://doi.org/10.1016/j.agrformet.2011.02.004, 2011. a
McDowell, N. G., Marshall, J. D., Hooker, T. D., and Musselman, R.: Estimating CO2 flux from snowpacks at three sites in the Rocky Mountains, Tree Physiol., 20, 745–753, https://doi.org/10.1093/treephys/20.11.745, 2000. a
Merbold, L., Eugster, W., Stieger, J., Zahniser, M., Nelson, D., and Buchmann, N.: Greenhouse gas budget (CO2, CH4 and N2O) of intensively managed grassland following restoration, Glob. Change Biol., 20, 1913–1928, https://doi.org/10.1111/gcb.12518, 2014. a
Migliavacca, M., Sonnentag, O., Keenan, T. F., Cescatti, A., O'Keefe, J., and Richardson, A. D.: On the uncertainty of phenological responses to climate change, and implications for a terrestrial biosphere model, Biogeosciences, 9, 2063–2083, https://doi.org/10.5194/bg-9-2063-2012, 2012. a
Monson, R. K., Turnipseed, A. A., Sparks, J. P., Harley, P. C., Scott-Denton, L. E., Sparks, K., and Huxman, T. E.: Carbon sequestration in a high-elevation, subalpine forest, Glob. Change Biol., 8, 459–478, https://doi.org/10.1046/j.1365-2486.2002.00480.x, 2002. a
Montagnani, L., Manca, G., Canepa, E., Georgieva, E., Acosta, M., Feigenwinter, C., Janous, D., Kerschbaumer, G., Lindroth, A., Minach, L., Minerbi, S., Mölder, M., Pavelka, M., Seufert, G., Zeri, M., and Ziegler, W.: A new mass conservation approach to the study of CO2 advection in an alpine forest, J. Geophys. Res.-Atmos., 114, D07306, https://doi.org/10.1029/2008JD010650, 2009. a
Moors, E.: Water use of forests in the Netherlands, Tech. rep., Vrije Universiteit, Amsterdam, available at: http://edepot.wur.nl/213926 (last access: 26 April 2019), 2012. a
Morellato, L. P. C., Alberti, L. F., and Hudson, I. L.: Applications of Circular Statistics in Plant Phenology: a Case Studies Approach, in: Phenological Research, Springer, Dordrecht, https://doi.org/10.1007/978-90-481-3335-2_16, 339–359, 2010. a, b
Morente-López, J., Lara-Romero, C., Ornosa, C., and Iriondo, J. M.: Phenology drives species interactions and modularity in a plant–flower visitor network, Sci. Rep., 8, 9386, https://doi.org/10.1038/s41598-018-27725-2, 2018. a
Morin, X., Roy, J., Sonié, L., and Chuine, I.: Changes in leaf phenology of three European oak species in response to experimental climate change, New Phytol., 186, 900–910, https://doi.org/10.1111/j.1469-8137.2010.03252.x, 2010. a
Pabon-Moreno, D. E., Musavi, T., Migliavacca, M., Reichstein, M., Römermann, C., and Mahecha, M. D.: Code-repository for the research paper: 11Ecosystem Physio-phenology revealed using circular statistics”, Zenodo, https://doi.org/10.5281/zenodo.3921892, 2020. a
Pastorello, G., Trotta, C., Canfora, E., et al.: The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data, Scientific Data, 7, 225 pp., https://doi.org/10.1038/s41597-020-0534-3, 2020. a, b
Peichl, M., Gažovič, M., Vermeij, I., Goede, E. d., Sonnentag, O., Limpens, J., and Nilsson, M. B.: Peatland vegetation composition and phenology drive the seasonal trajectory of maximum gross primary production, Sci. Rep., 8, 8012, https://doi.org/10.1038/s41598-018-26147-4, 2018. a, b, c
Peñuelas, J., Rutishauser, T., and Filella, I.: Phenology Feedbacks on Climate Change, Science, 324, 887–888, https://doi.org/10.1126/science.1173004, 2009. a, b
Pilegaard, K., Ibrom, A., Courtney, M. S., Hummelshøj, P., and Jensen, N. O.: Increasing net CO2 uptake by a Danish beech forest during the period from 1996 to 2009, Agr. Forest Meteorol., 151, 934–946, https://doi.org/10.1016/j.agrformet.2011.02.013, 2011. a
Post, E. and Forchhammer, M. C.: Climate change reduces reproductive success of an Arctic herbivore through trophic mismatch, Philos. T. Roy. Soc. B-Biol., 363, 2367–2373, https://doi.org/10.1098/rstb.2007.2207, 2008. a
Prescher, A.-K., Grünwald, T., and Bernhofer, C.: Land use regulates carbon budgets in eastern Germany: From NEE to NBP, Agr. Forest Meteorol., 150, 1016–1025, https://doi.org/10.1016/j.agrformet.2010.03.008, 2010. a
Rambal, S., Joffre, R., Ourcival, J. M., Cavender-Bares, J., and Rocheteau, A.: The growth respiration component in eddy CO2 flux from a Quercus ilex mediterranean forest, Glob. Change Biol., 10, 1460–1469, https://doi.org/10.1111/j.1365-2486.2004.00819.x, 2004. a
Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., Bernhofer, C., Buchmann, N., Gilmanov, T., Granier, A., Grünwald, T., Havránková, K., Ilvesniemi, H., Janous, D., Knohl, A., Laurila, T., Lohila, A., Loustau, D., Matteucci, G., Meyers, T., Miglietta, F., Ourcival, J.-M., Pumpanen, J., Rambal, S., Rotenberg, E., Sanz, M., Tenhunen, J., Seufert, G., Vaccari, F., Vesala, T., Yakir, D., and Valentini, R.: On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm, Glob. Change Biol., 11, 1424–1439, https://doi.org/10.1111/j.1365-2486.2005.001002.x, 2005. a
Rey, A., Pegoraro, E., Tedeschi, V., Parri, I. D., Jarvis, P. G., and Valentini, R.: Annual variation in soil respiration and its components in a coppice oak forest in Central Italy, Glob. Change Biol., 8, 851–866, https://doi.org/10.1046/j.1365-2486.2002.00521.x, 2002. a
Richardson, A. D., Braswell, B. H., Hollinger, D. Y., Jenkins, J. P., and Ollinger, S. V.: Near-surface remote sensing of spatial and temporal variation in canopy phenology, Ecol. Appl., 19, 1417–1428, https://doi.org/10.1890/08-2022.1, 2009. a
Richardson, A. D., Andy Black, T., Ciais, P., Delbart, N., Friedl, M. A., Gobron, N., Hollinger, D. Y., Kutsch, W. L., Longdoz, B., Luyssaert, S., Migliavacca, M., Montagnani, L., William Munger, J., Moors, E., Piao, S., Rebmann, C., Reichstein, M., Saigusa, N., Tomelleri, E., Vargas, R., and Varlagin, A.: Influence of spring and autumn phenological transitions on forest ecosystem productivity, Philos. T. Roy. Soc. B-Biol., 365, 3227–3246, https://doi.org/10.1098/rstb.2010.0102, 2010. a
Richardson, A. D., Keenan, T. F., Migliavacca, M., Ryu, Y., Sonnentag, O., and Toomey, M.: Climate change, phenology, and phenological control of vegetation feedbacks to the climate system, Agr. Forest Meteorol., 169, 156–173, https://doi.org/10.1016/j.agrformet.2012.09.012, 2013. a, b, c
Ryan, E. M., Ogle, K., Zelikova, T. J., LeCain, D. R., Williams, D. G., Morgan, J. A., and Pendall, E.: Antecedent moisture and temperature conditions modulate the response of ecosystem respiration to elevated CO2 and warming, Glob. Change Biol., 21, 2588–2602, https://doi.org/10.1111/gcb.12910, 2015. a
Saleska, S. R., Miller, S. D., Matross, D. M., Goulden, M. L., Wofsy, S. C., da Rocha, H. R., de Camargo, P. B., Crill, P., Daube, B. C., de Freitas, H. C., Hutyra, L., Keller, M., Kirchhoff, V., Menton, M., Munger, J. W., Pyle, E. H., Rice, A. H., and Silva, H.: Carbon in Amazon Forests: Unexpected Seasonal Fluxes and Disturbance-Induced Losses, Science, 302, 1554–1557, https://doi.org/10.1126/science.1091165, 2003. a
Schimel, D., Pavlick, R., Fisher, J. B., Asner, G. P., Saatchi, S., Townsend, P., Miller, C., Frankenberg, C., Hibbard, K., and Cox, P.: Observing terrestrial ecosystems and the carbon cycle from space, Glob. Change Biol., 21, 1762–1776, https://doi.org/10.1111/gcb.12822, 2015. a
Schmid, H. P., Grimmond, C. S. B., Cropley, F., Offerle, B., and Su, H.-B.: Measurements of CO2 and energy fluxes over a mixed hardwood forest in the mid-western United States, Agr. Forest Meteorol., 103, 357–374, https://doi.org/10.1016/S0168-1923(00)00140-4, 2000. a
Scott, R. L., Cable, W. L., and Hultine, K. R.: The ecohydrologic significance of hydraulic redistribution in a semiarid savanna, Water Resour. Res., 44, W02440, https://doi.org/10.1029/2007WR006149, 2008. a
Serrano-Ortiz, P., Domingo, F., Cazorla, A., Were, A., Cuezva, S., Villagarcía, L., Alados-Arboledas, L., and Kowalski, A. S.: Interannual CO2 exchange of a sparse Mediterranean shrubland on a carbonaceous substrate, J. Geophys. Res.-Biogeosci., 114, G04015, https://doi.org/10.1029/2009JG000983, 2009. a
Stocker, T. F., Qin, D., Plattner, G.-K. et al.: Climate change 2013: The physical science basis, Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change, 1535, Cambridge university press Cambridge, United Kingdom and New York, NY, USA, 2013. a
Suni, T., Rinne, J., Reissell, A., Altimir, N., Keronen, P., Rannik, U., Dal Maso, M., Kulmala, M., and Vesala, T.: Long-term measurements of surface fluxes above a Scots pine forest in Hyytiala, southern Finland, 1996–2001, Boreal Environ. Res., 8, 287–301, 2003. a
Tedeschi, V., Rey, A., Manca, G., Valentini, R., Jarvis, P. G., and Borghetti, M.: Soil respiration in a Mediterranean oak forest at different developmental stages after coppicing, Glob. Change Biol., 12, 110–121, https://doi.org/10.1111/j.1365-2486.2005.01081.x, 2006. a
Thum, T., Aalto, T., Laurila, T., Aurela, M., Kolari, P., and Hari, P.: Parametrization of two photosynthesis models at the canopy scale in a northern boreal Scots pine forest, Tellus B, 59, 874–890, https://doi.org/10.1111/j.1600-0889.2007.00305.x, 2007. a
Treuhaft, R. N., Law, B. E., and Asner, G. P.: Forest Attributes from Radar Interferometric Structure and Its Fusion with Optical Remote Sensing, BioScience, 54, 561–571, 2004. a
Urbanski, S., Barford, C., Wofsy, S., Kucharik, C., Pyle, E., Budney, J., McKain, K., Fitzjarrald, D., Czikowsky, M., and Munger, J. W.: Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res.-Biogeosci., 112, G02020, https://doi.org/10.1029/2006JG000293, 2007. a
Valentini, R., Angelis, P. D., Matteucci, G., Monaco, R., Dore, S., and Mucnozza, G. E. S.: Seasonal net carbon dioxide exchange of a beech forest with the atmosphere, Glob. Change Biol., 2, 199–207, https://doi.org/10.1111/j.1365-2486.1996.tb00072.x, 1996. a
van der Molen, M. K., van Huissteden, J., Parmentier, F. J. W., Petrescu, A. M. R., Dolman, A. J., Maximov, T. C., Kononov, A. V., Karsanaev, S. V., and Suzdalov, D. A.: The growing season greenhouse gas balance of a continental tundra site in the Indigirka lowlands, NE Siberia, Biogeosciences, 4, 985–1003, https://doi.org/10.5194/bg-4-985-2007, 2007. a
Von Mises, R.: Über die “Ganzzahligkeit” der Atomgewichte und verwandte Fragen, Phys. Z., 19, 490–500, 1918. a
Wang, X. and Wu, C.: Estimating the peak of growing season (POS) of China's terrestrial ecosystems, Agr. Forest Meteorol., 278, 107639, https://doi.org/10.1016/j.agrformet.2019.107639, 2019. a, b, c
Wohlfahrt, G., Hammerle, A., Haslwanter, A., Bahn, M., Tappeiner, U., and Cernusca, A.: Seasonal and inter-annual variability of the net ecosystem CO2 exchange of a temperate mountain grassland: Effects of weather and management, J. Geophys. Res.-Atmos., 113, D08110, https://doi.org/10.1029/2007JD009286, 2008. a
Xu, L. and Baldocchi, D. D.: Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature, Tree Physiol., 23, 865–877, https://doi.org/10.1093/treephys/23.13.865, 2003. a
Xu, L. and Baldocchi, D. D.: Seasonal variation in carbon dioxide exchange over a Mediterranean annual grassland in California, Agr. Forest Meteorol., 123, 79–96, https://doi.org/10.1016/j.agrformet.2003.10.004, 2004. a
Zhang, X., Friedl, M. A., Schaaf, C. B., Strahler, A. H., Hodges, J. C. F., Gao, F., Reed, B. C., and Huete, A.: Monitoring vegetation phenology using MODIS, Remote Sensing Environ., 84, 471–475, https://doi.org/10.1016/S0034-4257(02)00135-9, 2003. a
Zhou, S., Zhang, Y., Caylor, K. K., Luo, Y., Xiao, X., Ciais, P., Huang, Y., and Wang, G.: Explaining inter-annual variability of gross primary productivity from plant phenology and physiology, Agr. Forest Meteorol., 226-227, 246–256, https://doi.org/10.1016/j.agrformet.2016.06.010, 2016. a, b
Zhou, S., Zhang, Y., Ciais, P., Xiao, X., Luo, Y., Caylor, K. K., Huang, Y., and Wang, G.: Dominant role of plant physiology in trend and variability of gross primary productivity in North America, Sci. Rep., 7, 41366, https://doi.org/10.1038/srep41366, 2017. a
Zielis, S., Etzold, S., Zweifel, R., Eugster, W., Haeni, M., and Buchmann, N.: NEP of a Swiss subalpine forest is significantly driven not only by current but also by previous year's weather, Biogeosciences, 11, 1627–1635, https://doi.org/10.5194/bg-11-1627-2014, 2014. a





