Alkenone isotopes show evidence of active carbon concentrating mechanisms in coccolithophores as aqueous carbon dioxide concentrations fall below 7 µmol L⁻¹

Coccolithophores and other haptophyte algae acquire the carbon required for metabolic processes from the water in which they live. Whether carbon is actively moved across the cell membrane via a carbon concentrating mechanism, or passively through diffusion, is important for haptophyte biochemistry. The possible utilization of carbon concentrating mechanisms also has the potential to over-print one proxy method by which ancient atmospheric CO₂ concentration is reconstructed using alkenone isotopes. Here I show that carbon concentrating mechanisms are likely used when aqueous carbon dioxide concentrations are below 7 µmol L⁻¹. I compile published alkenone-based CO₂ reconstructions from multiple sites over the Pleistocene and recalculate them using a common methodology, which allows comparison to be made with ice core CO₂ records. Interrogating these records reveals that the relationship between proxy CO₂ and ice core CO₂ breaks down when local aqueous CO₂ concentration falls below 7 µmol L⁻¹. The recognition of this threshold explains why many alkenone-based CO₂ records fail to accurately replicate ice core CO₂ records, and it suggests the alkenone proxy is likely robust for much of the Cenozoic when this threshold was unlikely to be reached in much of the global ocean.

1 Introduction

Alkenones are long-chain (C₃₇₋₃₉) ethyl and methyl ketones (Fig. 1; Brassell et al., 1986; Rechka and Maxwell, 1987) produced by a restricted group of photosynthetic haptophyte algae (Conte et al., 1994). Produced by a narrow group of organisms which live exclusively in the photic zone, alkenones allow probing of algal biogeochemistry, and as alkenones are often preserved in the sedimentary record, alkenones can also provide information about past environmental conditions.

Two main proxy systems based on alkenone geochemistry exist: one allows reconstruction of sea surface temperature (SST) and relies on the changing degree of unsaturation of the C₃₇ alkenone (${\mathrm{U}}_{\mathrm{37}}^{{\mathrm{K}}^{\prime }}$) (Brassell et al., 1986), whilst a second for atmospheric CO₂ concentration is based on reconstructing the isotopic fractionation which takes place during photosynthesis (ε_p) (Laws et al., 1995; Bidigare et al., 1997). It is the second system using the stable carbon isotopic composition of the preserved alkenones for reconstructing atmospheric CO₂ concentration (referred to throughout as ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$) which is the focus of this study.

In the modern ocean, alkenones are produced primarily by two dominant coccolithophore species: Emiliania huxleyi and Gephyrocapsa oceanica. E. huxleyi first appeared 290 kyr ago and began to dominate over G. oceanica around 82 kyr ago (Gradstein et al., 2012; Raffi et al., 2006). However alkenones are commonly found in sediments throughout the Cenozoic, with the oldest reported detections from mid-Albian-aged black shales (Farrimond et al., 1986). Prior to the evolution of G. oceanica, alkenones were most likely produced by other closely related species from the Noelaerhabdaceae family (Marlowe et al., 1990; Volkman, 2000). Micropalaeontological and molecular data split the coccolith-bearing haptophytes into two distinct phylogenetic clades: the Isochrysidales and Coccolithales. The Isochrysidales contain the modern alkenone-producing taxa, including E. huxleyi and G. oceanica, and fossil reticulofenestrids. Meanwhile the non-alkenone-producers are separated into the order Coccolithales, which includes Coccolithus pelagicus and Calcidiscus leptoporus along with most other coccolithophores.

Proxies for atmospheric CO₂ concentration – including ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$, those based on the δ¹¹B of planktic foraminifera, geochemical modelling, and stomatal density – broadly agree that over the Cenozoic atmospheric pCO₂ declined from high levels (> 1000 µatm) in the “greenhouse” worlds of the Palaeocene and Eocene to close to modern-day values (around 400 µatm) in the Pliocene (Pagani et al., 2005, 2011; Pearson et al., 2009; Anagnostou et al., 2016; Foster et al., 2017; Sosdian et al., 2018; Super et al., 2018; Zhang et al., 2013; Beerling and Royer, 2011). However, recently discrepancies have emerged between ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and other CO₂ proxies at the < 400 µatm atmospheric CO₂ concentrations of the Pleistocene (i.e. Badger et al., 2019, 2013a, and compare Badger et al., 2013b, and Pagani et al., 2009, with Martínez-Botí et al., 2015). Whilst the long-standing differences between alkenone (Pagani et al., 1999), δ¹¹B (Foster et al., 2012), and stomatal proxies (Kürschner et al., 2008) in the Miocene CO₂ reconstructions have been partially resolved with new SST records (Super et al., 2018), differences remain in the Pliocene (Pagani et al., 2009; Badger et al., 2013b; Martínez-Botí et al., 2015) and Pleistocene (Badger et al., 2019).

Carbon concentrating mechanisms

One plausible reason for the discrepancies between ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and other proxies for atmospheric CO₂ is the operation of active carbon concentrating mechanisms (CCMs) in haptophytes. These are potentially important as ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ assumes purely passive uptake of carbon into the haptophyte cell purely via diffusion (Laws et al., 1995; Bidigare et al., 1997). The potential for CCMs to affect ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ has long been known (Laws et al., 1997, 2002; Cassar et al., 2006), and recent work has refocussed efforts on understanding CCMs in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ (Bolton et al., 2012; Bolton and Stoll, 2013; Stoll et al., 2019; Zhang et al., 2019, 2020). Coccolithophores are thought to have low-efficiency CCMs – especially compared to diatoms, dinoflagellates, and Phaeocystis – with evidence that CCMs play a minor role in coccolithophore biochemistry in the CO₂-replete worlds of the early Cenozoic (Bolton et al., 2012; Reinfelder, 2011). Direct evidence from experimentation with the marine diatom Phaeodactylum tricornutum suggests that both passive diffusive uptake and active CCMs operate at the same time, with active uptake used to moderate internal cell CO₂ concentrations to minimize energy use during transport to carboxylation sites (Laws et al., 1997). CO₂, unlike some other nutrients, is abundant within the water column, especially when considering the dissolved inorganic carbon (DIC) reservoir which includes bicarbonate (${\mathrm{HCO}}_{\mathrm{3}}^{-}$), carbonate (${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$), and dissolved CO₂([CO₂]_(aq)). However, due to the relatively slow diffusion of dissolved [CO₂]_(aq) through water and the slow kinetics of the bicarbonate-to-[CO₂]_(aq) transformation, surface water [CO₂]_(aq) can still be depleted by photosynthetic activity. This can become particularly problematic in species which form blooms and at the cell boundary of species with limited motility. It should be no surprise therefore that many marine photosynthetic organisms have evolved with mechanisms to concentrate carbon within the cell.

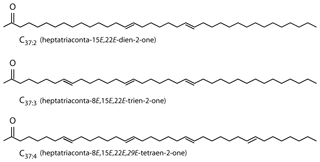
Figure 1 Alkenones are C₃₇ unsaturated methyl ketones (Brassell et al., 1986; Rechka and Maxwell, 1987).

The enzyme carbonic anhydrase (CA) can catalyse the dehydration of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ to [CO₂]_(aq) to speed up availability of carbon if the [CO₂]_(aq) reservoir is depleted and has been observed in several haptophytes, including coccolithophores (Rost et al., 2003; Riebesell et al., 2007). The exact contribution of CA remains unclear, but two possible mechanisms for CCMs have been postulated (Reinfelder, 2011): (1) CA catalyses dehydration of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ at the cell surface, which then allows increased CO₂ to diffuse into the cell passively, and (2) ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ is transported into the cell and then converted by CA. Both of these options will likely impact the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy, firstly by changing the effective [CO₂]_(aq) within the cell (and so impacting ε_p) and secondly by imparting another carbon isotopic fractionation during CA catalysation which is not considered by the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy system. However CA activity in coccolithophores does not appear to be regulated by CO₂ as it is in diatoms and Phaeocystis (Rost et al., 2003), which may indicate a less-well-developed CCM in coccolithophores.

Calcifying coccolithophores (which include alkenone producers E. huxleyi and G. oceanica) may be able to utilize ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ directly as a carbon source (Trimborn et al., 2007), with precipitation of CaCO₃ providing an acid for the dehydration of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, but this still requires sufficient ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ entering the cell, and it is unclear whether calcification aids DIC acquisition (Riebesell et al., 2000; Zondervan et al., 2002). The light-dependent leak of carbon (as CO₂ and DIC) back from haptophyte cells (including the coccolithophore E. huxleyi) to seawater (Tchernov et al., 2003) suggests that CCMs are energy intensive and can concentrate DIC within the cell. Even with active CCMs, it appears that in the ocean coccolithophores are CO₂ limited under some circumstances (Riebesell et al., 2007).

2 Materials and methods

Calculating CO₂ from alkenone δ¹³C values: the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy

In this study I use the now large number of published ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ records which overlap with ice core records of atmospheric CO₂ concentration (Tables 1 and 2) to explore the relationship between ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and CCMs in the Pleistocene, where our understanding of atmospheric CO₂ concentration is best.

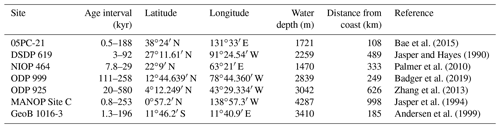
Multiple records of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ have been published for the Pleistocene (Fig. 2, Table 1), allowing direct comparison with ice-core-based CO₂ records (Table 2). These records are globally distributed in longitude but are concentrated at low-latitude sites, largely as there is a general preference for sites which have (in the modern ocean) surface waters close to equilibrium with the atmosphere (Fig. 2, Table 1). In longer-term palaeoclimate studies there has also been a preference for low-latitude gyre sites in the belief that these sites are more likely to be oceanographically stable over long time intervals (Pagani et al., 1999). Most of the records included here (Table 1, Fig. 2) were generated with the aim to reconstruct atmospheric CO₂ concentration; however one, the MANOP Site C of Jasper et al. (1994), was used to explicitly reconstruct changing disequilibrium due to oceanographic frontal changes over time and so is excluded from the following analysis.

Bae et al. (2015)Jasper and Hayes (1990)Palmer et al. (2010)Badger et al. (2019)Zhang et al. (2013)Jasper et al. (1994)Andersen et al. (1999)

Table 1 Sites with Pleistocene ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ records. Note that the MANOP Site C record was generated to track changes in surface water–atmosphere equilibrium, not atmospheric pCO₂, so, although it is included here for completeness, it is not included in the analysis. Distance from the coast is calculated from the intermediate-resolution version of GSHHG and computed using Generic Mapping Tools (Wessel and Smith, 1996; Wessel et al., 2019).

The full record for ODP Site 925 extends to 38.62 Ma.

Rubino et al. (2013)MacFarling Meure et al. (2006)Monnin et al. (2001, 2004)Marcott et al. (2014)Ahn and Brook (2014)Bereiter et al. (2012)Bereiter et al. (2012)Schneider et al. (2013)Petit et al. (1999)

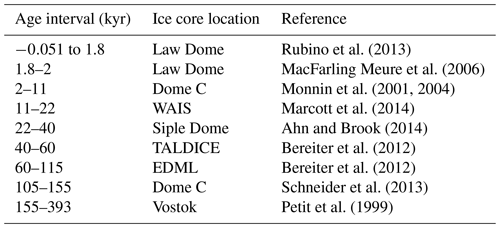
Table 2 Sources of ice core data, as compiled by Bereiter et al. (2015). WAIS – West Antarctic Ice Sheet; TALDICE – TALos Dome Ice CorE; and EDML – EPICA Dronning Maud Land. Age given as gas age relative to 1950.

Whilst these sites do only span a relatively small latitudinal extent, the diversity of settings does allow for investigation of any secondary controls on alkenone δ¹³C values (δ¹³C_alkenone) – in particular, differences in oceanographic setting and SST to test the hypothesis that low [CO₂]_(aq) breaks the relationship between δ¹³C_alkenone and atmospheric CO₂ concentration, as might be expected if haptophytes are able to actively take up carbon from seawater to meet metabolic demand (i.e. activate CCMs).

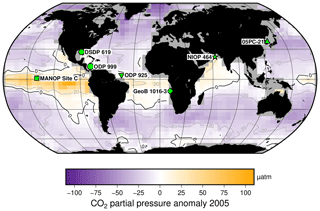
Figure 2 Study sites relative to mean annual surface ocean CO₂ disequilibrium for 2005. Sites are globally distributed in longitude but restricted in latitude, as generally sites are chosen to be close to surface water equilibrium with the atmosphere. Sites used for this study are indicated, over the mean annual surface ocean disequilibrium for 2005 calculated from Takahashi et al. (2014). The MANOP Site C (Jasper et al., 1994) was chosen to study the disequilibrium at that site, so it is shown here but not used in the following analyses. Site symbols are used throughout the figures: ODP 999 – circle; 05PC-21 – triangle; ODP 925 – inverted triangle; DSDP 619 – hexagon; MANOP Site C – square; NIOP 464 – star; and GeoB 1016-3 – diamond.

To facilitate fair comparison between sites and consistent comparison with the ice core records, all ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ records were recalculated using a consistent approach. The approach is based on Bidigare et al. (1997), which updated the initial approach of Jasper and Hayes (1990) to ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$. This approach removes some additional corrections used in the original publication of the records (such as growth rate adjustment for NIOP 464; Palmer et al., 2010) but does allow for direct comparison to be made. For all sites the “b” term was estimated using modern-day surface $\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]$ (Bidigare et al., 1997; Pagani et al., 2009)

An overview of how ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ data are typically generated is given in Badger et al. (2013b). Briefly, to calculate ε_p requires the stable carbon isotopic composition of the dissolved CO₂ (${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}}$) and haptophyte biomass (δ¹³C_org). The isotopic fractionation between δ¹³C_alkenone and δ¹³C_org is first corrected assuming a constant fractionation (ε_alkenone) of 4.2 ‰ (Garcia et al., 2013; Popp et al., 1998; Bidigare et al., 1997):

$$\begin{array}{}\text{(1)}& {\mathit{\epsilon }}_{\mathrm{alkenone}}={\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{alkenone}}+\mathrm{1000}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{org}}+\mathrm{1000}}}-\mathrm{1}.\end{array}$$

The isotopic composition of DIC is estimated using (ideally) the δ¹³C value of planktic foraminifera and the temperature-dependent fractionation between calcite and [CO₂]_(g) experimentally determined by Romanek et al. (1992), where T is sea surface temperature in degrees Celsius (SST):

$$\begin{array}{}\text{(2)}& {\mathit{\epsilon }}_{\mathrm{calcite}-{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}=\mathrm{11.98}-\mathrm{0.12}T.\end{array}$$

The value of the carbon isotopic composition of CO_2(g) (${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}$) can then be calculated:

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}={\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{carbonate}}+\mathrm{1000}}{{\mathit{\epsilon }}_{\mathrm{calcite}-{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}/\mathrm{1000}+\mathrm{1}}}-\mathrm{1000}.\end{array}$$

From this ${\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}}$ can be calculated using the relationship experimentally determined by Mook et al. (1974),

$$\begin{array}{}\text{(4)}& {\mathit{\epsilon }}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}-{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}={\displaystyle \frac{-\mathrm{373}}{T+\mathrm{273.15}}}+\mathrm{0.19},\end{array}$$

and

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\displaystyle }{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}}=& {\displaystyle }\left({\displaystyle \frac{{\mathit{\epsilon }}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}-{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{g}\right)}}}{\mathrm{1000}}}+\mathrm{1}\right)\\ {\displaystyle }& {\displaystyle }\times \left({\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{c}\left(\mathrm{g}\right)}}+\mathrm{1000}\right)\\ {\displaystyle }& {\displaystyle }-\mathrm{1000}.\end{array}\end{array}$$

Finally ε_p can be calculated:

$$\begin{array}{}\text{(6)}& {\mathit{\epsilon }}_{\text{p}}=\left({\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{{\mathrm{CO}}_{\mathrm{2}\left(\mathrm{aq}\right)}}+\mathrm{1000}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{org}}+\mathrm{1000}}}-\mathrm{1}\right)\times \mathrm{1000},\end{array}$$

and from that [CO₂]_(aq) is calculated using the isotopic fractionation during carbon fixation (ε_f) and b, which represents the summation of physiological factors:

$$\begin{array}{}\text{(7)}& {\left[{\mathrm{CO}}_{\mathrm{2}}\right]}_{\text{(aq)}}={\displaystyle \frac{b}{{\mathit{\epsilon }}_{\text{f}}-{\mathit{\epsilon }}_{\text{p}}}}.\end{array}$$

Here ε_f is assumed to be a constant 25 ‰ (Bidigare et al., 1997). In the modern ocean the b term, which accounts for physiological factors such as cell size and growth rate, shows a close correlation with $\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]$ (Bidigare et al., 1997; Pagani et al., 2009). However, the relationship between b, growth rate, and $\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]$ has recently been questioned (Zhang et al., 2019, 2020) but for the purposes of this analysis is assumed to hold. This is discussed further below. Values for SST, δ¹³C_alkenone, δ¹³C_carbonate, salinity, and $\left[{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\right]$ are either taken from the original publications or estimated from modern ocean estimates (Takahashi et al., 2009; Antonov et al., 2010; Garcia et al., 2013; Locarnini et al., 2013).

Providing that the atmosphere is in equilibrium with surface water, the concentration of atmospheric CO₂ can be calculated from [CO₂]_(aq) (and vice versa if atmospheric CO₂ concentration is known) using Henry's law:

$$\begin{array}{}\text{(8)}& p{\mathrm{CO}}_{\mathrm{2}}={\displaystyle \frac{{\left[{\mathrm{CO}}_{\mathrm{2}}\right]}_{\text{(aq)}}}{K_{\mathrm{H}}}}.\end{array}$$

The solubility coefficient (K_H) is dependent on salinity and SST, and here it is calculated following the parameterization of Weiss (1970, 1974).

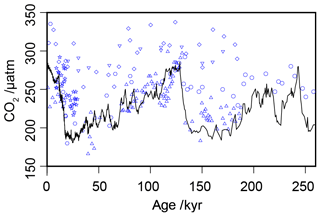
Figure 3 Compiled ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based estimates of atmospheric CO₂ concentration over the past 260 kyr (blue circles), with the ice core compilation of Bereiter et al. (2015) shown as the solid black line. Full sources for the ice core and ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ records are in Tables 1 and 2.

3 Results

3.1 Multi-site comparisons between ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and the ice core records

Across the six sites included in this analysis, there are 217 ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based estimates of atmospheric CO₂ concentration over the past 260 kyr for comparison with the ice core records (Table 2; Bereiter et al., 2015). When all ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ estimates are considered together over 260 kyr, this compilation of proxy-based records fails to replicate the ice core record (Fig. 3). This has already been noted at specific sites (e.g. Site 999 in the Caribbean; Badger et al., 2019), but this is the first time that all available records coincident with the Pleistocene ice core records have been compiled using a common methodology. Notably the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based estimates are rarely lower than time-equivalent ice core estimate, but frequently higher. Given that haptophytes require carbon to satisfy metabolic demand, this is perhaps unsurprising; if at times of low carbon availability haptophytes can switch from passive to active uptake to satisfy metabolic demand, it would be times of low atmospheric CO₂ concentration (and so lower [CO₂]_(aq)) when the active uptake is most likely to be needed. As ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based estimates of atmospheric CO₂ concentration rely on the assumption of a purely diffusive uptake of carbon, it is therefore likely that the proxy would perform worse at times of low atmospheric CO₂ concentration.

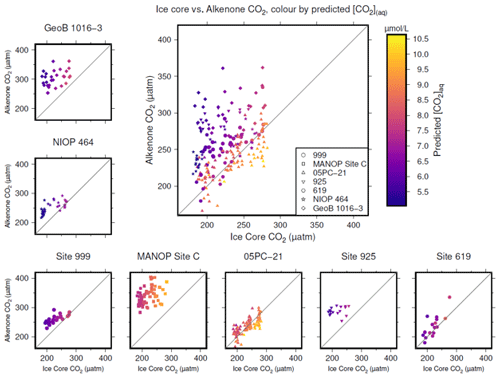
Figure 4 Crossplots of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based atmospheric CO₂ concentration (y axes) vs. the time-equivalent estimate from ice core records (x axes; Bereiter et al., 2015; Table 2). The large panel compiles all sites, with the exception of MANOP Site C, as explained in the text. Symbols are coloured by predicted [CO₂]_(aq) for each site and time as explained in the text. Full sources for alkenone data are shown in Table 1. A 1:1 line is included in all plots for comparison.

The haptophytes do not directly interact with the atmosphere, obtaining their carbon from dissolved carbon. As it is not only atmospheric CO₂ concentration which controls the concentration of dissolved carbon ([CO₂]_(aq)) but also temperature, alkalinity, and other oceanographic factors which control the equilibrium state between surface waters at the atmosphere (Fig. 2), the multiple sites in different settings now give the opportunity to test whether other factors are important in controlling the accuracy of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$.

To produce time-equivalent estimates of atmospheric CO₂ concentration for comparison with the ice core records, a simple linear interpolation of the Bereiter et al. (2015) compilation was initially used (Fig. 4). This assumes that both the age model of the ice core and the published age models of the sites are correct and equivalent. This is almost certainly not the case, and so for the calculations below, a ±3000 year uncertainty is included for ages of both the ice core and ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ values. Figure 4 shows that ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based atmospheric CO₂ concentration agree with ice core CO₂ at some sites and at some times, but not throughout. Sites 05-PC21 (Bae et al., 2015) and DSDP Site 619 (Jasper and Hayes, 1990) perform quite well throughout, whilst ODP Site 999 (Badger et al., 2019) and NIOP 464 (Palmer et al., 2010) only appear to agree at higher values of CO₂, and at ODP Site 925 (Zhang et al., 2013) and GeoB 1016-3 (Andersen et al., 1999) there is very little overlap between the two methods of reconstructing atmospheric CO₂ concentration.

To explore whether [CO₂]_(aq) is an important influence on ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$, I calculate predicted [CO₂]_(aq) ([CO₂]_{(aq)−predicted}) for each of the samples. To calculate [CO₂]_{(aq)−predicted}, the time-equivalent value of atmospheric CO₂ concentration from the ice core record is used in combination with Eq. (8) to calculate [CO₂]_(aq) at the time of alkenone production for each sample. Reconstructed estimates of SST and salinity are used as for ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ above, along with any estimated surface water–atmosphere disequilibrium. Points in Fig. 4 are then coloured by [CO₂]_{(aq)−predicted}.

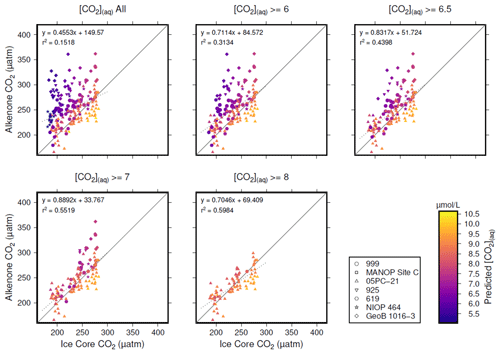
Figure 5 Crossplots of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based atmospheric CO₂ concentration (Table 1; y axes) vs. the time-equivalent estimate from ice core records (x axes; Bereiter et al., 2015; Table 2). The sample of published vales of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ was progressively restricted by [CO₂]_{(aq)−predicted}, indicated by the subplot titles. Individual values are coloured by [CO₂]_{(aq)−predicted}, and sites indicated by shape (see key). Coefficients of determination and equations of best fit are shown in each panel, along with a 1:1 line.

Inspection of Fig. 4 suggests a connection between ([CO₂]_{(aq)−predicted}) and the skill of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ to reconstruct atmospheric CO₂ concentration. The points clustering around the 1:1 line are lighter in colour (so with higher [CO₂]_{(aq)−predicted}), whilst points falling away from the 1:1 line have lower [CO₂]_{(aq)−predicted}. To explore this relationship, I progressively restricted the included samples on the basis of [CO₂]_{(aq)−predicted} and at each stage calculated a Pearson correlation coefficient (r) and coefficient of determination (r²) for each subset. Under this analysis the correlation progressively increased as more of the low [CO₂]_{(aq)−predicted} samples were excluded (Fig. 5). All analyses were performed in R (R Core Team, 2020) using RStudio (RStudio Team, 2020). This suggests that the fidelity of the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ depends on the concentration of [CO₂]_(aq), improving at higher levels of [CO₂]_(aq).

To further investigate this potential relationship, I progressively exclude samples based on [CO₂]_{(aq)−predicted} with a step size of 0.05 µmol L⁻¹, again calculating Pearson correlation coefficients and coefficients of determination between ice core and ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ for each subsample of the population. The result is shown in Fig. 6. Here the analysis shows, similar to Fig. 5, that, as the samples with lowest [CO₂]_{(aq)−predicted} are progressively removed, the correlation between ice core and ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ increases. Furthermore, this continues only up until [CO₂]_{(aq)−predicted} reaches 7 µmol L⁻¹. Above this, the coefficient of determination plateaus, until the subsample reaches such a small size that spurious correlations become important (Fig. 6b).

3.2 Sensitivity and uncertainty tests

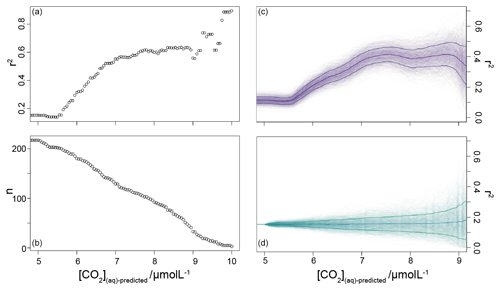
Figure 6 Coefficient of determination (a) of a reducing sample of all compiled ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ (Table 1) vs. the time-equivalent estimate from ice core records (Bereiter et al., 2015; Table 2). The sample reduces stepwise by 0.05 µmol L⁻¹, and the number of records in each subsample is shown in panel (b). Panel (c) shows a 1000-member Monte Carlo analysis, whereby uncertainty in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and age is considered, as detailed in the text. Panel (d) shows a similar 1000-member Monte Carlo analysis, but with random sampling of the whole ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ population so that the number of samples is equivalent to the dataset shown in panel (c); i.e. the size of the sample follows that shown in panel (b). Means and 1σ uncertainties are shown as the bold lines.

It is possible that the pattern seen in Fig. 6b could emerge from a dataset shaped with increasing density surrounding the 1:1 correlation line without being driven by changes in [CO₂]_{(aq)−predicted}. To explore this possibility, I ran a series of sensitivity experiments. In these, rather than reducing the sample by filtering by [CO₂]_{(aq)−predicted}, the whole dataset (Table 1) was randomly ordered and then stepwise subsampled. To make this equivalent to the [CO₂]_{(aq)−predicted} analysis above, I set the size of each subsample to be equal to each step in the original analysis. This produces a randomly selected but same-sized subsample such that the size of the subsample reduces in the same way as shown in Fig. 6b). Pearson correlation coefficients and coefficients of determination were calculated for each subsample as above, and I repeated this 1000 times, with the order of each sample randomized each time.

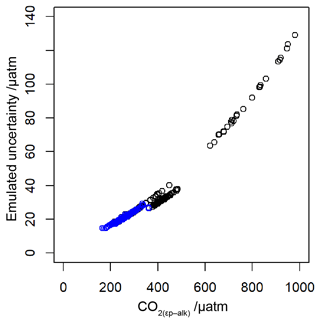
To allow for possible age model uncertainties, a 3000-year (1σ) uncertainty was also applied to each sample. This uncertainty was applied to the age of each sample prior to sampling of the ice core record, and it is applied as a normally distributed uncertainty. Uncertainty in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ measurements is typically calculated using Monte Carlo modelling of all the parameters (i.e. Pagani et al., 1999; Badger et al., 2013a, b); however this was not done in all the published work (Table 1), and some differences in approach were found across the published work. Therefore to create ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ uncertainty estimates for each value in this study, I emulate the uncertainties based on the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ value. I built a simple emulator (Fig. 7) by running Monte Carlo uncertainty estimates for all of the included datasets (Table 1) using the same estimates of uncertainty for each variable in the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ calculation as applied in Badger et al. (2013a, b). This then allows the uncertainty to be included in the [CO₂]_{(aq)−predicted} calculation as well as ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$, and it allowed for uncertainty estimates to be site-ambivalent.

The result is shown in Fig. 6c and d, and it suggests that the 7 µmol L⁻¹ break point remains valid. The absolute value of r² is reduced, even at higher [CO₂]_{(aq)−predicted}, but this would be expected given the addition of uncertainty in the age model, as the published age is most likely to align with the ice core. Given the rapid rate of change at deglaciations, this effect is likely to be particularly pronounced in this dataset as many records have high temporal resolution around deglaciations in order to attempt to resolve them. Any small age model offset introduced by the error modelling in these intervals also clearly has the potential to induce large differences between the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and ice core values. Figure 6c and d clearly demonstrate that it is the filtering by [CO₂]_{(aq)−predicted} rather than any spurious correlations which determines the shape of the data in Fig. 6a.

Figure 7 Emulated uncertainty in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$, generated by running Monte Carlo uncertainty models for all sites in Table 1, applying the same approach to uncertainty as Badger et al. (2013a, b). Estimates used in this study are highlighted in blue.

4 Discussion

The plateau in r² in Fig. 6a and c suggests that below a [CO₂]_{(aq)−predicted} of ∼7 µmol L⁻¹ ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ is no longer as good a predictor of ice core CO₂ as when [CO₂]_{(aq)−predicted} > 7 µmol L⁻¹. This is clear from comparing the relationship between samples where [CO₂]_{(aq)−predicted} < 7 µmol L⁻¹ with those where [CO₂]_{(aq)−predicted} > 7 µmol L⁻¹ in Fig. 8. Here the r² for the former of 0.15 is substantially less than the latter of 0.55. I suggest that this is because below this threshold the fundamental assumption of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$, that carbon is passively taken up by haptophytes, no longer holds true. One obvious explanation for why this would be the case is that at low levels of [CO₂]_(aq) haptophytes have to rely more on active uptake of carbon via CCMs in order to satisfy metabolic demand. Similar behaviour has been recognized in some culture studies (Laws et al., 1997, 2002; Cassar et al., 2006), with some evidence that the diatom Phaeodactylum tricornutum has a similar CCM threshold of 7 µmol L⁻¹ (Laws et al., 1997). Whilst the evidence for the mechanism of CCM is poorer for coccolithophores than it is for diatoms, any CCM would be expected to compromise the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy, either by increased supply of [CO₂]_(aq) or by further carbon isotopic fractionation effects during carbon transport, or both (Stoll et al., 2019).

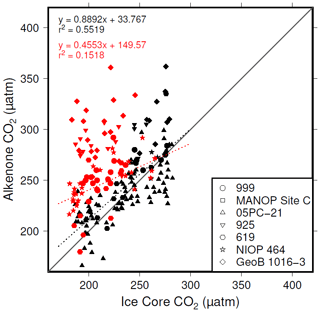
Figure 8 Correlations between ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ and ice core CO₂, where [CO₂]_{(aq)−predicted} > 7 µmol L⁻¹ (black symbols) and [CO₂]_{(aq)−predicted} < 7 µmol L⁻¹ (red symbols).

By applying a threshold value for [CO₂]_{(aq)−predicted} of 7 µmol L⁻¹ to the published records (Table 1), values of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ which are influenced by active CCMs can be eliminated. Recognition of this new threshold value of [CO₂]_{(aq)−predicted} allows for a new record of Pleistocene ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ to be compiled. This compilation then much better replicates the glacial–interglacial pattern of CO₂ change over the last 260 kyr (Fig. 9). Whilst this present compilation does rely on ice core CO₂ records to estimate [CO₂]_{(aq)−predicted}, and therefore has little direct utility as a CO₂ record, it does demonstrate that recognition of a threshold response allows accurate CO₂ reconstruction using ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$. This may represent the point at which isotopic effects of CCMs (plausibly through increased CA activity or ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ dehydration to meet C demand) overwhelm the assumptions of the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy. This, as well as the behaviour shown in Fig. 6a and c, suggests that from the standpoint of the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy CCMs may effectively be considered either active or not, and that when [CO₂]_(aq) is plentiful passive uptake dominates, at least sufficiently in most oceanographic settings that ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ can accurately record atmospheric CO₂ concentration. This implies that, if areas of the ocean (or intervals of time) with low [CO₂]_(aq) can be avoided, accurate reconstructions of atmospheric CO₂ concentration can be acquired using ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$.

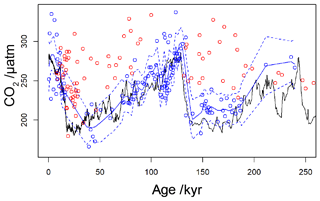
Figure 9 Revised compilation of Pleistocene ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ vs. ice core records. The compiled published records (Table 1) are shown as circles, coloured red where [CO₂]_{(aq)−predicted} is below a threshold of 7 µmol⁻¹ and blue where [CO₂]_{(aq)−predicted} > 7 µmol⁻¹. The solid blue line is a loess filter (span 0.1) through the [CO₂]_{(aq)−predicted} > 7 µmol⁻¹ values, with 95 % confidence intervals (dashed blue line). The black line is the ice core compilation of Bereiter et al. (2015) (Table 2).

As [CO₂]_(aq) is affected by both SST via the temperature dependance of the Henry's law constant and atmospheric CO₂ concentration, for ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ to be effective in reconstructing atmospheric CO₂ concentration, areas of warm water (i.e. tropical or shallow shelf regions) under relatively low atmospheric CO₂ concentration must be avoided. However, as the atmospheric CO₂ control renders the global surface ocean sufficiently replete with [CO₂]_(aq) at Pliocene-like levels of atmospheric CO₂ concentration and above (Martínez-Botí et al., 2015) at all but the warmest surface ocean temperatures, ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ is likely to be a reliable system for most of the Cenozoic. It is only in the Pleistocene that atmospheric CO₂ concentration is low enough for CCMs to be widely active across the surface ocean, with the low-CO₂ glacials providing the most difficulty (Badger et al., 2019). This finding aligns well with evidence that CCMs developed in coccolithophores as a response to declining atmospheric CO₂ concentration through the Cenozoic and were developing in [CO₂]_(aq)-limited parts of the ocean in the late Miocene at the earliest, and likely not widespread until the Plio-Pleistocene (Bolton et al., 2012; Bolton and Stoll, 2013).

There have been recent attempts to correct for CCMs in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$-based reconstructions of atmospheric CO₂ concentrations (Zhang et al., 2019; Stoll et al., 2019; Zhang et al., 2020). However, these assume that CCMs are always active and crucially do not fundamentally break the relationship between ε_p values and atmospheric CO₂ concentration. However if this is not the case, and the relationship between ε_p values and atmospheric CO₂ concentration fails at Pleistocene levels of atmospheric CO₂, then Pleistocene records cannot be used to develop corrections of ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ to be applied throughout the Cenozoic. If, as suggested by the analyses presented here, CCMs only act at low [CO₂]_(aq), and largely only in conditions prevalent throughout the late Pliocene and Pleistocene, it is plausible that corrections based on Pleistocene records could overcompensate for CCMs in the rest of the Cenozoic, when the assumption of passive carbon uptake inherent in ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ as traditionally applied may still be valid.

5 Conclusions

Reconstructions of past atmospheric CO₂ concentration with proxy tools like ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ are critical for understanding how the Earth's climate system operates, as long as the tools used can be relied upon to be accurate and precise. This re-analysis of existing Pleistocene ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ records reveals that below a critical threshold of [CO₂]_(aq) of 7 µmol⁻¹ the relationship between δ¹³C_alkenone and atmospheric CO₂ concentration breaks down, plausibly because below this threshold haptophytes are able to actively take up carbon using CCMs in order to satisfy metabolic demand.

Although reconstructing the low levels of atmospheric CO₂ concentration in the Pleistocene glacials and areas of the global ocean where [CO₂]_(aq) is less than 7 µmol⁻¹ will be impossible, for much of the Cenozoic the ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ proxy retains utility. If care is taken to avoid regions and oceanographic settings where [CO₂]_(aq) is expected to be abnormally low, ${\mathrm{CO}}_{\mathrm{2}({\mathit{\epsilon }}_{\mathrm{p}}-\mathrm{alk})}$ remains an important and useful proxy to understand the Earth system.