the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Geographic variability in freshwater methane hydrogen isotope ratios and its implications for global isotopic source signatures
Peter M. J. Douglas
Emerald Stratigopoulos
Sanga Park
Dawson Phan
There is growing interest in developing spatially resolved methane (CH4) isotopic source signatures to aid in geographic source attribution of CH4 emissions. CH4 hydrogen isotope measurements (δ2H–CH4) have the potential to be a powerful tool for geographic differentiation of CH4 emissions from freshwater environments, as well as other microbial sources. This is because microbial δ2H–CH4 values are partially dependent on the δ2H of environmental water (δ2H–H2O), which exhibits large and well-characterized spatial variability globally. We have refined the existing global relationship between δ2H–CH4 and δ2H–H2O by compiling a more extensive global dataset of δ2H–CH4 from freshwater environments, including wetlands, inland waters, and rice paddies, comprising a total of 129 different sites, and compared these with measurements and estimates of δ2H–H2O, as well as δ13C-CH4 and δ13C–CO2 measurements. We found that estimates of δ2H–H2O explain approximately 42 % of the observed variation in δ2H–CH4, with a flatter slope than observed in previous studies. The inferred global δ2H–CH4 vs. δ2H–H2O regression relationship is not sensitive to using either modelled precipitation δ2H or measured δ2H–H2O as the predictor variable. The slope of the global freshwater relationship between δ2H–CH4 and δ2H–H2O is similar to observations from incubation experiments but is different from pure culture experiments. This result is consistent with previous suggestions that variation in the δ2H of acetate, controlled by environmental δ2H–H2O, is important in determining variation in δ2H–CH4. The relationship between δ2H–CH4 and δ2H–H2O leads to significant differences in the distribution of freshwater δ2H–CH4 between the northern high latitudes (60–90∘ N), relative to other global regions. We estimate a flux-weighted global freshwater δ2H–CH4 of −310 ± 15 ‰, which is higher than most previous estimates. Comparison with δ13C measurements of both CH4 and CO2 implies that residual δ2H–CH4 variation is the result of complex interactions between CH4 oxidation, variation in the dominant pathway of methanogenesis, and potentially other biogeochemical variables. We observe a significantly greater distribution of δ2H–CH4 values, corrected for δ2H–H2O, in inland waters relative to wetlands, and suggest this difference is caused by more prevalent CH4 oxidation in inland waters. We used the expanded freshwater CH4 isotopic dataset to calculate a bottom-up estimate of global source δ2H–CH4 and δ13C-CH4 that includes spatially resolved isotopic signatures for freshwater CH4 sources. Our bottom-up global source δ2H–CH4 estimate (−278 ± 15 ‰) is higher than a previous estimate using a similar approach, as a result of the more enriched global freshwater δ2H–CH4 signature derived from our dataset. However, it is in agreement with top-down estimates of global source δ2H–CH4 based on atmospheric measurements and estimated atmospheric sink fractionations. In contrast our bottom-up global source δ13C-CH4 estimate is lower than top-down estimates, partly as a result of a lack of δ13C-CH4 data from C4-plant-dominated ecosystems. In general, we find there is a particular need for more data to constrain isotopic signatures for low-latitude microbial CH4 sources.
- Article
(5746 KB) - Full-text XML
-
Supplement
(245 KB) - BibTeX
- EndNote
Methane (CH4) is an important greenhouse gas that accounts for approximately 25 % of current anthropogenic global warming, but we do not have a complete understanding of the current relative or absolute fluxes of different CH4 sources to the atmosphere (Schwietzke et al., 2016; Saunois et al., 2019), nor is there consensus on the causes of recent decadal-scale changes in the rate of increase in atmospheric CH4 (Kai et al., 2011; Pison et al., 2013; Rice et al., 2016; Schaefer et al., 2016; Worden et al., 2017; Thompson et al., 2018; Turner et al., 2019). Freshwater ecosystems are an integral component of the global CH4 budget. They are one of the largest sources of atmospheric CH4 and are unequivocally the largest natural, or non-anthropogenic, source (Bastviken et al., 2011; Saunois et al., 2019). At the same time the geographic distribution of freshwater CH4 emissions, changes in the strength of this source through time, and the relative importance of wetland versus inland water CH4 emissions all remain highly uncertain (Pison et al., 2013; Schaefer et al., 2016; Ganesan et al., 2018; Saunois et al., 2019; Turner et al., 2019). Gaining a better understanding of freshwater CH4 emissions on a global scale is of great importance for understanding potential future climate feedbacks related to CH4 emissions from these ecosystems (Bastviken et al., 2011; Koven et al., 2011; Yvon-Durocher et al., 2014; Zhang et al., 2017). It is also necessary in order to better constrain the quantity and rate of change of other CH4 emissions sources, including anthropogenic sources from fossil fuels, agriculture, and waste (Kai et al., 2011; Pison et al., 2013; Schaefer et al., 2016).
Isotopic tracers, particularly δ13C, have proven to be very useful in constraining global CH4 sources and sinks (Kai et al., 2011; Nisbet et al., 2016; Rice et al., 2016; Schaefer et al., 2016; Schwietzke et al., 2016; Nisbet et al., 2019). However, δ13C source signatures cannot fully differentiate CH4 sources, leaving residual ambiguity in source apportionment (Schaefer et al., 2016; Schwietzke et al., 2016; Worden et al., 2017; Turner et al., 2019). Applying additional isotopic tracers to atmospheric CH4 monitoring has the potential to greatly improve our understanding of CH4 sources and sinks (Turner et al., 2019; Saunois et al., 2020). Recently developed laser-based methods, including cavity ring-down spectroscopy, quantum cascade laser absorption spectroscopy, and tunable infrared laser direct absorption spectroscopy, in addition to continued application of isotope ratio mass spectrometry (Chen et al., 2016; Röckmann et al., 2016; Yacovitch et al., 2020) could greatly enhance the practicality of atmospheric δ2H–CH4 measurements at greater spatial and temporal resolution, similar to recent developments for δ13C-CH4 measurements (Zazzeri et al., 2015; Miles et al., 2018). δ2H–CH4 measurements have proven useful in understanding past CH4 sources in ice core records (Whiticar and Schaefer, 2007; Mischler et al., 2009; Bock et al., 2010, 2017) but have seen only limited use in modern atmospheric CH4 budgets (Kai et al., 2011; Rice et al., 2016), in part because of loosely constrained source terms, as well as relatively sparse atmospheric measurements. Atmospheric inversion models have shown that increased spatial and temporal resolution of δ2H–CH4 measurements could provide substantial improvements in precision for global and regional methane budgets (Rigby et al., 2012).
δ2H–CH4 measurements could prove especially useful in understanding freshwater CH4 emissions. Freshwater δ2H–CH4 is thought to be highly dependent on δ2H–H2O (Waldron et al., 1999a; Whiticar, 1999; Chanton et al., 2006). Since δ2H–H2O exhibits large geographic variation as a function of temperature and fractional precipitation (Rozanski et al., 1993; Bowen and Revenaugh, 2003), δ2H–CH4 measurements have the potential to differentiate freshwater CH4 sources by latitude. This approach has been applied in some ice core studies (Whiticar and Schaefer, 2007; Bock et al., 2010), but geographic source signals remain poorly constrained, in part because of small datasets and because of incompletely understood relationships between δ2H–H2O and δ2H–CH4. In contrast, recent studies of modern atmospheric δ2H–CH4 have typically not accounted for geographic variation in freshwater CH4 sources (Kai et al., 2011; Rice et al., 2016). Relatedly, other studies have found an important role for variation in δ2H–H2O in controlling δ2H–CH4 from biomass burning (Umezawa et al., 2011) and from plants irradiated by UV light (Vigano et al., 2010), as well as the δ2H of H2 produced by wood combustion (Röckmann et al., 2016).
In addition to variance caused by δ2H–H2O, a number of additional biogeochemical variables have been proposed to influence δ2H–CH4 in freshwater environments. These include differences in the predominant biochemical pathway of methanogenesis (Whiticar et al., 1986; Whiticar, 1999; Chanton et al., 2006), the extent of methane oxidation (Happell et al., 1994; Waldron et al., 1999a; Whiticar, 1999; Cadieux et al., 2016), isotopic fractionation resulting from diffusive gas transport (Waldron et al., 1999a; Chanton, 2005), and differences in the thermodynamic favorability or enzymatic reversibility of methanogenesis (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). These influences on δ2H–CH4 have the potential to complicate geographic signals but also provide the potential to differentiate ecosystem sources, if specific ecosystems are characterized by differing rates and pathways of methanogenesis, rates of CH4 oxidation, or gas transport processes. A recent study proposed that freshwater δ13C-CH4 could be differentiated geographically based on ecosystem differences in the prevalence of different methanogenic pathways and in the predominance of C4 plants, in addition to the geographic distribution of wetland ecosystems (Ganesan et al., 2018). δ2H–CH4 measurements have the potential to complement this approach by providing an additional isotopic parameter for differentiating ecosystem and geographic CH4 source signatures.
In order to use δ2H–CH4 as an indicator of freshwater ecosystem contributions to global and regional CH4 emissions budgets, a clearer understanding of freshwater δ2H source signals and how they vary by geographic location, ecosystem type, and other variables is needed. In order to address this need, we have assembled and analyzed a dataset of 897 δ2H–CH4 measurements from 129 individual ecosystems, or sites, derived from 40 publications (Schoell, 1983; Woltemate et al., 1984; Burke and Sackett, 1986; Whiticar et al., 1986; Burke et al., 1988; Burke, 1992; Burke et al., 1992; Lansdown et al., 1992; Lansdown, 1992; Martens et al., 1992; Wassmann et al., 1992; Happell et al., 1993; Levin et al., 1993; Happell et al., 1994; Wahlen, 1994; Bergamaschi, 1997; Chanton et al., 1997; Hornibrook et al., 1997; Tyler et al., 1997; Zimov et al., 1997; Bellisario et al., 1999; Popp et al., 1999; Waldron et al., 1999b; Chasar et al., 2000; Marik et al., 2002; Nakagawa et al., 2002a, b; Chanton et al., 2006; Walter et al., 2006, 2008; Alstad and Whiticar, 2011; Brosius et al., 2012; Sakagami et al., 2012; Bouchard et al., 2015; Stolper et al., 2015; Wang et al., 2015; Cadieux et al., 2016; Douglas et al., 2016; Thompson et al., 2016; Lecher et al., 2017). We have advanced existing datasets of freshwater δ2H–CH4 (Whiticar et al., 1986; Waldron et al., 1999a; Sherwood et al., 2017) in the following key attributes: (1) compiling a significantly larger dataset than was previously available; (2) compiling paired δ13C-CH4 data for all sites, δ13C–CO2 data for 50 % of sites, and δ2H–H2O data for 47 % of sites; (3) compiling geographic coordinates for all sites, providing the ability to perform spatial analyses and compare with gridded datasets of precipitation isotopic composition; and (4) classifying all sites by ecosystem and sample type (dissolved vs. gas samples), allowing for a clearer differentiation of how these variables influence δ2H–CH4.
Using this dataset we applied statistical analyses to address key questions surrounding the global distribution of freshwater δ2H–CH4, the variables that control this distribution, and its implications for atmospheric δ2H–CH4. Specifically, we investigated the nature of the global dependence of δ2H–CH4 on δ2H–H2O and whether this relationship results in significant differences in freshwater δ2H–CH4 by latitude. We also assessed whether variability in δ13C-CH4, δ13C–CO2, and αC was correlated with δ2H–CH4 and whether there are significant differences in δ2H–CH4 between different ecosystem and sample types. Finally, we used our dataset, combined with other isotopic datasets (Sherwood et al., 2017) and flux estimates (Saunois et al., 2020), to estimate the global δ2H–CH4 and δ13C-CH4 of global emissions sources, and we compared this with previous estimates based on atmospheric measurements or isotopic datasets (Whiticar and Schaefer, 2007; Rice et al., 2016; Sherwood et al., 2017).
2.1 Isotope nomenclature
Hydrogen and carbon isotope ratios are primarily discussed as delta values, using the generalized formula (Coplen, 2011)
where R is the ratio of the heavy isotope to the light isotope, and the standard is Vienna Standard Mean Ocean Water (VSMOW) for δ2H and Vienna Pee Dee Belemnite (VPDB) for δ13C. δ values are expressed in per mil (‰) notation.
We also refer to the isotopic fractionation factor between two phases, or α, which is defined as
Specifically, we discuss the carbon isotope fractionation factor between CO2 and CH4 (αC) and the hydrogen isotope fractionation factor between H2O and CH4 (αH).
2.2 Dataset compilation
2.2.1 Literature survey
To identify datasets we used a set of search terms (methane OR CH4 AND freshwater OR wetland OR peatland OR swamp OR marsh OR lake OR pond OR “inland water” AND “hydrogen isotope” OR “δD” OR “δ2H”) in Google Scholar to find published papers that discussed this measurement. We also identified original publications using previously compiled datasets (Waldron et al., 1999a; Sherwood et al., 2017). Data for 90 % of sites were from peer-reviewed publications. Data from 13 sites were from a PhD dissertation (Lansdown, 1992).
2.2.2 Dataset structure
Most samples were associated with geographic coordinates in data tables or text documentation, or with specific geographic locations such as the name of a town or city. In a few cases we identified approximate geographic locations based on text descriptions of sampling sites, with the aid of Google Earth software. Sampling sites were defined as individual water bodies or wetlands as identified in the relevant study. In one study where a number of small ponds were sampled from the same location, we grouped ponds of a given type as a single site (Bouchard et al., 2015). We divided sampling sites into six ecosystem categories: (1) lakes and ponds (hereafter lakes), (2) rivers and floodplains (hereafter rivers), (3) bogs, (4) fens, (5) swamps and marshes, and (6) rice paddies. Most data (seven of eight sites) in the rivers category are from floodplain lake or delta environments. Swamps and marshes were combined as one category because of a small number of sites and because there is no clear indication of biogeochemical differences between these ecosystems. To make these categorizations we relied on site descriptions in the data source publications. We also analyzed data in two larger environment types, inland waters (lakes and rivers) and wetlands (bogs, fens, swamps and marshes, and rice paddies), which correspond to two flux categories (freshwaters and natural wetlands) documented by Saunois et al. (2020). While rice paddies are an anthropogenic ecosystem; they are wetlands where microbial methanogenesis occurs under generally similar conditions to natural wetlands, and therefore we included them as wetlands in our analysis. In some cases the type of wetland was not specified. We did not differentiate between ombrotrophic and minerotrophic peatlands since most publications did not specify this difference, although it has been inferred to be important for δ13C-CH4 distributions (Hornibrook, 2009). For studies of bogs and fens that sampled by soil depth we have only included sample measurements from the upper 50 cm. This is based on the observation of large-scale isotopic variability with soil depth in these ecosystems (Hornibrook et al., 1997; Waldron et al., 1999b) and the observation that shallow peat is typically the dominant source of atmospheric emissions (Waldron et al., 1999b; Bowes and Hornibrook, 2006; Shoemaker et al., 2012), which is our primary focus in this study. Other wetland ecosystems were not sampled by soil depth.
We also categorized samples by the form in which CH4 was sampled, differentiating between dissolved CH4 and CH4 emitted through diffusive fluxes, which we group as dissolved CH4, and gas-phase samples, including bubbles sampled either by disturbing sediments or by collecting natural ebullition fluxes. In some cases the sampling method or type of sample was not specified, or samples were a mix of both categories, which we did not attempt to differentiate.
Where possible (78 % of sites), δ2H–CH4 and δ13C-CH4 values, as well as δ13C–CO2 and δ2H–H2O, were gathered from data files or published tables. In a number of publications, representing 22 % of sites, data were only available graphically. For these studies we used WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/, last access: 15 August 2017) software to extract data for these parameters. Previous studies have shown that user errors from WebPlotDigitizer are typically small, with 90 % of user-generated data within 1 % of the actual value (Drevon et al., 2017). Based on this, we estimate a typical error for δ2H–CH4 data of less than 3 ‰. Studies where data were derived from graphs are identified in Supplement Table S1 (Douglas et al., 2020b).
2.2.3 Estimates of δ2H–H2O and its effects on δ2H–CH4
To estimate δ2H–H2O for sites where it was not measured, we relied on estimates of the isotopic composition of precipitation (δ2Hp), derived from the Online Isotopes in Precipitation Calculator v.3.1 (OIPC3.1; http://www.waterisotopes.org, last access: 10 December 2020; Bowen and Wilkinson, 2002; Bowen and Revenaugh, 2003; Bowen et al., 2005). Inputs for δ2Hp estimates are latitude, longitude, and elevation. We estimated elevation for each site surface elevation at the site's geographic coordinates reported by Google Earth. We tabulated estimates of both annual and growing season precipitation-amount-weighted δ2Hp, where the growing season is defined as months with a mean temperature greater than 0 ∘C. We then analysed whether annual or growing season δ2Hp is a better estimate of environmental δ2H–H2O for both wetlands and inland waters by comparing these values with measured δ2H–H2O for sites with measurements (see Sect. 3.2). Based on this analysis, we then identified a “best-estimate” δ2H–H2O value for each site, using an approach similar to that of Waldron et al. (1999a). Namely, we apply measured δ2H–H2O where available and estimates based on the regression analyses detailed in Sect. 3.2 for sites without measurements.
To account for the effects of δ2H–H2O on δ2H–CH4, we introduce the term δ2H–CH4,W0, which is the estimated δ2H–CH4 of a sample if it had formed in an environment where δ2H–H2O = 0 ‰. This is defined by the equation
where δ2H–H2O is the best-estimate value for each site described above, and b is the slope of the regression relationship of δ2H–H2O vs. δ2H–CH4 for the entire dataset, as reported in Sect. 3.3. We also performed the same calculation separately for the subset of sites with measured δ2H–H2O. We analyze δ2H–CH4,W0 instead of αH because, as discussed in Sect. 3.3, the global relationship between δ2Hp vs. δ2H–CH4 does not correspond to a constant value of αH, and therefore deviations from the global empirical relationship are more clearly expressed as a residual as opposed to a fractionation factor.
2.3 Statistical analyses
For all statistical analyses we use site-level mean isotopic values. This avoids biasing our analyses towards sites with a large number of measurements, since there are large differences in the number of samples analyzed per site (n ranges from 66 to 1). To calculate αC we used average δ13C-CH4 and δ13C–CO2 at a given site. This approach entails some additional uncertainty in this variable but was necessary because at many sites these measurements were not made on the same samples.
We perform a set of linear regression analyses δ2H–CH4 against other isotopic variables, in addition to latitude. All statistical analyses were performed in MATLAB. We considered p<0.05 to be the threshold for identifying significant regression relationships. We chose to perform unweighted regression, as opposed to weighted regression based on the standard error of sample measurements, for two reasons. First, a small number of sites with a large number of measurements, and therefore small standard error, had a disproportionate effect on weighted regression results. Second, in environmental research unweighted regression is frequently less biased than weighted regression (Fletcher and Dixon, 2012). Based on a test proposed by Fletcher and Dixon (2012), unweighted regression is appropriate for this dataset. We used analysis of covariance to test for significant differences between regression relationships.
To compare isotopic data (δ2H–CH4 and δ13C-CH4) between groups (i.e. latitudinal bands, ecosystem types, sample types), we used non-parametric statistical tests to test whether the groups were from different distributions. We used non-parametric tests because some sample groups were not normally distributed, as determined by a Shapiro–Wilk test (Shapiro and Wilk, 1965). For comparing differences between the distributions of two groups we used the Mann–Whitney U test (Mann and Whitney, 1947), whereas when comparing differences between the distributions of more than two groups we used the Kruskal–Wallis H test (Kruskal and Wallis, 1952), combined with Dunn's test to compare specific sample group pairs (Dunn, 1964). We considered p<0.05 to be the threshold for identifying groups with significantly different distributions.
When comparing δ13C-CH4 by latitude and ecosystem, we combined the data from this study with additional data from Sherwood et al. (2017) (32 additional sites) where δ2H–CH4 was not measured to make our dataset as representative as possible. To our knowledge this combined dataset is the largest available compiled dataset of freshwater δ13C-CH4, although there are many more δ13C-CH4 measurements that have not yet been aggregated. We did not include these additional data when analysing differences by sample type, as sample type was not specified in the dataset of Sherwood et al. (2017).
2.4 Estimation of global atmospheric CH4δ2H and δ13C source values
To better understand how latitudinal differences in wetland isotopic source signatures influence atmospheric δ2H–CH4 and δ13C-CH4, we calculated a bottom-up mixing model of δ2H–CH4 and δ13C-CH4. For this calculation we ascribed all CH4 sources a flux (derived from Saunois et al., 2020; see details below) and a δ2H and δ13C value, and we calculated the global atmospheric source value using an isotopic mixing model. Because of non-linearity when calculating mixtures using δ2H values, we performed the mixing equation using isotopic ratios (see Sect. 2.1). The mixing equation is as follows:
where fn is the fractional flux for each source term (i.e. the ratio of the source flux to total flux), and Rn is the isotope ratio for each source term.
Values for the flux, δ2H, and δ13C applied for each source term are shown in Table 1. We used bottom-up source fluxes from Saunois et al. (2020) for the period 2008–2017. For categories other than wetlands, inland waters, and rice paddies, we used global fluxes and isotope values, since geographically resolved isotopic source signature estimates are not available. For these sources we used δ2H and δ13C values published by Sherwood et al. (2017), using the mean value for each source term. For wetlands, inland waters, and rice paddies, we used geographically resolved (60–90∘ N, 30–60∘ N, 90∘ S–30∘ N) fluxes derived from Saunois et al. (2019) for the period 2008–2017 and mean δ2H–CH4 for these latitudinal bands from this study.
Table 1Estimates of source-specific fluxes, δ2H–CH4, and δ13C-CH4 and their uncertainties, used in mixing models and Monte Carlo analyses.
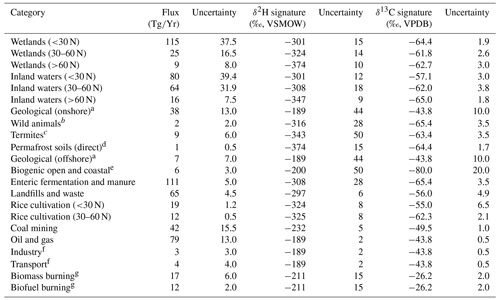
a No specific isotopic measurements in the database (Sherwood et al., 2017). We applied the mean isotopic values for oil and gas and applied the standard deviation of for oil and gas as the uncertainty. b No specific isotopic measurements in database (Sherwood et al., 2017). We used the isotopic values and uncertainties from livestock. c Only one δ2H measurement in database (Sherwood et al., 2017). We applied 50 ‰ as a conservative uncertainty estimate. d No specific isotopic measurement in database (Sherwood et al., 2017). We used the isotopic values and uncertainties for high-latitude wetlands. e No specific isotopic measurements in database (Sherwood et al., 2017). We applied approximate isotopic values based on Whiticar (1999) and conservatively large uncertainty estimates. f No specific isotopic measurements in database (Sherwood et al., 2017). We used the isotopic values and uncertainties for oil and gas. g We applied all isotopic measurements of biomass burning to both the biomass burning and biofuel burning categories. We did not correct for the relative proportion of C3 and C4 plant combustion sources (see Sect. 2.4).
To calculate mean δ13C-CH4 from wetlands, inland waters, and rice paddies for different latitudinal bands, we combined the data from this study along with additional data from Sherwood et al. (2017) (32 additional sites) to make our estimated source signatures as representative as possible. To our knowledge this combined dataset is the largest available compiled dataset of freshwater δ13C-CH4 (see Sect. 2.3). Sites dominated by C4 plants are notably underrepresented in this combined dataset. In addition, the biomass burning dataset of Sherwood e al. (2017) contains very few data from C4 plant combustion. We performed a separate estimate of global source δ13C-CH4 that attempted to correct for these likely biases by making two adjustments: (1) using the estimated low-latitude wetland δ13C-CH4 signature of Ganesan et al. (2018) (−56.7 ‰), which takes into account the predicted spatial distribution of C4-plant-dominated wetlands and (2) using the biomass burning δ13C-CH4 signature of Schwietzke et al. (2016) (−22.3 ‰), which is weighted by the predicted contribution from C4 plant combustion. We did not attempt to take into account δ13C-CH4 from ruminants feeding on C4 plants. For the C4-plant-corrected δ13C-CH4 estimate, we applied the same uncertainties that are reported in Table 1.
Since fluxes from other natural sources are not differentiated for the period 2008–2017, we calculated the proportional contribution of each category of other natural sources for the period 2000–2009 (Saunois et al., 2020), and we applied this to the total flux from other natural sources for 2008–2017. Inland waters and rice paddies do not have geographically resolved fluxes reported in Saunois et al. (2020). Therefore, we calculated the proportion of other natural sources attributed to inland waters from 2000–2009 (71 %), and we applied this proportion to the geographically resolved fluxes of other natural sources. Similarly, we calculated the proportion of agricultural and waste sources attributed to rice agriculture from 2008–2017 (15 %), and we applied this to the geographically resolved fluxes of agricultural and waste fluxes.
To estimate uncertainty in the modelled total source δ2H and δ13C values, we conducted Monte Carlo analyses (Thompson et al., 1992). We first estimated the uncertainty for each flux, δ2H, and δ13C term. Flux uncertainties were defined as one-half of the range of estimates provided by Saunois et al. (2020). For sources where fluxes were calculated as a proportion of a larger flux, we applied the same proportional calculation to uncertainty estimates. In cases where one-half of the range of reported studies was larger than the flux estimate, we set the uncertainty to be equal to the flux estimate to avoid negative fluxes in the mixing model. Isotopic source signal uncertainties were defined as the 95 % confidence interval of the mean value for a given source category. For some sources there are insufficient data to calculate a 95 % confidence interval, and we applied a conservative estimate of uncertainty for these sources, as detailed in Table 1. Confidence intervals for fossil fuel isotopic source signatures do not take into account variation in emissions fluxes and isotopic values between regions or resource types (i.e. conventional vs. unconventional reservoirs). This variation is difficult to quantify with available datasets but could imply additional uncertainty in global source signatures. We recalculated the δ2H and δ13C mixing models 10 000 times, each time sampling inputs from the uncertainty distribution for each variable. We assumed all uncertainties were normally distributed. We interpret the 2σ standard deviation of the resulting Monte Carlo distributions as an estimate of the uncertainty of our total atmospheric CH4 source isotopic values. To examine how the Monte Carlo analyses were specifically influenced by uncertainty in isotopic source signatures vs. flux estimates, we conducted sensitivity tests where we set the uncertainty in either isotopic source signatures or flux estimates to zero. We also used the mixing model and Monte Carlo method to estimate the mean flux-weighted freshwater δ2H–CH4 and δ13C-CH4, using only the inputs for freshwater environments (wetlands, inland waters, and rice cultivation) from Table 1 (see Sect. 3.5).
3.1 Dataset distribution
The dataset is primarily concentrated in the Northern Hemisphere (Fig. 1a) but is distributed across a wide range of latitudes between 3∘ S and 73∘ N (Fig. 1c). The majority of sampled sites are from North America (Fig. 1b), but there are numerous sites from Eurasia. A much smaller number of sites are from South America and Africa. We define three latitudinal bands for describing geographic trends: low latitudes (3∘ S to 30∘ N), mid-latitudes (30 to 60∘ N), and high-latitudes (60 to 90∘ N). This definition was used primarily because it corresponds with a commonly applied geographic classification of CH4 fluxes (Saunois et al., 2020).
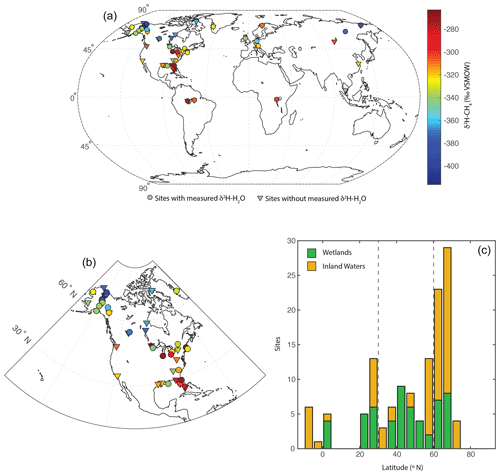
Figure 1Distribution of sites shown (a) on a global map, with site mean CH4-δ2H values indicated in relation to a colour bar. Sites with and without measured δ2H–H2O are differentiated: (b) on a map of North America and (c) as a histogram of sites by latitude, differentiated between wetlands and inland waters. Dashed lines in (c) indicate divisions between low-latitude, mid-latitude, and high-latitude sites.
A total of 74 of 129 sites are classified as inland waters, primarily lakes (n=66), with a smaller number from rivers (n=8). To our knowledge, all of the inland water sites are natural ecosystems and do not include reservoirs. A total of 55 sites are classified as wetlands, including 16 bogs, 14 swamps and marshes, 12 fens, and 8 rice paddies. For the majority of sites (n=84) gas samples were measured, whereas studies at 36 sites measured dissolved CH4 or diffusive fluxes.
3.2 Use of δ2Hp as an estimator for freshwater δ2H–H2O
As discussed in Sect. 2.2.3, we regressed annual and growing season δ2Hp against measured δ2H–H2O to determine which is a better estimator for sites where δ2H–H2O is not measured. We performed this analysis separately for wetland and inland water environments because these broad environmental categories have distinct hydrological characteristics. For all regression analyses we found strong correlations, with R2 values between 0.82 and 0.88 (Fig. 2). For wetlands, regression using annual δ2Hp produces a slightly better fit and also produces a slope within uncertainty of 1 (Fig. 2a), suggesting that variation in annual δ2Hp scales proportionately with variation in measured δ2H–H2O. However, the intercept of this relationship was significantly greater than 0 (19 ± 9 ‰). We interpret this intercept as indicating that evaporative isotopic enrichment is generally important in controlling δ2H–H2O in wetlands. A slope slightly greater than 1 is also consistent with evaporative enrichment, since greater evaporation rates would be expected in low-latitude environments with higher δ2H–H2O. These results are consistent with detailed studies of wetland isotope hydrology that indicate a major contribution from groundwater, with highly dampened seasonal variability relative to precipitation, but also indicate evaporative enrichment of water isotopes in shallow soil water (Sprenger et al., 2017; David et al., 2018).
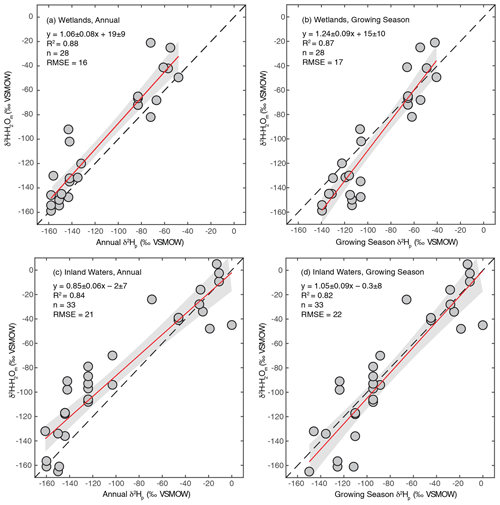
Figure 2Scatter plots of annual or growing season δ2Hp vs. measured δ2H–H2O for wetland (a, b) and inland water (c, d) sites. The red lines indicate the best fit, with a 95 % confidence interval (grey envelopes), and the dashed black lines are the 1:1 relationship.
For inland waters, regression with growing season δ2Hp produces a relationship that is within error of the 1:1 line (Fig. 2c), in contrast to annual δ2Hp, which produces a flatter slope (Fig. 2d). We infer that seasonal differences in δ2Hp are important in determining δ2H–H2O in the inland water environments analyzed, especially at high latitudes, implying that these environments generally have water residence times on subannual timescales. This finding is generally consistent with evidence for seasonal variation in lake water isotopic compositions that is dependent on lake water residence times (Tyler et al., 2007; Jonsson et al., 2009). Lake water residence times vary widely, primarily as a function of lake size, but isotopic data imply that small lakes have water residence times of less than a year (Brooks et al., 2014), resulting in seasonal isotopic variability (Jonsson et al., 2009). Isotopic enrichment of lake water is highly variable but is typically minor in humid and high-latitude regions (Jonsson et al., 2009; Brooks et al., 2014), which characterizes most of our study sites.
Based on these results we combine measured and estimated δ2H–H2O to determine a best-estimate value for each site, an approach similar to that of Waldron et al. (1999a). For sites with measured δ2H–H2O values we use that value. For inland water sites without measured δ2H–H2O we use modelled growing season δ2Hp since the regression of this against measured δ2H–H2O is indistinguishable from the 1:1 line (Fig. 2d). For wetland sites without measured δ2H–H2O, we estimate δ2H–H2O using the regression relationship with annual precipitation δ2H–H2O shown in Fig. 2a. The root-mean-square errors (RMSE) of these relationships (16 ‰ for wetlands, 22 ‰ for inland waters) provide an estimate of the uncertainty associated with estimating δ2H–H2O using δ2Hp. Given the uncertainty associated with estimating δ2H–H2O using δ2Hp, for all analyses presented below that depend on δ2H–H2O values we also analyse the dataset only including sites with measured δ2H–H2O.
3.3 Relationship between δ2H–H2O and δ2H–CH4
We carried out regression analyses of δ2H–H2O vs. δ2H–CH4, both using best-estimate δ2H–H2O as described in Sect. 3.2 (Fig. 3a) and only including sites with measured δ2H–H2O (Fig. 3b). In addition we analysed the relationship for all sites using annual (Fig. 3c) and growing season (Fig. 3d) δ2Hp. Identifying the relationship between modelled δ2Hp and δ2H–CH4 is of value because this could be used to create gridded global predictions of δ2H–CH4 based on gridded datasets of δ2Hp (Bowen and Revenaugh, 2003), as well as to predict the distribution of δ2H–CH4 under past and future global climates using isotope enabled Earth system models (Zhu et al., 2017).
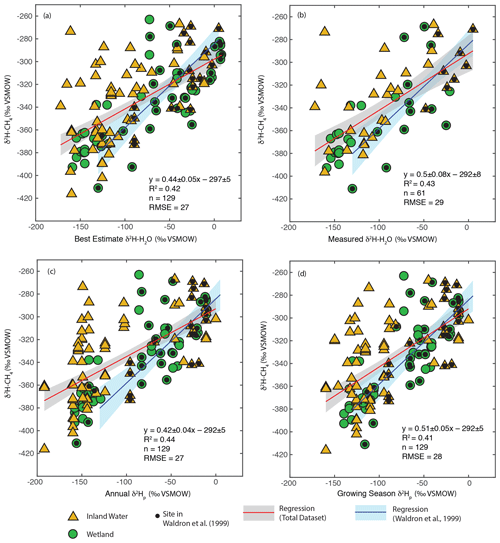
Figure 3Scatter plots of δ2H–CH4 vs. (a) best-estimate δ2H–H2O, (b) measured δ2H–H2O, (c) annual δ2Hp, and (d) growing season δ2Hp. Sites that were included in the analysis of Waldron et al. (1999a) are indicated. The regression relationship for the total dataset in each plot is shown by the red line, with its 95 % confidence interval (grey envelope). The regression relationship and confidence interval for the dataset of Waldron et al. (1999a) are shown in blue. Uncertainties for reported regression relationships are standard errors.
δ2H–CH4 is significantly positively correlated with δ2H–H2O when using all four methods of estimating δ2H–H2O (Fig. 3, Supplement Table S2). This is the case when analysing all sites together, as well as when analysing wetlands and inland waters separately (Douglas et al., 2020b, Supplement Table S2, Fig. 4). There is no significant difference in regression relationships, based on analysis of covariance, when δ2H–CH4 is regressed against best-estimate δ2H–H2O, measured δ2H–H2O, or modelled δ2Hp, nor is there a major difference in R2 values or RMSE (Douglas et al., 2020b, Supplement Table S2). Regression with wetland sites consistently results in a higher R2 values and lower RMSE than regression with inland water sites.
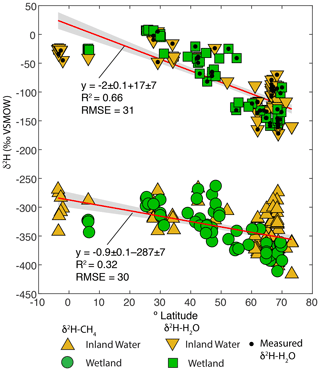
Figure 4Scatter plots of δ2H–CH4 and best-estimate δ2H–H2O, vs. latitude (∘ N). Sites with measured δ2H–H2O are indicated. Envelopes indicate 95 % confidence intervals for regression lines.
Given the similar results when regressing with estimated or measured δ2H–H2O, we infer that using either the “best-estimate” δ2H–H2O or modelled δ2Hp, instead of measured δ2H–H2O, to predict δ2H–CH4 does not result in substantial additional error. This implies that isotope-enabled Earth system models (ESMs) could be used to predict the distribution of freshwater δ2H–CH4 under past and future climates based on modelled δ2Hp, although the substantial scatter in Fig. 3c and d should be taken into account. The Southern Hemisphere is highly underrepresented in the δ2H–CH4 dataset. However, the mechanisms linking δ2H–CH4 with δ2H–H2O should not differ in the Southern Hemisphere, and we argue that the relationships observed in this study are suitable to predict Southern Hemisphere freshwater δ2H–CH4. The choice of predicting δ2H–CH4 using growing-season vs. annual precipitation δ2Hp could be important, with steeper slopes overall when regressing against growing season δ2Hp. Based on our analysis in Sect. 3.2, we suggest that annual δ2Hp may be more appropriate for estimating wetland δ2H–CH4, while growing season δ2Hp may be more appropriate for estimating inland water δ2H–CH4. Forthcoming research will combine gridded datasets of wetland distribution (Ganesan et al., 2018), modelled annual δ2Hp (Bowen and Revenaugh, 2003), and the regression relationships from this study to predict spatially resolved wetland δ2H–CH4 at a global scale (Stell et al., 2021).
Overall, our results are broadly consistent with those of Waldron et al. (1999a), and confirm the finding of that study that δ2H–H2O is the predominant predictor of global variation in δ2H–CH4. All of the regression slopes produced using our dataset are flatter than the regression relationship found by Waldron et al. (1999a) using a smaller dataset (0.68 ± 0.1), although the slopes are not significantly different based on analysis of covariance. Based on this result we infer that the true global relationship is likely flatter than that estimated by Waldron et al. (1999a). The difference between the regression relationships reported here and that of Waldron et al. (1999a) is largely a result of a much greater number of samples from the high latitudes (Fig. 1c), where δ2H–H2O values are typically lower. The small number of high-latitude sites sampled by Waldron et al. (1999a) are skewed towards the low end of the high-latitude δ2H–CH4 data from this study (Fig. 3). A similarly flatter slope (0.54 ± 0.05) was found by Chanton et al. (2006) when combining a dataset of δ2H–CH4 from Alaskan wetlands, which are included in this study, with the dataset of Waldron et al. (1999a). Based on the range of R2 values shown in Fig. 3, we estimate that δ2H–H2O explains approximately 42 % of variability in δ2H–CH4, implying substantial residual variability, with greater residual variability for inland water sites than for wetlands (Douglas et al., 2020b, Supplement Table S2).
Given that δ2H–H2O is strongly influenced by latitude we examined whether δ2H–CH4 is also significantly correlated with latitude. There is indeed a significant negative relationship between latitude and δ2H–CH4, indicating an approximate decrease of 0.9 ‰ per degree latitude (Fig. 4). The slope is significantly flatter than that for latitude vs. δ2H–H2O in this dataset (−2 ‰ per degree latitude), which is consistent with the inferred slope for δ2H–H2O vs. δ2H–CH4 (0.44 to 0.5). There is greater scatter in δ2H–CH4 at higher latitudes, especially for inland waters, but it is unclear whether this is simply a result of a larger sample set or of differences in the underlying processes controlling δ2H–CH4. We discuss latitudinal differences in δ2H–CH4 in further detail in Sect. 3.5.
Comparison of δ2H–H2O vs. δ2H–CH4 relationships between environmental and experimental studies
To further understand the processes controlling the observed freshwater δ2H–H2O vs. δ2H–CH4 relationships, we compared them to results from pure culture and incubation experiments across a wide range of δ2H–H2O values (Fig. 5), focusing on regression against best-estimate δ2H–H2O. The regression slopes for both wetlands and inland waters (0.5 and 0.42) are within error of the in vitro relationship compiled by Waldron et al. (1999a) (0.44), based on laboratory incubations from three separate studies (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998). The intercept for the wetland and inland water regressions is higher than that for the in vitro relationship, although only the difference with inland waters is significant. In contrast, the regression slope for pure-culture acetoclastic methanogenesis experiments is much flatter (0.18 to 0.2) (Valentine et al., 2004b; Gruen et al., 2018), consistent with the prediction that one hydrogen atom is exchanged between water and the acetate methyl group during CH4 formation (Pine and Barker, 1956; Whiticar, 1999). The large difference in intercept between the two acetate pure culture datasets is likely a function of differences in the δ2H of acetate between the experiments but could also be influenced by differences in kinetic isotope effects (Valentine et al., 2004b).
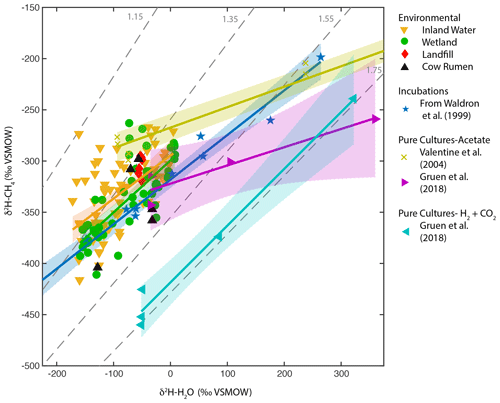
Figure 5Scatter plots of δ2H–CH4 vs. δ2H–H2O for wetlands, inland waters, landfills, and cow rumen, compared with incubation and pure-culture experiments. Regression lines and confidence intervals corresponding to each dataset (except landfills and cow rumen) are shown. Dashed grey lines indicate constant values of αH. Regression line statistics are listed in Supplement Table S2. Plotted δ2H–H2O values are best-estimate values for wetlands and inland waters, measured values for culture experiments, and a combination of measured values and annual δ2Hp for landfills and cow rumen (see Supplement Table S3 for more details, Douglas et al., 2020b).
Pure-culture hydrogenotrophic methanogenesis experiments (Gruen et al., 2018) yield a regression slope that is consistent with a constant αH value, although αH can clearly vary depending on experimental or environmental conditions (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). The wetland, inland water, and in vitro regression relationships are not consistent with a constant value of αH (Fig. 5). Our comparison supports previous inferences that the in vitro line of Waldron et al. (1999a) provides a good estimate of the slope of environmental δ2H–H2O vs. δ2H–CH4 relationships. This slope is likely controlled by the relative proportion of acetoclastic and hydrogenotrophic methanogenesis, the net kinetic isotope effect associated with these two methanogenic pathways, and variance in δ2H of acetate (Waldron et al., 1998, 1999a; Valentine et al., 2004a), but the relative importance of these variables remains uncertain.
In particular, the δ2H of acetate methyl hydrogen is probably influenced by environmental δ2H–H2O and therefore likely varies geographically as a function of δ2Hp, as originally hypothesized by Waldron et al. (1999a). To our knowledge there are no measurements of acetate or acetate-methyl δ2H from natural environments with which to test this hypothesis. In general, variability in the δ2H of environmental organic molecules in lake sediments and wetlands, including fatty acids and cellulose, is largely controlled by δ2H–H2O (Huang et al., 2002; Sachse et al., 2012; Mora and Zanazzi, 2017), albeit with widely varying fractionation factors. The δ2H of methoxyl groups in plants has also been shown to vary as a function of δ2H–H2O (Vigano et al., 2010). Furthermore, culture experiments with acetogenic bacteria imply that there is rapid isotopic exchange between H2 and H2O during chemoautotrophic acetogenesis (Valentine et al., 2004a), implying that the δ2H of chemoautotrophic acetate is also partially controlled by environmental δ2H–H2O. Incubation experiments, such as those included in the in vitro line (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998), probably contain acetate-δ2H that varies as a function of ambient δ2H–H2O, given that the acetate in these incubation experiments was actively produced by fermentation and/or acetogenesis during the course of the experiment. This differs from pure cultures of methanogens, where acetate is provided in the culture medium and therefore does not vary in its δ2H value (Valentine et al., 2004b; Gruen et al., 2018).
3.4 Relationship of δ2H–CH4 with δ13C-CH4, δ13C–CO2, and αC
As shown in Fig. 3, there is a large amount of residual variability in δ2H–CH4 that is not explained by δ2H–H2O. Several biogeochemical variables have been proposed to influence freshwater δ2H–CH4 independently of δ2H–H2O, including the predominant biochemical pathway of methanogenesis (Whiticar et al., 1986; Whiticar, 1999; Chanton et al., 2006), the extent of methane oxidation (Happell et al., 1994; Waldron et al., 1999a; Whiticar, 1999; Cadieux et al., 2016), isotopic fractionation resulting from diffusive gas transport (Waldron et al., 1999a; Chanton, 2005), and differences in the thermodynamic favorability or reversibility of methanogenesis (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). These variables are also predicted to cause differences in δ13C-CH4, δ13C–CO2, and αC. Therefore, we analysed co-variation between δ2H–CH4,W0 (see definition in Sect. 2.2.3) and δ13C-CH4, δ13C–CO2, and αC to see whether it could partially explain the residual variability in δ2H–CH4 (Fig. 6).
In order to facilitate interpretation of isotopic co-variation, we estimated approximate vectors of predicted isotopic co-variation for the four variables being considered (Fig. 6). We emphasize that these vectors are uncertain, and while they can be considered indicators for the sign of the slope of co-variation and the relative magnitude of expected isotopic variability, they are not precise representations of the slope or intercept of isotopic co-variation. In reality, isotopic co-variance associated with these processes likely varies depending on specific environmental conditions, although the sign of co-variance should be consistent. The starting point for the vectors is arbitrarily set to typical isotopic values for inferred acetoclastic methanogenesis in freshwater systems (Whiticar, 1999). We based the vectors for differences in the dominant methanogenic pathway and methane oxidation in Figs. 8, 5, and 10 in Whiticar (1999). These figures are widely applied to interpret environmental isotopic data related to CH4 cycling. However, we note that both environmental and experimental research has questioned whether differences in the dominant methanogenic pathway have an influence on δ2H–CH4 (Waldron et al., 1998, 1999a). Differences in δ2H–CH4 between hydrogenotrophic and acetoclastic methanogenesis are likely highly dependent on both the δ2H of acetate and the carbon and hydrogen kinetic isotope effects for both methanogenic pathways, both of which are poorly constrained in natural environments and are likely to vary between sites (see Sect. 3.3). We did not differentiate between anaerobic and aerobic methane oxidation, and the vectors shown are similar to experimental results for aerobic methane oxidation (Wang et al., 2016).
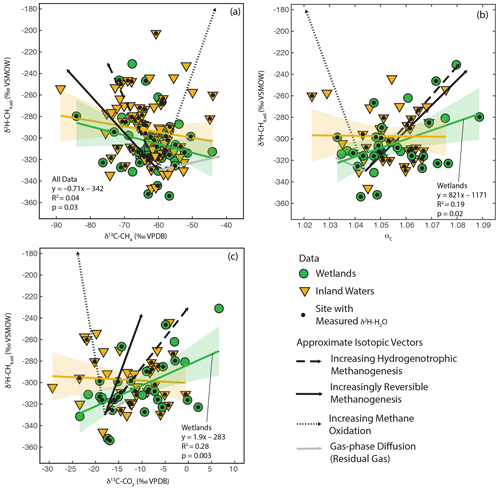
Figure 6Scatter plots of δ2H–CH4,w0 vs. (a) δ13C-CH4, (b) αc, and (c) δ13C–CO2. Approximate vectors for isotopic co-variation related to four biogeochemical variables are shown. See details in Sect. 3.4 and the Supplement. Regression relationships are shown for wetland and inland water sites, with envelopes indicating 95 % confidence intervals. Regression statistics are shown here for relationships with significant correlations (p<0.05). All regression statistics are detailed in Supplement Table S4 (Douglas et al., 2020b).
The vector for isotopic fractionation related to gas-phase diffusion is based on the calculations of Chanton (2005) and indicates isotopic change for residual gas following a diffusive loss. Gas–liquid diffusion is predicted to have a much smaller isotopic effect (Chanton, 2005). The vector for differences in enzymatic reversibility is based on experiments where CH4 and CO2 isotopic compositions were measured together with changes in methane production rate or Gibbs free energy (Valentine et al., 2004b; Penning et al., 2005). We note that these studies did not measure δ2H–CH4 in the same experiments as δ13C-CH4 or δ13C–CO2, implying large uncertainty in the co-variance vectors. More detail on the estimated vectors is provided in the Supplement.
We observe significant positive correlations between δ2H–CH4,W0, calculated using best estimate δ2H–H2O, and both δ13C–CO2 and αC for wetland sites (Douglas et al., 2020b, Fig. 6b, c; Supplement Table S4). We do not observe a significant correlation between these variables for inland water sites or for the dataset as a whole. We also observe a weak but significant negative correlation between δ2H–CH4,W0 and δ13C-CH4 for all sites but not for data disaggregated into wetlands and inland water categories (Fig. 6a). The correlations shown in Fig. 6 should be interpreted with caution, since repeating this analysis only using sites with measured δ2H–H2O does not result in any significant correlations (Douglas et al., 2020b, Supplement Table S4). It is unclear whether this different result when using best-estimate or measured δ2H–H2O represents a bias related to estimating δ2H–H2O using δ2Hp or is an effect of the much smaller sample size for sites with δ2H–H2O measurements. If accurate, the observed significant positive correlations in Fig. 6b and c suggest that residual variability in δ2H–CH4 in wetlands is more strongly controlled by biogeochemical variables related to methanogenesis, namely differences in methanogenic pathway or thermodynamic favorability, than post-production processes such as diffusive transport and CH4 oxidation. For inland water sites our analysis suggests that no single biogeochemical variable has a clear effect in controlling residual variability in δ2H–CH4.
Overall, our results are not consistent with arguments that residual variability in freshwater δ2H–CH4 is dominantly controlled by either differences in methanogenic pathway (Chanton et al., 2006) or post-production processes (Waldron et al., 1999a). Instead they highlight the combined influence of a complex set of variables and processes that are difficult to disentangle on an inter-site basis using δ13C measurements alone. It is also important to note the likely importance of variables that could influence δ13C-CH4 or δ13C–CO2 but not necessarily affect δ2H–CH4, including variance in the δ13C of soil or sediment organic matter (Conrad et al., 2011; Ganesan et al., 2018), diverse metabolic and environmental sources and sinks of CO2 in aquatic environments, and Rayleigh fractionation associated with CH4 carbon substrate depletion (Whiticar, 1999). Finally, the possible role of other carbon substrates, such as methanol, in CH4 production could be important in controlling isotopic co-variation. Culture experiments suggest that CH4 produced from methanol has low δ13C and δ2H values relative to other pathways (Krzycki et al., 1987; Penger et al., 2012; Gruen et al., 2018), although the importance of this difference in environmental CH4 is unclear.
Further research examining intra-site isotopic co-variation, which largely avoids complications associated with estimating δ2H–H2O, would help to more clearly resolve the relative importance of these processes and how they vary between environments. Expanded research using methyl fluoride to inhibit acetoclastic methanogenesis (Penning et al., 2005; Penning and Conrad, 2007; Conrad et al., 2011), with a particular focus on δ2H–CH4 measurements, would also help to clarify the importance of methanogenic pathway on isotopic co-variation. Finally, an expanded application of measurements of clumped isotopes, which have distinctive patterns of variation related to these processes (Douglas et al., 2016, 2017; Young et al., 2017; Douglas et al., 2020a), would also be of value in determining their relative importance in controlling δ2H–CH4 values in freshwater environments.
3.5 Differences in δ2H–CH4 and δ13C-CH4 by latitude
When analysing all sites together, we found a significant difference in the distribution of δ2H–CH4 between high-latitude sites (median: −351 ‰) and both low- (median: −298 ‰) and mid-latitude sites (median: −320 ‰) (Fig. 7a). However, we did not find a significant difference in the distribution of low- and mid-latitude sites. Similar differences were found when the data were disaggregated into wetland and inland water sites. We also found that the distribution of δ13C-CH4 for low-latitude sites (median: −61.6 ‰) was significantly higher than for high-latitude sites (median: −63.0 ‰) but that mid-latitude sites (median: −60.3 ‰) were not significantly different from the other two latitudinal zones (Fig. 7b). The observed difference by latitudinal zone in δ13C-CH4 appears to be driven primarily by latitudinal differences between inland water sites, where a similar pattern is found. In wetland sites we found no significant differences in the distribution of δ13C-CH4 by latitude.
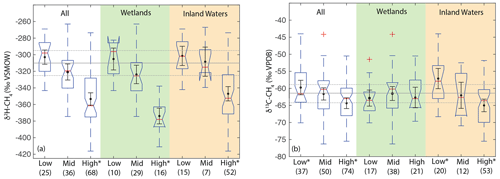
Figure 7Boxplots of (a) δ2H–CH4 and (b) δ13C-CH4 for sites differentiated by latitude, for all data, wetlands, and inland waters. Numbers in parentheses indicate the number of sites for each category. Red lines indicate medians, boxes indicate 25th and 75th percentiles, whiskers indicate 95th and 5th percentiles, and outliers are shown as red crosses. Notches indicate the 95 % confidence intervals of the median value; where notches overlap the edges of the box this indicates the median confidence interval exceeds the 75th or 25th percentile. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the estimated flux-weighted mean values for global freshwater CH4, and dashed lines indicate the 95 % confidence interval of this value. Asterisks in (a) indicate that high-latitude sites have significantly different distributions from other latitudinal bands. Asterisks in (b) indicate groups that have significantly different distributions from one another, within a specific environmental category. Two extremely low outliers (<−80 ‰; high-latitude wetland and inland water) are not shown in (b).
Estimates of flux-weighted mean freshwater δ2H–CH4 and δ13C-CH4, calculated using the Monte Carlo approach described in Sect. 2.4, are −310 ± 15 ‰ (Fig. 7a) and −61.5 ± 3 ‰ (Fig. 7b) respectively. Flux-weighted mean values for natural wetlands (not including inland waters or rice paddies) are −310 ± 25 ‰ for δ2H–CH4 and −63.9 ± 3.3 ‰ for δ13C-CH4. Flux-weighted mean values for inland waters are −309 ± 31 ‰ for δ2H–CH4 and −60 ± 5.7 ‰ for δ13C-CH4. As discussed in Sect. 2.4 there are limited data in our dataset or that of Sherwood et al. (2017) from C4-plant-dominated wetlands, and therefore our low-latitude and flux-weighted mean δ13C-CH4 values for wetlands are probably biased towards low values.
Differences in δ2H–CH4 by latitude have the potential to aid in geographic discrimination of freshwater methane sources, both because it is based on a clear mechanistic linkage with δ2H–H2O (Figs. 3 and 4) and because geographic variation in δ2H–H2O is relatively well understood (Bowen and Revenaugh, 2003; Bowen et al., 2005). However, recent studies of atmospheric δ2H–CH4 variation have typically not accounted for geographic variation in source signals. As an example, Rice et al. (2016) apply a constant δ2H–CH4 of −322 ‰ for both low-latitude (0–30∘ N) and high-latitude (30–90∘ N) wetland emissions. Based on our dataset this estimate is an inaccurate representation of wetland δ2H–CH4 for either 0–30∘ N (mean: −305 ± 13 ‰) or 30–90∘ N (mean: −345 ± 11 ‰). Studies of ice core measurements have more frequently differentiated freshwater δ2H–CH4 values as a function of latitude. For example, Bock et al., (2010) differentiated δ2H–CH4 between tropical (−320 ‰) and boreal (−370 ‰) wetlands. This tropical wetland signature is significantly lower than our estimate of low-latitude wetland δ2H–CH4, although the boreal wetland signature is similar to our mean value for high-latitude wetlands (−374 ± 10 ‰). Overall, our results imply that accounting for latitudinal variation in freshwater δ2H–CH4, along with accurate latitudinal flux estimates, is important for developing accurate estimates of global freshwater δ2H–CH4 source signatures.
Our analysis indicates significant differences in the distribution of freshwater δ13C-CH4 between the low- and high-latitudes, but mid-latitude sites cannot be differentiated. Furthermore our results do not indicate significant latitudinal differences in δ13C-CH4 for wetland sites in particular. This is in contrast to previous studies that have inferred significant differences in wetland δ13C-CH4 by latitude (Bock et al., 2010; Rice et al., 2016; Ganesan et al., 2018). An important caveat is that we have not analyzed a comprehensive dataset of freshwater δ13C-CH4, for which there are much more published data than for δ2H–CH4, although our analysis does comprise the largest dataset of freshwater δ13C-CH4 compiled to date (see Sect. 2.3). In addition, our analysis does not take into account the geographic distribution of different ecosystem categories, although we do not find significant differences in δ13C-CH4 between ecosystem categories (Fig. 8; Sect. 3.6). Low-latitude ecosystems dominated by C4 plants are underrepresented in both our dataset and that of Sherwood et al. (2017), and accounting for this would likely lead to a more enriched low-latitude wetland δ13C-CH4. In contrast, high-latitude ecosystems, including bogs, are relatively well represented in these datasets (Fig. 8), and we suggest that inferences of especially low δ13C-CH4 in high-latitude wetlands (Bock et al., 2010; Rice et al., 2016; Ganesan et al., 2018) are not consistent with the compiled dataset of in situ measurements. However, we note that atmospheric estimates of high-latitude wetland δ13C-CH4 (∼ −68 ± 4 ‰; Fisher et al., 2011) are lower than the median or mean value shown in Fig. 7b and are in close agreement with the relatively low values predicted by Ganesan et al. (2018). Ombrotrophic and minerotrophic peatlands have distinctive δ13C-CH4 signatures (Bellisario et al., 1999; Bowes and Hornibrook, 2006; Hornibrook, 2009), with lower signatures in ombrotrophic peatlands. We did not differentiate peatlands by trophic status, and it is possible that the dataset of high-latitude wetland in situ measurements is biased towards minerotrophic peatlands with relatively high δ13C-CH4.
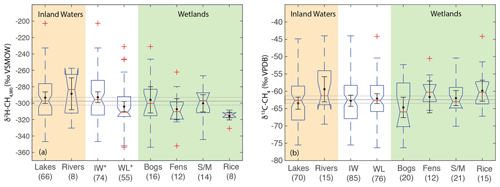
Figure 8Boxplots of (a) δ2H–CH4,W0 and (b) δ13C-CH4 for sites differentiated by ecosystem type. Numbers in parentheses indicate the number of sites for each category. Boxplot parameters are as in Fig. 7. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the mean values across all categories, and the dashed lines indicate the 95 % confidence interval of this value. Two extremely low outliers (<−80 ‰; lake and fen) are not shown in (b). IW – inland waters; WL – wetlands; S/M – swamps and marshes. Asterisks in A indicate that inland waters and wetlands have significantly different distributions.
Latitudinal differences in δ13C-CH4 inferred by Ganesan et al. (2018) were based on two key mechanisms: (1) differences in methanogenic pathway between different types of wetlands, especially between minerotrophic fens and ombrotrophic bogs; and (2) differential inputs of organic matter from C3 and C4 plants. Because inferred latitudinal differences in δ13C-CH4 and δ2H–CH4 are caused by different mechanisms, they could be highly complementary in validating estimates of freshwater emissions by latitude. It is also important to note that previous assessments of latitudinal differences in δ13C-CH4 did not include inland water environments. Our analysis suggests that latitudinal variation in δ13C-CH4 in inland waters may be more pronounced than in wetlands, although the mechanisms causing this difference will need to be elucidated with further study. A benefit of geographic discrimination based on δ2H–CH4 is that the same causal mechanism applies to all freshwater emissions, including both wetlands and inland waters.
Potential for geographic discrimination of other microbial methane sources based on δ2H–CH4
We speculate that latitudinal differences in δ2H–CH4 should also be observed in other fluxes of microbial methane from terrestrial environments, including enteric fermentation in livestock and wild animals, manure ponds, landfills, and termites. This is because microbial methanogenesis in all of these environments will incorporate hydrogen from environmental water and therefore will be influenced by variation in precipitation δ2H. There are limited data currently available to test this prediction, but δ2H–CH4 data from cow rumen and landfills are available with either specified locations or δ2H–H2O (Burke, 1993; Levin et al., 1993; Liptay et al., 1998; Bilek et al., 2001; Wang et al., 2015; Teasdale et al., 2019). These data plot in a range that is consistent with the δ2H–CH4 vs. δ2H–H2O relationships for freshwater CH4 (Fig. 5). Landfill data are only available for a very small range of estimated δ2H–H2O, making it impossible to assess for geographic variation currently. δ2H–CH4 data from cow rumen span a much wider range and express substantial variation that is independent of δ2H–H2O but largely overlap measurements from freshwater environments. Based on these limited data, variation observed in incubation studies that simulate landfill conditions (Schoell, 1980; Waldron et al., 1998), and our understanding of the influence of δ2H–H2O on microbial δ2H–CH4 (Fig. 6), we suggest that both landfill and cow rumen δ2H–CH4 likely varies geographically as a function of δ2H–H2O. If validated, this variation could also be used to distinguish these CH4 sources geographically. More data are clearly needed to test this conjecture, and it will also be important to evaluate how closely annual or seasonal δ2Hp corresponds to environmental δ2H–H2O in both landfills and cow rumen. Relatedly, the δ2H of CH4 emitted by biomass burning or directly by plants has also been shown to vary as a function of δ2H–H2O (Vigano et al., 2010; Umezawa et al., 2011).
3.6 Differences in δ2H–CH4 and δ13C-CH4 by ecosystem
When comparing ecosystems, we analyze δ2H–CH4,W0 values to account for variability related to differences in δ2H–H2O. Ecosystem types are not evenly distributed by latitude and therefore have different distributions of δ2H–H2O values. Our analysis does not find a significant difference in the distribution of δ2H–CH4,W0 between ecosystems, which could be partly a result of small sample sizes for most ecosystem categories (Fig. 8). Comparing the broader categories of inland waters and wetlands, we do observe a significant difference in δ2H–CH4,W0 distributions, with inland waters shifted towards higher values (median: −296 ‰) than wetlands (median: −311 ‰). We repeated this analysis only including sites with measured δ2H–H2O and found the same results in terms of category differences (Supplement Fig. S1). We did not observe any significant differences in δ13C-CH4 distributions between ecosystems, nor was there a significant difference in δ13C-CH4 distributions between inland waters and wetlands.
The significant difference in the distribution of δ2H–CH4,W0 between inland waters and wetlands is primarily a result of the difference in δ2H–CH4 between these environments in the high latitudes (Figs. 3, 4, and 7). We suggest this difference could be related to a greater overall prevalence of CH4 oxidation in inland waters. As shown in Fig. 6, the lack of positive co-variation between δ2H–CH4,W0 and δ13C–CO2 and αC could be interpreted to support a greater role for CH4 oxidation in controlling δ2H–CH4,W0 in inland waters relative to wetlands, although this result requires further validation. In lakes that undergo seasonal overturning and water column oxygenation, there may be a greater overall effect of CH4 oxidation than there is in wetlands typically. The absence of significant differences between ecosystems in terms of δ13C-CH4 (Fig. 8b) is in contrast to previous studies that have suggested that fens and bogs in particular have distinctive δ13C-CH4 (Ganesan et al., 2018). Bogs in particular have a very wide distribution of δ13C-CH4 that could represent differences between minerotrophic and ombrotrophic bogs (Hornibrook, 2009), which we did not differentiate in our dataset. This result should be interpreted with caution given that our dataset is not a comprehensive compilation of published δ13C-CH4 data, although it is the largest compiled dataset available (Sect. 2.3). We argue that inferred differences in δ13C-CH4 between wetland ecosystem categories should be further verified with more comprehensive data assimilation and additional measurements.
3.7 Differences in δ2H–CH4 and δ13C-CH4 by sample type
As with comparing ecosystems, when comparing sample types we analyze δ2H–CH4,W0 values to normalize for variability related to differences in δ2H–H2O, since sample types are not distributed evenly by latitude. When comparing sample types, dissolved CH4 samples do not have a significantly different δ2H–CH4,W0 distribution for the dataset as a whole, nor is there a significant difference between these groups in wetland sites (Fig. 9a). There is, however, a significant difference in inland water sites, with dissolved CH4 samples having a more enriched distribution (median: −270 ‰) vs. gas samples (median: −302 ‰). We repeated this analysis only including sites with measured δ2H–H2O and found the same results in terms of category differences (Supplement Fig. S2). We did not observe a significant difference in the distribution of δ13C between dissolved and gas-phase CH4 samples, either for the dataset as a whole or when the dataset was disaggregated into wetlands and inland waters (Fig. 9b).
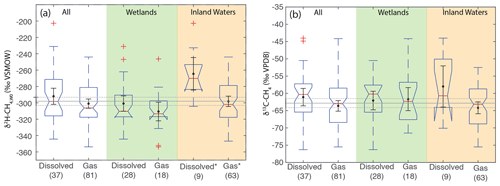
Figure 9Boxplots of (a) δ2H–CH4,W0 and (b) δ13C-CH4 for sites differentiated by sample type. Numbers in parentheses indicate the number of sites for each category. Boxplot parameters are as in Fig. 7. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the mean values across all categories, and the dashed lines indicate the 95 % confidence interval of this value. Two extremely low outliers (<−80 ‰; dissolved wetland and gas inland water) are not shown in (b). Asterisks in (a) indicate that dissolved and gas-phase CH4 samples from inland water sites have significantly different distributions.
We suggest that the higher δ2H–CH4,W0 in dissolved vs. gas samples for inland waters could be a result of generally greater oxidation of dissolved CH4 in inland water environments, potentially as a result of longer exposure to aerobic conditions in lake or river water columns. This is in contrast to wetlands, where aerobic conditions are generally limited to the uppermost layers of wetlands proximate to the water table. However, our dataset for inland-water-dissolved CH4 is quite small (n=9), and more data are needed to test this hypothesis. Furthermore, it is unclear why oxidation in inland water dissolved CH4 would be more strongly expressed in terms of δ2H–CH4,W0 (Fig. 9a) than δ13C (Fig. 9b).
Overall, our data imply that isotopic differences between dissolved and gas-phase methane are relatively minor on a global basis, especially in wetlands. This result could imply that the relative balance of diffusive vs. ebullition gas fluxes does not have a large effect on the isotopic composition of freshwater CH4 emissions. However, our study does not specifically account for isotopic fractionation occurring during diffusive or plant-mediated transport (Hornibrook, 2009), and most of our dissolved sample data are of in situ dissolved CH4 and not diffusive fluxes. More isotopic data specifically focused on diffusive methane emissions, for example using measurements of gas sampled from chambers, would help to resolve this question, as would more comparisons of the isotopic composition of diffusive and ebullition CH4 emissions from the same ecosystem.
3.8 Estimates of global emissions source δ2H–CH4 and δ13C-CH4
Our mixing model estimates a global source δ2H–CH4 of −278 ± 15 ‰ and a global source δ13C-CH4 of −56.4 ± 2.6 ‰ (Fig. 10). Monte Carlo sensitivity tests that only included uncertainty in either isotopic source signatures or flux estimates suggest that larger uncertainty is associated with isotopic source signatures (12 ‰ for δ2H; 2.2 ‰ for δ13C) than with flux estimates (8 ‰ for δ2H; 1.4 ‰ for δ13C). When correcting for wetland and biomass burning emissions from C4 plant ecosystems, as described in Sect. 2.4, our estimate of global source δ13C-CH4 increases to −55.2 ± 2.6 ‰. Our estimate of global source δ2H–CH4 is substantially higher than a previous bottom-up estimate using a similar approach (−295 ‰; Fig. 10) (Whiticar and Schaefer, 2007). This difference can be largely attributed to the application of more depleted δ2H–CH4 source signatures for tropical wetlands (−360 ‰), and to a lesser extent boreal wetlands (−380 ‰), by Whiticar and Schaefer (2007).
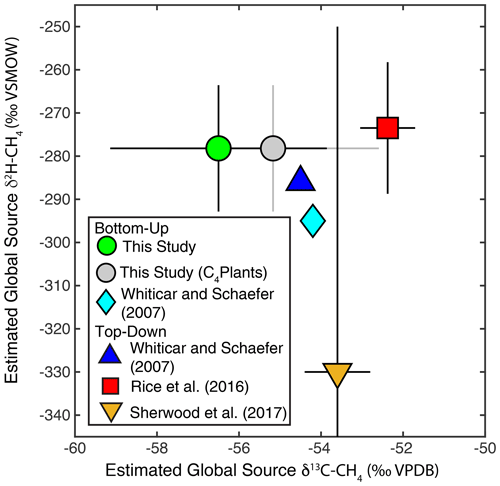
Figure 10Comparison of estimates of dual-isotope global source δ2H–CH4 and δ13C-CH4 from this and previous studies. Error bars from this study indicate the 2σ standard deviation from Monte Carlo analysis. Grey dot and error bars indicate an estimate corrected for the lack of data from wetlands and biomass burning in C4 plant environments, as described in Sect. 2.4. Error bars for Rice et al. (2016) indicate the range of values estimated in that study between 1977–2005. Error bars for Sherwood et al. (2017) reflect the combined measurement uncertainty and uncertainty in sink fractionations reported in that study. Whiticar and Schaefer (2007) did not provide uncertainties for their estimates.
Our bottom-up estimate of global source δ2H–CH4 substantially overlaps the range of top-down estimates (−258 to −289 ‰) based on atmospheric δ2H–CH4 measurements from 1977–2005 and a box model of sink fluxes and kinetic isotope effects (Rice et al., 2016) (Fig. 10). It is also within error of simpler top-down estimates calculated based on mean atmospheric measurements and estimates of a constant sink fractionation factor (Whiticar and Schaefer, 2007; Sherwood et al., 2017). Sherwood et al. (2017) estimate a very wide range of possible global source δ2H–CH4 values based on a relatively large atmospheric sink fractionation with large uncertainty (−235 ± 80 ‰). This range overlaps with our bottom-up estimate, although its mid-point is substantially lower than our estimate. We argue that the box-model method used to account for sink fractionations applied by Rice et al. (2016) probably provides a more accurate representation of global-source isotopic composition than the other top-down estimates shown in Fig. 10. The estimates of Rice et al. (2016) are also supported by the results of a global inversion model. Overall, the overlap between our bottom-up estimate of global source δ2H–CH4 with top-down estimates is encouraging and suggests that the estimates of emission source δ2H–CH4 signatures applied in this study are reasonably accurate. However, as discussed below, there is still substantial scope to further constrain these estimates and to reduce uncertainty.
Our bottom-up estimate of global source δ13C-CH4 is lower than the other top-down and bottom-up estimates shown in Fig. 10. As discussed above, there is likely a bias in our freshwater CH4 isotopic database in that it includes very few wetland sites from C4-plant-dominated ecosystems. When correcting for this, as well as for CH4 emissions from combustion of C4 plants (Fig. 10), our estimate shifts to a more enriched value that is within uncertainty of other estimates. Clearly, accounting for the effect of C4 plants in wetland and biomass burning CH4 emissions, and potentially also in enteric fermentation emissions, is important for accurate estimates of global source δ13C-CH4. As discussed below, other sources of error in both isotopic source signatures and inventory-based flux estimates could also partially account for our relatively low global source δ13C-CH4 estimate. For example, variation in fossil fuel isotopic signatures between regions and resource types is potentially an additional source of uncertainty that is not accounted for in this estimate.
Previous studies have argued, on the basis of comparing atmospheric measurements and emissions source δ13C-CH4 signatures, that there are biases in global emissions inventories, specifically that fossil fuel emissions estimates are too low and that either microbial emissions estimates are too high (Schwietzke et al., 2016) or that biomass burning estimates are too high (Worden et al., 2017). We argue that greater analysis of δ2H–CH4 measurements could be valuable for evaluating these and other emissions scenarios, as has been suggested previously (Rigby et al., 2012). This is especially true for determining the relative proportion of fossil fuel and microbial emissions, since these sources have widely differing δ2H–CH4 signatures (Table 1). Currently, atmospheric δ2H–CH4 measurements are not a routine component of CH4 monitoring programs, but we argue that based on both their value in constraining emissions sources and sinks (Rigby et al., 2012) and the increasing practicality of high-frequency measurements (Chen et al., 2016; Röckmann et al., 2016; Yacovitch et al., 2020), there should be a renewed focus on these measurements.
The uncertainty in our bottom-up estimates, the overall greater uncertainty associated with isotopic source signatures in our Monte Carlo calculations, and the apparent discrepancies for δ13C-CH4 shown in Fig. 10 also imply that isotopic source signatures for specific sources could be greatly improved. As noted by Rigby et al. (2012), the impact of improved isotopic source signatures increases as measurement precision improves. We have discussed above the importance of increased data assimilation and measurements from tropical wetlands, with a particular focus on C4-plant-dominated ecosystems. Using the isotopic source signal uncertainties and emissions fluxes shown in Table 1, we identified the sources with the greatest flux-weighted uncertainty in isotopic signatures. Based on this analysis, the greatest uncertainty for global source δ2H–CH4 estimates comes from source signatures for enteric fermentation and manure, low-latitude wetlands, onshore geological emissions, low-latitude and mid-latitude inland waters, termites, and landfills. We identified the same source categories as having the greatest flux-weighted uncertainty for δ13C-CH4, with the exception of termites, but we repeat the caveat that the underlying dataset is less comprehensive for δ13C-CH4. We argue that these source categories should be considered priorities for future emissions source isotopic characterization through data assimilation and additional measurements. As discussed in Sect. 3.5, evaluation of possible latitudinal variation in enteric fermentation and landfill δ2H–CH4 is particularly promising.
Our analysis of an expanded isotopic dataset for freshwater CH4 confirms the previous finding that δ2H–H2O is the primary determinant of δ2H–CH4 on a global scale (Waldron et al., 1999a) but also finds that the slope of this relationship is probably flatter than was inferred previously (Fig. 3). This flatter slope is primarily the result of the inclusion of a much larger number of high-latitude sites with low δ2H–H2O in our dataset. We find that the inferred relationship between δ2H–CH4 and δ2H–H2O is not highly sensitive to whether measured δ2H–H2O, modelled δ2Hp, or a combination of the two (i.e. a best-estimate) is used to estimate δ2H–H2O. This implies that gridded datasets of δ2Hp or isotope-enabled climate models could be used to predict the distribution of δ2H–CH4 in the present, as well as under past and future climates. Our analysis also suggests that annual δ2Hp may be a better predictor for wetland δ2H–CH4, while seasonal δ2Hp may be a better predictor of inland water δ2H–CH4. The slope of δ2H–CH4 vs. δ2H–H2O in both wetlands and inland waters agrees well with that found in incubation experiments (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998, 1999a), and we concur with previous inferences that this slope is partly controlled by variation in the δ2H of acetate as a function of δ2H–H2O (Waldron et al., 1999a). Analysis of co-variation in δ2H–CH4,W0 with δ13C-CH4, δ13C–CO2, and αC suggests that residual variation in δ2H–CH4 is influenced by a complex set of biogeochemical variables, including both variable isotopic fractionation related to methanogenesis and post-production isotopic fractionation related to CH4 oxidation and diffusive gas transport. A significant positive correlation between δ2H–CH4,W0 and both δ13C–CO2 and αC in wetlands suggests that hydrogen isotope fractionation related to methanogenesis pathway or enzymatic reversibility may be more important in these environments, but this result is dependent on the method used to estimate δ2H–H2O and requires further validation.
The dependence of δ2H–CH4 on δ2H–H2O leads to clear latitudinal differences in δ2H–CH4, with particularly low values from high-latitude sites (Figs. 4, 7a). The mechanism for latitudinal differences in δ2H–CH4 is distinct from proposed mechanisms for latitudinal differences in δ13C-CH4 (Ganesan et al., 2018), implying that these two isotopic tracers are complementary in differentiating geographic emissions sources. We estimate a global flux-weighted δ2H–CH4 signature from freshwater environments of −310 ± 15 ‰, which is enriched relative to values used in previous source apportionment studies (Rice et al., 2016; Bock et al., 2017). We observe a significantly higher δ2H–CH4,W0 distribution in inland waters relative to wetlands (Fig. 8a), which we suggest is a result of greater rates of CH4 oxidation in inland waters. We do not find significant differences between more specific ecosystem categories, nor do we find significant differences in δ2H–CH4,W0 between sample types (Fig. 9a), with the exception of higher values in dissolved CH4 relative to gas-phase CH4 in inland water environments.
Our bottom-up estimate of the global δ2H–CH4 source signature, −278 ± 15 ‰, is higher than previous bottom-up estimates (Whiticar and Schaefer, 2007) but is within the range of top-down estimates based on atmospheric measurements and modelled sink fractionations (Rice et al., 2016). In contrast, our bottom-up estimate of global δ13C-CH4, −56.4 ± 2.6 ‰, is low relative to top-down estimates, which is partially explained by a lack of data from C4-plant-dominated ecosystems in the freshwater CH4 isotopic dataset. The agreement between bottom-up and top-down global δ2H–CH4 estimates suggests that our current understanding of δ2H–CH4 source signatures, when combined with inventory-based flux estimates (Saunois et al., 2020), is consistent with atmospheric measurements. This supports the argument that increased measurements and modelling of atmospheric δ2H–CH4 could help to constrain global CH4 budgets (Rigby et al., 2012). However, there is clearly a need to better constrain source signatures for both δ2H–CH4 and δ13C-CH4, especially from low-latitude microbial sources.
The datasets used in this paper (Supplement Tables S1–S4) are publicly available at https://doi.org/10.6084/m9.figshare.13194833.v2 (Douglas et al., 2020b).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-18-3505-2021-supplement.
PMJD designed the project, assisted with compiling the data, analyzed the data, and wrote the manuscript; ES and JP compiled the data and assisted with analyzing the data and editing the manuscript; DP developed code for mixing model and Monte Carlo calculations and assisted with analyzing the data and editing the manuscript.
The authors declare that they have no conflict of interest.
We thank all of the researchers whose published data made this analysis possible (see Supplement Table S1). We also thank Susan Waldron, Edward Hornibrook, and the anonymous reviewer for constructive feedback.
This research has been supported by the Natural Sciences and Engineering Research Council of Canada (grant no. 2017-03902) and by McGill Science Undergraduate Research Awards.
This paper was edited by Caroline P. Slomp and reviewed by Susan Waldron, Edward Hornibrook, and one anonymous referee.
Alstad, K. P. and Whiticar, M. J.: Carbon and hydrogen isotope ratio characterization of methane dynamics for Fluxnet Peatland Ecosystems, Org. Geochem., 42, 548–558, 2011.
Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M., and Enrich-Prast, A.: Freshwater methane emissions offset the continental carbon sink, Science, 331, 50–50, 2011.
Bellisario, L., Bubier, J., Moore, T., and Chanton, J.: Controls on CH4 emissions from a northern peatland, Global Biogeochem. Cy., 13, 81–91, 1999.
Bergamaschi, P.: Seasonal variations of stable hydrogen and carbon isotope ratios in methane from a Chinese rice paddy, J. Geophys. Res.-Atmos., 102, 25383–25393, 1997.
Bilek, R., Tyler, S., Kurihara, M., and Yagi, K.: Investigation of cattle methane production and emission over a 24-hour period using measurements of δ13C and δD of emitted CH4 and rumen water, J. Geophys. Res.-Atmos., 106, 15405–15413, 2001.
Bock, M., Schmitt, J., Möller, L., Spahni, R., Blunier, T., and Fischer, H.: Hydrogen isotopes preclude marine hydrate CH4 emissions at the onset of Dansgaard-Oeschger events, Science, 328, 1686–1689, 2010.
Bock, M., Schmitt, J., Beck, J., Seth, B., Chappellaz, J., and Fischer, H.: Glacial/interglacial wetland, biomass burning, and geologic methane emissions constrained by dual stable isotopic CH4 ice core records, P. Natl. Acad. Sci. USA, 114, E5778–E5786, 2017.
Bouchard, F., Laurion, I., Prėskienis, V., Fortier, D., Xu, X., and Whiticar, M. J.: Modern to millennium-old greenhouse gases emitted from ponds and lakes of the Eastern Canadian Arctic (Bylot Island, Nunavut), Biogeosciences, 12, 7279–7298, https://doi.org/10.5194/bg-12-7279-2015, 2015.
Bowen, G. J. and Revenaugh, J.: Interpolating the isotopic composition of modern meteoric precipitation, Water Resour. Res., 39, 1299, https://doi.org/10.1029/2003WR002086, 2003.
Bowen, G. J. and Wilkinson, B.: Spatial distribution of δ18O in meteoric precipitation, Geology, 30, 315–318, 2002.
Bowen, G. J., Wassenaar, L. I., and Hobson, K. A.: Global application of stable hydrogen and oxygen isotopes to wildlife forensics, Oecologia, 143, 337–348, 2005.
Bowes, H. L. and Hornibrook, E. R.: Emission of highly 13C-depleted methane from an upland blanket mire, Geophys. Res. Lett., 33, L04401, https://doi.org/10.1029/2005GL025209, 2006.
Brooks, J. R., Gibson, J. J., Birks, S. J., Weber, M. H., Rodecap, K. D., and Stoddard, J. L.: Stable isotope estimates of evaporation: inflow and water residence time for lakes across the United States as a tool for national lake water quality assessments, Limnol. Oceanogr., 59, 2150–2165, 2014.
Brosius, L., Walter Anthony, K., Grosse, G., Chanton, J., Farquharson, L., Overduin, P. P., and Meyer, H.: Using the deuterium isotope composition of permafrost meltwater to constrain thermokarst lake contributions to atmospheric CH4 during the last deglaciation, J. Geophys. Res.-Biogeo. (2005–2012), 117, G01022, https://doi.org/10.1029/2011JG001810, 2012.
Burke Jr., R.: Shallow aquatic sediments, Bacterial Gas. Conference, Milan, 25–26 September 1989, Editions Technip, Paris, France, 1992.
Burke Jr., R. A. and Sackett, W. M.: Stable hydrogen and carbon isotopic compositions of biogenic methanes from several shallow aquatic environments, in: Organic Marine Geochemistry, edited by: Sohn, M. L., ACS Publications, Washington D.C., USA, 297–313, 1986.
Burke Jr., R. A., Barber, T. R., and Sackett, W. M.: Methane flux and stable hydrogen and carbon isotope composition of sedimentary methane from the Florida Everglades, Global Biogeochem. Cy., 2, 329–340, 1988.
Burke Jr., R. A., Barber, T. R., and Sackett, W. M.: Seasonal variations of stable hydrogen and carbon isotope ratios of methane in subtropical freshwater sediments, Global Biogeochem. Cy., 6, 125–138, 1992.
Burke Jr., R. A.: Possible influence of hydrogen concentration on microbial methane stable hydrogen isotopic composition, Chemosphere, 26, 55–67, 1993.
Cadieux, S. B., White, J. R., Sauer, P. E., Peng, Y., Goldman, A. E., and Pratt, L. M.: Large fractionations of C and H isotopes related to methane oxidation in Arctic lakes, Geochim. Cosmochim. Ac., 187, 141–155, 2016.
Chanton, J., Whiting, G., Blair, N., Lindau, C., and Bollich, P.: Methane emission from rice: Stable isotopes, diurnal variations, and CO2 exchange, Global Biogeochem. Cy., 11, 15–27, 1997.
Chanton, J. P.: The effect of gas transport on the isotope signature of methane in wetlands, Org. Geochem., 36, 753–768, 2005.
Chanton, J. P., Fields, D., and Hines, M. E.: Controls on the hydrogen isotopic composition of biogenic methane from high-latitude terrestrial wetlands, J. Geophys. Res.-Biogeo. (2005–2012), 111, G04004, https://doi.org/10.1029/2005JG000134, 2006.
Chasar, L., Chanton, J., Glaser, P. H., and Siegel, D.: Methane concentration and stable isotope distribution as evidence of rhizospheric processes: Comparison of a fen and bog in the Glacial Lake Agassiz Peatland complex, Ann. Bot., 86, 655–663, 2000.
Chen, Y., Lehmann, K. K., Peng, Y., Pratt, L., White, J., Cadieux, S., Sherwood Lollar, B., Lacrampe-Couloume, G., and Onstott, T. C.: Hydrogen Isotopic Composition of Arctic and Atmospheric CH4 Determined by a Portable Near-Infrared Cavity Ring-Down Spectrometer with a Cryogenic Pre-Concentrator, Astrobiology, 16, 787–797, 2016.
Conrad, R., Noll, M., Claus, P., Klose, M., Bastos, W. R., and Enrich-Prast, A.: Stable carbon isotope discrimination and microbiology of methane formation in tropical anoxic lake sediments, Biogeosciences, 8, 795–814, https://doi.org/10.5194/bg-8-795-2011, 2011.
Coplen, T. B.: Guidelines and recommended terms for expression of stable-isotope-ratio and gas-ratio measurement results, Rapid Commun. Mass Sp., 25, 2538–2560, 2011.
David, K., Timms, W., Hughes, C. E., Crawford, J., and McGeeney, D.: Application of the pore water stable isotope method and hydrogeological approaches to characterise a wetland system, Hydrol. Earth Syst. Sci., 22, 6023–6041, https://doi.org/10.5194/hess-22-6023-2018, 2018.
Douglas, P. M. J., Stolper, D., Smith, D., Walter Anthony, K., Paull, C., Dallimore, S., Wik, M., Crill, P., Winterdahl, M., Eiler, J., and Sessions, A. L.: Diverse origins of Arctic and Subarctic methane point source emissions identified with multiply-substituted isotopologues, Geochim. Cosmochim. Ac., 188, 163–188, 2016.
Douglas, P. M. J., Stolper, D. A., Eiler, J. M., Sessions, A. L., Lawson, M., Shuai, Y., Bishop, A., Podlaha, O. G., Ferreira, A. A., and Neto, E. V. S.: Methane clumped isotopes: progress and potential for a new isotopic tracer, Org. Geochem., 113, 262–282, 2017.
Douglas, P. M. J., Gonzalez Moguel, R., Walter Anthony, K. M., Wik, M., Crill, P. M., Dawson, K. S., Smith, D. A., Yanay, E., Lloyd, M. K., and Stolper, D. A.: Clumped isotopes link older carbon substrates with slower rates of methanogenesis in northern lakes, Geophys. Res. Lett., 47, e2019GL086756, https://doi.org/10.1029/2019GL086756, 2020a.
Douglas, P. M. J., Stratigopoulos, E., Park, J., and Phan, D.: Data for geographic variability in freshwater methane hydrogen isotope ratios and its implications for emissions source apportionment and microbial biogeochemistry, figshare [Dataset], https://doi.org/10.6084/m9.figshare.13194833.v2, 2020b.
Drevon, D., Fursa, S. R., and Malcolm, A. L.: Intercoder reliability and validity of WebPlotDigitizer in extracting graphed data, Behav. Modif., 41, 323–339, 2017.
Dunn, O. J.: Multiple comparisons using rank sums, Technometrics, 6, 241–252, 1964.
Fisher, R. E., Sriskantharajah, S., Lowry, D., Lanoisellé, M., Fowler, C., James, R., Hermansen, O., Lund Myhre, C., Stohl, A., Greinert, J., and Nisbet, E. G.: Arctic methane sources: Isotopic evidence for atmospheric inputs, Geophys. Res. Lett., 38, L21803, https://doi.org/10.1029/2011GL049319, 2011.
Fletcher, D. and Dixon, P. M.: Modelling data from different sites, times or studies: weighted vs. unweighted regression, Method. Ecol. Evolut., 3, 168–176, 2012.
Ganesan, A., Stell, A., Gedney, N., Comyn-Platt, E., Hayman, G., Rigby, M., Poulter, B., and Hornibrook, E.: Spatially resolved isotopic source signatures of wetland methane emissions, Geophys. Res. Lett., 45, 3737–3745, 2018.
Gruen, D. S., Wang, D. T., Könneke, M., Topçuoğlu, B. D., Stewart, L. C., Goldhammer, T., Holden, J. F., Hinrichs, K.-U., and Ono, S.: Experimental investigation on the controls of clumped isotopologue and hydrogen isotope ratios in microbial methane, Geochim. Cosmochim. Ac., 237, 339–356, 2018.
Happell, J. D., Chanton, J. P., Whiting, G. J., and Showers, W. J.: Stable isotopes as tracers of methane dynamics in Everglades marshes with and without active populations of methane oxidizing bacteria, J. Geophys. Res.-Atmos., 98, 14771–14782, 1993.
Happell, J. D., Chanton, J. P., and Showers, W. S.: The influence of methane oxidation on the stable isotopic composition of methane emitted from Florida swamp forests, Geochim. Cosmochim. Ac., 58, 4377–4388, 1994.
Hornibrook, E. R.: The stable carbon isotope composition of methane produced and emitted from northern peatlands, edited by: Baird, A., Belyea, L., Comas, X., Reeve, A., and Slater, L., American Geophysical Union, Geophys. Monogr. Ser., 184, 187–203, 2009.
Hornibrook, E. R., Longstaffe, F. J., and Fyfe, W. S.: Spatial distribution of microbial methane production pathways in temperate zone wetland soils: stable carbon and hydrogen isotope evidence, Geochim. Cosmochim. Ac., 61, 745–753, 1997.
Huang, Y., Shuman, B., Wang, Y., and Webb III, T.: Hydrogen isotope ratios of palmitic acid in lacustrine sediments record late Quaternary climate variations, Geology, 30, 1103–1106, 2002.
Jonsson, C. E., Leng, M. J., Rosqvist, G. C., Seibert, J., and Arrowsmith, C.: Stable oxygen and hydrogen isotopes in sub-Arctic lake waters from northern Sweden, J. Hydrol., 376, 143–151, 2009.
Kai, F. M., Tyler, S. C., Randerson, J. T., and Blake, D. R.: Reduced methane growth rate explained by decreased Northern Hemisphere microbial sources, Nature, 476, 194–197, 2011.
Koven, C. D., Ringeval, B., Friedlingstein, P., Ciais, P., Cadule, P., Khvorostyanov, D., Krinner, G., and Tarnocai, C.: Permafrost carbon-climate feedbacks accelerate global warming, P. Natl. Acad. Sci. USA, 108, 14769–14774, 2011.
Kruskal, W. H. and Wallis, W. A.: Use of ranks in one-criterion variance analysis, J. Am. Stat. Assoc., 47, 583–621, 1952.
Krzycki, J., Kenealy, W., DeNiro, M., and Zeikus, J.: Stable carbon isotope fractionation by Methanosarcina barkeri during methanogenesis from acetate, methanol, or carbon dioxide-hydrogen, Appl. Environ. Microbiol., 53, 2597–2599, 1987.
Lansdown, J., Quay, P., and King, S.: CH4 production via CO2 reduction in a temperate bog: A source of 13C-depIeted CH4, Geochim. Cosmochim. Ac., 56, 3493–3503, 1992.
Lansdown, J. M.: The carbon and hydrogen stable isotope composition of methane released from natural wetlands and ruminants, PhD Dissertation, University of Washington, 1992.
Lecher, A. L., Chuang, P. C., Singleton, M., and Paytan, A.: Sources of methane to an Arctic lake in Alaska: An isotopic investigation, J. Geophys. Res.-Biogeo., 122, 753–766, 2017.
Levin, I., Bergamaschi, P., Dörr, H., and Trapp, D.: Stable isotopic signature of methane from major sources in Germany, Chemosphere, 26, 161–177, 1993.
Liptay, K., Chanton, J., Czepiel, P., and Mosher, B.: Use of stable isotopes to determine methane oxidation in landfill cover soils, J. Geophys. Res.-Atmos., 103, 8243–8250, 1998.
Mann, H. B. and Whitney, D. R.: On a test of whether one of two random variables is stochastically larger than the other, Ann. Mathemat. Stat., 18, 50–60, 1947.
Marik, T., Fischer, H., Conen, F., and Smith, K.: Seasonal variations in stable carbon and hydrogen isotope ratios in methane from rice fields, Global Biogeochem. Cy., 16, 41-41–41-11, 2002.
Martens, C. S., Kelley, C. A., Chanton, J. P., and Showers, W. J.: Carbon and hydrogen isotopic characterization of methane from wetlands and lakes of the Yukon-Kuskokwim delta, western Alaska, J. Geophys. Res.-Atmos. (1984–2012), 97, 16689–16701, 1992.
Miles, N. L., Martins, D. K., Richardson, S. J., Rella, C. W., Arata, C., Lauvaux, T., Davis, K. J., Barkley, Z. R., McKain, K., and Sweeney, C.: Calibration and field testing of cavity ring-down laser spectrometers measuring CH4, CO2, and δ13CH4 deployed on towers in the Marcellus Shale region, Atmos. Meas. Tech., 11, 1273–1295, https://doi.org/10.5194/amt-11-1273-2018, 2018.
Mischler, J. A., Sowers, T. A., Alley, R. B., Battle, M., McConnell, J., Mitchell, L., Popp, T., Sofen, E., and Spencer, M.: Carbon and hydrogen isotopic composition of methane over the last 1000 years, Global Biogeochem. Cy., 23, GB4024, https://doi.org/10.1029/2009GB003460, 2009.
Mora, G. and Zanazzi, A.: Hydrogen isotope ratios of moss cellulose and source water in wetlands of Lake Superior, United States reveal their potential for quantitative paleoclimatic reconstructions, Chem. Geol., 468, 75–83, 2017.
Nakagawa, F., Yoshida, N., Sugimoto, A., Wada, E., Yoshioka, T., Ueda, S., and Vijarnsorn, P.: Stable isotope and radiocarbon compositions of methane emitted from tropical rice paddies and swamps in Southern Thailand, Biogeochemistry, 61, 1–19, 2002a.
Nakagawa, F., Yoshida, N., Nojiri, Y., and Makarov, V.: Production of methane from alasses in eastern Siberia: Implications from its 14C and stable isotopic compositions, Global Biogeochem. Cy., 16, 14-11–14-15, 2002b.
Nisbet, E., Dlugokencky, E., Manning, M., Lowry, D., Fisher, R., France, J., Michel, S., Miller, J., White, J., and Vaughn, B.: Rising atmospheric methane: 2007–2014 growth and isotopic shift, Global Biogeochem. Cy., 30, 1356–1370, 2016.
Nisbet, E. G., Manning, M., Dlugokencky, E., Fisher, R., Lowry, D., Michel, S., Myhre, C. L., Platt, S. M., Allen, G., and Bousquet, P.: Very strong atmospheric methane growth in the 4 years 2014–2017: Implications for the Paris Agreement, Global Biogeochem. Cy., 33, 318–342, 2019.
Penger, J., Conrad, R., and Blaser, M.: Stable carbon isotope fractionation by methylotrophic methanogenic archaea, Appl. Environ. Microbiol., 78, 7596–7602, 2012.
Penning, H. and Conrad, R.: Quantification of carbon flow from stable isotope fractionation in rice field soils with different organic matter content, Org. Geochem., 38, 2058–2069, 2007.
Penning, H., Plugge, C. M., Galand, P. E., and Conrad, R.: Variation of carbon isotope fractionation in hydrogenotrophic methanogenic microbial cultures and environmental samples at different energy status, Glob. Change Biol., 11, 2103–2113, 2005.
Pine, M. J. and Barker, H.: Studies on the methane fermentation XII.: The pathway of hydrogen in the acetate fermentation, J. Bacteriol., 71, 644–648, 1956.
Pison, I., Ringeval, B., Bousquet, P., Prigent, C., and Papa, F.: Stable atmospheric methane in the 2000s: key-role of emissions from natural wetlands, Atmos. Chem. Phys., 13, 11609–11623, https://doi.org/10.5194/acp-13-11609-2013, 2013.
Popp, T. J., Chanton, J. P., Whiting, G. J., and Grant, N.: Methane stable isotope distribution at a Carex dominated fen in north central Alberta, Global Biogeochem. Cy., 13, 1063–1077, 1999.
Rice, A. L., Butenhoff, C. L., Teama, D. G., Röger, F. H., Khalil, M. A. K., and Rasmussen, R. A.: Atmospheric methane isotopic record favors fossil sources flat in 1980s and 1990s with recent increase, P. Natl. Acad. Sci. USA, 113, 10791–10796, 2016.
Rigby, M., Manning, A., and Prinn, R.: The value of high-frequency, high-precision methane isotopologue measurements for source and sink estimation, J. Geophys. Res.-Atmos., 117, D12312, https://doi.org/10.1029/2011JD017384, 2012.
Röckmann, T., Eyer, S., van der Veen, C., Popa, M. E., Tuzson, B., Monteil, G., Houweling, S., Harris, E., Brunner, D., Fischer, H., Zazzeri, G., Lowry, D., Nisbet, E. G., Brand, W. A., Necki, J. M., Emmenegger, L., and Mohn, J.: In situ observations of the isotopic composition of methane at the Cabauw tall tower site, Atmos. Chem. Phys., 16, 10469–10487, https://doi.org/10.5194/acp-16-10469-2016, 2016.
Rozanski, K., Araguás-Araguás, L., and Gonfiantini, R.: Isotopic patterns in modern global precipitation, Geophys. Monogr. Ser., 78, 1–36, 1993.
Sachse, D., Billault, I., Bowen, G. J., Chikaraishi, Y., Dawson, T. E., Feakins, S. J., Freeman, K. H., Magill, C. R., McInerney, F. A., and van der Meer, M. T. J.: Molecular paleohydrology: Interpreting the hydrogen-isotopic composition of lipid biomarkers from photosynthesizing organisms, Ann. Rev. Earth Planet. Sci., 40, 221–249, 2012.
Sakagami, H., Takahashi, N., Hachikubo, A., Minami, H., Yamashita, S., Shoji, H., Khlystov, O., Kalmychkov, G., Grachev, M., and De Batist, M.: Molecular and isotopic composition of hydrate-bound and dissolved gases in the southern basin of Lake Baikal, based on an improved headspace gas method, Geo.-Mar. Lett., 32, 465–472, 2012.
Saunois, M., Stavert, A. R., Poulter, B., Bousquet, P., Canadell, J. G., Jackson, R. B., Raymond, P. A., Dlugokencky, E. J., Houweling, S., Patra, P. K., Ciais, P., Arora, V. K., Bastviken, D., Bergamaschi, P., Blake, D. R., Brailsford, G., Bruhwiler, L., Carlson, K. M., Carrol, M., Castaldi, S., Chandra, N., Crevoisier, C., Crill, P. M., Covey, K., Curry, C. L., Etiope, G., Frankenberg, C., Gedney, N., Hegglin, M. I., Höglund-Isaksson, L., Hugelius, G., Ishizawa, M., Ito, A., Janssens-Maenhout, G., Jensen, K. M., Joos, F., Kleinen, T., Krummel, P. B., Langenfelds, R. L., Laruelle, G. G., Liu, L., Machida, T., Maksyutov, S., McDonald, K. C., McNorton, J., Miller, P. A., Melton, J. R., Morino, I., Müller, J., Murguia-Flores, F., Naik, V., Niwa, Y., Noce, S., O'Doherty, S., Parker, R. J., Peng, C., Peng, S., Peters, G. P., Prigent, C., Prinn, R., Ramonet, M., Regnier, P., Riley, W. J., Rosentreter, J. A., Segers, A., Simpson, I. J., Shi, H., Smith, S. J., Steele, L. P., Thornton, B. F., Tian, H., Tohjima, Y., Tubiello, F. N., Tsuruta, A., Viovy, N., Voulgarakis, A., Weber, T. S., van Weele, M., van der Werf, G. R., Weiss, R. F., Worthy, D., Wunch, D., Yin, Y., Yoshida, Y., Zhang, W., Zhang, Z., Zhao, Y., Zheng, B., Zhu, Q., Zhu, Q., and Zhuang, Q.: The Global Methane Budget 2000–2017, Earth Syst. Sci. Data, 12, 1561–1623, https://doi.org/10.5194/essd-12-1561-2020, 2020.
Schaefer, H., Fletcher, S. E. M., Veidt, C., Lassey, K. R., Brailsford, G. W., Bromley, T. M., Dlugokencky, E. J., Michel, S. E., Miller, J. B., and Levin, I.: A 21st-century shift from fossil-fuel to biogenic methane emissions indicated by 13CH4, Science, 352, 80–84, 2016.
Schoell, M.: The hydrogen and carbon isotopic composition of methane from natural gases of various origins, Geochim. Cosmochim. Ac., 44, 649–661, 1980.
Schoell, M.: Genetic characterization of natural gases, AAPG Bull., 67, 2225–2238, 1983.
Schwietzke, S., Sherwood, O. A., Bruhwiler, L. M., Miller, J. B., Etiope, G., Dlugokencky, E. J., Michel, S. E., Arling, V. A., Vaughn, B. H., and White, J. W.: Upward revision of global fossil fuel methane emissions based on isotope database, Nature, 538, 88–91, 2016.
Shapiro, S. S. and Wilk, M. B.: An analysis of variance test for normality (complete samples), Biometrika, 52, 591–611, 1965.
Sherwood, O. A., Schwietzke, S., Arling, V. A., and Etiope, G.: Global Inventory of Gas Geochemistry Data from Fossil Fuel, Microbial and Burning Sources, version 2017, Earth Syst. Sci. Data, 9, 639–656, https://doi.org/10.5194/essd-9-639-2017, 2017.
Shoemaker, J., Varner, R., and Schrag, D.: Characterization of subsurface methane production and release over 3 years at a New Hampshire wetland, Geochim. Cosmochim. Ac., 91, 120–139, 2012.
Sprenger, M., Tetzlaff, D., Tunaley, C., Dick, J., and Soulsby, C.: Evaporation fractionation in a peatland drainage network affects stream water isotope composition, Water Resour. Res., 53, 851–866, 2017.
Stell, A. C., Douglas, P. M. J., Rigby, M., and Ganesan, A. L.: The impact of spatially varying wetland source signatures on the atmospheric variability of δD-CH4, Philos. T. R. Soc. A, in press, 2021.
Stolper, D., Martini, A., Clog, M., Douglas, P., Shusta, S., Valentine, D., Sessions, A., and Eiler, J.: Distinguishing and understanding thermogenic and biogenic sources of methane using multiply substituted isotopologues, Geochim. Cosmochim. Ac., 161, 219–247, 2015.
Sugimoto, A. and Wada, E.: Hydrogen isotopic composition of bacterial methane: CO2 H2 reduction and acetate fermentation, Geochim. Cosmochim. Ac., 59, 1329–1337, 1995.
Teasdale, C. J., Hall, J. A., Martin, J. P., and Manning, D. A.: Discriminating methane sources in ground gas emissions in NW England, Q. J. Eng. Geol. Hydrogeol., 52, 110–122, 2019.
Thompson, H. A., White, J. R., Pratt, L. M., and Sauer, P. E.: Spatial variation in flux, δ13C and δ2H of methane in a small Arctic lake with fringing wetland in western Greenland, Biogeochemistry, 131, 17–33, 2016.
Thompson, K. M., Burmaster, D. E., and Crouch, E. A.: Monte Carlo techniques for quantitative uncertainty analysis in public health risk assessments, Risk Anal., 12, 53–63, 1992.
Thompson, R. L., Nisbet, E., Pisso, I., Stohl, A., Blake, D., Dlugokencky, E., Helmig, D., and White, J.: Variability in atmospheric methane from fossil fuel and microbial sources over the last three decades, Geophys. Res. Lett., 45, 11499–11508, 2018.
Turner, A. J., Frankenberg, C., and Kort, E. A.: Interpreting contemporary trends in atmospheric methane, P. Natl. Acad. Sci. USA, 116, 2805–2813, 2019.
Tyler, J. J., Leng, M. J., and Arrowsmith, C.: Seasonality and the isotope hydrology of Lochnagar, a Scottish mountain lake: implications for palaeoclimate research, The Holocene, 17, 717–727, 2007.
Tyler, S., Bilek, R., Sass, R., and Fisher, F.: Methane oxidation and pathways of production in a Texas paddy field deduced from measurements of flux, δ13C, and δD of CH4, Global Biogeochem. Cy., 11, 323–348, 1997.
Umezawa, T., Aoki, S., Kim, Y., Morimoto, S., and Nakazawa, T.: Carbon and hydrogen stable isotopic ratios of methane emitted from wetlands and wildfires in Alaska: Aircraft observations and bonfire experiments, J. Geophys. Res.-Atmos., 116, D15305, https://doi.org/10.1029/2010JD015545, 2011.
Valentine, D., Sessions, A., Tyler, S., and Chidthaisong, A.: Hydrogen isotope fractionation during H2 CO2 acetogenesis: hydrogen utilization efficiency and the origin of lipid-bound hydrogen, Geobiology, 2, 179–188, 2004a.
Valentine, D. L., Chidthaisong, A., Rice, A., Reeburgh, W. S., and Tyler, S. C.: Carbon and hydrogen isotope fractionation by moderately thermophilic methanogens, Geochim. Cosmochim. Ac., 68, 1571–1590, 2004b.
Vigano, I., Holzinger, R., Keppler, F., Greule, M., Brand, W. A., Geilmann, H., Van Weelden, H., and Röckmann, T.: Water drives the deuterium content of the methane emitted from plants, Geochim. Cosmochim. Ac., 74, 3865–3873, 2010.
Wahlen, M.: Carbon dioxide, carbon monoxide and methane in the atmosphere: abundance and isotopic composition, in: Stable Isotopes in Ecology and Environmental Science, edited by: Lathja, K. and Michener, R. H., Blackwell, Malden, MA, USA, 93–113, 1994.
Waldron, S., Watson-Craik, I. A., Hall, A. J., and Fallick, A. E.: The carbon and hydrogen stable isotope composition of bacteriogenic methane: a laboratory study using a landfill inoculum, Geomicrobiol. J., 15, 157–169, 1998.
Waldron, S., Lansdown, J., Scott, E., Fallick, A., and Hall, A.: The global influence of the hydrogen iostope composition of water on that of bacteriogenic methane from shallow freshwater environments, Geochim. Cosmochim. Ac., 63, 2237–2245, 1999a.
Waldron, S., Hall, A. J., and Fallick, A. E.: Enigmatic stable isotope dynamics of deep peat methane, Global Biogeochem. Cy., 13, 93–100, 1999b.
Walter, K., Chanton, J. P., Chapin, F. S., Schuur, E. A. G., and Zimov, S. A.: Methane production and bubble emissions from arctic lakes: Isotopic implications for source pathways and ages, J. Geophys. Res.-Biogeo., 113, G00A08, https://doi.org/10.1029/2007JG000569, 2008.
Walter, K. M., Zimov, S., Chanton, J. P., Verbyla, D., and Chapin, F. S.: Methane bubbling from Siberian thaw lakes as a positive feedback to climate warming, Nature, 443, 71–75, 2006.
Wang, D. T., Gruen, D. S., Sherwood Lollar, B., Hinrichs, K.-U., Stewart, L. C., Holden, J. F., Hristov, A. N., Pohlman, J. W., Morrill, P. L., Könneke, M., Delwiche, K. B., Reeves, E. P., Sutcliffe, C. N., Ritter, D. J., Seewald, J. S., McIntosh, J. C., Hemond, H. F., Kubo, M. D., Cardace, D., Hoehler, T. M., and Ono, S.: Nonequilibrium clumped isotope signals in microbial methane, Science, 348, 428–431, 2015.
Wang, D. T., Welander, P. V., and Ono, S.: Fractionation of the methane isotopologues 13CH4, 12CH3D, and 13CH3D during aerobic oxidation of methane by Methylococcus capsulatus (Bath), Geochim. Cosmochim. Ac., 192, 186–202, 2016.
Wassmann, R., Thein, U., Whiticar, M., Rennenburg, H., Seiler, W., and Junk, W.: Methane emissions from the Amazon floodplain: characterization of production and transport, Global Biogeochem. Cy., 6, 3–13, 1992.
Whiticar, M. and Schaefer, H.: Constraining past global tropospheric methane budgets with carbon and hydrogen isotope ratios in ice, Philos. T. Ro. Soc. A, 365, 1793–1828, 2007.
Whiticar, M. J.: Carbon and hydrogen isotope systematics of bacterial formation and oxidation of methane, Chem. Geol., 161, 291–314, 1999.
Whiticar, M. J., Faber, E., and Schoell, M.: Biogenic methane formation in marine and freshwater environments: CO2 reduction vs. acetate fermentation – Isotope evidence, Geochim. Cosmochim. Ac., 50, 693–709, 1986.
Woltemate, I., Whiticar, M., and Schoell, M.: Carbon and hydrogen isotopic composition of bacterial methane in a shallow freshwater lake, Limnol. Oceanogr., 29, 985–992, 1984.
Worden, J. R., Bloom, A. A., Pandey, S., Jiang, Z., Worden, H. M., Walker, T. W., Houweling, S., and Röckmann, T.: Reduced biomass burning emissions reconcile conflicting estimates of the post-2006 atmospheric methane budget, Nat. Commun., 8, 1–11, 2017.
Yacovitch, T. I., Daube, C., and Herndon, S. C.: Methane emissions from offshore oil and gas platforms in the Gulf of Mexico, Environ. Sci. Technol., 54, 3530–3538, 2020.
Young, E., Kohl, I., Sherwood Lollar, B., Etiope, G., Rumble, D., Li, S., Haghnegahdar, M., Schauble, E., McCain, K., Foustoukos, D., Sutclife, C., Warr, O., and Ballentine, C.: The relative abundances of resolved CH2D2 and 13CH3D and mechanisms controlling isotopic bond ordering in abiotic and biotic methane gases, Geochim. Cosmochim. Ac., 203, 235–264, 2017.
Yvon-Durocher, G., Allen, A. P., Bastviken, D., Conrad, R., Gudasz, C., St-Pierre, A., Thanh-Duc, N., and Del Giorgio, P. A.: Methane fluxes show consistent temperature dependence across microbial to ecosystem scales, Nature, 507, 488–491, 2014.
Zazzeri, G., Lowry, D., Fisher, R., France, J., Lanoisellé, M., and Nisbet, E.: Plume mapping and isotopic characterisation of anthropogenic methane sources, Atmos. Environ., 110, 151–162, 2015.
Zhang, Z., Zimmermann, N. E., Stenke, A., Li, X., Hodson, E. L., Zhu, G., Huang, C., and Poulter, B.: Emerging role of wetland methane emissions in driving 21st century climate change, P. Natl. Acad. Sci. USA, 114, 9647–9652, 2017.
Zhu, J., Liu, Z., Brady, E., Otto-Bliesner, B., Zhang, J., Noone, D., Tomas, R., Nusbaumer, J., Wong, T., and Jahn, A.: Reduced ENSO variability at the LGM revealed by an isotope-enabled Earth system model, Geophys. Res. Lett., 44, 6984–6992, 2017.
Zimov, S., Voropaev, Y. V., Semiletov, I., Davidov, S., Prosiannikov, S., Chapin, F. S., Chapin, M., Trumbore, S., and Tyler, S.: North Siberian lakes: a methane source fueled by Pleistocene carbon, Science, 277, 800–802, 1997.





