Geographic variability in freshwater methane hydrogen isotope ratios and its implications for global isotopic source signatures

There is growing interest in developing spatially resolved methane (CH₄) isotopic source signatures to aid in geographic source attribution of CH₄ emissions. CH₄ hydrogen isotope measurements (δ²H–CH₄) have the potential to be a powerful tool for geographic differentiation of CH₄ emissions from freshwater environments, as well as other microbial sources. This is because microbial δ²H–CH₄ values are partially dependent on the δ²H of environmental water (δ²H–H₂O), which exhibits large and well-characterized spatial variability globally. We have refined the existing global relationship between δ²H–CH₄ and δ²H–H₂O by compiling a more extensive global dataset of δ²H–CH₄ from freshwater environments, including wetlands, inland waters, and rice paddies, comprising a total of 129 different sites, and compared these with measurements and estimates of δ²H–H₂O, as well as δ¹³C-CH₄ and δ¹³C–CO₂ measurements. We found that estimates of δ²H–H₂O explain approximately 42 % of the observed variation in δ²H–CH₄, with a flatter slope than observed in previous studies. The inferred global δ²H–CH₄ vs. δ²H–H₂O regression relationship is not sensitive to using either modelled precipitation δ²H or measured δ²H–H₂O as the predictor variable. The slope of the global freshwater relationship between δ²H–CH₄ and δ²H–H₂O is similar to observations from incubation experiments but is different from pure culture experiments. This result is consistent with previous suggestions that variation in the δ²H of acetate, controlled by environmental δ²H–H₂O, is important in determining variation in δ²H–CH₄. The relationship between δ²H–CH₄ and δ²H–H₂O leads to significant differences in the distribution of freshwater δ²H–CH₄ between the northern high latitudes (60–90^∘ N), relative to other global regions. We estimate a flux-weighted global freshwater δ²H–CH₄ of −310 ± 15 ‰, which is higher than most previous estimates. Comparison with δ¹³C measurements of both CH₄ and CO₂ implies that residual δ²H–CH₄ variation is the result of complex interactions between CH₄ oxidation, variation in the dominant pathway of methanogenesis, and potentially other biogeochemical variables. We observe a significantly greater distribution of δ²H–CH₄ values, corrected for δ²H–H₂O, in inland waters relative to wetlands, and suggest this difference is caused by more prevalent CH₄ oxidation in inland waters. We used the expanded freshwater CH₄ isotopic dataset to calculate a bottom-up estimate of global source δ²H–CH₄ and δ¹³C-CH₄ that includes spatially resolved isotopic signatures for freshwater CH₄ sources. Our bottom-up global source δ²H–CH₄ estimate (−278 ± 15 ‰) is higher than a previous estimate using a similar approach, as a result of the more enriched global freshwater δ²H–CH₄ signature derived from our dataset. However, it is in agreement with top-down estimates of global source δ²H–CH₄ based on atmospheric measurements and estimated atmospheric sink fractionations. In contrast our bottom-up global source δ¹³C-CH₄ estimate is lower than top-down estimates, partly as a result of a lack of δ¹³C-CH₄ data from C₄-plant-dominated ecosystems. In general, we find there is a particular need for more data to constrain isotopic signatures for low-latitude microbial CH₄ sources.

1 Introduction

Methane (CH₄) is an important greenhouse gas that accounts for approximately 25 % of current anthropogenic global warming, but we do not have a complete understanding of the current relative or absolute fluxes of different CH₄ sources to the atmosphere (Schwietzke et al., 2016; Saunois et al., 2019), nor is there consensus on the causes of recent decadal-scale changes in the rate of increase in atmospheric CH₄ (Kai et al., 2011; Pison et al., 2013; Rice et al., 2016; Schaefer et al., 2016; Worden et al., 2017; Thompson et al., 2018; Turner et al., 2019). Freshwater ecosystems are an integral component of the global CH₄ budget. They are one of the largest sources of atmospheric CH₄ and are unequivocally the largest natural, or non-anthropogenic, source (Bastviken et al., 2011; Saunois et al., 2019). At the same time the geographic distribution of freshwater CH₄ emissions, changes in the strength of this source through time, and the relative importance of wetland versus inland water CH₄ emissions all remain highly uncertain (Pison et al., 2013; Schaefer et al., 2016; Ganesan et al., 2018; Saunois et al., 2019; Turner et al., 2019). Gaining a better understanding of freshwater CH₄ emissions on a global scale is of great importance for understanding potential future climate feedbacks related to CH₄ emissions from these ecosystems (Bastviken et al., 2011; Koven et al., 2011; Yvon-Durocher et al., 2014; Zhang et al., 2017). It is also necessary in order to better constrain the quantity and rate of change of other CH₄ emissions sources, including anthropogenic sources from fossil fuels, agriculture, and waste (Kai et al., 2011; Pison et al., 2013; Schaefer et al., 2016).

Isotopic tracers, particularly δ¹³C, have proven to be very useful in constraining global CH₄ sources and sinks (Kai et al., 2011; Nisbet et al., 2016; Rice et al., 2016; Schaefer et al., 2016; Schwietzke et al., 2016; Nisbet et al., 2019). However, δ¹³C source signatures cannot fully differentiate CH₄ sources, leaving residual ambiguity in source apportionment (Schaefer et al., 2016; Schwietzke et al., 2016; Worden et al., 2017; Turner et al., 2019). Applying additional isotopic tracers to atmospheric CH₄ monitoring has the potential to greatly improve our understanding of CH₄ sources and sinks (Turner et al., 2019; Saunois et al., 2020). Recently developed laser-based methods, including cavity ring-down spectroscopy, quantum cascade laser absorption spectroscopy, and tunable infrared laser direct absorption spectroscopy, in addition to continued application of isotope ratio mass spectrometry (Chen et al., 2016; Röckmann et al., 2016; Yacovitch et al., 2020) could greatly enhance the practicality of atmospheric δ²H–CH₄ measurements at greater spatial and temporal resolution, similar to recent developments for δ¹³C-CH₄ measurements (Zazzeri et al., 2015; Miles et al., 2018). δ²H–CH₄ measurements have proven useful in understanding past CH₄ sources in ice core records (Whiticar and Schaefer, 2007; Mischler et al., 2009; Bock et al., 2010, 2017) but have seen only limited use in modern atmospheric CH₄ budgets (Kai et al., 2011; Rice et al., 2016), in part because of loosely constrained source terms, as well as relatively sparse atmospheric measurements. Atmospheric inversion models have shown that increased spatial and temporal resolution of δ²H–CH₄ measurements could provide substantial improvements in precision for global and regional methane budgets (Rigby et al., 2012).

δ²H–CH₄ measurements could prove especially useful in understanding freshwater CH₄ emissions. Freshwater δ²H–CH₄ is thought to be highly dependent on δ²H–H₂O (Waldron et al., 1999a; Whiticar, 1999; Chanton et al., 2006). Since δ²H–H₂O exhibits large geographic variation as a function of temperature and fractional precipitation (Rozanski et al., 1993; Bowen and Revenaugh, 2003), δ²H–CH₄ measurements have the potential to differentiate freshwater CH₄ sources by latitude. This approach has been applied in some ice core studies (Whiticar and Schaefer, 2007; Bock et al., 2010), but geographic source signals remain poorly constrained, in part because of small datasets and because of incompletely understood relationships between δ²H–H₂O and δ²H–CH₄. In contrast, recent studies of modern atmospheric δ²H–CH₄ have typically not accounted for geographic variation in freshwater CH₄ sources (Kai et al., 2011; Rice et al., 2016). Relatedly, other studies have found an important role for variation in δ²H–H₂O in controlling δ²H–CH₄ from biomass burning (Umezawa et al., 2011) and from plants irradiated by UV light (Vigano et al., 2010), as well as the δ²H of H₂ produced by wood combustion (Röckmann et al., 2016).

In addition to variance caused by δ²H–H₂O, a number of additional biogeochemical variables have been proposed to influence δ²H–CH₄ in freshwater environments. These include differences in the predominant biochemical pathway of methanogenesis (Whiticar et al., 1986; Whiticar, 1999; Chanton et al., 2006), the extent of methane oxidation (Happell et al., 1994; Waldron et al., 1999a; Whiticar, 1999; Cadieux et al., 2016), isotopic fractionation resulting from diffusive gas transport (Waldron et al., 1999a; Chanton, 2005), and differences in the thermodynamic favorability or enzymatic reversibility of methanogenesis (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). These influences on δ²H–CH₄ have the potential to complicate geographic signals but also provide the potential to differentiate ecosystem sources, if specific ecosystems are characterized by differing rates and pathways of methanogenesis, rates of CH₄ oxidation, or gas transport processes. A recent study proposed that freshwater δ¹³C-CH₄ could be differentiated geographically based on ecosystem differences in the prevalence of different methanogenic pathways and in the predominance of C₄ plants, in addition to the geographic distribution of wetland ecosystems (Ganesan et al., 2018). δ²H–CH₄ measurements have the potential to complement this approach by providing an additional isotopic parameter for differentiating ecosystem and geographic CH₄ source signatures.

In order to use δ²H–CH₄ as an indicator of freshwater ecosystem contributions to global and regional CH₄ emissions budgets, a clearer understanding of freshwater δ²H source signals and how they vary by geographic location, ecosystem type, and other variables is needed. In order to address this need, we have assembled and analyzed a dataset of 897 δ²H–CH₄ measurements from 129 individual ecosystems, or sites, derived from 40 publications (Schoell, 1983; Woltemate et al., 1984; Burke and Sackett, 1986; Whiticar et al., 1986; Burke et al., 1988; Burke, 1992; Burke et al., 1992; Lansdown et al., 1992; Lansdown, 1992; Martens et al., 1992; Wassmann et al., 1992; Happell et al., 1993; Levin et al., 1993; Happell et al., 1994; Wahlen, 1994; Bergamaschi, 1997; Chanton et al., 1997; Hornibrook et al., 1997; Tyler et al., 1997; Zimov et al., 1997; Bellisario et al., 1999; Popp et al., 1999; Waldron et al., 1999b; Chasar et al., 2000; Marik et al., 2002; Nakagawa et al., 2002a, b; Chanton et al., 2006; Walter et al., 2006, 2008; Alstad and Whiticar, 2011; Brosius et al., 2012; Sakagami et al., 2012; Bouchard et al., 2015; Stolper et al., 2015; Wang et al., 2015; Cadieux et al., 2016; Douglas et al., 2016; Thompson et al., 2016; Lecher et al., 2017). We have advanced existing datasets of freshwater δ²H–CH₄ (Whiticar et al., 1986; Waldron et al., 1999a; Sherwood et al., 2017) in the following key attributes: (1) compiling a significantly larger dataset than was previously available; (2) compiling paired δ¹³C-CH₄ data for all sites, δ¹³C–CO₂ data for 50 % of sites, and δ²H–H₂O data for 47 % of sites; (3) compiling geographic coordinates for all sites, providing the ability to perform spatial analyses and compare with gridded datasets of precipitation isotopic composition; and (4) classifying all sites by ecosystem and sample type (dissolved vs. gas samples), allowing for a clearer differentiation of how these variables influence δ²H–CH₄.

Using this dataset we applied statistical analyses to address key questions surrounding the global distribution of freshwater δ²H–CH₄, the variables that control this distribution, and its implications for atmospheric δ²H–CH₄. Specifically, we investigated the nature of the global dependence of δ²H–CH₄ on δ²H–H₂O and whether this relationship results in significant differences in freshwater δ²H–CH₄ by latitude. We also assessed whether variability in δ¹³C-CH₄, δ¹³C–CO₂, and α_C was correlated with δ²H–CH₄ and whether there are significant differences in δ²H–CH₄ between different ecosystem and sample types. Finally, we used our dataset, combined with other isotopic datasets (Sherwood et al., 2017) and flux estimates (Saunois et al., 2020), to estimate the global δ²H–CH₄ and δ¹³C-CH₄ of global emissions sources, and we compared this with previous estimates based on atmospheric measurements or isotopic datasets (Whiticar and Schaefer, 2007; Rice et al., 2016; Sherwood et al., 2017).

2 Methods

2.1 Isotope nomenclature

Hydrogen and carbon isotope ratios are primarily discussed as delta values, using the generalized formula (Coplen, 2011)

$$\begin{array}{}\text{(1)}& \mathit{\delta }={\displaystyle \frac{\left(R_{\mathrm{sample}}-R_{\mathrm{standard}}\right)}{R_{\mathrm{standard}}}},\end{array}$$

where R is the ratio of the heavy isotope to the light isotope, and the standard is Vienna Standard Mean Ocean Water (VSMOW) for δ²H and Vienna Pee Dee Belemnite (VPDB) for δ¹³C. δ values are expressed in per mil (‰) notation.

We also refer to the isotopic fractionation factor between two phases, or α, which is defined as

$$\begin{array}{}\text{(2)}& {\mathit{\alpha }}_{a-b}={\displaystyle \frac{R_a}{R_b}}={\displaystyle \frac{{\mathit{\delta }}_a+\mathrm{1}}{{\mathit{\delta }}_b+\mathrm{1}}},\end{array}$$

Specifically, we discuss the carbon isotope fractionation factor between CO₂ and CH₄ (α_C) and the hydrogen isotope fractionation factor between H₂O and CH₄ (α_H).

2.2 Dataset compilation

2.2.1 Literature survey

To identify datasets we used a set of search terms (methane OR CH₄ AND freshwater OR wetland OR peatland OR swamp OR marsh OR lake OR pond OR “inland water” AND “hydrogen isotope” OR “δD” OR “δ²H”) in Google Scholar to find published papers that discussed this measurement. We also identified original publications using previously compiled datasets (Waldron et al., 1999a; Sherwood et al., 2017). Data for 90 % of sites were from peer-reviewed publications. Data from 13 sites were from a PhD dissertation (Lansdown, 1992).

2.2.2 Dataset structure

Most samples were associated with geographic coordinates in data tables or text documentation, or with specific geographic locations such as the name of a town or city. In a few cases we identified approximate geographic locations based on text descriptions of sampling sites, with the aid of Google Earth software. Sampling sites were defined as individual water bodies or wetlands as identified in the relevant study. In one study where a number of small ponds were sampled from the same location, we grouped ponds of a given type as a single site (Bouchard et al., 2015). We divided sampling sites into six ecosystem categories: (1) lakes and ponds (hereafter lakes), (2) rivers and floodplains (hereafter rivers), (3) bogs, (4) fens, (5) swamps and marshes, and (6) rice paddies. Most data (seven of eight sites) in the rivers category are from floodplain lake or delta environments. Swamps and marshes were combined as one category because of a small number of sites and because there is no clear indication of biogeochemical differences between these ecosystems. To make these categorizations we relied on site descriptions in the data source publications. We also analyzed data in two larger environment types, inland waters (lakes and rivers) and wetlands (bogs, fens, swamps and marshes, and rice paddies), which correspond to two flux categories (freshwaters and natural wetlands) documented by Saunois et al. (2020). While rice paddies are an anthropogenic ecosystem; they are wetlands where microbial methanogenesis occurs under generally similar conditions to natural wetlands, and therefore we included them as wetlands in our analysis. In some cases the type of wetland was not specified. We did not differentiate between ombrotrophic and minerotrophic peatlands since most publications did not specify this difference, although it has been inferred to be important for δ¹³C-CH₄ distributions (Hornibrook, 2009). For studies of bogs and fens that sampled by soil depth we have only included sample measurements from the upper 50 cm. This is based on the observation of large-scale isotopic variability with soil depth in these ecosystems (Hornibrook et al., 1997; Waldron et al., 1999b) and the observation that shallow peat is typically the dominant source of atmospheric emissions (Waldron et al., 1999b; Bowes and Hornibrook, 2006; Shoemaker et al., 2012), which is our primary focus in this study. Other wetland ecosystems were not sampled by soil depth.

We also categorized samples by the form in which CH₄ was sampled, differentiating between dissolved CH₄ and CH₄ emitted through diffusive fluxes, which we group as dissolved CH₄, and gas-phase samples, including bubbles sampled either by disturbing sediments or by collecting natural ebullition fluxes. In some cases the sampling method or type of sample was not specified, or samples were a mix of both categories, which we did not attempt to differentiate.

Where possible (78 % of sites), δ²H–CH₄ and δ¹³C-CH₄ values, as well as δ¹³C–CO₂ and δ²H–H₂O, were gathered from data files or published tables. In a number of publications, representing 22 % of sites, data were only available graphically. For these studies we used WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/, last access: 15 August 2017) software to extract data for these parameters. Previous studies have shown that user errors from WebPlotDigitizer are typically small, with 90 % of user-generated data within 1 % of the actual value (Drevon et al., 2017). Based on this, we estimate a typical error for δ²H–CH₄ data of less than 3 ‰. Studies where data were derived from graphs are identified in Supplement Table S1 (Douglas et al., 2020b).

2.2.3 Estimates of δ²H–H₂O and its effects on δ²H–CH₄

To estimate δ²H–H₂O for sites where it was not measured, we relied on estimates of the isotopic composition of precipitation (δ²H_p), derived from the Online Isotopes in Precipitation Calculator v.3.1 (OIPC3.1; http://www.waterisotopes.org, last access: 10 December 2020; Bowen and Wilkinson, 2002; Bowen and Revenaugh, 2003; Bowen et al., 2005). Inputs for δ²H_p estimates are latitude, longitude, and elevation. We estimated elevation for each site surface elevation at the site's geographic coordinates reported by Google Earth. We tabulated estimates of both annual and growing season precipitation-amount-weighted δ²H_p, where the growing season is defined as months with a mean temperature greater than 0 ^∘C. We then analysed whether annual or growing season δ²H_p is a better estimate of environmental δ²H–H₂O for both wetlands and inland waters by comparing these values with measured δ²H–H₂O for sites with measurements (see Sect. 3.2). Based on this analysis, we then identified a “best-estimate” δ²H–H₂O value for each site, using an approach similar to that of Waldron et al. (1999a). Namely, we apply measured δ²H–H₂O where available and estimates based on the regression analyses detailed in Sect. 3.2 for sites without measurements.

To account for the effects of δ²H–H₂O on δ²H–CH₄, we introduce the term δ²H–CH_4,W0, which is the estimated δ²H–CH₄ of a sample if it had formed in an environment where δ²H–H₂O = 0 ‰. This is defined by the equation

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}^{\mathrm{2}}{\text{H-CH}}_{\mathrm{4},\mathrm{W}\mathrm{0}}=\mathit{\delta }{}^{\mathrm{2}}{\text{H-CH}}_{\mathrm{4}}-\left(b\times \mathit{\delta }{}^{\mathrm{2}}{\text{H-H}}_{\mathrm{2}}\mathrm{O}\right),\end{array}$$

where δ²H–H₂O is the best-estimate value for each site described above, and b is the slope of the regression relationship of δ²H–H₂O vs. δ²H–CH₄ for the entire dataset, as reported in Sect. 3.3. We also performed the same calculation separately for the subset of sites with measured δ²H–H₂O. We analyze δ²H–CH_4,W0 instead of α_H because, as discussed in Sect. 3.3, the global relationship between δ²H_p vs. δ²H–CH₄ does not correspond to a constant value of α_H, and therefore deviations from the global empirical relationship are more clearly expressed as a residual as opposed to a fractionation factor.

2.3 Statistical analyses

For all statistical analyses we use site-level mean isotopic values. This avoids biasing our analyses towards sites with a large number of measurements, since there are large differences in the number of samples analyzed per site (n ranges from 66 to 1). To calculate α_C we used average δ¹³C-CH₄ and δ¹³C–CO₂ at a given site. This approach entails some additional uncertainty in this variable but was necessary because at many sites these measurements were not made on the same samples.

We perform a set of linear regression analyses δ²H–CH₄ against other isotopic variables, in addition to latitude. All statistical analyses were performed in MATLAB. We considered p<0.05 to be the threshold for identifying significant regression relationships. We chose to perform unweighted regression, as opposed to weighted regression based on the standard error of sample measurements, for two reasons. First, a small number of sites with a large number of measurements, and therefore small standard error, had a disproportionate effect on weighted regression results. Second, in environmental research unweighted regression is frequently less biased than weighted regression (Fletcher and Dixon, 2012). Based on a test proposed by Fletcher and Dixon (2012), unweighted regression is appropriate for this dataset. We used analysis of covariance to test for significant differences between regression relationships.

To compare isotopic data (δ²H–CH₄ and δ¹³C-CH₄) between groups (i.e. latitudinal bands, ecosystem types, sample types), we used non-parametric statistical tests to test whether the groups were from different distributions. We used non-parametric tests because some sample groups were not normally distributed, as determined by a Shapiro–Wilk test (Shapiro and Wilk, 1965). For comparing differences between the distributions of two groups we used the Mann–Whitney U test (Mann and Whitney, 1947), whereas when comparing differences between the distributions of more than two groups we used the Kruskal–Wallis H test (Kruskal and Wallis, 1952), combined with Dunn's test to compare specific sample group pairs (Dunn, 1964). We considered p<0.05 to be the threshold for identifying groups with significantly different distributions.

When comparing δ¹³C-CH₄ by latitude and ecosystem, we combined the data from this study with additional data from Sherwood et al. (2017) (32 additional sites) where δ²H–CH₄ was not measured to make our dataset as representative as possible. To our knowledge this combined dataset is the largest available compiled dataset of freshwater δ¹³C-CH₄, although there are many more δ¹³C-CH₄ measurements that have not yet been aggregated. We did not include these additional data when analysing differences by sample type, as sample type was not specified in the dataset of Sherwood et al. (2017).

2.4 Estimation of global atmospheric CH₄δ²H and δ¹³C source values

To better understand how latitudinal differences in wetland isotopic source signatures influence atmospheric δ²H–CH₄ and δ¹³C-CH₄, we calculated a bottom-up mixing model of δ²H–CH₄ and δ¹³C-CH₄. For this calculation we ascribed all CH₄ sources a flux (derived from Saunois et al., 2020; see details below) and a δ²H and δ¹³C value, and we calculated the global atmospheric source value using an isotopic mixing model. Because of non-linearity when calculating mixtures using δ²H values, we performed the mixing equation using isotopic ratios (see Sect. 2.1). The mixing equation is as follows:

$$\begin{array}{}\text{(4)}& R_{\mathrm{mix}}=f_{\mathrm{1}}{R}_{\mathrm{1}}+f_{\mathrm{2}}{R}_{\mathrm{2}}+f_n{R}_n,\end{array}$$

where f_n is the fractional flux for each source term (i.e. the ratio of the source flux to total flux), and R_n is the isotope ratio for each source term.

Values for the flux, δ²H, and δ¹³C applied for each source term are shown in Table 1. We used bottom-up source fluxes from Saunois et al. (2020) for the period 2008–2017. For categories other than wetlands, inland waters, and rice paddies, we used global fluxes and isotope values, since geographically resolved isotopic source signature estimates are not available. For these sources we used δ²H and δ¹³C values published by Sherwood et al. (2017), using the mean value for each source term. For wetlands, inland waters, and rice paddies, we used geographically resolved (60–90^∘ N, 30–60^∘ N, 90^∘ S–30^∘ N) fluxes derived from Saunois et al. (2019) for the period 2008–2017 and mean δ²H–CH₄ for these latitudinal bands from this study.

Table 1 Estimates of source-specific fluxes, δ²H–CH₄, and δ¹³C-CH₄ and their uncertainties, used in mixing models and Monte Carlo analyses.

^a No specific isotopic measurements in the database (Sherwood et al., 2017). We applied the mean isotopic values for oil and gas and applied the standard deviation of for oil and gas as the uncertainty. ^b No specific isotopic measurements in database (Sherwood et al., 2017). We used the isotopic values and uncertainties from livestock. ^c Only one δ²H measurement in database (Sherwood et al., 2017). We applied 50 ‰ as a conservative uncertainty estimate. ^d No specific isotopic measurement in database (Sherwood et al., 2017). We used the isotopic values and uncertainties for high-latitude wetlands. ^e No specific isotopic measurements in database (Sherwood et al., 2017). We applied approximate isotopic values based on Whiticar (1999) and conservatively large uncertainty estimates. ^f No specific isotopic measurements in database (Sherwood et al., 2017). We used the isotopic values and uncertainties for oil and gas. ^g We applied all isotopic measurements of biomass burning to both the biomass burning and biofuel burning categories. We did not correct for the relative proportion of C₃ and C₄ plant combustion sources (see Sect. 2.4).

To calculate mean δ¹³C-CH₄ from wetlands, inland waters, and rice paddies for different latitudinal bands, we combined the data from this study along with additional data from Sherwood et al. (2017) (32 additional sites) to make our estimated source signatures as representative as possible. To our knowledge this combined dataset is the largest available compiled dataset of freshwater δ¹³C-CH₄ (see Sect. 2.3). Sites dominated by C₄ plants are notably underrepresented in this combined dataset. In addition, the biomass burning dataset of Sherwood e al. (2017) contains very few data from C₄ plant combustion. We performed a separate estimate of global source δ¹³C-CH₄ that attempted to correct for these likely biases by making two adjustments: (1) using the estimated low-latitude wetland δ¹³C-CH₄ signature of Ganesan et al. (2018) (−56.7 ‰), which takes into account the predicted spatial distribution of C₄-plant-dominated wetlands and (2) using the biomass burning δ¹³C-CH₄ signature of Schwietzke et al. (2016) (−22.3 ‰), which is weighted by the predicted contribution from C₄ plant combustion. We did not attempt to take into account δ¹³C-CH₄ from ruminants feeding on C₄ plants. For the C₄-plant-corrected δ¹³C-CH₄ estimate, we applied the same uncertainties that are reported in Table 1.

Since fluxes from other natural sources are not differentiated for the period 2008–2017, we calculated the proportional contribution of each category of other natural sources for the period 2000–2009 (Saunois et al., 2020), and we applied this to the total flux from other natural sources for 2008–2017. Inland waters and rice paddies do not have geographically resolved fluxes reported in Saunois et al. (2020). Therefore, we calculated the proportion of other natural sources attributed to inland waters from 2000–2009 (71 %), and we applied this proportion to the geographically resolved fluxes of other natural sources. Similarly, we calculated the proportion of agricultural and waste sources attributed to rice agriculture from 2008–2017 (15 %), and we applied this to the geographically resolved fluxes of agricultural and waste fluxes.

To estimate uncertainty in the modelled total source δ²H and δ¹³C values, we conducted Monte Carlo analyses (Thompson et al., 1992). We first estimated the uncertainty for each flux, δ²H, and δ¹³C term. Flux uncertainties were defined as one-half of the range of estimates provided by Saunois et al. (2020). For sources where fluxes were calculated as a proportion of a larger flux, we applied the same proportional calculation to uncertainty estimates. In cases where one-half of the range of reported studies was larger than the flux estimate, we set the uncertainty to be equal to the flux estimate to avoid negative fluxes in the mixing model. Isotopic source signal uncertainties were defined as the 95 % confidence interval of the mean value for a given source category. For some sources there are insufficient data to calculate a 95 % confidence interval, and we applied a conservative estimate of uncertainty for these sources, as detailed in Table 1. Confidence intervals for fossil fuel isotopic source signatures do not take into account variation in emissions fluxes and isotopic values between regions or resource types (i.e. conventional vs. unconventional reservoirs). This variation is difficult to quantify with available datasets but could imply additional uncertainty in global source signatures. We recalculated the δ²H and δ¹³C mixing models 10 000 times, each time sampling inputs from the uncertainty distribution for each variable. We assumed all uncertainties were normally distributed. We interpret the 2σ standard deviation of the resulting Monte Carlo distributions as an estimate of the uncertainty of our total atmospheric CH₄ source isotopic values. To examine how the Monte Carlo analyses were specifically influenced by uncertainty in isotopic source signatures vs. flux estimates, we conducted sensitivity tests where we set the uncertainty in either isotopic source signatures or flux estimates to zero. We also used the mixing model and Monte Carlo method to estimate the mean flux-weighted freshwater δ²H–CH₄ and δ¹³C-CH₄, using only the inputs for freshwater environments (wetlands, inland waters, and rice cultivation) from Table 1 (see Sect. 3.5).

3 Results and discussion

3.1 Dataset distribution

The dataset is primarily concentrated in the Northern Hemisphere (Fig. 1a) but is distributed across a wide range of latitudes between 3^∘ S and 73^∘ N (Fig. 1c). The majority of sampled sites are from North America (Fig. 1b), but there are numerous sites from Eurasia. A much smaller number of sites are from South America and Africa. We define three latitudinal bands for describing geographic trends: low latitudes (3^∘ S to 30^∘ N), mid-latitudes (30 to 60^∘ N), and high-latitudes (60 to 90^∘ N). This definition was used primarily because it corresponds with a commonly applied geographic classification of CH₄ fluxes (Saunois et al., 2020).

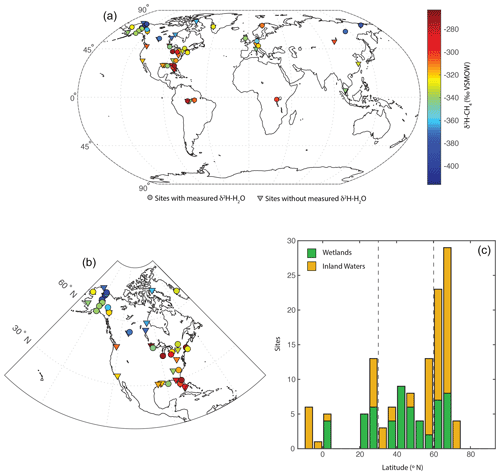
Figure 1 Distribution of sites shown (a) on a global map, with site mean CH₄-δ²H values indicated in relation to a colour bar. Sites with and without measured δ²H–H₂O are differentiated: (b) on a map of North America and (c) as a histogram of sites by latitude, differentiated between wetlands and inland waters. Dashed lines in (c) indicate divisions between low-latitude, mid-latitude, and high-latitude sites.

A total of 74 of 129 sites are classified as inland waters, primarily lakes (n=66), with a smaller number from rivers (n=8). To our knowledge, all of the inland water sites are natural ecosystems and do not include reservoirs. A total of 55 sites are classified as wetlands, including 16 bogs, 14 swamps and marshes, 12 fens, and 8 rice paddies. For the majority of sites (n=84) gas samples were measured, whereas studies at 36 sites measured dissolved CH₄ or diffusive fluxes.

3.2 Use of δ²H_p as an estimator for freshwater δ²H–H₂O

As discussed in Sect. 2.2.3, we regressed annual and growing season δ²H_p against measured δ²H–H₂O to determine which is a better estimator for sites where δ²H–H₂O is not measured. We performed this analysis separately for wetland and inland water environments because these broad environmental categories have distinct hydrological characteristics. For all regression analyses we found strong correlations, with R² values between 0.82 and 0.88 (Fig. 2). For wetlands, regression using annual δ²H_p produces a slightly better fit and also produces a slope within uncertainty of 1 (Fig. 2a), suggesting that variation in annual δ²H_p scales proportionately with variation in measured δ²H–H₂O. However, the intercept of this relationship was significantly greater than 0 (19 ± 9 ‰). We interpret this intercept as indicating that evaporative isotopic enrichment is generally important in controlling δ²H–H₂O in wetlands. A slope slightly greater than 1 is also consistent with evaporative enrichment, since greater evaporation rates would be expected in low-latitude environments with higher δ²H–H₂O. These results are consistent with detailed studies of wetland isotope hydrology that indicate a major contribution from groundwater, with highly dampened seasonal variability relative to precipitation, but also indicate evaporative enrichment of water isotopes in shallow soil water (Sprenger et al., 2017; David et al., 2018).

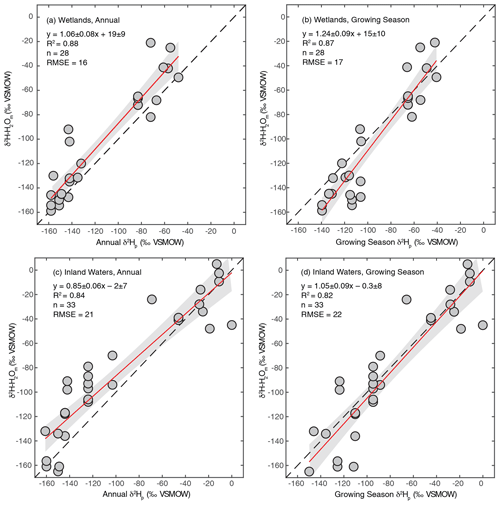
Figure 2 Scatter plots of annual or growing season δ²H_p vs. measured δ²H–H₂O for wetland (a, b) and inland water (c, d) sites. The red lines indicate the best fit, with a 95 % confidence interval (grey envelopes), and the dashed black lines are the 1:1 relationship.

For inland waters, regression with growing season δ²H_p produces a relationship that is within error of the 1:1 line (Fig. 2c), in contrast to annual δ²H_p, which produces a flatter slope (Fig. 2d). We infer that seasonal differences in δ²H_p are important in determining δ²H–H₂O in the inland water environments analyzed, especially at high latitudes, implying that these environments generally have water residence times on subannual timescales. This finding is generally consistent with evidence for seasonal variation in lake water isotopic compositions that is dependent on lake water residence times (Tyler et al., 2007; Jonsson et al., 2009). Lake water residence times vary widely, primarily as a function of lake size, but isotopic data imply that small lakes have water residence times of less than a year (Brooks et al., 2014), resulting in seasonal isotopic variability (Jonsson et al., 2009). Isotopic enrichment of lake water is highly variable but is typically minor in humid and high-latitude regions (Jonsson et al., 2009; Brooks et al., 2014), which characterizes most of our study sites.

Based on these results we combine measured and estimated δ²H–H₂O to determine a best-estimate value for each site, an approach similar to that of Waldron et al. (1999a). For sites with measured δ²H–H₂O values we use that value. For inland water sites without measured δ²H–H₂O we use modelled growing season δ²H_p since the regression of this against measured δ²H–H₂O is indistinguishable from the 1:1 line (Fig. 2d). For wetland sites without measured δ²H–H₂O, we estimate δ²H–H₂O using the regression relationship with annual precipitation δ²H–H₂O shown in Fig. 2a. The root-mean-square errors (RMSE) of these relationships (16 ‰ for wetlands, 22 ‰ for inland waters) provide an estimate of the uncertainty associated with estimating δ²H–H₂O using δ²H_p. Given the uncertainty associated with estimating δ²H–H₂O using δ²H_p, for all analyses presented below that depend on δ²H–H₂O values we also analyse the dataset only including sites with measured δ²H–H₂O.

3.3 Relationship between δ²H–H₂O and δ²H–CH₄

We carried out regression analyses of δ²H–H₂O vs. δ²H–CH₄, both using best-estimate δ²H–H₂O as described in Sect. 3.2 (Fig. 3a) and only including sites with measured δ²H–H₂O (Fig. 3b). In addition we analysed the relationship for all sites using annual (Fig. 3c) and growing season (Fig. 3d) δ²H_p. Identifying the relationship between modelled δ²H_p and δ²H–CH₄ is of value because this could be used to create gridded global predictions of δ²H–CH₄ based on gridded datasets of δ²H_p (Bowen and Revenaugh, 2003), as well as to predict the distribution of δ²H–CH₄ under past and future global climates using isotope enabled Earth system models (Zhu et al., 2017).

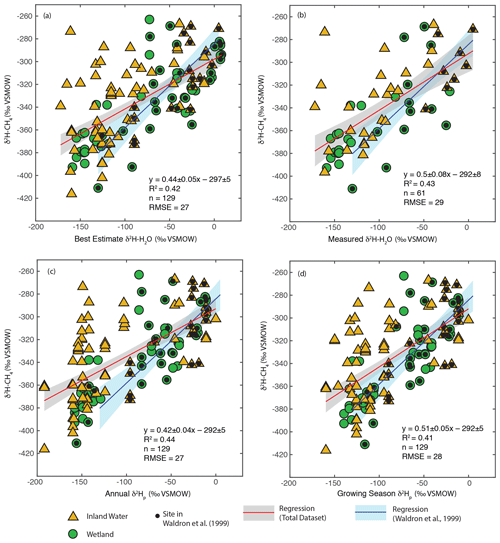
Figure 3 Scatter plots of δ²H–CH₄ vs. (a) best-estimate δ²H–H₂O, (b) measured δ²H–H₂O, (c) annual δ²H_p, and (d) growing season δ²H_p. Sites that were included in the analysis of Waldron et al. (1999a) are indicated. The regression relationship for the total dataset in each plot is shown by the red line, with its 95 % confidence interval (grey envelope). The regression relationship and confidence interval for the dataset of Waldron et al. (1999a) are shown in blue. Uncertainties for reported regression relationships are standard errors.

δ²H–CH₄ is significantly positively correlated with δ²H–H₂O when using all four methods of estimating δ²H–H₂O (Fig. 3, Supplement Table S2). This is the case when analysing all sites together, as well as when analysing wetlands and inland waters separately (Douglas et al., 2020b, Supplement Table S2, Fig. 4). There is no significant difference in regression relationships, based on analysis of covariance, when δ²H–CH₄ is regressed against best-estimate δ²H–H₂O, measured δ²H–H₂O, or modelled δ²H_p, nor is there a major difference in R² values or RMSE (Douglas et al., 2020b, Supplement Table S2). Regression with wetland sites consistently results in a higher R² values and lower RMSE than regression with inland water sites.

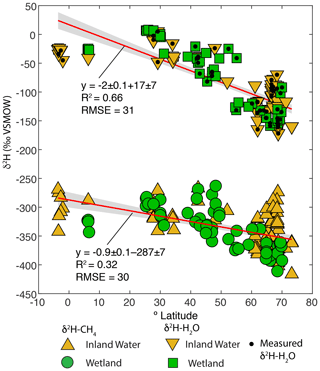
Figure 4 Scatter plots of δ²H–CH₄ and best-estimate δ²H–H₂O, vs. latitude (^∘ N). Sites with measured δ²H–H₂O are indicated. Envelopes indicate 95 % confidence intervals for regression lines.

Given the similar results when regressing with estimated or measured δ²H–H₂O, we infer that using either the “best-estimate” δ²H–H₂O or modelled δ²H_p, instead of measured δ²H–H₂O, to predict δ²H–CH₄ does not result in substantial additional error. This implies that isotope-enabled Earth system models (ESMs) could be used to predict the distribution of freshwater δ²H–CH₄ under past and future climates based on modelled δ²H_p, although the substantial scatter in Fig. 3c and d should be taken into account. The Southern Hemisphere is highly underrepresented in the δ²H–CH₄ dataset. However, the mechanisms linking δ²H–CH₄ with δ²H–H₂O should not differ in the Southern Hemisphere, and we argue that the relationships observed in this study are suitable to predict Southern Hemisphere freshwater δ²H–CH₄. The choice of predicting δ²H–CH₄ using growing-season vs. annual precipitation δ²H_p could be important, with steeper slopes overall when regressing against growing season δ²H_p. Based on our analysis in Sect. 3.2, we suggest that annual δ²H_p may be more appropriate for estimating wetland δ²H–CH₄, while growing season δ²H_p may be more appropriate for estimating inland water δ²H–CH₄. Forthcoming research will combine gridded datasets of wetland distribution (Ganesan et al., 2018), modelled annual δ²H_p (Bowen and Revenaugh, 2003), and the regression relationships from this study to predict spatially resolved wetland δ²H–CH₄ at a global scale (Stell et al., 2021).

Overall, our results are broadly consistent with those of Waldron et al. (1999a), and confirm the finding of that study that δ²H–H₂O is the predominant predictor of global variation in δ²H–CH₄. All of the regression slopes produced using our dataset are flatter than the regression relationship found by Waldron et al. (1999a) using a smaller dataset (0.68 ± 0.1), although the slopes are not significantly different based on analysis of covariance. Based on this result we infer that the true global relationship is likely flatter than that estimated by Waldron et al. (1999a). The difference between the regression relationships reported here and that of Waldron et al. (1999a) is largely a result of a much greater number of samples from the high latitudes (Fig. 1c), where δ²H–H₂O values are typically lower. The small number of high-latitude sites sampled by Waldron et al. (1999a) are skewed towards the low end of the high-latitude δ²H–CH₄ data from this study (Fig. 3). A similarly flatter slope (0.54 ± 0.05) was found by Chanton et al. (2006) when combining a dataset of δ²H–CH₄ from Alaskan wetlands, which are included in this study, with the dataset of Waldron et al. (1999a). Based on the range of R² values shown in Fig. 3, we estimate that δ²H–H₂O explains approximately 42 % of variability in δ²H–CH₄, implying substantial residual variability, with greater residual variability for inland water sites than for wetlands (Douglas et al., 2020b, Supplement Table S2).

Given that δ²H–H₂O is strongly influenced by latitude we examined whether δ²H–CH₄ is also significantly correlated with latitude. There is indeed a significant negative relationship between latitude and δ²H–CH₄, indicating an approximate decrease of 0.9 ‰ per degree latitude (Fig. 4). The slope is significantly flatter than that for latitude vs. δ²H–H₂O in this dataset (−2 ‰ per degree latitude), which is consistent with the inferred slope for δ²H–H₂O vs. δ²H–CH₄ (0.44 to 0.5). There is greater scatter in δ²H–CH₄ at higher latitudes, especially for inland waters, but it is unclear whether this is simply a result of a larger sample set or of differences in the underlying processes controlling δ²H–CH₄. We discuss latitudinal differences in δ²H–CH₄ in further detail in Sect. 3.5.

Comparison of δ²H–H₂O vs. δ²H–CH₄ relationships between environmental and experimental studies

To further understand the processes controlling the observed freshwater δ²H–H₂O vs. δ²H–CH₄ relationships, we compared them to results from pure culture and incubation experiments across a wide range of δ²H–H₂O values (Fig. 5), focusing on regression against best-estimate δ²H–H₂O. The regression slopes for both wetlands and inland waters (0.5 and 0.42) are within error of the in vitro relationship compiled by Waldron et al. (1999a) (0.44), based on laboratory incubations from three separate studies (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998). The intercept for the wetland and inland water regressions is higher than that for the in vitro relationship, although only the difference with inland waters is significant. In contrast, the regression slope for pure-culture acetoclastic methanogenesis experiments is much flatter (0.18 to 0.2) (Valentine et al., 2004b; Gruen et al., 2018), consistent with the prediction that one hydrogen atom is exchanged between water and the acetate methyl group during CH₄ formation (Pine and Barker, 1956; Whiticar, 1999). The large difference in intercept between the two acetate pure culture datasets is likely a function of differences in the δ²H of acetate between the experiments but could also be influenced by differences in kinetic isotope effects (Valentine et al., 2004b).

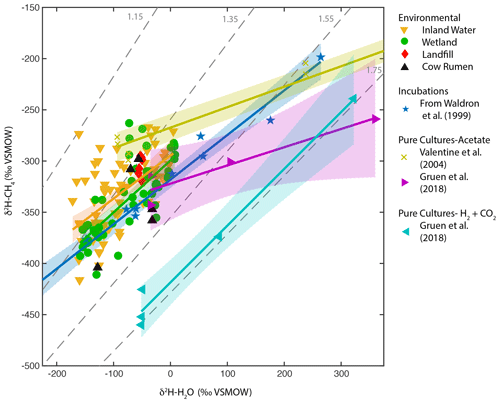
Figure 5 Scatter plots of δ²H–CH₄ vs. δ²H–H₂O for wetlands, inland waters, landfills, and cow rumen, compared with incubation and pure-culture experiments. Regression lines and confidence intervals corresponding to each dataset (except landfills and cow rumen) are shown. Dashed grey lines indicate constant values of α_H. Regression line statistics are listed in Supplement Table S2. Plotted δ²H–H₂O values are best-estimate values for wetlands and inland waters, measured values for culture experiments, and a combination of measured values and annual δ²H_p for landfills and cow rumen (see Supplement Table S3 for more details, Douglas et al., 2020b).

Pure-culture hydrogenotrophic methanogenesis experiments (Gruen et al., 2018) yield a regression slope that is consistent with a constant α_H value, although α_H can clearly vary depending on experimental or environmental conditions (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). The wetland, inland water, and in vitro regression relationships are not consistent with a constant value of α_H (Fig. 5). Our comparison supports previous inferences that the in vitro line of Waldron et al. (1999a) provides a good estimate of the slope of environmental δ²H–H₂O vs. δ²H–CH₄ relationships. This slope is likely controlled by the relative proportion of acetoclastic and hydrogenotrophic methanogenesis, the net kinetic isotope effect associated with these two methanogenic pathways, and variance in δ²H of acetate (Waldron et al., 1998, 1999a; Valentine et al., 2004a), but the relative importance of these variables remains uncertain.

In particular, the δ²H of acetate methyl hydrogen is probably influenced by environmental δ²H–H₂O and therefore likely varies geographically as a function of δ²H_p, as originally hypothesized by Waldron et al. (1999a). To our knowledge there are no measurements of acetate or acetate-methyl δ²H from natural environments with which to test this hypothesis. In general, variability in the δ²H of environmental organic molecules in lake sediments and wetlands, including fatty acids and cellulose, is largely controlled by δ²H–H₂O (Huang et al., 2002; Sachse et al., 2012; Mora and Zanazzi, 2017), albeit with widely varying fractionation factors. The δ²H of methoxyl groups in plants has also been shown to vary as a function of δ²H–H₂O (Vigano et al., 2010). Furthermore, culture experiments with acetogenic bacteria imply that there is rapid isotopic exchange between H₂ and H₂O during chemoautotrophic acetogenesis (Valentine et al., 2004a), implying that the δ²H of chemoautotrophic acetate is also partially controlled by environmental δ²H–H₂O. Incubation experiments, such as those included in the in vitro line (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998), probably contain acetate-δ²H that varies as a function of ambient δ²H–H₂O, given that the acetate in these incubation experiments was actively produced by fermentation and/or acetogenesis during the course of the experiment. This differs from pure cultures of methanogens, where acetate is provided in the culture medium and therefore does not vary in its δ²H value (Valentine et al., 2004b; Gruen et al., 2018).

3.4 Relationship of δ²H–CH₄ with δ¹³C-CH₄, δ¹³C–CO₂, and α_C

As shown in Fig. 3, there is a large amount of residual variability in δ²H–CH₄ that is not explained by δ²H–H₂O. Several biogeochemical variables have been proposed to influence freshwater δ²H–CH₄ independently of δ²H–H₂O, including the predominant biochemical pathway of methanogenesis (Whiticar et al., 1986; Whiticar, 1999; Chanton et al., 2006), the extent of methane oxidation (Happell et al., 1994; Waldron et al., 1999a; Whiticar, 1999; Cadieux et al., 2016), isotopic fractionation resulting from diffusive gas transport (Waldron et al., 1999a; Chanton, 2005), and differences in the thermodynamic favorability or reversibility of methanogenesis (Valentine et al., 2004b; Stolper et al., 2015; Douglas et al., 2016). These variables are also predicted to cause differences in δ¹³C-CH₄, δ¹³C–CO₂, and α_C. Therefore, we analysed co-variation between δ²H–CH_4,W0 (see definition in Sect. 2.2.3) and δ¹³C-CH₄, δ¹³C–CO₂, and α_C to see whether it could partially explain the residual variability in δ²H–CH₄ (Fig. 6).

In order to facilitate interpretation of isotopic co-variation, we estimated approximate vectors of predicted isotopic co-variation for the four variables being considered (Fig. 6). We emphasize that these vectors are uncertain, and while they can be considered indicators for the sign of the slope of co-variation and the relative magnitude of expected isotopic variability, they are not precise representations of the slope or intercept of isotopic co-variation. In reality, isotopic co-variance associated with these processes likely varies depending on specific environmental conditions, although the sign of co-variance should be consistent. The starting point for the vectors is arbitrarily set to typical isotopic values for inferred acetoclastic methanogenesis in freshwater systems (Whiticar, 1999). We based the vectors for differences in the dominant methanogenic pathway and methane oxidation in Figs. 8, 5, and 10 in Whiticar (1999). These figures are widely applied to interpret environmental isotopic data related to CH₄ cycling. However, we note that both environmental and experimental research has questioned whether differences in the dominant methanogenic pathway have an influence on δ²H–CH₄ (Waldron et al., 1998, 1999a). Differences in δ²H–CH₄ between hydrogenotrophic and acetoclastic methanogenesis are likely highly dependent on both the δ²H of acetate and the carbon and hydrogen kinetic isotope effects for both methanogenic pathways, both of which are poorly constrained in natural environments and are likely to vary between sites (see Sect. 3.3). We did not differentiate between anaerobic and aerobic methane oxidation, and the vectors shown are similar to experimental results for aerobic methane oxidation (Wang et al., 2016).

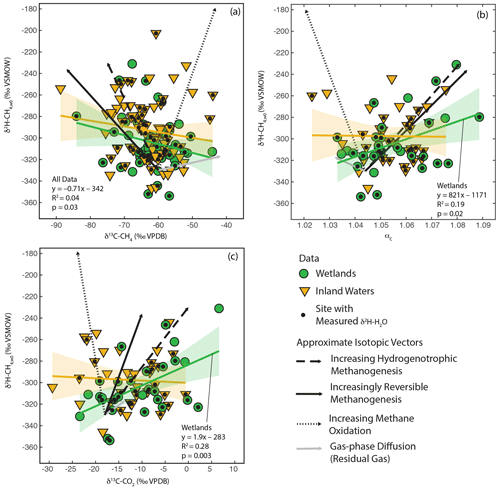
Figure 6 Scatter plots of δ²H–CH_4,w0 vs. (a) δ¹³C-CH₄, (b) α_c, and (c) δ¹³C–CO₂. Approximate vectors for isotopic co-variation related to four biogeochemical variables are shown. See details in Sect. 3.4 and the Supplement. Regression relationships are shown for wetland and inland water sites, with envelopes indicating 95 % confidence intervals. Regression statistics are shown here for relationships with significant correlations (p<0.05). All regression statistics are detailed in Supplement Table S4 (Douglas et al., 2020b).

The vector for isotopic fractionation related to gas-phase diffusion is based on the calculations of Chanton (2005) and indicates isotopic change for residual gas following a diffusive loss. Gas–liquid diffusion is predicted to have a much smaller isotopic effect (Chanton, 2005). The vector for differences in enzymatic reversibility is based on experiments where CH₄ and CO₂ isotopic compositions were measured together with changes in methane production rate or Gibbs free energy (Valentine et al., 2004b; Penning et al., 2005). We note that these studies did not measure δ²H–CH₄ in the same experiments as δ¹³C-CH₄ or δ¹³C–CO₂, implying large uncertainty in the co-variance vectors. More detail on the estimated vectors is provided in the Supplement.

We observe significant positive correlations between δ²H–CH_4,W0, calculated using best estimate δ²H–H₂O, and both δ¹³C–CO₂ and α_C for wetland sites (Douglas et al., 2020b, Fig. 6b, c; Supplement Table S4). We do not observe a significant correlation between these variables for inland water sites or for the dataset as a whole. We also observe a weak but significant negative correlation between δ²H–CH_4,W0 and δ¹³C-CH₄ for all sites but not for data disaggregated into wetlands and inland water categories (Fig. 6a). The correlations shown in Fig. 6 should be interpreted with caution, since repeating this analysis only using sites with measured δ²H–H₂O does not result in any significant correlations (Douglas et al., 2020b, Supplement Table S4). It is unclear whether this different result when using best-estimate or measured δ²H–H₂O represents a bias related to estimating δ²H–H₂O using δ²H_p or is an effect of the much smaller sample size for sites with δ²H–H₂O measurements. If accurate, the observed significant positive correlations in Fig. 6b and c suggest that residual variability in δ²H–CH₄ in wetlands is more strongly controlled by biogeochemical variables related to methanogenesis, namely differences in methanogenic pathway or thermodynamic favorability, than post-production processes such as diffusive transport and CH₄ oxidation. For inland water sites our analysis suggests that no single biogeochemical variable has a clear effect in controlling residual variability in δ²H–CH₄.

Overall, our results are not consistent with arguments that residual variability in freshwater δ²H–CH₄ is dominantly controlled by either differences in methanogenic pathway (Chanton et al., 2006) or post-production processes (Waldron et al., 1999a). Instead they highlight the combined influence of a complex set of variables and processes that are difficult to disentangle on an inter-site basis using δ¹³C measurements alone. It is also important to note the likely importance of variables that could influence δ¹³C-CH₄ or δ¹³C–CO₂ but not necessarily affect δ²H–CH₄, including variance in the δ¹³C of soil or sediment organic matter (Conrad et al., 2011; Ganesan et al., 2018), diverse metabolic and environmental sources and sinks of CO₂ in aquatic environments, and Rayleigh fractionation associated with CH₄ carbon substrate depletion (Whiticar, 1999). Finally, the possible role of other carbon substrates, such as methanol, in CH₄ production could be important in controlling isotopic co-variation. Culture experiments suggest that CH₄ produced from methanol has low δ¹³C and δ²H values relative to other pathways (Krzycki et al., 1987; Penger et al., 2012; Gruen et al., 2018), although the importance of this difference in environmental CH₄ is unclear.

Further research examining intra-site isotopic co-variation, which largely avoids complications associated with estimating δ²H–H₂O, would help to more clearly resolve the relative importance of these processes and how they vary between environments. Expanded research using methyl fluoride to inhibit acetoclastic methanogenesis (Penning et al., 2005; Penning and Conrad, 2007; Conrad et al., 2011), with a particular focus on δ²H–CH₄ measurements, would also help to clarify the importance of methanogenic pathway on isotopic co-variation. Finally, an expanded application of measurements of clumped isotopes, which have distinctive patterns of variation related to these processes (Douglas et al., 2016, 2017; Young et al., 2017; Douglas et al., 2020a), would also be of value in determining their relative importance in controlling δ²H–CH₄ values in freshwater environments.

3.5 Differences in δ²H–CH₄ and δ¹³C-CH₄ by latitude

When analysing all sites together, we found a significant difference in the distribution of δ²H–CH₄ between high-latitude sites (median: −351 ‰) and both low- (median: −298 ‰) and mid-latitude sites (median: −320 ‰) (Fig. 7a). However, we did not find a significant difference in the distribution of low- and mid-latitude sites. Similar differences were found when the data were disaggregated into wetland and inland water sites. We also found that the distribution of δ¹³C-CH₄ for low-latitude sites (median: −61.6 ‰) was significantly higher than for high-latitude sites (median: −63.0 ‰) but that mid-latitude sites (median: −60.3 ‰) were not significantly different from the other two latitudinal zones (Fig. 7b). The observed difference by latitudinal zone in δ¹³C-CH₄ appears to be driven primarily by latitudinal differences between inland water sites, where a similar pattern is found. In wetland sites we found no significant differences in the distribution of δ¹³C-CH₄ by latitude.

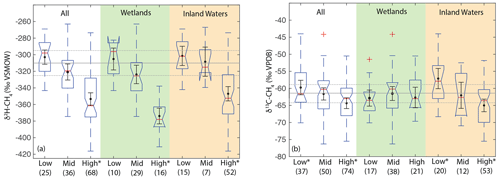
Figure 7 Boxplots of (a) δ²H–CH₄ and (b) δ¹³C-CH₄ for sites differentiated by latitude, for all data, wetlands, and inland waters. Numbers in parentheses indicate the number of sites for each category. Red lines indicate medians, boxes indicate 25th and 75th percentiles, whiskers indicate 95th and 5th percentiles, and outliers are shown as red crosses. Notches indicate the 95 % confidence intervals of the median value; where notches overlap the edges of the box this indicates the median confidence interval exceeds the 75th or 25th percentile. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the estimated flux-weighted mean values for global freshwater CH₄, and dashed lines indicate the 95 % confidence interval of this value. Asterisks in (a) indicate that high-latitude sites have significantly different distributions from other latitudinal bands. Asterisks in (b) indicate groups that have significantly different distributions from one another, within a specific environmental category. Two extremely low outliers (<−80 ‰; high-latitude wetland and inland water) are not shown in (b).

Estimates of flux-weighted mean freshwater δ²H–CH₄ and δ¹³C-CH₄, calculated using the Monte Carlo approach described in Sect. 2.4, are −310 ± 15 ‰ (Fig. 7a) and −61.5 ± 3 ‰ (Fig. 7b) respectively. Flux-weighted mean values for natural wetlands (not including inland waters or rice paddies) are −310 ± 25 ‰ for δ²H–CH₄ and −63.9 ± 3.3 ‰ for δ¹³C-CH₄. Flux-weighted mean values for inland waters are −309 ± 31 ‰ for δ²H–CH₄ and −60 ± 5.7 ‰ for δ¹³C-CH₄. As discussed in Sect. 2.4 there are limited data in our dataset or that of Sherwood et al. (2017) from C₄-plant-dominated wetlands, and therefore our low-latitude and flux-weighted mean δ¹³C-CH₄ values for wetlands are probably biased towards low values.

Differences in δ²H–CH₄ by latitude have the potential to aid in geographic discrimination of freshwater methane sources, both because it is based on a clear mechanistic linkage with δ²H–H₂O (Figs. 3 and 4) and because geographic variation in δ²H–H₂O is relatively well understood (Bowen and Revenaugh, 2003; Bowen et al., 2005). However, recent studies of atmospheric δ²H–CH₄ variation have typically not accounted for geographic variation in source signals. As an example, Rice et al. (2016) apply a constant δ²H–CH₄ of −322 ‰ for both low-latitude (0–30^∘ N) and high-latitude (30–90^∘ N) wetland emissions. Based on our dataset this estimate is an inaccurate representation of wetland δ²H–CH₄ for either 0–30^∘ N (mean: −305 ± 13 ‰) or 30–90^∘ N (mean: −345 ± 11 ‰). Studies of ice core measurements have more frequently differentiated freshwater δ²H–CH₄ values as a function of latitude. For example, Bock et al., (2010) differentiated δ²H–CH₄ between tropical (−320 ‰) and boreal (−370 ‰) wetlands. This tropical wetland signature is significantly lower than our estimate of low-latitude wetland δ²H–CH₄, although the boreal wetland signature is similar to our mean value for high-latitude wetlands (−374 ± 10 ‰). Overall, our results imply that accounting for latitudinal variation in freshwater δ²H–CH₄, along with accurate latitudinal flux estimates, is important for developing accurate estimates of global freshwater δ²H–CH₄ source signatures.

Our analysis indicates significant differences in the distribution of freshwater δ¹³C-CH₄ between the low- and high-latitudes, but mid-latitude sites cannot be differentiated. Furthermore our results do not indicate significant latitudinal differences in δ¹³C-CH₄ for wetland sites in particular. This is in contrast to previous studies that have inferred significant differences in wetland δ¹³C-CH₄ by latitude (Bock et al., 2010; Rice et al., 2016; Ganesan et al., 2018). An important caveat is that we have not analyzed a comprehensive dataset of freshwater δ¹³C-CH₄, for which there are much more published data than for δ²H–CH₄, although our analysis does comprise the largest dataset of freshwater δ¹³C-CH₄ compiled to date (see Sect. 2.3). In addition, our analysis does not take into account the geographic distribution of different ecosystem categories, although we do not find significant differences in δ¹³C-CH₄ between ecosystem categories (Fig. 8; Sect. 3.6). Low-latitude ecosystems dominated by C₄ plants are underrepresented in both our dataset and that of Sherwood et al. (2017), and accounting for this would likely lead to a more enriched low-latitude wetland δ¹³C-CH₄. In contrast, high-latitude ecosystems, including bogs, are relatively well represented in these datasets (Fig. 8), and we suggest that inferences of especially low δ¹³C-CH₄ in high-latitude wetlands (Bock et al., 2010; Rice et al., 2016; Ganesan et al., 2018) are not consistent with the compiled dataset of in situ measurements. However, we note that atmospheric estimates of high-latitude wetland δ¹³C-CH₄ (∼ −68 ± 4 ‰; Fisher et al., 2011) are lower than the median or mean value shown in Fig. 7b and are in close agreement with the relatively low values predicted by Ganesan et al. (2018). Ombrotrophic and minerotrophic peatlands have distinctive δ¹³C-CH₄ signatures (Bellisario et al., 1999; Bowes and Hornibrook, 2006; Hornibrook, 2009), with lower signatures in ombrotrophic peatlands. We did not differentiate peatlands by trophic status, and it is possible that the dataset of high-latitude wetland in situ measurements is biased towards minerotrophic peatlands with relatively high δ¹³C-CH₄.

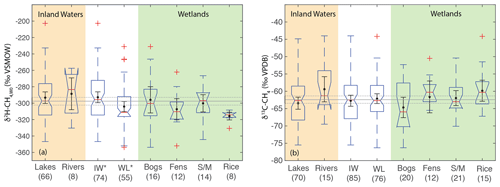
Figure 8 Boxplots of (a) δ²H–CH_4,W0 and (b) δ¹³C-CH₄ for sites differentiated by ecosystem type. Numbers in parentheses indicate the number of sites for each category. Boxplot parameters are as in Fig. 7. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the mean values across all categories, and the dashed lines indicate the 95 % confidence interval of this value. Two extremely low outliers (<−80 ‰; lake and fen) are not shown in (b). IW – inland waters; WL – wetlands; S/M – swamps and marshes. Asterisks in A indicate that inland waters and wetlands have significantly different distributions.

Latitudinal differences in δ¹³C-CH₄ inferred by Ganesan et al. (2018) were based on two key mechanisms: (1) differences in methanogenic pathway between different types of wetlands, especially between minerotrophic fens and ombrotrophic bogs; and (2) differential inputs of organic matter from C₃ and C₄ plants. Because inferred latitudinal differences in δ¹³C-CH₄ and δ²H–CH₄ are caused by different mechanisms, they could be highly complementary in validating estimates of freshwater emissions by latitude. It is also important to note that previous assessments of latitudinal differences in δ¹³C-CH₄ did not include inland water environments. Our analysis suggests that latitudinal variation in δ¹³C-CH₄ in inland waters may be more pronounced than in wetlands, although the mechanisms causing this difference will need to be elucidated with further study. A benefit of geographic discrimination based on δ²H–CH₄ is that the same causal mechanism applies to all freshwater emissions, including both wetlands and inland waters.

Potential for geographic discrimination of other microbial methane sources based on δ²H–CH₄

We speculate that latitudinal differences in δ²H–CH₄ should also be observed in other fluxes of microbial methane from terrestrial environments, including enteric fermentation in livestock and wild animals, manure ponds, landfills, and termites. This is because microbial methanogenesis in all of these environments will incorporate hydrogen from environmental water and therefore will be influenced by variation in precipitation δ²H. There are limited data currently available to test this prediction, but δ²H–CH₄ data from cow rumen and landfills are available with either specified locations or δ²H–H₂O (Burke, 1993; Levin et al., 1993; Liptay et al., 1998; Bilek et al., 2001; Wang et al., 2015; Teasdale et al., 2019). These data plot in a range that is consistent with the δ²H–CH₄ vs. δ²H–H₂O relationships for freshwater CH₄ (Fig. 5). Landfill data are only available for a very small range of estimated δ²H–H₂O, making it impossible to assess for geographic variation currently. δ²H–CH₄ data from cow rumen span a much wider range and express substantial variation that is independent of δ²H–H₂O but largely overlap measurements from freshwater environments. Based on these limited data, variation observed in incubation studies that simulate landfill conditions (Schoell, 1980; Waldron et al., 1998), and our understanding of the influence of δ²H–H₂O on microbial δ²H–CH₄ (Fig. 6), we suggest that both landfill and cow rumen δ²H–CH₄ likely varies geographically as a function of δ²H–H₂O. If validated, this variation could also be used to distinguish these CH₄ sources geographically. More data are clearly needed to test this conjecture, and it will also be important to evaluate how closely annual or seasonal δ²H_p corresponds to environmental δ²H–H₂O in both landfills and cow rumen. Relatedly, the δ²H of CH₄ emitted by biomass burning or directly by plants has also been shown to vary as a function of δ²H–H₂O (Vigano et al., 2010; Umezawa et al., 2011).

3.6 Differences in δ²H–CH₄ and δ¹³C-CH₄ by ecosystem

When comparing ecosystems, we analyze δ²H–CH_4,W0 values to account for variability related to differences in δ²H–H₂O. Ecosystem types are not evenly distributed by latitude and therefore have different distributions of δ²H–H₂O values. Our analysis does not find a significant difference in the distribution of δ²H–CH_4,W0 between ecosystems, which could be partly a result of small sample sizes for most ecosystem categories (Fig. 8). Comparing the broader categories of inland waters and wetlands, we do observe a significant difference in δ²H–CH_4,W0 distributions, with inland waters shifted towards higher values (median: −296 ‰) than wetlands (median: −311 ‰). We repeated this analysis only including sites with measured δ²H–H₂O and found the same results in terms of category differences (Supplement Fig. S1). We did not observe any significant differences in δ¹³C-CH₄ distributions between ecosystems, nor was there a significant difference in δ¹³C-CH₄ distributions between inland waters and wetlands.

The significant difference in the distribution of δ²H–CH_4,W0 between inland waters and wetlands is primarily a result of the difference in δ²H–CH₄ between these environments in the high latitudes (Figs. 3, 4, and 7). We suggest this difference could be related to a greater overall prevalence of CH₄ oxidation in inland waters. As shown in Fig. 6, the lack of positive co-variation between δ²H–CH_4,W0 and δ¹³C–CO₂ and α_C could be interpreted to support a greater role for CH₄ oxidation in controlling δ²H–CH_4,W0 in inland waters relative to wetlands, although this result requires further validation. In lakes that undergo seasonal overturning and water column oxygenation, there may be a greater overall effect of CH₄ oxidation than there is in wetlands typically. The absence of significant differences between ecosystems in terms of δ¹³C-CH₄ (Fig. 8b) is in contrast to previous studies that have suggested that fens and bogs in particular have distinctive δ¹³C-CH₄ (Ganesan et al., 2018). Bogs in particular have a very wide distribution of δ¹³C-CH₄ that could represent differences between minerotrophic and ombrotrophic bogs (Hornibrook, 2009), which we did not differentiate in our dataset. This result should be interpreted with caution given that our dataset is not a comprehensive compilation of published δ¹³C-CH₄ data, although it is the largest compiled dataset available (Sect. 2.3). We argue that inferred differences in δ¹³C-CH₄ between wetland ecosystem categories should be further verified with more comprehensive data assimilation and additional measurements.

3.7 Differences in δ²H–CH₄ and δ¹³C-CH₄ by sample type

As with comparing ecosystems, when comparing sample types we analyze δ²H–CH_4,W0 values to normalize for variability related to differences in δ²H–H₂O, since sample types are not distributed evenly by latitude. When comparing sample types, dissolved CH₄ samples do not have a significantly different δ²H–CH_4,W0 distribution for the dataset as a whole, nor is there a significant difference between these groups in wetland sites (Fig. 9a). There is, however, a significant difference in inland water sites, with dissolved CH₄ samples having a more enriched distribution (median: −270 ‰) vs. gas samples (median: −302 ‰). We repeated this analysis only including sites with measured δ²H–H₂O and found the same results in terms of category differences (Supplement Fig. S2). We did not observe a significant difference in the distribution of δ¹³C between dissolved and gas-phase CH₄ samples, either for the dataset as a whole or when the dataset was disaggregated into wetlands and inland waters (Fig. 9b).

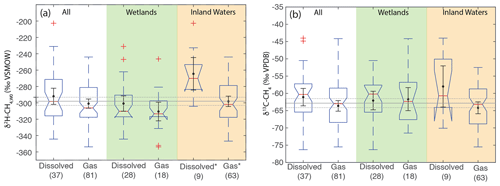
Figure 9 Boxplots of (a) δ²H–CH_4,W0 and (b) δ¹³C-CH₄ for sites differentiated by sample type. Numbers in parentheses indicate the number of sites for each category. Boxplot parameters are as in Fig. 7. Black points and error bars indicate the category mean and 95 % confidence interval of the mean. Grey lines indicate the mean values across all categories, and the dashed lines indicate the 95 % confidence interval of this value. Two extremely low outliers (<−80 ‰; dissolved wetland and gas inland water) are not shown in (b). Asterisks in (a) indicate that dissolved and gas-phase CH₄ samples from inland water sites have significantly different distributions.

We suggest that the higher δ²H–CH_4,W0 in dissolved vs. gas samples for inland waters could be a result of generally greater oxidation of dissolved CH₄ in inland water environments, potentially as a result of longer exposure to aerobic conditions in lake or river water columns. This is in contrast to wetlands, where aerobic conditions are generally limited to the uppermost layers of wetlands proximate to the water table. However, our dataset for inland-water-dissolved CH₄ is quite small (n=9), and more data are needed to test this hypothesis. Furthermore, it is unclear why oxidation in inland water dissolved CH₄ would be more strongly expressed in terms of δ²H–CH_4,W0 (Fig. 9a) than δ¹³C (Fig. 9b).

Overall, our data imply that isotopic differences between dissolved and gas-phase methane are relatively minor on a global basis, especially in wetlands. This result could imply that the relative balance of diffusive vs. ebullition gas fluxes does not have a large effect on the isotopic composition of freshwater CH₄ emissions. However, our study does not specifically account for isotopic fractionation occurring during diffusive or plant-mediated transport (Hornibrook, 2009), and most of our dissolved sample data are of in situ dissolved CH₄ and not diffusive fluxes. More isotopic data specifically focused on diffusive methane emissions, for example using measurements of gas sampled from chambers, would help to resolve this question, as would more comparisons of the isotopic composition of diffusive and ebullition CH₄ emissions from the same ecosystem.

3.8 Estimates of global emissions source δ²H–CH₄ and δ¹³C-CH₄

Our mixing model estimates a global source δ²H–CH₄ of −278 ± 15 ‰ and a global source δ¹³C-CH₄ of −56.4 ± 2.6 ‰ (Fig. 10). Monte Carlo sensitivity tests that only included uncertainty in either isotopic source signatures or flux estimates suggest that larger uncertainty is associated with isotopic source signatures (12 ‰ for δ²H; 2.2 ‰ for δ¹³C) than with flux estimates (8 ‰ for δ²H; 1.4 ‰ for δ¹³C). When correcting for wetland and biomass burning emissions from C₄ plant ecosystems, as described in Sect. 2.4, our estimate of global source δ¹³C-CH₄ increases to −55.2 ± 2.6 ‰. Our estimate of global source δ²H–CH₄ is substantially higher than a previous bottom-up estimate using a similar approach (−295 ‰; Fig. 10) (Whiticar and Schaefer, 2007). This difference can be largely attributed to the application of more depleted δ²H–CH₄ source signatures for tropical wetlands (−360 ‰), and to a lesser extent boreal wetlands (−380 ‰), by Whiticar and Schaefer (2007).

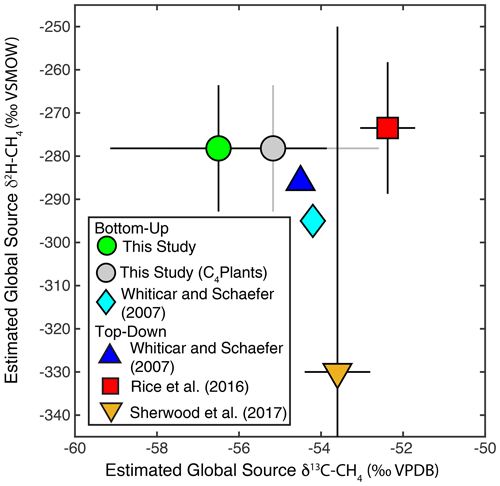
Figure 10 Comparison of estimates of dual-isotope global source δ²H–CH₄ and δ¹³C-CH₄ from this and previous studies. Error bars from this study indicate the 2σ standard deviation from Monte Carlo analysis. Grey dot and error bars indicate an estimate corrected for the lack of data from wetlands and biomass burning in C₄ plant environments, as described in Sect. 2.4. Error bars for Rice et al. (2016) indicate the range of values estimated in that study between 1977–2005. Error bars for Sherwood et al. (2017) reflect the combined measurement uncertainty and uncertainty in sink fractionations reported in that study. Whiticar and Schaefer (2007) did not provide uncertainties for their estimates.

Our bottom-up estimate of global source δ²H–CH₄ substantially overlaps the range of top-down estimates (−258 to −289 ‰) based on atmospheric δ²H–CH₄ measurements from 1977–2005 and a box model of sink fluxes and kinetic isotope effects (Rice et al., 2016) (Fig. 10). It is also within error of simpler top-down estimates calculated based on mean atmospheric measurements and estimates of a constant sink fractionation factor (Whiticar and Schaefer, 2007; Sherwood et al., 2017). Sherwood et al. (2017) estimate a very wide range of possible global source δ²H–CH₄ values based on a relatively large atmospheric sink fractionation with large uncertainty (−235 ± 80 ‰). This range overlaps with our bottom-up estimate, although its mid-point is substantially lower than our estimate. We argue that the box-model method used to account for sink fractionations applied by Rice et al. (2016) probably provides a more accurate representation of global-source isotopic composition than the other top-down estimates shown in Fig. 10. The estimates of Rice et al. (2016) are also supported by the results of a global inversion model. Overall, the overlap between our bottom-up estimate of global source δ²H–CH₄ with top-down estimates is encouraging and suggests that the estimates of emission source δ²H–CH₄ signatures applied in this study are reasonably accurate. However, as discussed below, there is still substantial scope to further constrain these estimates and to reduce uncertainty.

Our bottom-up estimate of global source δ¹³C-CH₄ is lower than the other top-down and bottom-up estimates shown in Fig. 10. As discussed above, there is likely a bias in our freshwater CH₄ isotopic database in that it includes very few wetland sites from C₄-plant-dominated ecosystems. When correcting for this, as well as for CH₄ emissions from combustion of C₄ plants (Fig. 10), our estimate shifts to a more enriched value that is within uncertainty of other estimates. Clearly, accounting for the effect of C₄ plants in wetland and biomass burning CH₄ emissions, and potentially also in enteric fermentation emissions, is important for accurate estimates of global source δ¹³C-CH₄. As discussed below, other sources of error in both isotopic source signatures and inventory-based flux estimates could also partially account for our relatively low global source δ¹³C-CH₄ estimate. For example, variation in fossil fuel isotopic signatures between regions and resource types is potentially an additional source of uncertainty that is not accounted for in this estimate.

Previous studies have argued, on the basis of comparing atmospheric measurements and emissions source δ¹³C-CH₄ signatures, that there are biases in global emissions inventories, specifically that fossil fuel emissions estimates are too low and that either microbial emissions estimates are too high (Schwietzke et al., 2016) or that biomass burning estimates are too high (Worden et al., 2017). We argue that greater analysis of δ²H–CH₄ measurements could be valuable for evaluating these and other emissions scenarios, as has been suggested previously (Rigby et al., 2012). This is especially true for determining the relative proportion of fossil fuel and microbial emissions, since these sources have widely differing δ²H–CH₄ signatures (Table 1). Currently, atmospheric δ²H–CH₄ measurements are not a routine component of CH₄ monitoring programs, but we argue that based on both their value in constraining emissions sources and sinks (Rigby et al., 2012) and the increasing practicality of high-frequency measurements (Chen et al., 2016; Röckmann et al., 2016; Yacovitch et al., 2020), there should be a renewed focus on these measurements.

The uncertainty in our bottom-up estimates, the overall greater uncertainty associated with isotopic source signatures in our Monte Carlo calculations, and the apparent discrepancies for δ¹³C-CH₄ shown in Fig. 10 also imply that isotopic source signatures for specific sources could be greatly improved. As noted by Rigby et al. (2012), the impact of improved isotopic source signatures increases as measurement precision improves. We have discussed above the importance of increased data assimilation and measurements from tropical wetlands, with a particular focus on C₄-plant-dominated ecosystems. Using the isotopic source signal uncertainties and emissions fluxes shown in Table 1, we identified the sources with the greatest flux-weighted uncertainty in isotopic signatures. Based on this analysis, the greatest uncertainty for global source δ²H–CH₄ estimates comes from source signatures for enteric fermentation and manure, low-latitude wetlands, onshore geological emissions, low-latitude and mid-latitude inland waters, termites, and landfills. We identified the same source categories as having the greatest flux-weighted uncertainty for δ¹³C-CH₄, with the exception of termites, but we repeat the caveat that the underlying dataset is less comprehensive for δ¹³C-CH₄. We argue that these source categories should be considered priorities for future emissions source isotopic characterization through data assimilation and additional measurements. As discussed in Sect. 3.5, evaluation of possible latitudinal variation in enteric fermentation and landfill δ²H–CH₄ is particularly promising.

4 Conclusions

Our analysis of an expanded isotopic dataset for freshwater CH₄ confirms the previous finding that δ²H–H₂O is the primary determinant of δ²H–CH₄ on a global scale (Waldron et al., 1999a) but also finds that the slope of this relationship is probably flatter than was inferred previously (Fig. 3). This flatter slope is primarily the result of the inclusion of a much larger number of high-latitude sites with low δ²H–H₂O in our dataset. We find that the inferred relationship between δ²H–CH₄ and δ²H–H₂O is not highly sensitive to whether measured δ²H–H₂O, modelled δ²H_p, or a combination of the two (i.e. a best-estimate) is used to estimate δ²H–H₂O. This implies that gridded datasets of δ²H_p or isotope-enabled climate models could be used to predict the distribution of δ²H–CH₄ in the present, as well as under past and future climates. Our analysis also suggests that annual δ²H_p may be a better predictor for wetland δ²H–CH₄, while seasonal δ²H_p may be a better predictor of inland water δ²H–CH₄. The slope of δ²H–CH₄ vs. δ²H–H₂O in both wetlands and inland waters agrees well with that found in incubation experiments (Schoell, 1980; Sugimoto and Wada, 1995; Waldron et al., 1998, 1999a), and we concur with previous inferences that this slope is partly controlled by variation in the δ²H of acetate as a function of δ²H–H₂O (Waldron et al., 1999a). Analysis of co-variation in δ²H–CH_4,W0 with δ¹³C-CH₄, δ¹³C–CO₂, and α_C suggests that residual variation in δ²H–CH₄ is influenced by a complex set of biogeochemical variables, including both variable isotopic fractionation related to methanogenesis and post-production isotopic fractionation related to CH₄ oxidation and diffusive gas transport. A significant positive correlation between δ²H–CH_4,W0 and both δ¹³C–CO₂ and α_C in wetlands suggests that hydrogen isotope fractionation related to methanogenesis pathway or enzymatic reversibility may be more important in these environments, but this result is dependent on the method used to estimate δ²H–H₂O and requires further validation.

The dependence of δ²H–CH₄ on δ²H–H₂O leads to clear latitudinal differences in δ²H–CH₄, with particularly low values from high-latitude sites (Figs. 4, 7a). The mechanism for latitudinal differences in δ²H–CH₄ is distinct from proposed mechanisms for latitudinal differences in δ¹³C-CH₄ (Ganesan et al., 2018), implying that these two isotopic tracers are complementary in differentiating geographic emissions sources. We estimate a global flux-weighted δ²H–CH₄ signature from freshwater environments of −310 ± 15 ‰, which is enriched relative to values used in previous source apportionment studies (Rice et al., 2016; Bock et al., 2017). We observe a significantly higher δ²H–CH_4,W0 distribution in inland waters relative to wetlands (Fig. 8a), which we suggest is a result of greater rates of CH₄ oxidation in inland waters. We do not find significant differences between more specific ecosystem categories, nor do we find significant differences in δ²H–CH_4,W0 between sample types (Fig. 9a), with the exception of higher values in dissolved CH₄ relative to gas-phase CH₄ in inland water environments.

Our bottom-up estimate of the global δ²H–CH₄ source signature, −278 ± 15 ‰, is higher than previous bottom-up estimates (Whiticar and Schaefer, 2007) but is within the range of top-down estimates based on atmospheric measurements and modelled sink fractionations (Rice et al., 2016). In contrast, our bottom-up estimate of global δ¹³C-CH₄, −56.4 ± 2.6 ‰, is low relative to top-down estimates, which is partially explained by a lack of data from C₄-plant-dominated ecosystems in the freshwater CH₄ isotopic dataset. The agreement between bottom-up and top-down global δ²H–CH₄ estimates suggests that our current understanding of δ²H–CH₄ source signatures, when combined with inventory-based flux estimates (Saunois et al., 2020), is consistent with atmospheric measurements. This supports the argument that increased measurements and modelling of atmospheric δ²H–CH₄ could help to constrain global CH₄ budgets (Rigby et al., 2012). However, there is clearly a need to better constrain source signatures for both δ²H–CH₄ and δ¹³C-CH₄, especially from low-latitude microbial sources.