the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Revised fractional abundances and warm-season temperatures substantially improve brGDGT calibrations in lake sediments
Jonathan H. Raberg
David J. Harning
Sarah E. Crump
Greg de Wet
Aria Blumm
Sebastian Kopf
Áslaug Geirsdóttir
Gifford H. Miller
Julio Sepúlveda
Distributions of branched glycerol dialkyl glycerol tetraethers (brGDGTs) are frequently employed for reconstructing terrestrial paleotemperatures from lake sediment archives. Although brGDGTs are globally ubiquitous, the microbial producers of these membrane lipids remain unknown, precluding a full understanding of the ways in which environmental parameters control their production and distribution. Here, we advance this understanding in three ways. First, we present 43 new high-latitude lake sites characterized by low mean annual air temperatures (MATs) and high seasonality, filling an important gap in the global dataset. Second, we introduce a new approach for analyzing brGDGT data in which compound fractional abundances (FAs) are calculated within structural groups based on methylation number, methylation position, and cyclization number. Finally, we perform linear and nonlinear regressions of the resulting FAs against a suite of environmental parameters in a compiled global lake sediment dataset (n = 182). We find that our approach deconvolves temperature, conductivity, and pH trends in brGDGTs without increasing calibration errors from the standard approach. We also find that it reveals novel patterns in brGDGT distributions and provides a methodology for investigating the biological underpinnings of their structural diversity. Warm-season temperature indices outperformed MAT in our regressions, with the mean temperature of months above freezing yielding the highest-performing model (adjusted R2 = 0.91, RMSE = 1.97 ∘C, n = 182). The natural logarithm of conductivity had the second-strongest relationship to brGDGT distributions (adjusted R2 = 0.83, RMSE = 0.66, n = 143), notably outperforming pH in our dataset (adjusted R2 = 0.73, RMSE = 0.57, n = 154) and providing a potential new proxy for paleohydrology applications. We recommend these calibrations for use in lake sediments globally, including at high latitudes, and detail the advantages and disadvantages of each.
- Article
(3033 KB) - Full-text XML
-
Supplement
(19381 KB) - BibTeX
- EndNote
Paleotemperature records from lake sediment archives are highly sought after in studies of terrestrial paleoclimate. Bacterial branched glycerol dialkyl glycerol tetraether (brGDGT) lipids have solidified themselves as an important tool in this pursuit (Fig. A1; Schouten et al., 2013). First isolated from peat (Sinninghe Damsté et al., 2000), these membrane lipids have since been measured in increasingly diverse settings, from marine, soil, lacustrine, and riverine locations (Hopmans et al., 2004; Weijers et al., 2006; Pearson et al., 2011; De Jonge et al., 2014b, respectively) to hot springs, fossil bones, groundwater, deep ocean trenches, and methane seeps (Li et al., 2014; Dillon et al., 2018; Ding et al., 2018; Xiao et al., 2020; Zhang et al., 2020, respectively). Their ubiquity in nature has given them widespread applicability as environmental proxies; brGDGTs have been used to reconstruct temperature in a variety of archives including lake sediments (e.g., de Wet et al., 2016), marine sediments (e.g., Dearing Crampton-Flood et al., 2018), peat (e.g., Zheng et al., 2017), loess (e.g., Lu et al., 2019), and fossil bone (e.g., Zhao et al., 2020). They have additionally been used to reconstruct lake water pH (e.g., Cao et al., 2017). As the microbial producers of brGDGTs remain elusive (Sinninghe Damsté et al., 2018), these paleoclimate reconstructions currently rely on empirical calibrations at both the regional and global levels.
At the heart of brGDGT calibrations is the observation that the degrees of alkyl-chain methylation and cyclization are correlated to environmental temperature and pH, respectively. These relationships were first quantified by the methylation index and cyclization ratio of branched tetraethers (MBT and CBT) in a global soil dataset (Weijers et al., 2007). The authors proposed physiological explanations for both connections, positing that an increase in methylation number will enhance membrane fluidity, a desirable trait in cold environments, while a greater number of cyclic moieties could improve proton permeability, an advantageous adaptation at high pH. These physiological responses have precedent in other bacterial lipid classes (Beales, 2004; Reizer et al., 1985; Yuk and Marshall, 2004) and appear to function for brGDGTs as well. However, genomic analyses of environmental samples (van Bree et al., 2020; De Jonge et al., 2019; Weber et al., 2018) have suggested that differences in brGDGT distributions may also stem from shifts in bacterial community composition. Variations in the position of alkyl-chain methylations (Fig. A1; De Jonge et al., 2014a) further complicate the picture, with most studies showing 5-methyl brGDGT isomers to correlate better with temperature than their 6-methyl counterparts (e.g., Russell et al., 2018) but others arriving at the opposite result (e.g., Dang et al., 2018). These isomeric variations have additionally been shown to correlate with pH in lake sediments (Dang et al., 2016). These discoveries highlight the multifaceted nature of the empirical relationship between brGDGTs and environmental gradients and the need for further study.
Without a clear mechanistic understanding of the dependencies of brGDGTs on environmental parameters and no brGDGT-producing model organisms currently available for laboratory experimentation, researchers have relied on statistical methods to construct empirical brGDGT calibrations. The majority of recent calibrations have employed a variety of statistical techniques to construct linear or polynomial regressions using brGDGT fractional abundances (FAs; De Jonge et al., 2014a; Martínez-Sosa et al., 2021; Pérez-Angel et al., 2020). The fractional abundance fxi of a compound xi in a set of n compounds is defined as
where any x is the absolute abundance of the given compound in the set. For brGDGTs, these FAs are traditionally calculated using all 15 commonly measured compounds (Fig. A1),
where xi is any given compound in the denominator. By grouping together all 15 common brGDGTs, this approach makes no prior assumptions about the relationships between the compounds themselves and maximizes the degrees of freedom available when exploring a dataset. As relationships between brGDGTs and environment parameters are not yet fully understood, this indiscriminate approach is appropriate. However, by lumping compounds of various types and abundances into the denominator, the approach can also dampen meaningful trends and obscure important relationships, especially for less abundant molecules. This adverse effect has been recognized for other lipid biomarkers and has led to, for example, the exclusion of crenarchaeol from the TEX86 index (Schouten et al., 2002) and tetra-unsaturated alkenones from the index (Prahl and Wakeham, 1987). Numerous ratio-based indices have been developed for brGDGTs that similarly exclude low-abundance (e.g., MBT′; Peterse et al., 2012) or problematic (e.g., ; De Jonge et al., 2014a) compounds. However, a selective approach to fractional abundance calculations has been hitherto unexplored.
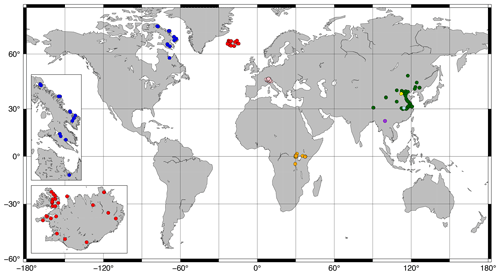
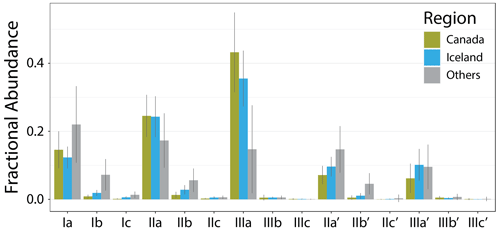
Figure 1Map of sites included in this study. Red and blue: Iceland and Canada (this study; see insets); orange: Russell et al. (2018); green: Dang et al. (2018); pink: Weber et al. (2018); yellow: Cao et al. (2020); light blue: Qian et al. (2019); purple: Ning et al. (2019).
On the other side of the calibration equations are the environmental variables that are regressed against brGDGT indices and FAs. Mean annual air temperature (MAT) has been the traditional target of brGDGT calibrations in lake sediments (e.g., Tierney et al., 2010; Loomis et al., 2012). It was recognized early on, however, that brGDGT-derived temperatures in cold regions may more accurately reflect warm-season temperatures (Pearson et al., 2011; Sun et al., 2011), a hypothesis that was strongly supported in high-latitude lake sediments (Foster et al., 2016; Peterse et al., 2014; Shanahan et al., 2013). Since the methodological advances that allowed for the separation of 5- and 6-methyl isomers (De Jonge et al., 2014b) and the development of new calibrations, both modern studies (Cao et al., 2020; Dang et al., 2018; Hanna et al., 2016) and paleo studies (Crump et al., 2019; Harning et al., 2020; Super et al., 2018; Thomas et al., 2018) have continued to support a warm-season bias. Additionally, a recent Bayesian calibration found the mean temperature of months above freezing (MAF) to be the only mode to significantly correlate with brGDGT distributions in a global lake sediment dataset (Martínez-Sosa et al., 2021). However, as the source organisms of brGDGTs remain incompletely known, other measures of warm-season temperature such as peak warmth or cumulative heat may prove to be more biologically relevant. Furthermore, the nature of the warm-season bias has yet to be tested thoroughly in the regions in which it is most pronounced – namely those with low MAT and high seasonality. As these are the regions that are currently experiencing the most rapid climate change (Landrum and Holland, 2020), their temperature histories are of high interest (Miller et al., 2010), and the quantification of the brGDGT warm-season bias is an important target of study.
Outside of temperature, lake water pH is the most common focus of calibration studies (e.g., Russell et al., 2018). However, numerous other variables including conductivity (Shanahan et al., 2013; Tierney et al., 2010), dissolved oxygen (DO; Colcord et al., 2017; Weber et al., 2018; van Bree et al., 2020; Yao et al., 2020), nutrient availability (Loomis et al., 2014a), and lake mixing regime (van Bree et al., 2020; Loomis et al., 2014b) have been shown to be potentially important controls on brGDGT distributions. Modern calibrations do not currently exist for these environmental variables, largely due to the complexity of the relationships and data limitations.
Uncertainties in the physical sources of brGDGTs on the landscape add an additional challenge for calibration efforts. BrGDGTs produced in soils and rivers can contribute to the lacustrine lipid pool to varying degrees, and the exact proportion of soil- and lake-derived brGDGTs at a particular site requires detailed study to quantify (e.g., Naeher et al., 2014; Guo et al., 2020; van Bree et al., 2020). Further complicating the matter, multiple sources of brGDGTs have been observed within lakes, including at varying depths (e.g., Yao et al., 2020) and within the sediment itself (e.g., Buckles et al., 2014). The intensive studies required to disentangle these various sources are absent for the vast majority of lakes in most calibration studies, undoubtedly contributing to their reported uncertainties. Furthermore, without a clear understanding of where brGDGTs are being produced, it can be difficult to determine which environmental variables are most appropriate to reconstruct. For example, lacustrine brGDGTs were successfully calibrated to lake water temperature at a site in Greenland (Zhao et al., 2021), but such an effort would likely be less successful for a lake with substantial soil input.
In this study, we aim to improve lake sediment calibrations for brGDGTs in three ways. First, we extend the global calibration dataset to include high-latitude sites by adding surface sediment from 43 lakes in the eastern Canadian Arctic, Northern Quebec, and Iceland. Second, we selectively group brGDGTs based on their three structural variables – methylation number, methylation position, and cyclization number – and use FAs calculated within these structural sets to investigate isolated relationships between environmental parameters and each structural variable in turn. Finally, we analyze the relationship between the compiled global dataset and MAT, four warm-season temperature indices, pH, conductivity, DO, and lake geometry and generate empirical calibrations for use in lake sediments globally.
2.1 Study sites and sample collection
Surface sediments (0–0.5, 0–1, or 0–2 cm; Ekman box corer or core-top sediment) were collected from 43 lakes (26 from Iceland; 16 from Baffin Island, Arctic Canada; 1 from Northern Quebec; Fig. 1 insets) between 2003 and 2019. For 28 of these lakes, water temperature, pH, conductivity, and DO were measured at the time of sampling during the summers of 2017–2020 using a multiparameter probe (HydroLab HL4, OTT HydroMet). These parameters were additionally measured beneath the lake ice in February–May of 2018–2020 for 11 lakes. All but one of these lakes experienced depleted bottom water oxygen levels under the ice relative to ice-free conditions. We therefore assume that our ice-free water chemistry profiles do not capture the minimum DO (DOmin) levels experienced by our Canadian and Icelandic lakes and exclude them from our analysis of DOmin, with the exception of the site from Northern Quebec, which contained a summer oxycline. All other water chemistry parameters were averaged across all depths and seasons before being used in calibrations.
Previously published data from 36 lakes in central Europe (Weber et al., 2018), 65 lakes in East Africa (Russell et al., 2018), and 38 lakes in China (Cao et al., 2020; Dang et al., 2018; Ning et al., 2019; Qian et al., 2019) were added to the dataset for a total of 182 data points (Fig. 1). Average brGDGT FAs were used for lakes with multiple surface sediment samples. Lake surface areas (SAs) were taken from published datasets or estimated using DigitalGlobe imagery. Lake volumes were estimated by approximating each lake basin as a hemiellipsoid (. Water chemistry parameters were taken from the literature where available or else excluded from our analyses. The number of data points for each environmental parameter is available in Table S1 in the Supplement. Some parameters were correlated in the dataset, most notably conductivity and pH (r = 0.75; Table S2 in the Supplement).
2.2 Sample extraction and analysis
Roughly 1 g of freeze-dried sediment was extracted using either an accelerated solvent extractor (ASE 200 DIONEX; 10 samples) or a modified Bligh and Dyer (BD; 33 samples) method. We provide a comparison of both extraction methods below. For the ASE method, samples were extracted twice using 9:1 (v:v) dichloromethane:methanol (DCM:MeOH) at 100 ∘C and 2000 psi. Total lipid extracts (TLEs) were redissolved in 99:1 (v:v) hexane:isopropanol (Hex:IPA) and filtered (0.45 µm, PTFE) before analysis. The remaining 33 samples were extracted using a modified BD procedure (Wörmer et al., 2013). Briefly, sediment was vortexed and sonicated in Mix A ( mM phosphate buffer (aq., pH 7.4) [, ]). The mixture was then centrifuged at 3000 rpm and 10 ∘C for 10 min, and the supernatant was collected in a glass separatory funnel. The process was performed twice with Mix A, twice with Mix B ( % trichloroacetic acid buffer (aq., pH 2) [, ]), and once with Mix C (DCM:MeOH [1:5, v:v]). Equal volumes of HPLC-grade water and DCM were added to induce separation. The organic fraction was collected and dried under a nitrogen stream. The aqueous phase was washed once with DCM, and the organic fraction was added to the extract. The TLE was then redissolved in 99:1 (v:v) Hex:IPA and filtered (0.45 µm, PTFE) before analysis.
We analyzed brGDGTs using a Thermo Scientific UltiMate 3000 high-performance liquid chromatography instrument coupled to a Q Exactive Focus Orbitrap-Quadrupole high-resolution mass spectrometer (HPLC-MS) via an atmospheric pressure chemical ionization (APCI). We achieved chromatographic separation using a slightly modified version (Crump et al., 2019; Harning et al., 2019; Pérez-Angel et al., 2020) of the HPLC method described by Hopmans et al. (2016). Due to observed deterioration of chromatography over time, we lowered the initial concentration of eluent B from 18 % to 14 % to maintain optimal separation of the 5- and 6-methyl isomers. A C46 GDGT internal standard (Huguet et al., 2006) was added to the TLE immediately after extraction and was used to quantify brGDGT yields. Peaks with a signal-to-noise ratio of at least 2:1 were considered for analysis.
2.3 Comparison of ASE and BD extraction methods
To ensure that brGDGT distributions were agnostic to our extraction method, we extracted three surface sediments, two suspended particulate matter (SPM) samples (2.5 L lake water filtered onto 0.3 µm glass fiber filters), and three soils from Baffin Island using the ASE and BD methods in parallel (Fig. S1 in the Supplement). The mean difference in (Eq. A3) between the two extraction methods was 0.006 ± 0.004, or 2 ± 2 %. This translates to a -derived temperature difference of 0.2 ± 0.2 ∘C using recent calibrations for soils (Naafs et al., 2017) and lake sediments (Russell et al., 2018), which is well below their respective RMSEs of 5.3 and 2.14 ∘C (Fig. S2 in the Supplement). To test for compound-specific differences, we calculated percent differences in FAs between the two methods. For compounds with FAs > 0.05 in the ASE method, the mean absolute percent difference compared to BD was 4 ± 3 %. For the lower abundance compounds (FA ≤ 0.05), this difference was higher (19 ± 17 %). No biases in the FA differences were found in either case (difference less than the standard deviation).
We further extracted the BD sample residue with the ASE method to determine whether any brGDGTs remained after BD extraction. On average, we recovered only an additional 0.8 ± 0.6 % brGDGTs. These residual brGDGTs had a similar to that of the original BD extract (mean difference = 0.02 ± 0.01, equivalent to 0.5 ± 0.4 ∘C) and were not present in high enough abundances to significantly affect the overall BD distributions (Fig. S2). We therefore conclude that there are no significant differences between samples extracted with the two methods and treat them identically in the analyses that follow.
2.4 Air temperatures
Monthly air temperature averages were gathered using the following methods. For nine sites on Baffin Island, 1 year of in situ 2 m air temperature data from five temperature loggers (1 to 4 h resolution, Thermochron iButtons, Maxim Integrated Products) was converted to a 30-year monthly climate normal (1971 to 2000) using a transfer function to relate local data to nearby meteorological stations (Department of Environment, Government of Canada). For the remaining Canadian sites as well as all sites in Iceland, we used the WorldClim database (Fick and Hijmans, 2017) to generate 30-year climate normals for the same time period (1970 to 2000). Monthly temperatures for central European sites were derived using monthly altitudinal lapse rates constructed from climate normals (1970 to 2013) of 148 meteorological stations (Federal Office of Meteorology and Climatology: MeteoSwiss). Monthly temperature data were not available for the East African lakes. However, the seasonality (standard deviation of monthly temperatures) of these lakes is low (0.5 ± 0.2 ∘C in the WorldClim database, or < 2 % of range of the dataset). We therefore approximate all monthly temperatures to be equivalent to MAT for these lakes. Monthly temperature data from all other studies were either published or provided by the authors.
We used the above monthly air temperatures to calculate MAT and four warm-season temperature indices. Three of these indices represent an average temperature for the warmer portion of the year: mean temperature of months above freezing (MAF), mean summer temperature (MST; mean of June, July, and August in the Northern Hemisphere and December, January, and February in the Southern Hemisphere), and mean warmest month temperature (WMT). These indices capture average temperatures for the warm season but are unaffected by its duration. We therefore additionally calculate the summer warm index (SWI), defined as the cumulative sum of all monthly temperatures above 0 ∘C. This index represents an important control on vegetation patterns at high latitudes and is a useful alternative to the growing degree days above 0 ∘C (GDD0) index when daily temperature data are not available (e.g., Raynolds et al., 2008). For our five in situ temperature loggers in the eastern Canadian Arctic for which sub-daily temperature data are available, GDD0 and SWI are highly correlated (R2 = 0.998). We also quantified shoulder season temperatures by calculating averages of the first and last, or first and last two, positive-degree months. However, the monthly resolution of the dataset proved too coarse to apply this method robustly.
2.5 Statistical methods
To construct calibrations between brGDGT FAs and environmental variables, we used the following method. Each FA was first regressed alone against the environmental variable being investigated. Compounds with a correlation p value ≥ 0.01 were considered non-significant and removed from further analysis (Pérez-Angel et al., 2020). Fits were then constructed from the remaining compounds using two independent approaches. The first approach was stepwise forward selection/backwards elimination (SFS/SBE) using the MASS package (Venables and Ripley, 2002) in R (R Core Team, 2021). This approach finds the best fit by sequentially adding (SFS) or removing (SBE) terms in a generalized linear model and evaluating the resulting fit using the Bayesian information criterion (BIC; Schwarz, 1978). The approach is common for constructing brGDGT calibrations (e.g., Dang et al., 2018; Russell et al., 2018), but it is not exhaustive. We therefore additionally used the leaps package (Lumley, 2020) in R to evaluate all possible linear combinations of fitting variables (the “combinatoric” approach; Pérez-Angel et al., 2020). We again used the BIC to select the best fit. For both methods, we imposed the additional criterion that each of the resulting fitting variables must itself be statistically significant (p < 0.01). To help avoid overfitting, we additionally used the adjusted R2 to evaluate calibration performances. Some of our variables (conductivity, depth, surface area to depth, and volume) spanned multiple orders of magnitude. We performed regressions against the natural logarithm of these variables, which greatly improved their normality.
We applied this calibration procedure to the FAs of each brGDGT structural set and subset defined below (Sect. 3). In the subset-specific calibrations, it was sometimes possible for a single compound to dominate (FA = 1; see Sect. S1.4 in the Supplement). These samples were generally clear outliers resulting from the low natural abundances of all other members of the subset, and they were therefore removed from the subset-specific calibration models. We additionally tested for linear regressions against a number of previously defined brGDGT indices. A summary of these indices and their definitions is provided in the Appendix.
All correlations reported in the text and figures were significant (p < 0.01) except those marked with an asterisk or with a p value provided. All R2 values reported in the text and figures are adjusted R2.
The structure of brGDGTs can vary in three (currently observed) ways: methylation number, methylation position, and cyclization number. These variations result in 15 commonly measured brGDGTs (Fig. A1). The standard approach in brGDGT analysis is to calculate fractional abundances using all 15 of these compounds (Eq. 2). By mathematically mixing brGDGTs with varying methylation number, methylation position, and cyclization number, however, this approach risks convoluting the influences of disparate environmental variables. Here, we present a method of grouping brGDGTs that highlights one type of structural variation (e.g., methylation number) while holding one or both of the others constant. By calculating FAs within each group, we aim to deconvolve the influences of temperature, pH, and other environmental variables on the structural variations in brGDGTs.
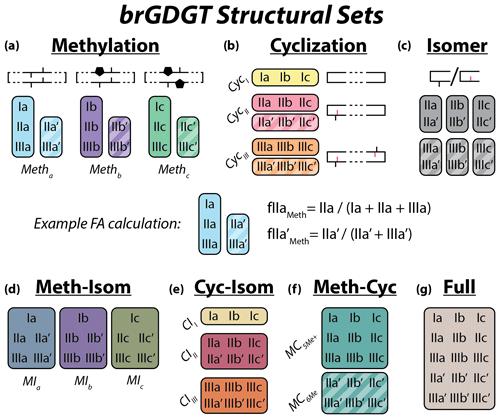
Figure 2Schematic of the basic (a–c) and combined (d–g) brGDGT structural sets. Fractional abundances are calculated within each boxed group independently (Eqs. 3–9 and Table A1). Schematic structures highlight the defining alkyl-chain moieties, with cyclopentane rings filled in for emphasis and C6 methylations denoted in red. Complete structures are available in Fig. A1.
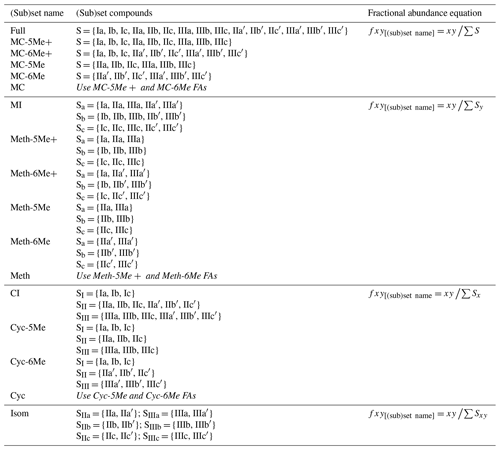
To explore how changes in methylation number alone relate to environmental parameters, we constructed the Methylation (Meth) set (Fig. 2a). This set was generated by grouping brGDGTs with the same number of cyclopentane rings and the same methylation positions. Fractional abundances calculated within the Meth set solely reflect changes in methylation number, while ring number and isomer designation are held constant. Within the Meth set, we defined the Meth-5Me and Meth-6Me subsets as those that contained only 5- and 6-methyl lipids, respectively. As the tetramethylated brGDGTs (Ia, Ib, and Ic) are neither 5-methyl nor 6-methyl isomers, we generated versions of these two subsets that excluded (Meth-5Me, Meth-6Me) and included (Meth-5Me+, Meth-6Me+) these compounds (Fig. S3a–d in the Supplement). We found that the correlation between 5-methyl isomers and temperature was significantly improved when the tetramethylated compounds were included in their FA calculations, while the opposite was true for the 6-methyl compounds (see discussion in Sect. 4.2.2). We therefore grouped the tetramethylated compounds with the 5-methyl compounds (and not with the 6-methyl compounds) when generating the Meth set. FAs for the Meth set were calculated using Eq. (3),
where fxy and xy are the fractional and absolute abundances of the brGDGT with Roman numeral x (I, II, or III) and letter y (a, b, or c), and tetramethylated compounds are grouped with 5-methyl isomers.
We next defined the Cyclization (Cyc) set to examine the relationship of brGDGT ring number with environmental variables (Fig. 2b). The Cyc set was formed by grouping brGDGTs with the same number and position of methylations. With these variables held constant, variations in the Cyc FAs reflect only variations in the number of cyclopentane moieties. We defined the Cyc-5Me and Cyc-6Me subsets as those containing only 5- and 6-methyl isomers, respectively (Fig. S3e and f). FAs for the Cyc set were calculated using Eq. (4),
where fxy and xy are the fractional and absolute abundances of the 5- or 6-methyl brGDGT with Roman numeral x (I, II, or III) and letter y (a, b, or c).
Third, we defined the Isomer (Isom) set to isolate changes in the relative abundances of brGDGT isomers (Fig. 2c). The Isom set was constructed by grouping brGDGTs with the same number of methylations and cyclizations. Its FAs are solely a measure of the relative abundances of 5- and 6-methyl isomers, without the convoluting influence of ring or methylation number variations. The isomeric diversity of brGDGTs is large, however, and there are structural variations that are not controlled for within this set. For example, hexamethylated brGDGTs have two isomers: one with methylations on different alkyl chains (e.g., at C5 and C5′) and another with methylations on the same chain (e.g., C5 and C24; De Jonge et al., 2013). As these compounds coelute, they cannot be treated independently at this time. Additionally, it is unclear whether brGDGT-IIIa′′ (Weber et al., 2015), which contains both a C5 and a C6′ methylation, should be grouped with 5- or 6-methyl brGDGTs, or whether the three recently identified 7-methyl brGDGTs (Ding et al., 2016) should be included in the Isom series. As these compounds are rarely reported, we excluded them from our analysis here, but we suggest the possibility of expanding the Isom set to include them in the future should more data become available. The Isom FAs were calculated using Eq. (5),
where fxy and xy are the fractional and absolute abundances of the 5- or 6-methyl brGDGT with Roman numeral x (I, II, or III) and letter y (a, b, or c) and “isomers” refers to 5- and 6-methyl brGDGTs. The Isom set contained groups of two compounds each, making their FAs redundant. We therefore used only the 6-methyl FAs in our analysis.
The Meth, Cyc, and Isom sets each allow only one structural component of brGDGTs to vary. It is possible, however, that two structural alterations occur in tandem in response to the same environmental variable. We therefore defined three additional sets that hold one variable constant while allowing the other two to vary. The first is the Meth–Isom (MI) combination set (Fig. 2d). In this set, brGDGTs with the same ring number are grouped together, while both methylation number and position are allowed to vary. The Cyc–Isom (CI; Fig. 2e) set is analogously constructed by holding methylation number constant, while the Meth–Cyc (MC; Fig. 2f) set holds methylation position constant (again treating tetramethylated brGDGTs as 5-methyl compounds, Fig. S3g–j). Finally, we defined the Full set (Fig. 2g), which takes the standard approach of allowing all three structural characteristics to vary freely by grouping all 15 commonly measured brGDGTs together. The FAs of the combined sets are calculated using Eqs. (6)–(9).
Here fxy and xy are the fractional and absolute abundances of the 5- or 6-methyl brGDGT with Roman numeral x (I, II, or III) and letter y (a, b, or c), and tetramethylated compounds are treated as 5-methyl isomers. An expanded guide to FA calculations is provided in Table A1.

Figure 3Adjusted R2 values for a linear regression of environmental parameters against the fractional abundance (FA) of brGDGT-Ia calculated within different structural sets. Colors denote the strengths of the relationships, from the minimum to the maximum observed coefficients of determination, with white being the median of the dataset. “Compounds” denote all brGDGTs used in the FA calculation. All values are significant (p < 0.01) unless marked with an asterisk.
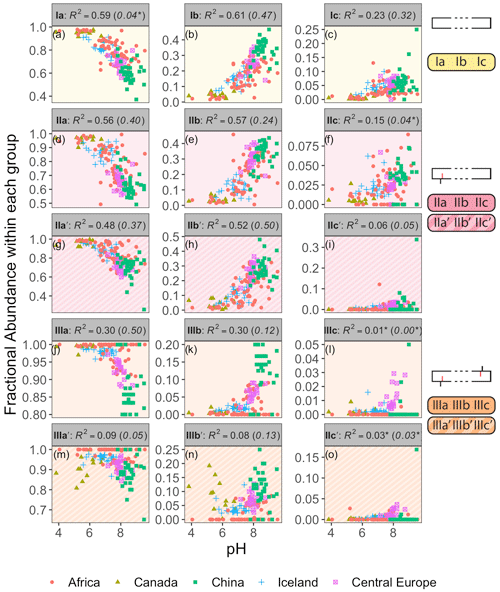
As a proof of concept, we show that the fractional abundance of just one compound, brGDGT-Ia, can be calculated within different structural sets to provide either a strong temperature or pH correlation, without a strong cross-correlation. When the standard FA is calculated using all 15 compounds (fIaFull), a moderate correlation is found with MAF (R2 = 0.61) and none with pH (R2 = 0.04, p = 0.014; Fig. 3). When cyclization is held constant by using the MI set, correlation with MAF increases (R2 = 0.75) while that with pH remains uncorrelated (R2 = 0.13). The temperature correlation increases further when isomer designation is controlled for as well (, R2 = 0.88), with an R2 nearly matching that of (R2 = 0.89) and the pH correlation remaining low (R2 = 0.27). In contrast, the correlation with temperature disappears for the analogous 6-methyl subset (, R2 = 0.08). Finally, allowing only ring number to vary (fIaCyc) effectively erases the correlation with temperature (R2 = 0.18) and instead provides a correlation with pH that, while modest, is already higher than any reported for a lake sediment calibration to date (R2 = 0.59).
4.1 Distributions of brGDGTs in Icelandic and Canadian lake sediments
The new Icelandic and Canadian lake sediments bolster the global dataset on the cold end, extending the lowest MAT from −0.2 to −18 ∘C and containing 28 of the 30 coldest samples by MAT. The low temperatures are reflected in the brGDGT distributions of these sediments (Fig. 4), which contain on average a higher fIIIaFull and lower fIaFull than the other samples in this dataset. Additionally, the Canadian and Icelandic datasets provide important end-member samples, including those with the highest fIIIaFull, fIIIbFull, and fIIIcFull and the lowest or second lowest fIaFull, fIbFull, and fIcFull. The new samples also contain some of the lowest fractional abundances of 6-methyl isomers, providing low end-member values for , , and and below-average values for the hexamethylated 6-methyl brGDGTs.
4.2 Temperature relationships with brGDGTs
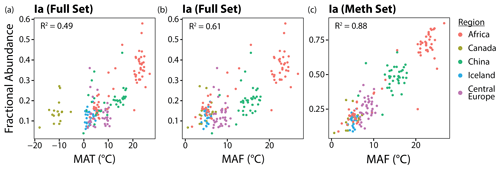
In this section, we show that two adjustments can be made to significantly improve the correlations between brGDGT FAs and temperature in lake sediments: (1) replace MAT with a warm-season temperature index and (2) use FAs calculated within the Meth structural set. The effect of these two adjustments on one representative compound, brGDGT-Ia, is shown from left to right in Fig. 5. The relationship between temperature and fIa is improved from a weak but significant correlation with a large error (R2 = 0.49; RMSE = 7.00 ∘C) to a stronger correlation with a smaller error (R2 = 0.88; RMSE = 2.42 ∘C). The two adjustments are detailed in the following sections.
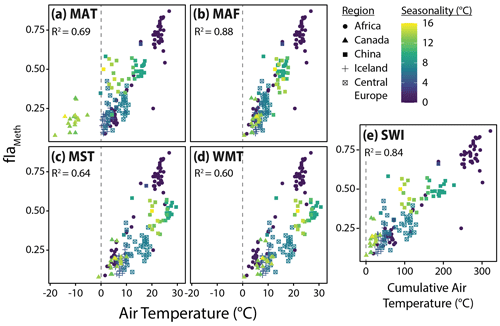
Figure 6Relationships between fIaMeth and the five air temperature variables tested in this study, (a) mean annual temperature (MAT), (b) months above freezing (MAF), (c) mean summer temperature (MST), (d) warmest month temperature (WMT), and (e) summer warmth index (SWI). Colors indicate air temperature seasonality (standard deviation of mean monthly temperatures). Dashed lines indicate mean or cumulative temperatures of 0 ∘C for reference. R2 values for the relationship between fIaMeth and each temperature variable are provided in each subplot.
4.2.1 Warm-season temperatures outperform MAT
To assess the possibility of a warm-season bias in brGDGT temperature reconstructions, we tested the relationships between brGDGTs and five air temperature indices: MAT, MAF, MST, WMT, and SWI (Sect. 2.4). The correlation between these variables and the FA of one representative compound, fIaMeth, is shown in Fig. 6. In all cases, substituting MAT with a warm-season temperature variable draws samples with strong seasonality into the main body of data. MAF performs best for brGDGT-Ia (R2 = 0.88), with high-seasonality lakes falling progressively out of alignment for SWI (R2 = 0.84), MST (R2 = 0.64), and WMT (R2 = 0.60). This result was upheld when performing temperature calibrations; MAF outperformed all other measures of temperature examined in this study (Sect. 4.4.1).
A possible explanation for the success of the MAF temperature index is that the activity of brGDGT-producing microbes may be heavily depressed under lake ice and/or in frozen soils (Cao et al., 2020; Pearson et al., 2011; Peterse et al., 2014; Shanahan et al., 2013). However, studies employing sub-seasonal sampling of sediment traps and suspended particulate matter in two midlatitude lakes have shown that brGDGTs are produced within the water column throughout the year, despite the presence of ice cover (Loomis et al., 2014b; Woltering et al., 2012). These and other studies employing similar sampling techniques (van Bree et al., 2020; Hu et al., 2016; Miller et al., 2018; Weber et al., 2018) have additionally found production of brGDGTs to be dependent on the degree and timing of lake mixing vs. stratification. Though heightened biological activity may still be the underlying driver of the observed warm-season bias, these depth- and time-resolved studies paint a complex picture of brGDGT production in lakes that precludes a simple explanation. Unfortunately, as knowledge of the timing, extent, and temperature of ice cover and mixing events is lacking for the vast majority of lakes in this study, these effects cannot be tested here. We therefore stress the empirical nature of our MAF calibrations and the need for further study.
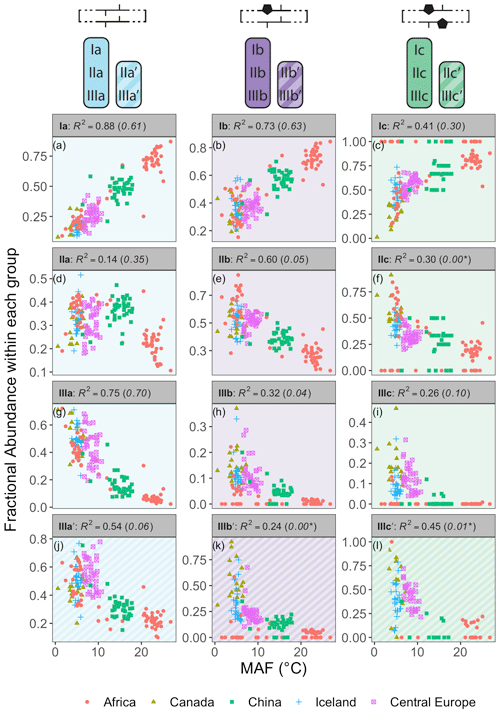
Figure 7Relationships between the average air temperature of months above freezing (MAF) and brGDGT FAs calculated within the Meth set. R2 values are provided for each subplot, with R2 values for the standard Full FAs given in parentheses for comparison. P values were < 0.01 except where marked with an asterisk. Note that plots of IIa′, IIb′, and IIc′ are redundant because they exactly mirror those of IIIa′, IIIb′, and IIIc′, respectively, and are therefore not shown.
4.2.2 Temperature and the Methylation set
The Methylation set provided the strongest relationships between brGDGT FAs and MAF (Fig. 7). This set both strengthened existing correlations (e.g., fIaMeth, Fig. 7a) compared to the standard approach (Full set, R2 values in parentheses in Fig. 7) and generated new ones (e.g., fIIbMeth, Fig. 7e). Furthermore, many relationships between FAs and temperature were revealed to be qualitatively similar regardless of ring number. For example, the FAs of all tetramethylated compounds (fIaMeth, fIbMeth, fIcMeth) had a strong positive linear relationship with temperature (Fig. 7a–c), while those of the 5-methyl pentamethylated compounds all had a noisier negative relationship (Fig. 7d–f). The hexamethylated FA trends were less clear in part due to their lower abundances, but all were negatively correlated with temperature, and nonlinearities were apparent (Fig. 7g–l). These analogous trends show that the number of methylations responds similarly to temperature regardless of the number of cyclopentane rings. Within a paleoclimate lens, this observation opens up the possibility of independent temperature calibrations for un-, mono-, and bicyclized brGDGTs (Sect. 4.4.1). From a biological standpoint, it could imply that methylation and cyclization play their biological roles independently, as the former appears to vary more or less freely of the latter.
The brGDGT temperature response appears to be agnostic to methylation position as well (Fig. 7g–i vs. j–l), but only when the tetramethylated brGDGTs (Ia, Ib, and Ic) are excluded from 6-methyl FA calculations. The Meth-5Me+ subset (Fig. S3a) showed strong relationships between 5-methyl brGDGTs and MAF (R2 ≤ 0.88; Fig. S4 in the Supplement). On the other hand, the analogous Meth-6Me+ subset (Fig. S3c) was broadly uncorrelated with MAF (R2 ≤ 0.29; Fig. S5 in the Supplement). At present, there is no known mechanism whereby an additional methylation at the C5 position would have an influence on membrane physiology in a way that a methylation at C6 would not (though the magnitude of the effect may be stronger closer to the less fluid membrane surface; see discussion in Sect. S3). At first glance, then, the markedly different responses of the Meth-5Me+ and Meth-6Me+ subsets to changes in temperature do not appear to support a physiological basis for the empirical relationship between temperature and brGDGT methylation number. However, when tetramethylated brGDGTs were excluded from the FA calculations for these compounds (Meth-5Me and Meth-6Me subsets; Fig. S3b and d), statistically significant and qualitatively similar temperature relationships did become visible for both isomer types (Figs. S6 and S7 in the Supplement). An analogous result was found for the MC set (Figs. S3g–j and S8–S11 in the Supplement). It is not clear at this time why the inclusion of tetramethylated brGDGTs improved temperature correlations for 5-methyl compounds but weakened them for 6-methyl compounds. The discrepancy may imply one or a combination of the following: (1) the isomers are produced by different organisms; (2) the isomers serve distinct biological functions, either in addition to or apart from a temperature response; or (3) the currently measured tetramethylated brGDGTs (Ia, Ib, and Ic) are not the precursors of 6-methyl brGDGTs. Regardless, this result allows us to combine the higher-performing Meth-5Me+ and Meth-6Me subsets to generate the Meth set (Fig. 2a), which maximizes the temperature responses of all 15 commonly measured brGDGTs (Fig. 7).
While the Meth set highlights the relationships between brGDGT FAs and temperature, it simultaneously weakens those with other environmental variables. FAs calculated in the standard Full set contain conductivity and pH dependencies (R2 ≤ 0.66 and 0.50, respectively; Figs. S25 and S32 in the Supplement) that are greatly reduced in the Meth set (R2 ≤ 0.40 and 0.28, respectively; Figs. S19 and S26 in the Supplement). This is evidence that many of the conductivity and pH relationships visible in the Full FAs are in fact due to the mathematical mixing of brGDGTs with different cyclization numbers and isomer designations. Holding these variations constant in the Meth FAs largely removes the effects of these environmental variables (e.g., fIIaMeth in Fig. S19d). DO dependencies are weak in both the Full and Meth sets, but slightly weaker in the latter (R2 ≤ 0.40 and 0.35, respectively, Figs. S39 and S33 in the Supplement). The Methylation set thus improves compound-specific correlations with temperature while decreasing their dependencies on other environmental variables.
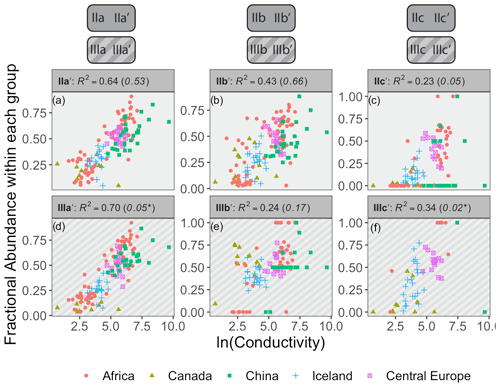
Figure 8Relationships between the natural logarithm of conductivity and brGDGT FAs calculated within the Isom set. R2 values are provided for each subplot, with R2 values for the standard Full FAs given in parentheses for comparison. P values were < 0.01 except where marked with an asterisk. Note that plots of 5-methyl compounds are redundant because they exactly mirror those of their 6-methyl counterparts; only the 6-methyl FAs are shown.
4.3 Conductivity and pH relationships with brGDGTs
While pH is the traditional secondary target of brGDGT calibrations after temperature, numerous works have suggested that conductivity plays an important role in controlling brGDGT distributions (e.g., Shanahan et al., 2013; Tierney et al., 2010). Conductivity and pH often plot nearly colinearly in principal component analyses (Dang et al., 2018; Russell et al., 2018; Shanahan et al., 2013) and were moderately correlated (r = 0.75) in this dataset (Table S2). This correlation is not surprising, as pH will affect conductivity both directly (through the concentration of H3O+/OH−) and indirectly (by altering the solubility of various ions). Furthermore, both pH and conductivity can be affected by the same factors, such as catchment lithology and precipitation chemistry (see Wetzel, 2001). BrGDGT FAs in this study showed similar relationships with pH and conductivity but also displayed potentially important differences. We therefore treat them separately in our analyses but discuss them together in this section.
4.3.1 The Isomer set and conductivity
Conductivity provided the strongest compound-specific correlations with brGDGT FAs after temperature (Figs. 8 and S23 in the Supplement). Of the basic brGDGT sets (Meth, Cyc, and Isom), the Isom set had the highest statistical performance (Fig. 8). The FAs of all 6-methyl brGDGTs showed a positive linear correlation with conductivity in this set, with coefficients of determination as high as R2 = 0.70 (Fig. 8d). Furthermore, this positive correlation was broadly independent of both methylation number and cyclization number, indicating that methylation position varies with conductivity irrespective of other structural properties. The 6-methyl brGDGTs were also all positively correlated with pH, but more weakly so (R2 ≤ 0.54, Fig. S28 in the Supplement). A relationship between brGDGT isomers and pH in lake sediments has been previously observed and quantified by the isomerization of branched tetraethers (IBT, Eq. A14; Ding et al., 2015) and the isomer ratio of 6-methyl isomers (IR6Me, Eq. A8; Dang et al., 2016). However, these indices were more closely tied to conductivity (IBT R2 = 0.65, IR6Me R2 = 0.66) than pH (IBT R2 = 0.55, IR6Me R2 = 0.49) in our dataset. These results indicate that isomer abundances are primarily dependent on conductivity but have some relation to pH as well. Temperature correlations were also present in the Isom subset (R2 ≤ 0.57 with MAF, Fig. S14 in the Supplement). Further study is needed to elucidate whether temperature acts as a secondary control on isomer abundances or whether these correlations are simply due to the inherent connection between MAF and conductivity in our dataset (r = 0.70, Table S1). DO provided little to no correlation in the Isom set (R2 ≤ 0.38, Fig. S35 in the Supplement).
4.3.2 The Cyclization set and pH
The Cyclization set highlighted the relationship between brGDGTs and pH. As pH increased, all cyclized brGDGTs were found in greater relative abundance (Fig. 9). This result reinforces previous observations that higher ring number is associated with higher pH, as has been quantified by the CBT (Weijers et al., 2007), #ringstetra (Sinninghe Damsté, 2016), degree of cyclization (DC; Baxter et al., 2019), and related indices (see Appendix). However, this pH relationship has thus far been demonstrated primarily in soils; the single-compound FAs of the Cyc subset already provide the strongest pH correlations (R2 = 0.61, Fig. 9b) yet reported in lake sediments. The Cyc set also reveals that compounds with structural similarities exhibit analogous responses to pH. For example, all monocyclized brGDGTs show a nonlinear increase with pH (Fig. 9b, e, h, k, and n), while uncyclized brGDGTs all exhibit a nonlinear decrease (Fig. 9a, d, g, j, and m). These trends are apparent regardless of methylation number or methylation position, suggesting that ring number is broadly independent of both. This independence may imply that alkyl-chain cyclization serves its biological function(s) regardless of the number and position of methylations present. It also allows for the construction of independent pH calibrations for tetra-, penta-, and hexamethylated brGDGTs (Sect. 4.4.2).
Though the Cyc set FAs were most strongly correlated with pH (R2 ≤ 0.61), they also exhibited robust relationships with conductivity (R2 ≤ 0.57; Fig. S20 in the Supplement). All cyclized compounds showed positive correlations with conductivity, and this increase was largely independent of methylation number or position. These results indicate that ring number is primarily dependent on pH, but is correlated with conductivity in a similar manner. The brGDGT indices showed an analogous result; all cyclization indices (CBT and related indices, #ringstetra and related indices, and DC; see Appendix) correlated most strongly with pH, but also exhibited weaker relationships with conductivity. The Cyc set exhibited little to no correlation with either temperature (R2 ≤ 0.25) or DO (R2 ≤ 0.08), suggesting that neither of these environmental variables plays an important role in controlling brGDGT cyclization.
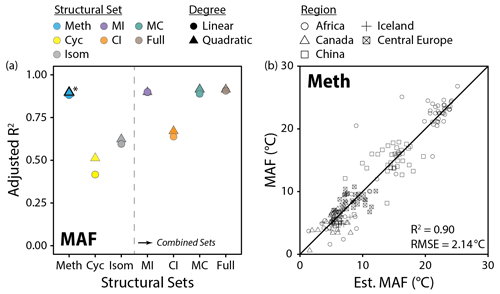
Figure 10(a) Performance (adjusted R2) of all linear and quadratic fits for the mean air temperature of months above freezing (MAF) and brGDGT fractional abundances (FAs) calculated within the basic (Meth, Cyc, Isom; left of dashed line) and combined (Meth–Isom (MI), Cyc–Isom (CI), Meth–Cyc (MC), and Full sets; right of dashed line) structural sets. Results of both the SFS/SBE and combinatoric fitting methods are plotted. The fit we suggest for general use (Meth set, quadratic, SFS/SBE; Eq. 10) is bolded and marked with an asterisk in (a) and plotted in (b). “Est. MAF” is the MAF temperature estimated using this suggested fit.
4.3.3 The combined Cyclization–Isomer set strengthens both conductivity and pH trends
Though the strongest conductivity trends were displayed by the Isom set (R2 ≤ 0.70), correlations were also present in the Cyc FAs (R2 ≤ 0.57, Fig. S20). Similarly, the Cyc set contained the highest pH dependencies (R2 ≤ 0.61), but notable relationships were visible in the Isom set as well (R2 ≤ 0.54, Fig. S28). To take advantage of all of these conductivity and pH relationships, we therefore used the combined Cyc–Isom set, which holds only methylation number constant while allowing both cyclization number and methylation position to vary (Fig. 2). Both conductivity and pH trends were strengthened in this combination set (R2 ≤ 0.73 and 0.62, Figs. S23 and S30 in the Supplement, respectively), especially for the uncyclized compounds. However, temperature correlations were also increased in the CI set (R2 ≤ 0.60, Fig. S16 in the Supplement), a potentially convoluting influence that may not be desired.
4.4 Calibrations
For each set, combined set, and subset defined in Sect. 3, we performed linear and quadratic regressions against temperature, conductivity, pH, dissolved oxygen, and lake geometry variables using SFS/SBE and combinatoric fitting methods. We found temperature and conductivity to provide the strongest empirical calibrations with brGDGTs, followed by pH and dissolved oxygen, and discuss our recommended calibrations below.
4.4.1 Temperature calibrations
For each structural set and subset defined in Sect. 3, we performed regressions of subset-specific brGDGT FAs against five temperature variables to generate multiple global-scale calibrations. Of the temperature indices that we tested, MAF provided the fit with the highest statistical significance (R2 = 0.91), followed closely by MST (R2 = 0.90), SWI (R2 = 0.89), and WMT (R2 = 0.88). MAT provided calibrations with high statistical performance as well (R2 ≤ 0.87). However, these fits showed clear seasonality biases in their residuals, resulting in substantial over-estimations of MAT for cold sites (Fig. S40 in the Supplement). Furthermore, they often relied heavily on low-abundance compounds as fitting variables (IIc, IIb′, IIIc, IIIc′, IIIb, and IIIb′). We therefore do not recommend a brGDGT MAT calibration and focus our discussion on the warm-season temperature indices, especially MAF. We note, however, that MAF is equal to MAT in warmer climates or lower latitudes and that MAF calibrations may be interpreted as reconstructing MAT in these cases.
Methylation number was the single most important structural variable for temperature calibrations. The Meth set, which allowed only methylation number to vary, provided a MAF calibration (R2 = 0.90, Fig. 10b) that was on par with other recent global and regional lake sediment calibrations (R2 = 0.85 to 0.94; Dang et al., 2018; Russell et al., 2018; Martínez-Sosa et al., 2021). The MI, MC, and Full sets, which additionally allowed for changes in cyclization number and/or methylation position, added little to the calibration performance (R2 = 0.90 to 0.91, Fig. 10a). Furthermore, sets which held methylation number constant – Cyc, Isom, and CI – performed markedly worse (R2 = 0.51, 0.63, and 0.67, respectively, Fig. 10a). Analogous results were found using RMSE to compare fit performance (Fig. S41a in the Supplement). These results indicate that effectively all of the temperature dependence of the 15 commonly measured brGDGTs is captured by methylation number alone.
Within the Meth set, independent calibrations were generated for the Metha, Methb, and Methc subsets as well. These subsets consist of only un-, mono-, and bicyclized compounds, respectively (Fig. 2a). As the FAs of these subsets were calculated independently, we were able to test for temperature calibrations of each subset alone. The Metha subset provided the strongest of the subset MAF fits (R2 = 0.88). This calibration has the notable advantage of employing only the three most abundant brGDGTs typically found in nature, Ia, IIa, and IIIa, which may allow for temperatures to be reproduced with high fidelity from even organic-lean samples. Furthermore, since it uses only non-cyclized, 5-methyl brGDGTs, it may be less subject to influence by the environmental factors that impact cyclization numbers and isomer ratios. MAF calibrations were also obtained using only the monocyclized (Methb, R2 = 0.79) and bicyclized (Methc, R2 = 0.74) brGDGTs. These fits represent, to our knowledge, the first calibrations that make use of only cyclized brGDGTs. This is a noteworthy result as it shows conclusively what can be seen by eye in Fig. 7; the relationship between temperature and methylations is a broad feature of brGDGTs that is present regardless of the number of rings on the carbon backbone. These un-, mono-, and bicyclized calibrations may find use in the case that one or more brGDGTs are suspected to be influenced by variables other than temperature.
Of the brGDGT temperature indices that we tested (see Appendix), performed best. This index correlated better with MAF (R2 = 0.89) than any other warm-season variable (SWI R2 = 0.84; MST R2 = 0.70; MAT R2 = 0.70; WMT R2 = 0.66). The slope and intercept of the MAF/ calibration (MAF = −0.5 (± 0.4) + 30.4 (± 0.8) ⋅ ) were similar to the MAT/ calibration presented by Russell et al. (2018) (MAT = −1.21 + 32.42 ⋅ ). This may suggest that -derived temperatures using the Russell et al. (2018) calibration in cold regions are best considered to reconstruct MAF rather than MAT. Though was previously found to correlate well with temperature in highly alkaline lakes on a regional scale (R2 = 0.75; Dang et al., 2018), it was not correlated with any temperature variable in our global dataset (R2 ≤ 0.12). Finally, we note that the community index (De Jonge et al., 2019), which was associated with bacterial community changes in geothermally heated Icelandic soils, is identical to our fIaMeth. This may suggest that the strong connection between fIaMeth and MAF could also be driven at least in part by changes in microbial community composition. However, genomic data are not currently available for the majority of the sites in this study to test this hypothesis.
MAF provided the strongest temperature calibrations at the global level in this study. Unlike for MAT, these calibrations yielded unbiased residuals at the cold end (Fig. 10b), encouraging their application in cold regions with high seasonality in particular. However, we note that the range of MAF values in our combined Canadian and Icelandic dataset is small (6.6 ∘C, or 3.2 ∘C without the warm and cold endmembers) compared to that of MAT (22.9 ∘C), especially in relation to the MAF calibration error (RMSE = 2.14 ∘C, Fig. 10b). While the global-scale MAF calibrations presented here are valid for application at high latitudes, they may therefore prove unable to resolve smaller temperature variations in paleoclimate archives from those regions. Regional high-latitude calibrations aimed at improving this temperature resolution are the subject of ongoing work.
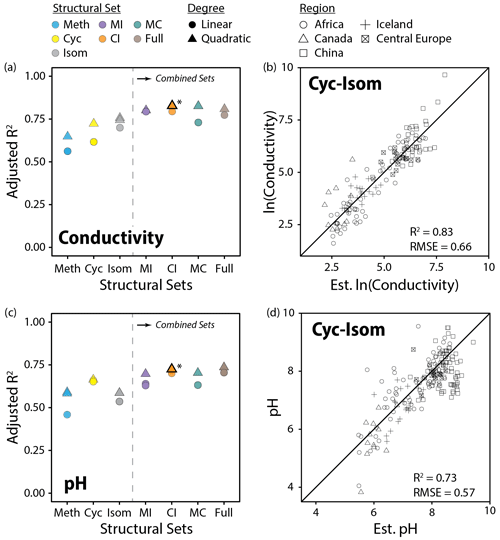
Figure 11Performance (adjusted R2) of all linear and quadratic fits for lake water conductivity (a) and pH (c) and brGDGT fractional abundances (FAs) calculated within the basic (Meth, Cyc, Isom; left of dashed lines) and combined (Meth–Isom (MI), Cyc–Isom (CI), Meth–Cyc (MC), and Full sets; right of dashed lines) structural sets. Results of both the SFS/SBE and combinatoric fitting methods are plotted. The fits we suggest for general use (CI set, quadratic, combinatoric, for both variables; Eqs. 12 and 13) are bolded and marked with an asterisk in (a) and (c) and plotted in (b) and (d). “Est. ln(Conductivity)” and “Est. pH” are the natural logarithm of lake water conductivity and pH estimated using these suggested fits.
4.4.2 Conductivity and pH calibrations
Conductivity outperformed pH in our calibrations (R2 = 0.83 vs. 0.74) and was the second most important predictor of brGDGT distributions in our dataset after temperature. Both cyclization number and methylation position were important to the success of these calibrations. The Cyc set, which allowed only cyclization number to change, provided a conductivity fit with R2 = 0.73 (Fig. 11a). The Isom set, which isolated trends in isomer abundances, generated a slightly stronger calibration with R2 = 0.76. When both of these structural properties were allowed to vary together in the CI set, the calibration was markedly improved (R2 = 0.83, Fig. 11b). In contrast, methylation number was a poorer predictor of conductivity alone (Meth set R2 = 0.65) and did not improve upon the CI correlation in the combined sets (MI R2 = 0.80; MC R2 = 0.83; Full R2 = 0.81). Similar results were found when using RMSE to compare fit performance (Fig. S41b). The CIIII and CIII subsets also provided conductivity calibrations with relatively high statistical performance (R2 = 0.75, 0.73). The CII subset performed worse (R2 = 0.65), likely due to the fact that no isomer variations are present in these FAs. These subset-specific fits are the first of their kind, and their success indicates that the relationship between brGDGTs and conductivity is present regardless of methylation number.
In addition to conductivity, the CI set also best captured the relationship between brGDGTs and pH (R2 = 0.73; Fig. 11c and d). The addition of methylation number variations in the Full set did not substantially improve the calibration (R2 = 0.74), indicating that the majority of the relationship between brGDGTs and pH is captured by cyclization number and methylation position. Of these two structural variables, cyclization number was more important for pH; the Cyc set calibration (R2 = 0.67) outperformed those from the Isom and Meth sets (R2 = 0.59 for both). Analogous results were found using RMSE (Fig. S41c). The CII, CIII, and CIIII subsets provided weaker but significant calibrations with comparable performances to one another (R2 = 0.67, 0.68, and 0.62, respectively), indicating again that pH relationships are more or less independent of methylation number.
4.4.3 Dissolved oxygen and lake geometry calibrations
There is increasing evidence that oxygen availability strongly affects lacustrine brGDGT distributions (van Bree et al., 2020; Colcord et al., 2017; Weber et al., 2018; Yao et al., 2020). We therefore tested for calibrations within our dataset with mean and minimum dissolved oxygen concentration (DOmean and DOmin). As lake morphology can be an important predictor of lake oxygen levels (Hutchinson, 1938; Nürnberg, 1995), we also tested the natural logarithms of maximum water depth (Depth), the ratio of lake surface area to maximum depth (), and approximate lake volume. None of the DO or lake geometry variables generated strong correlations with brGDGT distributions (Table S3 in the Supplement; Sect. S5.1 in the Supplement).
In light of the evidence that oxygen availability strongly affects lacustrine brGDGT distributions, it is perhaps surprising that we do not find a stronger correlation between brGDGTs and DO. However, the effects of DO on brGDGT distributions appear to be highly site-specific. For example, some detailed studies have found elevated levels of brGDGT-IIIa in low-oxygen conditions (Weber et al., 2018; Yao et al., 2020), but another found all of the most common brGDGTs except IIIa in abundance in the oxygen-depleted hypolimnion (van Bree et al., 2020). A third detailed study found no correlation between brGDGTs and oxygen at all (Loomis et al., 2014b), and no calibration study to date has found regional or global trends. The wide range of possible drivers of DO – mixing regimes, eutrophication state, and ice cover, to name a few – may play a role in the incoherent relationship between brGDGTs and DO in these studies and our own. Additionally, DO measurements are often taken at the time of sampling and are most likely not representative of the annual range. For the Canadian and Icelandic lakes in this study, for example, DO was depleted under lake ice relative to ice-free conditions in 10 out of 11 cases. Few of the lakes in our study have continuous DO monitoring data available, and most are from central Europe. Therefore, while our study does find some significant correlations between brGDGTs and DO, we do not recommend a calibration for general use and instead highlight the need for further study.
4.4.4 Recommended calibrations
The Meth, MC, MI, and Full sets all provided MAF temperature calibrations with comparable R2 (0.90 to 0.91) and RMSE (1.97 to 2.14 ∘C) values (Fig. 10a, Table S3). However, the Meth set provided the FAs with the strongest compound-specific relationships with MAF (R2 ≤ 0.88) in the modern dataset and exhibited little influence (R2 ≤ 0.49) from any other variable examined in this study. In contrast, the MC, MI, and Full sets all exhibited stronger relationships with pH and conductivity (Fig. 11a and c). We therefore recommend the highest-performing Meth calibration (Fig. 10b; Eq. 10; n = 182, R2 = 0.90, RMSE = 2.14 ∘C) for general use in lake sediments:
Importantly, Eq. (10) contains terms for fIIcMeth and fIIIbMeth, which may be equal to zero in organic-lean samples (e.g., Fig. 7f and h) and could thus result in unrealistic values for MAF. In these cases, we recommend applying subset-specific calibrations that exclude bicyclized (Eq. S1; n = 182, R2 = 0.89, RMSE = 2.19 ∘C) or both mono- and bicyclized (Eq. S2; n = 182, R2 = 0.88, RMSE = 2.33 ∘C) compounds. These calibrations offer flexibility in downcore applications with minimal sacrifice of statistical performance. Subset-specific calibrations are also available for mono- and bicyclized compounds alone (Eqs. S3 and S4).
The Full set MAF calibration provided the highest R2 and lowest RMSE in our dataset. This fit may be applicable in settings with good conductivity or pH control and may be useful for comparison with previous calibrations. It is therefore provided in Eq. (11) (n = 182, R2 = 0.91, RMSE = 1.97 ∘C):
The calibrations presented in Eqs. (10), (11), and (S1)–(S4) allow for the quantitative reconstruction of warm-season air temperatures from lake sediment archives, including those at high latitudes. The statistical performance of these fits is comparable to recently published calibrations (Russell et al. (2018): R2 = 0.94, RMSE = 2.14 ∘C, n = 65; Martínez-Sosa et al. (2021): R2 = 0.85, RMSE = 2.8 ∘C, n = 261; and Dang et al. (2018): R2 = 0.91, RMSE = 1.10 ∘C, n = 39). We do not recommend an independent MAT calibration due to residual seasonality biases (Fig. S40), though we note again that MAT is often identical to MAF in warm or low-seasonality settings.
Independent calibrations were generated for lake water conductivity and pH. However, we re-emphasize that these two variables are fundamentally related (Sect. 4.3), which may cause them to vary in tandem in a paleo-record. While we provide separate calibrations for conductivity and pH here, an examination of downcore trends in both reconstructed variables is recommended, along with an understanding of their relationships at the modern site.
The CI set generated the highest-performing conductivity calibration (R2 = 0.83, RMSE = 0.66; Fig. 11b, Table S3). The Full, MC, and MI sets provided calibrations that were statistically comparable (R2 = 0.80 to 0.83, RMSE = 0.65 to 0.70), but their FAs contained marked temperature dependencies (R2 ≤ 0.70, 0.77, and 0.75, respectively; Figs. S18, S17, and S15 in the Supplement). We therefore recommend the top CI fit for use (Eq. 12; n = 143, R2 = 0.83, RMSE = 0.66) and provide subset-specific calibrations for CII, CIII, and CIIII in the Supplement (Eqs. S5–S7 in the Supplement):
A brGDGT-based paleoconductivity reconstruction has yet to be attempted, but diatom-inferred conductivity records show the potential for this variable to provide valuable insight into changes in lake hydrology. These records have reconstructed changes in precipitation and evaporation balance, lake level fluctuations, meltwater influx events, and the isolation of a lake from the sea (Ng and King, 1999; Stager et al., 2013; Yang et al., 2004). The conductivity calibration in Eq. (12) thus enables brGDGTs to be tested as a new alternative or complementary proxy in paleohydrology reconstructions.
The Full and CI sets provided calibrations with pH that were statistically comparable to one another (R2 = 0.74 and 0.73, Fig. 11c, Table S3). Given the stronger temperature dependencies of the Full set, we recommend the CI calibration (Fig. 11d; Eq. 13; n = 154, R2 = 0.73, RMSE = 0.57) for use and provide its subset-specific calibrations (CII, CIII, and CIIII) in the Supplement (Eqs. S8–S10 in the Supplement):
The residuals of the fit in Eq. (13) have a weak but significant correlation with pH (R2 = 0.17), causing it to overestimate pH for acidic samples and underestimate it for alkaline ones. A similar bias in pH calibrations has been previously observed in soils (De Jonge et al., 2014b). We therefore caution the use of this calibration in acidic (pH < 5) or alkaline (pH > 9) conditions.
Previous work has demonstrated the value of brGDGT-derived pH records in studies of terrestrial paleoclimate (Cao et al., 2017; Fastovich et al., 2020; Tyler et al., 2010). However, these studies relied on calibrations generated from soils and/or analyses in which the 5- and 6-methyl isomers were not separated. The fit presented in Eq. (13) may improve such studies by providing a globally distributed pH calibration in lake sediments using the latest chromatographic methods, which improves upon the error of previously available calibrations (RMSE = 0.80, Russell et al., 2018).
The structural set calibrations for MAF, conductivity, and pH presented above offer potential advantages over traditional calibrations constructed using the standard Full set. The structural set FAs separate the effects of temperature from pH and conductivity in the modern dataset. The application of calibrations such as Eqs. (10), (12), and (13) could therefore provide some protection against the unwanted influences of other environmental variables downcore. Importantly, this advantage is gained without sacrificing the statistical performance of the calibration. Furthermore, the subset-specific calibrations such as Eqs. (S1) and (S2) use only the most abundant compounds, making it easier to apply brGDGT proxies to organic-lean samples where only some compounds are typically present above the detection limit.
We have shown that brGDGT structural sets and warm-season temperature indices improve compound-specific correlations with environmental parameters while advancing our biological understanding of the lipids themselves. Grouping brGDGTs into structural sets based on methylation number, methylation position, and cyclization number elucidated the relationships between environmental variables and brGDGT structures. These sets revealed that methylation number fully captures the relationship between brGDGT distributions and temperature. They also showed the relative abundance of 5- and 6-methyl isomers to be dependent on conductivity and cyclization number to be primarily tied to pH. The deconvolved relationships provided by these subsets allowed for the generation of calibrations with temperature and pH that relied on fewer compounds with robust modern trends, without sacrificing statistical performance. They additionally revealed conductivity to be the second-most important variable in controlling brGDGT distributions and provided a calibration for this oft-overlooked variable, which may find use as a proxy for precipitation/evaporation balances or hydrologic changes.
The structural sets also provided insight into the biological underpinnings of brGDGT structural diversity. The Meth, Cyc, and Isom sets gave evidence that methylation number, cyclization number, and methylation position vary more or less independently of one another across environmental gradients. They further revealed that the inclusion of tetramethylated compounds (Ia, Ib, Ic) enhances the temperature dependencies of 5-methyl compounds but erases those of their 6-methyl counterparts. Finally, the results linking methylation number to temperature and cyclization number to pH are consistent with a physiological explanation of brGDGT distributions (Weijers et al., 2007). However, an explanation for the connection between conductivity and methylation position has, to our knowledge, not yet been proposed and encourages further study. As the microbial producers of brGDGTs have yet to be identified and cultured, the structural set approach thus provides a valuable tool for investigating controls on brGDGT diversity with a biological lens.
Warm-season temperatures outperformed MAT as the most important predictors of brGDGT distributions, particularly in high-latitude environments. We introduced 43 new lake sediment samples from sites with low MAT and high seasonality. In conjunction with a global dataset, these samples showed a clear warm-season bias in brGDGT temperature relationships, with MAF providing the strongest fits in our dataset. The warm-season bias may suggest a direct or indirect connection to heightened primary productivity in the summer. Alternatively, it may be the result of a more complex relationship with dynamic lake processes such as mixing events. While further study is needed to unravel these complications, the strong empirical calibrations presented here support the use of the brGDGT paleotemperature proxy to quantitatively reconstruct warm-season air temperatures from high-latitude lake sediments.
In summary, the use of brGDGT structural sets and warm-season temperature indices deconvolved relationships between brGDGT structure and environmental gradients, revealed trends with biological implications, and tied brGDGT distributions to warm-season temperatures. Furthermore, they allowed for the construction of temperature and pH calibrations that rely on a smaller number of compounds with clearer modern trends compared to the traditional approach, without sacrificing statistical performance. Finally, we used the new structural set framework to generate the first brGDGT conductivity calibration in a global lake sediment dataset. Our results thus allow brGDGTs to be used to quantitatively reconstruct warm-season air temperatures and lake water conductivity and pH from lake sediment archives and provide a new methodology for the study of brGDGTs in the future.
Full and schematic structures of the 15 commonly measured brGDGTs are provided in Fig. A1. Table A1 details equations for calculating FAs within the structural sets.
We used the following previously defined brGDGT indices in this study: CBT (Weijers et al., 2007); MBT′ (Peterse et al., 2012); , , CBT5Me, CBT′, and Index1 (De Jonge et al., 2014b); IR6Me (Dang et al., 2016); #ringstetra, #ringspenta 5Me, and #ringspenta 6Me (Sinninghe Damsté, 2016); Degree of Cyclization (DC) as reformulated by Baxter et al. (2019); HP5 (Yao et al., 2020); isomerization of branched tetraethers (IBT; Ding et al., 2015); and community index (CI; De Jonge et al., 2019). Their equations are given below.
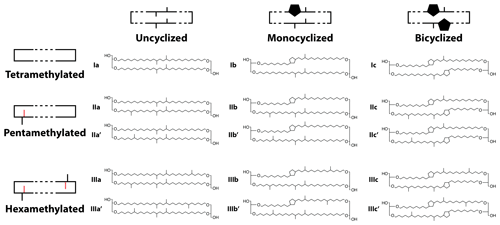
Figure A1Structures of the 15 commonly measured brGDGTs along with their schematic representations, with C6 methylations denoted in red in the schematics.
Biomarkers and associated metadata are provided in the Supplement and are archived at the PANGAEA data repository (https://doi.pangaea.de/10.1594/PANGAEA.931003, Raberg et al., 2021). Code for generating and plotting set-specific FAs in R is provided in the Supplement. Additional code, data, and calibration equations are available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-18-3579-2021-supplement.
GHM, JS, ÁG, JHR, SEC, DJH, and GdW designed the study and carried out the sampling. GHM, JS, ÁG, and SEC funded the research. JHR, AB, and DJH performed the laboratory work and processed the HPLC-MS data under the supervision of JS. JHR and SK generated the R code. JHR analyzed the data and interpreted the results. JHR wrote the manuscript with input from all authors. All authors contributed to the article and approved the submitted version.
The authors declare that they have no conflict of interest.
We thank the funding sources below for their support. We thank the Inuit of Nunavut for permitting access to their land and to sample soils and lake sediment (Scientific Research Licenses 01022 17R-M, 02034 18R-M, 02038 19R-M) and the Qikiqtani Inuit of Qikiqtarjuaq and Clyde River for assistance in the field. We thank the Nunavut Research Institute for logistical assistance and the Polar Continental Shelf Project for air support. Field research in Iceland benefited from the assistance of Ian Holmen, Sveinbjörn Steinthorsson, and Thor Blöndahl. We thank Yuki Weber and Shucheng Xie for providing additional temperature data, James Russell for a valuable discussion, and Lina Pérez-Angel for assistance with the calibration code. We additionally thank Nadia Dildar, Sebastian Cantarero, and Katie Rempfert for laboratory assistance and Chris Florian and Kate Zalzal for providing additional samples. The manuscript benefited from field assistance and/or discussions with Martha Raynolds, Shawnee Gowan, Helga Bueltmann, Elizabeth Thomas, Devon Gorby, Kayla Hollister, Kurt Lindberg, Nicolò Ardenghi, and Jamie McFarlin.
This research has been supported by the National Science Foundation (grant nos. OPP-1737712, OPP-1836981, DDRI-1657743, and EAR-1945484), the National Geographic Society (grant no. CP-019ER-17), a doctoral grant from the University of Iceland, a project grant from the University of Iceland Research Fund, and the University of Colorado Boulder.
This paper was edited by Sebastian Naeher and reviewed by two anonymous referees.
Baxter, A. J., Hopmans, E. C., Russell, J. M., and Sinninghe Damsté, J. S.: Bacterial GMGTs in East African lake sediments: Their potential as palaeotemperature indicators, Geochim. Cosmochim. Ac., 259, 155–169, https://doi.org/10.1016/j.gca.2019.05.039, 2019.
Beales, N.: Adaptation of Microorganisms to Cold Temperatures, Weak Acid Preservatives, Low pH, and Osmotic Stress: A Review, Compr. Rev. Food Sci. F., 3, 1–20, https://doi.org/10.1111/j.1541-4337.2004.tb00057.x, 2004.
Buckles, L. K., Weijers, J. W. H., Verschuren, D., and Sinninghe Damsté, J. S.: Sources of core and intact branched tetraether membrane lipids in the lacustrine environment: Anatomy of Lake Challa and its catchment, equatorial East Africa, Geochim. Cosmochim. Ac., 140, 106–126, https://doi.org/10.1016/j.gca.2014.04.042, 2014.
Cao, J., Rao, Z., Jia, G., Xu, Q., and Chen, F.: A 15 ka pH record from an alpine lake in north China derived from the cyclization ratio index of aquatic brGDGTs and its paleoclimatic significance, Org. Geochem., 109, 31–46, https://doi.org/10.1016/j.orggeochem.2017.02.005, 2017.
Cao, J., Rao, Z., Shi, F., and Jia, G.: Ice formation on lake surfaces in winter causes warm-season bias of lacustrine brGDGT temperature estimates, Biogeosciences, 17, 2521–2536, https://doi.org/10.5194/bg-17-2521-2020, 2020.
Colcord, D. E., Pearson, A., and Brassell, S. C.: Carbon isotopic composition of intact branched GDGT core lipids in Greenland lake sediments and soils, Org. Geochem., 110, 25–32, https://doi.org/10.1016/J.ORGGEOCHEM.2017.04.008, 2017.
Crump, S. E., Miller, G. H., Power, M., Sepúlveda, J., Dildar, N., Coghlan, M., and Bunce, M.: Arctic shrub colonization lagged peak postglacial warmth: Molecular evidence in lake sediment from Arctic Canada, Glob. Change Biol., 5, 1–13, https://doi.org/10.1111/gcb.14836, 2019.
Dang, X., Ding, W., Yang, H., Pancost, R. D., Naafs, B. D. A., Xue, J., Lin, X., Lu, J., and Xie, S.: Different temperature dependence of the bacterial brGDGT isomers in 35 Chinese lake sediments compared to that in soils, Org. Geochem., 119, 72–79, https://doi.org/10.1016/j.orggeochem.2018.02.008, 2018.
Dang, X. Y., Xue, J. T., Yang, H., and Xie, S. C.: Environmental impacts on the distribution of microbial tetraether lipids in Chinese lakes with contrasting pH: Implications for lacustrine paleoenvironmental reconstructions, Sci. China Earth Sci., 59, 939–950, https://doi.org/10.1007/s11430-015-5234-z, 2016.
De Jonge, C., Hopmans, E. C., Stadnitskaia, A., Rijpstra, W. I. C., Hofland, R., Tegelaar, E., and Sinninghe Damsté, J. S.: Identification of novel penta- and hexamethylated branched glycerol dialkyl glycerol tetraethers in peat using HPLC-MS2, GC-MS and GC-SMB-MS, Org. Geochem., 54, 78–82, https://doi.org/10.1016/j.orggeochem.2012.10.004, 2013.
De Jonge, C., Stadnitskaia, A., Hopmans, E. C., Cherkashov, G., Fedotov, A., and Sinninghe Damsté, J. S.: In situ produced branched glycerol dialkyl glycerol tetraethers in suspended particulate matter from the Yenisei River, Eastern Siberia, Geochim. Cosmochim. Ac., 125, 476–491, https://doi.org/10.1016/j.gca.2013.10.031, 2014a.
De Jonge, C., Hopmans, E. C., Zell, C. I., Kim, J. H., Schouten, S., and Sinninghe Damsté, J. S.: Occurrence and abundance of 6-methyl branched glycerol dialkyl glycerol tetraethers in soils: Implications for palaeoclimate reconstruction, Geochim. Cosmochim. Ac., 141, 97–112, https://doi.org/10.1016/j.gca.2014.06.013, 2014b.
De Jonge, C., Radujković, D., Sigurdsson, B. D., Weedon, J. T., Janssens, I., and Peterse, F.: Lipid biomarker temperature proxy responds to abrupt shift in the bacterial community composition in geothermally heated soils, Org. Geochem., 137, 103897, https://doi.org/10.1016/j.orggeochem.2019.07.006, 2019.
de Wet, G. A., Castañeda, I. S., DeConto, R. M., and Brigham-Grette, J.: A high-resolution mid-Pleistocene temperature record from Arctic Lake El'gygytgyn: A 50 kyr super interglacial from MIS 33 to MIS 31?, Earth Planet. Sc. Lett., 436, 56–63, https://doi.org/10.1016/j.epsl.2015.12.021, 2016.
Dearing Crampton-Flood, E., Peterse, F., Munsterman, D., and Sinninghe Damsté, J. S.: Using tetraether lipids archived in North Sea Basin sediments to extract North Western European Pliocene continental air temperatures, Earth Planet. Sc. Lett., 490, 193–205, https://doi.org/10.1016/j.epsl.2018.03.030, 2018.
Dillon, J. T., Lash, S., Zhao, J., Smith, K. P., van Dommelen, P., Scherer, A. K., and Huang, Y.: Bacterial tetraether lipids in ancient bones record past climate conditions at the time of disposal, J. Archaeol. Sci., 96, 45–56, https://doi.org/10.1016/j.jas.2018.05.009, 2018.
Ding, S., Xu, Y., Wang, Y., He, Y., Hou, J., Chen, L., and He, J.-S.: Distribution of branched glycerol dialkyl glycerol tetraethers in surface soils of the Qinghai–Tibetan Plateau: implications of brGDGTs-based proxies in cold and dry regions, Biogeosciences, 12, 3141–3151, https://doi.org/10.5194/bg-12-3141-2015, 2015.
Ding, S., Schwab, V. F., Ueberschaar, N., Roth, V.-N., Lange, M., Xu, Y., Gleixner, G., and Pohnert, G.: Identification of novel 7-methyl and cyclopentanyl branched glycerol dialkyl glycerol tetraethers in lake sediments, Org. Geochem., 102, 52–58, https://doi.org/10.1016/J.ORGGEOCHEM.2016.09.009, 2016.
Ding, S., Kohlhepp, B., Trumbore, S., Küsel, K., Totsche, K. U., Pohnert, G., Gleixner, G., and Schwab, V. F.: In situ production of core and intact bacterial and archaeal tetraether lipids in groundwater, Org. Geochem., 126, 1–12, https://doi.org/10.1016/j.orggeochem.2018.10.005, 2018.
Fastovich, D., Russell, J. M., Jackson, S. T., and Williams, J. W.: Deglacial temperature controls on no-analog community establishment in the Great Lakes Region, Quaternary Sci. Rev., 234, 106245, https://doi.org/10.1016/j.quascirev.2020.106245, 2020.
Fick, S. E. and Hijmans, R. J.: WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas, Int. J. Climatol., 37, 4302–4315, https://doi.org/10.1002/joc.5086, 2017.
Foster, L. C., Pearson, E. J., Juggins, S., Hodgson, D. A., Saunders, K. M., Verleyen, E., and Roberts, S. J.: Development of a regional glycerol dialkyl glycerol tetraether (GDGT)-temperature calibration for Antarctic and sub-Antarctic lakes, Earth Planet. Sc. Lett., 433, 370–379, https://doi.org/10.1016/j.epsl.2015.11.018, 2016.
Guo, J., Glendell, M., Meersmans, J., Kirkels, F., Middelburg, J. J., and Peterse, F.: Assessing branched tetraether lipids as tracers of soil organic carbon transport through the Carminowe Creek catchment (southwest England), Biogeosciences, 17, 3183–3201, https://doi.org/10.5194/bg-17-3183-2020, 2020.
Hanna, A. J. M., Shanahan, T. M., and Allison, M. A.: Distribution of branched GDGTs in surface sediments from the Colville River, Alaska: Implications for the MBT'/CBT paleothermometer in Arctic marine sediments, J. Geophys. Res.-Biogeo., 121, 1762–1780, https://doi.org/10.1002/2015JG003266, 2016.
Harning, D. J., Andrews, J. T., Belt, S. T., Cabedo-Sanz, P., Geirsdóttir, Á., Dildar, N., Miller, G. H., and Sepúlveda, J.: Sea Ice Control on Winter Subsurface Temperatures of the North Iceland Shelf During the Little Ice Age: A TEX86 Calibration Case Study, Paleoclimatology and Paleometeorology, 34, 1006–1021, https://doi.org/10.1029/2018PA003523, 2019.
Harning, D. J., Curtin, L., Geirsdóttir, Á., D'Andrea, W. J., Miller, G. H., and Sepúlveda, J.: Lipid Biomarkers Quantify Holocene Summer Temperature and Ice Cap Sensitivity in Icelandic Lakes, Geophys. Res. Lett., 47, 1–11, https://doi.org/10.1029/2019GL085728, 2020.
Hopmans, E. C., Weijers, J. W. ., Schefuß, E., Herfort, L., Sinninghe Damsté, J. S., and Schouten, S.: A novel proxy for terrestrial organic matter in sediments based on branched and isoprenoid tetraether lipids, Earth Planet. Sc. Lett., 224, 107–116, https://doi.org/10.1016/j.epsl.2004.05.012, 2004.
Hopmans, E. C., Schouten, S., and Sinninghe, J. S.: The effect of improved chromatography on GDGT-based palaeoproxies, Org. Geochem., 93, 1–6, https://doi.org/10.1016/j.orggeochem.2015.12.006, 2016.
Hu, J., Zhou, H., Peng, P., and Spiro, B.: Seasonal variability in concentrations and fluxes of glycerol dialkyl glycerol tetraethers in Huguangyan Maar Lake, SE China: Implications for the applicability of the MBT-CBT paleotemperature proxy in lacustrine settings, Chem. Geol., 420, 200–212, https://doi.org/10.1016/j.chemgeo.2015.11.008, 2016.
Huguet, C., Hopmans, E. C., Febo-Ayala, W., Thompson, D. H., Sinninghe Damsté, J. S., and Schouten, S.: An improved method to determine the absolute abundance of glycerol dibiphytanyl glycerol tetraether lipids, Org. Geochem., 37, 1036–1041, https://doi.org/10.1016/j.orggeochem.2006.05.008, 2006.
Hutchinson, G. E.: On the Relation between the Oxygen Deficit and the productivity and Typology of Lakes, Internationale Revue der gesamten Hydrobiologie und Hydrographie, 36, 336–355, https://doi.org/10.1002/iroh.19380360205, 1938.
Landrum, L. and Holland, M. M.: Extremes become routine in an emerging new Arctic, Nat. Clim. Change, 10, 1108–1115, https://doi.org/10.1038/s41558-020-0892-z, 2020.
Li, F., Zhang, C. L., Wang, S., Chen, Y., Sun, C., Dong, H., Li, W., Klotz, M. G., and Hedlund, B. P.: Production of branched tetraether lipids in Tibetan hot springs: A possible linkage to nitrite reduction by thermotolerant or thermophilic bacteria?, Chem. Geol., 386, 209–217, https://doi.org/10.1016/j.chemgeo.2014.08.015, 2014.
Loomis, S. E., Russell, J. M., Ladd, B., Street-Perrott, F. A., and Sinninghe Damsté, J. S.: Calibration and application of the branched GDGT temperature proxy on East African lake sediments, Earth Planet. Sc. Lett., 357–358, 277–288, https://doi.org/10.1016/j.epsl.2012.09.031, 2012.
Loomis, S. E., Russell, J. M., Eggermont, H., Verschuren, D., and Sinninghe Damsté, J. S.: Effects of temperature, pH and nutrient concentration on branched GDGT distributions in East African lakes: Implications for paleoenvironmental reconstruction, Org. Geochem., 66, 25–37, https://doi.org/10.1016/j.orggeochem.2013.10.012, 2014a.
Loomis, S. E., Russell, J. M., Heureux, A. M., D'Andrea, W. J., and Sinninghe Damsté, J. S.: Seasonal variability of branched glycerol dialkyl glycerol tetraethers (brGDGTs) in a temperate lake system, Geochim. Cosmochim. Ac., 144, 173–187, https://doi.org/10.1016/j.gca.2014.08.027, 2014b.
Lu, H., Liu, W., Yang, H., Wang, H., Liu, Z., Leng, Q., Sun, Y., Zhou, W., and An, Z.: 800-kyr land temperature variations modulated by vegetation changes on Chinese Loess Plateau, Nat. Commun., 10, 1958, https://doi.org/10.1038/s41467-019-09978-1, 2019.
Lumley, T.: leaps: Regression Subset Selection, CRAN repository, 2020.
Martínez-Sosa, P., Tierney, J. E., Stefanescu, I. C., Dearing Crampton-Flood, E., Shuman, B. N., and Routson, C.: A global Bayesian temperature calibration for lacustrine brGDGTs, Geochim. Cosmochim. Ac., 305, 87–105, https://doi.org/10.1016/j.gca.2021.04.038, 2021.
Miller, D. R., Habicht, M. H., Keisling, B. A., Castañeda, I. S., and Bradley, R. S.: A 900-year New England temperature reconstruction from in situ seasonally produced branched glycerol dialkyl glycerol tetraethers (brGDGTs), Clim. Past, 14, 1653–1667, https://doi.org/10.5194/cp-14-1653-2018, 2018.
Miller, G. H., Alley, R. B., Brigham-Grette, J., Fitzpatrick, J. J., Polyak, L., Serreze, M. C., and White, J. W. C.: Arctic amplification: Can the past constrain the future?, Quaternary Sci. Rev., 29, 1779–1790, https://doi.org/10.1016/j.quascirev.2010.02.008, 2010.
Naafs, B. D. A., Gallego-Sala, A. V., Inglis, G. N., and Pancost, R. D.: Refining the global branched glycerol dialkyl glycerol tetraether (brGDGT) soil temperature calibration, Org. Geochem., 106, 48–56, https://doi.org/10.1016/j.orggeochem.2017.01.009, 2017.
Naeher, S., Peterse, F., Smittenberg, R. H., Niemann, H., Zigah, P. K., and Schubert, C. J.: Sources of glycerol dialkyl glycerol tetraethers (GDGTs) in catchment soils, water column and sediments of Lake Rotsee (Switzerland) – Implications for the application of GDGT-based proxies for lakes, Org. Geochem., 66, 164–173, https://doi.org/10.1016/j.orggeochem.2013.10.017, 2014.
Ng, S. L. and King, R. H.: Development of a diatom-based specific conductivity model for the glacioisostatic lakes of Truelove Lowland: Implications for paleoconductivity and paleoenvironmental reconstructions in Devon Island lakes, N. W. T., Canada, J. Paleolimnol., 22, 367–382, https://doi.org/10.1023/A:1008022501117, 1999.
Ning, D., Zhang, E., Shulmeister, J., Chang, J., Sun, W., and Ni, Z.: Holocene mean annual air temperature (MAAT) reconstruction based on branched glycerol dialkyl glycerol tetraethers from Lake Ximenglongtan, southwestern China, Org. Geochem., 133, 65–76, https://doi.org/10.1016/j.orggeochem.2019.05.003, 2019.
Nürnberg, G. K.: Quantifying anoxia in lakes, Limnol. Oceanogr., 40, 1100–1111, https://doi.org/10.4319/lo.1995.40.6.1100, 1995.
Pearson, E. J., Juggins, S., Talbot, H. M., Weckström, J., Rosén, P., Ryves, D. B., Roberts, S. J., and Schmidt, R.: A lacustrine GDGT-temperature calibration from the Scandinavian Arctic to Antarctic: Renewed potential for the application of GDGT-paleothermometry in lakes, Geochim. Cosmochim. Ac., 75, 6225–6238, https://doi.org/10.1016/j.gca.2011.07.042, 2011.
Pérez-Angel, L. C., Sepúlveda, J., Molnar, P., Montes, C., Rajagopalan, B., Snell, K., Gonzalez-Arango, C., and Dildar, N.: Soil and Air Temperature Calibrations Using Branched GDGTs for the Tropical Andes of Colombia: Toward a Pan-Tropical Calibration, Geochem. Geophy. Geosy., 21, 1–18, https://doi.org/10.1029/2020gc008941, 2020.
Peterse, F., Meer, J. Van Der, Schouten, S., Weijers, J. W. H., Fierer, N., Jackson, R. B., Kim, J., and Damste, J. S. S.: Revised calibration of the MBT – CBT paleotemperature proxy based on branched tetraether membrane lipids in surface soils, Geochim. Cosmochim. Ac., 96, 215–229, https://doi.org/10.1016/j.gca.2012.08.011, 2012.
Peterse, F., Vonk, J. E., Holmes, R. M., Giosan, L., Zimov, N., and Eglinton, T. I.: Branched glycerol dialkyl glycerol tetraethers in Arctic lake sediments: Sources and implications for paleothermometry at high latitudes, J. Geophys. Res.-Biogeo., 119, 1738–1754, https://doi.org/10.1002/2014JG002639, 2014.
Prahl, F. G. and Wakeham, S. G.: Calibration of unsaturation patterns in long-chain ketone compositions for palaeotemperature assessment, Nature, 330, 367–369, https://doi.org/10.1038/330367a0, 1987.
Qian, S., Yang, H., Dong, C., Wang, Y., Wu, J., Pei, H., Dang, X., Lu, J., Zhao, S., and Xie, S.: Rapid response of fossil tetraether lipids in lake sediments to seasonal environmental variables in a shallow lake in central China: Implications for the use of tetraether-based proxies, Org. Geochem., 128, 108–121, https://doi.org/10.1016/j.orggeochem.2018.12.007, 2019.
Raberg, J. H., Harning, D. J., Crump, S. E., de Wet, G. A., Blumm, A., Kopf, S., Geirsdóttir, Á., Miller, G. H., and Sepúlveda, J.: brGDGT distributions and environmental parameters of lake sediments from the Eastern Canadian Arctic and Iceland, 2003–2019, PANGAEA [data set], https://doi.pangaea.de/10.1594/PANGAEA.931003, 2021.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/, last access: 15 February 2021.
Raynolds, M. K., Comiso, J. C., Walker, D. A., and Verbyla, D.: Relationship between satellite-derived land surface temperatures, arctic vegetation types, and NDVI, Remote Sens. Environ., 112, 1884–1894, https://doi.org/10.1016/j.rse.2007.09.008, 2008.
Reizer, J., Grossowicz, N., and Barenholz, Y.: The effect of growth temperature on the thermotropic behavior of the membranes of a thermophilic Bacillus. Composition-structure-function relationships, BBA-Biomembranes, 815, 268–280, https://doi.org/10.1016/0005-2736(85)90297-4, 1985.
Russell, J. M., Hopmans, E. C., Loomis, S. E., Liang, J., and Sinninghe Damsté, J. S.: Distributions of 5- and 6-methyl branched glycerol dialkyl glycerol tetraethers (brGDGTs) in East African lake sediment: Effects of temperature, pH, and new lacustrine paleotemperature calibrations, Org. Geochem., 117, 56–69, 2018.
Schouten, S., Hopmans, E. C., Schefuß, E., and Sinninghe Damsté, J. S.: Distributional variations in marine crenarchaeotal membrane lipids: A new tool for reconstructing ancient sea water temperatures?, Earth Planet. Sc. Lett., 204, 265–274, https://doi.org/10.1016/S0012-821X(02)00979-2, 2002.
Schouten, S., Hopmans, E. C., and Sinninghe Damsté, J. S.: The organic geochemistry of glycerol dialkyl glycerol tetraether lipids: A review, Org. Geochem., 54, 19–61, https://doi.org/10.1016/j.orggeochem.2012.09.006, 2013.
Schwarz, G.: Estimating the Dimension of a Model, Ann. Stat., 6, 461–464, https://doi.org/10.1214/aos/1176344136, 1978.
Shanahan, T. M., Hughen, K. A., and Van Mooy, B. A. S.: Temperature sensitivity of branched and isoprenoid GDGTs in Arctic lakes, Org. Geochem., 64, 119–128, https://doi.org/10.1016/j.orggeochem.2013.09.010, 2013.
Sinninghe Damsté, J. S.: Spatial heterogeneity of sources of branched tetraethers in shelf systems: The geochemistry of tetraethers in the Berau River delta (Kalimantan, Indonesia), Geochim. Cosmochim. Ac., 186, 13–31, https://doi.org/10.1016/j.gca.2016.04.033, 2016.
Sinninghe Damsté, J. S., Hopmans, E. C., Pancost, R. D., Schouten, S., and Geenevasen, J. A. J.: Newly discovered non-isoprenoid glycerol dialkyl glycerol tetraether lipids in sediments, Chem. Commun., 0, 1683–1684, https://doi.org/10.1039/b004517i, 2000.
Sinninghe Damsté, J. S., Rijpstra, W. I. C., Foesel, B. U., Huber, K. J., Overmann, J., Nakagawa, S., Kim, J. J., Dunfield, P. F., Dedysh, S. N., and Villanueva, L.: An overview of the occurrence of ether- and ester-linked iso-diabolic acid membrane lipids in microbial cultures of the Acidobacteria: Implications for brGDGT paleoproxies for temperature and pH, Org. Geochem., 124, 63–76, https://doi.org/10.1016/j.orggeochem.2018.07.006, 2018.
Stager, J. C., Ryves, D. B., King, C., Madson, J., Hazzard, M., Neumann, F. H., and Maud, R.: Late Holocene precipitation variability in the summer rainfall region of South Africa, Quaternary Sci. Rev., 67, 105–120, https://doi.org/10.1016/j.quascirev.2013.01.022, 2013.
Sun, Q., Chu, G., Liu, M., Xie, M., Li, S., Ling, Y., Wang, X., Shi, L., Jia, G., and Lü, H.: Distributions and temperature dependence of branched glycerol dialkyl glycerol tetraethers in recent lacustrine sediments from China and Nepal, J. Geophys. Res.-Biogeo., 116, G01008, https://doi.org/10.1029/2010JG001365, 2011.
Super, J. R., Chin, K., Pagani, M., Li, H., Tabor, C., Harwood, D. M., and Hull, P. M.: Late Cretaceous climate in the Canadian Arctic: Multi-proxy constraints from Devon Island, Palaeogeogr. Palaeoclim., 504, 1–22, https://doi.org/10.1016/j.palaeo.2018.03.004, 2018.
Thomas, E. K., Castañeda, I. S., McKay, N. P., Briner, J. P., Salacup, J. M., Nguyen, K. Q., and Schweinsberg, A. D.: A Wetter Arctic Coincident With Hemispheric Warming 8,000 Years Ago, Geophys. Res. Lett., 45, 10637–10647, https://doi.org/10.1029/2018GL079517, 2018.
Tierney, J. E. E., Russell, J. M. M., Eggermont, H., Hopmans, E. C. C., Verschuren, D., and Sinninghe Damsté, J. S. S.: Environmental controls on branched tetraether lipid distributions in tropical East African lake sediments, Geochim. Cosmochim. Ac., 74, 4902–4918, available at: https://www.sciencedirect.com/science/article/pii/S0016703710003236 (last access: 17 September 2018), 2010.
Tyler, J. J., Nederbragt, A. J., Jones, V. J., and Thurow, J. W.: Assessing past temperature and soil pH estimates from bacterial tetraether membrane lipids: Evidence from the recent lake sediments of Lochnagar, Scotland, J. Geophys. Res., 115, G01015, https://doi.org/10.1029/2009JG001109, 2010.
van Bree, L. G. J., Peterse, F., Baxter, A. J., De Crop, W., van Grinsven, S., Villanueva, L., Verschuren, D., and Sinninghe Damsté, J. S.: Seasonal variability and sources of in situ brGDGT production in a permanently stratified African crater lake, Biogeosciences, 17, 5443–5463, https://doi.org/10.5194/bg-17-5443-2020, 2020.
Venables, W. N. and Ripley, B. D.: Modern Applied Statistics with S, 4th Edn., Springer, New York, 2002.
Weber, Y., De Jonge, C., Rijpstra, W. I. C., Hopmans, E. C., Stadnitskaia, A., Schubert, C. J., Lehmann, M. F., Sinninghe Damsté, J. S., and Niemann, H.: Identification and carbon isotope composition of a novel branched GDGT isomer in lake sediments: Evidence for lacustrine branched GDGT production, Geochim. Cosmochim. Ac., 154, 118–129, https://doi.org/10.1016/j.gca.2015.01.032, 2015.
Weber, Y., Damsté, J. S. S., Zopfi, J., De Jonge, C., Gilli, A., Schubert, C. J., Lepori, F., Lehmann, M. F., and Niemann, H.: Redox-dependent niche differentiation provides evidence for multiple bacterial sources of glycerol tetraether lipids in lakes, P. Natl. Acad. Sci. USA, 115, 10926–10931, https://doi.org/10.1073/pnas.1805186115, 2018.
Weijers, J. W. H., Schouten, S., Spaargaren, O. C., and Sinninghe Damsté, J. S.: Occurrence and distribution of tetraether membrane lipids in soils: Implications for the use of the TEX86 proxy and the BIT index, Org. Geochem., 37, 1680–1693, https://doi.org/10.1016/j.orggeochem.2006.07.018, 2006.
Weijers, J. W. H., Schouten, S., van den Donker, J. C., Hopmans, E. C., and Sinninghe Damsté, J. S.: Environmental controls on bacterial tetraether membrane lipid distribution in soils, Geochim. Cosmochim. Ac., 71, 703–713, https://doi.org/10.1016/j.gca.2006.10.003, 2007.
Wetzel, R. G.: Salinity of Inland Waters, in: Limnology, edited by: Wetzel, R. G., Academic Press, San Diego, California, 169–186, 2001.
Woltering, M., Werne, J. P., Kish, J. L., Hicks, R., Sinninghe Damsté, J. S., and Schouten, S.: Vertical and temporal variability in concentration and distribution of thaumarchaeotal tetraether lipids in Lake Superior and the implications for the application of the TEX 86 temperature proxy, Geochim. Cosmochim. Ac., 87, 136–153, https://doi.org/10.1016/j.gca.2012.03.024, 2012.
Wörmer, L., Lipp, J. S., Schröder, J. M., and Hinrichs, K. U.: Application of two new LC-ESI-MS methods for improved detection of intact polar lipids (IPLs) in environmental samples, Org. Geochem., 59, 10–21, https://doi.org/10.1016/j.orggeochem.2013.03.004, 2013.
Xiao, W., Wang, Y., Liu, Y., Zhang, X., Shi, L., and Xu, Y.: Predominance of hexamethylated 6-methyl branched glycerol dialkyl glycerol tetraethers in the Mariana Trench: source and environmental implication, Biogeosciences, 17, 2135–2148, https://doi.org/10.5194/bg-17-2135-2020, 2020.
Yang, X., Wang, S., Kamenik, C., Schmidt, R., Shen, J., Zhu, L., and Li, S.: Diatom assemblages and quantitative reconstruction for paleosalinity from a sediment core of Chencuo Lake, southern Tibet, Sci. China, Ser. D, 47, 522–528, https://doi.org/10.1360/02yd0142, 2004.
Yao, Y., Zhao, J., Vachula, R. S., Werne, J. P., Wu, J., Song, X., and Huang, Y.: Correlation between the ratio of 5-methyl hexamethylated to pentamethylated branched GDGTs (HP5) and water depth reflects redox variations in stratified lakes, Org. Geochem., 147, 104076, https://doi.org/10.1016/j.orggeochem.2020.104076, 2020.
Yuk, H. G. and Marshall, D. L.: Adaptation of Escherichia coli O157:H7 to pH alters membrane lipid composition, verotoxin secretion, and resistance to simulated gastric fluid acid, Appl. Environ. Microb., 70, 3500–3505, https://doi.org/10.1128/AEM.70.6.3500-3505.2004, 2004.
Zhang, Z. X., Li, J., Chen, Z., Sun, Z., Yang, H., Fu, M., and Peng, X.: The effect of methane seeps on the bacterial tetraether lipid distributions at the Okinawa Trough, Mar. Chem., 225, 103845, https://doi.org/10.1016/j.marchem.2020.103845, 2020.
Zhao, B., Castañeda, I. S., Bradley, R. S., Salacup, J. M., de Wet, G. A., Daniels, W. C., and Schneider, T.: Development of an in situ branched GDGT calibration in Lake 578, southern Greenland, Org. Geochem., 152, 104168, https://doi.org/10.1016/j.orggeochem.2020.104168, 2021.
Zhao, J., Huang, Y., Yao, Y., An, Z., Zhu, Y., Lu, H., and Wang, Z.: Calibrating branched GDGTs in bones to temperature and precipitation: Application to Alaska chronological sequences, Quaternary Sci. Rev., 240, 106371, https://doi.org/10.1016/j.quascirev.2020.106371, 2020.
Zheng, Y., Pancost, R. D., Liu, X., Wang, Z., Naafs, B. D. A., Xie, X., Liu, Z., Yu, X., and Yang, H.: Atmospheric connections with the North Atlantic enhanced the deglacial warming in northeast China, Geology, 45, 1031–1034, https://doi.org/10.1130/G39401.1, 2017.