The motion of trees in the wind: a data synthesis

Interactions between wind and trees control energy exchanges between the atmosphere and forest canopies. This energy exchange can lead to the widespread damage of trees, and wind is a key disturbance agent in many of the world's forests. However, most research on this topic has focused on conifer plantations, where risk management is economically important, rather than broadleaf forests, which dominate the forest carbon cycle. This study brings together tree motion time-series data to systematically evaluate the factors influencing tree responses to wind loading, including data from both broadleaf and coniferous trees in forests and open environments.

We found that the two most descriptive features of tree motion were (a) the fundamental frequency, which is a measure of the speed at which a tree sways and is strongly related to tree height, and (b) the slope of the power spectrum, which is related to the efficiency of energy transfer from wind to trees. Intriguingly, the slope of the power spectrum was found to remain constant from medium to high wind speeds for all trees in this study. This suggests that, contrary to some predictions, damping or amplification mechanisms do not change dramatically at high wind speeds, and therefore wind damage risk is related, relatively simply, to wind speed.

Conifers from forests were distinct from broadleaves in terms of their response to wind loading. Specifically, the fundamental frequency of forest conifers was related to their size according to the cantilever beam model (i.e. vertically distributed mass), whereas broadleaves were better approximated by the simple pendulum model (i.e. dominated by the crown). Forest conifers also had a steeper slope of the power spectrum. We interpret these finding as being strongly related to tree architecture; i.e. conifers generally have a simple shape due to their apical dominance, whereas broadleaves exhibit a much wider range of architectures with more dominant crowns.

1 Introduction

Tree size and growth rate are influenced by their local wind environment (Bonnesoeur et al., 2016; MacFarlane and Kane, 2017) which in turn has an impact on forest carbon storage and dynamics. Monitoring the motion of trees in the wind can help us understand this interaction and model the risk of wind damage (Moore et al., 2018), which is a key driver of the forest carbon cycle in both temperate and tropical regions (Espírito-Santo et al., 2014; Schelhaas et al., 2003; Senf and Seidl, 2020).

Trees have characteristic and recognizable swaying patterns. This means that tree motion time series are distinct from each other and from the time series of local wind speeds. These tree motion characteristics are determined by tree size, shape, and, to a lesser extent, material properties (Dargahi et al., 2020; Jackson et al., 2019; Sellier and Fourcaud, 2009). Therefore, just as some types of trees have recognizable architectures, we expect them to have distinctive patterns of motion in response to wind loading. For example, trees in dense forests generally have a slender form with a small crown near the top (MacFarlane and Kane, 2017), which leads to a slow, pendulum-like motion (Sellier and Fourcaud, 2009).

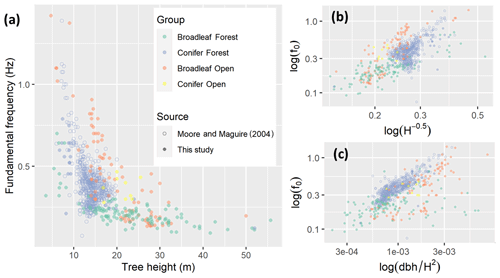
Previous data syntheses have focused on the fundamental sway frequency (f₀) of conifers and have found that larger, heavier trees sway more slowly than shorter, lighter ones (Moore and Maguire, 2004). This finding demonstrates that conifers can be approximated by a cantilever beam (i.e. a beam with distributed mass), but it is unclear whether this model extends to other types of trees. Jackson et al. (2019) demonstrated that tree architecture strongly influences f₀ using a combination of field data and finite element simulations. Additionally, a tree's f₀ has been observed to change over time in response to variations in tree mass and elasticity. These changes can be used as a proxy to measure phenology (Bunce et al., 2019; Gougherty et al., 2018) and water status of trees (Ciruzzi and Loheide, 2019) at high time resolution (e.g. every 10 min or hour) using low-cost sensors. Therefore, tree motion characteristics are expected to change with the seasons, with the presence or absence of leaves in deciduous trees and the freezing soil in high latitudes having important effects (Bunce et al., 2019).

Energy is transferred from the wind to a tree due to aerodynamic drag and is then dissipated by damping mechanisms in the tree. The balance between energy transfer from the wind to the tree and energy dissipation by damping determines a tree's risk of wind damage. A number of processes, both amplifying and damping the tree motion, have been suggested to become significant in the high wind speed regime, for example, damping by branching, whereby the branching patterns of open-grown trees increase damping efficiency by transferring energy to the outermost branches where it can be efficiently dissipated (de Langre, 2008, 2019; Spatz and Theckes, 2013; Theckes et al., 2011). Another example is the dynamic amplification of the tree motion as the peak energy of the wind spectrum approaches the natural frequency of the tree, inducing resonant effects (Blackburn et al., 1988; Ciftci et al., 2013; Holbo et al., 1980; Oliver and Mayhead, 1974; Rodriguez et al., 2008). We cannot measure these processes in the field, but the slope of the power spectrum (S_freq) can be used as an overall measure of energy transfer between wind and tree at different frequency ranges (van Emmerik et al., 2017, 2018). The spectrum of the tree is essentially the spectra of the wind, modified by the properties of the tree (Gardiner, 1992; Kerzenmacher and Gardiner, 1998; Mayer, 1987; Sellier et al., 2008). Therefore, the slope of the tree spectrum (S_freq) is the result of the energy transfer between wind and tree, as well as the energy transfer within the tree itself. We calculate S_freq for each hour of tree motion data and look for changes with increasing wind speed.

This study brings together data on tree motion from tropical, temperate, and boreal regions to explore key similarities and differences in the motion of these trees in the wind. We do this by comparing features calculated from the tree motion time-series data. While S_freq and f₀ are clearly important features of tree motion, thousands of other time-series features have been developed across multiple disciplines which may provide further insight. Fulcher and Jones (2017) compiled a set of over 7700 time-series features, and Lubba et al. (2019) distilled them to the most descriptive and minimally redundant 22 features (“catch22” features). We use these catch22 features, as well as f₀ and S_freq (and associated features described in the methods), to systematically explore the similarities and differences in the way trees move. We expect to find differences between conifers and broadleaves due to their different architectures (Jackson et al., 2019), as well as between open-grown trees and those in forests.

The specific questions we address are the following:

• Q1.

  What models best predict the fundamental frequency of broadleaf trees and conifers?

• Q2.

  Are characteristics of tree motion distinct between tree groups (conifers, broadleaves, forest, open-grown)?

• Q3.

  To what extent does increasing wind speed (or the change between summer and winter) change the characteristics of tree motion?

2 Methods

2.1 Description of the data

We collated data from 20 studies that included 243 trees and more than 1 million hours of tree motion data at resolutions ranging from 4 to 20 Hz. These collated data are now available online (Jackson et al., 2021). These studies used three types of sensor: (1) strain gauges which measure the bending strains at the base of the tree (Moore et al., 2005), (2) inclinometers measuring the changing inclination angle of the trunk (Bunce et al., 2019; Schindler et al., 2010), and (3) accelerometers measuring the acceleration at the top of the trunk (van Emmerik et al., 2017). We refer to these in general as measures of tree deflection. Five studies additionally measured branch motion, which is not used here but may provide further insight in future studies. Some data sets span multiple years, while others are confined to a short time during windy conditions. Most data sets contained tree height (H) and diameter at breast height (dbh) measurements and tree species data. Many of the individual studies in our data set did not measure high-resolution (>1 Hz) wind speeds because this requires sonic anemometers and so would substantially increase the cost of the field study. Also, in most cases the wind measurements were not in the same location as the trees, which hinders detailed analysis at high time resolution. We therefore focus on analyses which do not require high-resolution wind speed data (although we explore these data in Supplement S2). For the purposes of our analyses, we categorized trees as broadleaf or conifer and as open-grown or forest (as defined by the data owners). Table 1 gives an overview of the data sets.

2.2 Data processing and feature extraction

We resampled each time series to the lowest sampling frequency in the data set (4 Hz) to avoid sampling rate confounding our analysis. This frequency was sufficient to capture tree motion characteristics for all trees in our sample. Although each type of sensor measures a different property of tree motion, these properties are very strongly correlated and are complementary measures of tree motion. Each type of sensor has its own units, so absolute values are only comparable for this sensor type. All sensors are susceptible to a drift in the measurements resulting in an offset which varies slowly with temperature and other environmental factors. This is particularly evident in the strain gauges presumably because they are directly attached to the tree and so respond to the daily changes in tree diameter. We removed this offset using a 10 min high-pass Butterworth filter and applied the same filter to inclinometer and accelerometer data to ensure a fair comparison. This filter effectively removes the low-frequency (variations slower than 10 min) part of the tree motion, including any mean displacement and offset in the data. This period seems reasonable to capture most effects of wind–tree interaction, although open-grown trees exposed to strong winds may be displaced from their resting position for continuous long periods of time due to the mean wind speed on this timescale (Angelou et al., 2019; James et al., 2006). Therefore, different data filtering techniques may be more appropriate for open-grown trees (Angelou et al., 2019).

Table 1 Overview of the data sets used in this study. Links to download the data sets are provided in the “Data availability” section.

We selected 1 h samples during the windiest conditions available for each tree and calculated all tree motion features for all 243 trees in our data set. We first calculated features from the combined horizontal components of tree motion. We fitted an extreme value distribution and retained the shape parameter, k, which does not depend on the absolute values and so is comparable across sites. The scale and location parameters of the extreme value distribution depend on absolute values, and we did not use them in this study. Next, we calculated features from tree motion along a single axis of motion, since combining the two horizontal axes distorts important features such as f₀. The coordinate systems of each tree were not aligned with the wind direction. We therefore used a principal component analysis to select the axis with highest variance, the “stream-wise” component, and the perpendicular “cross-stream” component. We calculated the ratio of the explained variance in the two components, a measure of how elliptical the tree sway pattern is. We found that the cross-stream component did not contribute additional information, and so all analysis in this study used the stream-wise component of tree sway only. This is similar to using a time series from a single, horizontal axis of motion which is aligned with the dominant direction of the wind loading.

We centred and scaled the stream-wise component of tree sway and calculated the catch22 features (Lubba et al., 2019). These 22 features were selected to be maximally descriptive over a wide range of time-series data. Examples of these features are (1) the time interval between successive extreme events above the mean, (2) the mean error from forecasting the next value of the time series as the mean of the previous three, and (3) the centroid of the Fourier power spectrum. For more details of these features please see the Supplement and the original publications (Fulcher and Jones, 2017; Lubba et al., 2019).

We also calculated the power spectral density of the stream-wise component using Welch's method (Welch, 1967). We then calculated the slope of the power spectrum, S_freq, by fitting a linear model between log-transformed frequency and log-transformed power spectral density (van Emmerik et al., 2017). Since different frequency ranges represent different physical scales of energy transfer between wind and trees (see Fig. 1), we calculated this slope for multiple frequency ranges (0.05–0.8, 0.8–2, and 0.05–2 Hz). We test the sensitivity of this feature to different frequency ranges and fitting methods in the Supplement (S1) and found that the trends and differences between trees are not sensitive to the choice of frequency range, although the absolute values are. We tested calculating S_freq with reference to the tree's f₀, but this method proved too noisy at low wind speeds. Finally, we extracted the frequency, width, height, and dominance of the f₀ peak from the stream-wise component. The dominance was defined as the ratio of the fundamental peak height to the sum of all the heights of all other peaks in the spectrum (Jackson et al., 2019). In this study we focus on the features which help distinguish between tree types or are correlated with tree size. We do not discuss those features which do not meet these criteria, although these features may also exhibit interesting trends that warrant further study.

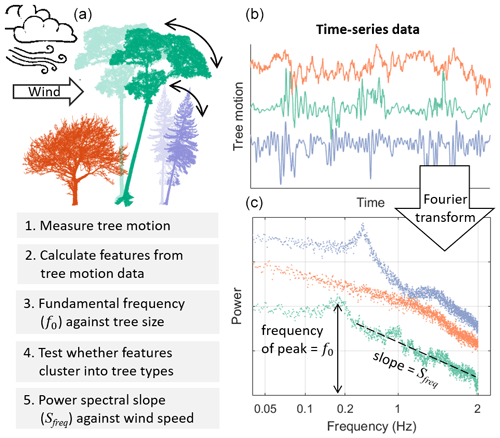
Figure 1 Overview of the study design. (a) Conceptual diagram of data collection showing three “types” of trees (colours) swaying in the wind. (b) A 5 min sample of tree motion data for three trees. (c) Fourier transformed data used to calculate the fundamental frequency, slope of the power spectrum, and related features.

2.3 Linear models of fundamental frequency against tree size and tree type

The aim of this analysis was to test whether the previously observed relationship between f₀ and tree size holds across the additional data in this study, especially the broadleaves. In addition to the detailed tree motion data for the 243 trees described above, we collated summary data on f₀ and tree size for a further 591 trees (Baker, 1997; Moore and Maguire, 2004). We used a linear regression on log-transformed data to explore the relationship between f₀ and tree size. We tested the simple pendulum model $\sqrt{\frac{\mathrm{1}}{H}}$, where H is the tree height, and a cantilever beam model $\frac{\mathrm{dbh}}{H^{\mathrm{2}}}$. This study improves upon previous work (Jackson et al., 2019) by (1) increasing the sample size in the underrepresented open-grown trees, (2) calculating f₀ in a consistent way across the 243 time series instead of using summary data, and (3) testing the simple pendulum model. Initial results showed that different models were more appropriate for conifers and broadleaves, so we performed a separate analysis for each tree type instead of using multiple linear regressions. We report the best fit models based on the coefficient of determination (R²) and Akaike's information criterion (AIC) (Pan, 2001).

2.4 Classifying tree types based on tree motion features

The aim in this analysis was to test whether different types of trees exhibited distinct, characteristic motion in the wind. We note that we could not account for systematic differences in wind conditions with these data. We first tested whether the trees grouped into the predefined groups (open-grown broadleaf, forest broadleaf, open-grown conifers, forest conifer) using a principal component analysis. We then used supervised methods (linear discriminant analysis and multinomial regression) to determine which two features best classified the trees into types. We also used a 10-fold cross-validation with a 50:50 training to testing data ratio to test whether the trees could be classified by type according to the features of their motion using a random forest model. We assessed the classification accuracy using Cohen's kappa (Cohen, 1960). We centred and scaled all features prior to analysis.

Note that our sample did not contain enough open-grown conifers to perform statistical analysis on this group. We therefore performed the above analysis on 89 forest broadleaves and the 63 open-grown broadleaves and the 63 forest conifers. The 17 open-grown conifers were projected onto the resulting axes in Fig. 3. Since the sample sizes in each group were not equal, we randomly resampled the larger groups to the size of the smallest (N=63) and repeated each analysis with this approach 50 times. We use this evenly sampled data set in the linear discriminant analysis and random forest classification analysis but not in the principal component analysis because it did not make a substantial difference.

We tested whether the classification analysis was likely impacted by the unequal tree size distributions in each tree type category. We used a subset of 169 trees (86 forest broadleaves, 54 forest conifers, and 29 open-grown broadleaves) for which we have raw tree motion data, as well as tree size data. We used a mixed-effects model (lme4) to predict tree size from the tree motion features and tree type (included in the model as a factor). We conducted separate analyses for tree height and dbh, and the best predictors were ordered using a two-way stepwise procedure based on minimizing AIC (Pan, 2001). The factor “tree type” was the seventh most explanatory feature in the model of height and ninth in the model of dbh (see Supplement S4 for details). This demonstrates that tree size is more strongly related to tree motion features than it is to tree type. Therefore, the relationship between tree type and tree motion features is unlikely to be confounded by differences in tree size, and hence the results of our classification analyses are valid.

2.5 Tracking changes in key tree motion characteristics with increasing wind speed

The aim of this analysis was to test whether the relationship between tree motion and wind speed varies between summer and winter and whether S_freq changes in a predictable way with wind speed. For the data sets with long-term tree motion and wind speed data (N=103 trees, 74 forest broadleaves and 29 forest conifers), we calculated each of the features described above for every hour of data available. We also calculated the hourly mean wind speed, the maxima, and 99th percentile of the tree deflection. We fitted a linear model to the relationship between tree deflection and squared wind speed for each tree separately and saved the coefficient, the slope of this fit line. We then calculated the ratio of the slope in summer (defined as 1 May–31 September) to the slope in winter. For deciduous trees, this ratio indicates whether the increased drag due to leaves in summer causes increased deflection or whether other mechanisms such as sheltering and damping compensate. We excluded trees with low sample sizes (<10 h), open-grown trees (due to low sample size), and tropical trees from this analysis. We therefore focussed on the comparison between deciduous forest broadleaves and forest conifers.

As the wind speed increases, both the drag coefficient and damping mechanisms will change (e.g. due to streamlining). The frequency range in which energy transfers from the wind to the tree will therefore shift, and this will be reflected in the slope of the power spectrum. Since our study contains a number of different forest structures, as well as open-grown trees, we cannot assume all sites have similar wind spectra. We therefore study the change in S_freq with wind speed for all 103 trees individually. We display these data by fitting a smoothing spline to them.

Figure 2 (a) Fundamental frequency against tree height on a linear scale. Small panels on log–log scales show fundamental frequency against (b) the simple pendulum model and (c) the cantilever beam model.

3 Results

3.1 Relationship between tree size and fundamental frequency

Figure 2 shows an overall decrease in f₀ with tree height, especially between 5 and 20 m. These short trees are mostly from conifer forests, the majority of which were included in a previous review (Moore and Maguire, 2004). The open-grown broadleaves display a similar sharp decrease in f₀ with height, although they are offset by approximately 0.5 Hz, which may be due to their wider stems. Table 2 shows that the best predictor of f₀ for the conifers was the cantilever beam model  $\left(f_{\mathrm{0}}\sim \frac{\mathrm{dbh}}{H^{\mathrm{2}}}\right)$ as demonstrated by Moore and Maguire (2004). This is unsurprising, since data from the previous review dominate this group of trees, but this relationship still holds in the new data for forest conifers. However, for both open-grown and forest broadleaves the simple pendulum model $\left(f_{\mathrm{0}}\sim \sqrt{\frac{\mathrm{1}}{H}}\right)$ was the best predictor of f₀. It is important to note that the taller trees in our study are almost exclusively broadleaves, and almost all were from a forest environment. Also, a mixed-effects model showed that f₀ was the feature most strongly correlated with tree height out of all the features in this study and that tree group, included in the model as a factor, was relatively unimportant (see Supplement S2 for details). This confirms that the trends we observed hold across groups, as well as within them, and do not represent group differences.

Table 2 Summary statistics for linear models predicting fundamental frequency using the cantilever beam model and the simple pendulum model for three groups of trees. The data were log-transformed prior to model fitting.

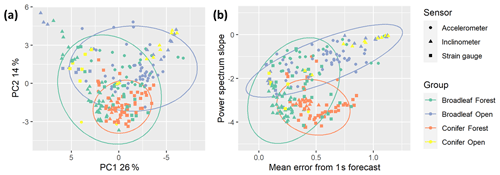
Figure 3 Features of tree motion from 229 trees during summer high (local) wind speed conditions projected on (a) first two principal component axes (arbitrary units) and (b) maximally discriminant axes (original units, unscaled). Ellipses represent Student's t distributions around the data and were only drawn around groups with sufficient samples: broadleaf forest (N=86), conifer forest (N=63), and broadleaf open (N=63).

3.2 Differences between types of trees

Figure 3 shows considerable overlap in the features of all groups of trees in this study. The trees from conifer forests are grouped together and cover a small proportion of the variance in both panels. The open-grown conifers seem to mainly overlap with the open-grown broadleaves, but we did not have enough samples to test this statistically. The forest broadleaves covered the largest area and overlapped with all other groups. We tested whether sample size affected this pattern by randomly sampling a subset of the forest broadleaves to the same sample size as the other types and repeating the analysis and found no substantial change in the distribution.

As expected, given that the catch22 features were designed to be minimally redundant, the principal components did not explain a large amount of the total variation across all features (Fig. 3a). The first principal component was driven by catch22 features, primarily the mean error from a rolling three-sample mean forecasting. The second principal component, while it only explained 14 % of the variation, helped distinguish between the groups of trees. The second principal component comprised mainly spectral features, specifically S_freq and the height of the fundamental frequency peak.

Figure 3b shows how the trees group along the two most discriminant features, determined using linear discriminant analysis and multinomial regression. It shows a clear separation between forest conifers and open-grown broadleaves, driven by S_freq, which is related not only to the damping efficiency of the tree but also to the energy spectrum of the local wind loading (see “Discussion”). We note that a mixed-effects model analysis showed that S_freq was strongly correlated with dbh but that tree group, included in the model as a factor, was not (see Supplement S2 for details). The x axis provides the best separation of forest broadleaves from the other groups based on the mean error from a 1 s forecast (predicting the fourth value from the previous three in a 4 Hz signal). This feature describes how predictable the signal is at short timescales and is likely influenced by both the speed and responsiveness of the tree motion, as well as the level of noise in the signal.

We performed multiple classification tasks using a random forest model with evenly balanced groups (N=63), a 50:50 training to testing data split, and a 10-fold cross-validation approach. In all cases we found that the stream-wise catch22 features improved classification ability compared to using only the features from the literature but that the cross-stream features added minimal further information. We found a moderate classification ability, Cohen's kappa = 0.646, for the three-group classification (omitting open-grown conifers due to lack of data). Two group classification analyses for the forest broadleaves against the other groups had slightly lower accuracy (kappa = 0.533 for open-grown broadleaves and kappa = 0.639 for forest conifers). However, the two-group classification between open-grown broadleaves and forest conifers resulted in a high accuracy, kappa = 0.90. These results align with our qualitative interpretation of the overlap between groups in Fig. 3, as described above.

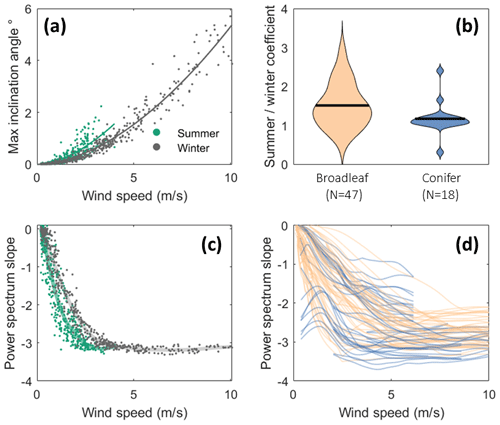
Figure 4 Changes in tree motion characteristics with wind speed for trees in forests. (a) Tree inclination angle against wind speed measured outside the forest for an example deciduous tree (Acer rubrum in Orange, Connecticut) in summer and winter with power-law fit lines overlaid. (b) Ratio of power-law fit slopes in summer and winter for all trees with >10 h of data in both seasons, excluding tropical trees. The horizontal black lines represent the median value. (c) Slope of the power spectrum (between 0.05 and 2 Hz) for a single tree (same as panel a) in summer and winter with smoothing splines overlaid. (d) Same as panel (c) but for all trees. Trends are approximated by smoothing splines, and summer and winter data are combined.

3.3 Changes in tree response with wind speed

Figure 4a shows a typical power-law relationship between tree deflection (in this case measured as inclination) and wind speed. Figure 4b shows how much more deflection occurs for a given wind speed in summer as compared to winter. As expected, we found that the deflection of the deciduous broadleaves increased more than that of the conifers (p<0.001) due to the presence of leaves in summer. Interestingly, we also observed an increase in some conifers, possibly due to soil conditions, and a decrease in a few broadleaves, possibly due to sheltering effects. We note that wind speeds were measured in different locations for each experiment, mostly outside the forest or at canopy height, meaning that the reported wind speeds do not represent inflow wind speed for each tree.

Figure 4c shows a sharp decrease in S_freq at low wind speeds, followed by a constant S_freq above 3–4 m/s. For this tree we found a slight difference between summer and winter, but there was no systematic difference across all deciduous trees, so we combined data from both seasons in the following analysis. Figure 4d shows S_freq for all trees with >10 h of data (N=93). As in Fig. 4c, we see an initial decline followed by a constant S_freq above a given threshold. Part of this trend is likely driven by noise at low wind speeds since the sensors will not reliably measure very low-level tree motion. However, since our data set contains a wide variety of sensors, some of which are extremely sensitive and which all exhibit similar patterns, we do not believe that the noise at low wind speeds is the (main) reason for the pattern. We found no systematic difference in this behaviour between types of trees.

4 Discussion

4.1 Key features of tree motion

As expected, we found that f₀ was a key feature of tree motion, being strongly correlated with tree height (Figs. 2 and S3–S4) and playing an important role in distinguishing between tree types. We showed that S_freq was stable at medium-high wind speeds (Fig. 4d) and this was the feature which best distinguished the different types of trees. The fact that two features previously used in the literature remain important when compared to the catch22 features, which were specifically designed for time-series classification, demonstrates that these two features capture key characteristics of tree motion. Interestingly, the width, height, and dominance of the fundamental frequency peak were not important features in this analysis; i.e. they did not explain much of the difference between tree types and were not strongly correlated with tree size.

We also found that a number of catch22 features were important for classifying tree types and were highly correlated with tree size (S3–S4). In particular, the mean error from a rolling three-sample mean forecast was important in distinguishing tree types (Fig. 3b). We interpret this feature as a measure of the regularity of the tree motion at 1 s timescales (all signals were analysed at 4 Hz). This regularity could be related to the wind conditions (i.e. a turbulent wind in a multi-layered forest leading to lower regularity) or the properties of the tree. For example, a small fast moving conifer would be less predictable, and a large broadleaf with complex branching architecture may be less affected by changes in wind loading and therefore be steadier and more predictable (Rodriguez et al., 2012; Theckes et al., 2011). We found that cross-stream features were superfluous in our analysis; i.e. the features from the literature and stream-wise catch22 features explained as much of the variability as was possible using this approach.

4.2 Differences in motion characteristics between tree types

We were surprised, given their differences in architecture, to find no clear separation between open-grown trees and forest trees in our clustering analyses (Fig. 3) and a relatively low accuracy in classifying these groups based on their motion. We did, however, observe that the open-grown conifers overlapped mostly with the open-grown broadleaves rather than the forest conifers, but the low sample size in this group (N=17) hindered any statistical analysis. Given their markedly divergent growth forms (MacFarlane and Kane, 2017), we expected open-grown trees to behave quite differently to the slender trees found in a forest environment (Q2). This lack of difference could be due to the diversity of broadleaves in this sample and difficulty of defining the boundary between open-grown and forest trees (in this study the data owners provided their own interpretation). This negative result may be interpreted as good news from a wind damage modelling point of view since it suggests that existing models (developed for conifer forests) may be generalizable to open-grown trees.

We found a consistent and distinct grouping of the forest conifers in both the supervised and unsupervised clustering analyses (Fig. 3) which is also reflected in the classification analysis. This was driven by their steeper S_freq, which suggests a difference in either the wind–tree energy transfer or the damping mechanisms. We also found that the f₀ of conifers was best predicted by the cantilever beam model (i.e. a beam with distributed weight) (Moore and Maguire, 2004). Broadleaves, however, were best approximated by the pendulum model (i.e. dominated by the weight of the crown) (Q1). This is likely due to the higher, heavier, and more distinct crowns of broadleaves determining the characteristics of their motion more strongly than the distributed crowns of conifers. Together, these findings support the theory that the motions of coniferous trees are relatively similar due to their simple architecture (Jackson et al., 2019), whereas the opposite is true of broadleaves in general. On this basis, we would expect emergent tropical trees, which also have a simple and consistent architecture, to respond to wind in a similarly predictable way. If this is the case (we did not have sufficient data from tall trees to test this theory here), this could enable a simple yet accurate wind damage model for tropical forests focussing only on the large trees which store the majority of the forest carbon (Bastin et al., 2015). We note that the conifers in this study were considerably smaller than the broadleaf trees. We suggest that the simpler pendulum model may be valid for a wider range of tree sizes than the cantilever beam model, and it would be interesting to test this for a range of tall conifers.

It is important to note that, in order to maximize the number of trees in our study, the clustering analyses did not incorporate any wind data. Therefore, differences in wind environment may confound differences in tree response. For example, the grouping of the conifers could be explained if patterns of wind flow over conifer forests are generally similar, but wind flow over broadleaf forests and open-grown trees is more variable. This emphasizes the importance of collecting high-resolution (>1 Hz) wind data alongside tree motion data to understand the details of this interaction. These data are currently lacking for open-grown trees and especially for tropical forests.

4.3 Trends with increasing wind speed and seasonal differences

As expected, maximum tree deflection (measured by either acceleration, inclination, or bending strain) increased with wind speed (Fig. 4a). We found that the gradient of this increase was generally steeper in summer for the deciduous trees (Q3) (Fig. 4b) presumably because their leaves provide a larger sail area. This effect is consistent with an increased drag on trees with leaves found in previous studies (Dellwik et al., 2019; Kane and Smiley, 2006). High wind speeds are more common in winter, so losing leaves will reduce a tree's risk of wind damage. However, for some deciduous trees this ratio was below 1, which could be explained by increased sheltering from nearby trees. We also found a slight increase in the tree deflection in summer for some conifers which could be explained by soil conditions or wood properties, especially in the sites which freeze in winter, although additional measurements would be required to test this.

The spectrum of the tree (characterized by S_freq) is essentially the spectra of the wind, modified by the properties of the tree. We observed a remarkably constant S_freq from medium to high wind speeds. This plateau in S_freq suggests that the frequencies at which energy is transferred from the wind to the tree do not change in the high wind speed regime. This plateau in S_freq suggests that no important additional damping or amplification mechanisms emerge above this threshold, meaning that wind damage risk is likely simply to increase with wind speed. We note that the classification analysis and correlation of features with tree size used these stable, high wind speed S_freq values.

We could not explain the fact that S_freq increased from low to medium wind speeds. We found a wide variation between individual trees in the shape of this curve, as well as the stable value, but we found no consistent difference between seasons, suggesting it is not driven by leaf streamlining processes.

4.4 Future research directions

A number of research questions arise from this study and the collation of this data set. Most importantly, does wind damage risk increase with tree height? Damage assessments after destructive windstorms have shown a larger proportion of tall trees uprooted or snapped (Magnabosco Marra et al., 2018; Rifai et al., 2016), which suggests that large trees are more vulnerable to wind damage. However, post-damage assessments may be confounded by other processes, such as disease or lightning, driving the observed pattern in tree mortality. Wind damage risk was measured directly on living trees and found to increase in two conifer forests (Duperat et al., 2020; Hale et al., 2012) and a tropical forest in Malaysia (Jackson et al., 2020). It would be highly valuable to extend this analysis across all trees with long-term data in this study to test whether this trend is consistent. However, the different types of sensors used to measure tree motion and their mounting positions made these data difficult to interpret in terms of risk across sites. We recommend the use of strain gauges to measure tree motion in this case since they provide comparable absolute values which can be related to the risk of mechanical damage. In addition, the low number of trees in each individual experiment limited the applicability of a mixed-effects model in this context. We note that this research question could be answered with local hourly wind speed measurements and therefore does not require sonic anemometers and so could be achieved at low-cost. To aid comparison between sites, locally measured wind speeds could be related to some near-surface reference wind speed available at hourly resolution, such as the hourly 10 m wind gust product provided by the European Centre for Medium-Range Weather Forecasts.

Collating this data set highlighted the paucity of data available for open-grown conifers, with the exception of James et al. (2006). The low number of these trees in our data set precluded statistical analysis, and further data collection in this area would be highly valuable. We also note the low representation of tropical forests, which are likely to be the most complex due to their structure and diversity. Neither of the two tropical sites in this study had high-resolution wind speed data for high wind periods.

A number of single-site studies have demonstrated intriguing relationships between fundamental frequency and ecological processes such as phenology, water status, rain interception, and drought (Bunce et al., 2019; Ciruzzi and Loheide, 2019; van Emmerik et al., 2018; Gougherty et al., 2018). Extending these analyses across the full data set would allow us to test how robust these relationships are and therefore whether trees can be used as indicators of ecological processes in other ecosystems. This could be particularly interesting in sites which freeze in winter since this will have a profound effect on the wood elasticity. Additional data collection for these purposes should use inertial measurement units (IMUs) which combine accelerometers, inclinometers, and magnetometers because the signals have a lower drift than the strain gauges.

In addition, there has been a long-standing debate on the potential role of resonance between the wind and the tree leading to wind damage (i.e. a high-energy frequency in the wind spectra coinciding with f₀) (Blackburn et al., 1988; Holbo et al., 1980; Oliver and Mayhead, 1974; Rodriguez et al., 2008; Schindler et al., 2010; Schindler and Mohr, 2018). Previous work used singular spectrum analysis to show that the oscillatory component of tree sway diminished with wind speed for four forest Scots pine trees (Schindler and Mohr, 2018). This result shows that no resonance between wind and tree occurs at the observed wind speeds and that resonance is unlikely to occur at higher wind speeds. It would be useful to test whether this result holds across all the trees in the current study.

The subset of data with high-resolution wind speed measurements could be used to explore energy transfer and damping efficiency of different trees. In particular, the identification of S_freq as a key feature of tree motion, possibly related to the drag factor and damping efficiency, warrants further exploration (van Emmerik et al., 2018). Further data collection aimed at understanding the mechanisms involved in energy transfer from the wind to the tree should use arrays of sonic anemometers above and below the canopy close to the target trees to collect high-resolution (>5 Hz) local wind speed data. We suggest future studies of this kind combine multiple sensors to measure tree motion and follow a standardized protocol to calibrate the sensors and so ensure data are comparable between studies.

5 Conclusions

In this study, we collated data on tree motion in order to explore the key similarities and differences amongst trees, as well as possible trends with tree size and wind speed. We compared trees and tested trends based on features extracted from the tree motion time series.

We found that trees in conifer forests exhibit similar responses to wind loading and that these were distinct from those of broadleaves, presumably as a result of their simpler branching architecture. However, we could not reliably distinguish between open-grown and forest broadleaves based on their motion in the wind despite their substantial architectural differences. Our analysis confirms previous studies showing that the fundamental frequency, which describes the speed of tree sway, is a robust feature with which to compare the motion of trees and which is strongly related to tree size. Future studies should examine how the fundamental frequency of trees changes over time since this is related to tree mass and elasticity and hence to a range of important ecological processes such as leaf phenology and water status.

We also found that the slope of the power spectrum, which is related to the wind–tree energy transfer, is an important feature in distinguishing tree types and displayed consistent trends with wind speed. All trees in this study exhibited a remarkably constant slope of the power spectrum from medium to high wind speeds in both summer and winter. This suggests that the relationship between wind loading and tree deflection is simply related to wind speed in the high wind speed range. This result could be an important contribution to estimating wind damage risk and understanding the role of wind in forest ecology more generally.