Importance of the forest state in estimating biomass losses from tropical forests: combining dynamic forest models and remote sensing

Disturbances, such as extreme weather events, fires, floods, and biotic agents, can have strong impacts on the dynamics and structures of tropical forests. In the future, the intensity of disturbances will likely further increase, which may have more serious consequences for tropical forests than those we have already observed. Thus, quantifying aboveground biomass loss of forest stands due to stem mortality (hereafter biomass loss rate) is important for the estimation of the role of tropical forests in the global carbon cycle. So far, the long-term impacts of altered stem mortality on rates of biomass loss have not been adequately described.

This study aims to analyse the consequences of long-term elevated stem mortality rates on forest dynamics and biomass loss rate. We applied an individual-based forest model and investigated the impacts of permanently increased stem mortality rates on the growth dynamics of humid, terra firme forests in French Guiana. Here, we focused on biomass, leaf area index (LAI), forest height, productivity, forest age, quadratic mean stem diameter, and biomass loss rate. Based on the simulation data, we developed a multiple linear regression model to estimate biomass loss rates of forests in different successional states from the various forest attributes.

The findings of our simulation study indicated that increased stem mortality altered the succession patterns of forests in favour of fast-growing species, which increased the old-growth forests' gross primary production, though net primary production remained stable. The stem mortality rate had a strong influence on the functional species composition and tree size distribution, which led to lower values in LAI, biomass, and forest height at the ecosystem level. We observed a strong influence of a change in stem mortality on biomass loss rate. Assuming a doubling of stem mortality rate, the biomass loss rate increased from 3.2 % yr⁻¹ to 4.5 % yr⁻¹ at equilibrium. We also obtained a multidimensional relationship that allowed for the estimation of biomass loss rates from forest height and LAI. Via an example, we applied this relationship to remote sensing data on LAI and forest height to map biomass loss rates for French Guiana. We estimated a countrywide mean biomass loss rate of 3.0 % yr⁻¹.

The approach described here provides a novel methodology for quantifying biomass loss rates, taking the successional state of tropical forests into account. Quantifying biomass loss rates may help to reduce uncertainties in the analysis of the global carbon cycle.

1 Introduction

Tropical forests represent an important pool in the global carbon cycle, as they store approximately 55 % of the amount of global forest carbon (471±93 PgC) in their living biomass (Pan et al., 2011). Intact tropical forests assimilate an average of 0.96±0.46 PgC of carbon per year (Hubau et al., 2020). This carbon sink behaviour of tropical forests has considerably reduced the growth rate of atmospheric carbon dioxide (Friedlingstein et al., 2019; Le Quéré et al., 2016). However, the carbon assimilation capacity of forests is affected by stem mortality due to disturbances, which can cause rapid, extensive carbon loss (Chambers et al., 2013; Fisher et al., 2008; Korner, 2003; Pugh et al., 2019; Seidl et al., 2014). Increased stem mortality due to disturbances has been related to a reduction in the carbon sink of tropical forests (Brienen et al., 2015; Hubau et al., 2020). A number of studies have discussed different climate-controlled mortality drivers, such as temperature (Clark et al., 2010), vapour pressure deficit (Trenberth et al., 2014), drought (Fauset et al., 2019; Phillips et al., 2010), and windthrow (Chambers et al., 2009; Magnabosco Marra et al., 2016; Marra et al., 2014; Negrón-Juárez et al., 2010, 2018; Rifai et al., 2016; Silvério et al., 2019). In addition, mechanical disturbances, such as insect calamities (Coley and Kursar, 2014), fires (Barlow et al., 2003; Brando et al., 2014; Slik et al., 2010), and lianas (Ingwell et al., 2010; Nepstad et al., 2007; Wright et al., 2015), may also lead to increased stem mortality. The expected increase in the frequency and intensity of those disturbances may result in an overall increase in stem mortality and its associated physiological mechanisms (McDowell et al., 2018). Higher levels of stem mortality thus present a major risk to climate mitigation efforts (e.g. REDD+: Reducing Emissions from Deforestation and Forest Degradation), as reductions in carbon assimilation rates and a decrease in the carbon stocks of tropical forests could counteract attempts to compensate for climate change (Gumpenberger et al., 2010; Körner, 2017; Le Page et al., 2013).

Mortality is a complex process because the causes leading to tree death can be diverse. Trees can die naturally from senescence or from forest disturbances, which may be abrupt or continuous and may have abiotic or biotic, allogenic or autogenic, and extrinsic or intrinsic causes (Franklin et al., 1987; McDowell et al., 2018). Furthermore, drivers of stem mortality often occur in combination, so the primary factors of death are not obvious (Franklin et al., 1987; McDowell et al., 2018). Stem mortality leads to temporal changes in stand structure, tree species composition, and releases of resources, particularly biomass (Franklin et al., 1987; Hülsmann et al., 2018). Consequently, tree death affects important forest growth processes, including tree growth and establishment, which are influenced by species-specific competition strategies (Snell et al., 2014) as well as by environmental and competitive factors such as light availability (Kuptz et al., 2010; Poorter, 1999; Uriarte et al., 2004). The influence of stem mortality on forest growth dynamics is determined by the disturbance intensity, which can range from the temporary loss of vitality to the mortality (Kindig and Stoddart, 2003) of individual trees, forest stands, and entire landscapes. Finally, stem mortality events are heterogeneously distributed such that spatial patterns can be scattered or clustered (Franklin et al., 1987). Empirical studies have already analysed the effects of short-term disturbances (i.e. intra-annual or over a few years) on increases in tropical stem mortality (e.g. Barlow et al., 2003; Brando et al., 2014; Chambers et al., 2009, 2013; Doughty et al., 2015; Holzwarth et al., 2013; Magnabosco Marra et al., 2016; Marra et al., 2014; McDowell et al., 2018; Negrón-Juárez et al., 2010, 2017; Nepstad et al., 2007; Phillips and Brienen, 2017; Slik et al., 2010; Stovall et al., 2019; Wright et al., 2015). Nevertheless, using empirical studies that are limited in space and time, it is difficult to quantify the long-term effects of permanently increased stem mortality levels and to assess the consequences of such alterations on the dynamics, structures, and successional states of forests. Also, new remote sensing technologies offer enhanced potential for measuring the vertical and horizontal structures of forests at country to global scales (e.g. Bi et al., 2015; Hall et al., 2011; Lefsky et al., 2002, 2005; Myneni et al., 2015; Simard et al., 2011; Le Toan et al., 2011). Remote sensing products have previously been used for large-scale identification of stem mortality following disturbances (e.g. Pugh et al., 2019; Senf and Seidl, 2020); however, the estimation of biomass loss rates due to stem mortality for forests at different states remains still uncertain.

In this context, individual-based forest gap models offer an approach to analysing forest dynamics (Botkin et al., 1972; Bugmann, 2001; Bugmann et al., 2019; Fischer et al., 2016; Shugart, 2002). Individual-based forest models are parameterized with forest inventory data to allow for the investigation of forest growth dynamics over longer periods. By simulating the growth, establishment, mortality, and competition among trees within a forest, these models can contribute to estimating the biomass gain and loss of tropical forests (e.g. Hiltner et al., 2018, 2021; Maréchaux and Chave, 2017). As a result of gap formation after tree falling (Fischer et al., 2016; Huth et al., 1998), simulation areas consist of a mosaic of forest stands on which the vertical and horizontal structures and dynamics of forests in different successional states are modelled (Botkin, 1993; Botkin et al., 1972; Bugmann, 2001; Fischer et al., 2016; Shugart, 1984). Structural state variables describing successional states of forests, such as tree size distributions and functional tree species compositions, play a major role in the estimation of the carbon budgets of forest stands and entire landscapes (Bohn and Huth, 2017; Fischer et al., 2018, 2019; Rödig et al., 2017, 2018, 2019; Rüger et al., 2020). Successional state variables of forests can be derived on large spatial scales (e.g. country to global levels) through a combination of individual-based forest gap modelling and remote sensing (Rödig et al., 2017, 2019; Shugart et al., 2015, 2018), as this allows for a quantification of the spatial variation in forest structure due to stem mortality (Rödig et al., 2017). The combination of individual-based forest gap models and remote sensing methods may also provide information on the spatial distribution of the annual rates of aboveground biomass loss due to stem mortality (hereafter biomass loss rate).

The aims of this study are to investigate the impacts of permanently increased stem mortality rates on forest dynamics, to provide a framework for estimating biomass loss rates in terra firme forests at different successional states, and to derive a sample map of biomass loss for an entire country (i.e. French Guiana). This biomass loss map represents an application example to demonstrate the synergetic benefits of linking an artificial dataset derived from an individual-based forest model with remote sensing data. Here, we address the following research questions in detail.

1. What are the consequences of permanently increased stem mortality rates on the dynamics of forest attributes (e.g. aboveground biomass, forest height, gross primary production, net primary production, leaf area index, quadratic mean stem diameter, mean forest age, and biomass loss rates) in tropical forests?

2. Can the biomass loss rates of tropical forests be estimated using various forest attributes that can also be derived from remote sensing?

2 Materials and methods

We applied the “terra firme” version of the dynamic individual-based forest model FORMIND (Fischer et al., 2016; Hiltner et al., 2018; Köhler and Huth, 2004) and simulated the effects of long-term increased stem mortality levels on the dynamics of multiple forest attributes (Fig. 1). This artificial dataset of forest dynamics covers a wide range of possible forest states such as the variability in tree species composition, successional state, and tree size distribution. We assume that we can use it to partially cover almost every state of forest stands in French Guiana (the so-called forest factory approach, see Bohn and Huth, 2017). We included aboveground biomass (hereafter biomass), mean forest height, gross primary production (GPP), net primary production (NPP), leaf area index (LAI), biomass turnover time (τ_B), quadratic mean stem diameter (QMD), mean forest age, and rate of biomass loss (m_AGB) in our assessment. We analysed all of these forest attributes in relation to the intensity of increased stem mortality. Each simulated forest used in the analysis has the area of 1 ha, with the forest states of each hectare differing from each other in each simulated time step and scenario. Then, we developed a multiple linear regression model by testing different forest state attributes, such as LAI and forest height, as proxy variables. In addition, we derived a sample map for the biomass loss rate and biomass residence time of an entire region by using values for forest height and LAI obtained from satellite products. Simulated terra firme forests of French Guiana served as a case study.

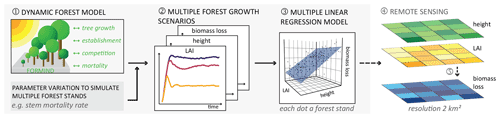
Figure 1 Framework developed for estimating biomass loss rates by linking a dynamic forest model and remote sensing. (1) A forest model was applied to (2) simulate the succession dynamics of forest stands of various forest attributes, such as LAI, forest height, and biomass loss rate, in a set of different stem mortality scenarios (results used to answer research question 1). A simulated forest stand has the area of 1 ha, with the forest states of each simulated hectare differing at each simulation time step and scenario. (3) Then, we developed a multiple linear regression model for the simulated forest states with LAI and forest height as proxy variables and biomass loss rate as the response (results to answer research question 2). (4) In addition, we applied the multiple linear regression model to remote sensing maps containing the values of the investigated forest attributes (LAI and forest height) to (5) derive a sample map of biomass loss.

2.1 Study region

The study region is French Guiana, 95 % of which is covered by humid, lowland terra firme forests (Hammond, 2005; Stach et al., 2009). These forests are characteristic for the Guiana Shield (Grau et al., 2017). The forests are generally species-rich, with an average of 150 to 200 tree species per hectare (Gourlet-Fleury et al., 2004), and are dense in biomass stock (Johnson et al., 2016; Rödig et al., 2017; Saatchi et al., 2011).

2.2 Forest model FORMIND

2.2.1 Model description

To analyse the forest dynamics under the impacts of different levels of disturbance, we applied the “terra firme parameterization” of the forest model FORMIND v3.2 (Fischer et al., 2016) and took relevant parameter values from Hiltner et al. (2018), including tree growth, mortality, and establishment (see Tables S1 and S2 in the Supplement). FORMIND is an individual-based forest gap model that describes forest dynamics, tree growth, and changes in forest structures on a simulation area (1 ha to multiple square kilometres) consisting of 20 by 20 m patches that interact with each other (see Fig. S1 in the Supplement), wherein trees are not positioned explicitly within a patch.

Every tree with a stem diameter at breast height (DBH) ≥0.1 m was simulated considering the following main processes at annual time steps: tree growth, establishment, mortality, and competition for light and space. The biomass gain of a tree results from the difference between photosynthetic production and respiratory losses (Fischer et al., 2016; Hiltner et al., 2018, 2021). In the model, stem mortality is a key driver of forest dynamics. Stem mortality increases if the space for canopy expansion is limited, which depends on a tree's position within the forest stand (self-thinning by crowding), whether tree growth is reduced (growth-dependent), and whether surrounding trees die after large trees fall (gap formation). Finally, each tree is subject to a stem mortality rate, which is stochastic. Here, we modified the stem mortality rate (Eq. 1) to induce heterogeneity in the horizontal and vertical forest structures (i.e. tree size distribution and functional species composition) of terra firme forests in French Guiana. Our study does not focus on short-term disturbances, but on the effects of long-term changes (>100 years) in the intensity of stem mortality. Possible factors altering stem mortality rates in the forest model include environmental drivers, such as sustained elevated temperatures, altered precipitation regimes, and reduced soil water availability. The stem mortality rate refers to individual trees at the stand level and is not stand-replacing.

For the generic forest model parameterization of French Guiana's terra firme forests, tree species were classified into eight plant functional types (PFTs) according to species-specific traits, i.e. the maximum incremental rates of DBH and maximum tree height. We assume here that major parts of the terra firme forests can be characterized on the basis of three functional species groups: light-requiring species, species with intermediate light requirements, and shade-tolerant species (see Table S2). This functional species diversity is considered to be sufficient to capture forest succession dynamics in tropical forests (Fischer et al., 2018; Rödig et al., 2017; Rüger et al., 2020). Detailed model descriptions can be found in Fischer et al. (2016), in Hiltner et al. (2018), and online at https://www.formind.org (last access: 22 February 2022).

2.2.2 Simulation settings

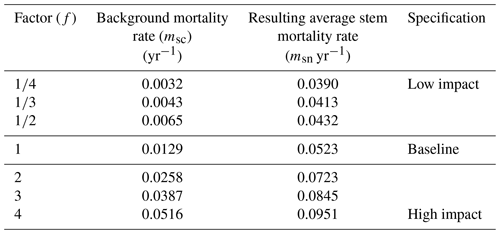
To investigate the effects of different stem mortality intensities on the dynamics and the structure of terra firme forests, we developed seven simulation scenarios: a baseline scenario and six scenarios with permanently altered stem mortality rates (Table 1). The baseline scenario is based on observed mortality rates (m_bl), which were computed by averaging the specific background mortality rates of all PFTs (Table  2). To obtain background mortality rates for the scenarios, the baseline's background mortality rate (m_bl) was multiplied by a factor (f) for each scenario (sc), resulting in the following equation:

$$\begin{array}{}\text{(1)}& m_{\mathrm{sc}}=f\cdot m_{\mathrm{bl}},\text{with}f\in \left\{{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}},{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}},{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}},\mathrm{2},\mathrm{3},\mathrm{4}\right\}.\end{array}$$

This resulted, in combination with the subsequent effects of the other types of modelled mortality (see Sect. 2.2.1), in different stem mortality rates at the stand level per simulated scenario (Table 1). The scenario with f=1 represented the baseline scenario. In this study, we simulated forest stands with an area of 1 ha consisting of interacting patches on which the forests grow (patch size 20 m × 20 m; see Fig. S1). The one-hectare stands extended over a total simulation area of 16 ha per scenario. Our assumption in the terra firme parameterization of FORMIND is that the 1 ha stands are not explicitly located in French Guiana. Forest dynamics were computed in an annual time step that started in year 0 on bare ground and ended after 300 years. In the baseline scenario, the biomass of a forest stand reached equilibrium after 210 years.

Table 1 Average stem mortality rate per simulation scenario and specification (see Eq. 1). Background mortality rate m_sc is the unweighted average over the mortality parameters of eight PFTs in the forest model. The resulting average stem mortality rate is the ratio of dead trees to the total number of trees in a simulated forest stand (averaged over the entire simulation time).

From the model outputs of all scenarios, we analysed the average development of multiple forest attributes (averaged over 16 ha), such as aboveground biomass (AGB), LAI, forest height (mean height of the tallest three trees per 40 m × 40 m; Rödig et al., 2017; Simard et al., 2011), gross primary production, net primary production, quadratic mean stem diameter (square root of the sum of squared stem diameters per tree divided by the number of trees in a stand), mean forest age (arithmetic mean age of the 25 oldest trees per simulated 1 ha area, selecting the oldest tree per patch), and biomass loss rate (m_AGB), which we defined as the annual proportion of dead biomass (AGB_dead) to total stand biomass (AGB_total):

$$\begin{array}{}\text{(2)}& m_{\mathrm{AGB}}={\mathrm{AGB}}_{\mathrm{dead}}\cdot {\mathrm{AGB}}_{\mathrm{total}}^{-\mathrm{1}}.\end{array}$$

In our forest model, we use a non-linear relationship between the AGB_t of a tree (t) and its stem diameter (D_t):

$$\begin{array}{}\text{(3)}& {\mathrm{AGB}}_{\mathrm{t}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}\cdot D_{\mathrm{t}}^{\mathrm{2}}\cdot H_{\mathrm{t}}\cdot F_{\mathrm{t}}\cdot {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{t}}}{{\mathit{\sigma }}_{\mathrm{t}}}},\end{array}$$

where H_t is the tree height, F_t is a form factor, ρ_t is the wood density, and σ_t is the fraction of aboveground biomass attributed to the stem (Fischer et al., 2016). Then, the tree biomasses are summed up to yield the total biomass, AGB_total. We also calculated the stem mortality rate (m_SN) as the ratio of the number of dead trees to the number of total trees in a forest stand at each simulation time step.

In addition, we computed the time over which each forest attribute reached the stable state (hereafter: equilibrium time) as well as the mean stand biomass turnover times (τ_B) with τ_B averaged over all successional states (simulated years 0–300). According to Carvalhais et al. (2014), turnover times can be defined as the ratio of the biomass stock to the flux (i.e. influx or outflux) of biomass. However, biomass outflux is not yet observable over large spatial scales (Thurner et al., 2016). Therefore, biomass outflux was defined as equaling biomass influx for forests in equilibrium (Carvalhais et al., 2014). Transferred to our study, the stock corresponds to the total biomass, influx to NPP, and outflux to dead biomass. Therefore, the following holds true for forests in equilibrium:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathit{\tau }}_{\mathrm{B}}& =\mathrm{stock}\cdot {\mathrm{flux}}^{-\mathrm{1}}={\mathrm{AGB}}_{\mathrm{total}}\cdot {\mathrm{NPP}}^{-\mathrm{1}}\\ & ={\mathrm{AGB}}_{\mathrm{total}}\cdot {\mathrm{AGB}}_{\mathrm{dead}}^{-\mathrm{1}}.\end{array}\end{array}$$

In our model, NPP of a stand is the sum of NPP values of all trees within this stand. Tree NPP is calculated as the difference between GPP and autotrophic respiration. The τ_B value can also be calculated from Eqs. (2) and (4) as the reciprocal of the biomass loss rate:

$$\begin{array}{}\text{(5)}& {\mathit{\tau }}_{\mathrm{B}}=\mathrm{1}\cdot m_{\mathrm{AGB}}^{-\mathrm{1}}\text{for}{m}_{\mathrm{AGB}}>\mathrm{0}.\end{array}$$

Using Eq. (5), we calculated τ_B by taking forest succession into account.

2.3 Derivation of a multiple linear regression model to estimate biomass loss rates

To estimate the biomass loss rates, we analysed a number of forest simulations which produced a large number of different forest stands each of 1 ha (averaged over 16 ha simulation areas) in different successional states (per simulated year) with unique functional species compositions and tree size distributions. Thus, we generated a total of 33 600 terra firme forest stands. We assumed that the rate of biomass loss can be related to other forest attributes (e.g. biomass, LAI, forest productivity, and forest height). For a multiple linear regression model, the temporal and spatial components are not important since forest states are considered independently of either. We acknowledged that when fitting linear regression models, it is important that the proxy variables do not strongly correlate. We tested this by using a covariance matrix with the Pearson's correlation coefficient of the proxy variables (Table S4). Then, we tested different linear and non-linear statistical models using different combinations of the proxy variables (see Table S3 and Fig. S15). Important selection criteria for the model type were good regression statistics and interpretability of the model equation. Furthermore, remote sensing products should be available for all proxy variables. Taking all of these criteria into account, the most suitable estimate was made by a multiple linear regression model which describes variations in m_AGB as a function of two proxy variables: LAI and forest height (Table S3). We estimated m_AGB (in units of yr⁻¹) as follows:

$$\begin{array}{}\text{(6)}& m_{\mathrm{AGB}}={\mathit{\beta }}_H\cdot H+{\mathit{\beta }}_L\cdot L+i+\mathit{\epsilon },\end{array}$$

where H is the forest height, L is the LAI, i is the y intercept, ε is the error term, and β_i represents the regression coefficients of the ith forest attribute. To test whether the linear regression model is robust, we simulated additional scenarios with altered productivity rates. Based on these new data together with the previous data, we fitted an alternative multiple linear regression model. Similarity between the two linear multiple regression models implied high robustness of the original model. For further information, see the Supplement (Figs. S10 and S11).

2.4 Estimation of the countrywide biomass loss rates

2.4.1 Input maps

To estimate forest height, we used a global map in the WGS-84 geographical projection with a pixel size of approximately 1 km (Simard et al., 2011; Fig. S5a). For the mapping of the forest height, Simard et al. (2011) used data from the Geoscience Laser Altimeter System (GLAS) aboard ICESat (Ice, Cloud, and land Elevation Satellite) collected in 2005. To create an LAI map, we used 139 data layers from the MCD15A2H version 6 Moderate Resolution Imaging Spectroradiometer (MODIS) Level 4 with a pixel size of 500 m and averaged the LAI values between 31 January 2004 and 31 December 2006 to reduce the overall LAI variance (Myneni et al., 2015). We harmonized and stacked the two input maps by first projecting the LAI map onto the coordinate reference system of the forest height map using the Geospatial Data Abstraction Library for French Guiana (https://www.gdal.org, last access: 22 February 2022). Resampling was conducted with the bilinear method. The spatial aggregation of the LAI map (Fig. S5b) was performed by calculating the mean values of pixels whose centres were within 1 km cells of the forest height map.

2.4.2 Output maps

The biomass loss rate was estimated for each pixel by applying the multiple linear regression model (Eq. 6) to the two input maps (see Fig. S5). We compared the density distributions of both input datasets with the ranges of FORMIND's simulation results (LAI and forest height). No correction factors were required for the extrapolations, since the most abundant combinations of value pairs of both datasets agree well, and only a few combinations differ (see Fig. S9). The biomass loss rates were then averaged over a pixel size of 2 km². We simulated forest stands of 1 ha with the forest model. This fine resolution allowed us to scale up to the accuracy of remote sensing products. We used a resolution of 2 km for the final biomass loss map, although the input data are available in 0.5 km (LAI, Myneni et al., 2015) and 1 km (forest height, Simard et al., 2011). Our regression model estimated negative biomass loss rates for a small portion of pixels, which were excluded from the biomass loss map. This was mainly the case for pixels without forest cover (see Fig. S5) according to a land use map published by Stach et al. (2009). To create the biomass turnover time map, we computed the reciprocal of each pixel for the biomass loss map (see Eq. 5).

We tested the reliability of the mapped biomass loss rate in the underlying input maps for the LAI and forest height via a sensitivity analysis regarding variations of ±30 % compared to the original input maps. We examined two methods to quantify the sensitivity of our study results concerning the input data. In a first experiment we modified the values of the two input maps by exactly +30 % and −30 % each (LAI and forest height). In a second experiment we sampled the input data for the LAI and forest height randomly using a uniform distribution. These values ranged between +30 % and −30 % of the original input values. This resulted in six new input maps (LAI_+30 %, H_+30 %, LAI_−30 %, H_−30 %, H_random, LAI_random). We then applied the multiple linear regression model (see Eq. 6) to some possible pairwise combinations of these new input maps (i.e. LAI${}_{+\mathrm{30}\mathit{\%}}-H_{+\mathrm{30}\mathit{\%}}$, LAI${}_{-\mathrm{30}\mathit{\%}}-H_{-\mathrm{30}\mathit{\%}}$, LAI${}_{+\mathrm{30}\mathit{\%}}-H_{-\mathrm{30}\mathit{\%}}$, LAI${}_{-\mathrm{30}\mathit{\%}}-H_{+\mathrm{30}\mathit{\%}}$, H_random−LAI_random) to obtain five uncertainty maps. We calculated Δm_AGB per pixel, which is defined as the difference between each of these uncertainty maps and the biomass loss map obtained from the original input maps. Thus, Δm_AGB represents the variation in the rate of biomass loss given 30 % variation in the input variables. Note that there are accompanying uncertainty products to the remote sensing products available that could be considered in follow-up studies to estimate error propagation. Furthermore, we compared our biomass loss map with forest plot data, provided by Brienen et al. (2015), and with map data of Johnson et al. (2016). Please refer to the Supplement for details on the computer software used in this study.

3 Results

3.1 Influence of increased stem mortality on forest succession dynamics

To analyse the influences of varying stem mortality intensities, we simulated succession dynamics, which were affected by competition among individual tree species belonging to species groups. Here, we show that successional stages can be differentiated based on the development of the total stand biomass (Fig. 2). After 40 years of forest succession, the simulated stand biomass peaked at 500 t_ODM ha⁻¹ (ODM: organic dry matter). This peak in stand biomass was caused by a high GPP of the pioneer species (GPP_pioneer=83 t_ODM ha⁻¹; Fig. S2a). After the early successional stage (years 0–40), the stand biomass fell slightly until year 100 due to the rapidly declining pioneer biomass, while the biomasses of other species increased (mid-successional stage; Fig. 2). After 100 years, the stand biomass stabilized at approximately 420 t_ODM ha⁻¹ yr⁻¹ (average over years 100–300), while the functional species composition reached a steady state after only 210 years (Fig. 2). In the late successional stage (gap dynamics), climax species and species with intermediate light requirements fixed 5 times more carbon in biomass than pioneer species (NPP of baseline scenario; Fig. S2b).

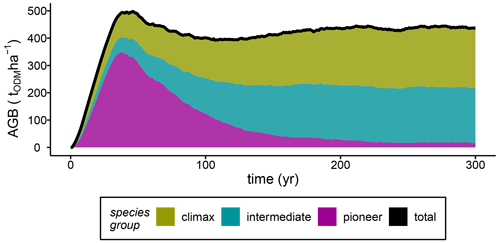
Figure 2 The baseline scenario's aboveground biomass (AGB) per species group and the total biomass for simulations of terra firme forests (ODM: organic dry matter).

Our simulation results reveal a sensitive response of the biomass loss rate to increased stem mortality intensities (Fig. 3a). At higher stem mortality levels, higher biomass loss with greater variance emerged and the biomass loss rate was on average greater than the stem mortality rate (see Fig. S4). At the level with the highest stem mortality, a peak in the biomass loss rates occurred at approximately 0.12 yr⁻¹ during the early phase of forest succession before levelling off at a value of 0.08 yr⁻¹ in the steady state (Fig. 3a). Due to the higher biomass loss rates, the light climate in the forest stand changed (Fig. 3c). The pioneer species were able to establish quickly in forest gaps. Hence, the GPP of the pioneer species was highest among all species groups (Fig. S2a), which also affected the productivity of the total stand (Figs. 3e–f, 4a). Despite the distinctly higher GPP values obtained in the case of higher biomass loss rates, NPP did not change distinctly among the different scenarios (Fig. 3f). Thus, the stem mortality rate had a strong influence on the species composition (e.g. higher pioneer GPPs; Fig. S2a) and forest structure (e.g. QMD and mean stand age; Fig. S3), which led to lower LAI, biomass, and mean forest height values at the ecosystem level than those of the reference (Fig. 3b–d). In addition, structural changes gave rise to modified forest stand dynamics, with unique succession patterns depending on the intensity of the disturbance due to stem mortality.

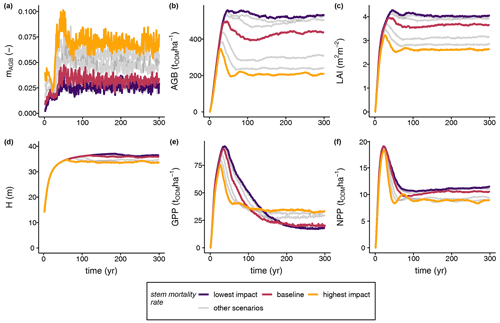
Figure 3 Simulation results of the (a) biomass loss rate (m_AGB), (b) aboveground biomass (AGB), (c) leaf area index (LAI), (d) mean forest height (H), (e) gross primary production (GPP), and (f) net primary production (NPP) of terra firme forest stands under different stem mortality intensities. Grey lines indicate the entire set of scenarios under varying stem mortality rates (Eq. 1) (ODM: organic dry matter; for further details see Table 1, Figs. S2 and S3).

Furthermore, we analysed how the stem mortality level affected the time needed to reach equilibrium (Fig. 4b). GPP responded particularly sensitively and inversely proportionally to the stem mortality rate, showing a strong decrease with rising stem mortality levels. In contrast, other forest attributes, such as biomass and NPP, had altogether shorter equilibrium times than that of GPP, responding inversely proportionally to the stem mortality level.

Finally, we evaluated the effect of increasing stem mortality rates on the turnover time of biomass (Eq. 5) in the forest stands while taking forest succession into account (Fig. 4c). The biomass turnover time τ_B was more than halved at a 4-fold higher stem mortality rate compared to the baseline (${\mathit{\tau }}_{\mathrm{B},(f=\mathrm{1})}=\mathrm{34}$, ${\mathrm{sd}}_{\mathrm{B},(f=\mathrm{1})}=\mathrm{12}$, ${\mathit{\tau }}_{\mathrm{B},(f=\mathrm{4})}=\mathrm{46}$, ${\mathrm{sd}}_{\mathrm{B},(f=\mathrm{4})}=\mathrm{43}$, ${\mathit{\tau }}_{\mathrm{B},(f=\mathrm{1}/\mathrm{4})}=\mathrm{15}$, ${\mathrm{sd}}_{\mathrm{B},(f=\mathrm{1}/\mathrm{4})}=\mathrm{5}$ years). Important forest properties are profoundly affected if the functional species composition, tree size distribution, or forest dynamics are changed.

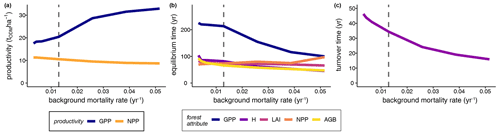
Figure 4 Influence of different mortality levels in simulated terra firme forests on (a) mature forests' mean GPP and mean NPP (averages over simulation years 250–300), (b) the time until the forest attributes reached equilibrium states, and (c) the mean biomass turnover times, represented as the reciprocal values of the biomass loss rate (see Eq. 5; averages over years 0–300). Dashed lines indicate the baseline scenario (GPP: gross primary production, NPP: net primary production, H: forest height, LAI: leaf area index, AGB: aboveground biomass, ODM: organic dry matter).

3.2 Estimation of biomass loss rates using single and multiple forest attributes

In a further analysis, we assessed how biomass loss rates can be derived from different proxy variables, such as the mean forest height and LAI. Including forests at different successional states, we tested the relationships between several single forest attributes and the rate of biomass loss but did not find distinct relationships (Fig. 5a–c; Table S3: regression model types 3–7). The biomass loss rates showed a widely scattered range of values and thus unclear relationships to all single forest attributes during the early successional stage (forest age <20 years; Fig. 5a–c). For instance, the LAI values of less-disturbed, old-growth forests (i.e. LAI =4 during the gap dynamics stage of mature forests) indicated similar biomass losses as forests in the early stages of succession. Relationships between single forest attributes and biomass loss rate seemed to be statistically significant (Table S3: regression model types 3–7); however, this was not useful because the relationships are clearly not linear (Fig. 5a–c). The relationships are strongly influenced by forest age and stem mortality rate.

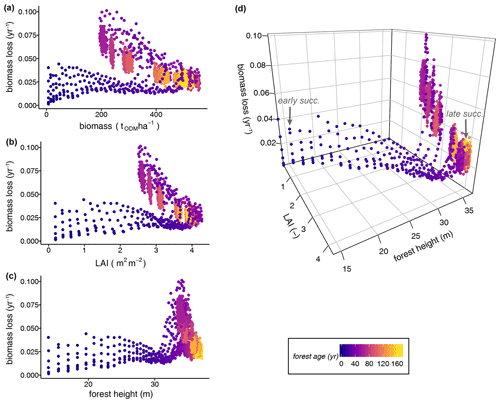
Figure 5 Dependence of biomass loss rates from the single attributes (a) biomass, (b) LAI, and (c) forest height versus (d) the multiple forest attributes (LAI and forest height) of simulated forest states, including all stem mortality scenarios. Each dot represents a terra firme forest stand with a unique forest structure (i.e. tree size distribution and functional species composition). All simulated years are included in the analyses. The colours of the dots show the mean forest ages characterizing the successional states (ODM: organic dry matter).

Figure 5d illustrates a three-dimensional relationship between LAI, forest height, and the rate of biomass loss. Only when combined in a multiple linear regression model did the LAI (L) and forest height (H) explain the biomass loss rates of forests at different successional states well (R²=0.731, RMSE =0.0093, p value =0.0; Fig. 6; Table S3):

$$\begin{array}{}\text{(7)}& m_{\mathrm{AGB}}=\mathrm{0.005698}\cdot H-\mathrm{0.033831}\cdot L-\mathrm{0.042064}+\mathit{\epsilon }.\end{array}$$

The LAI negatively influenced biomass loss rates, whereas forest height is positively correlated with it. The obtained residuals were normally distributed around the expected value (E(m_AGB)=0.0; Fig. S6b), and depending on the estimated biomass loss rates, the residuals were homoscedastic with overall only a small remaining trend (Figs. S6c; S7), which could be further improved by using a non-linear approach (e.g. generalized additive models; Fig. S15). Specifically, the residuals attributed to the LAI contained some “smile” effect (i.e. negative trend for 2.5 < LAI < 3.5 and positive trend for 3.5 < LAI < 4.5), and the ones attributed to forest height showed only a small remaining trend (see Fig. S7). On the basis of the selection criteria we have defined (see Sect. 2.3), we conclude that forest height and LAI can be used as proxy variables to estimate biomass loss rates using the linear approach.

The one-to-one comparisons of biomass loss rates for the simulated forest stands estimated by the multiple linear regression model (see Eq. 7) versus those simulated within the dynamic forest model fit well (Fig. 6). Other forest attributes, such as GPP and NPP, were not included in the multiple linear regression model because they did not improve the estimation of the biomass loss rates substantially (Table S3).

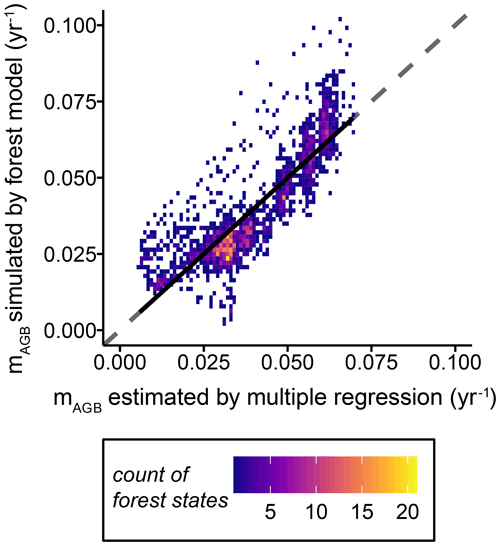
Figure 6 One-to-one density plot of biomass loss rates simulated by the dynamic forest model versus biomass loss rates estimated using a multiple linear regression model, with the forest height and leaf area index as proxy variables (Eq. 7 and Table S3). The dashed line shows the line of perfect fit. Each dot represents a forest stand with a unique forest structure (i.e. tree size distribution and functional species composition), while the colours represent the density distributions of the combinations. The black solid line indicates the mean deviation of the biomass loss rate simulated with the forest model from the estimated ones ($m_{\mathrm{AGB},\mathrm{DFM}}=\mathrm{1.0}\cdot m_{\mathrm{AGB},\mathrm{LM}}-\mathrm{0.0}+\mathit{\epsilon }$, R²=0.7312, RMSE =0.009, p value <0.01) (m_AGB: biomass loss rate).

3.3 Estimation of biomass loss rates from remote sensing by deriving a sample map

By combining simulated forest states with the maps of LAI and forest height obtained via remote sensing (Myneni et al., 2015; Simard et al., 2011), we derived a biomass loss map for terra firme forests of French Guiana (Fig. 7a). Based on this sample map, we obtained a mean biomass loss rate of 0.030 yr⁻¹ (standard deviation of 0.012 yr⁻¹; Fig. 7b). The values of biomass loss rate varied among regions, with higher values in the southern part of the country and lower rates in the northern part of the country. The highest biomass loss rates can be observed in the centre and at the southwestern country borders (m_AGB > 0.06). Such high values resulted from a combination of tall forest height together with low LAI values (Fig. S8). In the region surrounding the Paracou and Nourage sites, the biomass loss rates had values of 0.012 and 0.015 yr⁻¹, respectively, which agree well with the mean biomass loss rates we derived from the empirical data of the Brienen et al. (2015) study ($m_{\mathrm{AGB},\mathrm{Par}}=\mathrm{0.011}$ yr⁻¹, sd_Par=0.127 yr⁻¹; $m_{\mathrm{AGB},\mathrm{Nou}}=\mathrm{0.015}$ yr⁻¹, sd_Nou=0.027 yr⁻¹; Fig. 7c). The sensitivity analysis revealed the dependence of the mapped biomass loss on the quality of the input data (Fig. 7d, e). The sensitivity is moderate (i.e. Δm_AGB is small) if the LAI and forest height change uniformly by a certain amount (Fig. S14). If the changes in the LAI and forest height are contrary, the sensitivity of the mapped biomass loss is high (i.e. Δm_AGB is large), though we assume that a contrary change in the input data rarely occurs (Fig. S14). Considering forests at all successional states, we derived another sample map for biomass residence time (Fig. S12) calculated from the reciprocal of the biomass loss rate (Eq. 5). We estimated a mean countrywide biomass residence time of 40 years with a standard deviation of 9 years.

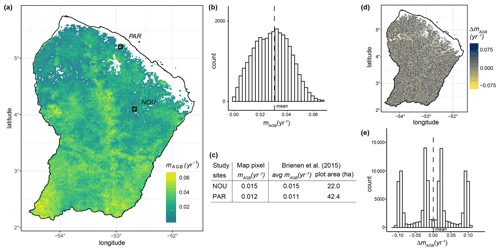
Figure 7 (a) Map of biomass loss for terra firme forests in French Guiana (∼2 km resolution) and (b) its histogram. The dashed line in (b) indicates the estimated countrywide mean (3.0 % with a standard deviation of 1.2 %). The black squares in the map show the locations of forest plots at Paracou (PAR) and Nourage (NOU), from which (c) census data were used to compare estimated and field-based biomass loss values. The census data originate from Brienen et al. (2015). (d) Sensitivity analysis for the mapped biomass loss rates of terra firme forests in French Guiana (see Fig. 7a) and (e) its histogram. The values for the input maps of leaf area index (LAI) and forest height were randomly sampled using a uniform distribution ranging ±30 % from their original values (see Fig. S4). Δm_AGB represents the variation in biomass loss rates given this variation in the input variables. For further results about the uncertainty analysis performed, see Figs. S7, S8, S9, S10, S11, and S14.

4 Discussion

4.1 Mechanism of tropical forests in dealing with the increasing intensity of stem mortality

In this study, we analysed dynamics in tropical forests in relation to stem mortality. We demonstrated that most of the analysed forest stand attributes (biomass, forest height, LAI, GPP, biomass loss rate, QMD) had specific responses during succession. Moreover, we showed that the rate of biomass loss is strongly affected by succession dynamics as well as by the stem mortality rate. The period until the stand's equilibrium was reached differed in duration among each simulation scenario. Additionally, the mean turnover time of biomass, i.e. the reciprocal value of biomass loss rate (Eq. 5), varied considerably.

There were multiple reasons for the unique succession patterns of each forest attribute. Succession dynamics are influenced by assimilation rates (e.g. photosynthesis rates, light requirements) and physiognomic characteristics (e.g. maximum stem diameter increment rates, maximum heights, and wood densities), both of which are specific to each species group (Hiltner et al., 2018). Functional traits are crucial in simulations of the succession dynamics in forests because they determine the competitiveness of species groups (Fischer et al., 2018; Rüger et al., 2020).

The relationship between successional stages and stem mortality rate has been investigated in empirical studies to estimate mortality in tropical forests (Aubry-Kientz et al., 2013; Chambers et al., 2013; Doughty et al., 2015; Holzwarth et al., 2013). Aubry-Kientz et al. (2013) introduced a method that estimated the stem mortality probability of terra firme forests at Paracou. Similar to our results, they found that the stem mortality probability depends on the successional stages of the forests as well as on the functional traits of species, such as the specific leaf area, wood density, stem diameter increment, and potential height.

Interestingly, we observed similar NPP values at different stem mortality levels for forests in equilibrium. Erb et al. (2016) argued that the NPP of vegetation is effectively independent of the stem mortality rate, which is supported by our results. The observed stability of NPP under different disturbance regimes can be explained by shifts within the functional species compositions and tree size distributions. Pioneer species, which typically have lower wood densities (Chave et al., 2009; Zanne et al., 2009) and lower potential heights than those of slow-growing climax and intermediate species (Hiltner et al., 2018), store less carbon in their living biomasses. Since pioneer species grow faster, they can bind as much carbon per time as slow-growing climax species. Therefore, at the forest stand level, higher stem mortality rates result in similar NPP values as those observed with lower stem mortality rates, although the individual trees show different growth behaviours. Our simulation results show how the carbon storage of forests in equilibrium changes across different levels of stem mortality rates, despite constant levels of NPP. Instead, our findings indicate that carbon storage depends on the functional species composition. At high stem mortality rates (e.g. a high-impact scenario), more pioneer trees of a younger age were present in the forest stands. Thus, to achieve a high forest carbon storage capacity, there is a trade-off between large, old, and less productive trees (e.g. climax species) and smaller, younger, and more productive trees (e.g. pioneer species).

4.2 Performance of the regression model for estimating biomass loss rates

One of the main findings of this study is that the simulated biomass loss rates of terra firme forests can be estimated using multiple linear relationships among several forest attributes. The premise was that all forest attributes used could be provided by remote sensing and could give information about the forest structure and productivity. We recognized the relationship between biomass loss rates to LAI and forest height when fitting many different statistical models with different simulated forest attributes (Table S3, Fig. S15). If stem mortality rates increased, this led to a higher biomass loss rate. However, it is impossible to directly infer stem mortality rates from biomass loss rates because forest structural state variables differed for each simulated forest stand, depending on its successional stage (Bohn and Huth, 2017; Rödig et al., 2017). For example, the stem number distribution of dying trees is not evenly distributed across tree size classes (Aubry-Kientz et al., 2013; Holzwarth et al., 2013; Muller-Landau et al., 2006; Rowland et al., 2015).

In our approach for identifying appropriate forest attributes to infer biomass loss rates, we considered results from empirical studies that have investigated stem mortality in tropical forests (Aubry-Kientz et al., 2013; Esquivel-Muelbert et al., 2019; Stovall et al., 2019). Esquivel-Muelbert et al. (2020) investigated the stem mortality of the Amazon by using empirical data to show that stem diameter growth rate and tree size are strong predictors. Fast-growing species with low wood densities are at a higher risk of mortality, whereas the effect of tree size varies. Aubry-Kientz et al. (2013) used functional traits, such as potential tree height and specific leaf area, to estimate the probability of stem mortality. Based on large-scale remote sensing observations, tree height was identified as an important predictor of stem mortality during drought, with large trees having twice the mortality rate of small trees, while environmental drivers (i.e. temperature, soil water, and competition) controlled the intensity of the height–mortality relationship (Stovall et al., 2019). The results of these studies underline the importance of productivity (e.g. increment rates and tree size), biomass, and functional characteristics (e.g. wood densities, potential stem diameter increment rates, leaf areas, and potential tree heights) of trees or tree species in the context of stem mortality. In our forest model, such characteristics are included in the derivation of stem mortality rates of specific PFTs (see Tables S1, S2). In forest gap models, forest structural state variables, such as the stem number distribution, tree size distribution, and functional species composition, of the dying trees emerge rather than being specified as input parameters (Botkin et al., 1972; Bugmann, 2001; Shugart, 2002). This fact is a useful model behaviour for estimating the biomass loss rate of simulated forest stands and, moreover, holds true for the derivation of other forest attributes, which we considered when fitting our regression model. Besides the LAI and forest height, we tested GPP, NPP, and biomass as proxy variables for the rate of biomass loss. On the forest stand level, however, these variables did not improve the performance of the multiple linear regression model substantially. These results suggest using forest height and LAI as proxy variables to estimate the biomass loss rates of forest stands. Despite the simplicity of the multiple linear regression model, meaning that we included only two proxy variables, its statistical performance proved to be robust (see Eq. 6; Table S3, Figs. S6, S7, S8, S9). Thus, it was possible to derive biomass loss rates from LAI and forest height with simulated data for forests in different successional states. It was important that the signs of the regression coefficients of our linear model plausibly reflected the relationships that were observed in the field. In the regression model, forest height was directly proportional, and LAI was indirectly proportional to the biomass loss rates of the forest stands. For example, tall forests with low LAI values resulted in high biomass loss rates (see Fig. S8). We would like to note that to further improve the regression model (e.g. further minimize the residual's remaining trend), additional proxy variables could be included, non-linear components can be acknowledged, and spatially variable effects of environmental factors on simulated forest states may be investigated in more detail. In this study, we tested non-linear statistical methods (see Fig. S15) and various forest attributes available as remote sensing products as potential proxy variables for the statistical models (see Tables S3, S4). We decided to use the simplest possible linear regression model (in terms of the number of included proxies and interpretability of the model equation) that estimated biomass loss rates best.

Using a forest model to derive the relationships among different forest attributes has several advantages. First, the simulated LAI and forest height data were generated mechanistically, integrating a broad spectrum of information about forest dynamics and successional states emerging from different physiological processes. This can lead to a lower level of noise in the simulation data compared to that in the observed field data. Nevertheless, forest models also include stochastic processes, including stem mortality rates and establishment (Bugmann, 2001; Fischer et al., 2016; Hiltner et al., 2018; Shugart, 2002). By using plant functional types to simulate forest dynamics, we reduced the possible uncertainties in species traits. Simplifications allow for a transferability of the regression analysis to forests with similar characteristics and succession states. These simplifications also enabled the estimation of the biomass loss rates of terra firme forests across the entirety of French Guiana. With the approach pursued here, it might be possible to derive regression models for estimating biomass loss rates in other locations worldwide. Forest model simulation results contain structural information about the conditions of forests in different successional states, allowing the data to be used as training data for the development of statistical regression models. Whether LAI and forest height are also suitable as proxy variables for the biomass loss rates of other forest types remains to be investigated.

4.3 Mapping of biomass loss rates of terra firme forests in French Guiana

We combined remote sensing maps of forest height (Simard et al., 2011) and LAI (Myneni et al., 2015) with forest modelling to derive a sample map of biomass loss rates in French Guiana. In doing so, we presented an innovative approach for estimating biomass loss rates in tropical forests. A comparison of estimated biomass loss rates with census-based values for two sites showed reasonable similarity, although in perspective, it would be important to further validate such maps using more field data (not available to us at present). In another comparison of biomass loss rates obtained for French Guiana with census-based values for the entire Guiana Shield (i.e. French Guiana, Suriname, Guyana, northern Brazil, eastern Venezuela; Johnson et al., 2016), our estimate is about 50 % higher, though it is noteworthy that Johnson et al. (2016) estimated the rate of biomass loss for the entire Guiana Shield, with higher values on average in French Guiana. Capabilities for improved projections of biomass loss rates are indispensable in the context of improved estimates of the role of tropical forests in the global carbon cycle (Anderegg et al., 2020; Friedlingstein et al., 2019; Friend et al., 2007; IPCC, 2014). Remote sensing by airborne and satellite-based instruments provides large-scale data on forests, such as the forest height (Simard et al., 2011) and LAI (Myneni et al., 2015). However, remote sensors can record measurements only at certain time points; hence, the successional stages of forest variables are uncertain in remotely sensed data. Such forest dynamics can be simulated by individual-based, dynamic forest models. A combination of remote sensing data and forest models therefore has the potential to improve predictions of large-scale ecosystem dynamics (Plummer, 2000; Shugart et al., 2015).

Forests can be in different successional stages due to disturbances that influence forest height and LAI (Dubayah et al., 2010; Kim et al., 2017). In the forest height and LAI maps, disturbed regions can be detected visually (see Fig. S5); these regions have been identified as disturbed areas in other studies (Asner and Alencar, 2010; Piponiot et al., 2016a; Stach et al., 2009). Such areas include disturbed areas in the floodplains of lakes and rivers, along the coast, near roads and settlements, and in the secondary forests of French Guiana, where the forest height and the crown coverage are, on average, lower than that in primary forests (Piponiot et al., 2016a; Stach et al., 2009; forest height map from Simard et al., 2011, in Fig. S5).

Remotely sensed products often include uncertainties. In this study, we demonstrated the sensitivity of the sample biomass loss map to variations in the LAI and forest height maps (Figs. 7d, S14). Accuracy of the input remote sensing data is beneficial.

Balanced deviations of LAI and forest height (e.g. LAI +30 % and H+30 %) result in smaller deviations in biomass loss rates than opposite deviations (e.g. LAI +30 % and H−30 %). Small-scale fluctuations in the LAI (e.g. on the individual tree level) were not captured due to the coarse resolution of the MODIS data (500 m). However, by using an individual-based dynamic forest model, the small-scale processes that manifest as variations in the LAI and forest height are accounted for in the simulations. Because simulated forest structures were the basis upon which the regression model was derived, the multiple linear regression model (Eq. 7) accounts for successional states and small-scale dynamics of forests. It is plausible that the LAI alone is not representative of the forest successional state. Therefore, we analysed forest succession (resulting from model-inherent processes), taking species diversity and interactions between trees into account, and we linked this information to the remote sensing products. Such approaches have already been successfully carried out in several studies (Rödig et al., 2017, 2018, 2019; Shugart et al., 2015). We obtained a good proxy for the successional state and, thus, for biomass loss rates only when forest height was also included in the analysis. It may also be the case that the forest height estimated by FORMIND and the forest height mapped by Simard et al. (2011) at the 1 km scale (Fig. S5a) are subject to a certain bias. Simard et al. (2011) used the mean height of the three tallest trees to validate the GLAS data at the footprint level, though not to validate the gridded 1 km data product, which tends to be shorter and less variable. The gridded product is based on a biome-level random forest model using other auxiliary data (e.g. percentage of tree cover, precipitation, altitude, temperature, conservation status) so that the variation in 1 km resolution forest height does not necessarily reflect the simulated variation in forest structure; rather, it reflects the predicted variation based on biome-level correlations with other factors.

4.4 Introduction of an alternative method for estimating biomass turnover time

Information on the carbon balance of forests is important for quantifying the biomass accumulation rates of trees. Various studies have estimated the turnover time of biomass, which we defined here as the reciprocal value of the rate of biomass loss, in forests worldwide (Carvalhais et al., 2014; Erb et al., 2016; Pugh et al., 2019). Carvalhais et al. (2014) were the first to estimate biomass turnover times for forests in equilibrium from biomass and GPP (see Eq. 4: $\mathit{\tau }={\mathrm{AGB}}_{\mathrm{total}}\cdot {\mathrm{NPP}}^{-\mathrm{1}}$). For the French Guiana region, the authors estimated biomass turnover times of approximately 20 to 40 years and discussed the fact that disturbances can shorten the biomass turnover time by increasing biomass loss rates. Our study quantifies the extent to which stem mortality leads to high biomass loss rates and thus to short biomass turnover times.

Erb et al. (2016) observed decreases caused by land use in the biomass turnover time. They found turnover times of 20 to 30 years for the French Guiana region, which are similar to our results (Fig. 4c). Pugh et al. (2019) showed that stand-replacing disturbances also shortened the biomass turnover times. We found that the biomass turnover time is strongly affected by succession dynamics and stem mortality rates. For our full simulation dataset, we found a mean biomass turnover time of 40 years (standard deviation of 20 years; Fig. S13). We derived an alternative framework to estimate the turnover time from biomass loss rates. This framework allows both turnover time and rate of biomass loss to be modelled in a simple way, considering succession dynamics and disturbances due to stem mortality.

4.5 Limitations and outlook

Our simulation results revealed complex relationships between stem mortality rate and biomass loss rate. The growth stage of a tree evidently has an effect on stem mortality, which often results in a U-shaped relationship of stem mortality as a function of the tree size distribution in a forest (Aubry-Kientz et al., 2013; Holzwarth et al., 2013; Muller-Landau et al., 2006). With regard to tree age, it is more likely that the youngest and oldest trees will die (Aubry-Kientz et al., 2013; Rüger et al., 2011) due to intense competition for light and space between the juvenile trees in the understorey and the senescence of the old trees in the canopy layer. Such mortality processes are often represented in forest models (Bugmann et al., 2019). Although empirical mortality algorithms which mechanistically describe the main causes of stem mortality and their effects on entire ecosystems (e.g. self-thinning, death of trees by crushing, and growth-dependent mortality) have already been developed, other causes of stem mortality with unclear signals are often summarized as stochastic processes (Bugmann et al., 2019; Hülsmann et al., 2017, 2018). In our study, biomass loss rates at the stand level arose from different mortality processes that occurred at the tree level (competition due to crowding, death of other trees by crushing, growth dependency, gap formation, and stochastic stem mortality). Compared to the U-shaped stem mortality distribution across stem diameter classes, the biomass loss rates of a forest stand depended in more complex ways on the functional species composition and the levels of carbon fluxes (GPP and NPP). We analysed the relationships between different levels of stem mortality rate with biomass loss rate, GPP, NPP, and biomass stock. It would be interesting to explore simulation results for different modes of stem mortality in future studies.

In our study, the effects of disturbances were represented in a simplified manner by modifying the mortality rates of tree species. We analysed the effects of permanently increasing the stem mortality rates in the studied forests. However, it is also necessary to consider the effects of discrete or continuously changing disturbance patterns (e.g. Barlow et al., 2003; Brando et al., 2014; Chambers et al., 2009, 2013; Doughty et al., 2015; Holzwarth et al., 2013; Magnabosco Marra et al., 2016; Marra et al., 2014; McDowell et al., 2018; Negrón-Juárez et al., 2010, 2017; Nepstad et al., 2007; Phillips and Brienen, 2017; Slik et al., 2010; Stovall et al., 2019; Wright et al., 2015). The impacts of single, discrete disturbance events (e.g. selective logging) on the dynamics of terra firme forests were studied by Hiltner et al. (2018). A follow-up study investigated the impacts of repeated logging events under continuously changing air temperatures and precipitation rates (Hiltner et al., 2021). If additional effects, such as climate change and forest management, were added to the dynamic forest model's simulations of the present study, the reasons for biomass losses could be determined more accurately. Assessing this aspect would be interesting for future studies in which the methodology presented here can be applied.

It was also found that the temporal patterns of establishing trees can change after disturbances such as modifications to the seed mortality of specific tree species, as such changes influence the competitive processes of trees within communities (Dantas de Paula et al., 2018). Here, we did not consider the influences of stem mortality rates on establishment processes, though this factor should be considered in future studies.

Regarding the mapping of the biomass loss rates in French Guiana, there are four important aspects. First, it is important to verify the quality of the forest model parameterization with field data as was done for biomass loss rates in this study and by Hiltner et al. (2018, 2021), who analysed biomass dynamics, tree size distribution, and functional species composition by comparing model results with data from forest inventories in French Guiana. The amount of available “ground truth data” was small, so a comprehensive validation of the simulation results and the biomass loss map was not possible. In future studies, the addition of more data sources will allow for more extensive validation of the study results. Second, a multiple linear regression model predicting biomass loss rates can be valid only for a certain type of forest. In mapping biomass loss rates at the country level, we assumed the predominance of a similar type of forest: the terra firme forests in French Guiana (Hammond, 2005). For this forest type, Stach et al. (2009) calculated a forest cover of 95 % of the country's land area. Third, site parameters across entire landscapes can be heterogeneous, affecting forest dynamics and structure. Various studies demonstrated that natural environmental factors, such as soil properties (Rödig et al., 2017; Soong et al., 2020), relief (Guitet et al., 2018), and climatic variations (Rödig et al., 2017; Wagner et al., 2012), as well as the silvicultural history (Hiltner et al., 2018; Piponiot et al., 2016b, 2019), can affect the succession dynamics and states of tropical forests. In this study, such spatially heterogeneous environmental influences on forest dynamics in terra firme forests are indirectly considered in the forest model and the regression model via stochastic stem mortality. Some of these environmental factors, which vary at the regional level, can be considered in future studies by including further processes (see Tables S1, S2, Fischer et al., 2016). Examples are (1) implementing the effects of forest management and fire, (2) taking into account the effects of weather variables such as temperature, rainfall variability, and solar radiation, and (3) varying the relationships describing tree geometry in space and time. Moreover, species diversity could play an important role, which was aggregated in this study using the plant functional type approach (Maréchaux and Chave, 2017). In further investigations, it is recommended that climatic and topographic effects or short-term disturbance events and forest management be implemented to further improve the approach developed here. Finally, changes in climatic conditions and tree coverage have an impact on forest height, LAI, and subsequently biomass loss rates. For example, drought, uprooting due to storms or flooding, forest fire, insect calamity, and forest management can be possible drivers of variability in the LAI. Furthermore, forest height can vary, e.g. due to uprooting from storms and flooding, fire, and forest management. Those environmental drivers may also interact with each other. The effects of tree coverage and climate as well as their importance for driving the maps of forest height and LAI and subsequently the estimations of biomass loss rates should be explored in follow-up studies.

5 Conclusions

Here, we developed a framework for estimating biomass loss rates in tropical forests. We analysed the effects of stem mortality rate and its relation to forest productivity, forest structure, and biomass based on the example of terra firme forests in French Guiana. By quantifying such effects through simulation experiments, it was possible to derive complex relationships between biomass loss rates and other forest attributes. Our approach revealed the strong influences of the succession states and stem mortality rates on the biomass loss rates of forests.

We also linked individual-based forest modelling with remote sensing so that an estimation of biomass loss rates due to stem mortality was feasible. The resulting sample map of biomass loss predicted that biomass is dying at a faster rate in the central, southern, and eastern regions than in the northern parts of French Guiana. The forest areas in the north and northeast are used for timber production, agricultural activities, and housing (Bovolo et al., 2018; Stach et al., 2009), whereas the forest areas in the south are predominantly natural rainforests (Hammond, 2005).

The approach we developed here can be easily transferred to other forest biomes (e.g. boreal and temperate forests) using forest models that capture biome-specific forest dynamics and available remote sensing products. Estimating the spatiotemporal distribution of forest biomass loss rates has recently been identified as particularly relevant for the monitoring of mortality hotspots (Hartmann et al., 2018). Moreover, improved estimations of the turnover times of carbon in forest stands have been made possible so that uncertainties in the global carbon cycle (Friend et al., 2014) can be reduced.