the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying biological carbon pump pathways with a data-constrained mechanistic model ensemble approach
Michael R. Stukel
Moira Décima
Michael R. Landry
The ability to constrain the mechanisms that transport organic carbon into the deep ocean is complicated by the multiple physical, chemical, and ecological processes that intersect to create, transform, and transport particles in the ocean. In this paper we develop and parameterize a data-assimilative model of the multiple pathways of the biological carbon pump (NEMUROBCP). The mechanistic model is designed to represent sinking particle flux, active transport by vertically migrating zooplankton, and passive transport by subduction and vertical mixing, while also explicitly representing multiple biological and chemical properties measured directly in the field (including nutrients, phytoplankton and zooplankton taxa, carbon dioxide and oxygen, nitrogen isotopes, and 234Thorium). Using 30 different data types (including standing stock and rate measurements related to nutrients, phytoplankton, zooplankton, and non-living organic matter) from Lagrangian experiments conducted on 11 cruises from four ocean regions, we conduct an objective statistical parameterization of the model and generate 1 million different potential parameter sets that are used for ensemble model simulations. The model simulates in situ parameters that were assimilated (net primary production and gravitational particle flux) and parameters that were withheld (234Thorium and nitrogen isotopes) with reasonable accuracy. Model results show that gravitational flux of sinking particles and vertical mixing of organic matter from the euphotic zone are more important biological pump pathways than active transport by vertically migrating zooplankton. However, these processes are regionally variable, with sinking particles most important in oligotrophic areas of the Gulf of Mexico and California Current, sinking particles and vertical mixing roughly equivalent in productive coastal upwelling regions and the subtropical front in the Southern Ocean, and active transport an important contributor in the eastern tropical Pacific. We further find that mortality at depth is an important component of active transport when mesozooplankton biomass is high, but it is negligible in regions with low mesozooplankton biomass. Our results also highlight the high degree of uncertainty, particularly amongst mesozooplankton functional groups, that is derived from uncertainty in model parameters. Indeed, variability in BCP pathways between simulations for a specific location using different parameter sets (all with approximately equal misfit relative to observations) is comparable to variability in BCP pathways between regions. We discuss the implications of these results for other data-assimilation approaches and for studies that rely on non-ensemble model outputs.
- Article
(17307 KB) -
Supplement
(3955 KB) - BibTeX
- EndNote
Marine phytoplankton in the surface ocean are responsible for approximately half of the world's photosynthesis (Field et al., 1998). However, as a result of their short lifetimes and active grazing by a diverse suite of zooplankton, most of the carbon dioxide fixed by phytoplankton will be respired back into the surface ocean on timescales of days to weeks (Steinberg and Landry, 2017). Long-term sequestration of this biologically fixed carbon dioxide requires that the organic matter produced by marine autotrophs be transported into the deep ocean through a suite of processes collectively referred to as the biological carbon pump (BCP) (Boyd et al., 2019; Ducklow et al., 2001; Volk and Hoffert, 1985). The BCP is estimated to transport 5–13 Pg C yr−1 into the deep ocean (Laws et al., 2000, 2011; Siegel et al., 2014; Henson et al., 2011). Our ability to constrain the magnitude of this globally important process (and its response to anthropogenic forcing) more accurately is hampered, however, by the diverse spatiotemporal scales over which these processes act and difficulties in quantifying rates in a heterogeneous three-dimensional ocean (Siegel et al., 2016; Burd et al., 2016; Boyd, 2015).
Attempts to predict future changes in the BCP are also complicated by the diverse pathways of organic matter flux into the deep ocean (Henson et al., 2022). Most research of the BCP has focused on sinking particles (Turner, 2015; Buesseler and Boyd, 2009; Martin et al., 1987; Honjo et al., 2008), which include diverse biologically produced material such as dead phytoplankton and zooplankton, fecal pellets, crustacean molts, and mucous feeding structures (Smayda, 1970; Kirchner, 1995; Bruland and Silver, 1981; Fowler and Small, 1972; Small et al., 1979; Alldredge, 1976; Hansen et al., 1996; Lebrato et al., 2013). Slowly sinking and suspended particles are also reshaped into rapidly sinking marine snow through abiotic aggregation processes (Passow et al., 1994; Burd and Jackson, 2009; Jackson, 2001; Alldredge, 1998). These sinking particles are continually transformed, remineralized, and modified by a community of particle-attached bacteria and protists and suspension- and flux-feeding mesozooplankton (Stukel et al., 2019a; Poulsen and Kiorboe, 2005; Steinberg et al., 2008; Simon et al., 2002; Boeuf et al., 2019).
Organic matter is also transported into the deep ocean through active transport by vertically migrating zooplankton and nekton (Steinberg et al., 2000; Longhurst et al., 1990; Archibald et al., 2019; Bianchi et al., 2013a) and by passive transport of dissolved and particulate organic matter that is subducted by ocean currents or mixed into the deep ocean (Levy et al., 2013; Carlson et al., 1994). The global magnitudes of these processes are highly uncertain because they are difficult to constrain from in situ measurements. Active transport is commonly believed to be responsible for a relatively small proportion (∼ 10 %–20 %) of the biological pump (Archibald et al., 2019; Hannides et al., 2009; Steinberg et al., 2000). However, if mortality at depth is included as part of active flux, it can be an important and at times dominant source of export, although such estimates are highly uncertain (Kelly et al., 2019; Kiko et al., 2020; Hernández-León et al., 2019). Similarly, investigations of the importance of passive transport initially focused on the role of refractory dissolved organic matter (Carlson et al., 1994; Copin-Montégut and Avril, 1993). Recent studies, however, highlight the importance and spatiotemporal variability of passive transport of particles via subduction, eddy mixing, mixed-layer shoaling, and vertical diffusion (Levy et al., 2013; Omand et al., 2015; Stukel et al., 2018b; Stukel and Ducklow, 2017; Resplandy et al., 2019). These passive transport processes can be driven both by large-scale flows and by mesoscale and submesoscale circulation near fronts and eddies (Resplandy et al., 2019; Llort et al., 2018; Omand et al., 2015; Stukel et al., 2017).
Numerical models are essential tools for investigating such processes that act across multiple spatiotemporal scales and integrate multiple physical, chemical, and biological drivers. Such models have, for instance, been crucial in elucidating spatial and temporal decoupling of phytoplankton production and sinking particle export (Plattner et al., 2005; Henson et al., 2015); quantifying spatial variability in the relative importance of different BCP pathways (Nowicki et al., 2022); determining the temporal horizon over which anthropogenic signals appear in the world ocean (Schlunegger et al., 2019); quantifying regional variability in subduction of organic matter (Levy et al., 2013); inverting oxygen, nutrient, and carbon standing stock measurements to estimate global carbon export rates (Schlitzer, 2000, 2002); and predicting climate change impacts on plankton communities and the BCP (Dutkiewicz et al., 2013; Hauck et al., 2015; Bopp et al., 2005; Oschlies et al., 2008; Yamamoto et al., 2018). Models have also been used to investigate the role of vertically migrating zooplankton in strengthening oxygen minimum zones (Bianchi et al., 2013a), mesoscale and submesoscale hotspots of particle subduction (Resplandy et al., 2019), and the impact of glacial/interglacial changes in iron deposition on the BCP (Parekh et al., 2006). Such investigations would be difficult or even impossible to undertake without models. Nevertheless, the models for varying processes differ substantially, and few are able to investigate the full potential parameter space or quantify the accuracy of simulated energy flows through multiple trophic levels. While accurate simulation of physical circulation is critical for simulating marine biogeochemistry (Doney et al., 2004), objective parameterization of biogeochemical models lags substantially behind similar approaches for physics. Indeed, the inability to constrain biogeochemical relationships accurately may be the primary limitation on our ability to objectively evaluate biogeochemical models (Anderson, 2005; Franks, 2009; Follows and Dutkiewicz, 2011; Ward et al., 2013). Recent advances in formal assimilation of biogeochemical properties into ocean models are beginning to allow objective model parameterization, a crucial first step for treating models as testable hypotheses (Xiao and Friedrichs, 2014a; Mattern and Edwards, 2019; Kaufman et al., 2018; Ford et al., 2018; Kriest et al., 2017; Shen et al., 2016; Oschlies, 2006; DeVries and Weber, 2017; Nowicki et al., 2022). Nevertheless, most of these approaches rely only on the assimilation of surface chlorophyll and/or other phytoplankton properties, thus leading to potentially high inaccuracies in parameterizing zooplankton dynamics (Shropshire et al., 2020; Löptien and Dietze, 2015). This is particularly important, because inaccurate parameterizations of mesozooplankton may lead to qualitatively and quantitatively inaccurate export dynamics (Cavan et al., 2017; Anderson et al., 2013). Accurate simulation of the BCP likely requires a focus on assimilation of data types crossing multiple trophic levels and both ecological and biogeochemical parameters.
In this study, we modify an existing, widely used biogeochemical model (NEMURO, Kishi et al., 2007) to focus specifically on the multiple pathways of the biological carbon pump. We refer to the new model as NEMUROBCP. We have three distinct goals in creating NEMUROBCP. The first is to mechanistically model the multiple BCP pathways (sinking particles, active transport by vertical migrants, and passive transport of organic matter by ocean circulation and mixing). Our second goal is to enable direct comparability between model results and field measurements of standing stocks and rates. This allows the model to act as a synthetic tool using diverse measured variables to enhance investigation of underlying and unmeasured processes (Dietze et al., 2013). Our third goal is a model that can be run efficiently in multiple physical configurations to allow extensive data assimilation and hypothesis testing. NEMUROBCP is designed with a core nitrogen-based module (including all biological components, nutrients, detritus, dissolved organic matter, and oxygen) that includes all three pathways of the BCP, along with submodules (that can be turned on or off) that model the carbon system, 234Th dynamics, and nitrogen isotopes. Here, we perform a Markov chain Monte Carlo statistical data assimilation to develop ensemble parameterizations of NEMUROBCP using 30 distinct types of field measurements from 49 Lagrangian experiments. We then investigate the model's ability to predict withheld measurements, conduct sensitivity analyses, and use the model to investigate the BCP in four ocean regions.
2.1 Core NEMUROBCP model
NEMUROBCP was developed from the NEMURO class of models originally developed for the North Pacific (Kishi et al., 2007, 2011; Yoshie et al., 2007) and includes several modifications adapted by Shropshire et al. (2020) that allow the model to be compared more directly to common field measurements. It also includes three optional modules that can be toggled on and off (the carbon system, nitrogen isotopes, and 234Th).
The core of NEMUROBCP is nitrogen-based and includes 19 state variables (Table 1): three nutrients (nitrate, ammonium, and silicic acid), two phytoplankton (small phytoplankton and diatoms), five zooplankton (protistan zooplankton, small non-vertically migrating mesozooplankton, small vertically migrating mesozooplankton, large non-vertically migrating mesozooplankton, large vertically migrating mesozooplankton), two dissolved organic pools (labile dissolved organic nitrogen and refractory dissolved organic nitrogen), four non-living particulate pools (small particulate nitrogen, large particulate nitrogen, small opal, and large opal), two chlorophyll state variables (one associated with small phytoplankton, the other with diatoms), and oxygen. As in Shropshire et al. (2020), the small and large mesozooplankton are defined based on size (< 1 and > 1 mm, respectively) rather than trophic status to allow direct comparison to common size-fractionated measurements. Relative to the original NEMURO model, key changes include (1) an explicit chlorophyll module (based on Li et al., 2010) that allows direct comparison to in situ chlorophyll measurements and gut pigment measurements made with herbivorous zooplankton; (2) division of dissolved organic matter into refractory and labile dissolved organic nitrogen to simulate subduction of refractory molecules; (3) division of detrital pools into slowly and rapidly sinking particles to simulate more accurately the gravitational pump; (4) division of mesozooplankton into epipelagic-resident taxa and vertical migrants to simulate active transport by diel vertical migrators; and (5) addition of a dissolved oxygen state variable that potentially limits heterotrophic growth in the mesopelagic ocean. NEMUROBCP also modifies key transfer functions by, for instance, allowing protists to feed on diatoms, since protistan grazers are often important diatom grazers (e.g., Landry et al., 2011). The transfer functions linking state variables in NEMUROBCP are shown in Fig. 1 and explained in detail in the Supplement. The 103 parameters in NEMUROBCP are explained in Supplement Table S1.
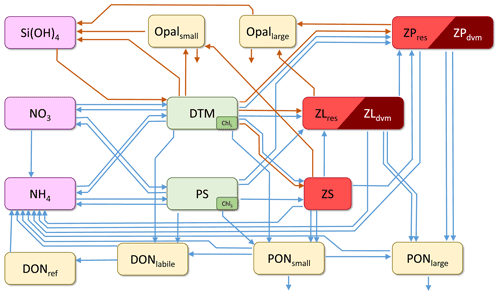
Figure 1Schematic depiction of the core NEMUROBCP model. Arrows show transfer functions (orange: Si flux; blue: N flux). Rectangles show state variables (SiOH3: silicic acid; NO3: nitrate; NH4: ammonium; Opalsmall: small biogenic silica; Opallarge: large biogenic silica; DONref: refractory dissolved organic nitrogen; DONlabile: labile dissolved organic nitrogen; PONsmall: small detritus; PONlarge: large detritus; DTM: diatoms; PS: small phytoplankton; Chll: diatom chlorophyll; chls: small phytoplankton chlorophyll; ZS: protistan zooplankton; ZLres: < 1 mm metazoan zooplankton that are resident in the euphotic zone; ZLdvm: < 1 mm diel vertically migrating metazoan zooplankton; ZPres: > 1 mm metazoan zooplankton that are resident in the euphotic zone; ZPdvm: > 1 mm diel vertically migrating metazoan zooplankton). Oxygen is also a state variable but is not shown in this figure.
Diel vertical migration is incorporated into NEMUROBCP via two alternate formulations (only the first one is used in this study). The first formulation is designed for computational efficiency when the model is run in a euphotic-zone-only configuration (NEMUROBCP,EUPONLY). In NEMUROBCP,EUPONLY diel vertically migrating taxa (LZDVM and PZDVM) only feed at night. During the day, their mortality and respiration do not contribute to detritus and dissolved nutrient pools but rather are treated as a loss of nitrogen from the model. The second formulation includes a true diel vertical migration model based on the model of Bianchi et al. (2013a) for use when the model explicitly represents mesopelagic layers. In this formulation (NEMUROBCP,DVM), vertically migrating zooplankton swim toward a target depth with a swimming speed of 3 cm s−1 (speed decreases as zooplankton approach the target depth). During the day, the target depth is defined as the depth of the 10−3 W m−2 isolume. At night, the target depth is defined as the mean depth of phytoplankton biomass. NEMUROBCP,DVM also includes a biological diffusion term that ensures that LZDVM and PZDVM are dispersed around the target depth rather than accumulating within a single model layer.
2.1.1 Optional carbon system submodule
The carbon system in NEMUROBCP includes dissolved inorganic carbon (DIC) and alkalinity as state variables. DIC is produced whenever there is net biological utilization of organic carbon and consumed whenever there is net biological production of organic carbon at fixed stoichiometric ratios of C : N = 106:16 (mol : mol). Calculation of other carbon system parameters (pH and partial pressure of CO2) and air–sea CO2 gas exchange is performed using procedures described in Follows et al. (2006).
2.1.2 Optional 234Th submodule
The 234Th submodule is based on the model of Resplandy et al. (2012). It adds a dissolved 234Th state variable (units are dpm: decays per minute), as well as state variables associated with 234Th bound to each of the nitrogen-containing particulate state variables (i.e., each phytoplankton, zooplankton, and detritus state variable). Dissolved 234Th is produced from the decay of 238U (which is assumed to be proportional to salinity, Owens et al., 2011). Dissolved 234Th adsorbs onto the aforementioned particulate pools following second-order rate kinetics. Particulate 234Th is returned to the dissolved pool through both desorption and destruction of particulate matter. 234Th is also lost from the dissolved and particulate phases through radioactive decay.
2.1.3 Optional 15N submodule
The nitrogen isotopes submodule is based on the NEMURO+15N model of Stukel et al. (2018a), following an earlier isotope model by Yoshikawa et al. (2005). The 15N submodule adds an additional 13 state variables that simulate the concentration of 15N in each nitrogen-containing state variable (nitrate, ammonium, all phytoplankton and zooplankton groups, both detritus classes, and both dissolved organic nitrogen pools). Isotopic fractionation occurs with most biological processes including nitrate uptake, ammonium uptake, exudation of organic matter by phytoplankton, excretion and egestion by zooplankton, remineralization of detritus and dissolved organic nitrogen, and nitrification.
2.2 Physical framework for model simulations
NEMUROBCP was developed so that it can be implemented in any physical framework. In this study, we used a simple one-dimensional physical framework to simulate the water column associated with Lagrangian experiments from which we derived our field data (see below). While this oversimplifies a system in which advection and diffusion play important roles in redistributing biological and chemical properties, we believe it is a reasonable short-term approximation, especially because we are explicitly simulating results from in situ Lagrangian experiments. In Lagrangian experiments, advection should play a reduced-to-negligible role in reshaping plankton time series, although we note that Lagrangian drifters (see below) explicitly track only the mixed layer, which may not be transported by the same currents as deeper layers. The use of a one-dimensional model does, however, allow us to perform more than 1 million simulations for each of the 49 Lagrangian experiments, something that would not be possible with a three-dimensional model grid. Our physical model framework simulates the euphotic zone with variable vertical spacing that increases with depth, chosen to match sampling depths from the field programs. Vertical layers are centered at 2, 5, 8, 12, 20, 25, 30, 35, 40, 45, 50, 55, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, and 160 m, although for each Lagrangian experiment we only model depths above the 0.1 % light level (which varied from 27 to 150 m). We simulate vertical mixing as a simple diffusive process using vertical eddy diffusivity coefficients that vary with depth and are estimated for each Lagrangian experiment using Thorpe-scale analyses from field measurements (Gargett and Garner, 2008). Initial and boundary conditions were determined from field measurements, although we sometimes had to estimate initial conditions from relationships with other measured parameters because all state variables were not measured for all experiments (e.g., if diatom biomass was not determined, we estimated it from a relationship between diatom biomass and total phytoplankton biomass). We ran the model for 30 d with constant vertical diffusion rates. While 30 d is an arbitrary model run time, it was chosen for multiple reasons: (1) it is long enough to reduce sensitivity to initial conditions, (2) it is the longest time period for which we would expect quasi-steady state conditions to be maintained in our study regions, and (3) it allows sufficient time for parameter sets to potentially drive some taxa to near extinction (i.e., it allows time for unreasonable parameter sets to, for instance, lead to competitive dominance of small phytoplankton and drive diatoms to extinction). We recognize that maintaining constant physical forcing introduces inaccuracy to our simulations and hence expect model–data mismatches, particularly during dynamic conditions (e.g., upwelling) when the system changes more rapidly. Model outputs were evaluated on the 30th day of the model simulation, and fluxes associated with different BCP pathways were quantified at the base of the euphotic zone (0.1 % light level), which varied between study sites. Since we only simulate the euphotic zone, the model was run in NEMUROBCP,EUPONLY configuration.
2.3 Field data
Field data come from 49 short-term (∼ 4 d) Lagrangian experiments conducted on 11 different cruises (Fig. 2) in the California Current Ecosystem (CCE) (Ohman et al., 2013), in the Costa Rica Dome (CRD) in the eastern tropical Pacific (Landry et al., 2016a), in the Gulf of Mexico (GoM) (Gerard et al., 2022), and at the Chatham Rise near the subtropical front in the Southern Ocean as part of the Salp Particle export and Oceanic Production (SalpPOOP) cruise (Décima et al., 2022). On these cruises a consistent sampling strategy involved utilization of an in situ incubation array with satellite-enabled surface drifter and 1×3 m “holey-sock” drogue centered at 15 m depth in the mixed layer (Landry et al., 2009). Samples for rate measurement experiments (see below) were incubated in polycarbonate bottles placed in mesh bags at six to eight depths spanning the euphotic zone on the incubation array (Landry et al., 2009). On 10 of the cruises, an identically drogued sediment trap array was deployed to capture sinking particles (Stukel et al., 2015).
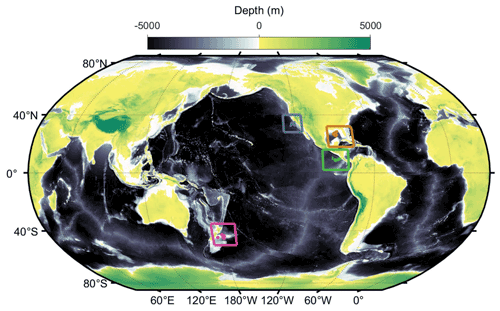
Figure 2Locations of our in situ Lagrangian experiments (blue: California Current Ecosystem; brown: Gulf of Mexico; green: Costa Rica Dome; magenta: Chatham Rise).
We assimilated a broad suite of standing stock and rate measurements across multiple trophic levels that included 466 measurements of NO concentration and 423 measurements of NH concentration (Knapp et al., 2021), 422 measurements each of silicic acid and 84 measurements of biogenic silica (Krause et al., 2015, 2016), 455 chlorophyll a measurements (Goericke, 2011), 193 measurements of small phytoplankton biomass by a combination of epifluorescence microscopy and flow cytometry (Taylor et al., 2012; Selph et al., 2021), 193 measurements of diatom biomass by epifluorescence microscopy (Taylor et al., 2012, 2016), 193 measurements of protistan zooplankton biomass by epifluorescence microscopy and/or light microscopy of Lugol's stained samples (Freibott et al., 2016), 44 measurements each of vertically integrated < 1 and > 1 mm epipelagic-resident mesozooplankton biomass, 43 measurements each of vertically integrated < 1 and > 1 mm diel vertically migrating mesozooplankton biomass, 413 measurements of particulate organic nitrogen and 28 measurements of dissolved organic nitrogen (Stephens et al., 2018), 342 measurements of net primary productivity by either H13CO or H14CO uptake methods (Morrow et al., 2018; Yingling et al., 2021), 149 measurements of nitrate uptake by incorporation of 15NO (Kranz et al., 2020; Stukel et al., 2016), 50 measurements of silicic acid uptake by incorporation of 32Si (Krause et al., 2015), 248 measurements each of whole phytoplankton community growth rates and whole phytoplankton community mortality rates due to protistan grazing determined by chlorophyll analyses of microzooplankton dilution experiments (Landry et al., 2009, 2021), 53 measurements each of small phytoplankton growth rates and small phytoplankton mortality rates due to protistan grazing determined by high-pressure liquid chromatography pigment analyses of microzooplankton dilution experiments combined with flow cytometry and epifluorescence microscopy (Landry et al., 2016b, 2021), 53 measurements each of diatom growth rates and diatom mortality rates due to protistan grazing determined by high-pressure liquid chromatography pigment analyses of microzooplankton dilution experiments combined with flow cytometry and epifluorescence microscopy (Landry et al., 2016b, 2021), 41 measurements each of vertically integrated < 1 and > 1 mm nighttime mesozooplankton grazing rates by the gut pigment method (Décima et al., 2016; Landry and Swalethorp, 2021), 41 measurements each of vertically integrated < 1 and > 1 mm daytime mesozooplankton grazing rates by the gut pigment method (Décima et al., 2016; Landry and Swalethorp, 2021), 37 measurements of sinking nitrogen using sediment traps (Stukel et al., 2019b; Stukel et al., 2021), 19 measurements of sinking biogenic silica using sediment traps (Krause et al., 2016; Stukel et al., 2019b), and 475 measurements of photosynthetically active radiation. Each of the above measurements was typically the mean of measurements taken at a specific depth (or vertically integrated) on multiple days of the Lagrangian experiment, thus allowing us to also quantify uncertainties for all measurements. Each of the above measurements also directly maps onto a specific standing stock or process in the model enabling direct model–data comparisons. Field data are listed in Supplement Tables S2–S4.
2.4 Data assimilation and objective model parameterization approach
Using the available datasets described above, our goal was to develop an automated and objective model parameterization method that would allow us to generate an ensemble of parameter sets for hypothesis testing or as prior distributions in future data-assimilation studies. We refer to this approach as objective ensemble parameterization with Markov chain Monte Carlo (OEPMCMC). We began by log-transforming most field measurements to normalize the data (some measurements, e.g., growth rates that can be positive or negative, were not transformed). We then defined a cost function,
where Nsites was the number of different sampling locations (i.e., 4 = CCE, CRD, GoM, and Chatham Rise), NLE,i was the number of Lagrangian experiments conducted at location i, NDT,i was the number of data types that were measured at site i, was the number of distinct observations of data type j at location i, and
where model is the model result corresponding to observation obs, and detlim is the detection limit for data type j. This is equivalent to stating that there is no model–data discrepancy if both the observation and the corresponding model result are below the experimental detection limit. Detection limits varied depending on measurement type. In practice the actual value of detlim was not very important to our results, because observations were seldom less than detlim. However, this formal definition is necessary with log-normally distributed errors, because occasionally the reported observational value was zero (or even negative).
Observational uncertainty was defined as
where is the standard deviation of multiple samples taken for the distinct observation k of data type j at location i (i.e., is the standard deviation of multiple measurements taken in the same depth layer over the course of a Lagrangian experiment), is the number of samples associated with observation k of data type j at location i, and ExpUnc is the experimental uncertainty (e.g., instrument accuracy) of observation k of data type j at location i. We chose to use the maximum of these two terms because, in most cases, the standard error of repeated measurements was greater than experimental uncertainty (and inherently incorporates experimental uncertainty). However, in some cases (e.g., if three measurements of nitrate at 12 m depth on a particular Lagrangian experiment reported the same value), the standard error of the measurements was an unrealistically low estimate of true uncertainty. We note that observational uncertainty can result from both instrument error and representativity error, and while we explicitly incorporate instrument error, we do not directly include all sources of representativity error. Representativity error refers to error due to unresolved scales and processes, observation-operator error, and errors associated with preprocessing and quality control (Janjić et al., 2018). Since our data are derived from direct in situ measurements, the latter two sources of representativity error are likely much less significant than errors resulting from unresolved scales and processes. Because we incorporate the standard deviation of multiple measurements taken at different depths and sampling times within a model layer in our measurement uncertainty, we include this dominant source of representativity error.
The cost function, J(p), gives equal weight to all measurement types within a specific Lagrangian experiment (e.g., if a Lagrangian experiment has 10 measurements of sinking nitrogen flux and 100 measurements of chlorophyll, J(p) gives each of those measurement types equal weight). It also gives different locations a weight proportional to the square root of the number of Lagrangian experiments at that site. That decision was made so that a more heavily sampled region (i.e., CCE) can provide more constraint to the model, while preventing that region from overwhelming the model results. We note that this is a comparatively weak cost function (relative to, for instance, likelihood), because it normalizes to the number of measurements. We chose a weak cost function, because it reflects the fact that uncertainty in initial conditions and physical forcing introduces a model–data misfit that is unassociated with parameter choice.
To investigate the parameter space, we performed a Markov chain Monte Carlo search (Metropolis et al., 1953). We first defined allowable ranges for all parameter values based on laboratory and field experiments, combined with results from prior model simulations (Supplement Table S1). These allowable ranges were broad and often spanned several orders of magnitude for a particular parameter. We then defined an initial guess for each parameter based primarily on values used in other NEMURO models (Kishi et al., 2007; Shropshire et al., 2020; Yoshie et al., 2007). We first ran 30 d simulations for all 49 Lagrangian experiments using the initial parameter values and calculated the cost function based on J(p1). We then perturbed the parameter set by adding to each parameter a random number drawn from a normal distribution with mean of 0 and standard deviation equal to a jump length of 0.02 times the width of the allowable range for that parameter. When newly selected values fell outside the allowable range, we mirrored them across the boundary. For many of the variables expected to follow a log-normal distribution (e.g., phytoplankton half-saturation constants), we log-transformed prior to the MCMC search. We then reran the 30 d model for all Lagrangian experiments and calculated a new cost associated with this parameter set, J(p2). We chose whether or not to accept this parameter set based on the relative cost functions of J(p1) and J(p2). If J(p2) was less than J(p1), we automatically accepted the new parameter set as a viable solution. If J(p2) was greater than J(p1), we accepted it with probability
We walked through the parameter solution space for a total of 1.1 million iterations (discarding the first 100 000 iterations as a “burn-in” period before the cost function stabilized at a relatively low value). In this way, we explored the correlated uncertainty in all parameters of the core model, except the temperature sensitivity coefficient. We chose not to vary the temperature sensitivity coefficient (TLIM), because it is fairly well constrained from experimental measurements and most model rates were directly correlated to TLIM; hence changes in TLIM lead to commensurate changes in so many other rate parameters that allowing it to vary would have made calculation of mean values of other parameters (e.g., maximum growth or grazing rates) almost meaningless.
We also saved model results associated with the BCP (e.g., sinking particle flux, net primary production, subduction rates, active transport) for the model simulations associated with each parameter set.
3.1 Objective model parameterization
In our Markov chain Monte Carlo (MCMC) exploration of the solution space, the cost function evaluated at our initial guess was 972. Over the first ∼ 100 000 iterations of the MCMC procedure, the cost function declined to approximately 100 and remained near this value for the remainder of the MCMC procedure (1 million additional simulations). We thus considered the first 100 000 iterations to be a burn-in period, and all results are based on the subsequent 1 000 000 solution sets. For this analysis set, the mean cost function was 98.2 % with a 95 % confidence interval (CI) of 83.8–115.3. For comparison, we also conducted an undirected MCMC exploration of the solution space (i.e., every solution was accepted regardless of relative change in cost function) that yielded a mean cost function of 3197 (CI = 1270–5657) after the burn-in period, with a minimum value of 740 (across the 1 000 000 simulations). The OEPMCMC procedure thus determined a set of 1 000 000 solutions for which the cost function was substantially reduced relative to either our initial parameter guess or a random sample of the solution space.
We investigated the 1 000 000 OEPMCMC solution sets to determine which parameters were well or poorly constrained by the data (Supplement Tables S1 and S2). We focus here on how well the field observations allowed the OEPMCMC approach to constrain the parameters relative to prior estimates of allowable ranges. This is distinct from the question of which parameters are most well constrained because some parameters were well known from prior knowledge (e.g., phytoplankton maximum growth rates) while others are poorly known (e.g., phytoplankton half-saturation constants). Some parameters were very well constrained by the data. Ten of the 101 variables were constrained to within 10 % of their allowed range (for log-transformed variables, 10 % of their log-transformed parameter space). Six of the 10 well-constrained variables were associated with phytoplankton bottom-up forcing, while only two parameters associated with zooplankton were well constrained by the data (the Ivlev constants for protistan grazing on small and large phytoplankton). The most-well-constrained parameter was the ammonium half-saturation constant for small phytoplankton which was assumed to vary from 0.001–1 mmol NH m−3 and was constrained by the OEPMCMC procedure to a 95 % CI of 0.0011–0.0065 mmol NH m−3. For metazoan zooplankton, all parameters except Ivlev constants had 95 % CIs that spanned > 60 % of the allowable range, and many exceeded 90 % of the allowable range. Overall, 25 parameters had 95 % CIs that spanned > 60 % of the allowable range, suggesting that those parameters were more strongly constrained by our prior estimates than by the field data (Supplement Table S1). We note that some well-constrained parameters were constrained by the data to fall within narrow bands near the middle of their prior allowable range (e.g., Vmax,SP, Fig. 3), and others were constrained to the edges of their allowable ranges (e.g., αSP, Fig. 3). While the latter case shows sensitivity of our model to our chosen priors, we do not consider this a flaw. Instead, it demonstrates that the data are providing strong constraint on the possible values of these parameters and effectively providing guidance for constraining these parameters in future studies.
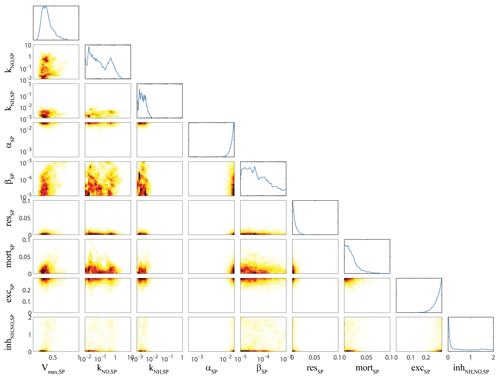
Figure 3OEPMCMC parameter distributions for bottom-up control of small phytoplankton. Line plots on top are probability density functions for individual parameters (see bottom for label and axes). Colored plots are heat maps showing joint parameter distributions. Parameters are maximum growth rate at 0 ∘C (Vmax,SP, units = d−1), half-saturation constant for nitrate uptake (KNO,SP, mmol N m−3), half-saturation constant for ammonium uptake (KNH,SP, mmol N m−3), initial slope of the photosynthesis–irradiance curve (αSP, m2 W−1 d−1), photoinhibition parameter (βSP, m2 W−1 d−1), respiration rate at 0 ∘C (resSP, d−1), linear mortality term at 0 ∘C (mortSP, d−1), excretion parameter (excSP, unitless), and ammonium inhibition of nitrate uptake (inh, m3 mmol N−1).
Next, we highlight analyses of bottom-up forcing on small phytoplankton (Fig. 3) and correlation of large phytoplankton (i.e., diatoms) bottom-up forcing with other model dynamics (Fig. 4) as examples of typical patterns of correlation among parameters. Small phytoplankton parameters were generally well constrained by the extensive datasets of phytoplankton growth rates, net primary production, and phytoplankton biomass (as assessed microscopically and/or by chlorophyll analyses). For instance, although we allowed the maximum growth rate of small phytoplankton (Vmax,SP) to vary from 0.1 to 1 d−1, the OEPMCMC procedure constrained Vmax,SP to 0.22 to 0.64 (at the 95 % CI). The least-well-constrained parameter related to small phytoplankton growth was the half-saturation constant for nitrate uptake, which varied from 0.011 to 1.3 mmol N m−3. Several of these phytoplankton parameters were also correlated in predictable manners. For instance, Vmax,SP was negatively correlated with the initial slope of the photosynthesis–irradiance curve (αSP, correlation coefficient ), because increased maximum growth rates and stronger light dependence (i.e., a slower rate of increase in photosynthesis with increasing light) offset each other to maintain similar realized growth rates under typical light-limited conditions. Vmax,SP was also positively correlated with the mortality rate (mort0.25), because commensurate changes in Vmax,SP and mortSP maintain similar net growth rates for small phytoplankton.
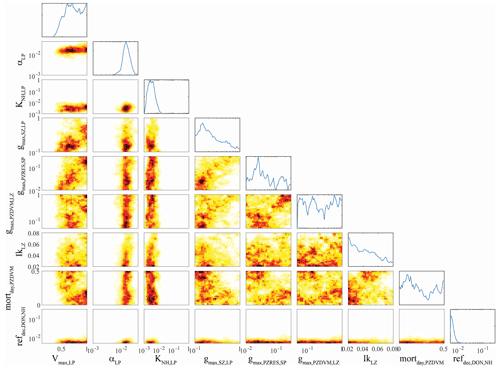
Figure 4OEPMCMC parameter distributions for large phytoplankton and some other model processes. Line plots on top are probability density functions for individual parameters (see bottom for label and axes). Colored plots are heat maps showing joint parameter distributions. Parameters are maximum growth rate at 0 ∘C (Vmax,LP, units = d−1), initial slope of the photosynthesis–irradiance curve (αLP, m2 W−1 d−1), half-saturation constant for NH uptake (KNH,LP, mmol N m−3), maximum grazing rate of small zooplankton on large phytoplankton (, d−1), maximum grazing rate of large (> 1 mm) epipelagic-resident mesozooplankton on small phytoplankton (, d−1), maximum grazing rate of large (> 1 mm) vertically migrating mesozooplankton on small (< 1 mm) mesozooplankton (, d−1), the Ikeda respiration parameter for small (< 1 mm) mesozooplankton, daytime mortality rate for small (< 1 mm) vertically migrating mesozooplankton (mortday,LZDVM, m3 mmol N−1 d−1), and remineralization rate of DON to NH (ref, d−1).
Parameters associated with large phytoplankton were typically less well constrained, although they did differ from parameters associated with small phytoplankton in several predictable ways. For instance, the maximum growth rate of large phytoplankton (Vmax,LP, mean = 0.72 d−1, 95 % CI was 0.43–0.99 d−1) was greater than the maximum growth rate of small phytoplankton (mean = 0.37 d−1, 95 % CI was 0.22–0.64 d−1) despite the fact that we used identical allowable ranges of 0.1–1 d−1. The half-saturation rate for large phytoplankton uptake of nitrate ( mmol N m−3) was also substantially greater than KNO,SP (0.25 mmol N m−3), although their half-saturation constants for ammonium uptake were similar. Unsurprisingly, the maximum growth rate of large phytoplankton was strongly correlated with the maximum grazing rate of protistan zooplankton on large phytoplankton (, ρ=0.35), because grazing by protistan zooplankton is often the dominant source of mortality for all phytoplankton (including diatoms). More surprisingly, Vmax,LP had an even stronger correlation with the maximum grazing rate of epipelagic-resident large (> 1 mm) mesozooplankton on small phytoplankton (, ρ = 0.43). We believe that this arises from a correlation between large mesozooplankton standing stock and . Since small phytoplankton are often the most abundant potential prey item, higher values allow large mesozooplankton (which preferentially graze large phytoplankton) to sustain higher biomass and prevent large phytoplankton from escaping grazing pressure, thus requiring a higher maximum growth rate to maintain their biomass.
Some correlations were unexpected. For instance, the initial slope of the photosynthesis–irradiance curve (αLP) was positively correlated with the remineralization rate of labile dissolved organic nitrogen to NH (ref, ρ=0.31). Both of these parameters were strongly constrained by the OEPMCMC procedure (αLP had an allowable prior range of 0.001–0.04 m2 W−1 d−1 but had a posterior 95 % CI of 0.008–0.03 m2 W−1 d−1; ref had an allowable range of 0.005–0.3 d−1 but a 95 % CI of 0.005–0.01 d−1). It is not clear why these parameters would be correlated, although it is likely related to the relative realized growth rates of large phytoplankton in the upper and lower euphotic zone. High values of αLP would promote higher realized growth rates in the deep euphotic zone; high values of ref would lead to higher realized growth rates in the nutrient-limited upper euphotic zone. The Ikeda parameter for small mesozooplankton (IkLZ, d−1), which sets the basal respiration of small (< 1 mm) mesozooplankton, was positively correlated with Vmax,LP (ρ=0.12), KNH,LP (ρ=0.16), and αLP (ρ=0.29). While the first and third correlations are not surprising (both lead to increased large phytoplankton growth which would support higher mesozooplankton respiration), it is surprising that IkLZ would be correlated with KNH,LP since higher half-saturation constants lead to lower realized phytoplankton growth rates. Vmax,LP was also negatively correlated with the daytime mortality rate of small (< 1 mm) vertically migrating mesozooplankton at their mesopelagic resting depth (mortday,LZDVM, ), which is opposite to what would be expected if large phytoplankton growth was necessary to support mesozooplankton mortality, but may reflect an indirect effect of intraguild competition between small mesozooplankton and protistan grazers (mortday,LZDVM was also negatively correlated with the Ivlev constant for small mesozooplankton grazing on protistan zooplankton (IvLZDVM,SZ, ), which would indicate that mesozooplankton mortality increases when their feeding rate on protists increases).
While these are only a subset of the multiple correlations, they highlight the complex, and often counterintuitive, relationships among many parameters. This analysis also clearly elucidates the importance of joint parameter sensitivity analyses. For instance, when model sensitivity to maximum large vertically migrating mesozooplankton grazing rates on small phytoplankton () was investigated with a maximum large phytoplankton growth rate (Vmax,LP) of ∼ 0.6 d−1, the analysis suggested that the model was only weakly sensitive to gmaxPZRES,SP and that the optimal value was near 0.03 d−1. However, when the same analysis was conducted with ∼ 1.0, the model was very sensitive to gmaxPZRES,SP, and the optimal value was 0.1–0.2 d−1.
3.2 Model–data comparison (assimilated data)
To determine whether the model was able to simulate assimilated measurements accurately, we compared model–data results with respect to two key processes related to export: net primary production and sinking particle flux at the base of the euphotic zone (Figs. 5 and 6, respectively). For most Lagrangian experiments, the model 95 % confidence interval bracketed the mean of the observed net primary production (Fig. 5). However, the model substantially underestimated net primary productivity for several experiments in the CCE (e.g., 605-1, 605-3, 704-4, 810-5, and 1604-4) conducted in near-coastal regions with recently upwelled high-nitrate water. The model–data discrepancy thus likely results from our assumption of a one-dimensional system with constant physics for 30 d. In reality, these Lagrangian experiments were heavily influenced by coastal upwelling processes missing in our one-dimensional model and experienced markedly non-linear dynamics as the water parcels were advected away from the upwelling source and nutrients drawn down over time (e.g., Landry et al., 2009). Contemporaneous nutrient input from directly below these water parcels was thus likely not the source of nitrogen supporting high production, as is assumed by our one-dimensional physical framework. In less dynamic regions (e.g., GoM), the model more faithfully simulated phytoplankton production.
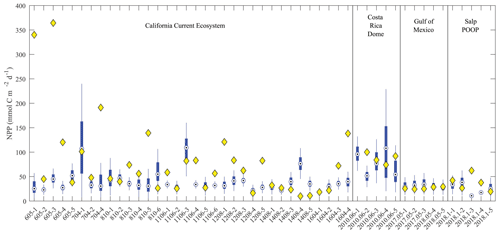
Figure 5Model–data net primary production comparison. Blue box plots show model results for each simulated Lagrangian experiment, with whiskers extending to 95 % confidence limits. Yellow diamonds show observations from Lagrangian experiments.
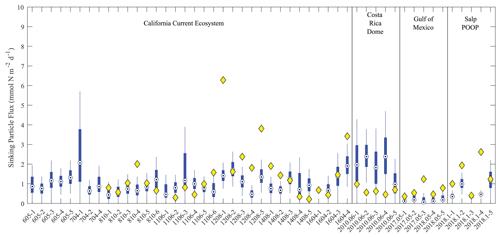
Figure 6Model–data sinking particle export comparison at the base of the euphotic zone. Blue box plots show model results for each simulated Lagrangian experiment, with whiskers extending to 95 % confidence limits. Yellow diamonds show observations from sediment trap deployments (no observations were available for nine experiments).
The model did a reasonable job simulating sinking particle export flux from the euphotic zone (Fig. 6). For the majority of experiments, observed export fell within the 95 % confidence interval of the model simulations. However, the simulated export flux range was quite substantial for most cycles. Indeed, the 95 % confidence intervals for export flux at single locations using the 1 000 000 MCMC solutions were at times as large as the confidence interval for mean observed flux across the 49 different Lagrangian experiments. This suggests that uncertainty in parameter estimation for the model is as important a source of error for export flux as variability between regions and seasons. The only region for which the model produced a stark bias in export flux relative to the observations was the CRD, where the model consistently overestimated export flux. This is not surprising for this region, because the CRD is dominated by Synechococcus, which contribute substantially less to export flux than larger phytoplankton (Saito et al., 2005; Stukel et al., 2013). In other regions, model underestimates of export flux were typically more notable than model overestimates (observations were seldom less than the lower bound of the model's 95 % confidence interval).
3.3 Model–data comparison (unassimilated data)
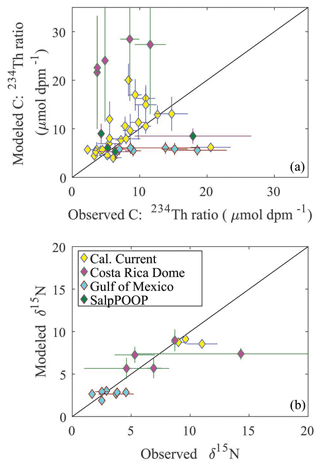
To assess the model's ability to simulate state variables and processes not included in the assimilation dataset, we utilized the thorium sorption and nitrogen isotope submodules and compared model results to measured total water column 234Th (Fig. 7), the C : 234Th ratio of sinking particles (Fig. 8a), and the δ15N of sinking particles (Fig. 8b). NEMUROBCP accurately simulated many properties of 234Th dynamics found in the field data. For instance, it did a reasonable job of estimating the shape and magnitude of vertical profiles, notably simulating low 234Th activity in surface waters and 234Th activity close to equilibrium with 238U in deeper waters. The model also captured some key aspects of inter- and intra-regional variability in 234Th activity, including much lower 234Th activity in coastal regions of the CCE (e.g., Fig. 7a, c, ah) relative to offshore regions (e.g., Fig. 7e, ad, ae). The model also accurately estimated the consistently high 234Th activity found in the GoM. The greatest model–data mismatch with respect to 234Th activity was found in the CRD (Fig. 7ai–am). In this region, the model was fairly accurate at predicting mixed layer 234Th activity, but the model consistently underestimated 234Th activity in the deep euphotic zone. The model was also reasonably effective at predicting the C : 234Th ratio of sinking particles. The model both accurately estimated the mean value of sinking particle C : 234Th ratios (median observation = 7.2 µmol C dpm−1; median model value for locations paired with observations = 7.7 µmol C dpm−1) and the range of C : 234Th values (observation = 2.2–20.5 µmol C dpm−1; model = 4.1–30.0 µmol C dpm−1). For most simulations, the modeled and observed C : 234Th ratios also showed very good agreement (Fig. 8a). However, the model consistently overestimated the C : 234Th ratio of sinking particles in the CRD, a region where the model was particularly poorly constrained and predicted a wide range of C : 234Th ratios. The model also substantially underestimated the C : 234Th ratio for several sediment trap collections in the GoM. Nevertheless, the overall model–data agreement with respect to 234Th dynamics is reassuring, especially since key parameters (e.g., thorium sorption and desorption coefficients) were not estimated by the OEPMCMC procedure but instead were taken directly from the literature.
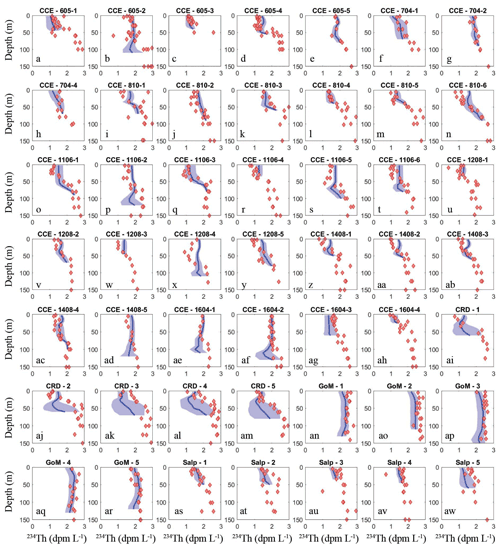
Figure 7Model–data water-column 234Th activity comparison. Dark blue lines show mean vertical profile of 234Th activity from MCMC model simulations, with lighter blue shading indicating 95 % CI. Red diamonds show observations. Each panel is for a separate Lagrangian experiment.
The model was also able to accurately simulate the δ15N of sinking particles, albeit with a more limited set of observations available (note that we did not simulate nitrogen isotopes for Lagrangian experiments from the SalpPOOP cruise, because the δ15N of deep-water nitrate, an important boundary value, was unknown in this region). The median observed δ15N of sinking particles was 4.6 compared to a model estimate of 6.1, while the observed range was 1.7–14.3 and the modeled range was 1.8–9.3 (Fig. 8b). The only simulation for which there was a substantial mismatch between model result and observation was from a single experiment in the CRD for which one sediment trap replicate had a very high measured δ15N value, while the other two replicates were near the simulated value.
3.4 Sensitivity analysis
The OEPMCMC approach allowed us to investigate uncertainty associated with all three pathways of the BCP (see the next two sections). First, we focus specifically on variability in model estimates of gravitational flux, as these can be directly compared to field measurements. When comparing modeled gravitational flux for different Lagrangian cycles, the median coefficient of variation (standard deviation mean) was 0.49, with a range of 0.29–1.38. This represents substantial uncertainty in sinking particle flux due solely to different potential parameter choices (Fig. 6). For instance, on the fifth Chatham Rise Lagrangian experiment (which was the experiment with coefficient of variation closest to the median), the mean model-predicted gravitational flux was 1.24 mmol N m−2 d−1 with a standard deviation of 0.62 mmol N m−2 d−1 and a 95 % confidence interval from 0.29 to 2.6 mmol N m−2 d−1. This shows that for a typical cycle, there was nearly an order of magnitude variability in export flux based solely on uncertainty in model parameterization. For comparison, across the 49 Lagrangian experiments for which we have sediment trap deployments near the base of the euphotic zone, the field observations of gravitational flux at the base of the euphotic zone ranged from 0.22–6.3 mmol N m−2 d−1. Thus, for a typical Lagrangian experiment, uncertainty in model parameterization introduced slightly less uncertainty in gravitational flux than variability across the multiple regions. For the fourth GoM Lagrangian experiment (the experiment with the highest coefficient of variation), the mean model-predicted gravitational flux was 0.23 mmol N m−2 d−1 with a standard deviation of 0.31 and a 95 % confidence interval from 0.0069–1.07 mmol N m−2 d−1. For this particular cycle, some likely parameter sets predicted gravitational flux nearly equal to the mean measured gravitational flux across the diverse regions we studied, while other likely parameter sets predicted export more than an order of magnitude lower than the lowest observed flux. This high degree of uncertainty should be considered when results of a single model simulation are considered and provides a strong argument for the importance of ensemble modeling.
To investigate the relationships among uncertainties in the three pathways of the BCP and uncertainties in parameters, we computed the R2 of ordinary least squares linear regressions of each BCP pathway as a function of each parameter. This approach allows us to quantify the percentage of variability in the export pathway explained by a linear relationship with a specific parameter. This is distinctly different from some traditional sensitivity analysis approaches that either compute the derivative of a model output with respect to different parameters or vary parameters by a fixed amount (e.g., ± 10 %). Unlike those approaches, our R2 approach explicitly accounts for the certainty with which different parameters are constrained. For instance, a model may be very sensitive to the maximum growth rate of diatoms; however, if that parameter is well constrained by laboratory experiments, field data, and/or data assimilation, then parameter uncertainty may not be the dominant source of uncertainty in model results. Our approach is thus well suited to determining which parameters especially merit future experimental focus.
Our results show that the R2 values for BCP pathways regressed against most parameters were ∼ 0.01 or less. However, some of the parameters were able to explain 10 % of the variability in specific BCP pathways. For instance, the linear mortality parameter for protistan zooplankton (mortSZ) explained 15 % of the variability in gravitational particle export (positive correlation) and 18 % of the variability in export due to vertical mixing (negative correlation). These correlations reflect the importance of protistan zooplankton in controlling phytoplankton populations without producing rapidly sinking particles. Multiple parameters had similar inverse correlations with gravitational particle export and export due to vertical mixing. For example, the assimilation efficiency of small epipelagic-resident mesozooplankton, the Ivlev constant for large mesozooplankton feeding on small mesozooplankton, and the sinking speed of fast-sinking detritus all had positive correlations with gravitational flux; the maximum grazing rate of small epipelagic-resident mesozooplankton on protistan zooplankton and the remineralization rate of fast-sinking detritus had negative correlations with gravitational flux. The remineralization rate of fast-sinking detritus explained the highest proportion of variability in gravitational flux (45 %). Only two parameters (the maximum grazing rate of large vertically migrating mesozooplankton on small mesozooplankton and the Ivlev constant for large mesozooplankton feeding on small protists) explained > 10 % of the variability in active transport (19 % and 18 %, respectively, with both positively correlated with active transport). Notably, none of the parameters most responsible for uncertainty in the BCP were related to phytoplankton bottom-up limitation. We do not believe that this reflects a lack of importance of bottom-up processes in the BCP. Rather, this reflects a much greater uncertainty in parameterizations for zooplankton and non-living organic matter, combined with the importance of these processes to the BCP (Cavan et al., 2017; Anderson et al., 2013).
As mentioned previously, two of the most important parameters for determining gravitational flux are the sinking speed (Lsink) and remineralization rate of fast-sinking particles to DON (ref). Notably, these two parameters are strongly related to the remineralization length scale for these particles (RLS = Lsink (ref + ref). We illustrate the impact of variability in RLS on model gravitational flux by focusing on two Lagrangian experiments representative of the CRD (CRD-1) and upwelling-influenced regions of the CCE (1604-3). RLS was strongly correlated with gravitational flux for each experiment (Pearson's ρ = 0.62 for both experiments, p ≪ 10−7). The relationship was not perfectly linear, however (Supplement Fig. S1a, b). Particularly for the CRD experiment, but also for the CCE experiment, there was a threshold effect such that RLS was only weakly correlated with gravitational flux at RLS > ∼ 150 m. This resulted from higher RLS values leading to decreased recycling in the system and hence reduced primary production. Comparison of the probability density functions for RLS determined by the OEPMCMC procedure with probability density functions for only those parameter sets that accurately predicted gravitational flux for these cycles (to ± 1 standard deviation of the observed value) shows that gravitational flux was more accurately predicted for the CCE experiment with RLS values slightly higher than the overall average of the whole dataset (median for the entire dataset was 85 m; median for parameter sets that accurately predicted export for this cycle was 115 m, Supplement Fig. S1c), while it was more accurately predicted for the CRD experiment with RLS values lower than the average for the dataset (median RLS for accurate parameter sets = 57 m, Supplement Fig. S1d). This highlights the sensitivity of the model to these parameters while suggesting differences in remineralization length scale between these specific regions, although we caution that RLS calculated above is only for fast-sinking detritus and does not account for the additional gravitational flux mediated by slowly sinking particles.
3.5 Model results: three pathways of export
We compared the relative magnitude of the three BCP pathways for all Lagrangian cycles and all OEPMCMC parameter sets (Fig. 9a). Results showed that export was typically dominated by some combination of gravitational flux and/or mixing flux (i.e., eddy subduction + vertical mixing). Active transport typically contributed a relatively small proportion of export from the base of the euphotic zone (mean = 2.8 %, 95 % CI = 0.02 %–16.5 %). Across the dataset, gravitational flux was the dominant export pathway (mean = 56.1 %, 7.1 %–99.6 %), although mixing was also an important source of export (mean = 41.1 %, 0 %–92.3 %). The large confidence intervals for each of these fluxes highlight the uncertainty in our estimates of the BCP pathways. They also, however, obscure distinct regional variability among the experiments analyzed in our study.
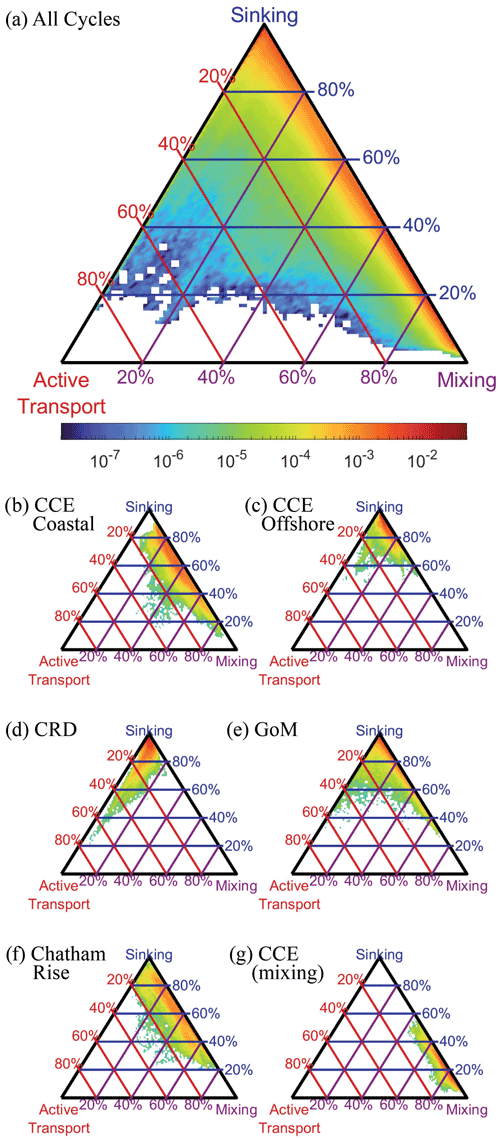
Figure 9Triangle diagrams showing the proportion of export due to each biological carbon pump pathway at the base of the euphotic zone. Locations near the upper apex of the triangle indicate dominance by sinking particles, locations near the bottom left indicate dominance by active transport, and locations near the bottom right show dominance by mixing. Colors represent the proportion of total model simulations with export patterns falling within a specific proportion of different export pathways. Lines indicate contours showing a constant proportion of one BCP pathway (i.e., red lines are constant proportions of active transport, blue lines are constant proportions of gravitational flux, and purple lines are constant proportions of mixing flux). (a) Results for all simulations, (b) results for a typical CCE coastal site (1604-3), (c) typical CCE oligotrophic site (1408-5), (d) typical Costa Rica Dome site (CRD-1), (e) typical Gulf of Mexico site (GoM-5), (f) typical Chatham Rise site (Salp-5), and (g) example of a CCE site (0605-3) dominated by mixing flux.
During upwelling-influenced experiments in the CCE, mixing and gravitational flux often contributed approximately equally to the BCP, with different parameter sets suggesting either dominance by mixing or gravitational flux. For instance, during CCE cycle 1604-3 (Fig. 9b) gravitational flux contributed an average of 61 % (29 %–84 %) of export, while mixing was responsible for 35 % (12 %–67 %). Not every CCE coastal cycle had a relatively even split, however, with some more dominated by sinking flux and others more dominated by mixing flux (e.g., CCE cycle 0605-3 which occurred during a dense coastal dinoflagellate bloom, Fig. 9g). In oligotrophic regions of the CCE and GoM, export was typically dominated by sinking flux, with relatively minor contributions from both mixing and active transport. For instance, during CCE cycle 1408-5 gravitational flux was responsible for 86 % (70 %–97 %) of export (Fig. 9c), while during GoM cycle 5 sinking was responsible for 89 % (66 %–98 %) of export (Fig. 9e). During CRD experiments, which had relatively high mesozooplankton biomasses relative to phytoplankton biomass, active transport was comparatively more important. For instance, during CRD cycle 1, active transport averaged 6.5 % (0.7 %–26 %) of export and was more important than mixing flux (4.3 %, 0.4 %–12 %, Fig. 9d). During the Chatham Rise experiments in the Southern Ocean, export patterns were comparable to those in the upwelling-influenced CCE, driven primarily by gravitational flux and mixing, with gravitational flux slightly more important.
Looking at patterns across regions and across the varying conditions on our Lagrangian experiments, the proportion of export driven by vertical mixing was correlated with vertical eddy diffusivity at the base of the euphotic zone (Spearman's ρ=0.64, p < 10−6). This is not surprising, since vertical diffusion drives particulate and dissolved organic matter flux across the euphotic zone. Because sinking and vertical mixing were the two dominant mechanisms of export, vertical eddy diffusivity also showed a strong inverse correlation with gravitational flux (Spearman's , p < 10−6). Across all simulations, organic matter mixed out of the euphotic zone was relatively evenly split between DOM and POM, but variability in POM flux was greater (mean = 3.4 ± 6.9 mmol N m−2 d−1) than variability in DOM (mean = 4.6 ± 5.5 mmol N m−2 d−1). For most simulations (72 %), DOM mixing flux exceeded POM mixing flux. However, POM mixing was greater for 66 % of the simulations with total mixing flux > 20 mmol N m−2 d−1. Flux of fast-sinking particles exceeded that of slow-sinking particles at the euphotic zone base for 90.5 % of simulations, with fast-sinking particles averaging of 2.3 mmol N m−2 d−1 (0.07–10.4 mmol N m−2 d−1) and slow-sinking particles averaging 0.35 mmol N m−2 d−1 (0.02–1.4 mmol N m−2 d−1).
3.6 Model results: diel vertical migration and active transport
In NEMUROBCP, active transport is driven by two processes: respiration/excretion and mortality at depth. The former is parameterized as a temperature- and size-dependent function representing basal respiration and is comparatively well constrained by prior experimental work. The latter is parameterized as a density-dependent function representing predator-induced mortality, a process that is highly uncertain because few studies have quantified zooplankton mortality in the mesopelagic ocean. We fit linear regressions to log-transformed active transport plotted against log-transformed mesozooplankton biomass (Fig. 10a) to determine a power law relationship predicting active transport from mesozooplankton biomass: AT = aBc, where AT is active transport (mmol N m−2 d−1), B is biomass (mmol N m−2), a = 0.0052 ± 6 × 10−6, and c = 1.29 ± 0.0004, R2=0.90, p ≪ 10−9. Similar relationships were also determined for the respiration/excretion component of active transport (E = aBc, a = 0.0037 ± 4 × 10−6, b = 1.02 ± 0.0005, R2= 0.87, p ≪ 10−9) and the mortality component of active transport (M = aBc, a = 0.00054 ± 10−6, b = 2.04 ± 0.001, R2= 0.89, p ≪ 10−9). As expected, since excretion is density-independent while mortality is density-dependent, the exponent of the excretion power law was ∼ 1 and the exponent of the mortality power law was ∼ 2. This led to mortality becoming a greater fraction of total active transport as mesozooplankton biomass increased (Fig. 10d). The transition from active transport dominated almost entirely by respiration to active transport comprised mostly of mortality at depth occurred rapidly as biomass increased past ∼ 5 mmol N m−2. As a result of the density-dependent parameterization of mortality, daytime mortality also increased with increasing zooplankton biomass (m = aBc, where m is specific mortality (h−1), a = 2.6 × 10−4 ± 5 × 10−6, and b = 0.995 ± 0.001, R2=0.68, p ≪ 10−9). This generated daily mortality rates (i.e., over a 12 h daytime period) of ∼ 0.3 % d−1 at a biomass of 1 mmol N m−2 and ∼ 6 % d−1 at a biomass of 20 mmol N m−2 (Fig. 10e). Overall mortality for vertically migrating mesozooplankton was approximately evenly split between the epipelagic and mesopelagic, although this ratio was poorly constrained by the model (Fig. 10f). For instance, 9 %–96 % of large-mesozooplankton mortality occurred in the mesopelagic (at the 95 % CI).
As suggested by the validation data, vertical migrator biomass was primarily found in the large (> 1 mm) mesozooplankton size class. The large mesozooplankton were also predominantly vertical migrators, while the small mesozooplankton were primarily epipelagic residents (Fig. 10g). Consequently, large mesozooplankton typically dominated active transport (Fig. 10h) even though small mesozooplankton usually contributed proportionally more to active transport than to biomass as a result of higher specific respiration rates (Fig. 10i).
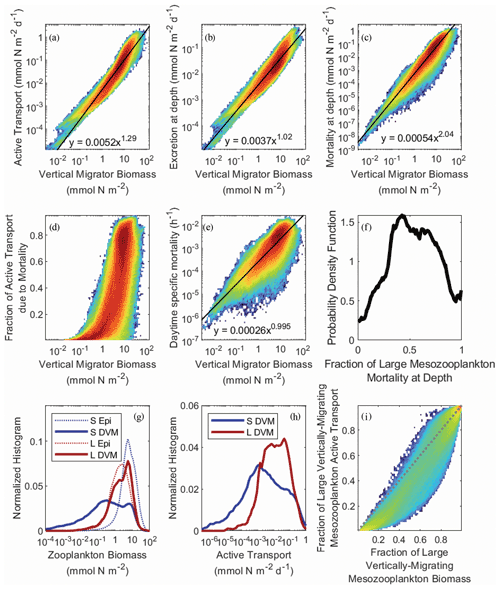
Figure 10Heat maps of active transport (a), active transport due to excretion in the deep ocean (b), active transport due to mesozooplankton mortality at depth (c), the fraction of active transport that was due to mortality at depth (d), and the daytime specific mortality experienced by mesozooplankton at their mesopelagic resting depths (e), all as a function of the total biomass of vertically migrating mesozooplankton (i.e., sum of both size classes). Black lines and equations in panels (a), (b), (c), and (d) were determined from ordinary least squares regressions of log-transformed data (see text for regression statistics). Panel (f) shows the probability density function for the fraction of large (> 1 mm) mesozooplankton mortality experienced during the day at their mesopelagic resting depths. Panels (g) and (h) show normalized histograms of log10-transformed zooplankton biomass and active transport, respectively. Dashed blue line is small epipelagic-resident zooplankton, solid blue is small DVM zooplankton, dashed red is large epipelagic-resident zooplankton, and solid red is large DVM zooplankton. Panel (i) shows the fraction of active transport mediated by large mesozooplankton (> 1 mm) as a function of their fraction of total vertically migrating mesozooplankton biomass. Dashed gray line is the 1:1 line.
It would be reasonable to assume that predator-induced mortality in the deep ocean would be negatively correlated with the abundance of diel vertical migrators, because high mortality would yield a competitive advantage for epipelagic-resident zooplankton. For the full dataset, however, we found a negligible correlation between the mesopelagic mortality term for large mesozooplankton (mortday,PZDVM) and large mesozooplankton biomass (Spearman's ). When investigating this correlation for individual experiments, the correlation was sometimes positive and sometimes negative. This lack of a correlation was driven by strong correlations between the mortday,PZDVM and both the assimilation efficiency of these zooplankton and their maximum grazing rate on smaller mesozooplankton. This led to a compensatory higher growth rate to offset the higher mortality rate and consequently to a reasonably strong correlation between mortday,PZDVM and the magnitude of export attributable to predation on large mesozooplankton in the deep ocean (ρ=0.25).
4.1 Biological carbon pump pathways
Gravitational flux is by far the most-well-studied pathway of the BCP, because it is the only pathway for which direct in situ flux measurements are possible. Nevertheless, incredibly sparse in situ sampling necessitates spatiotemporal extrapolation approaches to derive regional and global estimates of gravitational flux, including the use of forward models, inverse models, and satellite algorithms (e.g., Schlitzer, 2004; Laws et al., 2000; Hauck et al., 2015; DeVries and Weber, 2017). Satellite algorithms, as perhaps the most widely used and cited methods for deriving global estimates, deserve special attention. These approaches have delivered widely varying estimates of the magnitude of gravitational flux, and indeed the algorithms underlying such estimates often differ in the fundamental relationship predicted between sinking particle flux and phytoplankton biomass and production (Laws et al., 2000; Siegel et al., 2014; Henson et al., 2011; Dunne et al., 2005). Such studies typically estimate export flux from relationships with net primary production (or surface chlorophyll) and/or temperature because these properties are easily observable by satellite remote sensing. These studies, however, have reached widely differing conclusions about the relationships of these properties to export efficiency (e ratio = gravitational flux / net primary productivity). Indeed, the in situ data compiled here show no significant dependence of export efficiency on net primary productivity (NPP) or temperature (Fig. 11a), because export efficiency depends not just on temperature and phytoplankton production, but also the community composition of phytoplankton and zooplankton, physiological adaptations of important taxa, and a multitude of ecological interactions (Turner, 2015; Buesseler and Boyd, 2009; Guidi et al., 2016). Indeed, focusing only on the regions studied here, anomalously high Synechococcus abundances likely result in low export efficiency in the CRD (Stukel et al., 2013; Saito et al., 2005), salp blooms drive very high export in the Chatham Rise (Décima et al., 2022), and the diatom Thalassiosira seems to play a particularly important role in export in the CCE (Preston et al., 2019; Valencia et al., 2021). In the latter, diatom photophysiological health is a strong predictor of export (Brzezinski et al., 2015), although the diatoms likely sink mainly after grazing by metazooplankton (Morrow et al., 2018).
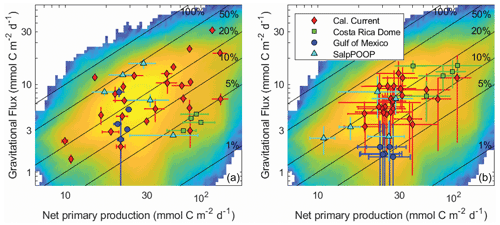
Figure 11Gravitational flux at the base of the euphotic zone as a function of net primary production for in situ data (a) and model results (b). Averages and standard deviations are shown for individual Lagrangian experiments. Nitrogen-based model results were converted to carbon units assuming a C : N ratio of 106:16 (mol : mol). The background in both figures is a heat map of all model results (i.e., all Lagrangian experiments and all parameter sets). Solid black lines show contours of constant e ratio (gravitational flux / net primary production).
Despite the diversity of processes that affect the BCP, many of which are not included in NEMUROBCP, our simulations reasonably reproduce the variability of export efficiency across the study regions, even though results for individual experiments are imprecise (Fig. 11). One important process that drives variability in export efficiency is temporal decoupling of production and export (Henson et al., 2015; Laws and Maiti, 2019; Kahru et al., 2020). Despite the use of constant physical forcing throughout our 30 d simulations, they exhibit distinct temporal variability in biogeochemical properties. We highlight results from one experiment in slightly aged, upwelled water off the California coast, using five different evenly spaced parameter sets (i.e., the 200 000th, 400 000th, 600 000th, 800 000th, and 1 000 000th parameter sets) chosen from our ensemble (Fig. 12). In each of these simulations, net primary production increases early in the simulations, rapidly in some, and more gradual in others (Fig. 12a). Net primary production soon diverges in all of the simulations, however, with some gradually decreasing after the first week and others exhibiting blooms. Gravitational flux was even more variable, with one simulation peaking almost immediately and others with substantial temporal lags between net primary production and export (Fig. 12b). This led to substantial temporal variability in export efficiency (Fig. 12c) and quite complex relationships between gravitational flux and net primary production (Fig. 12d).
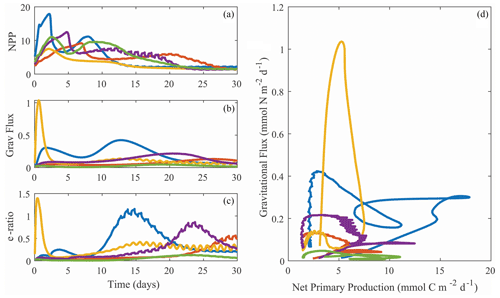
Figure 12Temporal variability in net primary production (a, mmol C m−2 d−1), gravitational flux (b, mmol N m−2 d−1), and export efficiency (c, unitless with a C : N conversion ratio of 106:16 mol : mol), along with a phase-space plot depicting the same data (d). All plots are from Lagrangian experiment 1604-3 (CCE upwelling region). Different colors are for simulations with ensemble parameter sets 2 × 105, 4 × 105, 6 × 105, 8 × 105, or 106.
Assessing the accuracy with which the model simulates export due to vertical mixing (variously called the eddy subduction pump, mixed layer pump, and/or physical pump) is more difficult. Previous studies to quantify this process have either relied on indirect biogeochemical proxies (Stukel and Ducklow, 2017; Llort et al., 2018) or numerical models (Omand et al., 2015; Levy et al., 2013; Stukel et al., 2018b; Nowicki et al., 2022) to quantify these processes. Our vertical mixing results should be considered with some caution due to our overly simplified one-dimensional physical framework, which conflates distinct processes including mesoscale subduction, diapycnal diffusion, mixed layer entrainment and detrainment, and gyre-scale Ekman pumping. Nevertheless, it is reassuring that our simulations from the CCE, which showed that vertical mixing out of the euphotic zone was often similar in magnitude to gravitational flux and at times even higher, is similar to results based on a Lagrangian particle model developed for the region (Stukel et al., 2018b). More realistic estimates for all regions could be derived by coupling NEMUROBCP and our parameter ensembles to a three-dimensional ocean simulation.
The magnitude of active transport mediated by diel vertically migrating zooplankton in the global ocean remains highly uncertain due to a paucity of measurements and the difficulty of constraining the amount of mortality occurring at depth. Studies that include only respiration and/or excretion of zooplankton at depth typically find that active transport is a relatively small fraction of gravitational flux (Steinberg et al., 2000; Hannides et al., 2009). However, more recent studies that have attempted to incorporate mortality experienced in the deep ocean have derived much larger estimates of active transport (Kelly et al., 2019; Kiko et al., 2020; Hernández-León et al., 2019). These studies should be considered highly uncertain, however, because they necessarily make large assumptions about the amount of zooplankton mortality occurring in the deep ocean, where it has never been directly quantified. Results from our study, which does include mortality at depth, suggest that active transport is a quantitatively important but never dominant component of carbon export out of the euphotic zone, in line with results from recent global estimates derived from a combination of satellite remote-sensing products and modeling approaches (Archibald et al., 2019; Nowicki et al., 2022).
One aspect of the BCP that our current euphotic-zone only simulations do not address is sequestration efficiency in the mesopelagic (Kwon et al., 2009; Marsay et al., 2015; Buesseler and Boyd, 2009). It is reasonable to surmise that the remineralization length scale will vary for different BCP pathways and be regionally variable as well. With gravitational flux, typically ∼ 50 % of particles will sink 100 m beneath the euphotic zone before remineralization, although remineralization length scales are highly variable and the spatial patterns are poorly understood (Buesseler and Boyd, 2009; Marsay et al., 2015). Meanwhile, vertically migrating zooplankton typically reside at depths of 200–600 m during the day and hence respire the majority of their carbon dioxide at this depth (Bianchi et al., 2013b), although it is unclear how the inclusion of mortality at depth into our understanding of active transport will affect the overall depth of penetration of actively transported carbon into the deep ocean. Stukel et al. (2018b), suggested that subducted particles in the southern CCE are mostly remineralized near the base of the euphotic zone, with little penetration into the mesopelagic, although in regions with deep convective mixing, signatures of subduction show substantial transport into the deep ocean (Omand et al., 2015; Llort et al., 2018). Nowicki et al. (2022) estimated that gravitational flux and active transport have similar sequestration timescales but that sequestration times for mixing were much shorter. In contrast, Boyd et al. (2019) surmised that active transport may have the greatest sequestration efficiency, followed by vertical mixing and then gravitational flux, although their synthesis was only able to draw from the few studies that have quantified these processes, and they note that determining the sensitivities of sequestration efficiencies to environmental drivers is crucial to predicting climate change impacts on marine carbon sequestration. We believe that future incorporation of our model ensemble approach into three-dimensional coupled modeling frameworks could be an important step forward in understanding the magnitude and uncertainty in these processes.
4.2 Data-assimilating biogeochemical models
Implicit to our OEPMCMC approach is the philosophical realization that our model (like all biogeochemical models) oversimplifies an incredibly complex system. Hence, we accept that no single solution set will accurately simulate all aspects of the BCP. Instead, we proposed a mechanistic–probabilistic approach that explicitly investigates the ecosystem uncertainty. This contrasts with some other data-assimilation approaches (e.g., gradient-based methods including the variational adjoint, Schartau et al., 2001; Friedrichs et al., 2007; Lawson et al., 1995) that seek to find a single solution that minimizes model–data misfit. While the variational-adjoint approach is computationally efficient and allows objective determination of a single solution that can then be used for high-resolution simulations (Mattern et al., 2017), our work shows that very different parameter sets can result in similar cost function values, despite generating distinctly different model outputs. For instance, different sets of parameters (all with approximately equivalent mismatch to our extensive suite of field measurements) predicted distinctly different functioning of the BCP in the CCE coastal region (with some parameter sets suggesting that subduction is most important and others suggesting that sinking particles are most important, Fig. 9b) and in the Costa Rica Dome (where some parameter sets suggested sinking was responsible for almost all carbon export, compared to other parameter sets that suggested almost equal importance of active transport, Fig. 9d). The results of a typical variational-adjoint data-assimilation approach (or any approach that determines results from a single “best” parameter set) would have selected only one of these possible parameter sets and assumed that it accurately depicted the ecosystem; our results more accurately quantify this true uncertainty.
Our approach has similarities with other biogeochemical model ensemble approaches. For instance, Doron et al. (2013) used an ensemble Kalman filter algorithm to assimilate surface chlorophyll data and determine regional variability in biogeochemical parameters for a simple ecosystem model. Gharamti et al. (2017a, b) used a modified approach to simultaneously estimate model parameters and state variable distributions to enable reasonably accurate ensemble predictions of modeled processes. These Kalman filter approaches are widely used in physical sciences for state estimation, reanalyses, and prediction purposes, although the data-assimilating state variable updates sacrifice true dynamical consistency. Meier et al. (2011) used dynamically consistent model ensembles generated from three different biogeochemical models forced with four climate projections and three different nutrient-loading scenarios to investigate increasing hypoxia in the Baltic Sea. Garnier et al. (2016) used a probabilistic version of the NEMO/PISCES model to generate a 60-member ensemble simulation of chlorophyll in the North Atlantic that accounts for uncertainties in biogeochemical parameters and sub-grid-scale processes. Gal et al. (2014) conducted a single model ensemble approach similar to ours in which they perturbed the most sensitive parameters in their model to investigate whether trends associated with different nutrient-loading scenarios were consistent across the ensemble, although their approach did not use data assimilation to determine the different parameter values used. Nowicki et al. (2022), building on previous work in DeVries and Weber (2017), used satellite-observed net primary production and phytoplankton size distributions to force a simple steady-state euphotic-zone food web model coupled to an organic matter transport and transformation model. The combined modeling system includes 42 parameters that are optimized to minimize mismatch with a suite of observations using a quasi-Newton algorithm. By making different assumptions related to the incorporated field data and optimizing parameters for each set of assumptions, the authors developed an ensemble of 124 ecosystem realizations. Ramondenc et al. (2020) used the statistical model check engine to assimilate laboratory and in situ observations to probabilistically constrain parameters associated with scyphozoan growth and degrowth. Vervatis et al. (2021a, b) conducted a model ensemble study of the Bay of Biscay in which they perturbed the atmospheric forcing, physical ocean parameterization, and biogeochemical sources and sinks (although, in contrast to our model, they did not vary the parameters but rather incorporated a spatiotemporally varying perturbation that acted directly on sources and sinks including photosynthesis, death, and grazing without modification to parameters). They found that chlorophyll was most sensitive to changes in atmospheric forcing and also highlight that the ensemble results can lead to improved simulation of plankton functional types. Anugerahanti et al. (2018) conducted a model ensemble approach in which, rather than modifying parameter values, they modified the functional form of key transfer functions associated with nutrient uptake, grazing, and mortality while simulating chlorophyll, nutrients, and primary production at five time-series sites. They discovered that the model was especially sensitive to modifications to the grazing and mortality functions. A further study (Anugerahanti et al., 2020) simultaneously perturbed physical circulation fields and the biogeochemical model and found that results were most sensitive to variability in the biological model. The result of these ensemble approaches is a probabilistic estimate of model outputs that (hopefully) accurately reflects true uncertainty in the system. Our OEPMCMC approach, by utilizing field data to automate the choice of parameter sets to be used in the model ensemble, allows us to generate 1 million different dynamically consistent model realizations that each fit the available data, while simultaneously exploring different regions of the solution space with regard to uncertainties in all of the modeled parameters. We consider this to be a reasonable tradeoff for the increased computational expense of our approach (relative to the variational-adjoint or Kalman filter approaches), while noting that each approach has distinct advantages or disadvantages for different applications.
An additional novelty of our study is the variety of different data types assimilated into the model (30 different rate and standing stock measurement types). Most data-assimilating biogeochemical models only incorporate data associated with nutrients and/or surface chlorophyll and other remotely sensed parameters (e.g., Xiao and Friedrichs, 2014b; Mattern et al., 2014; Wang et al., 2012). The incorporation of multiple data types spanning trophic levels and biogeochemical processes is important to model validation, because models can often reasonably simulate time series of one particular variable, with unrealistic dynamics of associated trophic levels. Ciavatta et al. (2014) found that assimilation of light attenuation coefficient data improved model prediction of light attenuation coefficient data but did not improve model estimates of surface chlorophyll and even degraded model performance in some regions. Furthermore, assimilation of only noisy standing stock data can lead to model overfitting and inability to retrieve accurate model parameters, even in an idealized model (Löptien and Dietze, 2015). The few studies that have attempted to incorporate many measurement types have focused on nutrient and phytoplankton parameters. For instance, Kim et al. (2021) assimilated standing stock data associated with nine model compartments along with net primary production and bacterial production into a model of an Antarctic coastal ecosystem but incorporated no metazoan zooplankton data. In a model simulating three distinct open-ocean regions, Luo et al. (2010) incorporated only one zooplankton parameter (mesozooplankton biomass) amongst 17 assimilated data types, mostly associated with non-living compartments. By contrast, we incorporate an extensive suite of group-specific protistan grazing rate measurements and biomass and grazing rate measurements for each of our four metazoan zooplankton groups. While these provide realistic bounds within which zooplankton dynamics can vary, zooplankton parameters still remain among the least constrained parameters in our model due to the difficulty of making zooplankton rate measurements (e.g., the paucity of grazing measurement relative to net primary production) and the fact that most zooplankton measurements (derived from net tows) inherently integrate over broad depth ranges. The weak constraints on zooplankton processes are particularly important in light of multiple studies that have shown that even subtle changes in grazing formulations can fundamentally alter the biogeochemical behaviors of models (Sailley et al., 2015; Gentleman and Neuheimer, 2008; Schartau et al., 2017; Chenillat et al., 2021; Sailley et al., 2013; Prowe et al., 2012) and the crucial roles of metazoan zooplankton for multiple pathways of the BCP (Buitenhuis et al., 2006; Steinberg and Landry, 2017).
4.3 Future directions
We have highlighted some of the insight about the BCP that can be gleaned from our ensemble data-assimilation approach. However, as noted previously, there are many limitations associated with using a simplified one-dimensional physical framework, and indeed a large portion of our study goal was to set the stage for more advanced uses of NEMUROBCP and OEPMCMC. One obvious future step is to incorporate NEMUROBCP into three-dimensional circulation models. Although NEMUROBCP was originally written in MATLAB, we are currently adapting it to Fortran compatible with circulation models such as ROMS, HYCOM, and MITgcm. Three-dimensional NEMUROBCP simulations may take different forms. One approach would be to use different parameter sets from the data ensemble in independent model runs to conduct three-dimensional global biogeochemical model ensembles. Notably, our different parameter sets are equally supported by assimilated field data, yet some predict very different ecosystem states (e.g., they vary in relative proportion of large/small phytoplankton, in turnover times for biota, in partitioning of organic matter between the particulate and dissolved phase, etc.). This ensemble modeling approach would thus allow quantification of BCP uncertainties in four dimensions. An alternate approach would be to use parameter distributions from one-dimensional simulations as prior estimates of parameters for data assimilation in a three-dimensional model. These prior estimates of each parameter (and the parameter covariance matrix) could be incorporated into the cost function for many different data-assimilation approaches. Comparison to satellite-observed or in situ time-series data would add powerful additional constraints on parameter values.
Another future use of the ensemble approach would be to simulate the results of specific Lagrangian experiments. In the current study, we developed an ensemble of plausible parameter sets that could be used for global ensemble models in the future or as prior distributions for future studies, while also assessing the uncertainty in parameter values. These goals informed our decision to conduct a joint parameter estimation that simultaneously utilized data from all available experiments (rather than estimating different parameter values for each experiment or each region). To simulate ecosystem dynamics for a specific experiment as accurately as possible, one would need to treat initial conditions and boundary values as unknown values to be determined during the optimization procedure. As such, the cost function should formally be defined as a function of these unknown values: , where IC represents the initial conditions (all state variables, all depths), BV is the boundary values (i.e., values of the state variables at the bottom boundary of the model), F is the physical forcing, and P is the parameter set. While this introduces a large number of additional unknown variables to solve for, it also justifies use of a more stringent cost function (e.g., the likelihood function). Thus to use NEMUROBCP to model a specific Lagrangian experiment (e.g., time-varying conditions during the North Pacific EXPORTS Lagrangian study, Siegel et al., 2021), we recommend treating our results for estimated global ranges of parameters as prior values in a Bayesian analysis to simultaneously constrain IC, BV, F, and P for that Lagrangian experiment.
In the current study, we incorporated a broad suite of standing stock and rate measurements spanning nutrients, phytoplankton, zooplankton, and non-living organic matter, because our goal was to simultaneously constrain all parameters in the model while investigating overall uncertainty in model outputs. However, Loptien and Dietze (2015) noted that specific parameters and processes can be better constrained if only the most relevant type of data are included. We thus suggest that targeted choice of data types to assimilate could allow the use of OEPMCMC for investigation of specific processes that are difficult to directly measure in situ. For instance, zooplankton mortality at depth has been hypothesized to be a potentially important component of the BCP (Kelly et al., 2019; Hernández-León et al., 2019), but estimates of zooplankton mortality at depth are typically derived from either allometric relationships between zooplankton size and life span or estimates of mortality made in the upper ocean (Brett and Groves, 1979; Hirst and Kiørboe, 2002; Ohman and Hirche, 2001). By incorporating only the data sources that offer the most constraint on zooplankton parameters (e.g., biomass and grazing rates of each zooplankton group), it may be possible to better constrain the fraction of mortality occurring in the deep ocean.
NEMUROBCP was built off of the NEMURO family of models (Kishi et al., 2007), and here we only added extra state variables essential for modeling BCP pathways from the euphotic zone into the mesopelagic. There are, of course, multiple additional processes that are important to simulating marine biogeochemistry and the BCP that are currently absent. Some additional processes that we consider priorities and plan to implement in future versions of NEMUROBCP include variable stoichiometry of organic matter, N2 fixation, and additional realism in the microbial community. Elemental stoichiometry (e.g., C : N : P) can vary substantially between different organic pools and across the different BCP pathways (Hannides et al., 2009; Singh et al., 2015), is predicted to change as a result of ocean acidification and/or increased temperature and stratification (Oschlies et al., 2008; Riebesell et al., 2007), and can affect the balance between carbon sequestration and nutrient supply and regeneration, leading to potentially enhanced carbon sequestration and growing oxygen minimum zones in a future ocean (Michaels et al., 2001; Oschlies et al., 2008; Riebesell et al., 2007). Adding variable stoichiometry to NEMUROBCP is simple but will require the addition of state variables associated with each model compartment that is allowed to vary in its elemental ratios, with substantial added computational costs. N2 fixation is simultaneously a source of new production in the absence of upwelling and a process that can substantially alter elemental stoichiometry in the open ocean. It could be introduced to the model through a state variable(s) simulating diazotrophs (Hood et al., 2001) or through implicit parameterization (Ilyina et al., 2013). NEMUROBCP might also benefit from added realism in microbial dynamics. The roles of heterotrophic bacteria in particle remineralization are currently included implicitly in the model. Explicit simulation of bacterial biomass and processes such as colonization of particles, microbial hotspots on sinking particles, production of hydrolytic enzymes, quorum sensing, and predator–prey dynamics with protists have the potential to more accurately simulate feedbacks that affect remineralization length scales in the ocean (Robinson et al., 2010; Simon et al., 2002; Mislan et al., 2014). Additionally, the model currently includes only two phytoplankton, which were explicitly identified as diatoms and non-diatoms in this data-assimilation exercise. The latter category subsumes a wide variety of different phytoplankton taxa into a group with transfer functions designed to simulate picophytoplankton (especially cyanobacteria). It thus excludes the presence of mixotrophs, which are abundant and diverse bacterivores in the open ocean, can survive low-nutrient and low-light conditions by supplementing their nutritional budget with phagotrophy, and may have distinctly different biogeochemical roles due to their decreased reliance on dissolved nutrients (Stoecker et al., 2017; Jones, 2000).
The data-assimilation approach utilized here is a computationally feasible method for incorporating a diverse suite of in situ measurements to objectively define parameter sets for ensemble modeling of the BCP. The 30 data types assimilated in this study improve constraints on ecosystem dynamics. However, some parameters, especially those related to metazoan zooplankton, remain poorly constrained by available data, despite assimilation of eight data types explicitly representing metazoan zooplankton rates and standing stocks. This likely results from a combination of the inherently patchy nature of many mesozooplankton populations (i.e., high measurement uncertainty) and the vertically integrated nature of zooplankton net tows which obscures simple relationships between predator abundance, prey abundance, and grazing rates.
The three BCP pathways were spatiotemporally variable across four study regions. Despite a very simple physical framework, distinct patterns were identified. Active transport was only a dominant contributor to the BCP in the CRD, where simulations predicted it to be responsible for 20 %–40 % of export from the euphotic zone. Near the subtropical front of the Southern Ocean and in upwelling-influenced regions of the CCE, both gravitational flux and vertical mixing were important components of the BCP, with the relative importance of the two determined more by differences between parameter sets than by differences between the conditions experienced during specific Lagrangian experiments. In offshore oligotrophic regions of the CCE and the GoM > 80 % of export was usually attributable to gravitational flux, although mixing dominated in a few experiments.
Our ensemble approach highlights uncertainties around model estimates of the BCP that arise from imprecisely defined parameters. Indeed, variability in many aspects of the BCP is as large comparing different (realistic) parameter sets within a specific location as it is across regions as distinctly different as the oligotrophic GoM and coastal CCE. Notably, different realistic parameter sets from our ensembles predict very different export efficiencies (and hence magnitudes of the gravitational pump) despite similar net primary production. This suggests that model validation against net primary production (or sea surface chlorophyll) data is insufficient to validate model skill in simulating BCP variability. The explicit representation of thorium and nitrogen isotope dynamics in NEMUROBCP should aid in future model validation efforts.
The core NEMUROBCP code is available on GitHub at https://github.com/mstukel/NEMURO_BCP (Stukel, 2022a). The code necessary to run the objective ensemble parameterization procedure can be found at https://github.com/mstukel/OEP_MCMC_NEMURObcp (Stukel, 2022b).
Field data used in this paper are available on either the CCE LTER Datazoo repository (https://oceaninformatics.ucsd.edu/datazoo/catalogs/ccelter/datasets) or the Biological and Chemical Oceanography Data Management Office repository: https://www.bco-dmo.org/project/834957, https://www.bco-dmo.org/project/819488, and https://www.bco-dmo.org/project/754878. For ease of access the data are also included in Supplement Tables S2–S4. The data file containing all model outputs (from all ensembles) is too large to deposit but can be generated from the code on GitHub. A summarized version (every 1000th iteration) is included as Supplement Table S5, and summary statistics are given in Supplement Table S1, with the correlation and covariance matrices given in Supplement Table S6.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-19-3595-2022-supplement.
MRS developed NEMUROBCP model and performed the simulations. MD led SalpPOOP project. MRL led the BLOOFINZ and FluZIE projects. MRS prepared the manuscript with contributions from all co-authors.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the captains and crews of the R/Vs Melville, Revelle, Knorr, Thompson, Sikuliaq, and Tangaroa and the NOAA ship Nancy Foster. We are also grateful to our many collaborators in the CCE LTER, BLOOFINZ-GoM, CRD FluZIE, and SalpPOOP Projects, especially Mark Ohman, Karen Selph, Thomas Kelly, Ralf Goericke, Scott Nodder, Andres Gutierrez-Rodriguez, Jeff Krause, and Karl Safi. This proposal was funded by US National Science Foundation awards OCE1756610 and 1851347 to Michael R. Stukel; OCE-0826626 to Michael R. Landry; and OCE-0417616, OCE-1026607, OCE-1637632, and OCE-1614359 to the CCE LTER program. It was also funded by the National Oceanic and Atmospheric Administration's RESTORE program grant (project title: Effects of nitrogen sources and plankton food-web dynamics on habitat quality for the larvae of ABT in the GoM; under federal funding opportunity NOAA-NOSNCCOS-2017-2004875); by the Ministry for Business, Innovation and Employment (MBIE) of New Zealand; by NIWA core programs Coast and Oceans Food Webs (COES) and Ocean Flows (COOF); and by the Royal Society of New Zealand Marsden Fast-Start award to Moira Décima.
This research has been supported by the National Science Foundation (grant nos. OCE-1756610, OCE-1851347, OCE-0826626, OCE‐0417616, OCE‐1026607, OCE‐1637632, and OCE‐1614359) and the National Oceanic and Atmospheric Administration's RESTORE program grant (project title: Effects of nitrogen sources and plankton food-web dynamics on habitat quality for the larvae of ABT in the GoM; under federal funding opportunity grant no. NOAA-NOSNCCOS-2017-2004875); by the Ministry for Business, Innovation and Employment (MBIE) of New Zealand; by NIWA core programs Coast and Oceans Food Webs (COES) and Ocean Flows (COOF); and by the Royal Society of New Zealand Marsden Fast-Start award.
This paper was edited by Marilaure Grégoire and reviewed by Vassilios Vervatis and one anonymous referee.
Alldredge, A.: The carbon, nitrogen and mass content of marine snow as a function of aggregate size, Deep-Sea Res. Pt. I, 45, 529–541, 1998.
Alldredge, A. L.: Discarded appendicularian houses as sources of food, surface habitats, and particulate organic matter in planktonic environments, Limnol. Oceanogr., 21, 14–23, 1976.
Anderson, T. R.: Plankton functional type modelling: running before we can walk?, J. Plankton Res., 27, 1073–1081, https://doi.org/10.1093/plankt/fbi076, 2005.
Anderson, T. R., Hessen, D. O., Mitra, A., Mayor, D. J., and Yool, A.: Sensitivity of secondary production and export flux to choice of trophic transfer formulation in marine ecosystem models, J. Mar. Sys., 125, 41–53, https://doi.org/10.1016/j.jmarsys.2012.09.008, 2013.
Anugerahanti, P., Roy, S., and Haines, K.: A perturbed biogeochemistry model ensemble evaluated against in situ and satellite observations, Biogeosciences, 15, 6685–6711, https://doi.org/10.5194/bg-15-6685-2018, 2018.
Anugerahanti, P., Roy, S., and Haines, K.: Perturbed biology and physics signatures in a 1-D ocean biogeochemical model ensemble, Front. Mar. Sci., 7, 549, https://doi.org/10.3389/fmars.2020.00549, 2020.
Archibald, K. M., Siegel, D. A., and Doney, S. C.: Modeling the impact of zooplankton diel vertical migration on the carbon export flux of the biological pump, Global Biogeochem. Cy., 33, 181–199, 2019.
Bianchi, D., Stock, C., Galbraith, E. D., and Sarmiento, J. L.: Diel vertical migration: Ecological controls and impacts on the biological pump in a one-dimensional ocean model, Global Biogeochem. Cy., 27, 478–491, https://doi.org/10.1002/gbc.20031, 2013a.
Bianchi, D., Galbraith, E. D., Carozza, D. A., Mislan, K. A. S., and Stock, C. A.: Intensification of open-ocean oxygen depletion by vertically migrating animals, Nat. Geosci., 6, 545–548, https://doi.org/10.1038/ngeo1837, 2013b.
Boeuf, D., Edwards, B. R., Eppley, J. M., Hu, S. K., Poff, K. E., Romano, A. E., Caron, D. A., Karl, D. M., and DeLong, E. F.: Biological composition and microbial dynamics of sinking particulate organic matter at abyssal depths in the oligotrophic open ocean, P. Natl. Acad. Sci. USA, 116, 11824–11832, https://doi.org/10.1073/pnas.1903080116, 2019.
Bopp, L., Aumont, O., Cadule, P., Alvain, S., and Gehlen, M.: Response of diatoms distribution to global warming and potential implications: A global model study, Geophys. Res. Lett., 32, L19606, https://doi.org/10.1029/2005gl023653, 2005.
Boyd, P. W.: Toward quantifying the response of the oceans' biological pump to climate change, Front. Mar. Sci., 2, 77, https://doi.org/10.3389/fmars.2015.00077, 2015.
Boyd, P. W., Claustre, H., Levy, M., Siegel, D. A., and Weber, T.: Multi-faceted particle pumps drive carbon sequestration in the ocean, Nature, 568, 327–335, https://doi.org/10.1038/s41586-019-1098-2, 2019.
Brett, J. and Groves, T.: Physiological energetics, Fish Physiol., 8, 280–352, 1979.
Bruland, K. W. and Silver, M. W.: Sinking rates of fecal pellets from gelatinous zooplankton (salps, pteropods, doliolids), Mar. Biol., 63, 295–300, 1981.
Brzezinski, M. A., Krause, J. W., Bundy, R. M., Barbeau, K. A., Franks, P., Goericke, R., Landry, M. R., and Stukel, M. R.: Enhanced silica ballasting from iron stress sustains carbon export in a frontal zone within the California Current, J. Geophys. Res.-Ocean., 120, 4654–4669, https://doi.org/10.1002/2015jc010829, 2015.
Buesseler, K. O. and Boyd, P. W.: Shedding light on processes that control particle export and flux attenuation in the twilight zone of the open ocean, Limnol. Oceanogr., 54, 1210–1232, https://doi.org/10.4319/lo.2009.54.4.1210, 2009.
Buitenhuis, E., Le Quere, C., Aumont, O., Beaugrand, G., Bunker, A., Hirst, A., Ikeda, T., O'Brien, T., Piontkovski, S., and Straile, D.: Biogeochemical fluxes through mesozooplankton, Global Biogeochem. Cy., 20, GB2003, https://doi.org/10.1029/2005GB002511, 2006.
Burd, A., Buchan, A., Church, M., Landry, M., McDonnell, A., Passow, U., Steinberg, D., and Benway, H.: Towards a transformative understanding of the ocean's biological pump: Priorities for future research, Hyatt Place New Orleans, New Orleans, LA, 36 pp., 2016.
Burd, A. B. and Jackson, G. A.: Particle Aggregation, Annu. Rev. Mar. Sci., 1, 65–90, https://doi.org/10.1146/annurev.marine.010908.163904, 2009.
Carlson, C. A., Ducklow, H. W., and Michaels, A. F.: Annual flux of dissolved organic carbon from the euphotic zone in the northwestern Sargasso Sea, Nature, 371, 405–408, https://doi.org/10.1038/371405a0, 1994.
Cavan, E. L., Henson, S. A., Belcher, A., and Sanders, R.: Role of zooplankton in determining the efficiency of the biological carbon pump, Biogeosciences, 14, 177–186, https://doi.org/10.5194/bg-14-177-2017, 2017.
Chenillat, F., Rivière, P., and Ohman, M. D.: On the sensitivity of plankton ecosystem models to the formulation of zooplankton grazing, PloS one, 16, e0252033, https://doi.org/10.1371/journal.pone.0252033, 2021.
Ciavatta, S., Torres, R., Martinez-Vicente, V., Smyth, T., Dall'Olmo, G., Polimene, L., and Allen, J. I.: Assimilation of remotely-sensed optical properties to improve marine biogeochemistry modelling, Prog. Oceanogr., 127, 74–95, 2014.
Copin-Montégut, G. and Avril, B.: Vertical distribution and temporal variation of dissolved organic carbon in the North-Western Mediterranean Sea, Deep-Sea Res. Pt. I, 40, 1963–1972, https://doi.org/10.1016/0967-0637(93)90041-Z, 1993.
Décima, M., Landry, M. R., Stukel, M. R., Lopez-Lopez, L., and Krause, J. W.: Mesozooplankton biomass and grazing in the Costa Rica Dome: amplifying variability through the plankton food web, J. Plankton Res., 38, 317–330, https://doi.org/10.1093/plankt/fbv091, 2016.
Décima, M., Stukel, M. R., Nodder, S. D., Gutiérrez-Rodríguez, A., Selph, K. E., Lopes dos Santos, A., Safi, K., Kelly, T. B., Deans, F., Latasa, M., Gorbunov, M. Y., and Pinkerton, M.: Salp population-blooms drive 5-fold increases in carbon export flux, Nat. Commun., https://doi.org/10.1101/2022.02.07.479467, in review, 2022.
DeVries, T. and Weber, T.: The export and fate of organic matter in the ocean: New constraints from combining satellite and oceanographic tracer observations, Global Biogeochem. Cy., 31, 535–555, 2017.
Dietze, M. C., Lebauer, D. S., and Kooper, R.: On improving the communication between models and data, Plant, Cell Environ., 36, 1575–1585, 2013.
Doney, S. C., Lindsay, K., Caldeira, K., Campin, J. M., Drange, H., Dutay, J. C., Follows, M., Gao, Y., Gnanadesikan, A., Gruber, N., Ishida, A., Joos, F., Madec, G., Maier-Reimer, E., Marshall, J. C., Matear, R. J., Monfray, P., Mouchet, A., Najjar, R., Orr, J. C., Plattner, G. K., Sarmiento, J., Schlitzer, R., Slater, R., Totterdell, I. J., Weirig, M. F., Yamanaka, Y., and Yool, A.: Evaluating global ocean carbon models: The importance of realistic physics, Global Biogeochem. Cy., 18, GB3017, https://doi.org/10.1029/2003gb002150, 2004.
Doron, M., Brasseur, P., Brankart, J.-M., Losa, S. N., and Melet, A.: Stochastic estimation of biogeochemical parameters from Globcolour ocean colour satellite data in a North Atlantic 3D ocean coupled physical–biogeochemical model, J. Mar. Sys., 117, 81–95, 2013.
Ducklow, H. W., Steinberg, D. K., and Buesseler, K. O.: Upper ocean carbon export and the biological pump, Oceanography, 14, 50–58, 2001.
Dunne, J. P., Armstrong, R. A., Gnanadesikan, A., and Sarmiento, J. L.: Empirical and mechanistic models for the particle export ratio, Global Biogeochem. Cy., 19, GB4026, https://doi.org/10.1029/2004GB002390, 2005.
Dutkiewicz, S., Scott, J. R., and Follows, M.: Winners and losers: Ecological and biogeochemical changes in a warming ocean, Global Biogeochem. Cy., 27, 463–477, 2013.
Field, C. B., Behrenfeld, M. J., Randerson, J. T., and Falkowski, P.: Primary production of the biosphere: Integrating terrestrial and oceanic components, Science, 281, 237–240, 1998.
Follows, M. J. and Dutkiewicz, S.: Modeling Diverse Communities of Marine Microbes, Ann. Rev. Mar. Sci., 3, 427–451, https://doi.org/10.1146/annurev-marine-120709-142848, 2011.
Follows, M. J., Ito, T., and Dutkiewicz, S.: On the solution of the carbonate chemistry system in ocean biogeochemistry models, Ocean Model., 12, 290–301, https://doi.org/10.1016/j.ocemod.2005.05.004, 2006.
Ford, D., Key, S., McEwan, R., Totterdell, I., and Gehlen, M.: Marine Biogeochemical Modelling and Data Assimilation for Operational Forecasting, Reanalysis, and Climate Research, in: New Frontiers in Operational Oceanography, edited by: Chassignet, E., Pascual, A., Tintore, J., and Verron, J., GODAE OceanView, 625–652, https://doi.org/10.17125/gov2018.ch22, 2018.
Fowler, S. W. and Small, L. F.: Sinking rates of euphausiid fecal pellets, Limnol. Oceanogr., 17, 293–296, 1972.
Franks, P. J. S.: Planktonic ecosystem models: perplexing parameterizations and a failure to fail, J. Plankton Res., 31, 1299–1306, https://doi.org/10.1093/plankt/fbp069, 2009.
Freibott, A., Taylor, A. G., Selph, K. E., Liu, H., Zhang, W., and Landry, M. R.: Biomass and composition of protistan grazers and heterotrophic bacteria in the Costa Rica Dome during summer 2010, J. Plankton Res., 38, 230–243, https://doi.org/10.1093/plankt/fbv107, 2016.
Friedrichs, M. A. M., Dusenberry, J. A., Anderson, L. A., Armstrong, R. A., Chai, F., Christian, J. R., Doney, S. C., Dunne, J., Fujii, M., Hood, R., McGillicuddy, D. J., Moore, J. K., Schartau, M., Spitz, Y. H., and Wiggert, J. D.: Assessment of skill and portability in regional marine biogeochemical models: Role of multiple planktonic groups, J. Geophys. Res.-Ocean., 112, 22, C08001, https://doi.org/10.1029/2006jc003852, 2007.
Gal, G., Makler-Pick, V., and Shachar, N.: Dealing with uncertainty in ecosystem model scenarios: application of the single-model ensemble approach, Environ. Modell. Softw., 61, 360–370, 2014.
Gargett, A. and Garner, T.: Determining Thorpe scales from ship-lowered CTD density profiles, J. Atmos. Ocean. Tech., 25, 1657–1670, 2008.
Garnier, F., Brankart, J.-M., Brasseur, P., and Cosme, E.: Stochastic parameterizations of biogeochemical uncertainties in a NEMO/PISCES model for probabilistic comparisons with ocean color data, J. Mar. Sys., 155, 59–72, 2016.
Gentleman, W. C. and Neuheimer, A. B.: Functional responses and ecosystem dynamics: how clearance rates explain the influence of satiation, food-limitation and acclimation, J. Plankton Res., 30, 1215–1231, https://doi.org/10.1093/plankt/fbn078, 2008.
Gerard, T., Lamkin, J., Kelly, T. B., Knapp, A. N., Laiz-Carrión, R., Malca, E., Selph, K. E., Shiroza, A., Shropshire, T. A., Stukel, M. R., Swalethorp, R., Yingling, N., and Landry, M. R.: Bluefin Larvae in Oligotrophic Ocean Foodwebs, Investigations of Nutrients to Zooplankton: Overview of the BLOOFINZ-Gulf of Mexico program, J. Plankton Res., fbac038, https://doi.org/10.1093/plankt/fbac038, 2022.
Gharamti, M., Samuelsen, A., Bertino, L., Simon, E., Korosov, A., and Daewel, U.: Online tuning of ocean biogeochemical model parameters using ensemble estimation techniques: application to a one-dimensional model in the North Atlantic, J. Mar. Sys., 168, 1–16, 2017a.
Gharamti, M., Tjiputra, J., Bethke, I., Samuelsen, A., Skjelvan, I., Bentsen, M., and Bertino, L.: Ensemble data assimilation for ocean biogeochemical state and parameter estimation at different sites, Ocean Modell., 112, 65–89, 2017b.
Goericke, R.: The size structure of marine phytoplankton – What are the rules?, Cal. Coop. Ocean. Fish., 52, 198–204, 2011.
Guidi, L., Chaffron, S., Bittner, L., Eveillard, D., Larhlimi, A., Roux, S., Darzi, Y., Audic, S., Berline, L., Brum, J. R., Coelho, L. P., Espinoza, J. C. I., Malviya, S., Sunagawa, S., Dimier, C., Kandels-Lewis, S., Picheral, M., Poulain, J., Searson, S., Tara Oceans Consortium, C., Stemmann, L., Not, F., Hingamp, P., Speich, S., Follows, M., Karp-Boss, L., Boss, E., Ogata, H., Pesant, S., Weissenbach, J., Wincker, P., Acinas, S. G., Bork, P., de Vargas, C., Iudicone, D., Sullivan, M. B., Raes, J., Karsenti, E., Bowler, C., and Gorsky, G.: Plankton networks driving carbon export in the oligotrophic ocean, Nature, 532, 465–470, https://doi.org/10.1038/nature16942, 2016.
Hannides, C. C. S., Landry, M. R., Benitez-Nelson, C. R., Styles, R. M., Montoya, J. P., and Karl, D. M.: Export stoichiometry and migrant-mediated flux of phosphorus in the North Pacific Subtropical Gyre, Deep-Sea Res. Pt. I, 56, 73–88, https://doi.org/10.1016/j.dsr.2008.08.003, 2009.
Hansen, J. L. S., Kiorboe, T., and Alldredge, A. L.: Marine snow derived from abandoned larvacean houses: Sinking rates, particle content and mechanisms of aggregate formation, Mar. Ecol. Prog. Ser., 141, 205–215, https://doi.org/10.3354/meps141205, 1996.
Hauck, J., Volker, C., Wolf-Gladrow, D. A., Laufkotter, C., Vogt, M., Aumont, O., Bopp, L., Buitenhuis, E. T., Doney, S. C., Dunne, J., Gruber, N., Hashioka, T., John, J., Le Quere, C., Lima, I. D., Nakano, H., Seferian, R., and Totterdell, I.: On the Southern Ocean CO2 uptake and the role of the biological carbon pump in the 21st century, Global Biogeochem. Cy., 29, 1451–1470, https://doi.org/10.1002/2015gb005140, 2015.
Henson, S. A., Sanders, R., Madsen, E., Morris, P. J., Le Moigne, F., and Quartly, G. D.: A reduced estimate of the strength of the ocean's biological carbon pump, Geophys. Res. Lett., 38, L04606, https://doi.org/10.1029/2011GL046735, 2011.
Henson, S. A., Yool, A., and Sanders, R.: Variability in efficiency of particulate organic carbon export: A model study, Global Biogeochem. Cy., 29, 33–45, https://doi.org/10.1002/2014gb004965, 2015.
Henson, S. A., Laufkötter, C., Leung, S., Giering, S. L. C., Palevsky, H. I., and Cavan, E. L.: Uncertain response of ocean biological carbon export in a changing world, Nat. Geosci., 15, 248–254, https://doi.org/10.1038/s41561-022-00927-0, 2022.
Hernández-León, S., Olivar, M. P., Fernández de Puelles, M. L., Bode, A., Castellón, A., López-Pérez, C., Tuset, V. M., and González-Gordillo, J. I.: Zooplankton and Micronekton Active Flux Across the Tropical and Subtropical Atlantic Ocean, Front. Mar. Sci., 6, 535, https://doi.org/10.3389/fmars.2019.00535, 2019.
Hirst, A. and Kiørboe, T.: Mortality of marine planktonic copepods: global rates and patterns, Mar. Ecol. Prog. Ser., 230, 195–209, 2002.
Honjo, S., Manganini, S. J., Krishfield, R. A., and Francois, R.: Particulate organic carbon fluxes to the ocean interior and factors controlling the biological pump: A synthesis of global sediment trap programs since 1983, Prog. Oceanogr., 76, 217–285, https://doi.org/10.1016/j.pocean.2007.11.003, 2008.
Hood, R. R., Bates, N. R., Capone, D. G., and Olson, D. B.: Modeling the effect of nitrogen fixation on carbon and nitrogen fluxes at BATS, Deep-Sea Res. Pt. II, 48, 1609–1648, 2001.
Ilyina, T., Six, K. D., Segschneider, J., Maier-Reimer, E., Li, H., and Núñez-Riboni, I.: Global ocean biogeochemistry model HAMOCC: Model architecture and performance as component of the MPI-Earth system model in different CMIP5 experimental realizations, J. Adv. Model. Earth Syst., 5, 287–315, https://doi.org/10.1029/2012ms000178, 2013.
Jackson, G. A.: Effect of coagulation on a model planktonic food web, Deep-Sea Res. Pt. I, 48, 95–123, 2001.
Janjić, T., Bormann, N., Bocquet, M., Carton, J. A., Cohn, S. E., Dance, S. L., Losa, S. N., Nichols, N. K., Potthast, R., Waller, J. A., and Weston, P.: On the representation error in data assimilation, Q. J. Roy. Meteorol. Soc., 144, 1257–1278, https://doi.org/https://doi.org/10.1002/qj.3130, 2018.
Jones, R. I.: Mixotrophy in planktonic protists: an overview, Freshwater Biol., 45, 219–226, 2000.
Kahru, M., Goericke, R., Kelly, T. B., and Stukel, M. R.: Satellite estimation of carbon export by sinking particles in the California Current calibrated with sediment trap data, Deep-Sea Res. Pt. II, 173, 104639, https://doi.org/10.1016/j.dsr2.2019.104639, 2020.
Kaufman, D. E., Friedrichs, M. A. M., Hemmings, J. C. P., and Smith Jr., W. O.: Assimilating bio-optical glider data during a phytoplankton bloom in the southern Ross Sea, Biogeosciences, 15, 73–90, https://doi.org/10.5194/bg-15-73-2018, 2018.
Kelly, T. B., Davison, P. R., Goericke, R., Landry, M. R., Ohman, M. D., and Stukel, M. R.: The Importance of Mesozooplankton Diel Vertical Migration for Supporting a Mesopelagic Ecosystem, Front. Mar. Sci., 6, 508, https://doi.org/10.3389/fmars.2019.00508, 2019.
Kiko, R., Brandt, P., Christiansen, S., Faustmann, J., Kriest, I., Rodrigues, E., Schütte, F., and Hauss, H.: Zooplankton-Mediated Fluxes in the Eastern Tropical North Atlantic, Front. Mar. Sci., 7, 358, https://doi.org/10.3389/fmars.2020.00358, 2020.
Kim, H. H., Luo, Y.-W., Ducklow, H. W., Schofield, O. M., Steinberg, D. K., and Doney, S. C.: WAP-1D-VAR v1.0: development and evaluation of a one-dimensional variational data assimilation model for the marine ecosystem along the West Antarctic Peninsula, Geosci. Model Dev., 14, 4939–4975, https://doi.org/10.5194/gmd-14-4939-2021, 2021.
Kirchner, M.: Microbial colonization of copepod body surfaces and chitin degradation in the sea, Helgolander Meeresun., 49, 201–212, 1995.
Kishi, M. J., Kashiwai, M., Ware, D. M., Megrey, B. A., Eslinger, D. L., Werner, F. E., Noguchi-Aita, M., Azumaya, T., Fujii, M., Hashimoto, S., Huang, D. J., Iizumi, H., Ishida, Y., Kang, S., Kantakov, G. A., Kim, H. C., Komatsu, K., Navrotsky, V. V., Smith, S. L., Tadokoro, K., Tsuda, A., Yamamura, O., Yamanaka, Y., Yokouchi, K., Yoshie, N., Zhang, J., Zuenko, Y. I., and Zvalinsky, V. I.: NEMURO – a lower trophic level model for the North Pacific marine ecosystem, Ecol. Model., 202, 12–25, https://doi.org/10.1016/j.ecolmodel.2006.08.021, 2007.
Kishi, M. J., Ito, S.-I., Megrey, B. A., Rose, K. A., and Werner, F. E.: A review of the NEMURO and NEMURO.FISH models and their application to marine ecosystem investigations, J. Oceanogr., 67, 3–16, 2011.
Knapp, A. N., Thomas, R. K., Stukel, M. R., Kelly, T. B., Landry, M. R., Selph, K. E., Malca, E., Gerard, T., and Lamkin, J.: Constraining the sources of nitrogen fueling export production in the Gulf of Mexico using nitrogen isotope budgets, J. Plankton Res., fbab049, https://doi.org/10.1093/plankt/fbab049, 2021.
Kranz, S. A., Wang, S., Kelly, T. B., Stukel, M. R., Goericke, R., Landry, M. R., and Cassar, N.: Lagrangian Studies of Marine Production: A Multimethod Assessment of Productivity Relationships in the California Current Ecosystem Upwelling Region, J. Geophys. Res.-Ocean., 125, e2019JC015984, https://doi.org/10.1029/2019jc015984, 2020.
Krause, J. W., Brzezinski, M. A., Goericke, R., Landry, M. R., Ohman, M. D., Stukel, M. R., and Taylor, A. G.: Variability in diatom contributions to biomass, organic matter production and export across a frontal gradient in the California Current Ecosystem, J. Geophys. Res.-Ocean., 120, 1032–1047, https://doi.org/10.1002/2014jc010472, 2015.
Krause, J. W., Stukel, M. R., Taylor, A. G., Taniguchi, D. A., De Verneil, A., and Landry, M. R.: Net biogenic silica production and the contribution of diatoms to new production and organic matter export in the Costa Rica Dome ecosystem, J. Plankton Res., 38, 216–229, https://doi.org/10.1093/plankt/fbv077, 2016.
Kriest, I., Sauerland, V., Khatiwala, S., Srivastav, A., and Oschlies, A.: Calibrating a global three-dimensional biogeochemical ocean model (MOPS-1.0), Geosci. Model Dev., 10, 127–154, https://doi.org/10.5194/gmd-10-127-2017, 2017.
Kwon, E. Y., Primeau, F., and Sarmiento, J. L.: The impact of remineralization depth on the air-sea carbon balance, Nat. Geosci., 2, 630–635, https://doi.org/10.1038/NGEO612, 2009.
Landry, M. R. and Swalethorp, R.: Mesozooplankton biomass, grazing and trophic structure in the bluefin tuna spawning area of the oceanic Gulf of Mexico, J. Plankton Res., fbab008, https://doi.org/10.1093/plankt/fbab008, 2021.
Landry, M. R., Ohman, M. D., Goericke, R., Stukel, M. R., and Tsyrklevich, K.: Lagrangian studies of phytoplankton growth and grazing relationships in a coastal upwelling ecosystem off Southern California, Prog. Oceanogr., 83, 208–216, https://doi.org/10.1016/j.pocean.2009.07.026, 2009.
Landry, M. R., Selph, K. E., Taylor, A. G., Décima, M., Balch, W. M., and Bidigare, R. R.: Phytoplankton growth, grazing and production balances in the HNLC equatorial Pacific, Deep-Sea Res. Pt. II, 58, 524-535, 2011.
Landry, M. R., De Verneil, A., Goes, J. I., and Moffett, J. W.: Plankton dynamics and biogeochemical fluxes in the Costa Rica Dome: introduction to the CRD Flux and Zinc Experiments, J. Plankton Res., 38, 167–182, https://doi.org/10.1093/plankt/fbv103, 2016a.
Landry, M. R., Selph, K. E., Decima, M., Gutierrez-Rodriquez, A., Stukel, M. R., Taylor, A. G., and Pasulka, A. L.: Phytoplankton production and grazing balances in the Costa Rica Dome, J. Plankton Res., 38, 366–379, https://doi.org/10.1093/plankt/fbv089, 2016b.
Landry, M. R., Selph, K. E., Stukel, M. R., Swalethorp, R., Kelly, T. B., Beatty, J. L., and Quackenbush, C. R.: Microbial food web dynamics in the oceanic Gulf of Mexico, J. Plankton Res., fbab021, https://doi.org/10.1093/plankt/fbab021, 2021.
Laws, E. A. and Maiti, K.: The relationship between primary production and export production in the ocean: Effects of time lags and temporal variability, Deep-Sea Res. Pt. I, 148, 100–107, https://doi.org/10.1016/j.dsr.2019.05.006, 2019.
Laws, E. A., Falkowski, P. G., Smith, W. O., Ducklow, H., and McCarthy, J. J.: Temperature effects on export production in the open ocean, Global Biogeochem. Cy., 14, 1231–1246, 2000.
Laws, E. A., D'Sa, E., and Naik, P.: Simple equations to estimate ratios of new or export production to total production from satellite-derived estimates of sea surface temperature and primary production, Limnol. Oceanogr. Meth., 9, 593–601, https://doi.org/10.4319/lom.2011.9.593, 2011.
Lawson, L. M., Spitz, Y. H., Hofmann, E. E., and Long, R. B.: A Data Assimilation Technique Applied to a Predator-Prey Model, Bull. Mathemat. Biol., 57, 593–617, 1995.
Lebrato, M., Mendes, P. D., Steinberg, D. K., Cartes, J. E., Jones, B. M., Birsa, L. M., Benavides, R., and Oschlies, A.: Jelly biomass sinking speed reveals a fast carbon export mechanism, Limnol. Oceanogr., 58, 1113–1122, https://doi.org/10.4319/lo.2013.58.3.1113, 2013.
Levy, M., Bopp, L., Karleskind, P., Resplandy, L., Ethe, C., and Pinsard, F.: Physical pathways for carbon transfers between the surface mixed layer and the ocean interior, Global Biogeochem. Cy., 27, 1001–1012, https://doi.org/10.1002/gbc.20092, 2013.
Li, Q. P., Franks, P. J. S., Landry, M. R., Goericke, R., and Taylor, A. G.: Modeling phytoplankton growth rates and chlorophyll to carbon ratios in California coastal and pelagic ecosystems, J. Geophys. Res.-Biogeo., 115, G04003, https://doi.org/10.29/2009JG001111, 2010.
Llort, J., Langlais, C., Matear, R., Moreau, S., Lenton, A., and Strutton, P. G.: Evaluating Southern Ocean Carbon Eddy-Pump From Biogeochemical-Argo Floats, J. Geophys. Res.-Ocean., 123, 971–984, https://doi.org/10.1002/2017jc012861, 2018.
Longhurst, A. R., Bedo, A. W., Harrison, W. G., Head, E. J. H., and Sameoto, D. D.: Vertical flux of respiratory carbon by oceanic diel migrant biota, Deep-Sea Res., 37, 685–694, 1990.
Löptien, U. and Dietze, H.: Constraining parameters in marine pelagic ecosystem models – is it actually feasible with typical observations of standing stocks?, Ocean Sci., 11, 573–590, https://doi.org/10.5194/os-11-573-2015, 2015.
Luo, Y. W., Friedrichs, M. A. M., Doney, S. C., Church, M. J., and Ducklow, H. W.: Oceanic heterotrophic bacterial nutrition by semilabile DOM as revealed by data assimilative modeling, Aquat. Microb. Ecol., 60, 273–287, https://doi.org/10.3354/ame01427, 2010.
Marsay, C. M., Sanders, R. J., Henson, S. A., Pabortsava, K., Achterberg, E. P., and Lampitt, R. S.: Attenuation of sinking particulate organic carbon flux through the mesopelagic ocean, P. Natl. Acad. Sci. USA, 112, 1089–1094, https://doi.org/10.1073/pnas.1415311112, 2015.
Martin, J. H., Knauer, G. A., Karl, D. M., and Broenkow, W. W.: Vertex: carbon cycling in the northeast Pacific, Deep-Sea Res., 34, 267–285, 1987.
Mattern, J. P. and Edwards, C. A.: A Simple Finite Difference-Based Approximation for Biogeochemical Tangent Linear and Adjoint Models, J. Geophys. Res.-Ocean., 124, 4–26, 2019.
Mattern, J. P., Fennel, K., and Dowd, M.: Periodic time-dependent parameters improving forecasting abilities of biological ocean models, Geophys. Res. Lett., 41, 6848–6854, https://doi.org/10.1002/2014gl061178, 2014.
Mattern, J. P., Song, H., Edwards, C. A., Moore, A. M., and Fiechter, J.: Data assimilation of physical and chlorophyll a observations in the California Current System using two biogeochemical models, Ocean Model., 109, 55–71, 2017.
Meier, H. M., Andersson, H. C., Eilola, K., Gustafsson, B. G., Kuznetsov, I., Müller-Karulis, B., Neumann, T., and Savchuk, O. P.: Hypoxia in future climates: A model ensemble study for the Baltic Sea, Geophys. Res. Lett., 38, L24608, https://doi.org/10.1029/2011GL049929, 2011.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of state calculations by fast computing machines, J. Chem. Phys., 21, 1087–1092, 1953.
Michaels, A. F., Karl, D. M., and Capone, D. G.: Element stoichiometry, new production and nitrogen fixation, Oceanogr. Soc., 14, 68–77, 2001.
Mislan, K. A. S., Stock, C. A., Dunne, J. P., and Sarmiento, J. L.: Group behavior among model bacteria influences particulate carbon remineralization depths, J. Mar. Res., 72, 183–218, https://doi.org/10.1357/002224014814901985, 2014.
Morrow, R. M., Ohman, M. D., Goericke, R., Kelly, T. B., Stephens, B. M., and Stukel, M. R.: Primary Productivity, Mesozooplankton Grazing, and the Biological Pump in the California Current Ecosystem: Variability and Response to El Niño, Deep-Sea Res. Pt. I, 140, 52–62, https://doi.org/10.1016/j.dsr.2018.07.012, 2018.
Nowicki, M., DeVries, T., and Siegel, D. A.: Quantifying the Carbon Export and Sequestration Pathways of the Ocean's Biological Carbon Pump, Global Biogeochem. Cy., 36, e2021GB007083, https://doi.org/10.1029/2021GB007083, 2022.
Ohman, M. D. and Hirche, H. J.: Density-dependent mortality in an oceanic copepod population, Nature, 412, 638–641, 2001.
Ohman, M. D., Barbeau, K., Franks, P. J. S., Goericke, R., Landry, M. R., and Miller, A. J.: Ecological Transitions in a Coastal Upwelling Ecosystem, Oceanography, 26, 210–219, 2013.
Omand, M. M., D'Asaro, E. A., Lee, C. M., Perry, M. J., Briggs, N., Cetinić, I., and Mahadevan, A.: Eddy-driven subduction exports particulate organic carbon from the spring bloom, Science, 348, 222–225, https://doi.org/10.1126/science.1260062, 2015.
Oschlies, A.: On the use of data assimilation in biogeochemical modelling, Ocean Weather Forecasting: An Integrated View of Oceanography, Springer, Dordrecht, 525–547, https://doi.org/10.1007/1-4020-4028-8_24, 2006.
Oschlies, A., Schulz, K. G., Riebesell, U., and Schmittner, A.: Simulated 21st century's increase in oceanic suboxia by CO2-enhanced biotic carbon export, Global Biogeochem. Cy., 22, GB4008, https://doi.org/10.1029/2007gb003147, 2008.
Owens, S. A., Buesseler, K. O., and Sims, K. W. W.: Re-evaluating the 238U-salinity relationship in seawater: Implications for the 238U-234Th disequilibrium method, Mar. Chem., 127, 31–39, https://doi.org/10.1016/j.marchem.2011.07.005, 2011.
Parekh, P., Follows, M. J., Dutkiewicz, S., and Ito, T.: Physical and biological regulation of the soft tissue carbon pump, Paleoceanography, 21, Pa3001, https://doi.org/10.1029/2005pa001258, 2006.
Passow, U., Alldredge, A. L., and Logan, B. E.: The role of particulate carbohydrate exudates in the flocculation of diatom blooms, Deep-Sea Res. Pt. I, 41, 335–357, 1994.
Plattner, G. K., Gruber, N., Frenzel, H., and McWilliams, J. C.: Decoupling marine export production from new production, Geophys. Res. Lett., 32, L11612, https://doi.org/10.1029/2005GL022660, 2005.
Poulsen, L. K. and Kiorboe, T.: Coprophagy and coprorhexy in the copepods Acartia tonsa and Temora longicornis: clearance rates and feeding behaviour, Mar. Ecol. Prog. Ser., 299, 217–227, 2005.
Preston, C. M., Durkin, C. A., and Yamahara, K. M.: DNA metabarcoding reveals organisms contributing to particulate matter flux to abyssal depths in the North East Pacific ocean, Deep-Sea Res. Pt. II, 173, 104708, https://doi.org/10.1016/j.dsr2.2019.104708, 2019.
Prowe, A. F., Pahlow, M., Dutkiewicz, S., Follows, M., and Oschlies, A.: Top-down control of marine phytoplankton diversity in a global ecosystem model, Prog. Oceanogr., 101, 1–13, 2012.
Ramondenc, S., Eveillard, D., Guidi, L., Lombard, F., and Delahaye, B.: Probabilistic modeling to estimate jellyfish ecophysiological properties and size distributions, Sci. Rep., 10, 1–13, 2020.
Resplandy, L., Martin, A. P., Le Moigne, F., Martin, P., Aquilina, A., Memery, L., Levy, M., and Sanders, R.: How does dynamical spatial variability impact 234Th-derived estimates of organic export?, Deep-Sea Res. Pt. I, 68, 24–45, https://doi.org/10.1016/j.dsr.2012.05.015, 2012.
Resplandy, L., Lévy, M., and Mcgillicuddy, D. J.: Effects of eddy-driven subduction on ocean biological carbon pump, Global Biogeochem. Cy., 33, 1071–1084, https://doi.org/10.1029/2018GB006125, 2019.
Riebesell, U., Schulz, K. G., Bellerby, R. G. J., Botros, M., Fritsche, P., Meyerhofer, M., Neill, C., Nondal, G., Oschlies, A., Wohlers, J., and Zollner, E.: Enhanced biological carbon consumption in a high CO2 ocean, Nature, 450, 545–548, https://doi.org/10.1038/nature06267, 2007.
Robinson, C., Steinberg, D. K., Anderson, T. R., Arístegui, J., Carlson, C. A., Frost, J. R., Ghiglione, J.-F., Hernández-León, S., Jackson, G. A., Koppelmann, R., Quéguiner, B., Ragueneau, O., Rassoulzadegan, F., Robison, B. H., Tamburini, C., Tanaka, T., Wishner, K. F., and Zhang, J.: Mesopelagic zone ecology and biogeochemistry – a synthesis, Deep-Sea Res. Pt. II, 57, 1504–1518, https://doi.org/10.1016/j.dsr2.2010.02.018, 2010.
Sailley, S. F., Vogt, M., Doney, S. C., Aita, M. N., Bopp, L., Buitenhuis, E. T., Hashioka, T., Lima, I., Le Quere, C., and Yamanaka, Y.: Comparing food web structures and dynamics across a suite of global marine ecosystem models, Ecol. Model., 261, 43–57, https://doi.org/10.1016/j.ecolmodel.2013.04.006, 2013.
Sailley, S. F., Polimene, L., Mitra, A., Atkinson, A., and Allen, J. I.: Impact of zooplankton food selectivity on plankton dynamics and nutrient cycling, J. Plankton Res., 37, 519–529, 2015.
Saito, M. A., Rocap, G., and Moffett, J. W.: Production of cobalt binding ligands in a Synechococcus feature at the Costa Rica upwelling dome, Limnol. Oceanogr., 50, 279–290, 2005.
Schartau, M., Oschlies, A., and Willebrand, J.: Parameter estimates of a zero-dimensional ecosystem model applying the adjoint method, Deep-Sea Res. Pt. II, 48, 1769–1800, https://doi.org/10.1016/s0967-0645(00)00161-2, 2001.
Schartau, M., Wallhead, P., Hemmings, J., Löptien, U., Kriest, I., Krishna, S., Ward, B. A., Slawig, T., and Oschlies, A.: Reviews and syntheses: parameter identification in marine planktonic ecosystem modelling, Biogeosciences, 14, 1647–1701, https://doi.org/10.5194/bg-14-1647-2017, 2017.
Schlitzer, R.: Applying the adjoint method for biogeochemical modeling: export of particulate organic matter in the world ocean, Geophys. Monogr., 114, 107–124, 2000.
Schlitzer, R.: Carbon export fluxes in the Southern Ocean: results from inverse modeling and comparison with satellite-based estimates, Deep-Sea Res. Pt. II, 49, 1623–1644, 2002.
Schlitzer, R.: Export production in the equatorial and North Pacific derived from dissolved oxygen, nutrient and carbon data, J. Oceanogr., 60, 53–62, https://doi.org/10.1023/B:JOCE.0000038318.38916.e6, 2004.
Schlunegger, S., Rodgers, K. B., Sarmiento, J. L., Frölicher, T. L., Dunne, J. P., Ishii, M., and Slater, R.: Emergence of anthropogenic signals in the ocean carbon cycle, Nat. Clim. Change, 9, 719–725, 2019.
Selph, K. E., Swalethorp, R., Stukel, M. R., Kelly, T. B., Knapp, A. N., Fleming, K., Hernandez, T., and Landry, M. R.: Phytoplankton community composition and biomass in the oligotrophic Gulf of Mexico, J. Plankton Res., fbab006, https://doi.org/10.1093/plankt/fbab006, 2021.
Shen, C., Shi, H., Liu, Y., Li, F., and Ding, D.: Discussion of skill improvement in marine ecosystem dynamic models based on parameter optimization and skill assessment, Chin. J. Oceanol. Limn., 34, 683–696, 2016.
Shropshire, T. A., Morey, S. L., Chassignet, E. P., Bozec, A., Coles, V. J., Landry, M. R., Swalethorp, R., Zapfe, G., and Stukel, M. R.: Quantifying spatiotemporal variability in zooplankton dynamics in the Gulf of Mexico with a physical-biogeochemical model, Biogeosciences, 17, 3385–3407, https://doi.org/10.5194/bg-17-3385-2020, 2020.
Siegel, D. A., Buesseler, K. O., Doney, S. C., Sailley, S. F., Behrenfeld, M. J., and Boyd, P. W.: Global assessment of ocean carbon export by combining satellite obervations and food-web models, Global Biogeochem. Cy., 28, 181–196, https://doi.org/10.1002/2013GB004743, 2014.
Siegel, D. A., Buesseler, K. O., Behrenfeld, M. J., Benitez-Nelson, C. R., Boss, E., Brzezinski, M. A., Burd, A., Carlson, C. A., D'Asaro, E. A., and Doney, S. C.: Prediction of the export and fate of global ocean net primary production: the EXPORTS science plan, Front. Mar. Sci., 3, 22, https://doi.org/10.3389/fmars.2016.00022, 2016.
Siegel, D. A., Cetinić, I., Graff, J. R., Lee, C. M., Nelson, N., Perry, M. J., Ramos, I. S., Steinberg, D. K., Buesseler, K., and Hamme, R.: An operational overview of the EXport Processes in the Ocean from RemoTe Sensing (EXPORTS) Northeast Pacific field deployment, Elementa Science of the Anthropocene, 9, 00107, https://doi.org/10.1525/elementa.2020.00107, 2021.
Simon, M., Grossart, H. P., Schweitzer, B., and Ploug, H.: Microbial ecology of organic aggregates in aquatic ecosystems, Aquat. Microb. Ecol., 28, 175–211, 2002.
Singh, A., Baer, S. E., Riebesell, U., Martiny, A. C., and Lomas, M. W.: C : N : P stoichiometry at the Bermuda Atlantic Time-series Study station in the North Atlantic Ocean, Biogeosciences, 12, 6389–6403, https://doi.org/10.5194/bg-12-6389-2015, 2015.
Small, L. F., Fowler, S. W., and Unlu, M. Y.: Sinking rates of natural copepod fecal pellets, Mar. Biol., 51, 233–241, 1979.
Smayda, T. J.: The suspension and sinking of phytoplankton in the sea, Oceanogr. Mar. Biol. Ann. Rev., 8, 353–414, 1970.
Steinberg, D. K. and Landry, M. R.: Zooplankton and the ocean carbon cycle, Annu. Rev. Mar. Sci., 9, 413–444, 2017.
Steinberg, D. K., Carlson, C. A., Bates, N. R., Goldthwait, S. A., Madin, L. P., and Michaels, A. F.: Zooplankton vertical migration and the active transport of dissolved organic and inorganic carbon in the Sargasso Sea, Deep-Sea Res. Pt. I, 47, 137–158, 2000.
Steinberg, D. K., Van Mooy, B. A. S., Buesseler, K. O., Boyd, P. W., Kobari, T., and Karl, D. M.: Bacterial vs. zooplankton control of sinking particle flux in the ocean's twilight zone, Limnol. Oceanogr., 53, 1327–1338, https://doi.org/10.4319/lo.2008.53.4.1327, 2008.
Stephens, B., Porrachia, M., Dovel, S., Roadman, M., Goericke, R., and Aluwihare, L.: Non-sinking organic matter production in the California Current, Global Biogeochem. Cy., 32, 1386–1405, https://doi.org/10.1029/2018GB005930, 2018.
Stoecker, D. K., Hansen, P. J., Caron, D. A., and Mitra, A.: Mixotrophy in the Marine Plankton, Annu. Rev. Mar. Sci., 9, 311–335, 2017.
Stukel, M. R. and Ducklow, H. W.: Stirring up the biological pump: Vertical mixing and carbon export in the Southern Ocean, Global Biogeochem. Cy., 31, 1420–1434, https://doi.org/10.1002/2017GB005652, 2017.
Stukel, M. R., Décima, M., Selph, K. E., Taniguchi, D. A. A., and Landry, M. R.: The role of Synechococcus in vertical flux in the Costa Rica upwelling dome, Prog. Oceanogr., 112/113, 49–59, https://doi.org/10.1016/j.pocean.2013.04.003, 2013.
Stukel, M. R., Kahru, M., Benitez-Nelson, C. R., Decima, M., Goericke, R., Landry, M. R., and Ohman, M. D.: Using Lagrangian-based process studies to test satellite algorithms of vertical carbon flux in the eastern North Pacific Ocean, J. Geophys. Res.-Ocean., 120, 7208–7222, https://doi.org/10.1002/2015JC011264, 2015.
Stukel, M. R., Benitez-Nelson, C., Décima, M., Taylor, A. G., Buchwald, C., and Landry, M. R.: The biological pump in the Costa Rica Dome: An open ocean upwelling system with high new production and low export, J. Plankton Res., 38, 348–365, https://doi.org/10.1093/plankt/fbv097, 2016.
Stukel, M. R., Aluwihare, L. I., Barbeau, K. A., Chekalyuk, A. M., Goericke, R., Miller, A. J., Ohman, M. D., Ruacho, A., Song, H., Stephens, B. M., and Landry, M. R.: Mesoscale ocean fronts enhance carbon export due to gravitational sinking and subduction, P. Natl. Acad. Sci. USA, 114, 1252–1257, https://doi.org/10.1073/pnas.1609435114, 2017.
Stukel, M. R., Décima, M., and Kelly, T. B.: A new approach for incorporating 15N isotopic data into linear inverse ecosystem models with Markov Chain Monte Carlo sampling, PloS one, 13, e0199123, https://doi.org/10.1371/journal.pone.0199123, 2018a.
Stukel, M. R., Song, H., Goericke, R., and Miller, A. J.: The role of subduction and gravitational sinking in particle export, carbon sequestration, and the remineralization length scale in the California Current Ecosystem, Limnol. Oceanogr., 63, 363–383, https://doi.org/10.1002/lno.10636, 2018b.
Stukel, M. R., Ohman, M. D., Kelly, T. B., and Biard, T.: The roles of suspension-feeding and flux-feeding zooplankton as gatekeepers of particle flux into the mesopelagic ocean, Front. Mar. Sci., 6, 397, https://doi.org/10.3389/fmars.2019.00397, 2019a.
Stukel, M. R., Kelly, T. B., Aluwihare, L. I., Barbeau, K. A., Goericke, R., Krause, J. W., Landry, M. R., and Ohman, M. D.: The Carbon: 234Thorium ratios of sinking particles in the California Current Ecosystem 1: Relationships with plankton ecosystem dynamics, Mar. Chem., 212, 1–15, https://doi.org/10.1016/j.marchem.2019.01.003, 2019b.
Stukel, M. R., Kelly, T. B., Landry, M. R., Selph, K. E., and Swalethorp, R.: Sinking carbon, nitrogen, and pigment flux within and beneath the euphotic zone in the oligotrophic, open-ocean Gulf of Mexico, J. Plankton Res., fbab001, https://doi.org/10.1093/plankt/fbab001, 2021.
Stukel, M. R.: NEMURO_bcp Code, Zenodo [code], https://doi.org/10.5281/zenodo.6928851, 2022a.
Stukel, M. R.: OEP_MCMC_NEMURObcp Code, Zenodo [code], https://doi.org/10.5281/zenodo.6928875, 2022b.
Taylor, A. G., Goericke, R., Landry, M. R., Selph, K. E., Wick, D. A., and Roadman, M. J.: Sharp gradients in phytoplankton community structure across a frontal zone in the California Current Ecosystem, J. Plankton Res., 34, 778–789, https://doi.org/10.1093/plankt/fbs036, 2012.
Taylor, A. G., Landry, M. R., Freibott, A., Selph, K. E., and Gutierrez-Rodriguez, A.: Patterns of microbial community biomass, composition and HPLC diagnostic pigments in the Costa Rica upwelling dome, J. Plankton Res., 34, 778–789, https://doi.org/10.1093/plankt/fbv086, 2016.
Turner, J. T.: Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump, Prog. Oceanogr., 130, 205–248, https://doi.org/10.1016/j.pocean.2014.08.005, 2015.
Valencia, B., Stukel, M. R., Allen, A. E., McCrow, J. P., Rabines, A., Palenik, B., and Landry, M. R.: Relating sinking and suspended microbial communities in the California Current Ecosystem: digestion resistance and the contributions of phytoplankton taxa to export, Environ. Microbiol., 23, 6734–6748, https://doi.org/10.1111/1462-2920.15736, 2021.
Vervatis, V. D., De Mey-Frémaux, P., Ayoub, N., Karagiorgos, J., Ciavatta, S., Brewin, R. J., and Sofianos, S.: Assessment of a regional physical–biogeochemical stochastic ocean model, Part 2: Empirical consistency, Ocean Model., 160, 101770, https://doi.org/10.1016/j.ocemod.2021.101770, 2021a.
Vervatis, V. D., De Mey-Frémaux, P., Ayoub, N., Karagiorgos, J., Ghantous, M., Kailas, M., Testut, C.-E., and Sofianos, S.: Assessment of a regional physical–biogeochemical stochastic ocean model, Part 1: Ensemble generation, Ocean Model., 160, 101781, https://doi.org/10.1016/j.ocemod.2021.101781, 2021b.
Volk, T. and Hoffert, M. I.: Ocean carbon pumps: Analysis of relative strengths and efficiencies in ocean-driven atmospheric CO2 changes, in: The Carbon Cycle and Atmospheric CO2: Natural Variations Archean to Present, edited by: Sundquist, E. T., and Broeker, W. S., American Geophysical Union, Washington, DC, 99–110, https://doi.org/10.1029/GM032p0099, 1985.
Wang, C. H., Li, X. Y., and Lv, X. Q.: Adjoint Assimilation of SeaWiFS data into a Marine Ecosystem Dynamical Model of the Bohai Sea and the North Yellow Sea, 18th Biennial Isem Conference on Ecological Modelling for Global Change and Coupled Human and Natural System, Procedia Environmental Sciences, 13, 2045–2061, https://doi.org/10.1016/j.proenv.2012.01.195, 2012.
Ward, B. A., Schartau, M., Oschlies, A., Martin, A. P., Follows, M. J., and Anderson, T. R.: When is a biogeochemical model too complex? Objective model reduction and selection for North Atlantic time-series sites, Prog. Oceanogr., 116, 49–65, https://doi.org/10.1016/j.pocean.2013.06.002, 2013.
Xiao, Y. and Friedrichs, M. A. M.: Using biogeochemical data assimilation to assess the relative skill of multiple ecosystem models in the Mid-Atlantic Bight: effects of increasing the complexity of the planktonic food web, Biogeosciences, 11, 3015–3030, https://doi.org/10.5194/bg-11-3015-2014, 2014a.
Xiao, Y. J. and Friedrichs, M. A. M.: The assimilation of satellite-derived data into a one-dimensional lower trophic level marine ecosystem model, J. Geophys. Res.-Ocean., 119, 2691–2712, https://doi.org/10.1002/2013jc009433, 2014b.
Yamamoto, A., Abe-Ouchi, A., and Yamanaka, Y.: Long-term response of oceanic carbon uptake to global warming via physical and biological pumps, Biogeosciences, 15, 4163–4180, https://doi.org/10.5194/bg-15-4163-2018, 2018.
Yingling, N., Kelly, T. B., Selph, K. E., Landry, M. R., Knapp, A. N., Kranz, S. A., and Stukel, M. R.: Taxon-specific phytoplankton growth, nutrient limitation, and light limitation in the oligotrophic Gulf of Mexico, J. Plankton Res., fbab028, https://doi.org/10.1093/plankt/fbab028, 2021.
Yoshie, N., Yamanaka, Y., Rose, K. A., Eslinger, D. L., Ware, D. M., and Kishi, M. J.: Parameter sensitivity study of the NEMURO lower trophic level marine ecosystem model, Ecol. Model., 202, 26–37, https://doi.org/10.1016/j.ecolmodel.2006.07.043, 2007.
Yoshikawa, C., Yamanaka, Y., and Nakatsuka, T.: An Ecosystem Model Including Nitrogen Isotopes: Perspectives on a Study of the Marine Nitrogen Cycle, J. Oceanogr., 61, 921–942, https://doi.org/10.1007/s10872-006-0010-5, 2005.