A robust initialization method for accurate soil organic carbon simulations

Changes in soil organic carbon (SOC) stocks are a major source of uncertainty for the evolution of atmospheric CO₂ concentration during the 21st century. They are usually simulated by models dividing SOC into conceptual pools with contrasted turnover times. The lack of reliable methods to initialize these models, by correctly distributing soil carbon amongst their kinetic pools, strongly limits the accuracy of their simulations. Here, we demonstrate that PARTY_SOC, a machine-learning model based on Rock-Eval^® thermal analysis, optimally partitions the active- and stable-SOC pools of AMG, a simple and well-validated SOC dynamics model, accounting for effects of soil management history. Furthermore, we found that initializing the SOC pool sizes of AMG using machine learning strongly improves its accuracy when reproducing the observed SOC dynamics in nine independent French long-term agricultural experiments. Our results indicate that multi-compartmental models of SOC dynamics combined with a robust initialization can simulate observed SOC stock changes with excellent precision. We recommend exploring their potential before a new generation of models of greater complexity becomes operational. The approach proposed here can be easily implemented on soil monitoring networks, paving the way towards precise predictions of SOC stock changes over the next decades.

1 Introduction

Soil organic carbon (SOC) plays an important role in sustaining soil functions and associated soil ecosystem services worldwide (IPCC, 2019). It is the largest terrestrial organic carbon reservoir, with the upper 2 m of soil storing 2400 Pg C, 3 times more carbon than the atmosphere (Jobbagy and Jackson, 2000). A mere 4 per 1000 annual decrease in SOC stocks (ca. 10 Pg C yr⁻¹) may double the global annual anthropogenic CO₂ emissions, while an equivalent increase may compensate them (Balesdent and Arrouays, 1999). This is the concept behind the 4 per 1000 initiative (Rumpel et al., 2018) that aims at increasing SOC stocks to fight global warming while ensuring food security, two Sustainable Development Goals of the United Nations (UN General Assembly, 2015). This initiative and other political headway have put the question of managing SOC stocks and assessing the global SOC sequestration potential at the top of political and scientific agendas (Vermeulen et al., 2019; FAO, 2019; Amelung et al., 2020). Despite this particular attention, the prediction of SOC stock changes remains very uncertain, which makes soils a major source of uncertainty for the evolution of atmospheric CO₂ concentration (Todd-Brown et al., 2014; He et al., 2016; Shi et al., 2018).

Models of SOC dynamics can predict future SOC stock evolution by simulating carbon transfer into the soil mostly through plant organic matter inputs and microbial SOC mineralization resulting in a CO₂ flux from the soil to the atmosphere. They can have structures of various complexities, reflecting our mechanistic understanding of SOC dynamics (Shi et al., 2018; Luo et al., 2016). However, most models dedicated to prediction, including those used in Earth system models, have a simple structure dividing SOC into conceptual pools with contrasted turnover times (Manzoni and Porporato, 2009; He et al., 2016; Todd-Brown et al., 2014). These multi-compartmental models of SOC dynamics are the best option we currently have to foster science-based SOC preservation and sequestration actions, given the strong uncertainty of more complex models (Cécillon, 2021a; Dangal et al., 2021; Lee et al., 2020; Shi et al., 2018; Crowther et al., 2019). Predictions of SOC stock evolution provided by such simple models are very sensitive to the initial distribution of SOC amongst the different kinetic pools (Luo et al., 2016; Smith and Falloon, 2000; Clivot et al., 2019). This makes the question of partitioning of SOC kinetic pools a priority for improving the accuracy of multi-compartmental SOC dynamics models (Luo et al., 2016; Taghizadeh-Toosi et al., 2020).

The most commonly used method to initialize the size of SOC kinetic pools is to run spin-up simulations until a steady-state equilibrium for SOC is reached, eventually matching the initial SOC stock measurement (Wutzler and Reichstein, 2007; Taghizadeh-Toosi et al., 2020). However, this method has two well-known limitations. First, climatic SOC input and land-use or land-cover data extending over long time periods required by this approach are highly uncertain. Second, assuming steady-state equilibrium for SOC at the onset of model simulations is often unrealistic. This is due to the history of the simulated sites that often includes disturbances (e.g. fire), as well as previous changes in climate, land use, and soil management that prevent SOC pools with slow turnover times from being at equilibrium (Wutzler and Reichstein, 2007; Herbst et al., 2018; Oberholzer et al., 2014; Poeplau et al., 2011; Clivot et al., 2019). Alternative initialization procedures are needed to address these issues (Wutzler and Reichstein, 2007; Bruun and Jensen, 2002; Taghizadeh-Toosi et al., 2020).

In some models of SOC dynamics, like the AMG model (Clivot et al., 2019), a default initial SOC pool size distribution is prescribed according to basic information on land-use history (i.e. long-term cropland vs. long-term grassland; Clivot et al., 2019). This approach does not take into account the effect of recent changes in land use or historical soil management practices on SOC pool distribution. To better reflect the effect of the frequent state of non-equilibrium of SOC on its partitioning into conceptual kinetic pools, another approach has been proposed, relating results from SOC fractionation methods with SOC kinetic pool sizes (e.g. Zimmermann et al., 2007a, or Skjemstad et al., 2004, for the RothC – Rothamsted carbon – model; Dangal et al., 2021, for the DAYCENT – Daily Century – model). However, this approach also suffers from important drawbacks. First, SOC fractionation procedures are tedious and cannot be implemented on large-scale studies, though this problem may be solved by using soil infrared spectroscopy or environmental variables and machine learning (Zimmermann et al., 2007b; Viscarra Rossel et al., 2019; Sanderman et al., 2021; Cotrufo et al., 2019; Lugato et al., 2021; Baldock et al., 2013; Barthès et al., 2008; Lee et al., 2020; Dangal et al., 2021). Second, their reproducibility is questionable (Poeplau et al., 2013, 2018), and third, their use of initializing model SOC pool sizes has never been properly validated. A proper validation would require showing that (1) the size of measured SOC fractions matches the one of model kinetic pools and that (2) simulations of SOC dynamics are more accurate using this initialization strategy, compared to default simulations (on independent validation sites while other model parameters remain constant). Reasonably good correspondence between measured or soil-spectroscopy-estimated SOC fractions and modelled SOC conceptual pools has been reported in a number of studies, though with some notable discrepancies (Leifeld et al., 2009b; Herbst et al., 2018; Zimmermann et al., 2007a; Dangal et al., 2021). Conversely, the studies that attempted to initialize model SOC pool sizes using a SOC fractionation scheme generally reported no improvement in the accuracy of simulations of SOC dynamics compared to a default or a spin-up initialization approach (Leifeld et al., 2009a; Nemo et al., 2016; Cagnarini et al., 2019). Only two studies showed that an initialization based on an SOC fractionation scheme yielded more accurate simulations of observed SOC dynamics, but this was at the cost of modifying the decomposition rate of SOC kinetic pools (Skjemstad et al., 2004; Luo et al., 2014).

An alternative approach using Rock-Eval^® thermal analysis has recently been proposed – under the name of the PARTY_SOC model – to estimate SOC kinetic pool sizes (Cécillon et al., 2018, 2021). PARTY_SOC is a machine-learning model trained on Rock-Eval^® data of soil samples from long-term experiments (LTEs) where the size of the centennially stable-SOC fraction can be estimated (e.g. sites including a bare fallow treatment). PARTY_SOC incorporates recent key elements of the new understanding of SOC dynamics (Dignac et al., 2017), showing that the centennially stable-SOC fraction has specific chemical and energetic characteristics that are measurable quickly (ca. 1 h per sample) and at a reasonable cost (less than USD 60) using Rock-Eval^®; it is thermally stable (i.e. high activation energy), and it is depleted in hydrogen (Barré et al., 2016; Hemingway et al., 2019; Gregorich et al., 2015; Poeplau et al., 2019; Chassé et al., 2021).

In this study, we tested if the PARTY_SOC machine-learning model, built on a totally independent dataset from north-western Europe, could be used to initialize the distribution of SOC pools of the simple AMG model (Clivot et al., 2019) and improve the accuracy of its simulations. The default version of AMG is currently the most accurate model for reproducing the observed SOC stock dynamics in diverse French agricultural LTEs at the pluri-decadal scale (Martin et al., 2019). The efficient use of this model at sites covering an important pedological and climatic variability (including oceanic, continental, and tropical climate) provides further support to its robustness (Levavasseur et al., 2020; Farina et al., 2021; Saffih-Hdadi and Mary, 2008). In this model, SOC is simply divided into two pools, the “stable SOC (C_S)” that is considered inert at the timescale of the simulation and the “active SOC (C_A)” that has a mean turnover time of a few decades. A recent study (Clivot et al., 2019) determined that the optimal initial proportion of stable SOC (C_S $/$ C₀) can deviate from the model's default value (0.65 in croplands) so that a more precise initialization of the C_S $/$ C₀ proportion would significantly improve AMG simulations of SOC dynamics. Here, we hypothesized that the SOC pool partitioning as determined by the PARTY_SOC machine-learning model (Cécillon et al., 2021, 2018) would be close to the mathematically optimal one for the AMG model, therefore, improving the accuracy of its SOC dynamics simulations compared to default initialization. We tested our hypothesis on 32 treatments from 9 independent French agricultural LTEs (experiment duration from 12 to 41 years with a median of 21 years) in which the AMG-optimal SOC pool partitioning could be determined by ex post optimization and for which topsoil samples collected at the onset of the experiment were available (Table 1). These LTEs were croplands established in different pedoclimates that have experienced contrasted soil management practices and land-use histories. All available initial topsoil samples were analysed with Rock-Eval^®, and the results were used in the European version of the PARTY_SOC model, PARTY_SOCv2.0_EU (Cécillon et al., 2021), to compute the centennially stable-SOC proportion of each topsoil sample.

2 Materials and methods

2.1 Experimental sites

This work was conducted on nine French agricultural LTEs (Supplement Fig. S1); s 7 LTEs including 29 treatments were selected from the dataset presented in Clivot et al. (2019), from sites with available initial topsoil samples. Two additional LTEs (Colmar and Feucherolles) including a total of three treatments were obtained from the dataset published in Levavasseur et al. (2020), selecting control treatments without organic amendments and with available initial topsoil samples. Basic site and topsoil characteristics are reported in Table 1 and Supplement Table S1. Information necessary to run AMG simulations on a total of 32 treatments (initial soil physicochemical properties, detailed information on management practices, and observed climatic data during all experiments) were obtained from Clivot et al. (2019) for the 29 treatments of the 7 sites and from Levavasseur et al. (2020) for the 3 treatments of the sites of Colmar and Feucherolles.

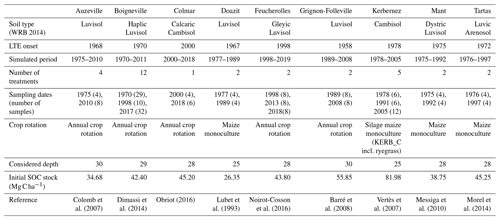
Table 1 Main information about the nine French agricultural long-term experiments used in this study. All sites had been croplands for at least 20 years before the onset of all experiments. Additional site information including climatic variability amongst sites and long-term history of land cover is provided in Supplement Table S1. WRB: World Reference Base.

2.2 Archive soil samples from experimental sites

Our final soil sample set included 181 topsoil samples. At each site the soil was sampled to include the whole ploughing depth (Table 1). At all sites, except Boigneville where the soil was sampled in five sublayers, the ploughing layer was sampled as one homogeneous layer. Of the final samples, 71 were from starting dates of the 9 LTEs; 24 were from LTEs intermediate dates; and 86 were from LTEs final dates. All samples were air-dried or dried at 40 ^∘C, sieved to <2 mm, and finely ground to <250 µm using a ball mill (Retsch, Germany).

2.3 Rock-Eval^® analysis of archive soil samples

All soil samples were analysed using a Rock-Eval 6^® Turbo apparatus (Vinci Technologies). The samples were first pyrolysed in an inert N₂ atmosphere, then oxidized under ambient air (O₂). The heating routine applied during pyrolysis was as described in Disnar et al. (2003), starting with a 3 min isotherm at 200 ^∘C followed by a heating ramp of 30 ^∘C min⁻¹ up to 650 ^∘C. For the oxidation step, a 1 min isotherm was kept at 300 ^∘C and was directly followed by a heating ramp of 20 ^∘C min⁻¹ until 850 ^∘C was reached, followed by a 5 min isotherm at 850 ^∘C (Baudin et al., 2015; adapted from Behar et al., 2001).

Based on 5 generated Rock-Eval^® thermograms, 18 parameters were calculated for each sample and were then used as predictors by the random forest model. These include total organic carbon (TOC; in g C per kg soil) – the amount of organic C released during the analysis as a proportion of sample weight; pyrolysed organic carbon (PC; in g C per kg soil) – the sum of C released as HC, CO, and CO₂ during the pyrolysis step; the ratio of PC to TOC ($\mathrm{PC}/\mathrm{TOC}$); the S2 peak area (g C per kg soil) – the hydrocarbon gas released within the range of the pyrolysis temperature ramp; the ratio of S2 to PC ($\mathrm{S}\mathrm{2}/\mathrm{PC}$); the PseudoS1 peak area (g C per kg soil) – the sum of C released as HC, CO, and CO₂ during the first 200 s of pyrolysis (after Khedim et al., 2021); the hydrogen index (HI; in mg HC g TOC⁻¹) – the amount of hydrocarbons released as a ratio of TOC; and the ratio of HI to the oxygen index ($\mathrm{HI}/\mathrm{OI}$_RE6) – where OI_RE6 is calculated as the amount of oxygen released as CO and CO₂ gases normalized to TOC. Finally, various temperature parameters (T70_{HC_PYR}, T90_{HC_PYR}, T30_{CO2_PYR}, T50_{CO2_PYR}, T70_{CO2_PYR}, T90_{CO2_PYR}, T70_{CO_OX}, T50_{CO2_OX}, T70_{CO2_OX}, and T90_{CO2_OX}; in ^∘C) are included in the predictor set. They describe evolution steps, namely at which temperature a specific amount (e.g. 30 %, 50 %, 70 %, or 90 %) of a given gas was released according to each thermogram (Cécillon et al., 2018). It is important to note that no pre-treatment of CaCO₃-containing samples was necessary before Rock-Eval^® analysis. The slow pyrolysis and oxidation steps of the Rock-Eval^® method allow for distinguishing carbon of organic and mineral form, since the latter is released above a given temperature. For the calculation of all of the above parameters, only the part of each thermogram corresponding to organic carbon was taken into account. For this purpose, upper temperature integration limits for Rock-Eval^® temperature parameters were set to 560 ^∘C for the CO and CO₂ pyrolysis thermograms and to 611 ^∘C for the CO₂ oxidation thermograms (Cécillon et al., 2018; Supplement Fig. S2). R scripts used for computing Rock-Eval^® parameters are available on the Zenodo platform (Cécillon, 2021b).

2.4 The PARTY_SOC machine-learning model

The most up-to-date European version of this model, calibrated on soils from north-western Europe, used in this study, is described in detail in Cécillon et al. (2021). This model uses the 18 above-mentioned Rock-Eval^® thermal analysis parameters as predictors and estimates the centennially stable-SOC proportion in a topsoil sample. The model consists of a trained non-parametric machine-learning algorithm, using the random forest approach to estimate centennially stable-SOC proportions in unknown topsoils from centred and scaled Rock-Eval^® parameters. In this study the obtained centennially stable-SOC proportion of each topsoil sample was converted to centennially stable-SOC content by multiplying the predicted proportion by the total SOC content. The PARTY_SOCv2.0_EU model, available on Zenodo (Cécillon, 2021b), was used without any adaptation.

2.5 The AMG model of soil organic carbon dynamics

The AMG model (Andriulo et al., 1999) was developed based on the two-compartment SOC model proposed by Hénin and Dupuis (1945). It is characterized by a simple structure consisting of three carbon pools: fresh organic matter and two SOC fractions, an active and a stable pool (Supplement Fig. S3). The model allows for the transfer of carbon from the fresh organic matter pool either to the atmosphere through microbial mineralization or into the active pool. Organic carbon from the active pool is also subject to mineralization, forming a second direct flux of CO₂ from the soil into the atmosphere. Soil organic matter (SOM) decomposition follows first-order kinetics with a rate defined by the coefficient of mineralization k (yr⁻¹), controlled by climatic conditions and soil characteristics. The h coefficient controls the yield of crop residue transformation into active carbon and depends on the type of fresh organic matter. No carbon exchange with the stable-SOC pool is possible, since it is considered inert and remains unchanged over the simulation period (here from 12 to 41 years; see Table 1). Considering the stable-SOC pool as mathematically inert at this timescale is in line with consistent observations of a significant pluri-decadal persistent SOC fraction in long-term bare fallows and C₃–C₄ vegetation change chronosequences (Barré et al., 2010; Balesdent et al., 2018).

The AMG model can be mathematically described by two simple equations (Clivot et al., 2019):

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{QC}={\mathrm{QC}}_{\mathrm{S}}+{\mathrm{QC}}_{\mathrm{A}},\text{(2)}& {\displaystyle \frac{{\mathrm{dQC}}_{\mathrm{A}}}{\mathrm{d}t}}={\sum }_i{m}_i{h}_i-k\cdot {\mathrm{QC}}_{\mathrm{A}},\end{array}$$

where QC is the total SOC stock (Mg C ha⁻¹), QC_S is the stable-SOC stock (Mg C ha⁻¹) defined as a fraction of the initial SOC stock QC₀ (see Sect. 2.6) constant for a specific treatment, QC_A is the active-SOC stock (Mg C ha⁻¹), t is the time in years, m_i is the annual C input from organic residue i (Mg C ha⁻¹ yr⁻¹), h is a coefficient representing the fraction of C inputs which is incorporated in SOM after 1 year related to the type of organic residue, and k is the mineralization rate constant associated with the active-C pool (yr⁻¹).

The AMG parameters (h and k) have been determined by experimental results (Clivot et al., 2019). This approach differs from most multi-compartmental SOC dynamics models for which decay rates of slower pools were calibrated indirectly, assuming an equilibrium state for SOC (Wutzler and Reichstein, 2007). The simple structure of the AMG model and the experimental determination of its decomposition rates make it less susceptible to the problem of equifinality compared to other multi-compartmental models of SOC dynamics (Clivot et al., 2019; Luo et al., 2016). Furthermore, AMG has been validated with δ¹³C tracer data of long-term alternative sequences of C₄ and C₃ crops (Mary et al., 2020).

The version of AMG used in this study was AMGv2, described in detail in Clivot et al. (2019). Input data necessary to run simulations of SOC stocks with AMG include crop type, annual crop yields, and information regarding management of crop residues. These are used to compute annual aboveground and belowground C inputs from plants, here according to the method proposed by Bolinder et al. (2007) and adapted by Clivot et al. (2019). The coefficient of mineralization k (yr⁻¹) is calculated according to soil characteristics (clay and carbonate contents, pH, and C:N ratio) and climatic conditions (mean annual temperature, precipitation, and potential evapotranspiration; Clivot et al., 2019).

2.6 Soil organic carbon pool partitioning in the AMG model

2.6.1 Default C_S $/$ C₀ initialization

Two default values can be used for initialization of the SOC pool distribution in AMG, depending on land-use history before the onset of simulations. The initial proportion of C_S $/$ C₀ equals 0.65 for sites with a long-term arable land-use history. Former long-term grassland sites are expected to have lower C_S $/$ C₀, and the value of 0.40 was used in previous studies (Saffih-Hdadi and Mary, 2008; Clivot et al., 2019). Since all sites used in this study had been under arable land for at least 20 years before the onset of the experiment, a default value of 0.65 was used.

2.6.2 PARTY_SOC-based initialization of C_S $/$ C₀

The PARTY_SOC-based initialization of C_S $/$ C₀ was derived from data obtained with Rock-Eval^® analysis of initial topsoil samples from each LTE. Here, C_S $/$ C₀ was estimated using the following simple four-step procedure: first, topsoil samples from the LTE's onset were analysed with Rock-Eval^®, and the 18 thermal parameters described in Sect. 2.3 were calculated for each sample. Second, the thermal parameters were used as input for the PARTY_SOC machine-learning model described in Sect. 2.4 which was run for this sample set resulting in a sample-specific prediction of the centennially stable-SOC proportion. Third, the obtained values were averaged per LTE. Fourth, the site mean of the centennially stable-SOC proportion was used (as C_S $/$ C₀) to initialize simulations of SOC stocks for the various treatments of every site (the site standard deviation is reported in Fig. 1 and in Supplement Table S2). Supported by the evident common land-use history shared by the multiple treatments of each site before the onset of simulations and because the SOC stocks and centennially stable-SOC contents were very homogeneous amongst each site, we also performed simulations of 17 treatments for which soil samples from the onset of the LTE were not available. In these cases, we considered that the C_S $/$ C₀ of the treatment was equal to the mean value of the respective site (Supplement Table S1 and S2).

2.6.3 Ex post optimization of C_S $/$ C₀

Following a least-squares optimization approach, the best fit of the AMG model on observed SOC stocks time series was obtained, and the optimal initial SOC pool partitioning (C_S $/$ C₀) was estimated accordingly for each site (Clivot et al., 2019). In sites with C₃–C₄ vegetation change chronosequences where δ¹³C long-term monitoring data were available, the model was adapted to simultaneously match the observed evolution of C, C₃, and C₄ stocks (Clivot et al., 2019) for a given treatment.

2.7 Calculation of the centennially stable-SOC content

The content of the centennially stable-SOC pool of each LTE at initial, intermediate, and final dates was estimated through multiplication of the PARTY_SOC estimates of the proportion of the centennially stable SOC at a given date by the corresponding total SOC content previously determined using elemental analysis (Clivot et al., 2019; Levavasseur et al., 2020). For example, for the onset of an LTE where t=0, C_S= C_S $/$ C₀ ⋅ C₀, where C_S is the stable-SOC content (g C per kg soil), and C₀ is the total SOC content (g C per kg soil) at time t=0.

2.8 Statistics

The fit between PARTY_SOC predictions of the centennially stable-SOC proportion and ex post AMG-optimized stable-SOC proportion was assessed by a linear regression model. The same approach was applied for the evaluation of the agreement between centennially stable-SOC content and ex post AMG-optimized stable-SOC content of initial samples. The evaluation of the performance of the AMG model, for the different SOC pool-partitioning initialization methods, was also based on simple linear regressions between simulated and observed SOC stock values. Statistical terms used to express the strength and the statistical significance of the relationships were the coefficient of determination (R²) and the associated probability value (p value). Prediction bias and model error were expressed as the mean difference (BIAS) and relative mean square error (RMSE). The relative root mean square error (RRMSE) and the normalized root mean square error (NRMSE) were used to compare the error of different datasets (with a different range of predictions) (Smith et al., 1996; Wallach, 2006; Otto et al., 2018).

$$\begin{array}{}\text{(3)}& {\displaystyle }{R}^{\mathrm{2}}={\left({\displaystyle \frac{{\sum }_{i=\mathrm{1}}^n\left(\left(O_i-\stackrel{\mathrm{‾}}{O}\right)\cdot \left(S_i-\stackrel{\mathrm{‾}}{S}\right)\right)}{\sqrt{\sum _{i=\mathrm{1}}^n{\left(O_i-\stackrel{\mathrm{‾}}{O}\right)}^{\mathrm{2}}}\cdot \sqrt{{\sum }_{i=\mathrm{1}}^n{\left(S_i-\stackrel{\mathrm{‾}}{S}\right)}^{\mathrm{2}}}}}\right)}^{\mathrm{2}},\text{(4)}& {\displaystyle }\mathrm{BIAS}={\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left(S_i-O_i\right),\text{(5)}& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n{\left(S_i-O_i\right)}^{\mathrm{2}}},\text{(6)}& {\displaystyle }\mathrm{RRMSE}={\displaystyle \frac{\mathrm{RMSE}}{\stackrel{\mathrm{‾}}{O}}},\text{(7)}& {\displaystyle }\mathrm{NRMSE}={\displaystyle \frac{\mathrm{RMSE}}{O_{\max }-O_{\min }}},\end{array}$$

where O and S are the observed and simulated values; n is the number of observations; $\stackrel{\mathrm{‾}}{O}$ and $\stackrel{\mathrm{‾}}{S}$ are the means of observations and simulations, respectively; and O_max and O_min are the maximum and the minimum value observed.

The observed and simulated total SOC stock change dQC was calculated as follows for each treatment:

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathrm{dQC}}_{\mathrm{obs}}={\mathrm{QC}}_{\mathrm{obs},t_{\mathrm{2}}}-{\mathrm{QC}}_{\mathrm{obs},t_{\mathrm{1}}},\text{(9)}& {\displaystyle }{\mathrm{dQC}}_{\mathrm{sim}}={\mathrm{QC}}_{\mathrm{sim},t_{\mathrm{2}}}-{\mathrm{QC}}_{\mathrm{obs},t_{\mathrm{1}}},\end{array}$$

where QC_obs is the observed SOC stock at time t, QC_sim is the SOC stock at time t simulated with AMG, and t₁ indicates the start and t₂ indicates the end of simulation period.

All data processing and statistical analyses were performed within the R programming environment (version 3.4.2) (R Core Team, 2017). For plotting, packages ggpmisc (Aphalo, 2016), reshape2 (Wickham, 2007), and ggplot2 (Wickham, 2016) were used.

3 Results

3.1 Accurate soil organic carbon pool partitioning

Centennially stable-SOC proportion values were predicted by the PARTY_SOC machine-learning model (Cécillon et al., 2021) using Rock-Eval^® data measured on initial topsoil samples. The mean value for each independent site was plotted against the stable SOC proportion as determined by ex post AMG optimization (Fig. 1). The initial centennially stable-SOC proportion values predicted with PARTY_SOC ranged from 0.44 to 0.74, with a mean value of 0.59, whereas ex post AMG-optimal estimations of stable-SOC proportion covered almost the same range, from 0.45 to 0.74, with a mean value of 0.61. The two approaches were strongly correlated (R²=0.63, significant at the p<0.05 level), with a linear regression slope close to 1 (a=0.9) and intercept close to 0 (b=0.04), showing an unbiased relationship between PARTY_SOC estimates of the centennially stable-SOC proportion and the ex post AMG-optimized stable-SOC proportion at the onset of the nine LTEs. Although a slight discrepancy was observed for higher stable-SOC proportion values, the results validate our hypothesis showing that the centennially stable-SOC proportion determined by Rock-Eval^® thermal analysis and the PARTY_SOC machine-learning model built on fully independent data provides a good estimate of the optimal stable-SOC proportion of the AMG model for unrelated French agricultural soils. When expressed as content (g C per kg soil), the fit between the PARTY_SOC predictions of the centennially stable SOC determined on initial topsoil samples and the ex post optimized stable-SOC content values was excellent (R²=0.95; Supplement Fig. S4; optimal stable-SOC content ranged from 4.37 to 12.75 g C per kg soil across the nine sites). Furthermore, the method appears to be reliable, since additional Rock-Eval^® measurements on topsoil samples from intermediate and final dates of the LTEs showed that the PARTY_SOC predictions of the centennially stable-SOC content remained remarkably constant during the experimental period at most sites (Supplement Fig. S5).

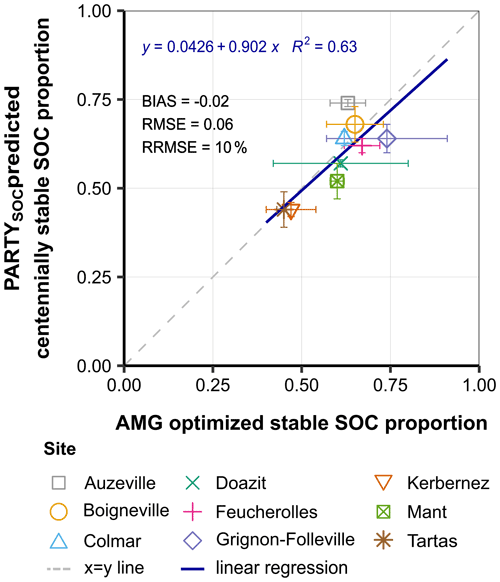
Figure 1 Performance of the PARTY_SOC model to predict the centennially stable-SOC proportion compared to the ex post AMG-optimized stable-SOC proportion. Points represent site-mean values based on initial topsoil samples from nine independent French long-term experiments. Statistics refer to the linear regression between x and y values (blue solid line). Horizontal error bars show the uncertainty associated with the AMG-optimal stable-SOC proportion, calculated as the standard deviation of treatment-wise AMG optimizations. Vertical error bars represent the prediction error of the centennially stable-SOC proportion values, calculated as the standard deviation of the PARTY_SOC model predictions on initial topsoil samples.

3.2 More accurate soil organic carbon simulations

In a second step, we investigated if a PARTY_SOC-based initialization of the SOC pool partitioning could improve the accuracy of SOC stock simulations of the AMG model. To do so, we compared SOC stock simulations obtained with three different initializations. We first ran AMG using the default initialization method for the SOC pool partitioning (C_S $/$ C₀ = 0.65, since all LTEs were under cropland for at least 2 decades before their onset; Table 1). Then, we ran AMG simulations using the PARTY_SOC-based initialization method by defining C_S $/$ C₀ as the site-mean centennially stable-SOC proportion determined by the PARTY_SOC model. Finally, we ran AMG using the ex post optimization method to initialize the SOC pool partitioning for each site. For all three initialization procedures, the simulated SOC stock change between the initial and last sampling date for each treatment of each site was plotted against the measured SOC stock change (Fig. 2a–c). Observed SOC stock change ranged from +6 to −24 Mg C ha⁻¹ for the 32 treatments. In spite of a rather good mean agreement (RMSE = 5.95 Mg C ha⁻¹), the AMG model initialized with the default procedure provided predictions of SOC stock change rather far from what was observed in two out of nine LTEs (Fig. 2a). Using the PARTY_SOC-based initialization method improved AMG simulations compared to the default method, bringing them much closer to the observed SOC stock changes (RMSE = 3.60 Mg C ha⁻¹; Fig. 2a, b). PARTY_SOC-based initialization of AMG resulted in unbiased simulations (BIAS = 0.06 Mg C ha⁻¹) and a strong decrease in the mean error of prediction. Unsurprisingly, AMG initialized using ex post optimized C_S $/$ C₀ proportions predicted SOC stock changes very close to the observed ones (RMSE = 2.12 Mg C ha⁻¹; Fig. 2c). AMG simulations from ex post optimized and PARTY_SOC-based initializations were remarkably comparable (Fig. 2b, c). The SOC stock simulations produced with AMG for each independent treatment are presented in Supplement Fig. S6.

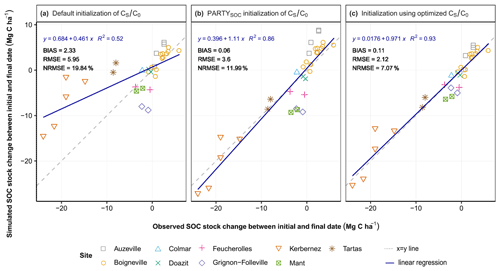
Figure 2 Observed vs. simulated change in SOC stocks between the initial and final date of 32 treatments from nine French long-term experiments. The three panels show the performance of the AMG model for three different initialization approaches. Initial SOC kinetic pool sizes were defined using (a) the default value for cropland (C_S $/$ C₀=0.65), (b) the centennially stable-SOC proportion predicted by the PARTY_SOC model, and (c) the ex post AMG-optimized C_S $/$ C₀ proportion. Statistics refer to the linear regression between x and y values (blue solid line). Points represent the values for the 32 treatments for which AMG simulations were run.

It is noteworthy that the PARTY_SOC-based initialization improved the fit between observed and simulated SOC stock change, compared to AMG default initialization, especially for treatments that experienced the greatest SOC stock loss (Fig. 2a, b). In treatments that experienced no SOC stock change or a slight increase in SOC stock, the PARTY_SOC-based initialization did not improve the simulations but resulted in highly reliable predictions, similarly to AMG default or optimized initialization methods (Fig. 2a–c). This is likely explained by the history of land cover and soil management practices of the different sites. Sites presenting treatments with no change or a slight increase in SOC stocks were predominantly sites with a long cropland history (e.g. site of Boigneville; Supplement Table S1), for which the default AMG C_S $/$ C₀ value of 0.65 is nearly optimal. Conversely, the two sites, Kerbernez and Tartas, where the ex post optimized C_S $/$ C₀ values were far below the default value (Fig. 1) have a more complex history of land use and soil management practices. The site of Kerbernez is former grassland (during the first half of the 20th century; Supplement Table S1) that was converted into cropland 2 decades before the implementation of its arable LTE, in 1958. The site of Tartas was cultivated for a longer time before the LTE onset; however it was turned to grassland for a period in the 19th century (Supplement Table S1) and received applications of poultry manure for several years before the LTE began. In these two sites, characterized by an AMG-optimal C_S $/$ C₀ much lower than the default value, the PARTY_SOC machine-learning model predicted values very close to the optimal C_S $/$ C₀ values (Fig. 1).

4 Discussion

Our study demonstrates that the PARTY_SOC method based on Rock-Eval^® thermal analysis (Cécillon et al., 2018, 2021) can estimate the initial SOC pool partitioning of the AMG model of SOC dynamics while improving its accuracy in a series of diverse and independent French LTEs. Contrary to previous studies (Skjemstad et al., 2004; Luo et al., 2014), no modifications of the decomposition rate of SOC kinetic pools were necessary to improve model predictions. The PARTY_SOC initialization method never severely affected the model simulations, while it strongly improved them at sites where SOC stocks were far from an equilibrium state due to historical changes in soil management or land use. Areas with past changes in land use and soil management represent a large yet poorly known part of arable land in France and Europe (Fuchs et al., 2015; Erb et al., 2017) where SOC stocks and slow-cycling SOC pools are far from equilibrium (Wutzler and Reichstein, 2007; Herbst et al., 2018; Clivot et al., 2019; Taghizadeh-Toosi et al., 2020). Therefore, by accounting for these legacy effects of site history on SOC pool partitioning, the PARTY_SOC-based initialization of the AMG model should result in more accurate simulations of SOC dynamics at a national or continental scale.

Our findings, combined with results reported in recent ensemble modelling studies (Martin et al., 2019; Farina et al., 2021), suggest that despite its simple structure and when properly initialized (e.g. using the PARTY_SOC model) the AMG model is unsurpassed for predicting observed SOC stock changes in French agricultural LTEs and is amongst the best available modelling frameworks of SOC dynamics in European arable land (Martin et al., 2019; Farina et al., 2021). Our results demonstrate that there is still potential to increase the accuracy of simple multi-compartmental models of SOC dynamics, bringing their simulations very close to the observed values of SOC stock changes. Developing other Rock-Eval^®-based initialization methods specifically designed to match the carbon pool design of other multi-compartmental SOC dynamics models such as RothC (Coleman et al., 1997) is a promising research area. More generally, we recommend that the potential of multi-compartmental SOC dynamics models be fully explored and exploited by soil biogeochemists before a new generation of models of increased complexity becomes operational. While new models including the diversity of microbial communities and related processes are emerging (Lehmann et al., 2020; Crowther et al., 2019), the uncertain structure and parametrization of more complex models is hindering their application as robust predictive tools (Shi et al., 2018). At the same time, simple conceptual models of SOC dynamics like AMG combined with novel initialization methods and data-based approaches such as PARTY_SOC show promising improvements (Cécillon, 2021a; Dangal et al., 2021; Lee et al., 2020). The low prediction error of the AMG model when its SOC pool distribution is initialized with the PARTY_SOC method even challenges the ability of more complex modelling approaches to achieve better performance, given the uncertainty on observed values of SOC stock changes (Schrumpf et al., 2011).

The continental or worldwide implementation of the AMG model with the PARTY_SOC-based initialization of SOC pools distribution will require additional work. First, the PARTY_SOC machine-learning model (Cécillon et al., 2018, 2021) will have to be validated on a wider range of pedoclimates. This method, initially built on LTEs coming from north-western Europe (Cécillon et al., 2018), has now been successfully extended to new soil types and a new climate (tropical; Cécillon et al., 2021). The good agreement between AMG-optimal stable-SOC proportion values and PARTY_SOC predictions reported here suggests that most agricultural LTEs with accurate AMG simulations could be used as reference sites for the PARTY_SOC model, lifting an important technical limitation to its geographical expansion (Cécillon et al., 2021). Second, the improved accuracy of model simulations using a PARTY_SOC-based initialization will also have to be demonstrated for a wider pedoclimatic range (i.e. worldwide LTEs; such as those referenced by the International Soil Carbon Network; Nave et al., 2015). Third, Rock-Eval^® data from the new application areas will be required. Rock-Eval^® is a high-throughput technique that is well adapted to the analysis of large soil sample sets provided by large-scale soil monitoring programmes. We recommend implementing Rock-Eval^® measurements in national and continental soil monitoring networks.

5 Conclusions

Combining Rock-Eval^® thermal analysis with the PARTY_SOC machine-learning model should be considered an emerging key approach with demonstrated ability to improve the accuracy of simulations of SOC dynamics, complementary to other SOC cycling proxies (Bailey et al., 2018; Wiesmeier et al., 2019). The progressive large-scale delivery of these complementary data related to SOC dynamics will strengthen model predictions of SOC stock changes at the national to global scale, necessary for implementing efficient climate change mitigation policies (FAO, 2020).