Single-species dinoflagellate cyst carbon isotope fractionation in core-top sediments: environmental controls, CO₂ dependency and proxy potential

Sedimentary bulk organic matter and various molecular organic components exhibit strong CO₂-dependent carbon isotope fractionation relative to dissolved inorganic carbon sources. This fractionation (ε_p) has been employed as a proxy for paleo-pCO₂. Yet, culture experiments indicate that CO₂-dependent ε_p is highly specific at genus and even species level, potentially hampering the use of bulk organic matter and non-species-specific organic compounds. In recent years, significant progress has been made towards a CO₂ proxy using controlled growth experiments with dinoflagellate species, also showing highly species-specific ε_p values. These values were, however, based on motile specimens, and it remains unknown whether these relations also hold for the organic-walled resting cysts (dinocysts) produced by these dinoflagellate species in their natural environment. We here analyze dinocysts isolated from core tops from the Atlantic Ocean and Mediterranean Sea, representing several species (Spiniferites elongatus, S. (cf.) ramosus, S. mirabilis, Operculodinium centrocarpum sensu Wall and Dale (1966) (hereafter referred to as O. centrocarpum) and Impagidinium aculeatum) using laser ablation–nano-combustion–gas-chromatography–isotope ratio mass spectrometry (LA/nC/GC-IRMS). We find that the dinocysts produced in the natural environment are all appreciably more ¹³C-depleted compared to the cultured motile dinoflagellate cells, implying higher overall ε_p values, and, moreover, exhibit large isotope variability. Where several species could be analyzed from a single location, we often record significant differences in isotopic variance and offsets in mean δ¹³C values between species, highlighting the importance of single-species carbon isotope analyses. The most geographically expanded dataset, based on O. centrocarpum, shows that ε_p correlates significantly with various environmental parameters. Importantly, O. centrocarpum shows a CO₂-dependent ε_p above ∼ 240 µatm pCO₂. Similar to other marine autotrophs, relative insensitivity at low pCO₂ is in line with active carbon-concentrating mechanisms at low pCO₂, although we here cannot fully exclude that we partly underestimated ε_p sensitivity at low pCO₂ values due to the relatively sparse sampling in that range. Finally, we use the relation between ε_p and pCO₂ in O. centrocarpum to propose a first pCO₂ proxy based on a single dinocyst species.

1 Introduction

Stable carbon isotope fractionation in marine autotrophs is governed for a large part by the carbon-fixing enzyme RuBisCO (e.g., Farquhar et al., 1989; Roeske and O'Leary, 1984), which implies most marine organic matter and therefore sedimentary marine organic matter is strongly ¹³C-depleted with respect to the dissolved inorganic carbon (DIC) source (CO₂ (aq), HCO${}_{\mathrm{3}}^{-}$ or CO${}_{\mathrm{3}}^{\mathrm{2}-}$), with the stable carbon isotope composition (δ¹³C) of organic matter ranging from −10 ‰ to −30 ‰ (Freeman and Hayes, 1992). While many groups of marine autotrophs show clear CO₂-dependent carbon isotope fractionation (ε_p), the exact relation strongly varies between marine phytoplankton groups, genera and cell morphologies (Popp et al., 1998; Boller et al., 2011, 2015; Brandenburg et al., 2022). Still, because of the assumed CO₂ dependency of RuBisCO fractionation, bulk marine organic matter and more specific organic compounds of marine autotrophs (e.g., lipids biomarkers) have been proposed and applied as pCO₂ proxies over the past decades (Freeman and Hayes, 1992; Naafs et al., 2016). The application of these pCO₂ proxies (e.g., Bijl et al., 2010; Pagani et al., 2011; Schoon et al., 2011; Witkowski et al., 2018) has provided constraints on past atmospheric pCO₂ and earth system sensitivity beyond the ice core record (e.g., Pagani et al., 2010; PALAEOSENS, 2012).

However, many of the organic compounds used for CO₂ reconstructions such as alkenones (e.g., Pagani, 2013), phytane (e.g., Witkowski et al., 2018), porphyrins (e.g., Freeman and Hayes, 1992) or bulk organic matter (e.g., Hayes et al., 1999) are not unique to a single species, genus and sometimes not even a group of organisms. This implies that reconstructions based on these compounds integrate interspecific differences in CO₂ dependency, which complicates the interpretation of such proxy records. Secondly, even if specific compounds derive from a single species or genus, they intrinsically derive from a multitude of individual organisms, differing in shape and size, affecting isotopic fractionation and hence limiting the accuracy of such CO₂ reconstructions.

Part of the uncertainties and biases in carbon isotope fractionation can be circumvented if the carbon isotopic fractionation of individual fossils can be analyzed. In recent years, significant progress has been made towards a CO₂ proxy based on the stable carbon isotope fractionation in organic walled dinoflagellate cysts (Burkhardt et al., 1999; Hoins et al., 2015, 2016a, b; Wilkes et al., 2017). A fraction (∼ 15 %) of modern dinoflagellates produces an organic resting cyst or dinocyst as an obligatory part of their lifecycle (Evitt, 1985). The organic resting cysts from autotrophic species have excellent preservation potential and are often highly oxidation-resistant (Zonneveld et al., 1997, 2019; Kodrans-Nsiah et al., 2008), and several ubiquitous extant genera and species, such as Spiniferites spp. and Operculodinium centrocarpum, have extremely long geological records (Fensome et al., 1996; Williams et al., 2004). The ecology and morphology of these long-ranging species seemingly remained unchanged for millions of years (Frieling and Sluijs, 2018). Most importantly, recent advances in methodology allow for analyses of species-specific single-cyst δ¹³C (van Roij et al., 2017; Sluijs et al., 2018). This presents the opportunity to quantify environmental controls on ε_p of individual dinoflagellate cysts and hence species to assess the potential to obtain more accurate paleo-pCO₂ estimates from sedimentary records.

Controlled growth experiments across a range of CO₂ levels representative of the last glacial (e.g., Barnola et al., 1987) and modern and future carbon emission scenarios (Eberlein et al., 2016; Hoins et al., 2016a, b, 2015; IPCC, 2014; Rost et al., 2006; Van de Waal et al., 2013; Wilkes et al., 2017) showed species-specific CO₂-dependent ε_p for multiple dinoflagellate species. From these, the species Protoceratium reticulatum and Gonyaulax spinifera (Hoins et al., 2015, 2016a, 2016b) are of particular interest as these produce the organic cyst species Operculodinium centrocarpum sensu Wall and Dale (1966), hereafter referred to as O. centrocarpum, and Spiniferites (cf.) ramosus, hereafter referred to as S. ramosus, respectively (Head, 1996; Zonneveld et al., 2013). These cyst species have their first occurrences in the geological records around ∼ 60 and 130 Ma (million years ago), for O. centrocarpum and S. ramosus, respectively (Williams et al., 2004), thus providing the potential for deep-time pCO₂ reconstructions.

Before ε_p values based on dinocysts can be used for reconstructing pCO₂, several fundamental questions need to be addressed. Although δ¹³C_DIC exerts a major control on dinocyst δ¹³C (Sluijs et al., 2018), it remains uncertain whether the CO₂ control on ε_p of motile cells from controlled growth experiments can be translated to their cysts formed in the natural environment. In addition, potential offsets in ε_p values between the motile cells and the cysts need to be established. This is especially important as the cell–cyst relations in carbon isotope ratios are not necessarily straightforward because bulk biomass such as cysts potentially deviates in δ¹³C values from the various cell components and potentially not by a constant offset (e.g., Freeman, 2001; Hayes, 2001; Pancost and Pagani, 2006; Schouten et al., 1998; Van de Waal et al., 2013; Wilkes et al., 2018).

We here present the first core-top data for single-species dinocysts to constrain the environmental controls on ε_p. We focus on the species O. centrocarpum and compare this data, when possible, to several species of Spiniferites (S. ramosus, S. mirabilis, S. elongatus) and Impagidinium aculeatum. The established environmental relations are subsequently evaluated using simple models converting carbon isotope fractionation in dinocysts into pCO₂ values for the surface waters.

2 Materials and methods

2.1 Materials

The primary dataset is based on 34 core-top samples (Table 1, Fig. 1), collected from the North Atlantic Ocean and Mediterranean Sea, with a secondary dataset based on pre-industrial sample material spanning ∼ 0–1500 common era (CE) from ENAM9606 for the North Atlantic (Richter et al., 2009). The core-top samples encompass a substantial natural pCO₂ (aq) gradient because the rate of cooling of the North Atlantic Current exceeds that of CO₂ uptake, whereas pCO₂ in the Mediterranean is close to or slightly above equilibrium with the atmosphere. Sample selection is further based on the dinocyst occurrence maps of Zonneveld et al. (2013), including only samples with an expected relative abundance of at least 10 %–20 % of the target species. Similarly, the coverage of environmental parameters such as sea surface temperature (SST), pCO₂ and difference in environmental settings was maximized during sample selection. Existing ocean databases are used for obtaining the relevant environmental parameters (Table 1).

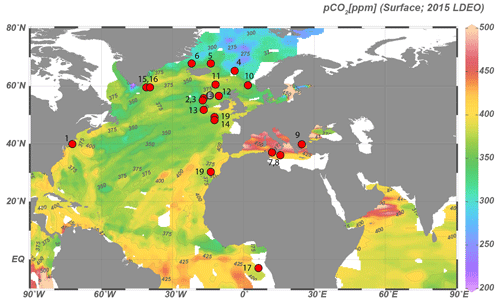
Figure 1 Locations of samples with sufficient Operculodinium centrocarpum and/or Spiniferites spp for dinoflagellate cyst δ¹³C analyses. Numbers correspond to localities listed in Table 1. Down-core data location (ENAM9606; 55.650^∘ N, 13.985^∘ W) is marked by a gray dot (“E”) between core top nos. 2, 3 and 12.

2.2 Methods

Using standard palynological techniques (see, e.g., Brinkhuis et al., 2003), ca. 5–10 g freeze-dried sediment of the upper 1–2 cm of core material was processed for each sample. This involved dissolving carbonates and silicate components using strong acids (HCl 30 % and HF 38 %–40 %). After acid steps, residues were pH-neutralized and sieved using an ultrasonic bath and 250 and 10 µm nylon mesh sieves to remove large and small particles, respectively. Subsequently, samples were transferred to glass test tubes with demineralized water and centrifuged at 3200 rpm for 10 min to obtain an optimum concentrate of the sample material. Prior to dinocyst selection, samples were stored in 4 mL glass vials in demineralized water.

Table 1 Core localities, analyzed species, number of measurements and normality of the carbon isotope data. Number of measurements is given as the total number and, in parentheses, the number of measurements used for environmental comparisons (see also results Sect. 3.4). Shapiro–Wilk (S–W) normality test on data: non-normal data distributions are indicated where p values are ^* < 0.1, ${}^{**}$ < 0.01 and ${}^{***}$ < 0.001; parentheses indicate the same for the data used for environmental comparisons. Site numbers correspond to those in Figs. 1 and 6a.

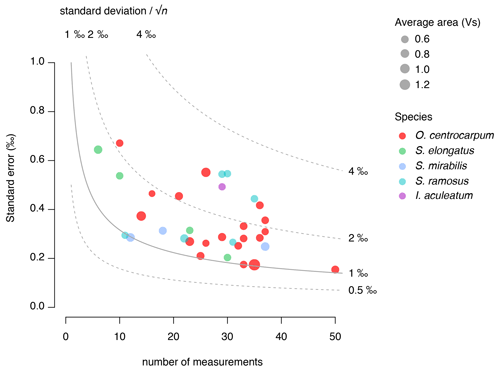
A micro-manipulator consisting of a Leica inverted microscope and a Narishige IM-9B micro-injector connected to a strung-out pipette was used to manually select individual dinocysts from a water droplet on a glass petri dish. Dinocyst selection followed a strict protocol, in which cyst morphology (primarily cyst shape and process length) was kept constant and the contribution of other organic particles was minimized. Specimens with darker coloration or amorphous organic matter adhering to the cyst or processes were avoided. In the case of O. centrocarpum, the morphological selection primarily involved selecting specimens of equal size and process length to avoid cysts that may be derived from different environments (e.g., Mertens et al., 2009). For Spiniferites, we were able to distinguish and separate three distinct morphological species in sufficient numbers: S. ramosus, S. elongatus and S. mirabilis. For all dinocyst species, the selected diameter excluding processes was in the order of ∼ 30–40 µm, except for S. mirabilis (∼ 60 µm), although constraining the exact size of each individual specimen was not feasible within the current analytical procedures. Stable carbon isotope analyses for individual samples are based on replicating the analyses of single of dinocysts, with ∼ 30 individual measurements being conducted to obtain a reasonably precise (∼ 0.3 ‰–0.4 ‰) sample average (van Roij et al., 2017). Given the size of the dinocysts used here (∼ 30–40 µm cyst diameter), three to seven specimens were required for each measurement, and hence ∼ 150 cysts were required to obtain sample averages (Table 1).

Dinocysts were placed on a 6 mm ∅ nickel sample tray, after which an identical second tray is added on top and compressed to fixate the dinocysts. Before placement in the ablation chamber, approximately ∼ 1 mm² of International Atomic Energy Agency CH-7 (IAEA-CH7) polyethylene standard (PE; certified δ¹³C value −32.15 ‰ ± 0.05 ‰; 1σ) was added to the sample tray. Stable carbon isotope analyses of the dinocysts followed the procedures described in previous work (van Roij et al., 2017; Sluijs et al., 2018), utilizing the recently developed ablation–nano-combustion–gas-chromatography–isotope ratio mass spectrometry (LA/nC/GC-IRMS) method. Fragments resulting from deep-ultraviolet LA were carried using a continuous helium flow in 0.32 mm capillaries and oxidized in a combustion oven at 940 ^∘C. The resultant CO₂ was transported to a GC combustion interface, dried in a Nafion tube using a He counterflow and subsequently into a Thermo Fisher DeltaV Advantage IRMS for isotope analysis. Each analytical run included five standards with signal intensity above 4 Vs (ca. 40 ng C; δ¹³C precision better than 0.5 ‰) to allow calibrating to the Vienna Peedee Belemnite (VPDB) scale. Direct visual monitoring of the ablation process was used as initial quality assessment of each individual measurement.

To calculate the fractionation factor ε_p of the dinocysts relative to dissolved inorganic carbon (DIC) from which the dinocyst was produced, we take the δ¹³C_DIC from the modeled grid of Tagliabue and Bopp (2008). As many dinoflagellate species, including those that produce O. centrocarpum and S. ramosus cysts, are able to utilize both HCO${}_{\mathrm{3}}^{-}$, which makes up the majority of DIC, and CO₂ for carbon fixation (Hoins et al., 2016a), we also compare the δ¹³C_DINO data to δ¹³C${}_{{\mathrm{CO}}_{\mathrm{2}}}$ and to overall seawater carbon partitioning.

ε_p-DIC is calculated as δ¹³C_DIC–δ¹³C_DINO, and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ is calculated as δ¹³C${}_{{\mathrm{CO}}_{\mathrm{2}}}$–δ¹³C_DINO. For the latter the δ¹³C of dissolved CO₂ is calculated from δ¹³C_DIC using the temperature-dependent fractionation between DIC and CO_2 (aq) (Mook et al., 1974). To evaluate the dominant contributions to ¹³C fractionation in dinocysts, we compare the ε_p-DIC and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ values to measured and interpolated physicochemical parameters. We test a suite of parameters, [NO${}_{\mathrm{3}}^{-}$], [PO${}_{\mathrm{4}}^{\mathrm{3}-}$], [Si], alkalinity, pCO₂, SST and sea surface salinity (SSS), which are extracted using Ocean Data View (https://odv.awi.de/, last access: 20 July 2020) from existing (gridded) datasets (Gouretski and Koltermann, 2004; Takahashi et al., 2014, 2016) (Supplement). Where possible, data are averaged over a grid of 4^∘ longitude and latitude around the sample position. This is both to reduce errors introduced by data scarcity and to account for potential lateral transport of dinocysts during sinking (Nooteboom et al., 2019). Carbonate chemistry is calculated using the R package seacarb (Gattuso et al., 2021), with alkalinity and pCO₂ as input variables to calculate the other relevant parameters of the carbonate system: the relative contributions of CO₂ (aq), HCO${}_{\mathrm{3}}^{-}$ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$, i.e., carbon speciation.

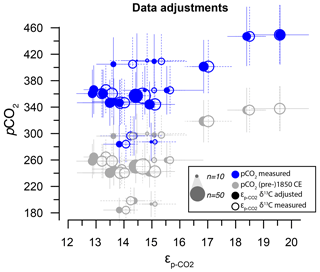
Ideally, all environmental parameters would be known for the different locations as would the time the dinoflagellates lived and encysted. This is, however, unfeasible because the dinocysts assemblage in core-top sediments (typically the upper 2 cm of sediment) integrates conditions over several centuries, assuming moderate to low average sediment accumulation rates (< 10 cm kyr⁻¹) that generally characterize open-ocean settings such as examined here. We therefore apply a rough correction for pCO₂, based on the assumption that local air–sea gas exchange has remained similar, that equals the atmospheric pCO₂ rise between the sampling date and 1850 CE. The correction from actual measurements to “pre-industrial” conditions for pCO₂ yields a substantial offset due to the ∼ 90 ppmv atmospheric pCO₂ rise from 1850 CE to the average sampling date (ca. 2000 CE). As this correction is broadly similar for all sample localities, it has only a small impact on the overall pattern in the CO₂ data (Fig. 3). We employed a Monte Carlo simulation to assess the potential impact of the pCO₂ correction by propagating (1) the 5 % analytical error in pCO₂ values and adding 45 ± 15 ppm to reflect a normally distributed mixture of modern and pre-industrial conditions and (2) a resampled uncertainty derived from the pCO₂ rise since pre-industrial times (1800–2000 CE). Both scenarios are set up to represent worst-case scenarios; a single error drawn from the error distribution is imposed on a sample basis and not a resampled average of the number of δ¹³C_DINO measurements within a sample, as that would reduce the error through averaging.

Changes in SST, SSS and nutrient concentrations are also expected, partly also by anthropogenic activity, but offsets in these parameters are generally subtle and more local compared to the changes in pCO₂ and hence would require site-specific reconstructions. Still, recent widespread eutrophication and enhanced productivity may impact the carbon isotope results through increased DIC uptake in algal blooms (i.e., counteracting the impact of enhanced pCO₂). However, as eutrophication has mainly affected coastal areas (Hallegraeff, 1993; Anderson et al., 2002), this is expected to play a minor factor at our, mostly open marine, sample localities (Fig. 1). Lastly, long-term natural changes in nutrients, SSS and SST also occur, and it is currently not possible to fully filter out the various anthropogenic offsets. With the exception of pCO₂, we hence assume all parameters (SST, SSS, nutrients) to have remained constant over the period the core-top samples represent.

3 Results

3.1 Carbon yields from dinocyst analyses

Despite our pre-screening to include only samples with high relative abundances of the target species, some of the selected samples contained too few dinocysts or at too low an abundance relative to other organic particles (amorphous organic matter, plant debris, pollen, non-dinocyst marine palynomorphs etc.) to be used in our study. Ultimately, out of the initial core-top sample set of 34 samples, 19 were found suitable for species-specific dinocyst stable carbon isotope analyses (Table 1).

Typically, ∼ 150 individual cysts were picked and analyzed for a total of 20–50 measurements, amounting to three to seven cysts per carbon isotope measurement. We calculate an average signal size of 0.2 Vs for a single cyst, which amounts to a carbon yield of ∼ 6–7 ng C per cyst (van Roij et al., 2017). Although the variability in signal intensity from individual measurements suggests there is substantial intra-sample (cyst–cyst) variability, no significant offsets in average carbon content per cyst were observed between samples, suggesting the average carbon content of the cysts within each of the analyzed populations is similar. Spiniferites mirabilis is the notable exception to this rule, as far fewer specimens of this species are needed for a single δ¹³C_cyst measurement. Based on the signal intensity per specimen, we estimate that this larger cyst species contains twice the amount of C compared to S. ramosus, S. elongatus and O. centrocarpum.

3.2 Carbon isotope data

3.2.1 Signal intensity

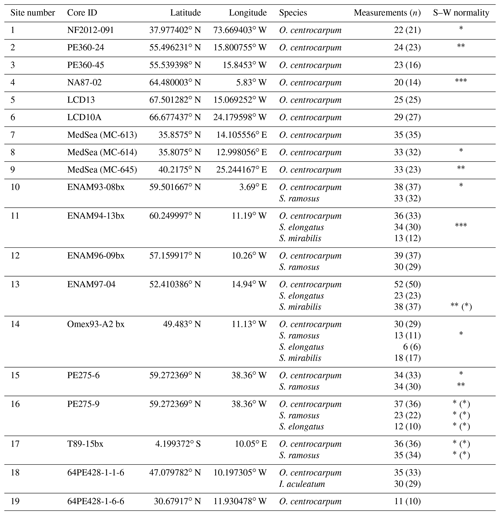
The 949 individual core-top analyses range in δ¹³C from ∼ −18.5 ‰ to −35.5 ‰ (all δ¹³C are relative to Vienna Peedee Belemnite (VPDB)), and the 137 down-core analyses range from ∼ −19.4 ‰ to −28.1 ‰. No relation was observed between δ¹³C and signal size (Vs), except at the very low end (≤ 0.2 Vs) (Fig. 2), in line with earlier analyses (van Roij et al., 2017). In this low range, the median of the δ¹³C values rises from −28 ‰ below 0.1 Vs to values between −22 ‰ and −25 ‰ above 0.2 Vs. In the ≤ 0.2 Vs range the δ¹³C averages of both the cysts and PE converge between −25 ‰ and −30 ‰, with substantial scatter. Poorer performance at such low C masses and signal intensities is expected, as these extremely small signal sizes and poor signal-to-noise ratio (below ∼ 3:1) approach the limit of our method. Consequently, even a very minor contamination source would bias values and result in larger scatter, as is also apparent in the PE standard at a similar signal intensity (van Roij et al., 2017; Fig. 2). Due to a worsening signal-to-noise ratio, we find that a noticeable degree of δ¹³C biasing from a background C source within the system is likely to occur at signal intensities ≤ 0.5 Vs and is particularly pronounced ≤ 0.2 Vs, and values for the standard and dinocysts converge around −27 ‰ in this range (Fig. 2a). A similar background δ¹³C value was also obtained after liquid nitrogen trapping (van Roij et al., 2017). The source of this C remains elusive. It is unlikely to be related to the ablation (etching) of the nickel plate or associated with the water used to pick samples from, as measured blanks for those result in much lower signal intensities and neither source would affect the measurements of the PE standard. Lastly, a significant contribution of atmospheric CO₂ (δ¹³C around −8 ‰) appears unlikely due to the δ¹³C signature of the background signal (−27 ‰). Though the origin of the background C remains unknown, we can use the trapping experiment to estimate the relevant background contribution (van Roij et al., 2017). We calculate the typical contribution is likely between 0.024 and 0.08 Vs, given a background C flux of 0.0008 Vs per second (van Roij et al., 2017) and a typical duration of measurements (30–50 s for δ¹³C_DINO and up to ∼ 100 s for PE standard).

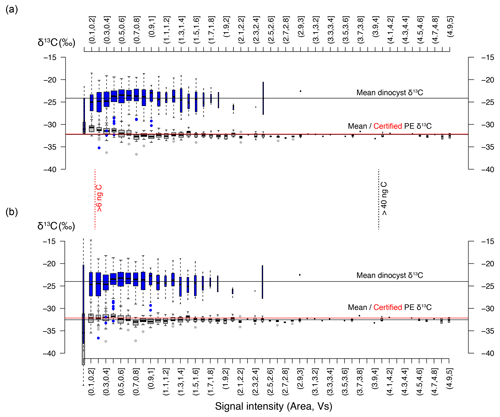
Figure 2 Signal intensity in volt seconds (Vs) versus carbon isotope value distribution within bins of 0.1 Vs. (a) The blue boxplots represent our new dinocyst δ¹³C, and the gray boxplots represent the previously published data for the PE standard (δ¹³C value −32.15 ‰ ± 0.05 ‰; 1σ). (b) Same as (a). but for background-corrected values (see Sect. 3.2). The vertical black and red lines represent cut-off values for individual PE standard measurements (>4 Vs; ∼ 42 ng C; 0.5 ‰ precision) and individual cyst measurements (>0.2 Vs; ∼ 6 ng C), respectively. The width of each boxplot is square-root-scaled with the number of measurements in the respective bins. Note that several bins at the high end do not contain any data.

Figure 3 Effects of δ¹³C and pCO₂ corrections (see also Fig. 2 and Sect. 3.2).

Before comparing our data with environmental variables, we therefore assess the impact of a very minor, but consistent, background contamination on the carbon isotope signal at low signal intensities (e.g., Fig. 2a). We find that a constant addition of ca. 0.04 Vs (≤ 1 ng C) of a background C source with a δ¹³C of −27 ‰ can explain the positive skewing in the standard PE δ¹³C. Using a simple isotope endmember and mass balance mixing model to correct for skewing (Fig. 2b), we calculated an average deviation from the measured PE and dinocyst values for intensities below 0.2 Vs in the order of $\left|\mathrm{2.6}\mathrm{‰}\right|$ and $\left|\mathrm{1.3}\mathrm{‰}\right|$, respectively. The standard deviation of the data increases approximately 3-fold (Fig. 2b) compared to the raw measurement data below 0.2 Vs but remains virtually unchanged above 0.2 Vs, and the calculated deviation from the measured value is also much reduced above 0.2 Vs ($\left|\mathit{<}\mathrm{0.3}\mathrm{‰}\right|$).

The data correction using our simple mixing model eliminates the skew towards −27 ‰ at low signal intensities and removes signal size δ¹³C dependency below 0.2 Vs for both the isotopically homogeneous PE and the heterogeneous dinocyst data (Fig. 2a, b). This suggests that our method of bias correction is warranted, but the increased variability at very low intensities and lack of independent control on the exact size and δ¹³C of the background contamination imply that the data associated with the lowest signal intensities remain significantly less reliable. We therefore apply a conservative cut-off and use only corrected data with a signal size above 0.2 Vs.

3.2.2 Skewed distributions and outlier omission

The drift-corrected δ¹³C_DINO is non-normally distributed in many core-top samples and also in different species (Table 1, Fig. 4). Distributions tend to be tailed towards lower values, exaggerated by the presence of a small number of outlier values. This is not due to analytical error or otherwise directly related to low signal intensity as we used a 0.2 Vs cut-off to eliminate samples with potentially unreliable signal-to-noise ratios (see above), and a minor correction for background C addition was sufficient to eliminate skewing at low signal intensities. The absence of such signals in the down-core samples (Supplement Fig. S1) suggests that the outliers and skewing in the sampled core-top populations could represent a real signal.

Figure 4 Carbon isotope measurements for multiple species; each panel represents a single sample after eliminating extremely small measurements sizes (< 0.2 Vs), carrying out background correction and removing outliers (± 2.5 interquartile range) (Sect. 3.2). Each box–whisker and δ¹³C distribution plot represents a set of measurements for a single species at their respective locality; note that tailing towards negative δ¹³C is common. Brackets above species δ¹³C populations indicate significant differences in means and variance for different species within a single sample.

Based on typical deep-ocean sedimentation rates in the range of centimeters per kiloyear, the core-top samples are expected to contain a mixed assemblage of dinocysts produced mostly within the last centuries to millennia but could also include cysts produced during the last few decades that are likely affected by anthropogenic influences. It is particularly relevant to consider because a steep δ¹³C decrease (∼ 2 ‰ since 1850 CE, of which > 1.5 ‰ occurs after 1950 CE) (Francey et al., 1999; Keeling et al., 2017) accompanies the pCO₂ rise (> 130 ppmv since 1850 CE, of which > 100 ppmv after 1950 CE). So even if enhanced carbon isotope fractionation at higher pCO₂ (Freeman and Hayes, 1992; Hoins et al., 2015; Brandenburg et al., 2022) did not play a role, the most recent specimens are likely to be impacted by decreasing δ¹³C_DIC.

As age integration in the modern era may result in a mixture of cysts representing a range of environmental conditions, especially with respect to CO₂ concentrations and δ¹³C_DIC, it is important to consider the potential age distribution of dinocysts before comparing δ¹³C_DINO and ε_p to environmental variables. In an ideal scenario, cysts produced after 1850 CE should be avoided in proxy-calibration efforts to eliminate a systematic bias towards the most recent times when atmospheric CO₂ was already elevated above pre-industrial Holocene background (∼ 280 ppmv). Because an accurate age correction for the Suess effect is technically unfeasible because the age distribution of δ¹³C_DINO measurements cannot be constrained, we illustrate the influence of δ¹³C_DINO data treatment (Fig. 3) and use Monte Carlo simulations of different error distributions to test the potential impact of the pCO₂ correction. We also compared both measured pCO₂ and pCO₂ around 1850 CE (see Sect. 2.2) to ε_p calculated using both our raw δ¹³C_DINO data and the δ¹³C_DINO data after drift correction and removal of statistical outliers identified within the sample-specific single-species populations. This final step of data treatment removed positive and negative measurement outliers from the sample- and species-specific δ¹³C population (outside ± 2.5 IQR), after eliminating the extremely low-signal intensities (< 0.2 Vs) and correcting for the drift induced by background C in the system.

Altogether, out of a 949 core-top measurements, we omit 43 measurements with signals < 0.2 Vs and 24 statistical outliers, which leaves 882 individual δ¹³C_DINO measurements: 560 for O. centrocarpum, 293 for Spiniferites (158 S. ramosus, 69 S. elongatus and 66 S. mirabilis) and 29 for I. aculeatum (Table 1). Most of the 67 omitted measurements have comparatively low δ¹³C, and the resulting δ¹³C of the populations is close to statistically indistinguishable from a normal distribution (Shapiro–Wilk p=0.05–0.1) or representative of a normal distribution (Table 1). Although the data treatment partly removed the negative skew on the δ¹³C_DINO distribution (Table 1), the combined effects of drift correction and outlier removal on sample and species-mean δ¹³C_DINO are generally small (Fig. 3). This is expected as drift correction averages only ∼ 0.25 ‰, and the negative and positive outliers represent only a small percentage of the total measurements (Table 1).

Distinctly non-normally distributed δ¹³C values were not previously observed in recent pollen and ancient dinocyst species analyzed with the same method (van Roij et al., 2016; Sluijs et al., 2018). The here presented down-core pre-industrial δ¹³C_DINO shows a similar mean, variance and data distribution to the nearby core-top samples (Supplement Fig. S1), suggesting that, at least for these nearby localities, the analyzed core-top specimens represent pre-industrial conditions. We find that an influence of the Suess effect and increased pCO₂ impacts on the δ¹³C_DINO data is the most likely factor to explain the appearance of a small number of predominantly ¹³C-depleted outliers and resulting (subtle) negative skewing of the δ¹³C distributions (Fig. 4).

We use the background and outlier-corrected δ¹³C_DINO data and compare these data with CO₂ conditions prevalent around 1850 CE (Fig. 6) and explore the effects of age integration by propagating different error distributions representative of the pCO₂ change since 1850 CE (Fig. 7b–d). For practical purposes, we assume all δ¹³C_DINO populations to be normally distributed for further statistical analyses. We then use the mean carbon isotope value (δ¹³C_DINO) and signal intensity in volt seconds (Vs) of each sample. The standard error of the mean ranges from ∼ 0.2 ‰ to 0.7 ‰ and depends primarily on the number of measurements in cases where n < 30, in line with expected values based on replicate measurements of the PE standard (van Roij et al., 2017) (Fig. 5).

Figure 5 Relation of standard error of δ¹³C_DINO (‰) with the number of measurements and signal intensity (area in volt seconds (Vs)). Colors correspond to the various analyzed species.

3.3 Environmental parameters and correlation

The range of measured δ¹³C_DINO values (∼ 5 ‰) far exceeds the variability in surface ocean δ¹³C_DIC (∼ 1 ‰) and δ¹³C${}_{{\mathrm{CO}}_{\mathrm{2}}}$ (∼ 2.5 ‰), implying the observed range likely reflects differences in fractionation related to changing uptake or leakage of different inorganic carbon phases (CO₂ and HCO${}_{\mathrm{3}}^{-}$; Sharkey and Berry, 1985; Hoins et al., 2016a), and this hence determines most of the variability in the δ¹³C_DINO data. Here, we quantitatively assess fractionation as a function of several environmental parameters.

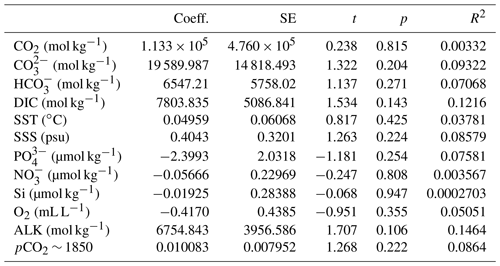
Table 2 Linear regression coefficients and significance for all samples where O. centrocarpum was analyzed (n=19), with ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ as dependent variable.

Table 3 As Table 2 but with ε_p-DIC as dependent variable.

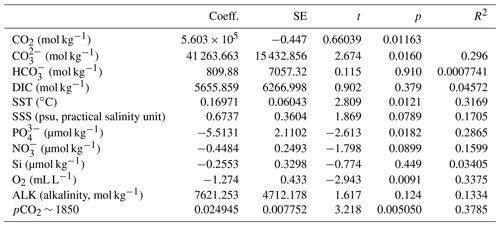
The simple (non-weighted) linear regressions show poor correlations between ε_p-DIC and δ¹³C_DIC for all environmental parameters, and the correlations slightly improve when compared to ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ (Tables 2, 3). However, none of the tested parameters individually explain the majority of the observed variance in ε_p-DIC (maximum R²; ∼ 0.1) or ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ (maximum R² with pCO₂; ∼ 0.38), despite high significance (low p values) of the regressions. The explained variance increases when polynomial regressions are applied. Several controlled growth experiments indeed show a non-linear response of ε_p as a function of pCO₂ of the growth medium (Hoins et al., 2015), although the number of data points in such experiments limits full mathematical descriptions of the trends within the pCO₂ range of this field study. Here, a second-order polynomial (quadratic) regression achieves an R² of ∼ 0.74 and ∼ 0.79 for the non-weighted and weighted versions, respectively.

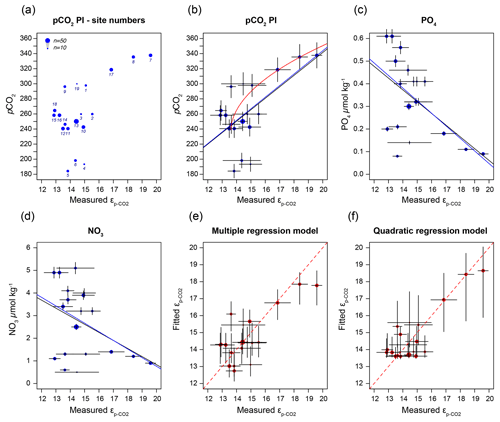
Figure 6 (a) Sample-specific ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ of O. centrocarpum relative to pre-industrial pCO₂; numbers correspond to localities listed in Table 1. (b) Regression analyses for ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ of O. centrocarpum relative to pCO₂ (measured and corrected to pre-industrial values); the black line represents simple linear regression, the blue line represents weighted linear regressions and the red line represents weighted quadratic regression. (c) Phosphate concentrations (PO${}_{\mathrm{4}}^{\mathrm{3}-}$). (d) Nitrate concentrations (NO${}_{\mathrm{3}}^{-}$). (e) Fitted values illustrating the multiple-regression model performance using parameters (a)–(c) relative to measured ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$. (f) Fitted values using only pre-industrial pCO₂ but applying a quadratic regression (red curve in panel b). Errors in panels (b)–(d) represent 5 % of the measured value and errors on the fitted values in panels (d) and (e) represent propagated errors in both measurements and environmental variables (as shown in panel b–d) using Monte Carlo simulations (n=1000) for regression models. Symbol size (top left corner of panel a) represents the number of measurements within each sample.

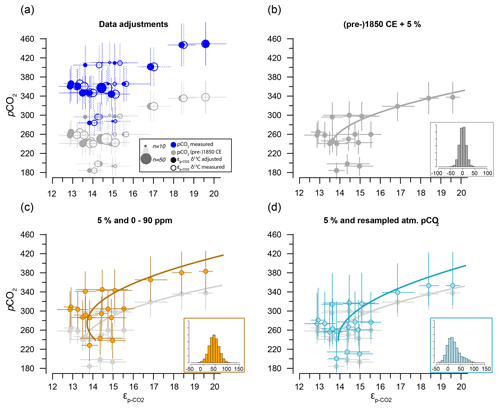
Figure 7 Sensitivity tests on the potential effect of anthropogenic carbon emissions. (a) Effects of data treatment on the difference between measured and adjusted pCO₂ and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ (same as Fig. 3). Open symbols indicate measured δ¹³C; closed symbols represent data after eliminating small signals (< 0.2 Vs) and outliers. Blue dots represent measured CO₂ values and gray dots indicate the CO₂ around 1850 CE. (b) Quadratic regression (red line in Fig. 6b) with propagated analytical error in pCO₂ and δ¹³C only, using CO₂ values around 1850 CE (gray filled symbols in panel a). (c) As in (b) but with the addition of a +45 ± 15 ppm error to reflect potential impact of anthropogenic CO₂ in orange. Gray dots and curve of panel (b) are added as a comparison. (d) As in (b) but with the addition of a CO₂ increase relative to pre-industrial values, sampled for the period 1800–2000 CE. Insets on the bottom right in panels (b), (c) and (d) show the combined error distributions imposed on pCO₂. All error bars in panels (b)–(d) on pCO₂ and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ are 2.5 %–97.5 % percentile ranges from Monte Carlo simulations (n=1000).

It is conceivable that other environmental parameters also significantly contribute to ε_p variability (Fig. 6). For example, [PO${}_{\mathrm{4}}^{\mathrm{3}-}$], [NO₃] and pCO₂ contribute significantly to a (linear) multiple-regression model, which takes the form of ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}=c+x$CO₂+yPO₄+zNO₃, where c, x, y and z are numerical constants. The multiple-regression model using these three parameters covers ∼ 58 % of the variance in O. centrocarpum ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ (not weighted) and 67 % when weighted to number of measurements per sample. Including more parameters, such as SST, oxygen concentrations or other carbonate system parameters, explains slightly more of the observed variance but does not significantly improve the model. The residual mean standard error (RSME) of the carbon–nitrogen–phosphorus (CNP)-ε_p multiple-regression model is ∼ 1.45 ‰ while a linear regression with only pCO₂ yields 1.7 ‰. Only weighted regressions are given here and reported ranges of the constants represent 1 standard error or equivalent percentiles in the case of Monte Carlo-simulated errors. These models have the following optimal formats:

• Equation (1), linear.

  $$\begin{array}{}\text{(1)}& {\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}=\mathrm{6.6}\pm \mathrm{2.1}+\mathrm{0.031}\pm \mathrm{0.008}p{\mathrm{CO}}_{\mathrm{2}}\end{array}$$

  (adjusted R²=0.48, p=0.001, RSME = 1.7 ‰) (Fig. 6b).

• Equation (2a), quadratic (data without error propagation and only suitable for use >240 μatm).

  $$\begin{array}{}\text{(2a)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& =\mathrm{40.8}\pm \mathrm{7.2}-\mathrm{0.23}\pm \mathrm{0.055}p{\mathrm{CO}}_{\mathrm{2}}\\ & +\mathrm{4.88}\times {\mathrm{10}}^{-\mathrm{4}}\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{2}}\end{array}\end{array}$$

  (adjusted R²=0.79, p < 0.001, RSME = 1.13 ‰) (Fig. 6b).

• Equation (2b), quadratic (Monte Carlo-constrained errors – analytical for pCO₂ and ${\mathit{\epsilon }}_{\mathit{\text{p-}}{\mathit{CO}}_{\mathit{2}}}$) (Fig. 7b).

  $$\begin{array}{}\text{(2b)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& ={\mathrm{35.6}}^{+\mathrm{5.8}}{/}_{-\mathrm{5.6}}-{\mathrm{0.19}}^{+\mathrm{0.045}}{/}_{-\mathrm{0.045}}p{\mathrm{CO}}_{\mathrm{2}}\\ & +{\mathrm{4.1}}^{+\mathrm{0.91}}{/}_{-\mathrm{0.88}}\times {\mathrm{10}}^{-\mathrm{4}}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{2}}.\end{array}\end{array}$$

• Equation (2c), quadratic (as Eq. 2b with additional 45 ± 15 ppm pCO₂ error) (Fig. 7c).

  $$\begin{array}{}\text{(2c)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& ={\mathrm{39.3}}^{+\mathrm{11.5}}{/}_{-\mathrm{8.8}}-{\mathrm{0.19}}^{+\mathrm{0.058}}{/}_{-\mathrm{0.076}}p{\mathrm{CO}}_{\mathrm{2}}\\ & +{\mathrm{3.4}}^{+\mathrm{1.3}}{/}_{-\mathrm{0.95}}\times {\mathrm{10}}^{-\mathrm{4}}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{2}}.\end{array}\end{array}$$

• Equation (2d), quadratic (as 2b with resampled pCO₂ rise 1800–2000 CE) (Fig. 7d).

  $$\begin{array}{}\text{(2d)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& ={\mathrm{29.8}}^{+\mathrm{11.0}}{/}_{-\mathrm{8.0}}-{\mathrm{0.13}}^{+\mathrm{0.061}}{/}_{-\mathrm{0.084}}p{\mathrm{CO}}_{\mathrm{2}}\\ & +{\mathrm{2.6}}^{+\mathrm{1.5}}{/}_{-\mathrm{1.1}}\times {\mathrm{10}}^{-\mathrm{4}}p{\mathrm{CO}}_{\mathrm{2}}^{\mathrm{2}}.\end{array}\end{array}$$

• Equation (3a), multiple-regression linear (Fig. 6e).

  $$\begin{array}{}\text{(3a)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& =\mathrm{6.0}\pm \mathrm{3.1}+\mathrm{0.034}\pm \mathrm{0.01}p{\mathrm{CO}}_{\mathrm{2}}\\ & +\mathrm{1.22}\pm \mathrm{0.47}{\mathrm{NO}}_{\mathrm{3}}-\mathrm{10.85}\pm \mathrm{3.7}{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\end{array}\end{array}$$

  (adjusted R²=0.67, p < 0.001, RSME = 1.45 ‰).

• Equation (3b) adjusted for application in the paleo-domain.

  $$\begin{array}{}\text{(3b)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}& =\mathrm{6.0}\pm \mathrm{3.1}+\mathrm{0.034}\pm \mathrm{0.01}p{\mathrm{CO}}_{\mathrm{2}}\\ & -\mathrm{1.1}\pm \mathrm{5.3}{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}.\end{array}\end{array}$$

• Equation (4), multiple-regression linear.

  $$\begin{array}{}\text{(4)}& \begin{array}{rl}{\mathit{\epsilon }}_{\text{p-DIC}}& =\mathrm{18.4}\pm \mathrm{3.1}+\mathrm{0.025}\pm \mathrm{0.01}p{\mathrm{CO}}_{\mathrm{2}}\\ & +\mathrm{1.45}\pm \mathrm{0.47}{\mathrm{NO}}_{\mathrm{3}}-\mathrm{11.1}\pm \mathrm{3.7}{\mathrm{PO}}_{\mathrm{4}}^{\mathrm{3}-}\end{array}\end{array}$$

  (adjusted R²=0.52, p=0.01, RSME = 1.44 ‰).

The two linear multiple-regression models are offset (Eqs. 3a and 4), primarily because of the carbon isotope fractionation between HCO${}_{\mathrm{3}}^{-}$ and CO₂. The slope with respect to pCO₂ also varies slightly between the models for ε_p-DIC and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ due to the temperature-dependent fractionation between HCO${}_{\mathrm{3}}^{-}$ and CO₂, but the slopes with NO${}_{\mathrm{3}}^{-}$ and PO${}_{\mathrm{4}}^{\mathrm{3}-}$ are indistinguishable. The quadratic regression seemingly better fits the variability observed in ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ compared to other (multiple) linear regressions and removes any structure in the residuals, potentially signaling a non-linear response in ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ to pCO₂. The quadratic regression also indicates insensitivity to pCO₂≤240 µatm and should not be used below this value (Fig. 6b). The Monte Carlo simulations of scenarios where an additional pCO₂ uncertainty is imposed as a normally distributed mixture of pre-industrial and modern values, offsetting pCO₂ by +45 ± 15 ppm (Fig. 7c, Eq. 2c), and a resampled uncertainty derived from the pCO₂ rise since pre-industrial times (Fig. 7d, Eq. 2d) shows that the parameters of the quadratic regression are fairly robust to these uncertainties (i.e., none of the parameters become insignificant at p>0.05), although the absolute pCO₂ values and errors increase.

4 Discussion

4.1 Absolute values, comparison to marine organic matter

The recorded δ¹³C_DINO range and absolute values (∼ −18 ‰ to −35 ‰) correspond well with global δ¹³C values previously reported for marine particulate organic matter (δ¹³C_POC) (e.g., Freeman and Hayes, 1992; Goericke and Fry, 1994) and modeled phytoplankton biomass (e.g., Magozzi et al., 2017; Tagliabue and Bopp, 2008). Consequently, ε_p-_DIC and ${\mathit{\epsilon }}_{\text{p-}{\mathrm{CO}}_{\mathrm{2}}}$ are also within the expected range for general marine particulate organic matter. However, the intra-sample variance of δ¹³C_DINO appears to be substantial, often spanning most of the full range (∼ 10 ‰) observed for δ¹³C_POC. Some of the observed variability might be related to the limited analytical precision during measurements of the extremely small numbers of carbon of individual dinocysts. Fully constraining the contribution of this analytical uncertainty to the observed variance is, however, not possible because of unresolvable micrometer-scale heterogeneity in the PE standard (van Roij et al., 2017; Sluijs et al., 2018). In most cases, the variance in δ¹³C_DINO is similar to that of the standard. Still, it is likely that some of the seasonal δ¹³C_DIC differences are also recorded in the δ¹³C_DINO and that some additional inter-specimen δ¹³C variance is present. This is to be expected since the δ¹³C populations from our integrated core-top samples span seasons and decades and thus also considerable variability in seawater properties and population change. In addition, growth-induced randomness and changes in δ¹³C and DIC in the cell's microenvironment likely contributed to inter-specimen variability. Note that in our data inter-specimen variability is still underestimated because we analyzed three to seven specimens per ablation event, as single-cyst carbon yield (∼ 7 ng C) from these cyst-sizes approached the limit for reliable measurements (van Roij et al., 2016). We minimized potential influence of differences in cell size or shape through manual selection. We thus analyzed a population where the pre-selection of similar-sized cysts restricts the variance in cell surface area and volume, unlike biomarker-based proxies for which the cell size has to be reconstructed independently (Henderiks and Pagani, 2007; Stoll et al., 2019). This approach could reduce scatter in the relation of ε_p to environmental variables (Popp et al., 1998).

4.2 Cell–cyst offset

One of the striking differences between the here generated data and the existing culture experiments is that carbon isotope fractionation of dinocysts in the natural environment appears to be much larger than that of motile cells from controlled growth (dilute batch) experiments (Hoins et al., 2015, 2016b). We find average ε_p values ranging between 13 ‰–20 ‰ and 23 ‰–29 ‰ with respect to CO₂ and DIC. Cultured cells of O. centrocarpum yielded not only a smaller overall ε_p but also a smaller range (∼ 8 ‰–12 ‰ and 18.5 ‰–20 ‰) across a larger CO₂ gradient, implying the cysts have a much steeper fractionation slope with CO₂ compared to the motile cells. Despite these differences, the average ε_p for Spiniferites species (S. ramosus, elongatus and mirabilis) is often somewhat larger than for O. centrocarpum (Fig. 4). This is consistent with culture experiments that showed larger CO₂ dependency and overall slightly larger ε_p in the motile species G. spinifera compared to P. reticulatum (Hoins et al., 2015).

While the cultured single strains and dinoflagellate populations in nature may behave somewhat differently, we do not expect that this alone underlies such a marked offset between the motile cultured cells and natural cysts. Natural cysts and cultured cells seem consistently offset in δ¹³C, although at present the exact amplitude of this offset cannot be determined. However, such an offset is in line with certain compounds in dinoflagellate cells being depleted in ¹³C relative to the bulk biomass (Schouten et al., 1998; Wilkes et al., 2017). The organic-walled dinocysts consist of mostly aliphatic and aromatic compounds, forming a complex biopolymer referred to as dinosporin (de Leeuw et al., 2006; Versteegh et al., 2007, 2012). Depending on the biosynthetic pathway of the cyst material and the derivation or degradation of the original compounds, this may result in offsets in δ¹³C values between cysts and the motile cells. A potential additional fractionation might be introduced during taphonomy and also later by the processing of sediments to concentrate the dinocysts from sediment samples. The sediment processing involves hydrochloric and hydrofluoric acids, which affects the more labile organic compounds. Last, it is conceivable that fractionation in the dilute batch experiments may be reduced by, e.g., higher-than-natural growth rates. This may be supported by chemostat culture experiments on Alexandrium tamarense (Wilkes et al., 2017), which show a (much) greater fractionation compared to the dilute batch experiments (Hoins et al., 2015). However, the enhanced fractionation recorded in chemostat experiments is likely an artifact of isotope equilibration times exceeding CO₂ uptake rates (Brandenburg et al., 2022; Zhang et al., 2022). The range of options cannot be narrowed down until cultured cysts are compared to their motile cells harvested from the same culture and treated with similar techniques as used for the sediments. Until these data become available, inferences on the origin and amplitude of the offsets between the cells and cysts of O. centrocarpum and Spiniferites remain speculative.

4.3 Environmental controls on carbon isotope fractionation

Carbon isotope fractionation is determined by RuBisCO and several environmental parameters, dominantly pCO₂ but also cell size and shape, growth rates, and nutrient or light regimes (e.g., Freeman and Hayes, 1992; Pagani, 2013; Popp et al., 1998; Stoll et al., 2019, and many others). In most cases, fractionation is pCO₂-dependent, and consequently ε_p in various groups and genera has been used as a paleo-pCO₂ proxy (e.g., Freeman and Hayes, 1992; Pagani, 2013; Rae et al., 2021). We performed a broad-spectrum multiple-regression analysis to identify environmental factors that contribute significantly to dinocyst ε_p. The most important parameter is pCO₂, in line with previous studies (Freeman and Hayes, 1992). A large part of the remaining variability can be attributed to growth rate and ultimately nutrient content, specifically nitrate and phosphate of the surface waters, in line with previous studies on phytoplankton and dinoflagellate carbon isotope fractionation (Popp et al., 1998; Hoins et al., 2016b; Wilkes et al., 2017; Wilkes and Pearson, 2019). We find that pCO₂ and ε_p are positively correlated, while NO${}_{\mathrm{3}}^{-}$ and PO${}_{\mathrm{4}}^{\mathrm{3}-}$ are negatively correlated with ε_p (Fig. 6c, d).

The inclusion of nutrient levels as environmental factors in the carbon isotope fractionation reduces the error in the fit between the measured and modeled fractionation. In the rare cases where paleo-nutrient concentrations are estimated, reconstructions usually cover only [PO${}_{\mathrm{4}}^{\mathrm{3}-}$], implying the [NO${}_{\mathrm{3}}^{-}$] in Eqs. (3a) and (4) has to be approximated from [PO${}_{\mathrm{4}}^{\mathrm{3}-}$]. As [PO${}_{\mathrm{4}}^{\mathrm{3}-}$] and [NO₃] are generally well-correlated (typically ∼ 1:10 [PO${}_{\mathrm{4}}^{\mathrm{3}-}$] : [NO₃]; here ∼ 1:8) in ocean waters, this is relatively straightforward. For application in the paleo-domain, however, nutrient ([PO${}_{\mathrm{4}}^{\mathrm{3}-}$]) reconstructions may not be available or may be considered too unreliable to provide meaningful constraints. In specific cases where accurate paleo-[PO₄] estimates or large changes are reconstructed, Eq. (3b) may be applied, in which [NO₃] is substituted for [PO${}_{\mathrm{4}}^{\mathrm{3}-}$] at a 1:8 ratio. However, unless there are clear changes in the nutrient regime or sufficient proxy constraints on the nutrient concentrations, we prefer a calibration based exclusively on carbon isotope fractionation and carbonate system parameters, including sea surface temperature to calculate δ¹³C${}_{{\mathrm{CO}}_{\mathrm{2}}}$ from δ¹³C_DIC to reconstruct pCO₂.

4.4 Influence of carbon-concentrating mechanisms: CO₂ insensitivity

As many phototrophs, including dinoflagellates, have mechanisms for concentrating CO₂ near the cell membrane, the sensitivity of carbon isotope fractionation to ambient CO₂ is expected to diminish below a certain concentration (M. R. Badger, 2003; M. P. S. Badger, 2021; Stoll et al., 2019). This is particularly the case as dinoflagellates utilize type II RuBisCO, which has generally poorer performance compared to type I RuBisCO at low CO₂ concentrations (Giordano et al., 2005). Indeed, substantial activity of the carboxyl anhydrase (CA) enzyme, which facilitates the conversion of HCO${}_{\mathrm{3}}^{-}$ to CO₂ inside the cell or near the membrane, was observed in numerous dinoflagellate species, including Lingulodinium (Lapointe et al., 2008), Symbiodinium (Leggat et al., 1999) and the here analyzed Operculodinium (Ratti et al., 2007). Also, here we find a relatively low sensitivity at the lower end of the CO₂ scale. The lower CO₂ values correspond to the northern-most locations, with trends below 240 µatm becoming somewhat obscured, at a minimum ε_p-CO₂ around 13 ‰ (Fig. 6b). However, part of this leveling of the proxy relationship may reflect the locally higher nutrient concentrations offsetting the higher CO₂. Though growth rates have a clear influence on ε_p in algal groups (Burkhardt et al., 1999), including dinoflagellates (Wilkes et al., 2017), the dilute batch culturing experiments conducted with P. reticulatum showed no clear influence of growth rates on ε_p (see also Sect. 4.2). It is also conceivable that higher growth rates influence ε_p indirectly through, for example, seasonally enhanced CO₂ drawdown, resulting in higher δ¹³C values in the remaining DIC. This effect may be enhanced by the relatively short growing season at the high latitudes. However, in culture experiments at low CO₂ concentrations with other dinoflagellate species, ¹³C fractionation was higher under nutrient-limiting conditions than under replete conditions (Hoins et al., 2016b). Because of these confounding factors, the influence of carbon-concentrating mechanisms on ε_p in O. centrocarpum is difficult to gauge with the presently available data and would ideally be tested using high nutrient or very low CO₂ concentrations.

Still, also in the relatively limited range the current ocean offers for testing pCO₂ proxies we have established a robust, albeit not overly sensitive, relation between pCO₂ and dinocyst δ¹³C. Our cyst-based calibration yields more conservative and arguably more realistic absolute CO₂ estimates and variability compared to available culture-based calibrations as it is based on the same compounds as will be analyzed in the paleo-domain. However, the low sensitivity at low CO₂ implies that, until better constraints become available, the proposed calibration is potentially less suitable for application across, for example, the Pleistocene glacial periods. Further, it is important to realize that the value of 240 µatm is based on the assumption that the ε_p-CO₂–pCO₂ relation originated from cysts that have not been affected by the Suess effect and thus represent a lower limit for CO₂ (in)sensitivity. While our data do not preclude fractionation smaller than the here observed minimum (∼ 13 ‰) during low-pCO₂ periods, increased sensitivity at higher CO₂ suggests that CO₂ above (minimum) 240 µatm and CO₂ variability can be reconstructed with reasonable precision.

4.5 Challenges of age control and potential caveats associated with anthropogenic carbon

A topic that warrants specific attention is the potential impact of anthropogenic carbon emissions on shaping the relation between δ¹³C_DINO and ε_p. Here, we assume that our outlier analyses preferentially excluded samples that were significantly affected by anthropogenic CO₂ and that, on average, the remainder of our core-top δ¹³C_DINO was not appreciably affected by either decreasing δ¹³C_DIC or elevated pCO₂. The similarity in pre-industrial down-core δ¹³C_DINO and that of three core-top localities in the North Atlantic corroborate the validity of this assumption locally, but these observations cannot be extrapolated to other regions. Unfortunately, sedimentation rates or other constraints for cyst production datums are not available. Further, if sedimentation rates were available for core-top localities, that would constitute an imperfect solution as it cannot provide the required dinocyst-specific age distribution needed to obtain an appropriate local pCO₂ correction to the datum of cyst production. This challenge may be unique to data such as those presented here, as studies on other substrates with pCO₂-proxy potential either could not generate data for individual single-celled organisms or have avoided the issue through other means, such as culture experiments (e.g., Pagani et al., 2002; Henehan et al., 2013), approaches that have other drawbacks.

Although we have no constraints on the ages of the cysts analyzed here, we can provide a meaningful test of the potential uncertainty added by our assumption that cysts are representative of pre-industrial conditions (Eq. 2a, b). The two scenarios that we have explored through Monte Carlo simulations show that, depending on the error distribution imposed on the assumed pCO₂ used in the quadratic regressions (Eq. 2a, b), the fitted regression shifts towards higher values (Fig. 7c) and may be steeper (Fig. 7d). These error-propagation case studies illustrate that our proposed pre-industrial transfer function (Eq. 2a, b), if it does indeed contain a substantial proportion of very recent dinocysts, is likely to lead to underestimated pCO₂ and perhaps pCO₂ variability when applied in the paleo-domain. Consequently, we recommend future studies target, for example, sediment trap collections and culture-derived dinocysts to validate the results obtained here.

5 Proxy potential, limitations and calibrations

Our new modern ocean single-species carbon isotope fractionation dataset shows promising trends with environmental variables, pCO₂ and nutrients. The selection of individual cysts allows control of cell size and species, which reduces uncertainty in proxy calibration and application compared to approaches based on organic substrates, which inevitably integrate entire communities. Although this approach has clear benefits, it also poses a unique challenge as the impact of anthropogenic carbon emissions on individual single-celled organisms must be considered. Based on our analyses, we expect this to be a relatively minor factor. In a worst-case scenario, however, we find that, although a helpful simplification, the assumption that all dinocysts from the core-top samples represent pre-industrial conditions may lead to an underestimate of pCO₂ and perhaps also pCO₂ variability when applied as a proxy in the paleo-domain.

In addition, many of the challenges associated with other proxies based on organic substrates are encountered here as well. For example, like in cultures (Hoins et al., 2016b), we observed an impact of nutrients on carbon isotope fractionation, possibly related to differences in growth rates. Similarly, at low pCO₂ values sensitivity is reduced, possibly because of carbon-concentrating mechanisms involved in dinoflagellate C uptake, as observed in culturing experiments (e.g., Hoins et al., 2016a). Another remaining challenge is the observed difference between the cultured populations and cysts from the core-top sediments. This is a pronounced difference, not only in the absolute isotope fractionation values but also in the slope of the CO₂ sensitivity, which appears to be much larger for the cysts and requires attention in future culture studies.

The offset in δ¹³C, combined with uncertainties in fractionation between the motile cells and dinocysts, implies that CO₂ reconstructions using culture-based calibrations are more likely to overestimate past pCO₂. Furthermore, the large spread in our data (∼ 5 ‰ between high and low CO₂) suggests that, due to this high sensitivity in the cysts, the method is also suited to study population dynamics.