Composite model-based estimate of the ocean carbon sink from 1959 to 2022

The ocean takes up around one-quarter of anthropogenically emitted carbon and is projected to remain the main carbon sink once global temperatures stabilize. Despite the importance of this natural carbon sink, estimates of its strength over the last decades remain uncertain, mainly due to too few and unevenly sampled observations and shortcomings in ocean models and their setups. Here, I present a composite model-based estimate of the annually averaged ocean carbon sink from 1959 to 2022 by combining the higher-frequency variability of the annually averaged estimates of the carbon sink from ocean models in hindcast mode and the long-term trends from fully coupled Earth system models. Ocean models in hindcast mode reproduce the observed climate variability, but their spin-up strategy likely leads to long-term trends that are too weak, whereas fully coupled Earth system models simulate their own internal climate variability but better represent long-term trends. By combining these two modelling approaches, I keep the strength of each approach and remove the respective weaknesses. This composite model-based estimate of the ocean carbon sink from 1959 to 2022 is 125±8 Pg C and is similar in magnitude to the best estimate of the Global Carbon Budget but 70 % less uncertain.

1 Introduction

The ocean is a major natural sink of anthropogenic carbon (Broecker et al., 1979; Sarmiento et al., 1992; Maier-Reimer and Hasselmann, 1987) and took up around one-quarter of carbon emissions from fossil fuels and land use change over the last decades (Friedlingstein et al., 2023; Terhaar et al., 2022; Müller et al., 2023; DeVries et al., 2023). Moreover, the ocean will continue taking up carbon over the 21st century (Terhaar et al., 2022) and beyond when temperatures are eventually stabilized (Silvy et al., 2024). Despite the importance of the ocean carbon sink for the global carbon cycle and hence the global climate, large uncertainties exist with respect to the magnitude, variability, and trends of the ocean carbon sink (DeVries et al., 2023; Terhaar et al., 2024; Friedlingstein et al., 2023).

Observation-based annually resolved estimates of the ocean carbon sink are built on direct observations of the partial pressure of CO₂ (pCO₂) at the ocean surface (Fay et al., 2021). While being built on observations is a strength of these observation-based pCO₂ products, it is also their weakness. As observations are scarce in space and time, they must be extrapolated by methods relying, among others, on artificial intelligence and machine learning, for example neural networks (Landschützer et al., 2015). However, even these cutting-edge extrapolation methods introduce biases in the strength of the decadal variability (Gloege et al., 2021) and trends (Hauck et al., 2023a; Terhaar, 2024). The data scarcity and uneven spacing in the past are impossible to overcome, and the question was raised of whether the different methods of extrapolating these observations have “hit the wall” (Gregor et al., 2019).

An alternative to observation-based pCO₂ products are global ocean biogeochemical models (GOBMs) that are forced with historical atmospheric reanalysis data, atmospheric CO₂, and radiative forcing from other radiative agents. As GOBMs are forced with these historical data, they represent the observed internal climate variability at the ocean surface and hence the high-frequency variability of the annually averaged ocean carbon sink, i.e. inter-annual to sub-decadal variability. However, differences in the simulated carbon sink by GOBMs are caused by differences in the simulated circulation and carbonate chemistry in these models (Terhaar et al., 2024), as well as different ways of setting up these GOBMs, e.g. the lengths of the spin-up or different atmospheric CO₂ during the pre-industrial spin-up (Terhaar et al., 2024). Moreover, using atmospheric forcing from sometime between 1959 and the present, the period for which atmospheric reanalysis data are provided, for the pre-industrial spin-up leads to a pre-industrial ocean that is too warm and hence transient warming in GOBMs that is too weak (Huguenin et al., 2022; Hollitzer et al., 2024) and deoxygenation that is too weak (Takano et al., 2023; Hollitzer et al., 2024). This pre-industrial ocean that is too warm and ocean warming that is too weak may also influence the ocean carbon sink and its trends through biases in the base state and transient changes in the stratification, solubility, or carbonate chemistry of the ocean. However, the sign and magnitude of that effect still remain unclear.

Another option to estimate the annually resolved ocean carbon sink are fully coupled Earth system models (ESMs) that are also forced with historical atmospheric CO₂ and radiative forcing from other radiative agents but dynamically simulate their atmosphere. Being dynamically coupled, ESMs do not simulate the phase of the observed internal climate variability and hence not the high-frequency variability of the annually averaged ocean carbon sink. However, ESMs from the most recent Phase 6 of the coupled model intercomparison project (CMIP6) are all set up in a common way, having the same atmospheric CO₂ during the pre-industrial spin-up and long enough spin-ups that allow the simulated ocean to reach its own equilibrium (Séférian et al., 2016). Furthermore, their pre-industrial atmospheric and ocean temperatures in ESMs are colder than their respective historical temperatures so that the simulated transient ocean warming aligns with observed ocean warming (Takano et al., 2023; Hollitzer et al., 2024). Finally, the simulated global ocean carbon sink could be adjusted for biases in the simulated ocean circulation and carbonate chemistry with observations (Terhaar et al., 2021a, 2022). Thus, ESMs from CMIP6 can be considered to robustly simulate the long-term trends of the ocean carbon sink and the externally forced decadal variability, which is mostly driven by changes in the atmospheric CO₂ growth rate (Terhaar, 2024; McKinley et al., 2020).

As both model estimates will not overcome their respective weaknesses in the near future, here I propose a new composite model-based estimate of the ocean carbon sink combining the inter-annual and sub-decadal variability of the ocean carbon sink from GOBMs and the externally forced decadal variability and long-term evolution of the ocean carbon sink from ESMs. The combined model-based estimate uses the strength and removes the weaknesses of the respective model estimates.

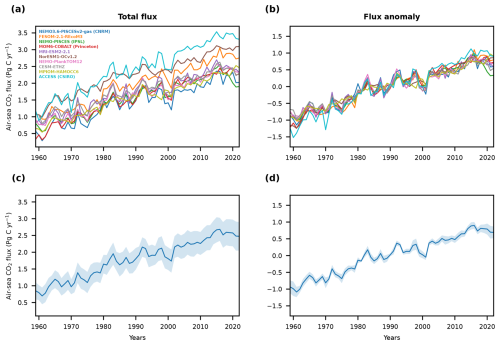
Figure 1 Global ocean carbon sink and its anomaly as simulated by global ocean biogeochemical models. The global ocean carbon sink as defined by the Global Carbon Budget 2023 (Friedlingstein et al., 2023) and (a) simulated by 10 global ocean biogeochemical models as well as (c) the multi-model mean and standard deviation. In addition, (b) the anomaly of the ocean carbon sink for the 10 global ocean biogeochemical models with respect to the mean flux from 1959 to 2022 in the respective GOBM and (d) the multi-model mean and standard deviation of that anomaly are shown.

2 Results

2.1 A new composite model-based estimate

The 10 GOBMs from the Global Carbon Budget 2023 simulate a global ocean carbon sink from 1959 to 2022 of various strengths (Friedlingstein et al., 2023) (Fig. 1a, c), but the flux anomaly with respect to the mean simulated carbon sink over the entire period is almost indistinguishable across these GOBMs (Fig. 1b, d). Small common differences in the anomalies exist in 1985 and 1998 for the GOBMs NorESM1-OCv1.2 (Schwinger et al., 2016) and MPIOM-HAMOCC6 (Lacroix et al., 2021a) (Fig. 1b), likely because both use the NCEP reanalysis data (Kanamitsu et al., 2002) to force the simulations and not the JRA55-do dataset (Tsujino et al., 2018) that is used by seven GOBMs or ERA5 reanalysis dataset (Hersbach et al., 2020) that is used by one GOBM. Furthermore, the ACCESS (CSIRO) model (Law et al., 2017) simulates slightly weaker anomalies at the beginning of the simulation and stronger anomalies at the end of the simulations, resulting in a larger trend of the anomalies over the entire period (Fig. 1b), although the model setup is not different to the others (Friedlingstein et al., 2023). While the differences in the anomalies might be too small due to the small diversity in atmospheric forcing datasets, even the difference in the anomalies between GOBMs that use different forcing data is much smaller than the difference of the absolute fluxes simulated by GOBMs (Fig. 1a), which was removed by calculating the anomalies. Thus, the overall strong agreement in simulated anomalies of the global ocean carbon sink across these 10 GOBMs as expressed by the small multi-model standard deviation and the strong agreement between GOBMs that use different atmospheric forcing data give high confidence in the multi-model mean estimate of the high-frequency variability of the simulated global ocean carbon sink by GOBMs (Fig. 1d).

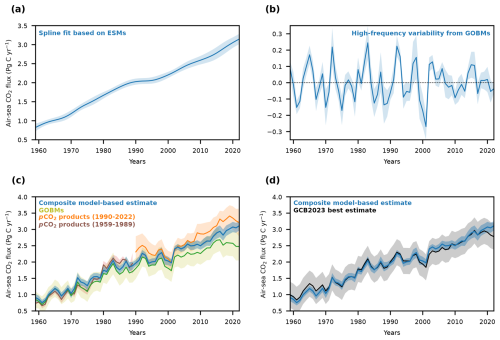
Figure 2 Composite model-based estimate of the ocean carbon sink and its two components. (a) A spline fit to the ocean carbon sink as simulated by ESMs and adjusted for biases in the ocean circulation and carbonate chemistry (Terhaar et al., 2022) as well as (b) the high-frequency variability of the ocean carbon sink anomalies as simulated by GOBMs that was derived after removing a spline fit to the simulated anomalies. The multi-model mean estimates are shown as blue lines and the multi-model standard deviation as blue shading. (c) The composite estimate is then the sum of the time series in (a) and (b). The uncertainties of the composite model-based estimates are the combined uncertainties of (a) and (b) plus the uncertainty from the spline fit (see the Appendix for details). In addition, estimates from the GOBMs (olive line and shading for multi-model mean and standard deviation) and the pCO₂ products from the Global Carbon Budget 2023 (Friedlingstein et al., 2023) (orange lines and shading show the multi-product mean and standard deviations over eight pCO₂ products from 1990 to 2022, and brown lines show the shading for the multi-product mean and standard deviation over two pCO₂ products from 1959 to 1989) are shown for comparison in (c) and the best estimate from the Global Carbon Budget 2023 (black line and shading for multi-model mean and uncertainty as reported in the Global Carbon Budget 2023) in (d).

As inter-model differences in the simulated high-frequency variability of the global ocean carbon sink by the GOBMs are small, here I combine this estimate of the high-frequency variability with an estimate of the long-term trend of the ocean carbon sink based on ESMs from CMIP6 to create a new composite model-based estimate of the global ocean carbon sink (Fig. 2c, Table A1). The long-term trend of the carbon sink is based on ESMs as these ESMs largely agree on the magnitude and long-term trends of the global ocean carbon sink after adjusting for biases in ocean circulation and carbonate chemistry (Terhaar et al., 2022). Furthermore, the multi-model mean of ESMs can represent the externally forced decadal trends (Li and Ilyina, 2018; Terhaar, 2024). The high-frequency variability was extracted here by removing a spline fit (Enting, 1987) from the simulated carbon sink estimate from each GOBM separately (Friedlingstein et al., 2023) (Fig. 2b). The low-frequency variability and long-term trends were calculated by fitting a spline fit (Enting, 1987) to the bias-adjusted simulated carbon sink from each ESM separately (Terhaar et al., 2022) (Fig. 2a). The ESMs were forced with historical forcing until 2014 and with forcing from the Shared Socioeconomic Pathway 1-2.6 (SSP1-2.6) (Riahi et al., 2017) after 2014 as the atmospheric CO₂ under that SSP (Meinshausen et al., 2020) is closest but still slightly above the observed atmospheric CO₂ (Lan et al., 2024). For the estimates of the long-term trend and short-term variabilities, it would have been possible to only use the members of the GOBM and ESM ensembles that have an ocean model component that is part of both ensembles to ensure consistency. However, I used all available GOBMs and ESMs as there is no indication that the short-term variability and long-term trend are linked and the largest number of GOBMs and ESMs in each ensemble allows best estimating both the short-term variability and long-term trend. The uncertainty of the composite estimate is the combination of the multi-model standard deviation of the high-frequency variability from GOBMs and that of the long-term trends from ESMs, as well as the uncertainty from the spline fit (see the Appendix for more details).

The ocean carbon sink estimated by this composite model-based estimate from 1959 to 2022 is 125±8 Pg C (Fig. 1c, Table A1). It increases from 1.00±0.10 Pg C yr⁻¹ in the 1960s to 2.78±0.16 Pg C yr⁻¹ in the 2010s. The increase in the ocean carbon sink slows down in the 1990s (decadal trend of 0.10 Pg C yr⁻¹ decade⁻¹) and accelerates afterwards (decadal trends of 0.55 and 0.56 Pg C yr⁻¹ decade⁻¹ in the 2000s and 2010s) as expected from the trends in atmospheric CO₂ and the eruption of Mount Pinatubo in the early 1990s (McKinley et al., 2020; Fay et al., 2023; Terhaar, 2024).

2.2 Comparison to previous estimates of the global ocean carbon sink

The new composite model-based estimate of the global ocean carbon sink differs from previous estimates by pCO₂ products and GOBMs in terms of magnitude, trend, and variability. The ocean carbon sink in the composite model-based estimate is 10 % (11 Pg C) larger than the estimate from GOBMs for the period from 1959 to 2022 (Fig. A1a). The absolute difference between the two estimates has some variability over time but remains on average the same until 2014. After 2014, the composite estimate becomes steadily larger and the difference rises from 0.24 Pg C yr⁻¹ (8 %) averaged from 2005 to 2014 to 0.65 Pg C yr⁻¹ (26 %) in 2022 (Fig. A1a). The difference before 2014 is due to a bias in the GOBMs in their simulated circulation and carbonate chemistry (Terhaar et al., 2024) that also exists in ESMs but was corrected for (Terhaar et al., 2022) (Fig. A1a). After 2014, the increasing difference may be explained by slightly different trajectories of atmospheric CO₂ in ESMs under SSP1-2.6 and the historical atmospheric CO₂. Recently it has been shown that the trend in the ocean carbon sink is sensitively related to changes in the trend of atmospheric CO₂. When combining this recently quantified relationship between changes in the trend of atmospheric CO₂ and trends in the ocean carbon sink across ESMs (Terhaar, 2024) with observations of atmospheric CO₂ and prescribed atmospheric CO₂ in SSP1-2.6 after 2014 to estimate the respective expected trends in the ocean carbon sink, the trend of the ocean carbon sink in ESMs should only have been 0.2 Pg C yr⁻¹ decade⁻¹ larger than in GOBMs. As the difference was 0.4 Pg C yr⁻¹ decade⁻¹ larger, the difference in the atmospheric CO₂ trajectory after 2014 thus explains around half of the difference of both estimates after 2014. The other half might be the spin-up strategy by GOBMs with an atmosphere that is too warm during pre-industrial times, which results in transient ocean warming that is too weak (Takano et al., 2023; Huguenin et al., 2022; Hollitzer et al., 2024), and hence there is too little loss of natural carbon to the atmosphere as a consequence of this warming. However, to quantify such an effect, simulations with GOBMs following the spin-up strategy by Huguenin et al. (2022) would have to be performed.

Compared to pCO₂ products, the composite estimate of the global ocean carbon sink is only 3 % (1 Pg C) larger for the period from 1959 and 1989 than the two pCO₂ products that provide estimates before 1990 and is 8 % (7 Pg C) smaller than all eight pCO₂ products on average for the period from 1990 to 2022 (Fig. A1b). The difference in the early 1990s and after 2000 might be due to overly strong decadal variability that has been shown to exist at least in one pCO₂ product (Gloege et al., 2021). This explanation is further supported by two studies, one that showed that extrapolating unevenly spaced observations in space and time leads to overly strong trends in the estimates of the ocean carbon sink by pCO₂ products (Hauck et al., 2023a) and one that used ESMs to show that the trends in pCO₂ products lie outside of what can be expected based on changes in the atmospheric CO₂ growth rate and climate variability (Terhaar, 2024). After 2019, the difference between the composite model-based estimate and the pCO₂ products decreases again, likely because of the above-discussed difference in observed atmospheric CO₂ and the prescribed atmospheric CO₂ in ESMs after 2014 following SSP1-2.6.

The composite estimate is almost identical to the best estimate of the ocean carbon sink provided by the Global Carbon Budget 2023 (Fig. 2d), which represents the average of the estimate by GOBMs and the pCO₂ products, until the atmospheric CO₂ differs in the ESMs after 2014. The composite estimate thus corroborates this best estimate by the Global Carbon Budget 2023. However, instead of simply averaging two independent but imperfect estimates, the composite model-based estimate uses the best available knowledge to remove the weaknesses of each model-based estimate and to only keep the strengths. As the composite model-based estimate explains the differences, its uncertainty is around 70 % smaller than that of the best estimate of the Global Carbon Budget 2023.

3 Conclusion

Overall, the composite model-based estimate of the global ocean carbon sink combines the strengths of two so far mostly separated model classes and successfully manages to account for the shortcomings in the different global ocean carbon sink estimates, i.e. the low bias in GOBMs due to the spin-up and the representation of the ocean circulation and carbonate chemistry as well as the bias towards decadal variability and trends in the pCO₂ products that are too large. The same method could also be applied to derive composite model-based estimates of regional and monthly resolved estimates of the ocean carbon sink. Regionally composite estimates might, however, have larger uncertainties as differences in regional carbon sink estimates are often larger than global estimates (DeVries et al., 2023; Yasunaka et al., 2023; Hauck et al., 2023b; Perez et al., 2023; Terhaar et al., 2021a, 2022, 2021c, 2024), possibly due to a compensation of regional carbon fluxes; e.g. a low Southern Ocean carbon uptake can be compensated for by a high North Atlantic Ocean carbon uptake.

Although this composite estimate provides an improvement to existing estimates of both model classes, GOBMs (Friedlingstein et al., 2023; DeVries et al., 2023) and ESMs (Terhaar et al., 2022), it still has shortcomings. One shortcoming is the forcing of ESMs with SSPs after 2014 that leads to carbon sink estimates that are slightly too high from 2015 to 2022. This shortcoming could be overcome if ESMs were run with observed atmospheric CO₂ after the historical forcing from CMIP6 ends in 2014. Another shortcoming is that all ESMs start in 1850 and are spun up with atmospheric CO₂, which leads to an underestimation of the ocean carbon sink (Bronselaer et al., 2017) of around 0.05–0.10 Pg C yr⁻¹ for ESMs for the period from 1959 to 2022 (Terhaar et al., 2024). This underestimation could be removed if ESMs were to start before the industrial revolution and the associated increase in atmospheric CO₂. Furthermore, the composite estimate cannot remove shortcomings or uncertainties that are inherent to both GOBMs and ESMs and that were not accounted for by emergent constraints (Terhaar et al., 2022), such as the often incorrect representation of the seasonal cycle of pCO₂ in both model classes (Rodgers et al., 2023; Joos et al., 2023). As it has been shown that the seasonal cycle changes in the future will affect the strength of the ocean carbon sink by 8 % until 2100 under a high-emission scenario (Fassbender et al., 2022), an incorrect representation at present likely also affects the simulated ocean carbon sink by ESMs and GOBMs and hence by the composite estimate. Other processes that are also still not simulated at all or not accurately simulated in GOBMs and ESMs and that might affect the ocean carbon sink are, for example, the ocean biological carbon pump (Doney et al., 2024; Laufkötter et al., 2015) and the land–ocean aquatic continuum (Séférian et al., 2020; Terhaar et al., 2024). Although improvements have been made in the past to account for these model weaknesses (Dinauer et al., 2022; Archibald et al., 2019; Lacroix et al., 2020; Terhaar et al., 2021b, 2019), more research is needed to improve simulated estimates of the ocean carbon sink.

The need for a composite model-based estimate of the global ocean carbon arose due to shortcomings in both model classes. As ESMs will always simulate an internal climate variability in a different phase than the observed one, this estimate remains a necessary fix until GOBMs are set up so that they can overcome their current weaknesses. To overcome current weaknesses, I recommend testing whether an improved spin-up strategy that accounts for the difference in atmospheric and surface ocean temperatures as well as radiation between the pre-industrial times and the mid-20th century, for example as proposed by Huguenin et al. (2022), may explain differences in the trends of the ocean carbon sink between GOBMs and ESMs. Furthermore, previous suggestions provided by Terhaar et al. (2024), such as a long enough spin-up and an early starting date with an associated atmospheric CO₂ during the spin-up, will likely also improve the carbon sink estimates by GOBMs. Once GOBMs are set up in a common way, emergent constraints could also be used in GOBMs to correct for biases in the ocean circulation and carbonate chemistry as was done for ESMs regionally and globally (Goris et al., 2018; Terhaar et al., 2021a, 2022, 2020; Bourgeois et al., 2022; Vaittinada Ayar et al., 2022). Until then, the composite model-based estimate of the global ocean annually averaged carbon sink provided here circumvents these shortcomings in GOBMs at present with the help of ESMs and thus provides a robust estimate of the global ocean carbon from 1959 to 2022.

Appendix A

A1 Estimates of the ocean carbon sink

Estimates of the ocean carbon sink, defined as the change in the globally integrated air–sea CO₂ flux since pre-industrial times due to increasing CO₂ and climate change, from pCO₂ products, GOBMs, and ESMs were used. Estimates of the global ocean carbon sink were directly taken for eight pCO₂ products (Table A2) and 10 GOBMs (Table A3) from the Global Carbon Budget 2023 (Friedlingstein et al., 2023) (https://doi.org/10.18160/gcp-2023, Global Carbon Project, 2023). In addition, the best estimate from the Global Carbon Budget 2023 was also directly taken from https://doi.org/10.18160/gcp-2023 (Global Carbon Project, 2023). For ESMs, estimates of the ocean carbon sink were calculated for 14 ESMs under historical forcing until 2014 and SSP1-2.6 from 2015 to 2022 following Terhaar et al. (2022) (Table A4).

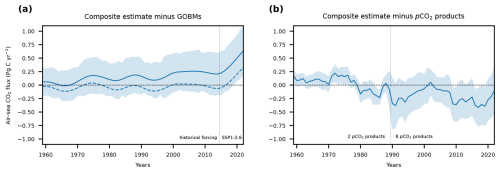
Figure A1 Difference in estimates of the global ocean carbon sink between the new composite estimate and estimates from GOBMs and pCO₂ products. Difference between the composite estimate of the global ocean carbon sink and the estimates (a) from GOBMs and (b) pCO₂ products from the Global Carbon Budget 2023 (Friedlingstein et al., 2023) The solid blue lines indicate the mean difference and the uncertainties show the combined uncertainties from the two respective estimates. The dashed line in (a) shows the difference between the composite estimate and the GOBMs when the ESMs are not adjusted before.

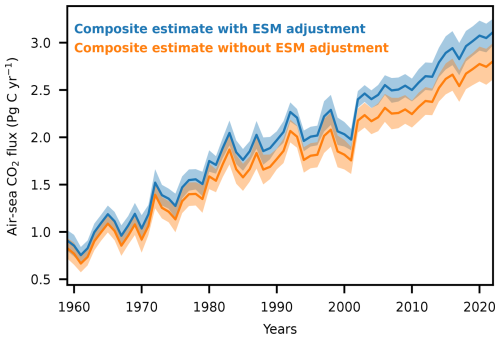
Figure A2 Difference in the composite model-based estimates with and without the adjustment for biases in the ocean carbon sink in Earth system models due to the circulation and surface ocean carbonate chemistry. The composite estimate is shown with the adjustment by Terhaar et al. (2022) (blue line) and without the adjustment (orange line).

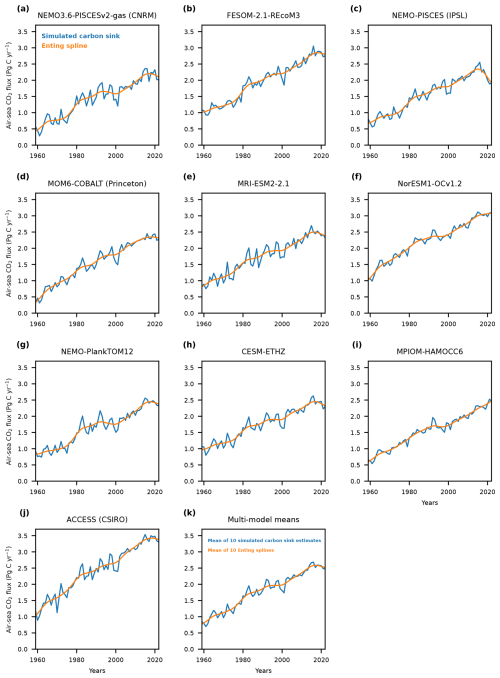
Figure A3 The annual ocean carbon sink as simulated by 10 global ocean biogeochemistry models with an Enting spline fit using a 15-year cutoff period. (a–j) The simulated annual ocean carbon sink for 10 models from the Global Carbon Budget 2023 (Friedlingstein et al., 2023) and the (k) multi-model average (blue lines). An Enting spline fit to each simulated carbon sink and the mean of all spline fits are shown as orange lines.

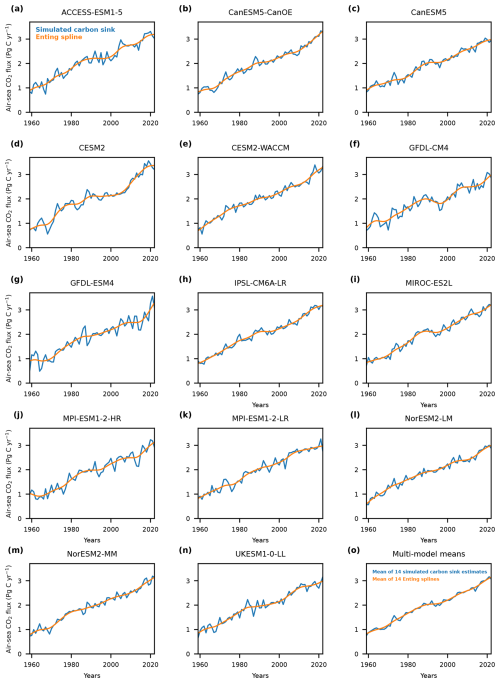
Figure A4 The annual ocean carbon sink as simulated by 14 Earth system models and adjusted for biases in circulation and surface ocean carbon chemistry with an Enting spline fit using a 15-year cutoff period. (a–n) The simulated annual ocean carbon sink for 14 models that were adjusted for biases in the circulation and surface ocean carbon chemistry and the (k) multi-model average (blue lines). An Enting spline fit to each simulated carbon sink and the mean of all spline fits are shown as orange lines.

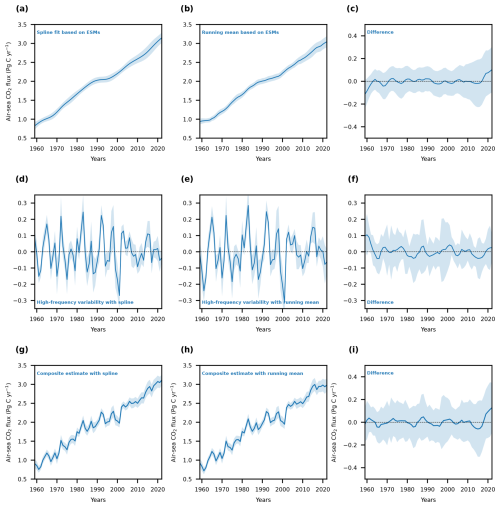
Figure A5 Difference in estimates of the global ocean carbon sink between the new composite estimate and estimates from GOBMs and pCO₂ products. Difference between the composite estimate of the global ocean carbon sink and the estimates (a) from GOBMs and (b) pCO₂ products from the Global Carbon Budget 2023 (Friedlingstein et al., 2023). The blue lines indicate the mean difference and the uncertainties show the combined uncertainties from the two respective estimates.

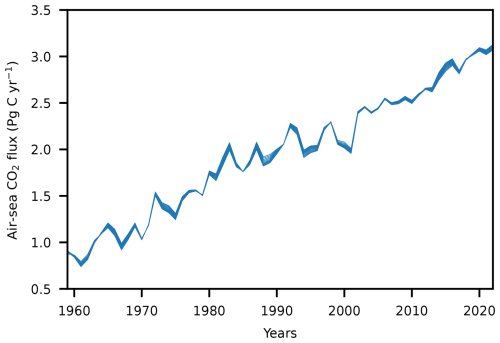
Figure A6 The global ocean carbon sink estimate by the composite model-based estimate using different cutoff periods. Each of the 11 lines here represents the global ocean carbon sink estimate by the composite model-based estimate using cutoff periods from 10 to 20 years.

Table A1 Annually averaged best estimates and uncertainties (1σ) of the global ocean carbon sink by the composite model-based estimate. All units are in Pg C yr⁻¹.

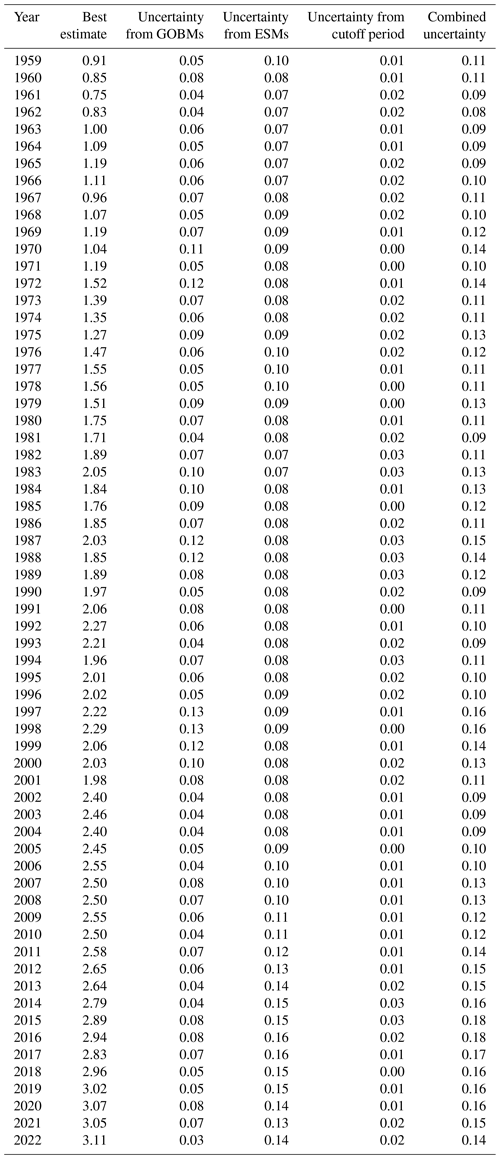
Table A2 Observation-based pCO₂ products from the Global Carbon Budget 2023 (Friedlingstein et al., 2023).

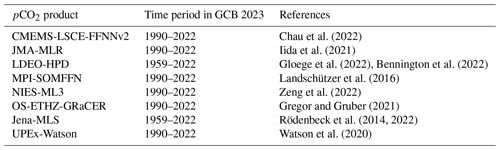
Table A3 Global ocean biogeochemical models from the Global Carbon Budget 2023 (Friedlingstein et al., 2023).

Table A4 List of Earth system models that were used in this study.

The carbon sink estimates from ESMs were adjusted for biases in each model's circulation and carbonate chemistry as described by Terhaar et al. (2022). Each model's annually averaged and globally integrated ocean carbon sink was adjusted based on three predictors that were previously identified to determine the strength of the ocean carbon sink. The rate by which surface water with high anthropogenic carbon is transported to the ocean interior and replaced by newly upwelled water was shown to be largely driven in ESMs by the surface ocean salinity in the Southern Ocean that largely determines the rate of formation of mode and intermediate waters in that region (Terhaar et al., 2021a) and the strength of the Atlantic Meridional Overturning Circulation that determines the strength of the subsurface water formation in the subpolar North Atlantic in ESMs (Terhaar et al., 2022). In addition, the globally averaged Revelle factor determines the amount of carbon that the surface ocean can take up for a given increase in CO₂ in the atmosphere in ESMs (Terhaar et al., 2022). These three predictors, the same as in Terhaar et al. (2022), were used here. For the target variable, however, here I did not use the ocean carbon sink estimates from 1997 to 2014 but the ocean carbon sink from 1959 to 2022, the period for which this new composite model-based estimate provides annual ocean carbon sink estimates. To calculate the adjustment factors, here I used SSP5-8.5 after 2014 for which three more ESMs provide output (Table A4) as the higher number of ESMs makes the fit between predictors and target variables more robust (r² decreases from 0.82 to 0.63 when only using the 14 ESMs that provide output for SSP1-2.6). The adjustment increases the mean carbon sink in the ESMs and hence the estimate of the composite estimate by 11 % and reduces the uncertainty by 12 % (Fig. A2). Hence, the main part of the reduction in uncertainty indeed stems from the combination of the two model classes and not from the adjustment to the ESMs by Terhaar et al. (2022). However, the adjustment is necessary to adjust for a known bias in the strength of the ocean carbon sink in ESMs (Terhaar et al., 2022).

Instead of using several different ESMs, one could also use large ensembles such as the GFDL-ESM2M large ensemble (Burger et al., 2022) or the CESM2 large ensemble (Rodgers et al., 2021). The advantage of such an ensemble with 30–50 ensemble members is indeed that the forced trend can be better isolated (Li and Ilyina, 2018). However, the disadvantage is that one model can have systematic biases in all its ensemble members. CESM2, for example, appears to have a strong low bias in the Southern Ocean sea surface salinity, hence the creation of mode and intermediate waters (Terhaar et al., 2021a). The underestimation of the mode and intermediate water then leads to too little carbon uptake in the Southern Ocean, with a strong global imprint (see Fig. 3 in Terhaar et al., 2022). The multi-model approach, on the other hand, has the distinct advantage that systematic biases in single models are averaged out to the best extent possible. Moreover, the use of these different models even allows correcting the multi-model estimate for biases that remain within the entire model ensemble (Terhaar et al., 2022). The disadvantage of the multi-model approach is that it has a smaller number of simulations so that the true forced trend may not be completely isolated, and some random variability may remain. However, as a spline fit is later fitted to the Earth system model output, that variability is largely removed as well. Although not all internal variability might be filtered out entirely by the multi-model ensemble, I use this multi-model ensemble to avoid biases in the magnitude of the long-term carbon sink that could arise from using a large ensemble of a single model.

A2 Separating high-frequency variability and long-term trends

The high-frequency variability and long-term trends of the annually averaged global carbon sink in ESMs and GOBMs were separated by fitting a spline following Enting (1987) to the respective ocean carbon sink estimate (Figs. A3 and A4). The fit itself represents the long-term trends and decadal variability, and the residual, the difference between the original time series and the spline fit, is defined as the high-frequency variability. Here I used an openly available Python implementation of this spline fitting method (https://github.com/friedrichs-repo/enting_spline, last access: 8 July 2024) with a cutoff period of 15 years. The cutoff period describes the period where 50 % of the signal is attenuated by the spline. A 15-year period was chosen to guarantee that all sub-decadal variability is removed from the original time series.

To test the sensitivity to the choice, a composite model-based estimate was also calculated using an 11-year running mean instead of a spline using Enting (1987) with a cutoff period of 15 years. The composite model-based estimate using the 11-year running mean is almost indistinguishable from the estimate using Enting (1987) with a cutoff period of 15 years but differs at the start and the end of the time series (Fig. A5). The running mean flattens at the ends of time series with strong trends because neither the smaller values before the beginning of the time series nor the potentially larger values after the end of the time series are included. Thus, I decided to rely on the spline fit from Enting (1987) here.

The spline fit itself also comes with uncertainties due to the choice of the cutoff period. Here, I calculated the composite model-based estimate using cutoff periods from 10 to 20 years (Fig. A6). The resulting composite model-based estimate is insensitive to the choice of the cutoff period. This insensitivity shows that it is essential that the inter-annual variability is taken from the GOBMs and the long-term trends from the ESMs. The variability in between, however, can be taken from either GOBMs or ESMs as the decadal variability and trends of the ocean carbon sink are mainly driven by the change in the trends in atmospheric CO₂, i.e. the growth rate of atmospheric CO₂ (McKinley et al., 2017, 2020; Fay et al., 2023; Terhaar, 2024), and other external forcing such as volcanoes (McKinley et al., 2020; Fay et al., 2023; Frölicher et al., 2013), which are prescribed in GOBMs and ESMs (until 2014) based on observations. As GOBMs have external forcing, such as volcanoes, prescribed and ESMs have it prescribed until 2014, the end of the historical period in CMIP6, the long-term effect of volcanoes is part of the long-term ESM estimate and the short-term variability due to volcanoes is part of the short-term variability from GOBMs. As the same spline and cutoff period are used to separate the long-term trend and short-term variability in GOBMs and ESMs, there is no double counting of the overall effect of volcanoes (Fay et al., 2023).

A3 Combining high-frequency variability and long-term trends to form the composite estimate

As described in the Results section, the composite estimate combines two components of the ocean carbon sink time series. One component is the short-term variability, and one component is the long-term trend. Mathematically, the ocean carbon sink can be separated into these two components:

$$\begin{array}{}\text{(A1)}& S_{\mathrm{OCEAN}}=S_{\mathrm{OCEAN}}^{\mathrm{STV}}+S_{\mathrm{OCEAN}}^{\mathrm{LTT}},\end{array}$$

where S_OCEAN is the total carbon sink, $S_{\mathrm{OCEAN}}^{\mathrm{STV}}$ is the short-term variability component, and $S_{\mathrm{OCEAN}}^{\mathrm{LTT}}$ is the long-term trend component. The ocean carbon sink of each GOBM ($S_{\mathrm{OCEAN}}^{\mathrm{GOBM}}$) and each ESM ($S_{\mathrm{OCEAN}}^{\mathrm{ESM}}$) (after adjustment for biases) was then separated into their short-term variability components ($S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{STV}}$ and $S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{STV}}$) and their long-term trend components ($S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{LTT}}$ and $S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{LTT}}$).

$$\begin{array}{}\text{(A2)}& {\displaystyle }{S}_{\mathrm{OCEAN}}^{\mathrm{GOBM}}=S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{STV}}+S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{LTT}}\text{(A3)}& {\displaystyle }{S}_{\mathrm{OCEAN}}^{\mathrm{ESM}}=S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{STV}}+S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{LTT}}\end{array}$$

Here I performed the separation using an Enting spline with a 15-year cutoff period as described in Sect. A2 and also tested the sensitivity of the results to a change in the cutoff period and to the use of a different method to extract the long-term trend, i.e. a running mean. The separation was performed for each model individually. If the same method is used to separate the short-term variability and the long-term trend in ESMs and GOBMs, there is no double counting of forcing that is present in both ensembles, such as volcanoes (Fay et al., 2023).

As described in the Introduction and Results sections, the historic short-term variability is more accurately simulated in GOBMs as they are forced with atmospheric reanalysis data, and the long-term trend is more accurately simulated in ESMs due to different ways of setting up these GOBMs, e.g. the lengths of the spin-up, different atmospheric CO₂ during the pre-industrial spin-up (Terhaar et al., 2024), and a pre-industrial ocean that is too warm and hence transient warming that is too weak in GOBMs (Huguenin et al., 2022; Hollitzer et al., 2024). Thus, the composite model-based estimate ($S_{\mathrm{OCEAN}}^{\mathrm{COMPOSITE}}$) is calculated as follows:

$$\begin{array}{}\text{(A4)}& S_{\mathrm{OCEAN}}^{\mathrm{COMPOSITE}}=S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{STV}}+S_{\mathrm{OCEAN}}^{\mathrm{ESMM}-\mathrm{LTT}}.\end{array}$$

The ocean model components in the GOBM and ESM ensembles are not the same. Thus, $S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{STV}}$ and $S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{LTT}}$ may be considered to be inconsistent. However, these two estimates do not need to be based on the same ocean model components, as there is no indication of a link between the long-term trend and short-term variability of the ocean carbon sink. Although it would be possible to only use the members of the GOBM and ESM ensembles that have an ocean model component that is used in an ESM and GOBM, I decided to use all available models in each ensemble as it allows getting the best available estimate of $S_{\mathrm{OCEAN}}^{\mathrm{GOBM}-\mathrm{STV}}$ and $S_{\mathrm{OCEAN}}^{\mathrm{ESM}-\mathrm{LTT}}$.

A4 Uncertainty estimates

The uncertainties of the composite model-based estimate of the ocean carbon sink are a combination of the multi-model standard deviation of the high-frequency estimates from the GOBMs and the long-term trends from the ESMs, as well as the uncertainty from the choice of the cutoff period that was used to calculate the spline (Table A1). The uncertainty of the cutoff period was calculated as the standard deviation of all 11 estimates with cutoff periods from 10 to 20 years (Fig. A6). The different uncertainties are added using error propagation, i.e. by calculating the square root of the sums of the squares of each uncertainty. The difference in the atmospheric CO₂ in the ESMs under SSP1-2.6 after 2014 was not explicitly added as an uncertainty but discussed as a caveat in the paper.