Toward more robust net primary production projections in the North Atlantic Ocean

Phytoplankton plays a crucial role in both climate regulation and marine biodiversity, yet it faces escalating threats due to climate change. Understanding future changes in phytoplankton biomass and productivity under climate change requires the utilization of Earth system models capable of resolving marine biogeochemistry. These models often differ significantly from one another, and most studies typically use the average response across an ensemble of models as the most reliable projection. However, in the North Atlantic, this straightforward method falls short of providing robust projections of phytoplankton net primary production (NPP) over the 21st century. A new inter-comparison approach was therefore developed and applied to eight models from the sixth phase of the Coupled Model Intercomparison Project (CMIP6) exhibiting substantial divergence in their NPP projections in the North Atlantic. The basin was first divided into three bioregions tailored to the characteristics of each model using a novel method based on a clustering procedure. The mechanisms controlling NPP projections were then identified in each model and in each bioregion, revealing two mechanisms responsible for a large part of model divergence: diazotrophy in the subtropical region and the presence of an ammonium pool in the subpolar region. This allowed for an informed selection of models in each region based on the way they represent these two mechanisms, resulting in reduced projection uncertainty, enhanced total NPP decrease in the subtropical region, and a strengthened increase in small phytoplankton NPP in the subpolar North Atlantic. These model selections enhanced the decreases in carbon export and phytoplankton biomass but had no impact on zooplankton biomass. This innovative approach has strong synergies with other widely used inter-comparison techniques, such as emergent constraints, and their combination would provide valuable insights into the future trajectory of the Earth's climate system.

1 Introduction

The world's oceans are facing increasing pressures due to climate change, leading to significant alterations in their physical and biogeochemical conditions. Sea surface temperature (SST) has risen by an average of 0.88 °C between 1850–1900 and 2011–2020 (Fox-Kemper et al., 2021), pH has declined by 0.016 to 0.020 units per decade in the subtropical regions since the 1980s (Canadell et al., 2021), and upper-ocean stratification has increased by 5.5 ± 1.0 % between 1960 and 2018 (Li et al., 2020). These changes pose a threat to the oceans' ability to provide essential environmental services that many people rely on, such as fisheries or carbon sequestration. Phytoplankton is key to many of these services, and understanding how climate change will impact it is of primary importance but still remains an open question.

The global distribution of phytoplankton is highly heterogeneous and is strongly influenced by ocean dynamics. The North Atlantic Ocean displays sharp contrasts, featuring a true “sea desert” in its subtropical section and one of the most productive regions on Earth in its subpolar part (Behrenfeld and Falkowski, 1997; Westberry et al., 2008). This high productivity is notably facilitated by a nutrient stream associated with the Atlantic Meridional Overturning Circulation (AMOC), which transports nutrients from equatorial and southern regions to the North Atlantic (Williams et al., 2006, 2011; Palter and Lozier, 2008), and by deep convection areas that bring large quantities of nutrients to the surface (Abot et al., 2023). This elevated productivity supports rich ecosystems and, combined with ocean dynamics, enables the North Atlantic Ocean to sequester large amounts of organic carbon through the biological carbon pump (Nowicki et al., 2022).

Climate change has both direct and indirect effects on phytoplankton net primary production (NPP). Directly, NPP increases with rising temperatures (Eppley, 1972; Sauterey et al., 2023). Indirectly, climate change impacts nutrient supply and light availability. Nutrient fluxes are influenced locally and regionally by increased vertical stratification, which reduces vertical supplies (Bopp et al., 2013), and globally by the projected decrease in the AMOC intensity (Whitt, 2019). Sea ice retreat reduces light limitation in the polar region (Vancoppenolle et al., 2013), while zooplankton grazing is also affected by global warming (Laufkötter et al., 2015; Rohr et al., 2023). The impacts of these mechanisms vary regionally and affect the different phytoplankton groups differently, potentially causing shifts in community structures and total abundance (Kléparski et al., 2023; Benedetti et al., 2021).

Given this intricate complexity, projecting the precise impact of climate change on phytoplankton NPP poses significant challenges. Earth system models (ESMs) from the Coupled Model Intercomparison Project (CMIP) include most of the above processes and thus offer a comprehensive approach to evaluating climate change impact on NPP. CMIP provides standardized experimental protocols (Eyring et al., 2016) based on shared socioeconomic pathways (O'Neill et al., 2014, 2016), enabling comparison of projections across models. Traditionally, all available models from the same CMIP phase are studied together and are used to assess a projection uncertainty around the multi-model mean (Bopp et al., 2013; Fu et al., 2016; Kwiatkowski et al., 2020; Tagliabue et al., 2021). Each model is given the same weight, and the multi-model mean is often considered the best available projection, as it is assumed to be less impacted by the particular sets of parameterizations used in individual models. However, Kwiatkowski et al. (2020) have shown that in the case of NPP projections with models from the sixth phase of CMIP (CMIP6), there was a strong divergence in NPP projections between models at the global scale. This was confirmed in particular regions such as the Indian and Atlantic oceans by Tagliabue et al. (2021). Thus, in terms of NPP, the multi-model mean contains little information and may not be considered a reliable estimate of its future evolution. An approach different from the multi-model mean is therefore needed to assess how NPP will respond to climate change under a given projection scenario.

Several approaches have already been proposed and shown to effectively reduce projection uncertainty. Some studies advocate for model weighting based on their ability to replicate past observations (Sanderson et al., 2017; Knutti et al., 2017), while others highlight the use of emergent constraints as a promising method for reducing projection uncertainty (Eyring et al., 2019; Kwiatkowski et al., 2017). Additionally, in-depth analyses have been conducted to explore the physical drivers of NPP, attributing model discrepancies to variations in ocean physics and their interactions with biogeochemical variables (Whitt, 2019; Xiu et al., 2018; Mousing et al., 2023). However, many of these studies tend to overlook the significant differences in the biogeochemical components of CMIP6 models (Kearney et al., 2021; Séférian et al., 2020). Yet, it is well-established that certain processes, depending on their inclusion and parameterization, can substantially influence NPP projections (Bopp et al., 2022; Rohr et al., 2023).

Building on these insights, the present study seeks to go a step further by linking part of the divergence in NPP projections to specific differences in the biogeochemical processes and pools represented across CMIP6 models. To achieve this, we identify the processes driving long-term NPP evolution under the SSP5-8.5 scenario in each model and use these insights to assess the reliability of their projections. This process-based evaluation will then inform a model selection aimed at reducing projection uncertainties.

The North Atlantic Ocean, a highly productive region with significant future divergence between model projections (Tagliabue et al., 2021), will serve as a case study. Given that the processes controlling NPP vary across different regions, we divide the North Atlantic Basin into three bioregions (polar, subpolar, and subtropical) using a clustering method and evaluate each subregion individually. Finally, we explore how our revised estimates of NPP projections influence carbon export and plankton biomass – key indicators of the biological carbon pump and marine ecosystem health – and how our approach integrates with the other methods mentioned above.

2 Methodology

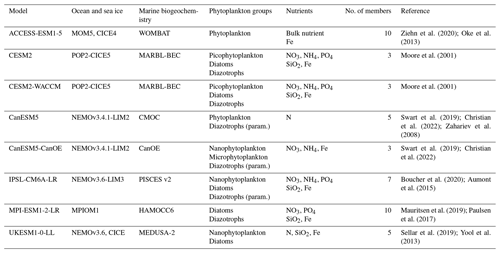
2.1 CMIP6 models

All the CMIP6 models assessed in this study include an ocean biogeochemistry component. For both the historical period and the SSP5-8.5 scenario (O'Neill et al., 2016), a prerequisite for each model was to have a minimum of three ensemble members with available outputs for primary production and for the five clustering variables employed to construct bioregions (chlorophyll a surface concentrations, sea surface temperature (SST), mixed-layer depth (MLD), sea ice concentration, and nitrate surface concentrations). Out of the 16 models with primary production projections under the SSP5-8.5 scenario, only 8 fulfill these criteria. Among the eight excluded models, six have only one member, and the remaining two (CNRM-ESM2-1 and MIROC-ES2L) lack one clustering variable for several or all members. Details about the characteristics of the remaining eight models can be found in Table 1.

Ziehn et al. (2020); Oke et al. (2013)Moore et al. (2001)Moore et al. (2001)Swart et al. (2019); Christian et al. (2022); Zahariev et al. (2008)Swart et al. (2019); Christian et al. (2022)Boucher et al. (2020); Aumont et al. (2015)Mauritsen et al. (2019); Paulsen et al. (2017)Sellar et al. (2019); Yool et al. (2013)

Table 1 Characteristics of the eight CMIP6 models studied. The phytoplankton group diazotrophs (param.) refers to models with an implicit representation of N₂ fixation.

Ensemble means for each model were computed to eliminate a maximum amount of natural variability, allowing us to focus on the impact of anthropogenic climate change. Trends were derived by averaging ensemble mean outputs over 20-year periods every 5 years from 1950–1970 to 2080–2100. These trends were calculated over the region between 10–80° N and 270–360° E, referred to as the North Atlantic Ocean in the subsequent analysis. The period 1950–1970 was taken as the reference, and all projections were expressed as the evolution between this reference period and 2080–2100.

The complexity of ESM marine biogeochemistry components varies significantly from one model to another. Among the eight models selected (Table 1), the simplest model (CMOC) only includes one nutrient and one phytoplankton class (Zahariev et al., 2008), whereas the most complex model (MARBL-BEC) features five nutrients and three phytoplankton classes (Moore et al., 2001; see Kearney et al. (2021) for a summary of the biogeochemistry components of CMIP6 models). Due to these differences, each model is studied individually to comprehensively grasp the mechanisms controlling NPP projections.

Three phytoplankton groups were considered in this study: diatoms, diazotrophs, and small phytoplankton. The last category encompasses classes labeled nanophytoplankton, picophytoplankton, and bulk phytoplankton when sensitivity to silicate is absent. In MPI-ESM1-2-LR, the bulk phytoplankton class is grouped with diatoms due to its reliance on SiO₂ (Ilyina et al., 2013), along with the large phytoplankton class in CanESM5-CanOE, despite the absence of SiO₂ in the model (Christian et al., 2022). Furthermore, CMIP6 models can be categorized into three groups based on their representation of diazotrophy:

• Models without any diazotrophy. These include ACCESS-ESM1-5 and UKESM1-0-LL.

• Models with an explicit group of diazotrophs. These include CESM2, CESM2-WACCM, and MPI-ESM1-2-LR. In these models, diazotroph growth rate is not constrained by nitrogen; they can utilize atmospheric N₂ but depend on PO₄ and Fe availability (Moore et al. (2001) for CESM2 and CESM2-WACCM; Paulsen et al. (2017) for MPI-ESM1-2-LR).

• Models with an implicit representation of diazotrophs. These include IPSL-CM6A-LR, CanESM5, and CanESM5-CanOE. N₂ fixation is parameterized, and its interaction with other nutrients varies based on this parameterization. In IPSL-CM6A-LR, the initial parameterization from PISCES v2 was used (Aumont et al., 2015; Bopp et al., 2022).

CMIP6 models can also be distinguished based on how they represent nitrogen and phosphorus (Table 1). Among the eight models studied, three (ACCESS-ESM1-5, CanESM5, and UKESM1-0-LL) use a unique bulk nutrient meant to represent both nitrogen and phosphorus. In contrast, three others (IPSL-CM6A-LR, CESM2, and CESM2-WACCM) include a PO₄ pool along with two nitrogen pools, NO₃ and NH₄. The CanESM5-CanOE model includes two nitrogen pools (NO₃ and NH₄) but lacks a PO₄ pool. Lastly, MPI-ESM1-2-LR represents both a PO₄ and an NO₃ pool but does not include NH₄. In these CMIP6 models, over our study region, there is an almost-perfect correlation between projected surface NO₃ concentrations and those integrated over the first 100 m (not shown). This makes surface nutrient concentrations an excellent proxy for changes occurring throughout the euphotic layer. Therefore, we chose to use surface concentrations for simplicity in the following analysis.

2.2 Construction of bioregions

The processes governing changes in NPP vary across different regions, necessitating a regional approach. Bioregions are the most suitable framework for conducting such a study because each bioregion corresponds to a specific production regime. However, their boundaries align with physical phenomena such as oceanic currents and sea ice, the precise localization of which varies among models. Consequently, fixed bioregions, like those established by Longhurst (2007) and used in Tagliabue et al. (2021), have limitations for inter-comparison studies.

To address this limitation, a novel approach was developed to establish bioregions tailored to the characteristics of each model. They were constructed using the self-organizing map (SOM) + hierarchical agglomerative clustering (HAC) procedure (defined in the following section), a robust method for extracting temporal and spatial patterns from large datasets. This procedure was first applied to the observed mean seasonal cycles over the recent historical period of five clustering variables, chosen for their relevance in explaining long-term NPP evolution and their availability in CMIP6 model outputs. The bioregions obtained were then replicated in each model. By employing this method, we ensured that each bioregion corresponded to a similar production regime across all models.

2.2.1 The SOM + HAC procedure

The SOM algorithm (Kohonen, 2013) is widely used for pattern identification and clustering analysis for large multi-variate datasets. In environmental sciences, it has been used to study precipitation patterns (Derouiche et al., 2022; Dilmi et al., 2017), monsoon weather regimes (Guèye et al., 2011)), phytoplankton biomes (El Hourany et al., 2021; Hofmann Elizondo et al., 2021), the oceanic circulation (Jouini et al., 2016), and aerosol concentrations (Yahi et al., 2013) or to identify biophysical regions in the Beaufort Sea (Hilborn and Devred, 2022). Similar to classical vector quantization procedures, such as k-means clustering, the SOM algorithm condensates the information contained in a multi-variate dataset into an optimal number of “neurons”, each associated with a vector characterizing a subset of the initial dataset. However, unlike k-means clustering, the neurons in the SOM algorithm are not independent. They are distributed over a 2D map with a topological constraint such that close neurons on the map are similar. Practically, this constraint means that, during the learning phase, neurons are not updated alone but as batches of close neurons, thus allowing the propagation of local updates to the global neuron map. This topological constraint allows for the preservation of the topological properties of the initial dataset. An advantage of the SOM algorithm over k-means clustering procedures is that it is robust to missing data (Vatanen et al., 2015), making it particularly interesting in the regions seasonally covered by sea ice.

When handling environmental data, the specific quantity of classes or neurons is not predetermined. In cases where the SOM is employed for vector quantization, a large number of neurons are utilized, each assigned to a geographic subregion. To determine major patterns among these neurons, an HAC is employed on them while preserving the topological constraints. This procedure is denoted SOM + HAC hereafter. The HAC produces a dendrogram offering various suggestions for estimating the number of classes. A balance is struck between the number of classes that can be logically explained and the number required to encompass the data's embedded information. This approach has demonstrated success in numerous studies (Farikou et al., 2015; Jouini et al., 2016; El Hourany et al., 2021; Baaklini et al., 2022).

2.2.2 The datasets used to build bioregions

To ensure that the bioregions obtained in each model were similar, they were first constructed from the observations before being reproduced in the models (see the following subsection). Here, we describe the datasets of observations used to build these bioregions.

Surface chlorophyll a concentrations were extracted from the GlobColour merged product distributed by the Copernicus Marine Service (MULTIOBS_GLO_PHY_TSUV_3D_MYNRT_015_012; Guinehut et al., 2012; Mulet et al., 2012). It provides daily outputs of surface chlorophyll concentrations over the global ocean from September 1997 to the present. Data from the period 2000–2020 were used.

Sea surface temperature and mixed-layer depth data were extracted from the Multi Observation Global Ocean 3D product from the Copernicus Marine Service (MULTIOBS_GLO_PHY_TSUV_3D_MYNRT_015_012). It provides weekly and monthly values of six variables, including SST and MLD, over the global ocean between 1993 and 2023, built from both in situ and satellite observations. Again, data from the period 2000–2020 were used.

NO₃ concentrations were extracted from the World Ocean Atlas 2018 database (Garcia et al., 2018), while sea ice concentration data came from the EUMETSAT OSI SAF SSMIS product v2.0, distributed by the Copernicus Climate Change Service, and covered the period 1998–2015.

2.2.3 Application of the clustering procedure

The SOM + HAC was first applied to the historical mean seasonal cycles of five clustering variables (surface chlorophyll concentrations, surface nitrate concentrations, mixed-layer depth, sea ice concentration, and sea surface temperature) computed from the datasets previously described. They were regridded to 1° × 1° regular grids, concatenated, and the coastal areas were excluded by removing values from grid cells adjacent to the continents. The North Atlantic Ocean was thus represented by 3335 grid points, each associated with a vector of dimension 60, corresponding to the five successive climatological seasonal cycles. To ensure equal weighting of all variables in the clustering process, the dataset was normalized beforehand. Several normalization methods, such as those outlined in Derouiche et al. (2022), Dilmi et al. (2017), and Hilborn and Devred (2022), can be employed. It was decided to normalize each seasonal cycle by dividing it by the absolute maximum value reached over the entire period and region. This normalization method has the advantage of preserving the dataset structure while ensuring all values fall within the range of −1 and 1. The selection of clustering variables resulted from a compromise between their relevance in explaining primary production variability in the North Atlantic Ocean and their availability in CMIP6 model outputs. For instance, silicate concentration was excluded, despite its acknowledged impact on primary production in the subpolar gyre (Hátún et al., 2017; Sieracki et al., 1993), as only five out of eight models provided the output.

The neurons obtained from the observations were then used to replicate similar bioregions in the CMIP6 models. In each model, a matrix akin to that of the observations was reproduced with the average seasonal cycles over the period 2000–2020, using the same normalization method and constants. Each grid point in each model was subsequently assigned to its nearest neuron based on Euclidean distance and to the cluster associated with that neuron, thereby reproducing the bioregions in each model. This assignment was carried out regardless of the distance between the grid point and the neuron. Consequently, the regions obtained were the closest to those built from the observations but could be rather different from them.

3 Results

3.1 Global projections

Primary production projections over the whole North Atlantic Ocean with CMIP6 models exhibit a large spread (Fig. 1a). Among the eight models, five (UKESM1-0-LL, CESM2, CESM2-WACCM, MPI-ESM1-2-LR, and CanESM5) project a strong decrease in net primary production (from −33.6 to −11.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ in 2080–2100 with respect to 1950–1970), while the remaining three (CanESM5-CanOE, IPSL-CM6A-LR, ACCESS-ESM1-5) project an increase (from +8.0 to +17.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$). On average, CMIP6 models project an NPP decrease of −10.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$. This range is similar to the one obtained with the first member of the 16 models used in Tagliabue et al. (2021). Therefore, the selected subset of eight models is considered representative of the broader ensemble of CMIP6 models.

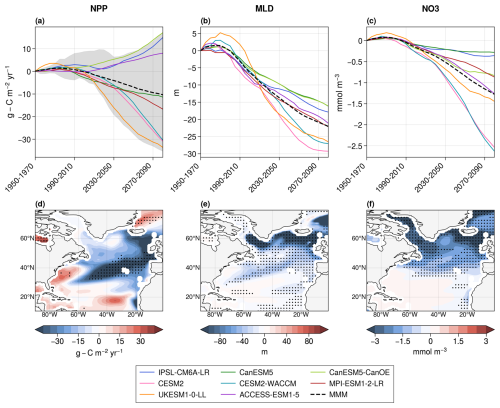
Figure 1 Projections of NPP (a), mixed-layer depth (b), and surface NO₃ concentrations (c) in the eight CMIP6 models over the whole North Atlantic Ocean. The dotted black lines are the multi-model means (MMMs), and the shaded area in the NPP panel corresponds to the range of projections with the first member of the 16 models used in Tagliabue et al. (2021). Multi-model means of the projected changes in NPP (d), mixed-layer depth (e), and surface NO₃ concentrations (f) between 1950–1970 and 2080–2100. Stippling indicates areas of robust projections, defined by an 80 % agreement in the sign of change across models.

There is confidence in the sign of NPP projections in the northeastern section of the subtropical gyre and along Greenland's eastern coast only (Fig. 1d). Confidence is defined here, following Kwiatkowski et al. (2020), as at least 80 % of the projections having the same sign. Models disagree on the sign of the future evolution of NPP in most of the subpolar gyre and in the southern subtropical gyre. This lack of confidence happens despite agreement between models on the sign of the long-term evolution of MLD and surface nitrate concentrations, particularly in the subpolar North Atlantic Ocean (Fig. 1e and f). On average over the region, all models project a decrease in MLD and NO₃ concentrations, with a multi-model mean decrease of −22.1 m and −1.3 mmol m⁻³, respectively.

3.2 Construction of the bioregions

The SOM + HAC procedure identified an optimal number of four bioregions in the observations: one subtropical region, one polar region, and two subpolar regions (Fig. 2). The subtropical bioregion, the largest at 20.8 million km², exhibits an oligotrophic regime characterized by very low nitrate and chlorophyll a concentrations (maximum annual values of 0.87 mmol m⁻³ and 0.16 mg m⁻³, respectively). It is situated over the subtropical gyre and the Caribbean Sea, bordered by the North Atlantic Current to the north. The polar region, the smallest at 1.0 million km², stands out due to the extensive presence of sea ice during winter and is further divided into two subregions: the Baffin Sea and the eastern Greenland Sea. The two subpolar regions, with surfaces of 3.3 and 4.8 million km², respectively, correspond to the intergyre region with the northern part of the Labrador Sea and the northern subpolar gyre with the Norwegian Sea. The latter region exhibits a deeper winter mixed layer, higher nitrate surface concentrations, and a delayed bloom compared to the former. However, the two regions do not significantly differ in terms of annual maximum chlorophyll a concentrations (0.76 mg m⁻³ in August for the former and 0.80 mg m⁻³ in September for the latter).

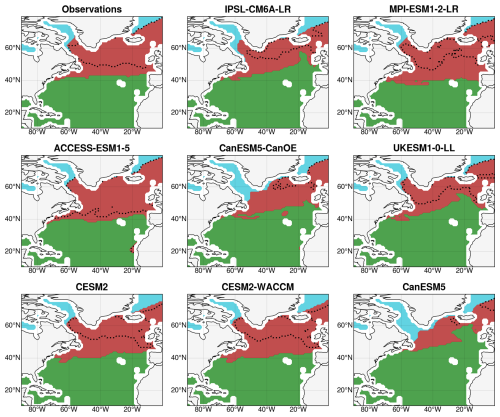
Figure 2 Bioregions built with the SOM + HAC procedure from the historical seasonal cycles of chlorophyll a concentrations, nitrate concentrations, SST, MLD, and sea ice concentration and their reproduction in CMIP6 models for the period 2000–2020. The subtropical region is in green, the subpolar region is in red, and the polar region is in cyan. The dotted black lines indicate the boundary between the two original subpolar bioregions.

Qualitatively, the models reproduce the historical bioregions obtained from observations fairly well, in terms of both localization and physical boundaries, despite variations in surfaces (Fig. 2). The subtropical region's surface ranges from 19.1 million km² in MPI-ESM1-2-LR to 24.1 million km² in CanESM5, while the polar region's surface varies from 0.9 million km² in MPI-ESM1-2-LR to 2.0 million km² in CanESM5. The overall subpolar region is relatively consistent across different models, but the relative importance of the subregions varies significantly from one model to another. It was decided to merge the subpolar subregions into one large subpolar region, supported by strong inter-model correlations between the projections of NPP in the two regions (r = 0.91; p = 0.002), indicating a similar dominant mechanism. The three resulting bioregions are presented for the observations and each model in Fig. 2. Each of these bioregions will now be studied successively to determine the mechanisms controlling NPP projections.

3.3 Regional analysis

3.3.1 Subtropical region

NPP projections strongly diverge in the subtropical region, with three models projecting an increase (up to +19.5 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ in 2080–2100 with respect to the 1950–1970 mean), while the remaining five project a decrease (down to −33.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) (Fig. 3a). These divergent groups align with those observed for the entire North Atlantic Ocean (Fig. 1a), suggesting that the subtropical region predominantly influences the basin-scale divergence of projections.

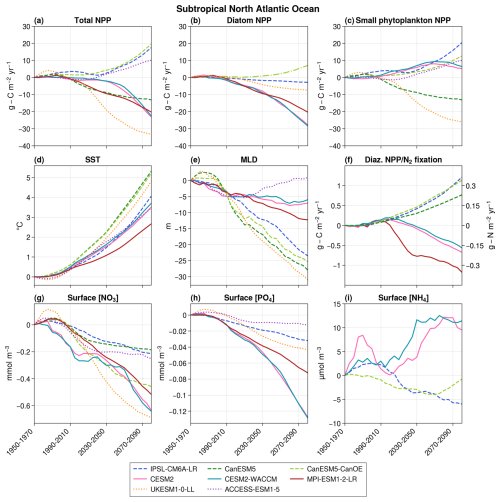
Figure 3 Projections over the subtropical bioregion of total NPP (a), diatom NPP (b), small phytoplankton NPP (c), SST (d), MLD (e), diazotrophs NPP/N₂ fixation (f), surface nitrate concentrations (g), surface phosphate concentrations (h), and surface ammonium concentrations (i). The average value over 1950–1970 is taken as the reference. The dotted lines represent models without diazotrophy, dashed lines correspond to models with parameterized N₂ fixation, and solid lines indicate models with an explicit diazotroph group. In panel (f), diazotroph NPP is shown on the left axis for models with an explicit diazotroph group, while N₂ fixation is plotted on the right axis for models with parameterized N₂ fixation. In panel (b), CanESM5-CanOE is represented by a dashed–dotted line to distinguish it from the other models. This distinction is made because it is the only model that includes a diatom group without SiO₂ and in which both diatoms and small phytoplankton are equally efficient at utilizing NH₄.

This substantial discrepancy occurs despite coherent evolutions across models for other crucial physical and biogeochemical variables (Fig. 3). Notably, sea surface temperature (SST) increases in all models (ranging from +2.7 °C in MPI-ESM1-2-LR to 5.3 °C in CanESM5), while surface NO₃ concentrations and surface PO₄ concentrations decrease (NO₃ concentrations from −0.19 to −0.69 mmol m⁻³; PO₄ concentrations from −0.01 to −0.13 mmol m⁻³). Mixed-layer depth and carbon export at 100 m depth both decrease in all models but one (ACCESS-ESM1-5 and IPSL-CM6A-LR, respectively), in which they increase after a period of decrease.

Small phytoplankton's NPP exhibits a strong discrepancy. The only variable able to cause this divergence is N₂ fixation, for which a clear separation appears between models with an implicit representation of diazotrophs, which project a strong increase in N₂ fixation, and those with an explicit representation, which project a decrease in diazotrophs' NPP (Fig. 3). As detailed in the Methodology section, CMIP6 models can be categorized into three groups according to their representation of N₂ fixation. We now examine each of these groups individually.

The two models with no diazotrophy project different primary production evolutions (ACCESS-ESM1-5 projects an increase of 10.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, while UKESM1-0-LL projects a decrease of −33.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$). In UKESM1-0-LL, the production of both small phytoplankton and diatoms decreases (Fig. 3). This discrepancy is mainly attributed to differences in annual maximum surface nitrate concentrations (1.0 and 0.3 mmol m⁻³ on average, respectively, in 2000–2020, whereas, according to the World Ocean Atlas 2018, the real value is 0.4 mmol m⁻³). In UKESM1-0-LL, nitrates are strongly limiting, and their declining trend (see Fig. 3g) leads to a decreased primary production for all phytoplankton groups. In ACCESS-ESM1-5, nitrates are not a strong limitation on average across the entire subtropical region, and the mechanisms causing NPP increase are more complex. Between 1950 and 2020, the opposing effects of rising SST and decreasing surface nutrient concentrations – partly due to mixed-layer shallowing – largely balance each other out, resulting in stable NPP. However, from 2020 to 2100, a recovery in MLD slows the decline in nutrient concentrations, allowing the SST effect to dominate, which leads to an increase in NPP.

The three models with an explicit representation of diazotrophs all project a decrease in both total primary production and N₂ fixation. This decrease affects both diazotrophs and diatoms in these models, while small phytoplankton primary production in CESM2 and CESM2-WACCM initially increases before decreasing (Fig. 3b, c, and f). This coherence across phytoplankton groups suggests that the mechanism influencing primary production evolution could affect all of them, ruling out nitrates as a potential candidate, as they do not impact diazotrophs. The only variable capable of explaining these evolutions is PO₄ concentrations, influencing all phytoplankton groups, consistently decreasing in all three models and known to limit N₂ fixation in the region in CESM models (Wang et al., 2019). Additionally, in CESM2 and CESM2-WACCM, small phytoplankton has a lower PO₄ half-saturation constant than diazotrophs and diatoms (0.00025, 0.0005, and 0.00125 mmol m⁻³, respectively; Moore et al., 2001), enabling them to thrive in environments with low PO₄ concentrations. This explains the initial increase in their primary production before declining when PO₄ concentrations become too low. Consequently, in models with an explicit representation of diazotrophs, decreasing PO₄ concentrations lead to a reduction in overall primary production, including diazotrophs, subsequently causing a decrease in N₂ fixation.

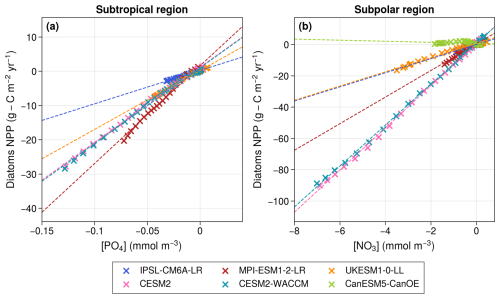
Figure 4 Scatter plots representing the change in diatom NPP relative to 1950–1970 versus the change in surface PO₄ concentrations in the subtropical region (a) and NO₃ concentrations in the subpolar region (b). CanESM5-CanOE appears only in the subpolar panel due to the absence of PO₄ in the model. The dashed lines represent linear regressions, all of which are significant at the p < 0.05 level, and show correlations greater than 0.96, except for CanESM5-CanOE, where the correlation is not significant (p = 0.11).

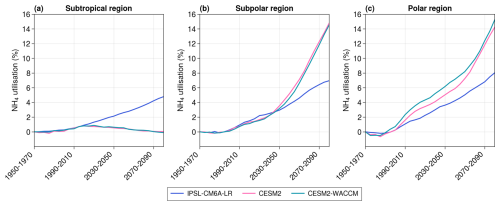
Figure 5 Projections of the proportion of total NPP using NH₄ rather than NO₃ as a nitrogen source in the subtropical (a), subpolar (b), and polar (c) regions. The average value over 1950–1970 is taken as the reference. CanESM5-CanOE is not included in this figure, despite its representation of NH₄, because the variable “intppnitrate”, used to construct this figure, is not available for that model.

The three models with parameterized diazotrophy exhibit contrasting behaviors in their total NPP projections. While IPSL-CM6A-LR and CanESM5-CanOE project an increase in total NPP, CanESM5 projects a decrease (Fig. 3a). In IPSL-CM6A-LR, the absence of effective control of PO₄ concentrations over N₂ fixation was identified as being responsible for the substantial increase in diazotrophy and primary production in subtropical oceans (Bopp et al., 2022). The increase in N₂ fixation replenishes the NH₄ pool (Aumont et al., 2015), leading to a greater proportion of total NPP being supported by NH₄ rather than NO₃ as a nitrogen source (Fig. 5a). This mechanism primarily benefits small phytoplankton, which are more efficient at consuming nutrients at low concentrations, such as NH₄ (Aumont et al., 2015). As a result, small phytoplankton NPP increases in IPSL-CM6A-LR despite the decline in NO₃ concentrations. The slight decrease in surface NH₄ concentrations can be explained by the increased consumption by small phytoplankton. However, this process does not benefit diatoms, whose long-term growth is regulated by PO₄ (Fig. 4a), leading to a decline in their NPP. In CanESM5-CanOE, N₂ fixation similarly replenishes the ammonium pool, and the same trends as in IPSL-CM6A-LR are observed for small phytoplankton NPP and surface NH₄ concentrations. Although we cannot compute the proportion of total NPP based on NH₄ versus NO₃ for CanESM5-CanOE due to the lack of data (Fig. 5), the similar behaviors between the models suggest that the mechanism is the same: the additional NH₄ from N₂ fixation supports the increase in small phytoplankton NPP. However, unlike IPSL-CM6A-LR, CanESM5-CanOE also shows an increase in diatom NPP. This can be attributed to the absence of PO₄ in CanESM5-CanOE, which cannot control diatom NPP, and the fact that, unlike in IPSL-CM6A-LR, the half-saturation constants for ammonium are the same for diatoms and small phytoplankton (Christian et al., 2022). As a result, diatoms are as efficient as small phytoplankton in consuming NH₄, allowing them to benefit from N₂ fixation and leading to a rise in their NPP. Finally, in CanESM5, a single nitrogen pool combines both ammonium and nitrate. Despite the strong increase in N₂ fixation, nitrogen concentrations in the subtropical region decrease overall (Fig. 3g), resulting in a decline in total NPP (Fig. 3a).

Diatom NPP decreases and is almost perfectly correlated with the evolution of surface PO₄ concentrations (r≥ 0.99, p≪ 0.01) in all models except CanESM5-CanOE (Fig. 4a). As explained in the previous paragraph, the different behavior of the diatom group in CanESM5-CanOE is explained by the absence of PO₄ in the model and by its high sensitivity to NH₄. In the remaining models, the inter-model spread in diatom NPP projections is primarily driven by differences in the sensitivity of diatoms to declining PO₄ concentrations.

The interactions between N₂ fixation, phosphates, and small phytoplankton therefore appear to be a strong diverging factor between models, with the potential to partially decouple total NPP from NO₃ concentrations. The models with the most realistic representations of diazotrophy (CESM2, CESM2-WACCM, and MPI-ESM1-2-LR) all project a decrease in NPP because of the declining PO₄ concentrations. The strong increases observed in some models are caused by either nitrate concentrations that are too high when no diazotrophy is represented or their unchecked influence by PO₄ concentrations, making such scenarios unlikely.

3.3.2 Subpolar region

NPP projections also significantly diverge in the subpolar region (Fig. 6a). Three models (CESM2, CESM2-WACCM, and UKESM1-0-LL) project a substantial decrease (−54.3, −53.7, and −44.7 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, respectively, in 2080–2100 with respect to 1950–1970), while three others (IPSL-CM6A-LR, CanESM5-CanOE, and ACCESS-ESM1-5) project a modest increase (+5.4, +6.6, and +3.8 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, respectively). The remaining two models project an intermediate decline (−12.7 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ in MPI-ESM1-2-LR and −10.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ in CanESM5). This disparity persists despite consistent trends across models for other physical and biogeochemical variables, such as SST, MLD, AMOC intensity, and NO₃ and PO₄ surface concentrations (Fig. 6). However, the breakdown of NPP projections into the different phytoplankton groups highlights that it is predominantly small phytoplankton that explains the model disagreement on the sign of total NPP future evolution (Fig. 6).

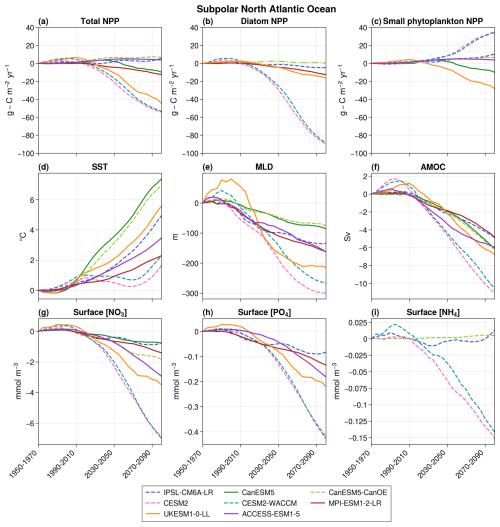
Figure 6 Projections over the subpolar bioregion of total NPP (a), diatom NPP (b), small phytoplankton NPP (c), SST (d), MLD (e), AMOC (f), surface nitrate concentrations (g), surface phosphate concentrations (h), and surface ammonium concentrations (i). The average value over 1950–1970 is taken as the reference. The dashed lines represent models with an ammonium pool, and solid lines indicate models without NH₄. In panel (b), CanESM5-CanOE is represented by a dashed–dotted line to distinguish it from the other models. This distinction is made because it is the only model that includes a diatom group without SiO₂ and in which both diatoms and small phytoplankton are equally efficient at utilizing NH₄.

Five out of seven models project an increase in small phytoplankton NPP, despite a consistent decrease in NO₃ and PO₄ concentrations across models (Fig. 6). Of these five, four (IPSL-CM6A-LR, CanESM5-CanOE, CESM2, and CESM2-WACCM) include an ammonium pool. In IPSL-CM6A-LR, CESM2, and CESM2-WACCM, the proportion of total NPP derived from NH₄ rather than NO₃ significantly increases (Fig. 5b). As observed in the subtropical region, this rise offsets the impact of decreasing NO₃ concentrations, leading to an increase in small phytoplankton NPP, along with a decrease in surface NH₄ concentrations in CESM2 and CESM2-WACCM. However, in these models, diatoms are strongly dependent on NO₃ (Fig. 4), and their NPP declines accordingly. For CanESM5-CanOE, it is not possible to compute the proportion of total NPP supported by NH₄ versus NO₃, but it can be hypothesized that NH₄ similarly sustains NPP, which would explain the slight increase in small phytoplankton NPP and the stagnation in diatom NPP. Notably, only in IPSL-CM6A-LR does the rise in small phytoplankton NPP fully compensate for the decline in diatom NPP, explaining the overall positive trend in total NPP.

The increased NPP of small phytoplankton in ACCESS-ESM1-5, where there is no NH₄ pool, was attributed to the absence of nitrate limitation (minimum annual concentration of 1.5 mmol m⁻³ over 2080–2100 despite a consistent decrease throughout the 21st century). The elevation in SST and the reduction in light limitation due to the shallowing of MLD can consequently enhance NPP. Conversely, in UKESM1-0-LL and CanESM5, nitrates exert strong limitations (minimum annual concentration of 0.04 and 0.003 mmol m⁻³, respectively, over 2080–2100), and their depletion leads to a reduction in NPP.

Diatom NPP consistently decreases across all models except CanESM5-CanOE. In all models but CanESM5-CanOE, projections of diatom NPP are strongly and significantly correlated with maximum annual surface NO₃ concentrations (r > 0.96, p≪ 0.01; Fig. 4b). Therefore, as in the subtropical region, the inter-model spread in diatom NPP projections is primarily driven by differences in the sensitivity of diatoms to declining NO₃ concentrations. In contrast, the increase in diatom NPP in CanESM5-CanOE, along with its lack of correlation with surface NO₃ concentrations, is likely influenced by NH₄. Unlike IPSL-CM6A-LR, CESM2, and CESM2-WACCM, CanESM5-CanOE uses identical ammonium uptake half-saturation constants for both small phytoplankton and diatoms (Christian et al., 2022). As a result, in this model, diatoms can utilize ammonium as efficiently as small phytoplankton, leading to similar behavior between the two groups. This likely explains why CanESM5-CanOE is the only model where the long-term evolution of diatoms is not controlled by macro-nutrient concentrations.

The strong increase in small phytoplankton's NPP observed in some CMIP6 models is therefore made possible by the presence of an ammonium pool, which is an alternative source of nitrogen and sustains NPP. NH₄ is only present in small concentrations but is quickly regenerated and is therefore preferentially used by small phytoplankton rather than diatoms, except in CanESM5-CanOE. This explains why diatoms cannot benefit from it and why they decrease with macro-nutrient concentrations.

3.3.3 Polar region

Primary production increases in all models in the polar region, ranging from +6.2 to +25.5 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ in 2080–2100 with respect to 1950–1970 (Fig. 7). These increases are mainly caused by sea ice retreat (on average, 36.4 % of the initial polar regions are still covered in sea ice in the winters of 2080–2100 against 95.5 % in 1950–1970), which leaves space for phytoplankton's growth and thus leads to an increase in NPP. Surface concentrations of NO₃ and PO₄ decrease across all models (Fig. 7g and h), driven by both changes in ocean physics and increased consumption by phytoplankton. The proportion of NPP relying on NH₄ rather than NO₃ increases in IPSL-CM6A-LR, CESM2, and CESM2-WACCM (Fig. 5c), thus leading to a decrease in surface NH₄ concentrations in the three models.

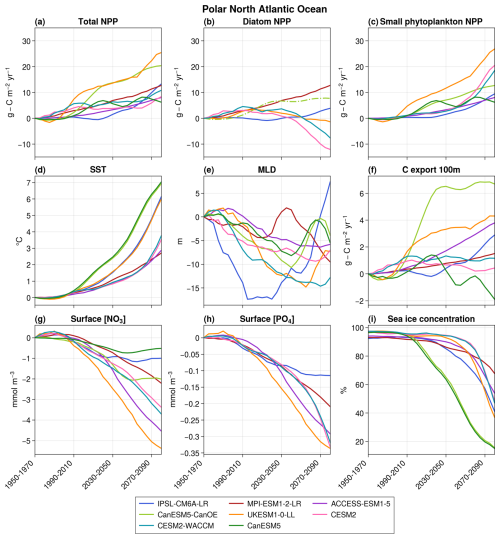
Figure 7 Projections over the polar bioregion of total NPP (a), diatom NPP (b), small phytoplankton NPP (c), SST (d), MLD (e), carbon export at 100 m (f), surface nitrate concentration (g), surface phosphate concentration (h), and sea ice concentration (i). The average value over 1950–1970 is taken as the reference for all variables except sea ice concentration. In panel (b), CanESM5-CanOE is represented by a dashed–dotted line to distinguish it from the other models. This distinction is made because it is the only model that includes a diatom group without SiO₂ and in which both diatoms and small phytoplankton are equally efficient at utilizing NH₄.

This increase in total NPP is observed in all models for small phytoplankton but not for diatoms, for which three models (CESM2, CESM2-WACCM, and UKESM1-0-LL) project a decrease in their primary production after an initial increase (Fig. 7). These three models are the most sensitive to a decrease in NO₃ concentrations, as they have the highest NO₃ half-saturation constants for diatoms of the six models (2.5 mmol m⁻³ for CESM2 and CESM2-WACCM, Moore et al., 2001; 0.75 mmol m⁻³ for UKESM1-0-LL, Yool et al., 2013). Moreover, they all reach very low annual minimum NO₃ concentrations (0.02, 0.02, and 0.19 mmol m⁻³, respectively, in 2080–2100 (not shown)), indicating a termination of the bloom by nitrates. Therefore, in these three models, after a first period in which the retreat of sea ice leads to an increase in primary production through the reduction in light limitation, nitrates become the main controlling factor of primary production, which leads to its decrease. In IPSL-CM6A-LR, nitrate concentrations are even lower than in the previous models (annual minimum of 0.01 mmol m⁻³ in 2080–2100), but diatoms are less sensitive to low nitrate concentrations (half-saturation constant of 0.39 mmol m⁻³, Aumont et al., 2015), and their primary production can keep increasing under the reduction in light limitation. In MPI-ESM1-2-LR and CanESM5-CanOE, nitrate concentrations are high throughout the 21st century (annual minimum concentration of 1.18 and 0.47 mmol m⁻³, respectively, in 2080–2100 despite a consistent decrease throughout the century) and never become limiting. Diatom primary production can therefore freely increase with sea ice retreat.

To summarize, climate change leads to an increase in small phytoplankton NPP in all CMIP6 models because of sea ice retreat. The fate of diatoms is the result of a compromise between their sensitivities to light and nitrates and the evolutions of NO₃ concentrations and sea ice, as was already the case in CMIP5 (Vancoppenolle et al., 2013). However, only a small portion of the Arctic was included in this study, and the results found cannot be expanded to the total Arctic Ocean.

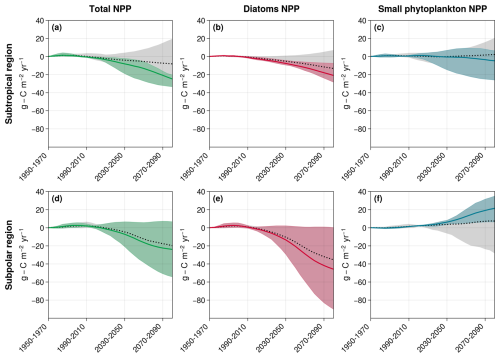
Figure 8 New estimates of total NPP (a, d), diatom NPP (b, e), and small phytoplankton's NPP (c, f) projections with the selected CMIP6 models in the subtropical (a–c) and subpolar (d–f) regions. The gray-shaded areas and the dotted black lines correspond to the projection inter-model spreads with all models and the associated multi-model means, respectively. The colored shaded areas and the plain lines correspond to the new inter-model spreads and multi-model means with the selected models. In the subtropical region, the selected models include MPI-ESM1-2-LR, CESM2, CESM2-WACCM, and UKESM1-0-LL. For the subpolar region, the selected models are IPSL-CM6A-LR, CanESM5-CanOE, CESM2, and CESM2-WACCM.

3.4 Toward more robust NPP projections

The model representation of small phytoplankton emerged as the main cause of divergence in NPP projections between models in the subtropical and subpolar North Atlantic Ocean. In the subtropical basin, differing representations of diazotrophy explain model disparities. When not adequately regulated by nutrients like PO₄, it has the potential to significantly boost small phytoplankton's NPP, while other nutrient concentrations decline. Only the three models explicitly representing diazotrophs represent these controls and project a decrease in NPP. The three models with an implicit representation of diazotrophs and no effective control from PO₄ are therefore not reliable for studying the evolution of small phytoplankton's NPP in the region. Among the models without diazotrophy, ACCESS-ESM1-5 emerged as overly rich in nutrients on average across the subtropical region, making it unreliable for projecting average NPP evolution. Thus, only four out of the eight models appeared dependable for projecting small phytoplankton's NPP evolution in the region (MPI-ESM1-2-LR, CESM2, CESM2-WACCM, and UKESM1-0-LL). They project an average decrease of −4.8 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from −26.0 to +6.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) against +2.2 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from −26.0 to +20.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) with all models (Fig. 8c). This selection also leads to a strengthening of diatom projected NPP decrease (Fig. 8b), thus resulting in a total NPP decrease of −24.9 (−33.4 to −20.3) $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ against −8.2 (−33.4 to +19.5) $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (Fig. 8a; Table 2).

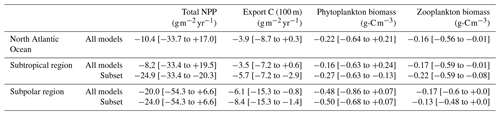
Table 2 Comparison of the mean projections of total NPP, carbon export at 100 m, and phytoplankton and zooplankton biomasses between 1950–1970 and 2080–2100 in the subtropical and subpolar regions for all models and for the subsets determined in each region (see Fig. 8). The values within the brackets correspond to inter-model spread.

In the subpolar region, NH₄ appeared to be able to sustain small phytoplankton's NPP in the models where it is present (IPSL-CM6A-LR, CanESM5-CanOE, CESM2, and CESM2-WACCM). If we hypothesize that ammonium will indeed play such a role in reality, models without an ammonium pool then tend to overestimate the impact of decreasing NO₃ concentrations on small phytoplankton. We can therefore set them aside and obtain narrowed estimates of small phytoplankton's NPP projections: +21.4 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from +6.4 to +35.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) instead of 7.3 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from −28.2 to +35.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) with all models (Fig. 8f). However, such a hypothesis would have no impact on total NPP because it would not affect diatoms (Fig. 8e): −24.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from −54.3 to +6.6 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) instead of −20.0 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ (from −54.3 to +6.6 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$) with all models (Fig. 8d and Table 2).

The selection of models based on the processes governing small phytoplankton NPP thus leads to narrowed projections for diatoms and total NPP in the subtropical region but not in the subpolar one. In the polar region, no discriminating mechanism was identified, and it was not possible to narrow projections using the same method.

3.5 Impact on carbon export and plankton biomass

NPP is closely linked with carbon export and plankton biomass, which are crucial variables for comprehending the future trajectory of the biological carbon pump and the effects of climate change on marine ecosystems. Consequently, the process-based selection of NPP models made previously can be used to estimate new projections of these other two variables.

Projections for carbon export across the global North Atlantic Ocean reveal significant disparities, ranging from −8.7 to +0.3 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$, with an average decrease of −3.9 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$. However, there is less uncertainty regarding the direction of its future changes compared to NPP projections (Table 2). While some models anticipate a slight increase in the subtropical region, all models project a decline in carbon export in the subpolar region. The model selection allows for a reduction in projection uncertainties in the subtropical region, resulting in a larger average decrease (−5.7 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ on average compared to −3.5 $\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{yr}}^{-\mathrm{1}}$ with all models). In the subpolar region, it does not reduce projection uncertainties but strengthens the average decrease (Table 2). The slight global increase in carbon export projected by some models is therefore explained by the strong increase in NPP they project in the subtropical region and is therefore unlikely to happen. The NPP process-based selection of models thus strengthens carbon export decrease at the end of the 21st century in the North Atlantic Ocean.

Phytoplankton biomass projections also exhibit a strong discrepancy, similar to that of NPP for the global North Atlantic Ocean and for the subtropical region (Table 2). However, the future evolution of phytoplankton biomass in the subpolar region is less uncertain compared to NPP, despite considerable model divergence (Table 2). The selection of models leads to a significant reduction in projection uncertainties in the subtropical region, where a new inter-model agreement on a future decrease in phytoplankton biomass emerges. The strong increases projected by some models are therefore caused by their inadequate representation of diazotrophy in the subtropical region, making such projections improbable.

All models agree on a decrease in zooplankton biomass across the global North Atlantic Ocean and in the two individual regions (Table 2). Both selections only slightly narrow projections in the two regions. This limited impact is due to the varying representations of zooplankton in CMIP6 models (Rohr et al., 2023), leading to a relative inter-model decoupling of phytoplankton and zooplankton. An analysis similar to the one conducted here should therefore be done to fully understand zooplankton projections in CMIP6 models.

4 Discussion

4.1 Model democracy and emergent constraints

NPP projections in the North Atlantic Ocean emerged as a case where the traditional approach of model inter-comparison studies through “model democracy” may not be adapted. This approach assumes that all ESMs are equally relevant and reliable for projecting future climate evolution (Knutti, 2010), whereas we showed here that some models, due to their representation or lack thereof of certain processes, are not dependable for projecting NPP in the region. A democratic multi-model mean computed with equal weights attributed to all models, as is done in Kwiatkowski et al. (2020) and Tagliabue et al. (2021), would therefore not be the optimal estimate of the future evolution of NPP.

However, we did not entirely set aside the model democracy approach because it was applied to model subsets in both regions. This application is questionable because it assumes independence among selected models, which is often not the case (Eyring et al., 2019). Some CMIP6 models are essentially variations of a similar base model (e.g., CESM2 and CESM2-WACCM) and share components and parameterizations (Masson and Knutti, 2011; Bishop and Abramowitz, 2013; Alexander and Easterbrook, 2015). This lack of independence results in systematic biases within the multi-model mean when model democracy is adopted. To address this issue, various studies have attempted to assign different weights to models based on their independence and ability to reproduce historical observations (Sanderson et al., 2015, 2017). While such efforts have sometimes improved agreement between multi-model means and observations (Räisänen et al., 2010; Knutti et al., 2017), the question of the validity of weighting methods for future projections remains unresolved. For example, in the context of NPP projections in the subtropical North Atlantic Ocean, the divergence of diazotrophy between models with effective PO₄ control and those without only arises around the year 2020 (Fig. 3). Consequently, weighting based solely on observations would likely overlook this divergence. Thus, process-based model selections, such as the one conducted here, and weighting methods are complementary techniques that should ideally be used together to combine their respective advantages.

Moreover, our approach failed at improving total NPP projections in the subpolar North Atlantic Ocean because we were not able to constrain diatoms. The discrepancy of diatom NPP projections arises from differences in sensitivity to a similar mechanism (Fig. 4), which prevents a process-based approach. However, it might set a good framework for an emergent constraint approach, which consists of exploiting an inter-model correlation between an observable variable and the response of another variable to climate change to constrain projections (Eyring et al., 2019; Sanderson et al., 2021). Emergent constrains have successfully been used to constrain projections of climate sensitivity (Cox et al., 2018), sea ice extent (Qu and Hall, 2014), extreme-precipitation events (O'Gorman, 2012), and NPP in the tropical ocean (Kwiatkowski et al., 2017). But, the reliability of emergent constraint outcomes is often hindered by the presence of systematic biases in large ensembles, stemming from model interdependence (Sanderson et al., 2021). Nevertheless, it is sometimes possible to enhance this reliability with the identification of a robust mechanism explaining the correlation used. Emergent constraints and process-based approaches are therefore complementary, particularly when competing mechanisms coexist. The case of NPP projections in the subpolar North Atlantic Ocean thus seems to be an ideal situation for combining a process-based method applied to small phytoplankton, carried out in this study, with an emergent constraint approach applied to the differing sensitivities of diatom NPP to nitrate concentrations. This will be the objective of a future study.

4.2 The influence of oceanic physics on NPP projection divergence

Divergences in NPP projections might in principle result from differences in both biogeochemical model components and the representation of physical processes, which may either amplify or mitigate the effects of biogeochemistry. In this study, we focused on the former, largely setting aside the latter. Our focus was motivated by the observation that, unlike NPP, the evolution with climate change of key oceanic parameters known to influence NPP, such as temperature, MLD, nutrient concentrations, and sea ice cover, had the same sign across all models. Specifically, all models indicated an increase in temperature, a decrease in nutrient concentrations, a reduction in MLD, and a decline in sea ice cover, while some projected an increase in NPP and others a decrease. However, we should point out that agreement on the sign of the evolution of these variables does not necessarily rule out their contribution to diverging NPP projections. The response of NPP to changes in MLD, for instance, is not always monotonic (Llort et al., 2019), and non-monotonicity may also result from complex interactions between physical and biogeochemical processes on seasonal timescales (Mousing et al., 2023). Future efforts are therefore needed to fully assess how differing physical mechanisms control NPP, further refining projection reliability and reducing uncertainty.

4.3 Estimation of climate change impacts on high trophic levels

CMIP model output serves as data inputs for the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP), an exercise aimed at examining the effects of climate change on human societies and ecosystems (Frieler et al., 2024). In the context of studying fisheries and marine ecosystems, CMIP models are used as inputs for marine ecosystem models. The connecting variable between plankton and higher trophic levels could be either NPP or the biomass of phytoplankton and zooplankton, depending on the marine ecosystem model employed (Tittensor et al., 2021). Additionally, some models rely on total NPP or biomass (Carozza et al., 2016), while others require inputs for each phytoplankton and zooplankton group, providing information on species composition (Cheung et al., 2016). Only a limited selection of CMIP models is incorporated into these studies. For the third phase of ISIMIP, specifically, only four CMIP6 models were chosen for marine ecosystem studies: GFDL-ESM4, UKESM1-0-LL, MPI-ESM1-2-HR, and IPSL-CM6A-LR. The biases exhibited by these models in projecting NPP and plankton biomass consequently influence the marine ecosystem models that employ them to investigate climate change impacts.

We demonstrated that IPSL-CM6A-LR lacks reliability in projecting NPP in the subtropical region due to its failure to represent PO₄ control over N₂ fixation. Conversely, UKESM1-0-LL lacks an NH₄ pool, likely resulting in an overestimation of NPP decrease in the subpolar region. These model deficiencies in projecting NPP directly affect phytoplankton biomass, and similar issues may arise for zooplankton biomass due to their disparate representations across CMIP6 models (Rohr et al., 2023). Such biases could significantly impact ISIMIP outcomes, which are subsequently used by policymakers to develop adaptation measures to climate change. Hence, it is imperative to identify these biases, assess the reliability of CMIP models in projecting variables used in ISIMIP studies, and estimate the repercussions of CMIP biases for ISIMIP results.

4.4 Perspectives on the future evolution of the biological carbon pump

Carbon export caused by the sinking of particulate organic matter is a key feature of the biological carbon pump, which helps to store carbon in the deep ocean and reduces atmospheric CO₂ concentrations. Depending on the remineralization depth of organic matter and the residency time of inorganic carbon in the deep ocean (Wilson et al., 2022), a decrease in carbon export caused by climate change might reduce the amount of carbon stored in the deep ocean and increase atmospheric CO₂ concentrations, thus forming a positive feedback mechanism. However, the sequestration time of the exported organic carbon strongly varies spatially (Nowicki et al., 2022). In the subtropical North Atlantic Ocean, it is only stored for a few decades, whereas it remains sequestered for several hundreds of years in the subpolar North Atlantic Ocean.

The strengthened decrease in carbon export obtained in both regions in this study therefore means that the North Atlantic biological carbon pump might be more affected by climate change than previously anticipated and on particularly long timescales for the subpolar region. However, because we were not able to reduce diatom NPP projection uncertainties in the region, the spread in carbon export projections remains very large.

Nevertheless, there is no quantitative relationship between carbon export and the efficiency of the biological carbon pump (DeVries et al., 2012). A reduction in the former does not necessarily mean a decrease in the latter. Further work is therefore needed to understand how the decrease in carbon export in the North Atlantic Ocean would affect the biological carbon pump, in both the short and the long term.

5 Conclusion

NPP is a key biogeochemical variable for which large uncertainties exist regarding its future evolution under climate change, particularly in the North Atlantic Ocean. The traditional approach to this problem, based on a multi-model mean computed through the model democracy approach, fails to provide informative projections for NPP in the region. We therefore developed a new methodology to exploit CMIP6 model diversity in order to gain new insights into the way NPP will be affected by climate change in the region. Thanks to an innovative regionalization of the North Atlantic Ocean, we were able to identify the processes responsible for the divergence of model projections and assess their likelihood of occurrence. This analysis allowed us to proceed to an informed selection of models in each bioregion, which gave us new estimates of the future evolution of NPP, along with carbon export and plankton biomasses, in the subtropical and subpolar bioregions.

CMIP6 model diversity was essential for conducting such an approach because it allowed us to identify the mechanisms responsible for projection divergence. The models set aside in the different bioregions should therefore not be discarded from the CMIP6 ensemble. Nevertheless, it is necessary to recognize that all models are not equally relevant depending on the region, the variable considered, and the question asked. A direct model democracy approach is therefore limited and should only be regarded as a first step in an inter-comparison study. It should be completed by more advanced methods, such as informed model selection, observation-based weighting, or emergent constraints, and by their combination. Moreover, when CMIP6 model outputs are used to assess the impacts climate change will have on ecosystems or human societies, the reliability of the models used to conduct these studies should be assessed in order to avoid strong biases stemming from CMIP6 models affecting the results.