Simulation of factors affecting Emiliania huxleyi blooms in Arctic and sub-Arctic seas by CMIP5 climate models: model validation and selection

The observed warming in the Arctic is more than double the global average, and this enhanced Arctic warming is projected to continue throughout the 21st century. This rapid warming has a wide range of impacts on polar and sub-polar marine ecosystems. One of the examples of such an impact on ecosystems is that of coccolithophores, particularly Emiliania huxleyi, which have expanded their range poleward during recent decades. The coccolithophore E. huxleyi plays an essential role in the global carbon cycle. Therefore, the assessment of future changes in coccolithophore blooms is very important.

Currently, there are a large number of climate models that give projections for various oceanographic, meteorological, and biochemical variables in the Arctic. However, individual climate models can have large biases when compared to historical observations. The main goal of this research was to select an ensemble of climate models that most accurately reproduces the state of environmental variables that influence the coccolithophore E. huxleyi bloom over the historical period when compared to reanalysis data. We developed a novel approach for model selection to include a diverse set of measures of model skill including the spatial pattern of some variables, which had not previously been included in a model selection procedure. We applied this method to each of the Arctic and sub-Arctic seas in which E. huxleyi blooms have been observed. Once we have selected an optimal combination of climate models that most skilfully reproduce the factors which affect E. huxleyi, the projections of the future conditions in the Arctic from these models can be used to predict how E. huxleyi blooms will change in the future.

Here, we present the validation of 34 CMIP5 (fifth phase of the Coupled Model Intercomparison Project) atmosphere–ocean general circulation models (GCMs) over the historical period 1979–2005. Furthermore, we propose a procedure of ranking and selecting these models based on the model's skill in reproducing 10 important oceanographic, meteorological, and biochemical variables in the Arctic and sub-Arctic seas. These factors include the concentration of nutrients (NO₃, PO₄, and SI), dissolved CO₂ partial pressure (pCO₂), pH, sea surface temperature (SST), salinity averaged over the top 30 m (SS_30 m), 10 m wind speed (WS), ocean surface current speed (OCS), and surface downwelling shortwave radiation (SDSR). The validation of the GCMs' outputs against reanalysis data includes analysis of the interannual variability, seasonal cycle, spatial biases, and temporal trends of the simulated variables. In total, 60 combinations of models were selected for 10 variables over six study regions using the selection procedure we present here. The results show that there is neither a combination of models nor one model that has high skill in reproducing the regional climatic-relevant features of all combinations of the considered variables in target seas. Thereby, an individual subset of models was selected according to our model selection procedure for each combination of variable and Arctic or sub-Arctic sea. Following our selection procedure, the number of selected models in the individual subsets varied from 3 to 11.

The paper presents a comparison of the selected model subsets and the full-model ensemble of all available CMIP5 models to reanalysis data. The selected subsets of models generally show a better performance than the full-model ensemble. Therefore, we conclude that within the task addressed in this study it is preferable to employ the model subsets determined through application of our procedure than the full-model ensemble.

1 Introduction

In the last 3 decades, the Arctic has been warming at more than twice the rate of the global average (Davy et al., 2018; Overland and Wang, 2010). This rapid warming has led to large changes in the physical environment, for example with the loss of sea ice extent and volume (Dai et al., 2019; Kwok, 2018), but it has also had a large impact on the Arctic ecosystem (Hoegh-Guldberg and Bruno, 2010; Johannessen and Miles, 2011). One group of species that has been affected by Arctic warming is coccolithophores such as Emiliania huxleyi (hereafter E. huxleyi). Reportedly, coccolithophores can affect the carbon and sulfur cycles in the surface ocean, at least within their bloom areas (Balch et al., 2016; Kondrik et al., 2018; Malin et al., 1993; Rivero-Calle et al., 2015; Winter et al., 2013). The effect of these algae on aquatic carbon chemistry results in changes to the carbon fluxes between the atmosphere and ocean (Balch et al., 2016; Morozov et al., 2019; Pozdnyakov et al., 2019; Shutler et al., 2013). Additionally, they contribute to the generation of sulfate aerosols, which scatter solar radiation in the atmosphere and act as cloud condensation nuclei, enabling cloud formation (Malin and Steinke, 2004). Therefore, the coccolithophores are responsible for both warming and cooling effects on the global climate (Charlson et al., 1987; Wang et al., 2018a, b).

Of all the coccolithophores, E. huxleyi is the most abundant and productive calcifying organism in the world ocean (McIntyre and Bé, 1967). It is a planktonic species growing at practically all latitudes (Brown and Yoder, 1994; Iglesias-Rodríguez et al., 2002; Moore et al., 2012) and in the eutrophic to oligotrophic marine waters (Paasche, 2001). The property of this photosynthesizing aquatic organism to produce not only organic carbon but also calcite, i.e. particulate inorganic carbon (PIC), imparts to E. huxleyi a special importance for the global ocean carbon cycle and, through intricate interactions, for CO₂ exchange fluxes between the ocean and atmosphere (Kondrik et al., 2019; Morozov et al., 2019; Shutler et al., 2013). Moreover, E. huxleyi blooms are known to (i) affect not only the carbon but also sulfur cycles in the surface ocean, at least within bloom zones, and arguably (ii) contribute to the generation of sulfate aerosols, which eventually enable cloud formation (Malin and Steinke, 2004). This gives E. huxleyi blooms a definite climatic dimension in the overall environmental impact of this phenomenon. The scale of the impact should indeed be very significant: such blooms not only release into the water huge amounts of PIC, in some cases reaching nearly 1×10⁶ t (Balch et al., 2016; Kondrik et al., 2018; Rivero-Calle et al., 2015), but they are very extensive, typically covering marine areas in excess of many hundreds of thousands, sometimes up to 1 million, of square kilometres. Besides this, they occur annually across the world ocean (Brown and Yoder, 1994; Iglesias-Rodríguez et al., 2002; Moore et al., 2012). Since changes of the regional climate have influenced the ecosystems of the Arctic seas, coccolithophores, particularly E. huxleyi, have increasingly expanded their range into polar waters (Henson et al., 2018; Rivero-Calle et al., 2015; Winter et al., 2013), which is thought to be due to climate warming (Fernandes, 2012; Flores et al., 2010; Kondrik et al., 2017; Okada and McIntyre, 1979; Winter et al., 1994).

Although E. huxleyi cells can adapt to diverse environmental conditions, the blooms of this alga exhibit remarkable interannual variations in extent, intensity, and localization (Balch et al., 2012; Iida et al., 2002; Kondrik et al., 2017; Morozov et al., 2013; Smyth et al., 2004). Importantly, the aforementioned spatio-temporal variations inherent in E. huxleyi blooms prove to be specific to individual marine environments, which indicates that E. huxleyi growth is generally conditioned by multiple forcing factors (FFs) acting through feedback mechanisms. Reportedly, the observed spatio-temporal variations are primarily driven by changes in sea surface temperature (SST); salinity; levels of photosynthetically active radiation (PAR); and nutrient and micronutrient availability, such as that of nitrate (NO₃), silicate (SI), ammonium (NH₄), phosphate (PO₄), and iron (Fe; Iglesias-Rodríguez et al., 2002; Krumhardt et al., 2017; Lavender et al., 2008; Zondervan, 2007). However, it has been found that, in addition to the above FFs, the water column stratification and wind speed (WS) at 10 m above the surface also condition the growth of E. huxleyi: a decrease in wind stress leads to formation of a shallow mixed layer and retention of algal cells within the zone of high levels of PAR (Raitsos et al., 2006). The intensity of water movements in general, and specifically water advection driven by ocean surface currents, was also highly consequential in this regard (Balch et al., 2016; Pozdnyakov et al., 2019). Among the other factors affecting E. huxleyi blooms are carbonate chemistry variables such as dissolved CO₂ partial pressure (pCO₂) and pH, which are considered to be very important (Tyrrell and Merico, 2004). There has been speculation that the ongoing increase in atmospheric CO₂ should damp and/or inhibit the growth of coccolithophores (Rivero-Calle et al., 2015); however, this is not supported by multiple observations (Kondrik et al., 2017; Morozov et al., 2013).

As the above FFs are susceptible to climate change, these factors are expected to exert their combined influence on the intensity, spatial extent, and possibly the seasonal duration of E. huxleyi blooms in the future. Given that the environmental influence of this phenomenon has both climatological and biogeochemical dimensions at least on a synoptic scale, it appears important to envisage how it will evolve in the midterm future. This can be done using either biological (e.g. Gregg et al., 2005) or statistical (e.g. Pozdnyakov et al., 2019) E. huxleyi bloom models, for which the prospective tendencies in FFs are employed. In turn, the tendencies in the FFs can be obtained from climate model output.

Today atmosphere–ocean coupled climate models are state-of-the-art tools for the projection of the future climate on decadal and centennial timescales (Otero et al., 2018; Taylor et al., 2012). In particular, the modern coupled atmosphere–ocean general circulation models (GCMs) include processes that govern the interactions between the ocean, atmosphere, land, sea ice, and carbon cycle. The fifth phase of the Coupled Model Intercomparison Project (CMIP5) provides the opportunity to use the model output from more than 30 GCMs (Taylor et al., 2012). The GCMs provide a large number of meteorological, oceanographic, and biochemical variables and so facilitate the comprehensive assessment of possible climate change impacts on marine ecosystems in the future. However, the studies which have evaluated the CMIP model's historical simulations have shown that the model outputs have a large spread compared to natural variability (Almazroui et al., 2017; Fu et al., 2013; Gleckler et al., 2008). The full CMIP5 model ensemble has been found to be skilful at simulating continent-wide surface air temperature and therefore useful for making robust assessments at these scales (IPCC, 2013). However, model skill at smaller spatial scales, such as for the Arctic, or even for specific Arctic seas, varies considerably from region to region and for different model variables (Overland et al., 2011). Therefore, it is important to find an approach for both model evaluation (comparison with historical climate) and selection of optimal models for each specific scientific task and region that gives a skill score to each model which encompasses all the relevant model variables and properties that are important for the scientific question to be addressed.

The main goal of the paper is to quantify how well CMIP5 models reproduce the main FFs that influence coccolithophore blooms in the Arctic and sub-Arctic seas. We propose a new approach for ranking and selecting CMIP5 models for their skill in capturing the historical environmental conditions in the Arctic and sub-Arctic seas (viz. the Barents, Bering, Greenland, Labrador, North, and Norwegian seas). We have chosen such a specific task as a case study in order to select model output to drive a model of coccolithophore blooms to predict how these will change in the future. We assume that a climate model that successfully represents the present-day conditions will also be skilful in future projections. Therefore, we select models based upon the validation of the models within the historical period.

Table 1 CMIP5 models used for simulation of selected variables: SST – sea surface temperature (in ^∘C), WS – 10 m wind speed (in m s⁻¹), SDSR – surface downwelling shortwave solar radiation (in W m⁻²), SS_30 m – sea salinity (averaged over top 30 m; in PSU), OCS – surface ocean current speed (in m s⁻¹), concentration of nutrients (NO₃, PO₄, and SI; in mol m⁻³), dissolved CO₂ partial pressure (pCO₂; in Pa), and pH (models available for respective variable are marked as “+”).

2 Materials and method

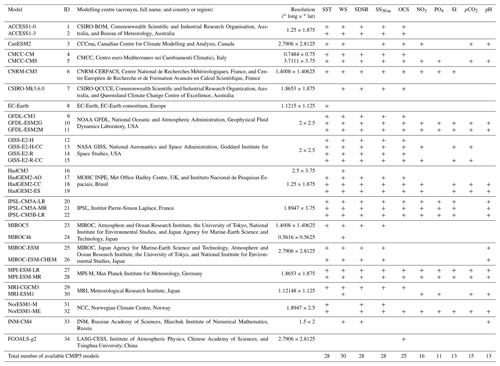
2.1 Data

34 CMIP5 GCMs' outputs for the historical period 1979–2005 were used in this study. The data are freely available in the ESGF portal (https://esgf-node.llnl.gov, last access: 10 December 2019). The list of climate models used is presented in Table 1. We analysed five oceanographic and meteorological variables, namely the SST; salinity averaged over 0–30 m (SS_30 m); surface WS at a height of 10 m; ocean surface current speed (OCS); surface shortwave downwelling solar radiation (SDSR); and five biochemical variables, namely concentration of nutrients (NO₃, PO₄, and SI), pCO₂, and pH. These FFs are known to affect the phytoplankton life cycle in sub-polar and polar latitudes (Iglesias-Rodríguez et al., 2002; Raitsos et al., 2006; Winter et al., 2013). The analysed CMIP5 GCMs are listed in Table 1: in total, we used outputs of 25 models for OCS; 28 for SS_30 m, SST, and SDSR; 30 for WS; 11 for PO₄; 13 for SI and pH; 15 for pCO₂; and 16 for NO₃. The number of models employed is different and was dictated by their availability in the ESGF portal. For validation of the climate models outputs, we used atmospheric and oceanic reanalyses: (i) ERA-Interim from the European Centre for Medium-Range Weather Forecasts (https://apps.ecmwf.int, last access: 29 March 2019; Dee et al., 2011) for SST, WS, and SDSR for the period from 1979 to 2005; (ii) GLORYS2V4 for the SS_30 m and OCS; and (iii) GLOBAL_REANALYSIS_BIO_001_029 (Perruche, 2018) for five biochemical variables – with both reanalyses from the European Copernicus Marine Environment Monitoring Service (http://marine.copernicus.eu, last access: 12 December 2019) for the period 1993–2005. The period for verification of the employed climate models was chosen based on the length of the reanalysis data and the limitations inherent in the “historical” runs of the GCMs, which usually terminate in 2005. The selected reanalyses are widely used in the literature and have been shown to be consistent with independent observational data (Agosta et al., 2015; Dee et al., 2011; Garric et al., 2017; Geil et al., 2013).

2.2 Methods for model selection

It is well established that the method of ensemble averaging can be used to reduce systematic model biases in the individual climate models (Flato et al., 2013; Gleckler et al., 2008; Knutti et al., 2010; Pierce et al., 2009; Reichler and Kim, 2008). There are two main approaches to employing climate model ensembles: (i) use of the full-ensemble average data for future trend analysis (Flato et al., 2013; Gleckler et al., 2008; Knutti et al., 2010; Reichler and Kim, 2008) and (ii) selection of an ensemble of the models from the entire set of available climate models yielding the best fit to the observational data for a historical period (Herger et al., 2018; Knutti et al., 2010; Taylor et al., 2012). We chose the second approach for analysing the ability of GCMs to reproduce main FFs that influence E. huxleyi bloom: nutrient concentrations (nitrate, phosphate, silicate), SS_30 m, SST, WS at a height of 10 m, SDSR, pH, pCO₂, and OCS.

There are many different approaches to ranking and selection climate models following validation with historical observations. For example, Agosta et al. (2015) ranked the CMIP5 models using only one statistical metric, namely a climate prediction index (CPI), “which is widely used in climatology studies for model evaluation and weighted projections” (Connolley and Bracegirdle, 2007; Franco et al., 2011; Murphy et al., 2004). Gleckler et al. (2008) evaluated the CMIP models and ranked them by analysing the climatology of the annual cycle, interannual variability, and relative errors. They found that the performance of the analysed models varied for different variables. Das et al. (2018) assessed 34 CMIP5 models using the following three criteria: the mean seasonal cycle, temporal trends, and spatial correlation. On this basis, the models were selected using a cumulative ranking approach. Fu et al. (2013) and Ruan et al. (2019) applied a score-based method using multiple criteria for the assessment of CMIP3 model performance: mean value, standard deviation, normalized root-mean-square error, linear correlation coefficient, Mann–Kendall test statistic Z, Sen's slope, and significance score. Further, Ruan et al. (2019) selected the top 25 % ranked CMIP5 models by applying a weight criterion from 0.5 to 1.0 to the different measures. Ruan et al. (2019) reported that the introduction of multiple criteria results in fewer uncertainties in the models' performance in comparison with the respective observation data.

Having tested the approaches cited above, we developed our own methodology which combines elements from some of these. We employ the multiple-criteria ranking method following Fu et al. (2013) and Ruan et al. (2019), but with the following modifications: (i) we took into consideration the Agosta et al. (2015) climate prediction index, (ii) analysed the features of spatial distribution of target variables (spatial biases and trends), (iii) ranked the models with the percentile method (25th, 50th, 75th) that is widely used in statistical analysis, and, finally, (iv) selected the top 25 % ranked CMIP5 models following Ruan et al. (2019).

2.2.1 Study regions

The target regions are six Arctic and sub-Arctic seas: the Barents, Bering, Greenland, Labrador, North, and Norwegian seas, where E. huxleyi blooms regularly occur (Kondrik et al., 2017). As mentioned above, the reason we chose the listed seas was that, in the context of global climate change, the Arctic and sub-Arctic seas have experienced the most pronounced changes in environmental variables due to the Arctic amplification. In addition, the target seas differ in physical and geographical conditions, which strongly affect their climate. While they are linked by common circulation patterns, e.g. with the warm-air advection coming into the Arctic from the Atlantic Ocean, the way in which this circulation affects the climate in a given sea is strongly affected by the local conditions. Therefore, we performed the validation and selection model procedure for each sea individually. Only specific areas within which intense growth and blooms of E. huxleyi frequently occur were selected in each sea, according to the results obtained by Kazakov et al. (2018) based on the Ocean Colour Climate Change Initiative dataset version 3.0 (https://esa-oceancolour-cci.org/, last access: 17 December 2019) for the period from 1998 to 2016. A comparison of the area-averaged values for the entire sea and only for the region of the regular occurrence of E. huxleyi blooms showed a significant difference. For example, it is about 2 ^∘C among all models for SST in the Barents Sea, where the E. huxleyi blooms cover the largest area of the sea compared to other seas. To identify the relevant study areas from a raster image that contained all blooming events over the period 1998–2016, we selected the areas where blooms occurred for more than one 8 d period (Fig. 1). For model validation we focused on sea-specific blooming periods: June–September for the Barents and Labrador seas, June–August for the Greenland Sea, May–July for the North Sea, May–August for the Norwegian Sea, and January–December for the Bering Sea (Kazakov et al., 2018). Thus, the results of the model validation can be used not only in terms of marine ecology-related issues (i.e. carbon cycle chemistry, water acidity, nutrients availability, etc.) but also for the purposes of forecasting region-specific climate-driven feedbacks between the environmental factors governing E. huxleyi growth.

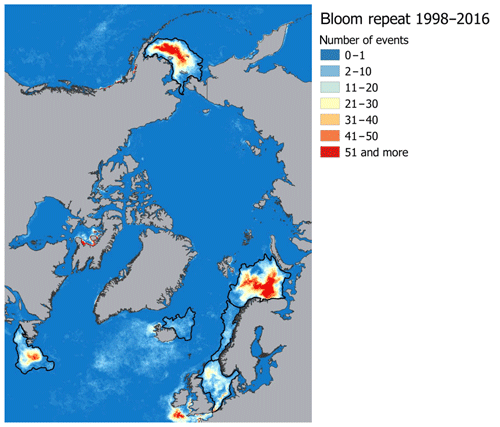
Figure 1 Spatial distribution of E. huxleyi blooms occurrence based on the Ocean Colour Climate Change Initiative dataset version 3.0 (Kazakov et al., 2018) for the Barents, Bering, Labrador, Greenland, North, and Norwegian seas. Black lines confine the territories where blooms occurred more than one 8 d period and show target sea areas.

2.2.2 Model evaluation measures

The CMIP5 climate models were validated against reanalysis data in order to assess how well they reproduce the regional features of the selected variables. The validation methodology for the GCMs' outputs included the analysis of the climatological-mean seasonal cycle, interannual variability, and analysis of the spatial distribution of climatological-mean biases and trends for selected variables averaged over the blooming period in each sea.

The seasonal cycle was analysed using the multi-year averaged monthly variables for all months of the year (i.e. a sample size of 12). Basic statistical measures were calculated, such as the root-mean-square deviation (RMSD), the correlation coefficient (r), and the standard deviation (SD; Fu et al., 2013; Gleckler et al., 2008; Kumar et al., 2015; Ruan et al., 2019). In addition, following Agosta et al. (2015), we calculated the CPI, which is a ratio of the model root-mean-square error to the standard deviation of observation data. This model evaluation statistic weighs the simulated data against the observations and is often used to validate model output (Agosta et al., 2015; Golmohammadi et al., 2014; Moriasi et al., 2007; Murphy et al., 2004; Stocker, 2004).

The interannual variability of the variables was analysed based on monthly variables solely for blooming periods (the sample size varied according to sub-region and variables combination; e.g. a sample size for SST in the Barents Sea was 108 monthly variables from June to September during 1979–2005). The same statistical measures for analysis of the seasonal cycle were used, viz. RMSD, r, SD, and CPI.

The spatial distribution of biases and trends between the model outputs and the reanalysis data was calculated for temporally averaged data in each grid point of the marine zone considered in this study.

2.2.3 Percentile ranking approach

For ranking models and selection of the model subset, we employed the percentile ranking approach, which is a compilation of the previously applied model ranking and the selection approaches with some modifications (see also Sect. 2.2). Following Fu et al. (2013) and Ruan et al. (2019), we used multiple criteria for model selection (RMSD, r, SD). Following Agosta et al. (2015) we analysed the CPI. In addition, we considered the differences in spatial distributions of biases and trends between the model outputs and the respective reanalysis data. Further, we ranked the models based on the percentile method (25th, 50th, 75th) for each statistical measure based on the amplitude of its values. Finally, we selected the top 25 % ranked CMIP5 models following Ruan et al. (2019) for each considered oceanographic, meteorological, and biochemical variables and the target region. Thus, for example, for a sample of 28 models, the top 25 % is a subset of seven models that showed the best total score, defined as the sum of scores of all statistical measures (marked bold in Table 2). However, if two or more models show the same score, they are all included in the selected model subset. Thus, the number of selected models varies from 3 to 11.

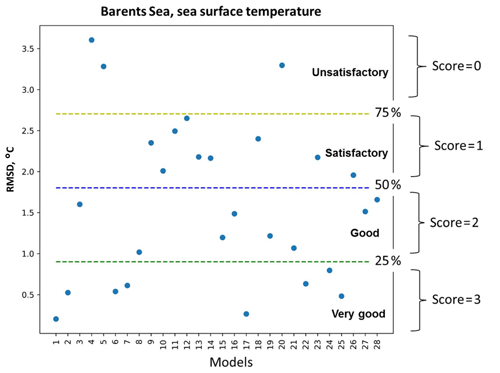
Figure 2 A schematic representation of the percentile ranking approach: division of RMSD values distribution of 28 models (see model names in Fig. 3) into four groups that are limited by 25th, 50th, and 75th percentiles and the relative assignment of scores from 3 to 0 to each group accordingly – very good, good, satisfactory, and unsatisfactory.

Figure 2 illustrates an example of the percentile ranking approach applied to the RMSD of SST in the Barents Sea. We divided the statistical measures into four groups based on the amplitude of the values and assigned a score to each model according to its group: (i) very good models (top 25th percentile of the distribution of the statistical measures) were given a score of 3, (ii) good models (between 50th and 25th percentile) were given a score of 2, (iii) satisfactory models (between 75th and 50th percentile) were given a score of 1, and (iv) unsatisfactory models (bottom 75th percentile) were given a score of 0. In the case of the correlation coefficient, the opposite applies; very good models with correlations scores above 0.75 were ranked with a score of 3, and this pattern continues.

Figure 3 Box plots of the spatial variability of SST biases (^∘C), which are calculated as the difference between the model and reanalysis data in the Barents Sea for E. huxleyi bloom season over the period from 1979 to 2005. Each box spreads from the lower quartile Q1 to the upper quartile Q3 of biases; the grey lines represent the medians. The dots show mean values. The lower “whiskers” are represented as Q1−1.5 standard deviation, and the upper whiskers are represented as Q3+1.5 standard deviation.

For ranking models based on the differences in the spatial distribution of biases and trends between model outputs and reanalysis, we used the absolute values of the mean and the spread of the spatial variation in model biases. For example, Fig. 3 displays the box plots of spatial variability in SST biases relevant to the studied area in the Barents Sea for the blooming season (June–September) and the study period 1979–2005. The mean bias varies from −6.6 (model no. 20) to 1.5 ^∘C (model no. 24) among the models, whereas the spread yielded by the model and that from observations has a wide range of values, from 7.3 (model no. 21) to 16.5 ^∘C (model no. 3). Thus it can be concluded from Fig. 3 that the analysis of spatial distribution of biases is very important; e.g. if we compare model no. 2 (ACCESS1-3) with model no. 3 (CanESM2), we can see that the means of these two models have a small difference (0.28 ^∘C), while the spread of spatial values for model no. 3 is much higher (by ∼6 ^∘C) than that for model no. 2. Application of the percentile ranking approach to model no. 2 (ACCESS1-3) and no. 3 (CanESM2) resulted in the inclusion of only the former in the model subset (see Table 3).

Table 2 presents all calculated statistics that were used to rank GCMs for SST in the Barents Sea as well as the final total score for each model. The spread of the total assigned scores is from 9 to 35. Based on this range we selected the top 25 % of GCMs. Thus, the best model ensemble for SST for the Barents Sea is the eight-model set: ACCESS1-0, ACCESS1-3, GFDL-CM3, HadGEM2-ES, MIROC-ESM, MIROC-ESM-CHEM, MPI-ESM-LR, and MPI-ESM-MR. The same procedure was performed for other target seas and variables.

Table 2 Results of the CMIP5 model performance for SST in the Barents Sea. Numbers in brackets indicate the models' scores (RMSD is the root-mean-square deviation – ^∘C; r is the correlation coefficient between models and reanalysis; CPI is climate prediction index; $\left|{\text{SD}}_{\mathrm{dif}}\right|$ is the modulus of the standard deviation difference – model minus reanalysis – ^∘C; $\left|{\text{Tr}}_{\mathrm{m}}\right|$ is the modulus of spatial trend mean difference – the model minus reanalysis – ${}^{\circ }\mathrm{C}{\mathrm{yr}}^{-\mathrm{1}}$; $\left|{\text{Tr}}_{\mathrm{a}}\right|$ is the modulus of spread of spatial trends difference – the model minus reanalysis – ${}^{\circ }\mathrm{C}{\mathrm{yr}}^{-\mathrm{1}}$; $\left|{\text{Br}}_{\mathrm{m}}\right|$ is the modulus of spatial bias mean difference – the model minus reanalysis – ^∘C; $\left|{\text{Br}}_{\mathrm{a}}\right|$ is the modulus of spread of spatial biases difference – the model minus reanalysis – ^∘C).

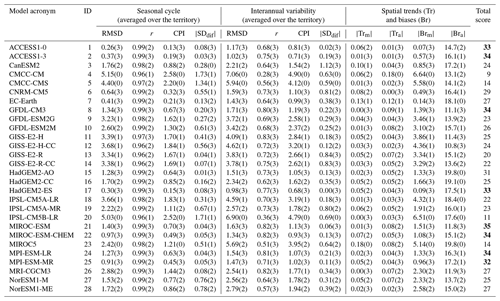
Table 3 The final model scores obtained using the percentile ranking approach for the five oceanographic and meteorological variables (sea surface temperature – SST; salinity averaged over 0–30 m – SS_30 m; surface wind speed at 10 m – WS; ocean surface current speed – OCS; and surface shortwave downwelling solar radiation – SDSR – for the Barents, Bering, Greenland, Labrador, North, and Norwegian seas based on different statistical measures; Fig. 2; Table 2). The white cells indicate a lack of model output for historical and RCP projections (RCP4.5, RCP8.5) in open data sources.

3 Results and discussion

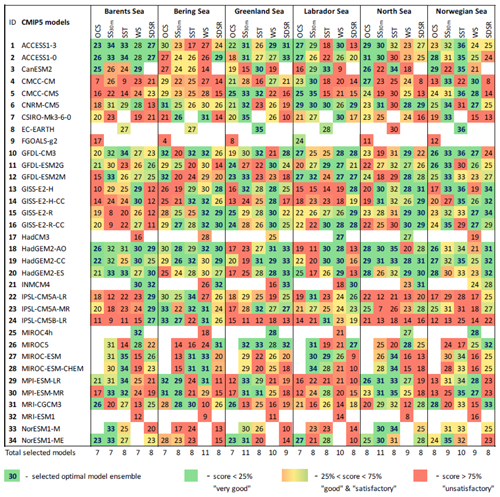
The results of model validation and ranking, as well as the selected CMIP5 model subsets in the Barents, Bering, Greenland, Labrador, North, and Norwegian seas, are presented in Table 3 (for five oceanographic and meteorological variables) and Table 4 (for five biochemical variables). Each number in these tables shows the final skill score for each combination of model, variable, and sea. For each individual column, a colour gradation was applied based on our percentile ranking approach: therefore, the same numbers in the tables can have different colours. For example, for OCS in the Barents Sea, the spread of the final model scores is from 7 to 26, whereas for SS_30 m it is from 8 to 34. Therefore, even model no. 3 CanESM2 has the total score 26 for SS_30 m (which is higher than that – 25 – for OCS); this model was not included in the SS_30 m selected model subset and is coloured red, whereas for OCS it is included in the selected model subset and highlighted in green. The final skill scores of those models, which were included in the selected model subsets, are marked in bold blue, and their total number is indicated at the bottom of each column.

Table 4 The final model scores obtained using the percentile ranking approach for the five biochemical variables (concentration of nutrients – NO₃, PO₄, and SI; dissolved CO₂ partial pressure – pCO₂; and pH) for the Barents, Bering, Greenland, Labrador, North, and Norwegian seas based on different statistical measures (Fig. 2; Table 2). The white cells indicate a lack of model output for historical and RCP projections (RCP4.5, RCP8.5) in open data sources.

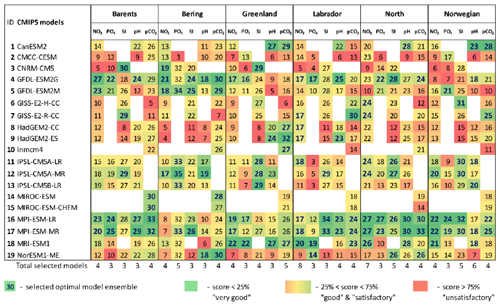
Analysing Tables 3–4, one can conclude that there is no model ensemble or single model which could simulate all variables equally well over the different target seas. However, some climate models show good results for many cases, e.g. ACCESS1-3, ACCESS1-0, GFDL-CM3, GISS-E2-R, GISS-E2-R-CC, HadGEM2-AO, HadGEM2-CC, HadGEM2-ES, INMCM4, MPI-ESM-LR, and MPI-ESM-MR. The models that have the lowest total scores across the majority of the target regions are CMCC-CM, FGOALS-g2, IPSL-CM5A-LR, IPSL-CM5A-MR, IPSL-CM5B-LR, MIROC5, and MRI-ESM1.

Such heterogeneity in the ability of climate models to reproduce the climate features in different seas can be partly explained. Climate models are often tuned to adequately reproduce global processes and globally averaged values (Mauritsen et al., 2012; Schmidt et al., 2017). An insufficient number of long time series of observations is available for model calibration, especially for marine waters. There are also very limited observations of climate processes in the Arctic which limit model development for the Arctic environment (Vihma et al., 2014).

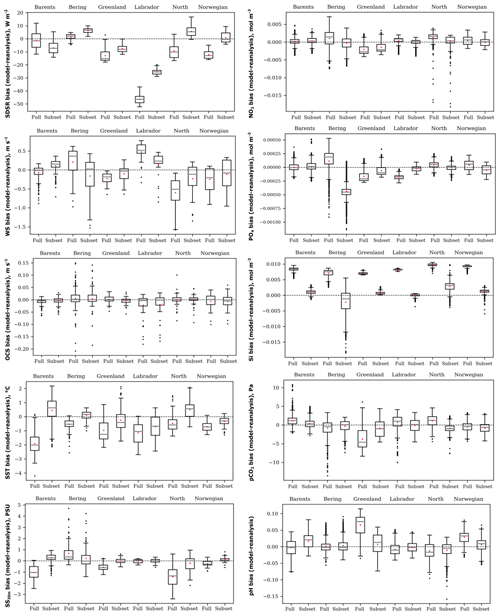
Figure 4 Box plots of the spatial distribution of biases (model ensemble minus reanalyses) of five oceanographic and meteorological (left) and five biochemical variables (right): sea surface temperature (SST), salinity averaged over 0–30 m (SS_30 m), surface wind speed at 10 m (WS), ocean surface current speed (OCS), surface shortwave downwelling solar radiation (SDSR), concentration of nutrients (NO₃, PO₄, and SI), dissolved CO₂ partial pressure (pCO₂), and pH for the Barents, Bering, Greenland, Labrador, North, and Norwegian seas averaged over the study period for comparison of full and selected model ensembles.

In order to verify our methodology, we compared the selected ensemble with the full-model ensemble for the time-averaged spatial distribution of biases, relative to reanalyses data for the historical period (1979 and 1993–2005), for each study variable in the six target seas (Fig. 4). The box plots (Fig. 4) show that the selected model ensemble mainly performs better than the full-model ensemble, i.e. the mean value (red dot) located closer to the zero line (dashed). The biggest difference between these two approaches obtained for the concentration of silicate (SI) is in favour of the ranking model approach.

Analysing the box plots of the selected model ensemble (Fig. 4), the lower spread of biases is obtained for OCS, SS_30 m, and concentration of silicate (SI). CMIP5 GCMs generally underestimate SDSR, especially over the Labrador Sea. Likewise, GCMs mainly underestimate WS except for the Labrador and Barents seas. For OCS all ensembles have a low spread of biases and a mean value located very close to zero, but they have many outliers (black dots). CMIP5 GCMs in different seas show heterogeneous results – they underestimate or overestimate SST, SS_30 m, and all biochemical variables. Also, Séférian et al. (2013) reported that CMIP5 GCMs differ enormously in biochemical variables, but they show fewer biases when compared to the previous model versions (CMIP3) for wind speed. Flato et al. (2013) found that CMIP5 models have higher biases (both positive and negative) for SST in polar regions and quite large negative biases relative to other latitudes for salinity in the Arctic. Rickard et al. (2016) summarized that oceanographic variables in CMIP5 models reveal better agreement across all models compared to biochemical ones. Lavoie et al. (2013) detected that GFDL and MPI models better represent nitrate concentrations, and the GFDL model best represents salinity among other considered models in the Labrador Sea. In our study, these models were also selected as the best for the Labrador Sea. It is quite difficult to compare obtained results with other already-published research because of using different models or a various number of models in full-ensemble and study regions. Some mentioned authors apply the full-model ensemble to other select models with better performance, but they did not compare these two approaches as we have done.

4 Conclusions

In the paper, we presented results of validation of 34 CMIP5 models compared to ERA-Interim, GLORYS2V4, and GLOBAL_REANALYSIS_BIO_001_029 reanalyses for the historical period (1979 and 1993–2005). Besides this we proposed the percentile ranking approach for selection climate model subsets that most accurately reproduce the state of 10 forcing factors affecting E. huxleyi blooms over the historical period in six Arctic and sub-Arctic seas, viz. the Barents, Bering, Labrador, Greenland, North, and Norwegian seas. In total 60 combinations of the most-skilful models were selected (10 variables and six target seas) based on different statistical measures: the root mean square error, correlation coefficient, standard deviation, climate prediction index (CPI), spatial biases, and trends. Our results show that there is no model ensemble or individual model which could best simulate all variables across all target seas. Despite the fact that the Arctic is often considered to be one single region in many studies, our results show that CMIP5 climate models do not have consistent performance across such a large area. However, the selected model ensembles show results with smaller biases than the full-model ensemble.

The results of the percentile ranking approach proposed in this paper show better performance (mean is closer to zero) of the selected model ensemble vs. the full-model ensemble for different variables and target seas. We can conclude that it is important to include a number of different evaluation criteria when selecting the best models from an ensemble, including the spatial pattern of model biases, and that the proposed methodology is a way of improving the model selection procedure that promises a better chance to identify more skilful models for the features we are interested in.

Given that the environmental impacts of E. huxleyi communities are diverse and encompass both climatological and marine ecology dimensions, the established sets of CMIP5 climatological models most closely simulating the environmental conditions under which this taxon grow open the way for envisaging how this phenomenon will further evolve in light of ongoing climate change. This can be done using the E. huxleyi bloom model, for which the changes in the forcing factors for E. huxleyi blooms will be employed. Finally, although the present study has been performed for the coccolithophore E. huxleyi which vegetates at Arctic and sub-Arctic latitudes, the reported methodological approach is not algal-specific and can be applied to studies of other algal species composing the phytoplankton communities in the world ocean.