Vertical partitioning of CO₂ production in a forest soil

Large amounts of total organic carbon are temporarily stored in soils, which makes soil respiration one of the major sources of terrestrial CO₂ fluxes within the global carbon cycle. More than half of global soil organic carbon (SOC) is stored in subsoils (below 30 cm), which represent a significant carbon (C) pool. Although several studies and models have investigated soil respiration, little is known about the quantitative contribution of subsoils to total soil respiration or about the sources of CO₂ production in subsoils. In a 2-year field study in a European beech forest in northern Germany, vertical CO₂ concentration profiles were continuously measured at three locations, and CO₂ production was quantified in the topsoil and the subsoil. To determine the contribution of fresh litter-derived C to CO₂ production in the three soil profiles, an isotopic labelling experiment, using ¹³C-enriched leaf litter, was performed. Additionally, radiocarbon measurements of CO₂ in the soil atmosphere were used to obtain information about the age of the C source in the CO₂ production. At the study site, it was found that 90 % of total soil respiration was produced in the first 30 cm of the soil profile, where 53 % of the SOC stock is stored. Freshly labelled litter inputs in the form of dissolved organic matter were only a minor source for CO₂ production below a depth of 10 cm. In the first 2 months after litter application, fresh litter-derived C contributed, on average, 1 % at 10 cm depth and 0.1 % at 150 cm depth to CO₂ in the soil profile. Thereafter, its contribution was less than 0.3 % and 0.05 % at 10 and 150 cm depths, respectively. Furthermore CO₂ in the soil profile had the same modern radiocarbon signature at all depths, indicating that CO₂ in the subsoil originated from young C sources despite a radiocarbon age bulk SOC in the subsoil. This suggests that fresh C inputs in subsoils, in the form of roots and root exudates, are rapidly respired, and that other subsoil SOC seems to be relatively stable. The field labelling experiment also revealed a downward diffusion of ¹³CO₂ in the soil profile against the total CO₂ gradient. This isotopic dependency should be taken into account when using labelled ¹³C and ¹⁴C isotope data as an age proxy for CO₂ sources in the soil.

1 Introduction

Soils are the world’s largest terrestrial organic carbon (C) pool, with an estimated global C stock of about 2400 Gt in first 2 m of the world’s soils (Batjes, 2014). The CO₂ efflux from soils, known as soil respiration, is the second-largest flux component in the global C cycle (Bond-Lamberty and Thomson, 2010; Raich and Potter, 1995) and can be divided into autotrophic respiration, due to roots and mycorrhizae, and heterotrophic respiration, due to the mineralisation of soil organic carbon (SOC) by decomposers. Global warming is expected to increase soil respiration by boosting the microbial decomposition of SOC (Bond-Lamberty et al., 2018; Hashimoto et al., 2015) and by greater root respiration (Schindlbacher et al., 2009; Suseela and Dukes, 2013). Although most of the CO₂ is produced in topsoils (<30 cm), a significant amount of CO₂ is produced in the subsoil (>30 cm; Davidson and Trumbore, 1995; Drewitt et al., 2005; Fierer et al., 2005; Jassal et al., 2005). Despite the fact that more than 50 % of global SOC stocks are stored in subsoils (Batjes, 2014; Jobbágy and Jackson, 2000), little is known about the amount and sources of CO₂ production in subsoils. Moreover, the mechanisms controlling CO₂ production in subsoils are still not fully understood. High apparent radiocarbon (¹⁴C) ages of SOC in subsoils (Rethemeyer et al., 2005; Torn et al., 1997) lead to an assumption of a high stability of C and a low turnover in subsoils. However, laboratory incubations of subsoil samples show similar mineralisation rates of SOC in both subsoils and topsoils (Agnelli et al., 2004; Salomé et al., 2010; Wordell-Dietrich et al., 2017), suggesting that subsoils also contain a labile fraction that should be taken into account as a source for soil respiration.

A range of studies have been conducted on CO₂ production in soils, but most of them have focused on spatial variations in temperature, water content and substrate supply (Borken et al., 2002; Davidson et al., 1998; Fang and Moncrieff, 2001) while ignoring the vertical partitioning of CO₂ production in the whole soil profile, which is essential for understanding soil C dynamics. One reason for this might be the measurement methods used to quantify sources and fluxes in the soil profile. Total CO₂ production can easily be measured at the soil surface with an open-bottom chamber, whereas vertical monitoring of CO₂ production needs the determination of CO₂ concentrations at several soil depths in order to estimate the CO₂ production, i.e. using the gradient method first described by De Jong and Schappert (1972). Basically, the CO₂ flux between the two depths can be calculated using the effective gas diffusion coefficient and the CO₂ gradient between the two depths. Recently, the development of low-cost sensors for temperature, soil moisture and CO₂ concentration has allowed greater use of the gradient method (Jassal et al., 2005; Maier and Schack-Kirchner, 2014; Pingintha et al., 2010; Tang et al., 2005). This method can help quantify CO₂ production in the entire soil profile, which is essential for an improved quantitative understanding of whole soil C dynamics, including the important contribution made by subsoil. To date, there have only been a few studies that have continuously determined CO₂ production in the whole soil profile in situ over a longer timescale (Goffin et al., 2014; Moyes and Bowling, 2012).

In the present study, the vertical distribution of the CO₂ concentration was measured, and CO₂ production rates were calculated over a 2-year period in a Dystric Cambisol in a temperate beech forest. The objectives of this study were (1) to quantify the contribution of CO₂ production in subsoils to total soil CO₂ production, and (2) to identify sources of CO₂ production along the soil profile using sources partitioning via isotopic data (¹³C and ¹⁴C). It was hypothesised that the majority of CO₂ in subsoils originates from young C sources and not from the mineralisation of old SOC.

2 Methods

2.1 Site description and subsoil observatories

The study site is located in a beech forest (Grinderwald) 35 km northwest of Hannover, Germany (52^∘34^′22^′′ N, 9^∘18^′49^′′ E). The vegetation is dominated by common beech trees (Fagus sylvatica) that were planted in 1916, and the soil is characterised as a Dystric Cambisol (IUSS Working Group WRB, 2015) developed on Pleistocene fluvial and aeolian sandy deposits from the Saale glaciation. The site is located around 100 m above sea level, with a mean annual temperature and precipitation of 9.7 °C and 762 mm (Deutscher Wetterdienst, Nienburg, 1981–2010) respectively. The soil texture of the site is mainly composed of the sand fraction with contents varying from 60 % (<30 cm) to 90 % (>120 cm), with SOC contents of 11.5 g kg⁻¹ down to (10 cm) 0.4 g kg⁻¹ (185 cm) (Heinze et al., 2018; Leinemann et al., 2016).

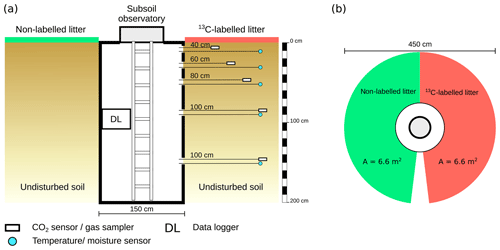
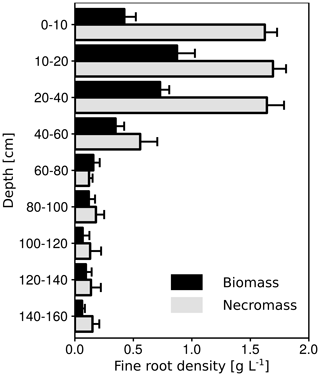
In July 2013, three subsoil observatories were installed using a stainless steel lysimeter vessel (1.6 m diameter and 2 m height) driven 2 m deep into the soil (Fig. 1a). Once the vessel had been inserted, the soil inside the containment was excavated by hand, and undisturbed soil cores (5.7 cm inner diameter, 4.0 cm height) were taken with five replicates at depths of 10, 30, 50, 90 and 150 cm from each subsoil observatory for soil diffusivity measurements. In addition, undisturbed soil samples in the observatories were taken to estimate fine root density. Thus, six samples were taken from the forest floor and six samples from each of the upper mineral soil layers (0–10, 10–20 and 20–40 cm) using a soil corer (3.5 cm diameter), and three samples were taken from each depth increment of the lower profile (40–200 cm depth), at 20 cm depth intervals, using a steel cylinder (12.3 cm diameter and 20 cm height). In the laboratory, the samples were gently washed over sieves of 0.25 mm mesh size to separate the roots from adhering soil particles. Under the stereo microscope, the rootlets were separated into live (biomass) and dead (necromass) roots and, subsequently, into fine (<2 mm in diameter) and coarse roots (>2 mm in diameter). All live and dead root samples were dried at 70 ^∘C for 48 h and weighed.

Figure 1 Photographs of (a) the lysimeter vessels used to drill the hole for the subsoil observatories, and (b) the polyethylene shaft used as the subsoil observatory.

After the lysimeter vessel was removed, a polyethylene shaft (1.5 m in diameter and 2.1 m height) was placed in the soil (Fig. 1b) and is referred to here as the subsoil observatory. The gap (≈ 5 cm) between the subsoil observatory and the surrounding undisturbed soil was refilled. The observatories were installed close to one other, with a maximum distance of 30 m between them.

To monitor the temperature and volumetric water content, combined temperature and moisture sensors (UMP-1; Umwelt-Geräte-Technik GmbH, Germany) were installed at depths of 10, 30, 50, 90 and 150 cm, with a horizontal distance of 100 cm from the wall of the subsoil observatories (Fig. 2a). Measurements were taken every 15 min and stored on a data logger inside the subsoil observatory. The CO₂ concentration in the soil air was monitored by solid-state infrared gas sensors (GMP221; Vaisala Oyj, Finland) with a measuring range of 0 %–10 % CO₂. To protect the polytetrafluoroethylene (PTFE) membrane of the CO₂ sensor from damage while being placed in the soil, the sensor was coated with an additional PTFE foil (616.13 P; FIBERFLON, Turkey) to allow gaseous diffusion and prevent water infiltration. The CO₂ concentration was measured every 3 h to reduce power consumption. The CO₂ sensors were turned on 15 min before the measurement itself, due to their warm-up time. In addition, PTFE suction cups (25 mm in diameter and 60 mm length) for soil air sampling with stainless steel tubing (2 mm inner diameter; ecoTech Umwelt-Meßsysteme GmbH, Germany) were installed adjacent to the CO₂ sensors. The gas samplers and CO₂ sensors were installed at the same depths as the temperature and moisture sensors. The horizontal distance of the gas samplers and CO₂ sensors from the subsoil observatory wall increased from 40 to 100 cm with increasing soil depth (Fig. 2a).

Figure 2 Schematic overview of the subsoil observatories, the installed sensors and the labelling experiment. (a) Side view of the subsoil observatory. (b) Top view of the labelled and control area.

2.2 Gas sampling and measurements

2.2.1 Soil respiration

The surface CO₂ efflux was measured using the closed-chamber method. A total of 30 PVC collars with a diameter of 10.4 cm and a height of 10 cm were installed 5 cm deep in the soil around the three subsoil observatories. The organic layer of 15 collars was removed in order to be able to distinguish between mineral soil respiration and total soil respiration. Soil respiration was measured with the EGM-3 SRC-1 soil respiration chamber (PP Systems, USA) and the LI-6400-09 soil chamber (LI-COR, Inc., USA). The measurement system was changed due to technical problems with the EGM-3 system; however, a comparison between the two systems revealed only minor differences. Each collar was measured three times per sampling day from March 2014 to March 2016, with sampling ranging from once a month to once a week. Annual soil respiration was derived from the linear interpolation of measured CO₂ fluxes from the collars. Furthermore, soil respiration was modelled by fitting an Arrhenius-type model (Eq. 1), introduced by Lloyd and Taylor (1994) and using soil temperature data from 10 cm depth, and the measured CO₂ fluxes as follows:

$$\begin{array}{}\text{(1)}& F_{\mathrm{0}}=a\times e^{\left(\frac{E_{\mathrm{0}}}{T+\mathrm{273.2}-T_{\mathrm{0}}}\times \frac{T-\mathrm{10}}{\mathrm{283.2}-T_{\mathrm{0}}}\right)},\end{array}$$

where F₀ is soil respiration (µmol m⁻² s⁻¹), a, E₀ and T₀ are fitted model parameters, and T is the soil temperature at 10 cm depth (in degrees Celsius).

2.2.2 ¹³CO₂ sampling and measurement

In addition to continuous CO₂ concentration monitoring, two gas samples per depth and subsoil observatory were taken at the end of the stainless steel tubing from the suction cups with a syringe and filled into 12 mL evacuated gas vials (Labco Exetainer; Labco Limited, UK). The sampling started in May 2014, with an interval of between once a month and once a week. The CO₂ concentration in the soil gas samples was analysed by gas chromatography (Agilent 7890A; Agilent Technologies, Inc., USA). The δ¹³C values of the CO₂ samples were measured by an isotope ratio mass spectrometer (Delta Plus with a GP interface and GC box; Thermo Fisher Scientific, Germany) connected to a PAL autosampler (CTC Analytics AG, Switzerland). The ¹³C results are expressed in parts per thousand (ppt) relative to the international standard of Vienna Pee Dee Belemnite (VPDB).

2.2.3 ¹⁴CO₂ sampling and measurement

Soil gas samples for radiocarbon analysis were taken in October and December 2014 in subsoil observatories 1 and 3. The CO₂ was sampled using a self-made molecular sieve cartridge as described in Wotte et al. (2017). Briefly, each stainless steel cartridge was filled with 500 mg zeolite type 13X (40/60 mesh, charge 5634; IVA Analysetechnik GmbH & Co. KG, Germany), which is used as an adsorbent for CO₂. The molecular sieve cartridges were connected to the installed gas samplers. The soil atmosphere of the corresponding depth was then pumped with an airflow of 7 mL min¹ over a desiccant (Drierite; W. A. Hammond Drierite Co. Ltd, USA) to the molecular sieve cartridge for 40 min to trap the CO₂ on the molecular sieve. Surface samples were taken from a respiration chamber (Gaudinski et al., 2000). The atmospheric CO₂ inside the chamber was removed prior to sampling by circulating an airflow of ≈ 1.5 L min⁻¹ from the chamber through a column filled with soda lime until the equivalent of 2–3 chamber volumes had been passed over the soda lime. Thereafter, the airflow was run over a desiccant and the molecular sieve cartridge for 10 min to collect the CO₂ sample.

In the laboratory, the adsorbed CO₂ was released from the molecular sieve cartridge by heating the molecular sieve under a vacuum (Wotte et al., 2017). The released CO₂ was purified cryogenically and sealed in a glass tube. The radiocarbon (¹⁴C) analysis was directly performed on the CO₂ with the gas ion source of the mini carbon dating system (MICADAS; Ionplus AG, Switzerland) at ETH Zurich (Ruff et al., 2010). The ¹⁴C concentrations are reported as fraction modern carbon (F¹⁴C), whereby F¹⁴C values of less than one denote that the majority of the C was fixed before the nuclear bomb tests in the 1960s, while values greater than one indicate C fixation after the bomb tests.

2.3 Labelling experiment

To trace the fate of fresh litter inputs in the soil and their contribution to the CO₂ released from different soil horizons, a ¹³C labelling experiment was performed. In January 2015, the leaf litter layer around the subsoil observatories was removed and replaced with a homogeneous mixture of 237 g ¹³C-labelled and 1575 g non-labelled young beech litter, which is equal to a litter input of 250 g m⁻². The labelled litter was distributed on a semi-circular area (6.6 m²) around the subsoil observatories (Fig. 2b). The labelled litter originated from young beech trees grown in a greenhouse in a ¹³CO₂-enriched atmosphere. The mixture of labelled and non-labelled litter had an average δ¹³C value of 1241 ‰ for subsoil observatory 1 (OB1) and a δ¹³C value of 1880 ‰ for subsoil observatories 2 (OB2) and 3 (OB3).

2.4 Diffusivity measurements

Gas transport along the soil profile is determined by the diffusivity of the soil. The diffusivity of the soil was determined at depths of 10, 30, 50, 90 and 150 cm, with five undisturbed core sample replicates per depth and per observatory. To account for different water contents, the undisturbed soil cores (5.7 cm in diameter and 4.0 cm height) were adjusted in the laboratory at different matrix potentials (−30, −60 and −300 hPa) to cover a wide range of soil moisture. After the moisture adjustment, the soil cores were attached to a diffusion chamber as described in Böttcher et al. (2011). The diffusion chamber was flushed with N₂ to initially establish a gas gradient between the chamber and the top of the sample as an atmospheric boundary condition. The increase in oxygen inside the ventilated chamber was measured over time with an oxygen dipping probe (DP-PSt3-L2.5-St10-YOP; PreSens Precision Sensing GmbH, Germany). Diffusivity and tortuosity factors (τ) were calculated with an inverse diffusion model (Schwen and Böttcher, 2013).

2.5 Data analysis

2.5.1 Gradient method

This method is based on the assumption that molecular diffusion is the main gas transport in the soil atmosphere. Therefore, gas fluxes, e.g. CO₂ fluxes in a soil profile, can be calculated from the CO₂ concentration gradient and the effective gas diffusion coefficient in the specific soil layer of interest.

In order to account for temperature and pressure dependencies of the CO₂ sensors, the CO₂ concentrations were corrected with a compensation algorithm for the GMP221 (S1) provided by the manufacturer (Niklas Piiroinen, Vaisala Oyj, Finland, personal communication, 2014). For the flux calculation, CO₂ volume concentrations were converted to CO₂ mole concentrations (Eq. 2) as follows:

$$\begin{array}{}\text{(2)}& C={\displaystyle \frac{C_{\mathrm{v}}\times p}{R\times T}},\end{array}$$

where C is the CO₂ mole concentration (µmol m⁻³), C_v is the CO₂ volume fraction (µmol mol⁻¹), p is the atmospheric pressure in Pascal (Pa), R is the universal gas constant (8.3144 J K⁻¹ mol⁻¹) and T is the soil temperature in kelvin (K) measured by temperature sensors at the corresponding soil depths. The CO₂ flux of a soil layer was calculated using Fick's first law (Eq. 3) as follows:

$$\begin{array}{}\text{(3)}& F=-D_{\mathrm{s}}\times {\displaystyle \frac{\mathrm{d}C}{\mathrm{d}z}},\end{array}$$

where F is the diffusive CO₂ flux (µmol m⁻² s⁻¹), D_s is the effective diffusivity in the soil atmosphere (m² s⁻¹) determined as described below, C is the CO₂ concentration (µmol m⁻³) and z is the depth (metres). The equation is based on the assumption that (1) molecular diffusion is the dominating transport process in the soil atmosphere and other transport mechanisms – i.e. convective CO₂ transport due to air pressure gradients or diffusion in the soil, and convective transport with soil water – are negligible, and (2) gas transport is 1D (e.g. De Jong and Schappert, 1972; Maier and Schack-Kirchner, 2014). The effective diffusivity D_s was calculated with Eq. (4) as follows:

$$\begin{array}{}\text{(4)}& D_{\mathrm{s}}=D_{\mathrm{0}}\times \mathit{\tau },\end{array}$$

where D₀ is the CO₂ diffusivity in free air. The pressure and temperature effect on D₀ were taken into account by the following:

$$\begin{array}{}\text{(5)}& D_{\mathrm{0}}=D_{a\mathrm{0}}\times \left({\displaystyle \frac{p_{\mathrm{0}}}{p}}\right)\times {\left({\displaystyle \frac{T}{T_{\mathrm{0}}}}\right)}^{\mathrm{1.75}},\end{array}$$

where D_a0 is a reference value of D₀ at standard conditions ($\mathrm{1.47}\times {\mathrm{10}}^{-\mathrm{5}}$ m² s⁻¹ at T₀ 293.15 K and p₀ 1.013×10⁵ Pa) (Jones, 1994). The dimensionless tortuosity factor τ at each depth was modelled as a function of the air-filled pore space ε for each soil depth. The model was derived from a power function fit from laboratory diffusion experiments (see above) on the undisturbed soil cores.

To account for the non-uniform vertical distribution of the soil water content in the soil profile, D_s was estimated as the harmonic average between the two measurement depths (Pingintha et al., 2010; Turcu et al., 2005) as follows:

$$\begin{array}{}\text{(6)}& D_{\mathrm{s}}={\displaystyle \frac{\mathrm{\Delta }{z}_{\mathrm{1}}+\mathrm{\Delta }{z}_{\mathrm{2}}}{\frac{\mathrm{\Delta }{z}_{\mathrm{1}}}{D_{\mathrm{s}{z}_{\mathrm{1}}}}+\frac{\mathrm{\Delta }{z}_{\mathrm{2}}}{D_{\mathrm{s}{z}_{\mathrm{2}}}}}},\end{array}$$

where Δz_1,2 (metres) is the thickness of the corresponding soil layer, and $D_{\mathrm{s}{z}_{\mathrm{1},\mathrm{2}}}$ is the effective diffusivity of the respective soil layer. Finally, assuming a constant flux between measured CO₂ at depth z_i and z_i+1, the CO₂ flux (F_i) was calculated by combining Eqs. (2)–(6) as follows:

$$\begin{array}{}\text{(7)}& F_i=\left({\displaystyle \frac{\mathrm{\Delta }{z}_i+\mathrm{\Delta }{z}_{i+\mathrm{1}}}{\frac{\mathrm{\Delta }{z}_i}{D_{\mathrm{s}{z}_i}}+\frac{\mathrm{\Delta }{z}_{i+\mathrm{1}}}{D_{\mathrm{s}{z}_{i+\mathrm{1}}}}}}\right)\times \left({\displaystyle \frac{C_{i+\mathrm{1}}-C_i}{z_{i+\mathrm{1}}-z_i}}\right),\end{array}$$

where F_i is the CO₂ flux (µmol m⁻² s⁻¹) at the upper boundary (z_i) between depth z_i and z_i+1 (metres). To calculate soil respiration (F₀) at the surface with the gradient method, a CO₂ concentration of 400 µmol mol⁻¹ at the soil surface and a constant D_s for the first 10 cm were assumed.

2.5.2 CO₂ production

The CO₂ production (P_i) in a soil layer was calculated as the difference between the flux (F_i) leaving the specific soil layer at the upper boundary (z_i) and the input flux (F_i+1) at the lower boundary (z_i+1) of the specific soil layer. Therefore, P_i had the unit of a flux (µmol m⁻² s⁻¹) (a similar approach was done by, for example, Gaudinski et al., 2000; Hashimoto et al., 2007; Fierer et al., 2005; Davidson et al., 2006).

$$\begin{array}{}\text{(8)}& P_i=F_i-F_{i+\mathrm{1}}.\end{array}$$

Total soil respiration was calculated as the sum of CO₂ production in all soil layers. Equation (8) is based on the assumption of a steady-state diffusion. Steady-state conditions for CO₂ concentration and volumetric water content were mostly given, except during a few heavy rain events where steady-state conditions were not met due to changing water contents in the profiles. Most soils exhibit increasing CO₂ concentrations with increasing soil depth. Therefore, CO₂ production is mostly positive with upward CO₂ fluxes. However, if the CO₂ concentration in a soil layer is greater than in the layers below, the calculated CO₂ production in the layers below can become negative (downward directed). Hence, in the present study, no CO₂ production was assumed when the calculated CO₂ production in a soil layer was negative. This approach was based on the assumption that there are no relevant CO₂ sinks in the soil profile. Furthermore, negative CO₂ production is considered as CO₂ storage, which will be released if the CO₂ concentration gradient or diffusion conditions change. In OB1, negative CO₂ production values were calculated in the first year at 30–50 cm depth (331 out of 365 d) and at 50–90 cm depth (359 out of 365 d). In the second year, negative values also occurred in OB1 at 30–50 cm depth (8 out of 308 d) and at 50–90 cm depth (182 out of 308 d).

Figure 3 Soil profile measurements of temperature (a), volumetric water content (b) and CO₂ concentration for the three observatories (OB). White bars represent periods without measurements.

2.5.3 Isotopic composition of CO₂

To determine the contribution of the labelled leaf litter to CO₂ in the soil atmosphere, we used the isotopic mixing equation (Eq. 9) as follows:

$$\begin{array}{}\text{(9)}& L=\mathrm{1}-\left({\displaystyle \frac{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{M}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{L}}}{{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{B}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{L}}}}\right),\end{array}$$

where δ¹³C_M is the isotopic signature of the gas sample, δ¹³C_L is the isotopic signature of the labelled leaf litter (1241 ‰ for OB1 and 1880 ‰ for OB2 and OB3), and δ¹³C_B is the average isotopic signature of the soil atmosphere for each observatory and depth before the labelled leaf litter was applied, assuming there was no change.

The CO₂ fluxes and productions for each layer and isotopologue of CO₂ (¹²CO₂ and ¹³CO₂) were calculated using the isotopic signature of the soil atmosphere and Eqs. (2)–(7). To account for different effective diffusivities of ¹²CO₂ and ¹³CO₂, the effective diffusivity D_s for ¹³CO₂ was adjusted, according to Cerling et al. (1991), as follows:

$$\begin{array}{}\text{(10)}& D_{\mathrm{s}}{=}^{\mathrm{12}}{D}_{\mathrm{s}}=\mathrm{1.0044}{\times }^{\mathrm{13}}{D}_{\mathrm{s}},\end{array}$$

where it is assumed that D_s is equivalent to ¹²D_s due to the fact that about 99 % of total CO₂ is ¹²CO₂.

To determine the contribution of the labelled leaf litter to the CO₂ production in a soil layer and accounting for diffusion effects, the isotopic signature of CO₂ production (δ¹³P-CO₂) in each soil layer was calculated with Eq. (11) as follows:

$$\begin{array}{}\text{(11)}& {\mathit{\delta }}^{\mathrm{13}}P\text{-}{\mathrm{CO}}_{\mathrm{2}}=\left({\displaystyle \frac{{}^{\mathrm{13}}P\text{-}{\mathrm{CO}}_{\mathrm{2}}}{R_{\mathrm{st}}{\times }^{\mathrm{12}}P\text{-}{\mathrm{CO}}_{\mathrm{2}}}}-\mathrm{1}\right)\times \mathrm{1000},\end{array}$$

where R_st is the isotopic ratio of the VPDB reference standard, while ¹³P-CO₂ and ¹²P-CO₂ are the CO₂ production for each isotopologue of the respective soil layer. Afterwards, Eq. (9) was used to calculate the amount of labelled leaf litter to total CO₂ production, where δ¹³C_B was substituted with the average isotopic signature of CO₂ production (Eq. 11) before the labelling, and δ¹³C_M was substituted with the isotopic signature of CO₂ production. The litter-derived CO₂ production was calculated by multiplying the amount of labelled leaf litter (L) with the total CO₂ production of the respective soil layer.

2.6 Statistical analysis

A Monte Carlo simulation was generated to determine the influence of the measurement uncertainties of the sensors, which were used for calculation of CO₂ fluxes and CO₂ production rates. It was assumed that each measurement error was normally distributed. The standard deviation was equal to the measurement accuracy, which was obtained from the corresponding manual. The distributions of CO₂, volumetric water content and temperature measurements were used for 1000 Monte Carlo simulations. Unless stated otherwise, the error bars in the final results represent the standard deviation of these simulations. All analyses were performed in R (version 3.3.2) for Linux (R Core Team, 2017).

3 Results

3.1 Temperature, water content and CO₂ concentration in the profile

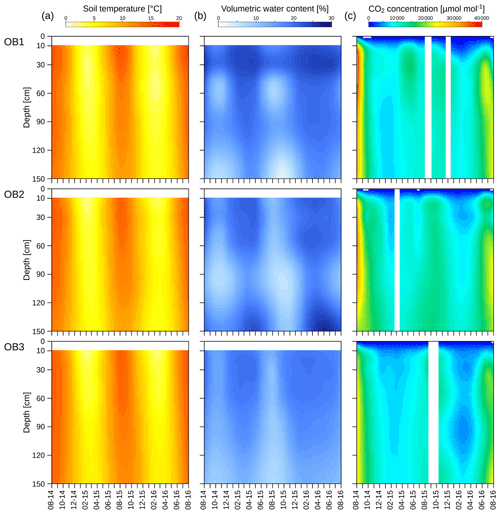
Soil temperature showed a distinct seasonality down to 150 cm, with the maximum and the minimum temperatures delayed with increasing soil depth (Fig. 3a). The minimum soil temperature was 0.3 and 4.0 ^∘C in January 2016 at 10 and 150 cm depths respectively. The maximum temperature was measured in July in the uppermost layer (16.6 ^∘C) and in August in the deepest layer (14.4 ^∘C). The annual amplitude of the soil temperature decreased from 16.3 ^∘C at 10 cm to 10.4 ^∘C at 150 cm. However, mean annual values showed no significant decline with soil depth and were 8.4 and 8.3 ^∘C at 10 and 150 cm respectively during the 2 years of observation. Variations in the mean soil temperatures between the three observatories were <1 ^∘C at all depths (Fig. S1).

The volumetric water contents also showed seasonal variations at all depths (Fig. 3b), with depletion during the summer. The minimum of the volumetric water content at 10 cm was reached in August (10 %), whereas the minimum at 150 cm was observed 2 months later in October (6 %). The water reservoir of the soil profile was refilled during the autumn and winter, reaching maximum values at 10 cm (23 %) and 150 cm (22 %) in April (Fig. 3b), which were delayed by 14 d in the deepest layer. In OB1 and OB3, the mean volumetric water content decreased with increasing soil depth. Only in OB2 did the mean water content increase at 150 cm (Fig. S2). The water content showed a greater variation between the three observatories than in the soil temperature (Fig. S2).

The CO₂ concentration in the soil pores followed a similar seasonality to the soil temperature (Fig. 3c), with a maximum during the summer and a minimum during the winter and early spring. The same behaviour was observed for both investigated years, while the values were higher during the first summer. The CO₂ concentration in the uppermost layer ranged from 1000 to 35 000 µmol mol⁻¹ and, thus, was in a similar range of results for the deepest layer, with 7500 to 35 000 µmol mol⁻¹. However, values were highly variable between the observatories, with OB2 and OB3 showing an increasing CO₂ concentration with greater soil depth, whereas OB1 yielded the highest CO₂ concentrations at 30 to 50 cm depth.

3.2 Soil respiration

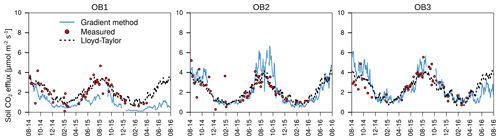
The mean annual mineral (without the organic layer) soil respiration determined with chamber measurements for the three observatories was 776±193 g C m⁻² yr⁻¹, with a small variability between the observatories (Table 1). The mineral soil respiration modelled with the Lloyd–Taylor function gave similar results for the same period. In contrast, soil respiration determined with the gradient method showed a high variability between the observatories, but was in the range of the directly measured respiration, except for OB1. This variability can be explained by the higher water content at OB1 and, consequently, the lower diffusion coefficient. The average diffusion coefficient at OB1 at 10 cm was less than half that at OB2 and OB3.

Table 1 Total soil respiration with and without the organic layer for the three observatories derived from soil surface measurements with linear interpolation (chamber), modelled with a Lloyd–Taylor function and derived from the gradient method based on CO₂ measurements along the soil profile for 1 year. Means and standard deviations are shown.

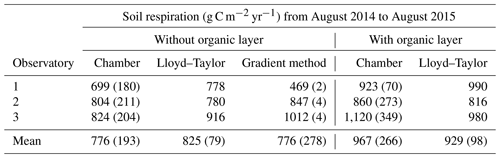
The organic layer increased total respiration by 13 % and 25 % respectively for the Lloyd–Taylor model and chamber measurements (Table 1). For all the methods and in all the observatories, soil respiration correlated well with soil temperature and soil moisture. The highest fluxes were measured when soil temperature (10 cm) was highest and water content (10 cm) was low (Figs. 3 and 4).

Figure 4 Mean daily soil respiration determined with the gradient method, measured with chambers and modelled with a Lloyd–Taylor function for the observatories (OB).

3.3 Vertical CO₂ production

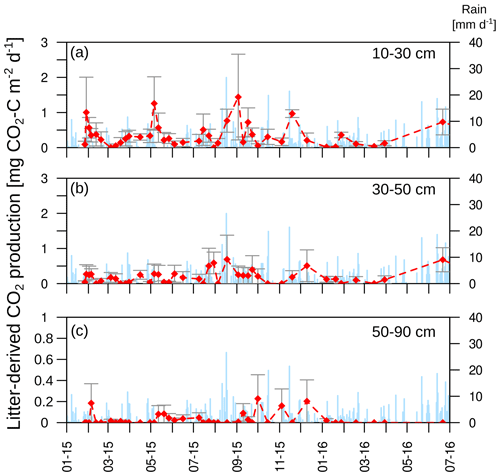
The mean CO₂ production rates decreased from 1.4 µmol m⁻² s⁻¹ in the uppermost layer (0–10 cm depth) to 0.03 µmol m⁻² s⁻¹ in the deepest layer (50–90 cm depth; Fig. 5). The CO₂ production followed the same seasonality as soil temperature and CO₂ concentration, with the highest production rates occurring during the summer and the lowest during the winter months in all soil layers. This seasonal variation was greatest in the top two layers of the soil (0–10 and 10–30 cm; Fig. 5a–d).

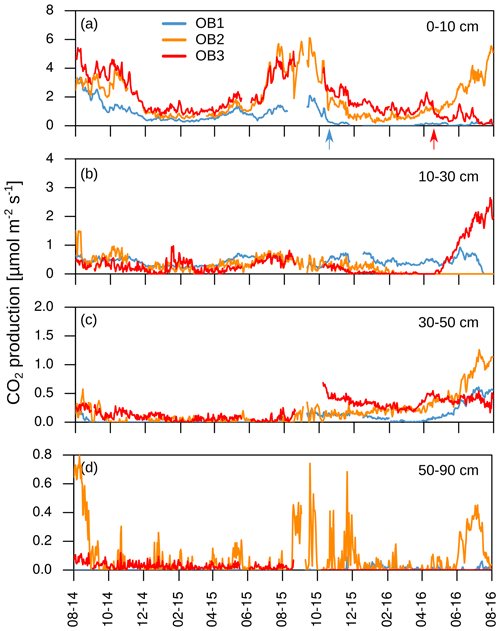
Figure 5 (a–d) Daily mean CO₂ production in each soil layer. Arrows indicate disturbances due to bioturbation of voles close to the CO₂ sensors at 10 cm depth (OB1 and OB3), which created macropores and changed diffusivity.

About 70±17 % of total soil respiration was produced in the first 10 cm of the soil profile where 21 % of the SOC stock (0–1.5 m) was stored. The CO₂ production at 10 to 30 cm accounted for 20 ± 14 % of the total soil respiration during the year, and 32 % of the SOC was located in this depth increment. The subsoil (>30 cm) accounted for 10 ± 9 % of total CO₂ production, with 47 % of the SOC stock stored in the subsoil.

The mean total CO₂ production showed no significant differences between the 2 years. The variation in total annual CO₂ production was greater between the three observatories (326–1008 g CO₂-C m⁻² yr⁻¹) than between the 2 studied years (Fig. 6). However, the CO₂ production in the different soil layers showed considerable changes with time; it increased by 500 % in the subsoil, from 30 to 50 cm, in the second year, which increased the contribution of subsoil CO₂ production from 4 % to 16 % of the total CO₂ production. This increase was observed at all three observatories. In contrast, the CO₂ production in the first 10 cm in OB1 and OB3 showed a decline from the first to the second year, which was probably caused by methodological variations and does not represent a real decrease in respiration activity since the bioturbation of animals (e.g. voles) might have had a strong influence on the diffusivity (Fig. 5a). Voles created macropores; therefore, the CO₂ gradient approach was not applicable. This was also indicated by a sudden and rapid drop in CO₂ production between 0 and 10 cm in OB1 (October 2015) (Fig. 5a).

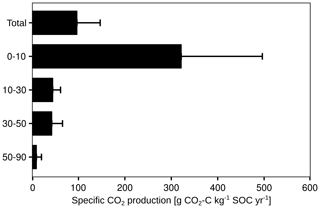
To take the different SOC contents of each soil layer into account, the cumulative CO₂ production was normalised to the SOC stock of the respective layer (Fig. 7). The specific CO₂ production decreased from 322 g CO₂-C kg⁻¹ SOC yr⁻¹ in the first 10 cm to 9 g CO₂-C kg⁻¹ SOC yr⁻¹ at 50 to 90 cm. It should be noted that the proportion of autotrophic respiration in the total CO₂ production could not be quantified.

3.4 Sources of CO₂ production

3.4.1 Contribution of fresh litter

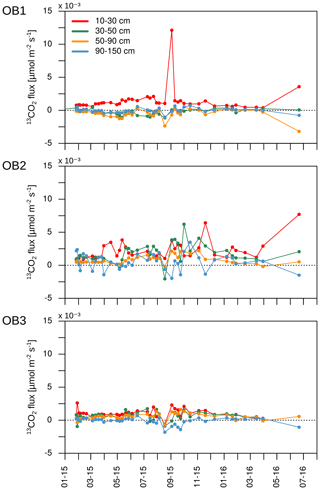
The isotopic signature of soil CO₂ (δ¹³CO₂) in the observatories before the start of the labelling experiment ranged from −25.4 ‰ to −21.8 ‰, with no significant differences between soil depths (Fig. 8a). The labelling experiment was conducted to assess the fate of fresh litter added on top of the organic layer into different C fractions (e.g. SOC and DOC), including soil CO₂. A total of 6 d after the application of the ¹³C-labelled leaf litter, CO₂ was already enriched in litter-derived C down to 90 cm depth in all the observatories. The isotopic signature ranged from 70 ‰ at 10 cm depth to −19 ‰ at 90 cm depth (Fig. 8b). Thus, the maximum contribution of litter-derived C to total CO₂ was 5 % at 10 cm depth 6 d after the litter replacement (Fig. 8c). At 90 cm, the maximum amount of litter-derived CO₂ was 0.6 % 2 weeks after the beginning of the labelling experiment (Fig. 8c). In addition, minor peaks with up to 0.8 % of CO₂ derived from the labelled litter were observed at all depths after rain events within the first 6 months of litter application. The average contribution of litter-derived CO₂ decreased with time and reached a range of 2.5 % to 0.2 % at 10 cm depth from January 2015 to July 2016. The total amount of labelled litter-derived C to the CO₂ production below 10 cm was 291 mg C m⁻² (±127) (Fig. 9), which accounted for 0.12 % of the total CO₂ production below 10 cm depth.

Assuming that diffusion is the main transport process of CO₂ in the soil atmosphere, the CO₂ flux between two soil layers can be calculated for each C isotope separately. As mentioned, a positive flux indicates the release of CO₂ from mineralisation or root respiration in the respective soil layer. A negative flux, in turn, represents the downward diffusion of CO₂ from the layer above. Due to the high ¹³C enrichment in the applied litter, negative ¹³CO₂ fluxes can indicate a downward diffusion of litter-derived CO₂ from the soil layer above (Fig. 10). On average for the three observatories, 20 out of 41 samplings had negative ¹³CO₂ fluxes below 90 cm depth, indicating a downward movement of labelled litter-derived CO₂. Furthermore, OB2 and OB3 had positive ¹³CO₂ fluxes between 10 and 90 cm, indicating a transport of labelled litter-derived C down the soil profile as dissolved organic carbon (DOC) and mineralisation of this DOC. Meanwhile, the observed ¹³C enrichment in CO₂ in OB1 below 30 cm depth might also be influenced by diffusion of labelled litter-derived ¹³CO₂ from the soil layer above (10 to 30 cm).

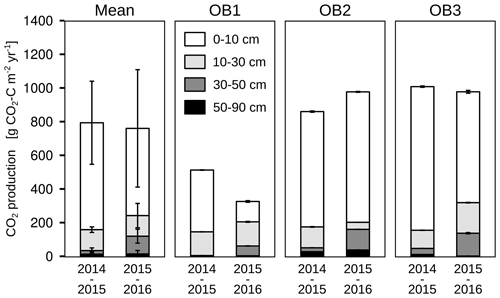
Figure 6 Cumulative CO₂ production for each soil layer, observatory (OB) and year of observation. Error bars represent the standard deviation.

Figure 7 Annual specific CO₂ production for the total CO₂ efflux. Mean (n=3) and standard deviation are shown.

3.4.2 Contribution of old C

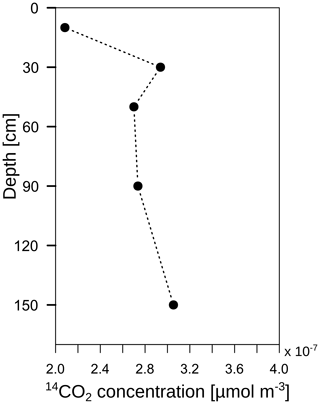
The radiocarbon content of the bulk SOC decreased strongly with increasing soil depth from close to atmospheric values (F¹⁴C 0.99) at 10 cm to an apparent age of about 3460 years before the present (F¹⁴C 0.65) at 110 cm depth (Fig. 11; grey triangles). In contrast, the ¹⁴C concentrations of the CO₂ in the soil atmosphere were relatively constant throughout the soil profile and for both samplings, with values in the range of 1.03–1.07 F¹⁴C and, thus, they derive mainly from the post-bomb period (Fig. 11; black dots). This indicates a young source of CO₂ production. Consequently, old subsoil SOC was not detected as a significant source of CO₂ production.

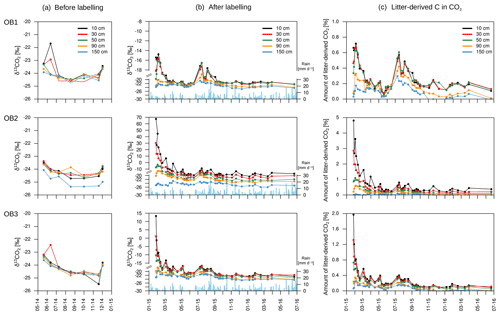
Figure 8 Isotopic signature of CO₂ at each depth and observatory (OB) before the addition of the labelled litter (a) and after the labelled litter addition (b), with daily precipitation data (blue bars). The relative amount of litter-derived CO₂ on total CO₂ at each depth and observatory (c). Please note the different y-axis ranges for (b) and (c).

Figure 9 (a–c) Litter-derived CO₂ production in each soil layer. Mean (n=3) and standard error are shown.

4 Discussion

4.1 Temperature, water content and CO₂ concentration in the profile

In all three subsoil observatories, increasing CO₂ concentrations with depth were observed. This has also been reported by other studies (Davidson et al., 2006; Drewitt et al., 2005; Fierer et al., 2005; Hashimoto et al., 2007; Moyes and Bowling, 2012). However, the increase was not continuous down to 150 cm depth. Higher CO₂ concentrations were observed between 30 and 50 cm depth, indicating a higher CO₂ production at this depth increment, which can be linked to the root distribution in the subsoil observatories (Fig. 12). About 82 % of the fine root biomass and necromass were found to be located between 0 and 50 cm and 18 % at the 30 to 50 cm depth. Therefore, the contribution of autotrophic respiration to CO₂ production and the mineralisation of dead roots were greater at these depths than in the deep subsoil (>50 cm). The CO₂ concentration in the soil pores is also controlled by abiotic factors such as effective diffusivity (D_s). The average effective diffusivity (D_s) at 10 cm was about 40 % lower than at 30 cm. Consequently, CO₂ accumulated in the soil pores below 10 cm depth due to the lower diffusion of CO₂ between the soil surface and 10 cm depth. The effective diffusivity was mainly controlled by soil water content, which reduced it. For example, the high CO₂ concentration in August 2014 (up to 40 000 µmol mol⁻¹) compared to August 2015 (up to 20 000 µmol mol⁻¹; Fig. 3c) can be explained by the higher volumetric water content in 2014 in all profiles. The high water content was related to more precipitation in July 2014 (120 mm) than in July 2015 (47 mm) and to less precipitation in August in both years (49 and 95 mm). Additionally, evapotranspiration was greater in August 2015 than in August 2014 due to a higher mean air temperature (18 and 15 ^∘C).

Figure 10 ¹³CO₂ fluxes for each observatory. Negative fluxes represent the diffusion of ¹³CO₂ from the soil layer above.

4.2 Soil respiration

The annual mean total respiration determined using the gradient method corresponded well with the results of the closed chamber measurements, indicating that the gradient method resulted in realistic flux estimations (Table 1; Fig. 4). This is in line with the results reported by other studies (Baldocchi et al., 2006; Tang et al., 2003; Liang et al., 2004). The differences in soil respiration between the methods can be attributed to the different spatial resolutions of the corresponding measurements. The chamber measurements were based on five spatial replicates for each subsoil observatory, covering a total measurement area of 1274 cm². Therefore, chamber measurements accounted for spatial variability in water content and soil CO₂ concentrations below the chamber, whereas the gradient method was based on one profile measurement for CO₂ and water content at each of the three observatories. Large differences in total respiration rates of up to 200 % were found among the three observatories with the gradient method. Both methods have advantages and disadvantages for determining total soil respiration. The gradient method does not alter the soil atmosphere CO₂ gradient, and is continuous and less time-consuming than chamber measurements, but it is vulnerable to the spatial heterogeneity of the soil structure, moisture content around the sensors and changes in diffusivity, e.g. due to bioturbation. For example, the higher soil respiration determined with the gradient method at OB2 and OB3 in summer (Fig. 4) is linked to lower soil moisture measured in 10 cm depth (Fig. 3b) and to higher total soil porosity (51 % at OB2 and 49 % at OB3 vs. 46 % at OB1). As a consequence, the effective diffusivity (Eq. 4) is higher, resulting in higher fluxes. Furthermore, the lower soil respiration of OB1 and OB3 in the second year, determined with the gradient method, was related to the bioturbation of voles, which increased the diffusivity around the CO₂ sensors and led to a lower CO₂ concentration in 10 cm depth, which in turn led to an underestimation of the total soil respiration (Fig. 4) by the gradient method.

Removing the organic layer in the soil collars was supposed to determine the contribution of CO₂ production in the organic layer to total soil respiration. Since the organic layer was only removed in the soil collars and not around the soil collars, it must be noted that the contribution of the organic layer to total soil respiration might be underestimated with the used method. However, the results are in line with findings from litter manipulation experiments, which reported a contribution of 9 % to 37 % of the organic layer to total soil respiration (Nadelhoffer et al., 2004; Bowden et al., 1993; Kim et al., 2005; Sulzman et al., 2005).

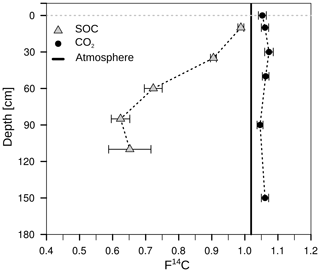
Figure 11 Mean ¹⁴C concentration (F¹⁴C) of bulk soil (grey triangles; data from Angst et al., 2016) and CO₂ in the soil atmosphere (black dots). The solid black lines represent the annual average F¹⁴C values in the atmosphere from 2014, measured at the Jungfraujoch alpine research station, Switzerland (Ingeborg Levin and Samuel Hammer, personal communication, 2015).

Figure 12 Mean fine root density for biomass and necromass of the subsoil observatories. Error bars represent the standard error.

4.3 Vertical CO₂ production

The vertically partitioned CO₂ flux revealed that more than 90 % of the total CO₂ efflux was produced in the topsoil (<30 cm). These results correspond well with other studies which have found that more than 70 % of total CO₂ efflux in temperate forests is produced in the upper 30 cm of the soil profile (Davidson et al., 2006; Fierer et al., 2005; Hashimoto et al., 2007; Jassal et al., 2005; Moyes and Bowling, 2012). Nevertheless, only 53 % of the SOC stock is stored in the first 30 cm, indicating that subsoil SOC on the site of the present study may have a slower turnover than the topsoil SOC. This is supported by the low ¹⁴C concentrations in SOC below 30 cm. However, the higher CO₂ production in the topsoil can be also related to a greater fine root biomass and necromass density (Fig. 12), which may serve as an indicator of autotrophic respiration and heterotrophic respiration in the rhizosphere. Even if the current study is unable to distinguish between autotrophic and heterotrophic respiration, the importance of autotrophic respiration to total soil respiration was shown in a large-scale girdling experiment by Högberg et al. (2001). They reported that autotrophic respiration accounted for up to 54 % of total soil respiration. As a consequence, autotrophic respiration should be higher in the topsoil than in the subsoil, due to the decreasing root bio- and necromass with increasing soil depth (Fig. 12).

It is remarkable that the CO₂ production at 30 to 50 cm increased from 23 g C m⁻² yr⁻¹ in the first year to 118 g C m⁻² yr⁻¹ in the second year of the study (Fig. 6). This can be explained in part by more precipitation in the second year (621 mm) than in the first year (409 mm), inducing fewer water-limiting conditions for plants and microbial activity. As a result, the mean volumetric water content was higher in the second year (18 % compared to 16 %) at 50 cm depth, which gave better conditions for the mineralisation of SOC by microorganisms (Cook et al., 1985; Moyano et al., 2012). Furthermore, the greater precipitation increased the input of DOC into the subsoil on the site of the present study, which is supported by the study of Leinemann et al. (2016), who investigated DOC fluxes in subsoil observatories for more than 60 weeks. They found a positive correlation between DOC fluxes, precipitation and water fluxes at 10, 50 and 150 cm depths. Furthermore, they showed that DOC fluxes declined by 92 % between a depth of 10 and 50 cm, which was attributed to mineral adsorption and microbial respiration of DOC (Leinemann et al., 2016).

Figure 13 Soil air ¹⁴CO₂ concentration in OB1 from December 2014.

4.4 Sources of CO₂ production

4.4.1 Young litter-derived CO₂

In this study, a unique labelling approach was used to estimate the contribution of aboveground litter to CO₂ production along a soil profile by applying stable isotope-enriched leaf litter to the soil surface. These results showed that litter-derived C did not significantly contribute to annual CO₂ production below 10 cm depth. Leaf litter is decomposed and washed into the mineral soil as DOC. Within 1 year, only 0.13 % of total CO₂ production between 10 and 90 cm originated from the labelled leaf litter. It should be considered that part of the measured ¹³CO₂ may derives from the turnover of the microbial necromass, which could lead to an overestimation of the litter-derived CO₂. However, the isotopic signature of the biomass at the study site ranges from −27 ‰ (10 cm) to −25.8 ‰ (90 cm; Sebastian Preußer and Ellen Kandeler, personal communication, 2020) which is lower than the isotopic signature of the soil atmosphere before the application of the labelled leaf litter. This indicates that the turnover of microbial biomass had no measurable effect on the isotopic signature of the soil atmosphere. Instead, it should be mentioned again that the determination of the CO₂ production is based on the assumption of steady-state conditions in the soil. Sudden changes in the CO₂ concentration or soil moisture, for example, after precipitation events can lead to a violation of this assumption, and the uncertainties in litter-derived CO₂ production increase for these periods. A non-steady-state model might be better to describe such periods, but a non-steady-state model may also require a higher spatial and temporal resolution of measurements (water content, CO₂ and ¹³CO₂) at depths of 0–10 cm. Nevertheless, further research should address this point. However, in periods without major precipitation events (before the ¹³CO₂ sampling) the contribution of litter-derived CO₂ to total CO₂ remained below 1 %. This indicates that, despite the uncertainties due to non-steady-state conditions, the mineralisation of DOC originating from the organic layer was a minor source of CO₂ production in the soil profile below 10 cm. The average DOC flux in the subsoil observatories in the first year was estimated to be 20 g C m⁻² yr⁻¹ at 10 cm depth and 2 g C m⁻² yr⁻¹ at 50 cm depth, indicating a DOC input of 18 g C m⁻² yr⁻¹ into the 10 and 50 cm depth increments (Leinemann et al., 2016). An assumed complete mineralisation of this DOC would account for 11 % of CO₂ production at this depth increment. Overall, most of the CO₂ production between a depth of 10 and 90 cm must be derived from autotrophic respiration and heterotrophic respiration in the rhizosphere.

4.4.2 Old SOC derived CO₂

The very similar radiocarbon contents of soil CO₂ produced at different depths, which were 1.06 F¹⁴C on average, revealed that ancient SOC components were not a major source of CO₂ production. The results indicate that the CO₂ originated mainly from young (several decades old) C sources, presumably mainly from root respiration, its exudates and DOC. Other studies have found similar results at a grassland site in California down to 230 cm depth (Fierer et al., 2005) and in temperate forests down to 100 cm (Gaudinski et al., 2000; Hicks Pries et al., 2017). In addition, Hicks Pries et al. (2017) incubated root-free soil from three depths (15, 50 and 90 cm) and compared the radiocarbon signature of the respired CO₂ with their results from the field. They found that CO₂ from the short-term incubations had the same modern signature as the field measurements despite the high ¹⁴C age of the bulk SOC at 90 cm depth (∼1000 yr BP; Hicks Pries et al., 2017). This supports the findings of the present experiment. Therefore, microbial respiration in temperate subsoils is mainly fed by relatively young C sources fixed less than 60 years ago.

4.4.3 Diffusion effects

A highly ¹³C-enriched CO₂ source was introduced to the top of a soil profile. Shortly afterwards, an enrichment of ¹³C was measured in CO₂ along the whole soil profile (Fig. 8b). However, this enrichment could not only be linked to the transport and mineralisation of litter-derived C along the soil profile (e.g. DOC in seepage water). The diffusion of ¹³CO₂ down the soil profile also has to be taken into account. According to Fick's first law, ¹³CO₂ diffuses into the soil profile following the ¹³CO₂ gradient independently from the ¹²CO₂. Thus, even though the total CO₂ concentration increased with soil depth, meaning an upward diffusion of ¹²CO₂, the ¹³CO₂ gradient could be the opposite due to ¹³C-enriched leaf litter, leading to a downward diffusion of ¹³CO₂. Consequently, this could lead to a misinterpretation of the pathways of subsoil ¹³CO₂ in tracer experiments. Furthermore, this effect should also be taken into consideration when interpreting ¹⁴CO₂ soil profile measurements as an indicator of the age of the mineralised SOC, as in other field studies (e.g. Davidson et al., 2006; Davidson and Trumbore, 1995; Fierer et al., 2005; Gaudinski et al., 2000). Downward diffusion of ¹⁴CO₂ might be an important factor for explaining the observed ¹⁴CO₂ profiles. If this downward diffusion is the case, the ¹⁴CO₂ gradient should not have a continuous decrease with soil depth since the ¹⁴CO₂ gradient is the driving factor for diffusion according to Eq. (3). In fact, ¹⁴CO₂ concentration at 30 cm depth in subsoil OB1 was greater than at 50 cm depth (Fig. 13), which in turn led to a downward diffusion of ¹⁴CO₂ from a depth of 30 to 50 cm. This might lead to a rejuvenation in the ¹⁴CO₂ soil profile and to an underestimation of the mineralisation of old SOC in subsoils.

5 Conclusions

The gradient method allowed total soil respiration to be partitioned vertically along a soil profile. Most of the CO₂ (90 %) was produced in the topsoil (<30 cm). However, the subsoil (>30 cm), which contained 47 % of the SOC stocks, accounted for 10 % of total soil respiration. This can be explained by a larger amount of stable SOC in subsoils compared to topsoils. However, the modern radiocarbon signature of CO₂ throughout the soil profiles indicated that mainly young carbon sources were being respired from roots and root exudates and autotrophic respiration. The contribution of old SOC to subsoil CO₂ production was too small to significantly alter the ¹⁴C concentrations in the soil atmosphere used to identify CO₂ sources. Furthermore, this study showed that the mineralisation of fresh litter-derived C only contributed to a small part of total soil respiration, underlining the importance of roots and the rhizosphere for subsoil CO₂ production.