the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modeling polar marine ecosystem functions guided by bacterial physiological and taxonomic traits
Jeff S. Bowman
Ya-Wei Luo
Hugh W. Ducklow
Oscar M. Schofield
Deborah K. Steinberg
Scott C. Doney
Heterotrophic marine bacteria utilize organic carbon for growth and biomass synthesis. Thus, their physiological variability is key to the balance between the production and consumption of organic matter and ultimately particle export in the ocean. Here we investigate a potential link between bacterial traits and ecosystem functions in the rapidly warming West Antarctic Peninsula (WAP) region based on a bacteria-oriented ecosystem model. Using a data assimilation scheme, we utilize the observations of bacterial groups with different physiological traits to constrain the group-specific bacterial ecosystem functions in the model. We then examine the association of the modeled bacterial and other key ecosystem functions with eight recurrent modes representative of different bacterial taxonomic traits. Both taxonomic and physiological traits reflect the variability in bacterial carbon demand, net primary production, and particle sinking flux. Numerical experiments under perturbed climate conditions demonstrate a potential shift from low nucleic acid bacteria to high nucleic acid bacteria-dominated communities in the coastal WAP. Our study suggests that bacterial diversity via different taxonomic and physiological traits can guide the modeling of the polar marine ecosystem functions under climate change.
- Article
(5413 KB) - Full-text XML
-
Supplement
(5137 KB) - BibTeX
- EndNote
Microbes regulate many key ecosystem functions in the marine food web. Unicellular primary producers fix organic carbon (i.e., an ecosystem function termed primary production), while heterotrophic marine bacteria and archaea (hereafter bacteria) utilize the fixed organic carbon for growth and biomass synthesis (i.e., an ecosystem function termed bacterial production, or BP; Azam et al., 1983). Thus, the variability in the abundance and activity of bacteria is central to understanding the balance between production and consumption of organic matter and ultimately particle export in the ocean. In flow cytometric analyses, bacteria cluster into two groups of cells with different nucleic acid content, including high nucleic acid (HNA) and low nucleic acid (LNA) cells (Bouvier et al., 2007; Gasol et al., 1999). These two groups are suggested to represent lineages (Schattenhofer et al., 2011; Vila-Costa et al., 2012) or physiological states (Bowman et al., 2017), in which HNA cells are generally larger in both cell and genome size compared to LNA cells (Bouvier et al., 2007; Calvo-Díaz and Morán, 2006). The significance of HNA versus LNA cells in determining distinct ecosystem states and functions has been investigated, but much is still unknown. In a recent study along the West Antarctic Peninsula (WAP), the high dimensionality of the bacterial community structure data was reduced via emergent self-organizing maps and subdivided into a small number of bacterial modes associated with specific taxonomic and functional traits (Bowman et al., 2017). Bowman et al. (2017) demonstrated that a combination of taxonomy, physiological structure (i.e., HNA and LNA cells), and abundance of bacterial communities explained up to 73 % of the variance in bulk BP. Their findings imply that physiological and taxonomic traits of bacteria may inform a predictive ecosystem model to further explore ecologically important questions including the following: would these bacterial traits reflect other important ecosystem functions such as the net primary production and particle sinking flux? If so, what would be the potential mechanisms and how will the relationship between bacterial traits and ecosystem functions be impacted by climate change?
The WAP is a rapidly warming marine ecosystem, with resulting changes in physical, ecological, and biogeochemical processes (Clarke et al., 2009; Cook et al., 2005; Ducklow et al., 2007; King, 1994; Meredith and King, 2005; Stammerjohn et al., 2008; Vaughan et al., 2003; Vaughan, 2006; Whitehouse et al., 2008). Routine monitoring through the Palmer Long-Term Ecological Research project (Palmer LTER; since 1991) has revealed climate-driven variations in seasonal phytoplankton accumulation (Saba et al., 2014; Schofield et al., 2017), bacterial dynamics (Bowman and Ducklow, 2015; Ducklow et al., 2012a; Kim and Ducklow, 2016; Luria et al., 2017, 2014), nutrient drawdown (Kim et al., 2016), and micro- and macrozooplankton dynamics (Garzio and Steinberg, 2013; Steinberg et al., 2015; Thibodeau et al., 2019). The wealth of Palmer LTER observations has enabled the construction of a numerical marine ecosystem model for the coastal WAP region (i.e., the WAP-1D-VAR v1.0 model; Kim et al., 2021) by adapting the regional test-bed models of other ocean basins (Friedrichs, 2001; Friedrichs et al., 2006, 2007; Luo et al., 2010, 2012). The WAP-1D-VAR v1.0 model is compared against roughly bi-weekly time-series observations over the growth season (October–March) near Palmer Station (64.77∘ S, 64.05∘ W; the mean depth ∼ 65 m, the bottom depth ∼ 75 m) that record seasonal variations in ecological processes modulated by variations in surface light, mixed layer depth, and surface sea-ice cover. The WAP-1D-VAR v1.0 model utilizes a data assimilation scheme to minimize the misfits between model results and observational data via a variational adjoint method (Lawson et al., 1995) that assimilates the available Palmer LTER data to objectively adjust the model parameters. Serving as a mechanistic model, assimilation of the Palmer LTER observations enables the model to constrain poorly measured bacterial processes (e.g., respiration, viral and grazing mortality, growth efficiency, carbon demand, and utilization of dissolved organic matter with varying lability) and to predict microbial system states in changing environments. Yet, incorporating molecular observations into a numerical ecosystem model is a challenge because of the difference in how levels of biological organization are treated in observations and models (Hellweger, 2020), as well as the high dimensionality of microbial molecular observations. One argument is that molecular-level changes in microbial dynamics may not directly translate into a clear picture of changes in community structure or resulting changes in bulk ecosystem functions.
In this study, we explore a potential link between bacterial traits and ecosystem functions in the warming coastal WAP using a bacteria-oriented ecosystem model modified from the WAP-1D-VAR v1.0 model (Kim et al., 2021). The bacterial traits examined in this study include physiological and taxonomic traits. For physiological traits, our model explicitly simulates the time-evolving dynamics of two ubiquitous bacterial groups with differing nucleic acid contents, the HNA group and the LNA group, by directly assimilating the group-specific carbon biomass observations estimated by flow cytometry. For taxonomic traits, taxonomic modes derived from bacterial 16S rRNA gene sequence data (Bowman et al., 2017) are compared to final model results at the corresponding time points with the assumption that bacterial taxonomy would provide information about bacterial ecosystem processes and structures. Our study indirectly incorporates bacterial molecular information into ecosystem-level dynamics, in contrast to genome-scale or gene-centric models predicting the time-evolving dynamics of microbial molecular processes.
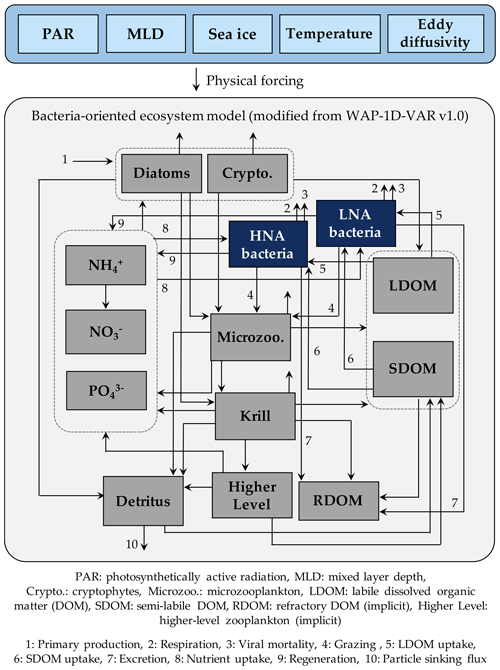
Figure 1Model structure. The model is forced by five different physical forcings, denoted as a horizontal row across the top of the schematic. As the ecosystem component, heterotrophic bacteria are divided into two groups of differing physiological states, including high nucleic acid (HNA) and low nucleic acid (LNA) bacterial compartments. The flows between the prognostic state variables with the name of the numbered flows in the legend only represent these two bacterial compartments.
2.1 Bacteria-oriented ecosystem model
The model is originally derived and modified from the one-dimensional (1-D) variational data assimilation planktonic ecosystem model for the coastal WAP region called the WAP-1D-VAR v1.0 model (Kim et al., 2021). The WAP-1D-VAR v1.0 model tracks C, N, and P of its state variables with flexible stoichiometry. For our study, we modify the original model's single bacterial compartment into HNA and LNA bacterial compartments and only discuss their C stocks and rates, as well as other state variables that remain the same as the WAP-1D-VAR v1.0 model. The state variables in this modified model include HNA and LNA bacteria, diatoms, cryptophytes, microzooplankton, krill, labile dissolved organic carbon (LDOC), semi-labile DOC (SDOC), ammonium (NH4), nitrate (NO3), phosphate (PO4), and particulate (carbon) detritus (Fig. 1). Refractory DOC (RDOC) and higher trophic levels are implicit to serve as model closure terms (i.e., they are source or sink terms of other explicit state variables, and their time derivatives are not calculated in the model). The model is forced by mixed layer depth (MLD), photosynthetically active radiation (PAR) at the ocean surface, surface sea-ice concentration, water-column temperature, and eddy diffusivity (Fig. S1 in the Supplement) using a constant time step of 1 h and a second-order Runge–Kutta scheme (Texts S1 and S2 in the Supplement). The model allows both LDOC and SDOC as substrate sources for bacteria, and it is the nutrient quota of bacteria that allows the lability of SDOC to vary. In contrast to LDOC pool that is entirely available for bacteria, a parameter controlling the lability of SDOC (rSDOC, Tables S2–S6 in the Supplement) regulates the size of the portion of SDOC that can be made available for bacterial uptake. Bacterial C growth is determined by their cellular nutrient quota, as well as available LDOC and SDOC concentrations (Kim et al., 2021).
Table 1Initial values of bacterial model parameters. Different initial values are assigned to the model parameters of high nucleic acid (HNA) and low nucleic acid (LNA) bacterial groups to simulate their distinct physiological processes and trophic interactions.

The time derivative of C biomass for each bacterial group is determined as follows:
where C is bacterial C biomass, is LDOC consumption, is SDOC consumption, RC is respiration, is RDOC excretion, is SDOC excretion, GZC is the amount of C biomass grazed by microzooplankton, and MC is mortality caused by viral attack (unit: mmol C m−3 for C and for the rest of the terms). The sum of the first three terms on the right-hand side in Eqs. (1) and (2) is defined as BP for each bacterial group (i.e., , ). Both CHNA and CHNA are constrained by the group-specific C biomass data estimated via flow cytometry, while only bulk BP (i.e., ), not the group-specific BP, is constrained by the observations due to the lack of the group-specific BP data at the study site. With the initial parameter values distinct to each bacterial group (Table 1), the model incorporates the observations of CHNA, CLNA, BP, and other state and rate variables to its built-in data assimilation scheme (Sect. 2.2) that optimizes the parameters and calculates the resulting C stock and flows of each bacterial group (Eqs. 1 and 2). In other words, the partitioning of BP into HNA and LNA groups is purely determined by parameter optimization using the information about other ecosystem observations.
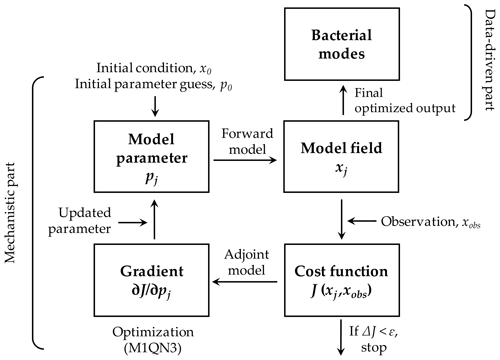
Figure 2Modeling framework. The modeling framework in this study consists of the mechanistic part as the processes associated with the bacteria-oriented ecosystem model (Fig. 1) and the data-driven part that represents how bacterial taxonomic modes are associated with the modeled bacterial and other key ecosystem functions. A variational adjoint method is employed for the parameter optimization and data assimilation processes (adapted from Glover et al., 2011). Gradient: the sensitivity of the total cost function with respect to the model parameter from optimization. Optimized model results are interpreted as a function of bacterial taxonomic and physiological traits.
2.2 Modeling framework
The modeling framework consists of the mechanistic and data-driven parts (Fig. 2). The mechanistic part represents prognostic, time-evolving microbial processes in the model (Fig. 1, Sect. 2.1) with its built-in data assimilation scheme via a variational adjoint method (Lawson et al., 1995). The data assimilation scheme minimizes the misfits between observations (i.e., assimilated data; Sect. 2.3) and model results by objectively optimizing a subset of model parameters (Friedrichs, 2001; Spitz et al., 2001; Ward et al., 2010; details in Text S3 in the Supplement). The data-driven part represents the pairing of the optimized model results from the mechanistic part and the bacterial taxonomic “modes” derived from 16S rRNA gene sequence abundance data (Bowman et al., 2017). We call this latter part data-driven because the high dimensionality of the bacterial community structure data is reduced to a single taxonomic mode using an unsupervised machine learning algorithm called Kohonen's self-organizing maps (Kohonen, 2001). Each taxonomic mode (mode hereafter) represents its specific taxonomic traits and is expressed as a single categorical variable without linear progression in between. For example, mode 1 is not necessarily closer to mode 3 than it is to mode 7. Modes are not necessarily correlated to the physiological traits of bacteria (i.e., HNA and LNA C biomass) despite being derived from the same samples. In other words, the taxonomic and physiological traits are independent of each other.
We select the nearshore Palmer LTER Station B (64.77∘ S, 64.05∘ W; ∼ 65 m) in the coastal WAP as the modeling site. The Station B datasets consist of roughly bi-weekly physical, chemical, and biological profiles collected via a profiling conductivity–temperature–density (CTD) rosette. Flow cytometric data for HNA and LNA C biomass and 16S rRNA gene amplicon data for taxonomic modes come from Arthur Harbour Station B at 10 m depth (situated 1 km from Station B) or Palmer Station seawater intake at 6 m depth (Bowman et al., 2017). Three upper-ocean depth levels, 0, 10, and 20 m (with the layer thickness of 2, 16, and 4 m, respectively), are modeled for four consecutive growth seasons, including November 2010–March 2011 (2010–11 hereafter), 2011–12, 2012–13, and 2013–14. However, only the results from 10 m are presented in detail because of the availability of the bacterial trait data at that depth. Despite the advantage of simulating the full water-column layers, it would be best to exclude the depth levels without bacterial trait observations, yet to include an adequate number of depth levels to simulate seasonal MLD and light impacts on bacterial dynamics. Thus, we choose to model three layers, that is, 0, 10, and 20 m, in a 1-D (vertical) water column.
The 1-D modeling of the coastal WAP region is justifiable given that the WAP shows relatively weak net advection compared with the Antarctic Circumpolar Current (ACC) or the subpolar gyres (Meredith et al., 2008, 2013). In addition, the CTD observations at Palmer Station do not show abrupt changes in physical and biogeochemical tracers as a result of lateral advection, with fairly homogeneous temperature and salinity distributions for the years and depths modeled in our study (Kim and Ducklow, 2016). There is a 6-month sampling gap in the austral autumn and winter months, so we optimize the model each year separately only for the austral spring to summer months. This results in each year possessing its own uniquely optimized parameter set that drives the minimized model–observation misfits for the given year. We also optimize the model for the climatological year, referred to as the climatological model, constructed by averaging 4-year observations (2010–11 to 2013–14; Text S4 in the Supplement). We do not average the whole Palmer LTER multi-decadal period (since 1991) because of the lack of HNA and LNA C biomass data except for those 4 years. Other modeling aspects (e.g., model initialization, spin-up, and bottom boundary conditions) are detailed in Text S4 and Kim et al. (2021).
2.3 Assimilated data
We assimilate the Palmer LTER observations from 0, 10, and 20 m that correspond to the compartments and flows in the model, including NO3, PO4, phytoplankton taxonomic-specific chlorophyll (Chl) for diatoms and cryptophytes (Schofield et al., 2017), microzooplankton C biomass (Garzio et al., 2013), bulk primary production (PP), bulk BP, HNA bacterial C biomass, LNA bacterial C biomass, SDOC, particulate organic carbon (POC), and particulate organic nitrogen (PON). Though not available in 2011–12, because of the importance in constraining the group-specific phytoplankton dynamics, the 4-year climatological value of the group-specific Chl is assimilated for 2011–12. NO3 is not assimilated in 2010–11, while POC, PON, and SDOC are not assimilated in 2012–13 and 2013–14 because of the lack of observations in those years. Krill C biomass is not assimilated due to the strong patchiness of their distribution with many zero values that may hinder proper model optimization, while microzooplankton C biomass (2010–11) from a single year's measurement is assimilated for all 4 model years to at least provide constraints on the parameter values for phytoplankton grazing. The model–observation misfits for microzooplankton are not examined because of the discrepancy in the timing and location of those data assimilated compared to our study.
SDOC is calculated by subtracting the background (RDOC) concentration (40.0 mmol C m−3) from climatological total DOC concentration. POC (PON) is assimilated to represent the model detrital pool, but its measurements contain living biomass from bottle filter experiments. Climatological observations show that living phytoplankton and bacterial biomass account for 26 % of total POC and 29 % of total PON, so these fractions are used to exclude living biomass from the bulk particulate material pool. When converting Chl to phytoplankton C biomass, the maximum Chl / N ratio is used along with the reference (Redfield) ratio of 0.15. BP () is derived from 3H-leucine incorporation rate () data using the conversion factor of 1.5 kg C mol−1 leucine incorporated (Ducklow, 2000). The bacterial group-specific C biomass (mmol C m−3) is estimated from bacterial abundance measured by flow cytometry (i.e., bulk bacterial C biomass multiplied by the fraction of each physiological group, fHNA or fLNA, with the conversion factor of 10 fg C cell−1; Fukuda et al., 1998).
2.4 Cost function and portability index
The total cost function is calculated to represent the misfit between observations and model results as follows:
where m and n represent assimilated data types and data points, respectively, M and Nm are the total number of assimilated data types and data points for data type m, respectively, σm is the target error for data type m, am,n is observations, and is model output. Hereafter, we present the total cost function as the total cost function normalized by M ( and normalized costs of individual data types () as the model–observation misfit equivalent to a reduced Chi-square estimate of the model goodness of fit (i.e., as a good fit from optimization, J′ ≫ 1 as a poor fit due to underestimation of the error variance or the fit not fully capturing the data, and J′ ≪ 1 as an overfitting of the data, fitting the noise, or overestimation of the error variance). The base-10 logarithm of Chl and PP is used in Eq. (3) to account for high productivity of the WAP waters and the approximate log-normal distribution of those data types (Campbell, 1995; Glover et al., 2018). The target error σm is calculated for each data type m as follows:
where is the climatological mean of the observations, and CVm is the adjusted coefficient of variation (CV) of the observations of each data type over 0, 10, and 20 m (due to observational error and seasonal and interannual variations). CVm values for the 4 modeled years in our study are higher than those across every measured depth within the mixed layer for an extended year period in the original WAP-1D-VAR v1.0 model (2002–03 to 2011–12; Kim et al., 2021) and are therefore reduced to the levels in the mixed layer to avoid an overestimated target error of each data type (Text S5 in the Supplement). The rationale behind using the adjusted CV in the target error calculation is based on Luo et al. (2010), in which all properties should be completely mixed in the mixed layer, a perfect measurement without significant errors should generate similar values at every measured depth within the mixed layer, and the average CV of all depth profiles can be used as CV in the target error calculation. The standard deviation is used as target errors of the log-converted data types. The CV of the log-converted data type is estimated as the average of ± 1 standard deviation in log space converted back into normal space (Doney et al., 2003; Glover et al., 2018).
We compute the portability index (Friedrichs et al., 2007) to evaluate the broader applicability of the optimized model parameter set for each year in predicting the dynamics of the other year as follows:
where is the normalized cross-validation total cost function when a model parameter set optimized for a given year is used to simulate another year, and is the normalized total cost function of the climatological model. A portability index value close to 1 indicates a more portable model or a system that is not particularly sensitive to year-to-year variations in optimized parameters, while an index value ≪ 1 indicates a less portable model or a system that is sensitive to year-to-year variations in optimized parameters.
2.5 Uncertainty analysis
The uncertainties of the optimized parameters are estimated using a finite difference approximation of the complete Hessian matrix during the iterative data assimilation process (i.e., the second derivatives of the cost function with respect to the model parameters). When computed at the minimum of the cost function value, the square root of a diagonal element in the inversed Hessian matrix represents the logarithm of the relative uncertainty of the corresponding optimized parameter. The absolute uncertainty of the optimized parameter is calculated as , where pf is the value of the optimized parameter, and σf is its relative uncertainty. We denote an optimized parameter with σf larger than 50 % as an “optimized” parameter, while an optimized parameter with σf smaller than 50 % is denoted as a “constrained” parameter (Text S3, Tables S2–S6). We then conduct Monte Carlo experiments to examine the impact of the uncertainties of the constrained parameters on the modeled fields. The Monte Carlo experiments consist of (1) creating an ensemble of parameter sets (N=1000) by randomly sampling values within the uncertainty ranges of the constrained parameters and (2) then performing a model simulation using each parameter set. All uncertainty estimates are calculated following standard error propagation rules and presented herein as ± 1 standard deviation.
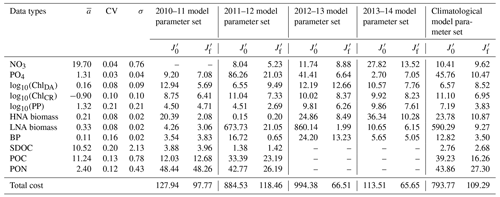
Table 2Data types, observed means, coefficient of variation, target errors, and costs before and after optimization. The observed mean (), coefficient of variation (CV), and target error (σ) of each assimilated data type used for calculating the normalized cost function (unitless; Eq. 3) before () and after optimization (). Data type unit: mmol N m−3 for nitrate (NO3); mmol P m−3 phosphate (PO4); mg m−3 for diatom chlorophyll (ChlDA) and cryptophyte chlorophyll (ChlCR); mmol C m−3 for HNA and LNA bacterial biomass, SDOC, and POC; mmol N m−3 for PON; and for primary production (PP) and bacterial production (BP). NO3 was not assimilated in 2010–11, while SDOC, POC, and PON were not assimilated in 2012–13 and 2013–14 (denoted as ”–” in the table).
3.1 Model skill assessment
The iterative optimization procedure reduced by 24 %–93 % the misfits between observations and model results for each year and for the climatological year compared to those obtained using the initial parameter values (Table 2). The optimized parameter sets satisfied the pre-set convergence criteria, including the local minima achieved by the total costs, low gradients of the total costs with respect to each optimized parameter, and positive eigenvalues of the Hessian matrix (details in Kim et al., 2021). The total costs were reduced by optimizing only a subset of the parameters: five–seven constrained and three–six optimized parameters (Tables S2–S6). The optimized parameters in common across all years were αDA (the initial slope of photosynthesis versus irradiance curve of diatoms, ), μHNA (the maximum HNA bacterial growth rate, d−1), μLNA (the maximum LNA bacterial growth rate, d−1), and gCR (the half-saturation density of cryptophytes in microzooplankton grazing, mmol C m−3). gHNA (the half-saturation density of HNA bacteria in microzooplankton grazing, mmol C m−3), gMZ (the half-saturation density of microzooplankton in krill grazing, mmol C m−3), and μKR (the maximum krill growth rate, d−1) were the next most frequently optimized, at least for 4 years out of a total of 5 modeled years including the climatological year.
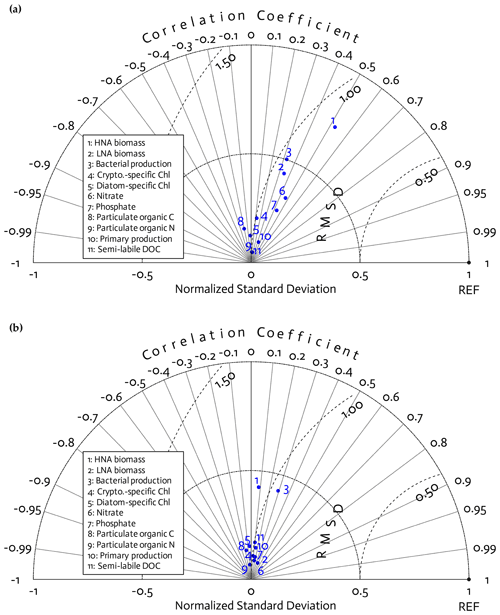
Figure 3Model skill assessment. A Taylor diagram using a polar-coordinate system summarizing the model–observational correspondence for each model stock and flow for individual annual simulations for the 4 modeled years together (2010–11 to 2013–14; a) and for the climatological year (b). The angular coordinate denotes the Pearson correlation coefficient (r), the distance from the origin denotes the standard deviation normalized by the standard deviation of the observations, and the distance from point (1,0), marked as REF on the x axis, describes the centered (bias removed) root-mean-square difference (RMSD) between model results and observations.
Because of this study's focus on the modeled bacterial and other ecosystem functions as a function of bacterial traits (Sect. 3.3) rather than of year (Figs. S2–S5 in the Supplement), we combined the observations and model results from all 4 years together for model skill assessment. According to the Taylor diagrams, model skills were overall similar among the 4 study years (Fig. 3a) and the climatological year (Fig. 3b). Three core variables in this study, including HNA biomass, LNA biomass, and BP, had better model–observation agreements than other data types, with relatively high correlations, a low centered (bias removed) root-mean-square difference (RMSD), and the normalized standard deviation closer to 1. These variables also had better fits to the 4-year seasonal cycles of the observations than other data types (Fig. S7 in the Supplement). However, the model skill for HNA biomass slightly degraded in the climatological model (Fig. 3b), with the insignificant correlation (p=0.61 versus r=0.53 and p=0.003 in Fig. 3a), lower normalized standard deviation, and higher RMSD than the 4 years together (Fig. 3a). After optimization, the models tended to underestimate PP with relatively larger errors than for other data types (Fig. S7), while its temporal and spatial (depth) variability was captured well as shown by high correlations (Fig. 3). By contrast, there were slight positive model biases for POC and PON (Fig. S7), and their variability was not well captured as shown by their negative correlations (Fig. 3).
Table 3Cross-validation cost and portability index. is the normalized optimized cost from the climatological model (equivalent to under the climatological model parameter set in Table 2), and is the normalized cross-validation cost (Eq. 5), in which, for example, under the row “2010–11 model parameter set” in Table 3 indicates the normalized cross-validation cost from simulating the 2010–11 model parameter set against 2011–12.
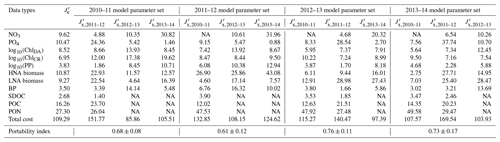
NA: not available.
Cross-validation cost analyses showed the increased model–observation misfits when a set of parameters optimized for a given year was applied to simulate another year's dynamics (Tables 2 and 3), suggesting that each year was best modeled using its own unique set of the optimized parameters. The magnitude of increase in the cost function varied by year pair, with the average portability index values indicating that the optimized model parameters for 2012–13 was most portable (0.76 ± 0.11), followed by those for 2013–14 (0.73 ± 0.17), 2010–11 (0.68 ± 0.08), and 2011–12 (0.61 ± 0.12; Table 3), though the differences were not always significantly different among the years.
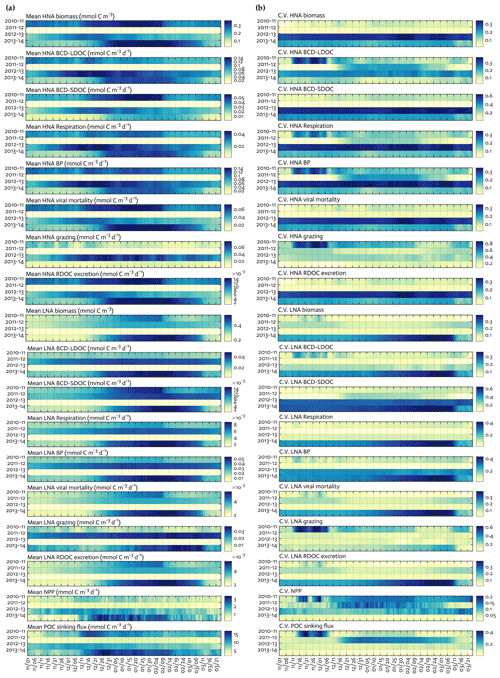
Figure 4Seasonal progression of modeled HNA and LNA bacterial carbon stocks and rates and key ecosystem functions across years. Seasonal patterns of HNA and LNA bacterial carbon stocks and flows, NPP and POC sinking flux at 10 m depth over the growth season (November–March) for each of the 4 simulation years (a), and coefficient of variation (the Monte-Carlo-derived standard deviation divided by each data point from Fig. 4a) from 1000 Monte Carlo experiments (b).
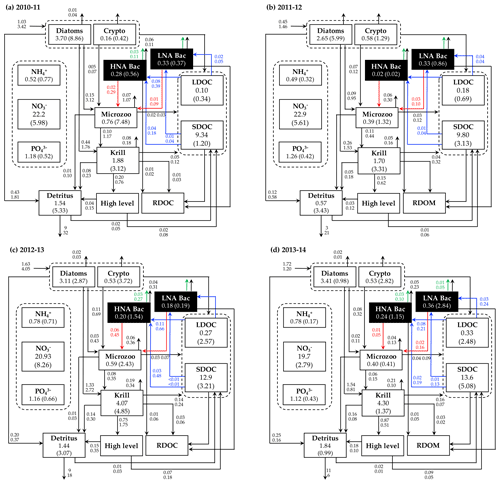
Figure 5Annual mean carbon stocks and flows. Carbon stocks (mmol C m−3) and flows (), particle sinking flux (), and other stocks (e.g., nutrients, mmol m−3) averaged over the growth season in each year are denoted as the numbers on the first row, while the numbers in the second row or in the parentheses are the standard deviation propagated from averaging over the growth season and the Monte-Carlo-derived uncertainties. Numbers around the arrows represent intercompartmental flows and do not necessarily balance to zero due to the build-up or loss in a compartment over the growth season. The magnitude of the N and P flows, as well as the flows smaller than 0.01 , are omitted. RDOC and higher levels are implicit.
3.2 Bacterial carbon stocks and flows
C stocks and flows for each bacterial group represented significant seasonal and interannual variability (Figs. 4a and S8 in the Supplement). Across years, HNA bacteria had significantly higher seasonal maximum values than their LNA counterparts when normalized by the group-specific biomass. These so-called cell-specific, seasonal maximum rates of the HNA group ranged from 0.10 ± 0.004 to 0.59 ± 0.24 d−1, 0.03 ± 0.001 to 0.18 ± 0.12 d−1, 0.07 ± 0.003 to 0.18 ± 0.08 d−1, 0.05 ± 0.002 to 0.57 ± 0.26 d−1, and 0.07 ± 0.03 to 0.36 ± 0.17 d−1 for LDOC uptake, SDOC uptake, respiration, BP, and grazing rates, respectively (Fig. 4). For the LNA group, the maximum cell-specific rates ranged from 0.01 ± 0.002 to 0.12 ± 0.02 d−1, 0.004 ± 0.002 to 0.03 ± 0.01 d−1, 0.01 ± 0.001 to 0.02 ± 0.002 d−1, 0.01 ± 0.003 to 0.13 ± 0.02 d−1, and 0.02 ± 0.0004 to 0.17 ± 0.03 d−1 for LDOC uptake, SDOC uptake, respiration, BP, and grazing rates, respectively (Fig. 4). For each year, C stocks and flows averaged over the growth season (Fig. 5) and those normalized by NPP (net primary production; normalized by NPP in 1 d for C stocks; Fig. S9 in the Supplement) summarized an annual snapshot of the group-specific bacterial dynamics. The annual mean LNA biomass was ∼ 17 times larger than that of HNA biomass in 2011–12 (Fig. 5b), in contrast to relatively similar average biomass values of both groups in other years (Fig. 5a, c, and d). Bacterial carbon demand (BCD; i.e., BCD = BP + bacterial respiration; blue arrows in Fig. 5) was mostly supported by LDOC (67 %–81 %) for both bacterial groups.
The rest of the modeled C stocks and flows fell into one of the following categories: (1) the variable for which a single year's values were assimilated (i.e., microzooplankton C biomass), (2) the variables for which observational values for the given year were assimilated (i.e., nutrients, POC or detritus, and SDOC), and (3) the variables that were not assimilated at all (i.e., krill C biomass, LDOC, NH4, and particle sinking flux). Compared to bacterial variables, there was little interannual variability in the average microzooplankton C biomass (Fig. 5). Even in the years when NO3, POC, and SDOC were not assimilated, their values were modeled similarly to those modeled in other assimilated years (Fig. 5). Modeled LDOC and NH4 were also within the reasonable ranges of their typically small values (< 1 µM).
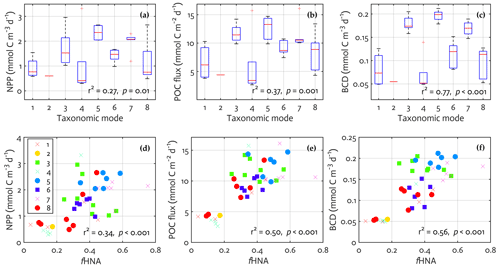
Figure 6Bacterial physiological and taxonomic association with modeled ecosystem functions. The results from linear regression of the key modeled ecosystem functions on a categorical predictor of the observed mode (a–c) and on the observed fraction of HNA cells (d–f). Regression statistics: (a) number of observations (N)=43, error degrees of freedom (df)=35, root-mean-square error (RMSE) = 0.68, r2 = 0.39, adjusted r2 = 0.27, F statistic value = 3.22, p value = 0.01; (b) N=43, df = 35, RMSE = 2.88, r2 = 0.48, adjusted r2 = 0.37, F statistic value = 4.55, p value = 0.001; (c) N=43, df = 35, RMSE = 0.03, r2 = 0.81, adjusted r2 = 0.77, F statistic value = 20.7, p value < 0.001; (d) N=43, df = 41, RMSE = 0.65, r2 = 0.36, adjusted r2 = 0.34, F statistic value = 22.8, p value < 0.001; (e) N=43, df = 41, RMSE = 2.57, r2 = 0.51, adjusted r2 = 0.50, F statistic value = 43.0, p value < 0.001; (f) N=43, df = 41, RMSE = 0.04, r2 = 0.57, adjusted r2 = 0.56, F statistic value = 53.5, p value < 0.001.
3.3 Bacterial physiological and taxonomic association with ecosystem functions
Each mode was dominated by unique bacterial taxa, thereby representing taxonomic traits (Fig. S10 in the Supplement). Candidatus Pelagibacter was the most abundant in mode 6 (Fig. S10c), Dokdonia sp. MED134 in mode 7 (Fig. S10d), Candidatus Thioglobus singularis PS1 in mode 1 (Fig. S10e), Owenweeksia hongkongensis DSM 17368 in mode 2 (Fig. S10f), Rhodobacteraceae in mode 5 (Fig. S10g), and Planktomarina temperata RCA23 in mode 4 (Fig. S10h). To explore a potential link between the bacterial taxonomic traits and the key ecosystem functions, we first extracted the modeled NPP, POC sinking flux, and BCD from the ecosystem model (i.e., the “final optimized output” in Fig. 2) at the time the bacterial samples and depth (10 m) were placed into a single mode derived from the observations. We then performed a linear regression with the mode as a factor, in which the mode is a categorical predictor with eight modes rather than an ordinal or continuous variable (i.e., equivalent to a one-way ANOVA with eight different categories). 27 %, 37 %, and 77 % of the total variance in the modeled NPP, POC sinking flux, and BCD were explained by the bacterial taxonomic mode (Fig. 6a–c). In particular, modes 3, 5, and 7 were associated with 2–3 times higher NPP, POC sinking flux, and BCD compared to when mode 4 dominated (two-sample t test with unequal sample size, p=0.02 for NPP and p < 0.001 for POC sinking flux and BCD) or to when mode 6 dominated (p=0.03 for NPP, p=0.003 for POC sinking flux, and p < 0.001 for BCD).
The observed mode was also positively correlated to the observed fHNA (r2 = 0.52, p < 0.001; not shown). Thus, we examined a potential link between the bacterial physiological traits and the key ecosystem functions as described above, using a linear regression with the observed fHNA as a predictor and the modeled ecosystem functions as dependent variables. The observed fHNA was positively correlated to the modeled NPP (r2 = 0.34, p < 0.001; Fig. 6d) and to a stronger extent to the modeled POC sinking flux (r2 = 0.50, p < 0.001; Fig. 6e) and to the modeled BCD (r2 = 0.56, p < 0.001; Fig. 6f). The stepwise addition of one predictor variable to the other predictor variable (i.e., fHNA adding to mode or vice versa) did not improve the model performance (not shown). These results suggest a clear link between the modeled ecosystem functions and the bacterial taxonomic (modes) and physiological (fHNA) trait observations.
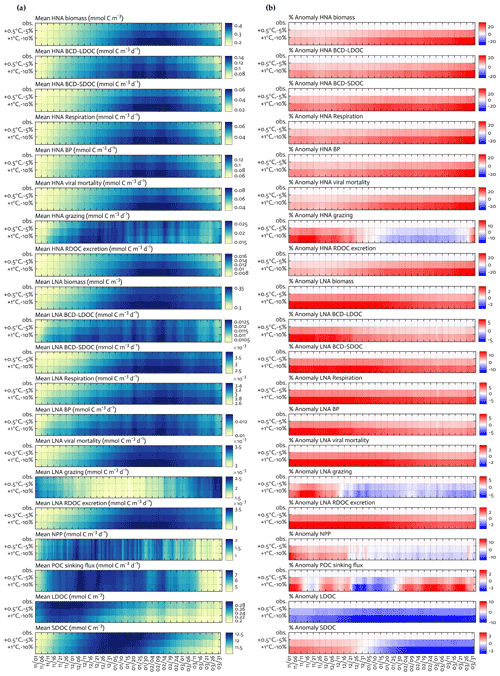
Figure 7Climate change experiments. Seasonal progression of the modeled HNA and LNA bacterial carbon stocks and rates and key ecosystem functions under observed physical forcing and climate change experiments (a) and the percent change in the corresponding variable compared to observed fields in the second and third row of each panel, with the first row of each panel as zero to represent base states (b). For example, the percent anomaly of HNA biomass in (b) = (HNA biomass under +1 ∘C and −10 % − HNA biomass under observed forcing) ⋅ 100HNA biomass under observed forcing.
3.4 Climate change experiments
We explored the responses of the modeled bacterial dynamics and other ecosystem functions (Sects. 3.2 and 3.3) to changing climates along the WAP (Fig. 7). Due to the varying portability of the optimized parameter sets among the 4 study years, we used the optimized parameter set for the climatological year (Table S6) to simulate an overall WAP system response under perturbed ocean temperatures (i.e., +0.5 ∘C and +1.0 ∘C relative to observed temperatures) and sea-ice forcing fields (i.e., 5 % and 10 % loss of sea-ice concentrations relative to observed sea-ice concentrations). These experiments were conducted under each perturbed condition separately (i.e., warming alone in Fig. S11 in the Supplement versus melting alone in Fig. S12 in the Supplement), as well as simultaneously (i.e., climate change; Fig. 7). We only analyzed the results from the climate change experiments, given that despite different impacts of each forcing change (i.e., the impact of warming on rate processes versus the impact of melting on light and photosynthesis but not MLD in our model), climate change would cause simultaneous changes in sea ice and water temperature along the WAP.
The climate change experiments resulted in a combination of changes in overall bacterial C stocks and rates, as well as the key ecosystem functions, and shifts in their seasonal timing (Fig. 7a) compared to the base state (the first row as the base state in Fig. 7a and b, while the second and third rows as anomalies under perturbed conditions in Fig. 7b). HNA bacterial C stock and rates responded more strongly to the perturbed climate conditions compared to their LNA counterparts. Under combined warming and melting (+1.0 ∘C and −10 %) conditions, there were the maximum increases in the HNA C stock and rates by 19 %–35 % (29 ± 89 % for biomass, 22 ± 67 % for LDOC uptake, 35 ± 111 % for SDOC uptake, 26 ± 79 % for respiration, 25 ± 78 % for BP, 29 ± 89 % for viral mortality, 19 ± 26 % for grazing, and 29 ± 89 % for RDOC excretion) compared to the maximum increases in the LNA C stock and rates by 3 %–15 % (3 ± 2 % for biomass, 6 ± 11 % for LDOC uptake, 15 ± 27 % for SDOC uptake, 8 ± 3 % for respiration, 7 ± 6 % for BP, 3 ± 2 % for viral mortality, 7 ± 18 % for grazing, and 3 ± 2 % for RDOC excretion). In contrast to bacterial C stocks and rates that increased consistently throughout the growth season, microzooplankton grazing rates showed seasonally mixed responses for both HNA and LNA cases, with the maximum decreases of 8 ± 32 % for HNA bacteria and of 4 ± 32 % for LNA bacteria. Similarly, there were the maximum increases in NPP and POC sinking flux by 14 ± 15 % and 3 ± 22 % and the maximum decreases in NPP and POC sinking flux by 4 ± 11 % and 3 ± 13 %, respectively. SDOC exhibited the maximum increase by 2 ± 1 % early in the season but became depleted strongly as the season progressed. LDOC decreased consistently in response to the perturbed conditions, with the maximum decrease by 10 ± 43 %.
4.1 Model skill assessment
Despite the important role that heterotrophic marine bacteria play in the ocean carbon cycle, the vast majority of mechanistic biogeochemical models neither include them as a model state variable nor explicitly simulate their physiological processes. Most models parameterize the bacterial remineralization of sinking organic matter with depth by fitting the power law functions or other similarly derived empirical approaches (Buesseler et al., 2020; Cael and Bisson, 2018). Cellular functions, taxa, and functional gene expression of other prokaryotes, such as cyanobacteria (Hellweger, 2010; Martín-Figueroa et al., 2000; Miller et al., 2013), or a diverse suite of microbial functional groups (Coles et al., 2017; Dutkiewicz et al., 2020) have been modeled so far. However, our study is the first to explicitly model heterotrophic bacterial groups of different physiological traits and to link their relationship with the key ecosystem functions.
Only a subset of the parameters was optimized in our model to simulate microbial and ecological patterns for each year, consistent with other data assimilation modeling studies (Friedrichs, 2001; Friedrichs et al., 2006, 2007; Luo et al., 2010, 2012). In general, optimization of this class of marine ecosystem model requires adjustment of a small number of independent parameters to achieve well-posed model solutions because of the highly cross-correlated nature of the parameters in the inherently nonlinear model equations (Fennel et al., 2001; Harmon and Challenor, 1997; Matear, 1996; Prunet et al., 1996a, b). In our study, most of the constrained parameters were directly associated with the bacterial processes, and there were overall better model–observation fits for the bacterial data types compared to other data types. These results provide confidence in the simulated bacterial C stocks and rates.
Optimization also sheds light on major unknown parameters in bacterial grazing processes involving gHNA and gLNA (the half-saturation densities of HNA and LNA bacteria in microzooplankton grazing, respectively). Microzooplankton grazing of the given bacterial group is simulated using a Holling type 2 density-dependent grazing function with a preferential prey selection on diatoms, cryptophytes, and the other bacterial group, in which a single microzooplankton maximum grazing rate is implemented for both bacterial groups for model simplicity purposes (Tables S2–S6 in the Supplement; Kim et al., 2021). Thus, it is the half-saturation density that determines the degree of preferential grazing by microzooplankton on the given bacterial group, the change in which may ultimately depend on the group-specific C biomass. Due to the lack of a priori knowledge on the relative magnitude of gHNA and gLNA, we assigned an identical initial parameter value (Table 1) to let the data assimilation scheme determine the values that best fit the overall observations. Compared to gLNA, smaller optimized gHNA values (Tables S2–S6) reflect preferential grazing of HNA cells by microzooplankton, consistent with previous speculations that grazers selectively remove larger and more active bacterial cells (del Giorgio et al., 1996; Gonzalez et al., 1990; Sherr et al., 1992), so HNA bacteria (Garzio et al., 2013). Together with the higher mean cell-specific grazing rates for HNA bacteria (Sect. 3.2), our results suggest preferential grazing of HNA cells by microzooplankton.
The portability index in our study reflects the extent to which a single model framework represented by its distinctly optimized parameters in the same model equations captures the observed variability in different years, given variable environmental forcing and the accompanying shift in plankton ecosystem structure. The model parameter set optimized for 2012–13 was the most portable, while the model parameter set optimized for 2011–12 was the least portable (Table 3), in which the most (n=7 out of total 11) and the least numbers (n=5 out of total 11) of parameters were constrained, respectively (Tables S3 and S4). The other two years exhibited intermediate levels of model portability, with similar portability index values characterized by the same number of the constrained parameters (n=6 out of total 10 for 2010–11 and n=6 out of total 12 for 2013–14; Tables S2 and S5). In other words, it is the number of the constrained parameters that matters the most in driving high model portability, suggesting a connection between overfitting and the portability of the optimized parameter sets. Also, varying degrees of portability across the 4 study years rendered it difficult to choose one particular year's model solution to perform the climate change experiments (Sects. 3.4 and 4.4), consistent with the characteristics of the original WAP-1D-VAR v1.0 model. Instead, better model skill was found by utilizing the parameters from assimilating the climatological observations (i.e., the climatological model).
4.2 Bacterial carbon stocks and flows
The fact that cell-specific BP, respiration, and SDOC uptake rates of HNA bacteria were significantly higher than those of LNA bacteria (Sect. 3.2) is mainly because of the way the parameter optimization was conducted (Text S3). The higher initial parameter values assigned for HNA bacterial growth, RDOC excretion, mortality, and respiration rates (Table 1) might drive not only their faster cell-specific growth rates but also their higher DOC uptake rates to coexist with their LNA counterparts when the loss rates were relatively large for HNA bacteria. Though driven by the model assumptions, the important aspect of these results lies in the fact that the model can leverage such assumptions to examine the implications for the WAP food-web dynamics and biogeochemistry. As with phylogenetic groups (Fuchs et al., 2000; Teira et al., 2009; Yokokawa et al., 2004), cell-specific bacterial growth rates are expected to differ among distinct bacterial physiological groups, but there are limited studies focusing on group-specific cell activities (Gasol et al., 1999; del Giorgio et al., 1996; Günter et al., 2008; Longnecker et al., 2005; Moràn et al., 2011). Moràn et al. (2011) showed that HNA bacteria greatly outgrew LNA bacteria in Waquoit Bay estuary, with a cell-specific growth rate of up to 2.26 d−1 for HNA cells versus < 0.5 d−1 for LNA cells. Other studies have demonstrated that HNA bacteria might depend on phytoplankton substrates more than LNA bacteria (Li et al., 1995; Morán et al., 2007; Scharek and Latasa, 2007). The hypothesis that WAP bacteria might rely on SDOC when limited by LDOC availability has received indirect support previously (Ducklow et al., 2011; Kim and Ducklow, 2016; Luria et al., 2017), providing the basis for bacterial SDOC utilization in our model formulation.
The model also captured the rest of the ecosystem variables fairly well. The modeled nutrient stocks were above the detection limits, indicating no evidence of macronutrient limitations at the study site. The WAP typically exhibits strong interannual variability in physical forcing and ecological and biogeochemical processes (Ducklow et al., 2007), but the lack of strong interannual variability in the modeled microzooplankton C biomass is due to assimilating their climatological observations. One exception is krill C biomass that was modeled 3–8 times larger than the maximum value from the available field measurement in 2017–2018 (0.57 mmol C m−3; not shown). It should be noted that there were inconsistences in the nature of the assimilated data types, including a single-year observation of microzooplankton C biomass (versus each year-specific observation of other variables) and two unassimilated data types (e.g., krill C biomass). Also, there can be compensating errors in krill grazing rate and metabolism values given that krill are mobile laterally. These observational limitations make it challenging to construct a complete bacterial C budget without significant uncertainties. A more complete assimilation of zooplankton data should be the next effort to improve the model fits and minimize uncertainties in the bacterial variables. Another source of uncertainty in our study is that the model forcing does not seem to have sufficient information to capture small-scale and high-frequency sources of variability (e.g., local circulation and tidal flow near Palmer Station), resulting in relatively low standard deviation values of the modeled bacterial and ecosystem variables than those of the observations (e.g., Figs. 3 and S2). By contrast, our model adequately captures seasonal variations in modeled ecosystem dynamics likely because such high frequency processes do not strongly rectify in the seasonal cycles in the WAP ecosystem.
4.3 Bacterial physiological and taxonomic association with ecosystem functions
The positive associations of the observed fHNA with the modeled NPP and POC sinking flux suggest a relatively strong resource control on these actively growing HNA cells compared to slow-growing LNA cells. This is consistent with previous studies showing increased HNA growth rates in response to enhanced phytoplankton-derived organic substrate (Morán et al., 2011) and more abundant HNA cells in areas or periods in which bacterial assemblages were predominantly controlled by resources rather than grazing (Morán et al., 2007). It has been hypothesized that due to minimal inputs of terrestrial organic matter, bacteria must ultimately rely on in situ NPP as an organic matter source in the WAP (Ducklow et al., 2012a), supporting the importance of resource control on these actively growing bacterial populations.
In our study, modes 3, 5, and 7, characterized by copiotrophic taxa with large genomes and more 16S rRNA gene copies (Bowman et al., 2017), were associated with high values of the modeled NPP, POC sinking flux, and BCD, while modes 4 and 6, characterized by taxa associated with more oligotrophic conditions, were associated with low values of the modeled NPP, POC sinking flux, and BCD. Dokdonia sp. MED134, a common bacterial species of the modes associated with high NPP, POC sinking flux, and BCD, is a proteorhodopsin-containing marine flavobacterium that grows faster with light (Gómez-Consarnau et al., 2007; Kimura et al., 2011) and in conditions under which resources are abundant (Gómez-Consarnau et al., 2007). Given the coastal WAP being primarily light-limited (Ducklow et al., 2012b), the correspondence of D. Dokdonia MED134 to high values of the modeled NPP suggests light-enhanced growth rates and cell yields from sufficient irradiance. By contrast, mode 4, dominated by Planktomarina temperata RCA23, is a slow-growing bacterium that specializes in using complex organic substrates (Giebel et al., 2013). These attributes are consistent with the high occurrence of mode 4 during the periods of low values of the modeled NPP and POC sinking flux. Candidatus Pelagibacter, abundant in mode 6, is generally known as an oligotrophic specialist with a low DOC requirement but often appears during Antarctic phytoplankton blooms (Delmont et al., 2014; Luria et al., 2014), the characteristics of which support its occurrence during the periods of high values of the modeled NPP. In summary, our study provides a novel numerical framework combining the dynamics of different ecosystem functions and microbial physiology and taxonomy. Certain modes represent distinct WAP ecosystem states, and the mode–state associations are reasonably explained from microbial perspectives. However, we did not investigate a seasonal succession and development in mode itself or the mode association of the key WAP ecosystem states. Future investigations should focus on including a few dominant or seasonally distinct modes in the data assimilation process in order to fully resolve the seasonality of the mode–ecosystem state associations along the WAP.
4.4 Climate change experiments
The WAP has experienced significant atmospheric and ocean warming and resulting changes in marine ecological processes, and further climate change is projected for the next several decades. The magnitudes of the perturbations used in the climate change experiments (+0.5 ∘C and +1.0 ∘C compared to observed temperature fields and −5 % and −10 % compared to observed sea-ice fields) are within the range of the long-term changes in temperature and sea-ice duration along the WAP continental shelf. The temperature of the ACC water that has direct access to the WAP shelf has shown a large increase after the 1980s, equivalent to a uniform warming of the upper 300 m layer by 0.7 ∘C (Ducklow et al., 2012b). The trend in the annual ice season duration is −1.5 d yr−1 over 1979–80 to 2017–18 field season (Henley et al., 2019). The degree of melting (5 %–10 %) chosen for the climate change experiments is translated into the shortening of the ice season duration by 1–3 d (not shown), falling within the range of the trend in Henley et al. (2019).
Under combined warming and melting conditions, we expected that increased NPP and phytoplankton accumulations early in the season would result in a significant build-up of all DOC pools. However, this was the case only for SDOC, and bacteria were soon LDOC-limited due to their preferential LDOC uptake for their primary C source. Nonetheless, the growth of bacteria and increased bacterial rates under LDOC limitation were still possible because bacteria depended on SDOC to meet the rest of their C demand, resulting in the strong depletion of the SDOC pool later in the season (Fig. 7b). In other words, bacteria were more likely resource-limited, in particular by the labile DOC pool, and SDOC subsequently played an increasingly important role. This change was particularly important in HNA bacteria, as shown by the relatively large increase in HNA bacterial C demand via SDOC compared to LNA bacteria. Temperature is often regarded as a major factor regulating physiological rates by changing the rate of enzymatic reactions (Kirchman et al., 2009; White et al., 1991). In our study, the modeled C stock and rates of HNA bacteria increased under the warming alone conditions (Fig. S11) but equally or more than under the melting alone conditions (i.e., increased photosynthesis and resource availability; Fig. S12). This suggests that temperature per se is not necessarily a more important limiting factor for bacterial growth, at least for HNA bacteria, than resource availability (Ducklow et al., 2012a), and warming may rather enhance HNA bacterial utilization of the already increased organic matter from the increased phytoplankton productivity. Also, future climate may impact the (re)distribution of bacterial taxonomic groups, with a potential shift to more abundant HNA cells in the WAP bacterial communities owing to their preferential SDOC utilization.
The major limitation of our climate change experiments is the short duration of the simulations. An ideal set of climate change simulations should be performed for longer-term periods, as well as continuously across many years. However, our study could not accommodate these requirements because of the limited observations and existing data gaps in each year. Despite these challenges, we were able to validate the capacity of the climatological model to partly reproduce the already observed, climate-driven trends of some ecosystem variables along the WAP. Under each year's forcing fields, the climatological model parameter set reproduced the interannual variability fairly well compared to the observed interannual variability, except for only a few cases (e.g., overestimated BP and HNA biomass in 2011–12, underestimated PP in 2012–13 and 2013–14; Table S7). The period of 2011–12 was characterized by a negative temperature anomaly (−0.13 ± 0.83 ∘C versus 0.03 ± 0.84 ∘C for the 4-year climatology) and a positive sea-ice anomaly (24 ± 38 % versus 21 ± 29 % for the 4-year climatology), with lower temperature and higher sea-ice concentrations than the other 3 years (all p < 0.05, two-sample t test). This coldest year had the lowest values of BP, HNA biomass, and PP observations (Table S7), consistent with increases in the modeled BP, HNA biomass, and PP under the combined warming and melting conditions. A combination of low HNA biomass, low PP, and low POC flux was also modeled in 2011–12, being largely responsible for driving the positive association of the observed fHNA with the modeled NPP and POC sinking across years (Sect. 4.3). Sea ice did not retreat until mid-December in 2011–12 (Fig. S1), and as a result of subsequently low light levels PP was modeled to be low. The low modeled PP drove both low HNA biomass and low particle sinking flux, reinforcing the strong resource control on these fast-growing bacterial populations and the conventional “high PP-high export” paradigm along the WAP.
Finally, our climate change simulations share similar results with those performed using the WAP-1D-VAR v1.0 model with one bacterial compartment (Kim et al., 2021). In the original WAP-1D-VAR v1.0 model, combined warming and reduced sea-ice conditions also increased NPP, net community production, POC sinking flux, bulk bacterial productivity and biomass, and SDOC, in contrast to LDOC that was strongly limited early in the season. This potential shift to a more productive and efficient export system state is partially in agreement with the speculations suggested by previous studies that warming may induce more recycling-favorable and microbial-dominated food webs (Moline et al., 2004; Sailley et al., 2013). Despite the increased productivity and plankton accumulations, LDOC may become strongly depleted, and, therefore, bacteria may need to depend more on SDOC to meet a significant part of their C demand (i.e., an increasingly important role of SDOC for bulk bacterial communities). Most of these results convey the same story as our experiments, thereby adding confidence to the results of the climate change experiments in our study. Yet, it should be noted that the increased complexity of bacterial dynamics in our study's bacteria-oriented model adds two important contributions to the original WAP ecosystem model including (1) the dominance of HNA bacteria over LNA bacteria in the warming WAP waters and (2) bacterial taxonomic (i.e., mode) and physiological (i.e., fHNA) traits being a significant indicator of the key WAP ecosystem functions.
Heterotrophic microbial diversity has seldom been considered in detail in the formulation and analysis of marine pelagic ecosystem models, reflecting in part the lack of suitable field data for model evaluation. Utilizing genomic products to prescribe the taxonomic aspects of bacterial dynamics, our study demonstrates the association of bacterial abundance with different physiological states, bacterial community structure, and key ecosystem functions. The modeling approach in our study enables the observations in different bacterial populations to constrain the group-specific processes and model parameters that have been poorly understood. These include the partitioning of BP specific to HNA and LNA groups, the partitioning of the bacterial uptake of DOC pools with different lability, and the half-saturation density of each bacterial group in microzooplankton grazing. The model also serves as an effective numerical platform to explore the WAP microbial response to changing climate conditions, in which ocean warming and melting sea ice would induce a potential shift to the dominance of HNA bacteria in more productive waters due to their increasing dependence on SDOC.
The Tangent linear and Adjoint Model Compiler (TAPENADE) used to construct an adjoint model is available online (https://team.inria.fr/ecuador/en/tapenade/, Inria at Sophia Antipolis, 2021). The original version of the model used in this study (WAP-1D-VAR model v1.0) is available from the project website: https://zenodo.org/record/5041139 (Kim et al., 2021) under the Creative Commons Attribution 4.0 International license. The exact version of the model used to produce the results, input data, and scripts to run the model and produce the plots for all the simulations presented in this article is available upon request.
Complete Palmer LTER time-series data used for data assimilation are available online (http://pal.lternet.edu/data, PAL-LTER, 2021). Surface downward solar radiation flux data used for physical forcing of the model simulations can be found at the National Centers for Environmental Prediction website (https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.surface.html, NOAA-ESRL, 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-19-117-2022-supplement.
HHK designed the study, performed the model simulations, and wrote the manuscript. JSB provided the observational data and helped with data analyses and interpretation. HWD, OMS, and DKS provided observational data. YWL contributed the model simulations. SCD supervised the study and significantly revised the manuscript.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study leverages the wealth of marine biogeochemical data collected by the Palmer LTER program along the WAP, and the authors thank the scientists, students, technicians, station support and logistical staff, and ship captains, officers, and crew involved. This research was supported, in part, by the US National Science Foundation Office of Polar Programs through award NSF PLR-1440435 and the US National Aeronautics and Space Administration Ocean Biology and Biogeochemistry Program through award NASA NNX14AL86G. Hyewon Heather Kim was also supported by the Investment in Science Fund and the Reuben F. and Elizabeth B. Richards Endowed Fund from Woods Hole Oceanographic Institution.
This research has been supported by the NASA (grant no. NNX14AL86G) and the NSF (grant no. PLR-1440435).
This paper was edited by Marilaure Grégoire and reviewed by three anonymous referees.
Azam, F., Fenchel, T., Field, J. G., Gray, J. S., Meyer-Reil, L. A., and Thingstad, F.: The ecological role of water-column microbes in the sea, Mar. Ecol. Prog. Ser., 257–263, available at: https://www.jstor.org/stable/24814647 (last access: 3 January 2022), 1983.
Bouvier, T., del Giorgio, P. A., and Gasol, J. M.: A comparative study of the cytometric characteristics of high and low nucleic-acid bacterioplankton cells from different aquatic ecosystems, Environ. Microbiol., 9, 2050–2066, https://doi.org/10.1111/j.1462-2920.2007.01321.x, 2007.
Bowman, J. S. and Ducklow, H. W.: Microbial communities can be described by metabolic structure: a general framework and application to a seasonally variable, depth-stratified microbial community from the coastal West Antarctic Peninsula, PloS one, 10, e0135868, https://doi.org/10.1371/journal.pone.0135868, 2015.
Bowman, J. S., Amaral-Zettler, L. A., Rich, J. J., Luria, C. M., and Ducklow, H. W.: Bacterial community segmentation facilitates the prediction of ecosystem function along the coast of the western Antarctic Peninsula, ISME J., 11, 1460–1471, https://doi.org/10.1038/ismej.2016.204, 2017.
Buesseler, K. O., Boyd, P. W., Black, E. E., and Siegel, D. A.: Metrics that matter for assessing the ocean biological carbon pump, P. Natl. Acad. Sci. USA, 117, 9679–9687, 2020.
Cael, B. B. and Bisson, K.: Particle flux parameterizations: Quantitative and mechanistic similarities and differences, Front. Mar. Sci., 5, 1–5, 2018.
Calvo-Díaz, A. and Morán, X. A. G.: Seasonal dynamics of picoplankton in shelf waters of the southern Bay of Biscay, Aquat. Microb. Ecol., 42, 159–174, https://doi.org/10.3354/ame042159, 2006.
Campbell, J. W.: The lognormal distribution as a model for bio-optical variability in the sea, J. Geophys. Res.-Oceans, 100, 13237–13254, https://doi.org/10.1029/95JC00458, 1995.
Clarke, A., Griffiths, H. J., Barnes, D. K., Meredith, M. P., and Grant, S. M.: Spatial variation in seabed temperatures in the Southern Ocean: implications for benthic ecology and biogeography, J. Geophys. Res.-Biogeo., 114, G03003, https://doi.org/10.1029/2008JG000886, 2009.
Coles, V. J., Stukel, M. R., Brooks, M. T., Burd, A., Crump, B. C., Moran, M. A., Paul, J. Hl., Satinsky, B. M., Yager, P. L., Zielinski, B. L., and Hood, R. R.: Ocean biogeochemistry modeled with emergent trait-based genomics, Science, 358, 1149–1154. https://doi.org/10.1126/science.aan5712, 2017.
Cook, A. J., Fox, A. J., Vaughan, D. G., and Ferrigno, J. G.: Retreating glacier fronts on the Antarctic Peninsula over the past half-century, Science, 308, 541–544. https://doi.org/10.1126/science.1104235, 2005.
del Giorgio, P. A., and Cole, J. J.: Bacterial growth efficiency in natural aquatic systems, Annu. Rev. Ecol. Syst., 29, 503–541, https://doi.org/10.1146/annurev.ecolsys.29.1.503, 1998.
del Giorgio, P. A., Gasol, J. M., Vaqué, D., Mura, P., Agustí, S., and Duarte, C. M.: Bacterioplankton community structure: protists control net production and the proportion of active bacteria in a coastal marine community, Limnol. Oceanogr., 41, 1169–1179, https://doi.org/10.4319/lo.1996.41.6.1169, 1996.
Delmont, T. O., Hammar, K. M., Ducklow, H. W., Yager, P. L., and Post, A. F.: Phaeocystis antarctica blooms strongly influence bacterial community structures in the Amundsen Sea polynya, Front Microbiol., 5, 646, https://doi.org/10.3389/fmicb.2014.00646, 2014.
Doney, S. C., Glover, D. M., McCue, S. J., and Fuentes, M.: Mesoscale variability of Sea-viewing Wide Field-of-view Sensor (SeaWiFS) satellite ocean color: Global patterns and spatial scales, J. Geophys. Res.-Oceans, 108, 3024, https://doi.org/10.1029/2001JC000843, 2003.
Ducklow, H. W., Schofield, O., Vernet, M., Stammerjohn, S., and Erickson, M.: Multiscale control of bacterial production by phytoplankton dynamics and sea ice along the western Antarctic Peninsula: a regional and decadal investigation, J. Marine Syst., 98, 26–39, https://doi.org/10.1016/j.jmarsys.2012.03.003, 2012a.
Ducklow, H., Clarke, A., Dickhut, R., Doney, S. C., Geisz, H., Huang, K., Martinson, D. G., Meredith, M. P., Moeller, H. V., Montes-Hugo, M., Schofield, O., Stammerjohn, S. E., Steinberg, D., and Fraser, W.: The marine system of the Western Antarctic Peninsula, in: Antarctic ecosystems: an extreme environment in a changing world, edited by: Rogers, A. D., Johnston, N. M., Murphy, E. J., and Clarke, A., 121–159, 2012b.
Ducklow, H. W.: Bacterial Production and Biomass in the Ocean, in: Microbial Ecology of the Oceans, second edn., John Wiley and Sons, Inc, 85–120, ISBN 978-0-470-28184-0, 2000.
Ducklow, H. W., Baker, K., Martinson, D. G., Quetin, L. B., Ross, R. M., Smith, R. C., Stammerjohn, S. E., Vernet, M., and Fraser, W.: Marine pelagic ecosystems: the west Antarctic Peninsula, Philos. T. R. Soc. B, 362, 67–94, https://doi.org/10.1098/rstb.2006.1955, 2007.
Ducklow, H. W., Myers, K. M., Erickson, M., Ghiglione, J. F., and Murray, A. E.: Response of a summertime Antarctic marine bacterial community to glucose and ammonium enrichment, Aquat. Microb. Ecol., 64, 205–220. https://doi.org/10.3354/ame01519, 2011.
Dutkiewicz, S., Cermeno, P., Jahn, O., Follows, M. J., Hickman, A. E., Taniguchi, D. A. A., and Ward, B. A.: Dimensions of marine phytoplankton diversity, Biogeosciences, 17, 609–634, https://doi.org/10.5194/bg-17-609-2020, 2020.
Fennel, K., Losch, M., Schröter, J., and Wenzel, M.: Testing a marine ecosystem model: sensitivity analysis and parameter optimization, J. Marine Syst., 28, 45–63, https://doi.org/10.1016/S0924-7963(00)00083-X, 2001.
Friedrichs, M. A.: Assimilation of JGOFS EqPac and SeaWiFS data into a marine ecosystem model of the central equatorial Pacific Ocean, Deep-Sea Res. Pt. II, 49, 289–319, https://doi.org/10.1016/S0967-0645(01)00104-7, 2001.
Friedrichs, M. A., Hood, R. R., and Wiggert, J. D.: Ecosystem model complexity versus physical forcing: Quantification of their relative impact with assimilated Arabian Sea data, Deep-Sea Res. Pt. II, 53, 576–600, https://doi.org/10.1016/j.dsr2.2006.01.026, 2006.
Friedrichs, M. A., Dusenberry, J. A., Anderson, L. A., Armstrong, R. A., Chai, F., Christian, J. R., and Wiggert, J. D.: Assessment of skill and portability in regional marine biogeochemical models: Role of multiple planktonic groups, J. Geophys. Res.-Oceans, 112, C08001, https://doi.org/10.1029/2006JC003852, 2007.
Fuchs, B. M., Zubkov, M. V., Sahm, K., Burkill, P. H., and Amann, R.: Changes in community composition during dilution cultures of marine bacterioplankton as assessed by flow cytometric and molecular biological techniques, Environ. Microbiol., 2, 191–201, https://doi.org/10.1046/j.1462-2920.2000.00092.x, 2000.
Fukuda, R., Ogawa, H., Nagata, T., and Koike, I.: Direct determination of carbon and nitrogen contents of natural bacterial assemblages in marine environments, Appl. Environ. Microb., 64, 3352–3358, https://doi.org/10.1128/AEM.64.9.3352-3358.1998, 1998.
Garzio, L. M. and Steinberg, D. K.: Microzooplankton community composition along the Western Antarctic Peninsula, Deep-Sea Res. Pt. I, 77, 36–49, https://doi.org/10.1016/j.dsr.2013.03.001, 2013.
Garzio, L. M., Steinberg, D. K., Erickson, M., and Ducklow, H. W.: Microzooplankton grazing along the Western Antarctic Peninsula, Aquat. Microb. Ecol., 70, 215–232. https://doi.org/10.3354/ame01655, 2013.
Gasol, J. M., Zweifel, U. L., Peters, F., Fuhrman, J. A., and Hagström, Å.: Significance of size and nucleic acid content heterogeneity as measured by flow cytometry in natural planktonic bacteria, Appl. Environ. Microb., 65, 4475–4483, https://doi.org/10.1128/AEM.65.10.4475-4483.1999, 1999.
Giebel, H.-A., Kalhoefer, D., Gahl-Janssen, R., Choo, Y.-J., Lee, K., Cho, J.-C., Tindall, B. J., Rhiel, E., Beardsley, C., Aydogmus, O. O., Voget, S., Daniel, R., Simon, M., Brinkhoff, T.: Planktomarina temperata gen. nov., sp. nov., belonging to the globally distributed RCA cluster of the marine Roseobacter clade, isolated from the German Wadden Sea, Int. J. Syst. Evol. Micr., 63, 4207–4217, https://doi.org/10.1099/ijs.0.053249-0, 2013.
Glover, D. M., Jenkins, W. J., and Doney, S. C.: Modeling methods for marine science, Cambridge University Press, https://doi.org/10.1017/CBO9780511975721, 2011.
Glover, D. M., Doney, S. C., Oestreich, W. K., and Tullo, A. W.: Geostatistical analysis of mesoscale spatial variability and error in SeaWiFS and MODIS/Aqua global ocean color data, J. Geophys. Res.-Oceans, 123, 22–39, https://doi.org/10.1002/2017JC013023, 2018.
Gómez-Consarnau, L., González, J. M., Coll-Lladó, M., Gourdon, P., Pascher, T., Neutze, R., Pedros-Alio, C., and Pinhassi, J.: Light stimulates growth of proteorhodopsin-containing marine Flavobacteria, Nature, 445, 210–213, https://doi.org/10.1038/nature05381, 2007.
Gonzalez, J. M., Sherr, E. B., and Sherr, B. F.: Size-Selective Grazing on Bacteria by Natural Assemblages of Estuarine Flagellates and Ciliates, Appl. Environ. Microbiol., 56, 583–589, https://doi.org/10.1128/aem.56.3.583-589.1990, 1990.
Günter, J., Zubkov, M. V., Yakushev, E., Labrenz, M., and Jürgens, K.: High abundance and dark CO2 fixation of chemolithoautotrophic prokaryotes in anoxic waters of the Baltic Sea, Limnol. Oceanogr., 53, 14–22, https://doi.org/10.4319/lo.2008.53.1.0014, 2008.
Harmon, R., and Challenor, P.: A Markov chain Monte Carlo method for estimation and assimilation into models, Ecol. Model., 101, 41–59, https://doi.org/10.1016/S0304-3800(97)01947-9, 1997.
Hellweger, F. L.: Resonating circadian clocks enhance fitness in cyanobacteria in silico, Ecol. Model., 221, 1620–1629, https://doi.org/10.1016/j.ecolmodel.2010.03.015, 2010.
Hellweger, F. L.: Combining Molecular Observations and Microbial Ecosystem Modeling: A Practical Guide, Annu. Rev. Mar. Sci., 12, 267–289, https://doi.org/10.1146/annurev-marine-010419-010829, 2020.
Henley, S. F., Schofield, O. M., Hendry, K. R., Schloss, I. R., Steinberg, D. K., Moffat, C., Peck, L. S., Costa, D. P., Bakker, D. C., Hughes, C., and Rozema, P. D.: Variability and change in the west Antarctic Peninsula marine system: research priorities and opportunities, Prog. Oceanogr., 173, 208–237, https://doi.org/10.1016/j.pocean.2019.03.003, 2019.
Kim, H., and Ducklow, H. W.: A decadal (2002–2014) analysis for dynamics of heterotrophic bacteria in an Antarctic coastal ecosystem: variability and physical and biogeochemical forcings, Frontiers in Marine Science, 3, 214, https://doi.org/10.3389/fmars.2016.00214, 2016.
Kim, H., Doney, S. C., Iannuzzi, R. A., Meredith, M. P., Martinson, D. G., and Ducklow, H. W.: Climate forcing for dynamics of dissolved inorganic nutrients at Palmer Station, Antarctica: an interdecadal (1993–2013) analysis, J. Geophys. Res.-Biogeo., 121, 2369–2389, https://doi.org/10.1002/2015JG003311, 2016.
Kim, H. H., Luo, Y.-W., Ducklow, H. W., Schofield, O. M., Steinberg, D. K., and Doney, S. C.: WAP-1D-VAR v1.0: development and evaluation of a one-dimensional variational data assimilation model for the marine ecosystem along the West Antarctic Peninsula, Geosci. Model Dev., 14, 4939–4975, https://doi.org/10.5194/gmd-14-4939-2021, 2021.
Kimura, H., Young, C. R., Martinez, A., and DeLong, E. F.: Light-induced transcriptional responses associated with proteorhodopsin-enhanced growth in a marine flavobacterium, ISME J., 5, 1641–1651, https://doi.org/10.1038/ismej.2011.36, 2011.
King, J. C.: Recent Climate Variability in the Vicinity of the Antarctic Peninsula, Int. J. Climatol., 14, 357–369, https://doi.org/10.1002/joc.3370140402, 1994.
Kirchman, David L., Xosé Anxelu G. Morán, and Hugh Ducklow: Microbial Growth in the Polar Oceans – Role of Temperature and Potential Impact of Climate Change, Nat. Rev. Microbiol., 7, 451–459, https://doi.org/10.1038/nrmicro2115, 2009.
Kohonen T.: Self-Organzing Maps, 3rd edn., Springer, Berlin, 2001.
Lawson, L. M., Spitz, Y. H., Hofmann, E. E., and Long, R. B.: A Data Assimilation Technique Applied to a Predator-Prey Model, B. Math. Biol., 57, 593–617, https://doi.org/10.1007/BF02460785, 1995.
Li, W. K. W., Jellett, J. F., and Dickie, P. M.: DNA Distributions in Planktonic Bacteria Stained with TOTO or TO-PRO, Limnol. Oceanogr., 40, 1485–1495, https://doi.org/10.4319/lo.1995.40.8.1485, 1995.
Longnecker, K., Sherr, B. F., and Sherr, E. B.: Activity and phylogenetic diversity of bacterial cells with high and low nucleic acid content and electron transport system activity in an upwelling ecosystem, Appl. Environ. Microb., 71, 7737–7749, https://doi.org/10.1128/AEM.71.12.7737-7749.2005, 2005.
Luo, Y. W., Friedrichs, M. A., Doney, S. C., Church, M. J., and Ducklow, H. W.: Oceanic heterotrophic bacterial nutrition by semilabile DOM as revealed by data assimilative modeling, Aquat. Microb. Ecol., 60, 273–287, https://doi.org/10.3354/ame01427, 2010.
Luo, Y. W., Ducklow, H. W., Friedrichs, M. A., Church, M. J., Karl, D. M., and Doney, S. C.: Interannual variability of primary production and dissolved organic nitrogen storage in the North Pacific Subtropical Gyre, J. Geophys. Res.-Biogeo., 117, G03019, https://doi.org/10.1029/2011JG001830, 2012.
Luria, C. M., Ducklow, H. W., and Amaral-Zettler, L. A.: Marine bacterial, archaeal and eukaryotic diversity and community structure on the continental shelf of the western Antarctic Peninsula, Aquat. Microb. Ecol., 73, 107–121, https://doi.org/10.3354/ame01703, 2014.
Luria, C. M., Amaral-Zettler, L. A., Ducklow, H. W., Repeta, D. J., Rhyne, A. L., and Rich, J. J.: Seasonal shifts in bacterial community responses to phytoplankton-derived dissolved organic matter in the Western Antarctic Peninsula, Front Microbiol., 8, 2117, https://doi.org/10.3389/fmicb.2017.02117, 2017.
Martín-Figueroa, E., Navarro, F., and Florencio, F. J.: The GS-GOGAT pathway is not operative in the heterocysts, Cloning and expression of glsF gene from the cyanobacterium Anabaena sp, PCC 7120, FEBS Lett., 476, 282–286, https://doi.org/10.1016/S0014-5793(00)01722-1, 2000.
Matear, R. J.: Parameter optimization and analysis of ecosystem models using simulated annealing: A case study at Station P, J. Mar. Res., 53, 571–607, https://doi.org/10.1357/0022240953213098, 1995.
Meredith, M. P., Brandon, M. A., Wallace, M. I., Clarke, A., Leng, M. J., Renfrew, I. A., Van Lipzig, N. P., and King, J. C.: Variability in the freshwater balance of northern Marguerite Bay, Antarctic Peninsula: results from δ18O, Deep-Sea Res. Pt. II, 55, 309–322, https://doi.org/10.1016/j.dsr2.2007.11.005, 2008.
Meredith, M. P., Venables, H. J., Clarke, A., Ducklow, H. W., Erickson, M., Leng, M. J., Lenaerts, J. T., and van den Broeke, M. R.: The freshwater system west of the Antarctic Peninsula: spatial and temporal changes, J. Climate, 26, 1669–1684, https://doi.org/10.1175/JCLI-D-12-00246.1, 2013.
Miller, T. R., Beversdorf, L., Chaston, S. D., and McMahon, K. D.: Spatiotemporal molecular analysis of cyanobacteria blooms reveals Microcystis-Aphanizomenon interactions, PloS one, 8, e74933, https://doi.org/10.1371/journal.pone.0074933, 2013.
Moline, M. A., Claustre, H., Frazer, T. K., Schofield, O., and Vernet, M.: Alteration of the food web along the Antarctic Peninsula in response to a regional warming trend, Glob. Change Biol., 10, 1973–1980, https://doi.org/10.1111/j.1365-2486.2004.00825.x, 2004.
Morán, X. A. G., Bode, A., Suárez, L. Á., and Nogueira, E.: Assessing the relevance of nucleic acid content as an indicator of marine bacterial activity, Aquat. Microb. Ecol., 46, 141–152, https://doi.org/10.3354/ame046141, 2007.
Morán, X. A. G., Ducklow, H. W., and Erickson, M.: Single-cell physiological structure and growth rates of heterotrophic bacteria in a temperate estuary (Waquoit Bay, Massachusetts), Limnol. Oceanogr., 56, 37–48, https://doi.org/10.4319/lo.2011.56.1.0037, 2011.
Prunet, P., Minster, J. F., Ruiz-Pino, D., and Dadou, I.: Assimilation of surface data in a one-dimensional physical-biogeochemical model of the surface ocean: 1. Method and preliminary results, Global Biogeochem. Cy., 10, 111–138, https://doi.org/10.1029/95GB03436, 1996a.
Prunet, P., Minster, J. F., Echevin, V., and Dadou, I.: Assimilation of surface data in a one-dimensional physical-biogeochemical model of the surface ocean: 2. Adjusting a simple trophic model to chlorophyll, temperature, nitrate, and pCO2 data, Global Biogeochem. Cy., 10, 139–158, https://doi.org/10.1029/95GB03435, 1996b.
Ruckstuhl, C., and Norris, J. R.: How do aerosol histories affect solar “dimming” and “brightening” over Europe?: IPCC-AR4 models versus observations, J. Geophys. Res.-Atmos., 114, D00D04, https://doi.org/10.1029/2008JD011066, 2009.
Saba, G. K., Fraser, W. R., Saba, V. S., Iannuzzi, R. A., Coleman, K. E., Doney, S. C., Ducklow, H. W., Martinson, D. G., Miles, T. N., Patterson-Fraser, D. L., and Stammerjohn, S. E.: Winter and spring controls on the summer food web of the coastal West Antarctic Peninsula, Nature Commun., 5, 1–8, https://doi.org/10.1038/ncomms5318, 2014.
Sailley, S. F., Ducklow, H. W., Moeller, H. V., Fraser, W. R., Schofield, O. M., Steinberg, D. K., Garzio, L. M., and Doney, S. C.: Carbon fluxes and pelagic ecosystem dynamics near two western Antarctic Peninsula Adélie penguin colonies: an inverse model approach, Mar. Ecol. Prog. Ser., 492, 253–272, https://doi.org/10.3354/meps10534, 2013.
Scharek, R. and Latasa, M.: Growth, grazing and carbon flux of high and low nucleic acid bacteria differ in surface and deep chlorophyll maximum layers in the NW Mediterranean Sea, Aquat. Microb. Ecol., 46, 153–161, https://doi.org/10.3354/ame046153, 2007.
Schattenhofer, M., Wulf, J., Kostadinov, I., Glöckner, F. O., Zubkov, M. V., and Fuchs, B. M.: Phylogenetic characterisation of picoplanktonic populations with high and low nucleic acid content in the North Atlantic Ocean, Syst. Appl. Microbiol., 34, 470–475, https://doi.org/10.1016/j.syapm.2011.01.008, 2011.
Schofield, O., Saba, G., Coleman, K., Carvalho, F., Couto, N., Ducklow, H., Finkel, Z., Irwin, A., Kahl, A., Miles, T., and Montes-Hugo, M.: Decadal variability in coastal phytoplankton community composition in a changing West Antarctic Peninsula, Deep-Sea Res. Pt. I, 124, 42–54, https://doi.org/10.1016/j.dsr.2017.04.014, 2017.
Sherr, B. F., Sherr, E. B., and McDaniel, J.: Effect of protistan grazing on the frequency of dividing cells in bacterioplankton assemblages, Appl. Environ. Microb., 58, 2381–2385, https://doi.org/10.1128/aem.58.8.2381-2385.1992, 1992.
Spitz, Y. H., Moisan, J. R., and Abbott, M. R.: Configuring an ecosystem model using data from the Bermuda Atlantic Time Series (BATS). Deep-Sea Res. Pt. II, 48, 1733–1768, https://doi.org/10.1016/S0967-0645(00)00159-4, 2001.
Stammerjohn, S. E., Martinson, D. G., Smith, R. C., Yuan, X., and Rind, D.: Trends in Antarctic annual sea ice retreat and advance and their relation to El Ni no–Southern Oscillation and Southern Annular Mode variability, J. Geophys. Res.-Oceans, 113, C03S90, https://doi.org/10.1029/2007JC004269, 2008.
Steinberg, D. K., Ruck, K. E., Gleiber, M. R., Garzio, L. M., Cope, J. S., Bernard, K. S., Stammerjohn, S. E., Schofield, O. M., Quetin, L. B., and Ross, R. M.: Long-term (1993–2013) changes in macrozooplankton off the Western Antarctic Peninsula, Deep-Sea Res. Pt. I, 101, 54–70, https://doi.org/10.1016/j.dsr.2015.02.009, 2015.
Teira, E., Martínez-García, S., Lønborg, C., and Álvarez-Salgado, X. A.: Growth rates of different phylogenetic bacterioplankton groups in a coastal upwelling system, Env. Microbiol. Rep., 1, 545–554, https://doi.org/10.1111/j.1758-2229.2009.00079.x, 2009.
Thibodeau, P. S., Steinberg, D. K., Stammerjohn, S. E., and Hauri, C.: Environmental controls on pteropod biogeography along the Western Antarctic Peninsula, Limnol. Oceanogr., 64, S240–S256, https://doi.org/10.1002/lno.11041, 2019.
Vaughan, D. G.: Recent trends in melting conditions on the Antarctic Peninsula and their implications for ice-sheet mass balance and sea level, Arct. Antarct. Alp. Res, 38, 147–152, https://doi.org/10.1657/1523-0430(2006)038[0147:RTIMCO]2.0.CO;2, 2006.
Vaughan, D. G., Marshall, G. J., Connolley, W. M., Parkinson, C., Mulvaney, R., Hodgson, D. A., King, J. C., Pudsey, C. J., and Turner, J.: Recent rapid regional climate warming on the Antarctic Peninsula, Climatic Change, 60, 243–274, https://doi.org/10.1023/A:1026021217991, 2003.
Vila-Costa, M., Gasol, J. M., Sharma, S., and Moran, M. A.: Community analysis of high-and low-nucleic acid-containing bacteria in NW Mediterranean coastal waters using 16S rDNA pyrosequencing, Environ. Microb., 14, 1390–1402, https://doi.org/10.1111/j.1462-2920.2012.02720.x, 2012.
Ward, B. A., Friedrichs, M. A., Anderson, T. R., and Oschlies, A.: Parameter optimisation techniques and the problem of underdetermination in marine biogeochemical models, J. Marine Syst., 81, 34–43, https://doi.org/10.1016/j.jmarsys.2009.12.005, 2010.
White, P. A., Kalff, J., Rasmussen, J. B., and Gasol, J. M.: The effect of temperature and algal biomass on bacterial production and specific growth rate in freshwater and marine habitats, Microb. Ecol., 21, 99–118, https://doi.org/10.1007/BF02539147, 1991.
Whitehouse, M. J., Meredith, M. P., Rothery, P., Atkinson, A., Ward, P., and Korb, R. E.: Rapid warming of the ocean around South Georgia, Southern Ocean, during the 20th century: forcings, characteristics and implications for lower trophic levels, Deep-Sea Res. Pt. I, 55, 1218–1228, https://doi.org/10.1016/j.dsr.2008.06.002, 2008.
Yokokawa, T., Nagata, T., Cottrell, M. T., and Kirchman, D. L.: Growth rate of the major phylogenetic bacterial groups in the Delaware estuary, Limnol. Oceanogr., 49, 1620–1629, https://doi.org/10.4319/lo.2004.49.5.1620, 2004.




