Ocean alkalinity enhancement – avoiding runaway CaCO₃ precipitation during quick and hydrated lime dissolution

Ocean alkalinity enhancement (OAE) is a method that can remove carbon dioxide (CO₂) from the atmosphere and counteract ocean acidification through the dissolution of alkaline minerals. Currently, critical knowledge gaps exist regarding the dissolution of different minerals suitable for OAE in natural seawater. Of particular importance is to understand how much alkaline mineral can be dissolved before secondary precipitation of calcium carbonate (CaCO₃) occurs, since secondary CaCO₃ precipitation reduces the atmospheric CO₂ uptake potential of OAE. Using two types of mineral proposed for OAE, quick lime (CaO) and hydrated lime (Ca(OH)₂), we show that both (<63 µm of diameter) dissolved in seawater within a few hours. No CaCO₃ precipitation occurred at a saturation state (Ω_A) of ∼5, but CaCO₃ precipitation in the form of aragonite occurred above an Ω_A value of 7. This limit is lower than expected for typical pseudo-homogeneous precipitation, i.e. in the presence of colloids and organic matter. Secondary precipitation at low Ω_A (∼ 7) was the result of heterogeneous precipitation onto mineral surfaces, most likely onto the added CaO and Ca(OH)₂ particles. Most importantly, runaway CaCO₃ precipitation was observed, a condition where significantly more total alkalinity (TA) was removed than initially added. Such runaway precipitation could reduce the OAE CO₂ uptake efficiency from ∼ 0.8 mol of CO₂ per mole of added TA down to 0.1 mol of CO₂ per mole of TA. Runaway precipitation appears to be avoidable by dilution below the critical Ω_A threshold of 5, ideally within hours of the mineral additions to minimise initial CaCO₃ precipitation. Finally, OAE simulations suggest that for the same Ω_A threshold, the amount of TA that can be added to seawater would be more than 3 times higher at 5 ^∘C than at 30 ^∘C. The maximum TA addition could also be increased by equilibrating the seawater to atmospheric CO₂ levels (i.e. to a pCO₂ of ∼ 416 µatm) during addition. This would allow for more TA to be added in seawater without inducing CaCO₃ precipitation, using OAE at its CO₂ removal potential.

1 Introduction

Modern climate change is considered one of the greatest threats to humankind (Hoegh-Guldberg et al., 2019; IPCC, 2021; The Royal Society and Royal Academy of Engineering, 2018). Global mean temperature has increased by 1.0 ^∘C since pre-industrial times and could reach +1.2–1.9 ^∘C in the next 20 years and +2.1–5.7 ^∘C by the end of this century (IPCC, 2021). Furthermore, about 26 % of all anthropogenic carbon dioxide (CO₂) emissions were taken up by the ocean through air–sea gas exchange between 1750 and 2020 (Friedlingstein et al., 2022). This has led to a decrease in the average open-ocean pH by 0.1 units in a process termed ocean acidification – OA (Bates et al., 2012; Canadell et al., 2007; Carter et al., 2019; Cyronak et al., 2014; Doney et al., 2009; Hoegh-Guldberg et al., 2007).

The aim of the 2015 Paris Agreement is to minimise the negative impacts of global warming and OA by limiting global warming to less than +2.0 ^∘C, ideally below +1.5 ^∘C, by the end of this century (Goodwin et al., 2018). However, the current and pledged reductions will likely not be enough, and additional CO₂ mitigation strategies are needed, such as ocean alkalinity enhancement – OAE (Gattuso et al., 2015; GESAMP, 2019; Lenton and Vaughan, 2009; The Royal Society and Royal Academy of Engineering, 2018). OAE could be an efficient approach for CO₂ removal (current emissions of 40 Gt yr⁻¹), with models suggesting a potential of 165 to 790 Gt (1 Gt = 10¹⁵ g) of atmospheric CO₂ removed by the year 2100 on a global scale if OAE were implemented today (Burt et al., 2021; Feng et al., 2017; IPCC, 2021; Keller et al., 2014; Köhler et al., 2013; Lenton et al., 2018). However, empirical data on OAE efficacies are limited, and safe thresholds for mineral dissolution are particularly lacking (National Academies of Sciences and Medicine, 2022).

OAE typically relies on the dissolution of alkaline minerals in seawater, releasing alkalinity similarly to natural rock-weathering processes (Kheshgi, 1995). Suitable candidates are magnesium-rich minerals such as brucite, periclase or forsterite and calcium-rich minerals such as quick and hydrated lime (Renforth and Henderson, 2017). Quick lime and hydrated lime are of particular interest due to their high solubility in seawater and rapid dissolution. Quick lime, i.e. calcium oxide (CaO), is obtained by the calcination of limestone, composed primarily of calcium carbonate (CaCO₃), which is present in large quantities within the earth's crust. Once heated to temperatures of ∼ 1200 ^∘C, each molecule of CaCO₃ breaks down into one molecule of CaO and one molecule of CO₂ (Ilyina et al., 2013; Kheshgi, 1995). Hence, for maximum OAE potential, carbon capture during calcination and subsequent storage would be necessary (Bach et al., 2019; Ilyina et al., 2013; Kheshgi, 1995; Renforth et al., 2013; Renforth and Kruger, 2013). CaO can be hydrated into calcium hydroxide (Ca(OH)₂), also known as hydrated lime. The addition of either CaO or Ca(OH)₂ to seawater leads to the dissociation of Ca(OH)₂ into one calcium Ca²⁺ and two hydroxyl ions OH⁻ (Feng et al., 2017; Harvey, 2008). Ignoring the non-linearities of the seawater carbonate system (i.e. changes in total alkalinity, TA, and dissolved inorganic carbon, DIC, are not 1:1), the chemical reaction of CO₂ and Ca(OH)₂ dissolution and the subsequent uptake of atmospheric CO₂ can be written as

$$\begin{array}{}\text{(1)}& \left(\mathrm{CaO}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\rightleftharpoons \mathrm{Ca}{\left(\mathrm{OH}\right)}_{\mathrm{2}}\right)+\mathrm{2}{\mathrm{CO}}_{\mathrm{2}}\to {\mathrm{Ca}}^{\mathrm{2}+}+\mathrm{2}{\mathrm{HCO}}_{\mathrm{3}}^{-}.\end{array}$$

The dissolution of CaO and Ca(OH)₂ and the subsequent addition of TA increase the pH of seawater, which changes the carbonate chemistry speciation (Zeebe and Wolf-Gladrow, 2001). DIC can be approximated as the sum of HCO${}_{\mathrm{3}}^{-}$ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ (ignoring the small contribution by CO₂). Similarly, TA can be approximated as the sum of HCO${}_{\mathrm{3}}^{-}$ and 2 CO${}_{\mathrm{3}}^{\mathrm{2}-}$ (ignoring the smaller contributions by boric and silicic acids and other minor components). Combining both DIC and TA equations reveals that CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentrations can be expressed as [CO${}_{\mathrm{3}}^{\mathrm{2}-}$] = TA − DIC. Hence, increasing TA at a constant DIC, e.g. by dissolving CaO or Ca(OH)₂, increases [CO${}_{\mathrm{3}}^{\mathrm{2}-}$], shifting the carbonate chemistry speciation towards a higher pH (Fig. A1) (Dickson et al., 2007; Wolf-Gladrow et al., 2007; Zeebe and Wolf-Gladrow, 2001). The subsequent shift in DIC speciation leads to a decrease in dissolved CO₂ concentrations, reducing the partial pressure of CO₂ (pCO₂) in seawater and increasing its atmospheric CO₂ uptake potential.

Depending on the amount of TA added and the initial seawater pCO₂, the TA-enriched seawater would either take up CO₂ from the atmosphere or reduce outgassing of CO₂. Factoring in the non-linearities of the carbonate system, about 1.6 mol of atmospheric CO₂ could be taken up per mole of dissolved CaO or Ca(OH)₂ (Köhler et al., 2010). Furthermore, dissolving CaO and Ca(OH)₂ can also counteract ocean acidification. During the dissolution of alkaline minerals, both pH and the CaCO₃ saturation state of seawater (Ω) increase through increasing Ca²⁺ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentrations. This makes OAE a dual solution for removing atmospheric CO₂ and mitigating OA (Feng et al., 2017; GESAMP, 2019; Harvey, 2008). However, there are important knowledge gaps in our understanding surrounding basic mineral dissolution in seawater (Feng et al., 2016; González and Ilyina, 2016; Mongin et al., 2021; Renforth and Henderson, 2017).

One knowledge gap is the critical Ω threshold beyond which CaCO₃ starts to precipitate inorganically. Such secondary precipitation constitutes the opposite of alkaline mineral dissolution and would decrease pH and Ω while simultaneously increasing the CO₂ concentration in seawater. This would decrease the ocean uptake's capacity for atmospheric CO₂, causing the opposite of the intended effect. Additionally, if all added alkalinity were precipitated, only 1 mol of atmospheric CO₂ per mole of Ca²⁺ would be removed, instead of ∼ 1.6 mol in the absence of CaCO₃ precipitation. If even more CaCO₃ precipitated, the efficiency of OAE would be further reduced. Under typical seawater conditions, CaCO₃ precipitation does not occur due to the absence of mineral-phase precipitation nuclei and the presence of precipitation inhibitors such as dissolved organic compounds, magnesium (Mg) or phosphate (Chave and Suess, 1970; De Choudens-Sanchez and Gonzalez, 2009; Pytkowicz, 1965; Rushdi et al., 1992; Simkiss, 1964). There are three types of CaCO₃ precipitation, (1) homogeneous (in the absence of any precipitation nuclei), (2) heterogeneous (in the presence of mineral phases) and (3) pseudo-homogeneous (in the presence of colloids and organic materials) (Marion et al., 2009; Morse and He, 1993). For pseudo-homogeneous precipitation, the critical threshold at which calcite precipitates spontaneously is at a calcite saturation state (Ω_C) of ∼ 18.8 (at a salinity of 35 and at a temperature of 21 ^∘C) (Marion et al., 2009). Assuming typical open-ocean carbonate chemistry (e.g. TA ∼ 2350 µmol kg⁻¹ and DIC ∼ 2100 µmol kg⁻¹), this threshold would be reached through an increase in TA of ∼ 810 µmol kg⁻¹. This corresponds to a critical threshold for Ω with respect to aragonite, i.e. Ω_A, of ∼ 12.3. The two other types of precipitation (i.e. homogeneous and heterogeneous) are more poorly constrained (Marion et al., 2009). Importantly, at current dissolved Mg and Ca concentrations in seawater, the CaCO₃ polymorph that is favoured during inorganic precipitation is aragonite rather than calcite (Morse et al., 1997; Pan et al., 2021). Therefore, aragonite saturation state Ω_A may be a more important determinant of critical runaway precipitation thresholds. No matter what mineral phase is precipitating, a better understanding of CaCO₃ precipitation under conditions relevant to OAE is needed.

To gain a better understanding of the consequences of CaO and Ca(OH)₂ dissolution for OAE, we conducted several dissolution experiments with CaO and Ca(OH)₂ to determine (1) how much alkaline material can be dissolved without inducing CaCO₃ precipitation, (2) what causes secondary CaCO₃ precipitation and (3) how secondary precipitation can be avoided.

2 Material and methods

2.1 Experimental setup

Two different calcium minerals were used, CaO powder from Ajax Finechem (CAS no. 1305-78-8) and industrial Ca(OH)₂ powder (hydrated lime 20 kg, Dingo). The elemental compositions of these powders were analysed using an Agilent 7700 inductively coupled plasma mass spectrometer (ICP-MS), coupled to a laser ablation unit (NWR213, Electro Scientific Industries, Inc). Samples were embedded in resin and instrument readings calibrated against standard reference materials, batch nos. 610 and 612, from the National Institute of Standards and Technology.

All dissolution experiments were conducted in natural seawater. The seawater was collected between September 2020 and June 2021, about 200 to 300 m from the shore, avoiding suspended sand or silt, at Broken Head, New South Wales, Australia (28^∘${\mathrm{42}}^{\prime }{\mathrm{12}}^{\prime \prime }$ S, 153^∘${\mathrm{37}}^{\prime }{\mathrm{03}}^{\prime \prime }$ E). Seawater was stored for up to 14 d at 4 ^∘C in the dark to slow bacterial metabolic activity and allow for all suspended particles to settle on the bottom before being sterile-filtered using a peristaltic pump, connected to a 0.2 µm Whatman Polycap 75 AS filter. For salinity measurements, about 200 mL of seawater was placed in a gas-tight polycarbonate container and allowed to equilibrate to room temperature overnight. The sample's conductivity and temperature were then measured with a Metrohm cell (6.017.080), connected to a 914 pH/Conductometer. The conductivity was recorded in millisiemens per centimetre (mS cm⁻¹) and the temperature in degrees Celsius (^∘C). Salinity was calculated according to Lewis and Perkin (1981) on the 1978 practical salinity scale. The salinity in each experiment is reported in Table A1.

2.2 OAE experiments

For each experiment, seawater was accurately weighed (in grams to 2 decimal places) into high-quality 2 L borosilicate 3.3 Schott DURAN beakers, and the temperature was controlled via a Tank chiller line TK-1000 set at 21 ^∘C, feeding a re-circulation water jacket (Fig. A2). A magnetic stir bar was placed in the beaker, and the natural seawater was constantly stirred at ∼ 200 rpm. To minimise gas exchange, a floating lid with various sampling ports was placed on top. Finally, after 1 h of equilibration, calculated quantities of weighed-in calcium alkaline compounds were added. Upon addition, samples for DIC and TA were taken at increasing time intervals to fully capture the dissolution kinetics and check for potential secondary precipitation. Furthermore, the pH was monitored at a frequency of 1 Hz for the first hour before alkalinity addition and over 4 h after addition to determine when alkalinity was fully released. Once the pH plateaued (corresponding to maximum TA release), the content of the beaker was carefully transferred to a clean Schott bottle to ensure that evaporation would not alter the DIC or TA concentrations. Bottles were kept in the dark for the duration of each experiment, i.e. up to 48 d, with the same constant stirring of ∼ 200 rpm at 21 ^∘C. Each bottle was exposed to UV light for at least 30 min after each sampling to inhibit bacterial growth.

2.2.1 CaO and Ca(OH)₂ dissolution

Following the beaker setup as described in Sect. 2.2, TA was added by sieving CaO and Ca(OH)₂ through a 63 µm mesh to avoid the formation of larger CaO or Ca(OH)₂ aggregates. The mesh was placed in a clean 50 mL upside-down Falcon tube cap to minimise the loss of material smaller than 63 µm, and the overall weight was recorded in milligrams. Then, the mesh was placed above the Schott bottle, and the mineral was added by gently tapping the side of the sieve. Finally, the sieve was placed in the same upside-down Falcon tube cap and weighed once again, thereby making sure that the desired amount had been added to the beaker. The weighing steps were carefully performed to avoid material loss between the bottle and the balance and were achieved in less than 5 min. Two alkalinity additions, +250 and +500 µmol kg⁻¹ with each calcium mineral powder, were performed (Table 1).

Table 1 Summary of experimental conditions. Please note that for comparability, more TA was added in the liquid than the sieved approaches to match the theoretical increases in calcium carbonate saturation state (see “Materials and methods” section for details).

n/a: not applicable.

2.2.2 Na₂CO₃ alkalinity, particles additions and filtration

Three further experiments assessed the role of mineral phases during secondary CaCO₃ precipitation observed in the previous experiments. The first experiment used a 1 M solution of sodium carbonate (Na₂CO₃, CAS number 497-19-8), freshly prepared on the day to limit CO₂ ingassing. Ultrapure Na₂CO₃ was accurately weighed (in mg with 2 decimal places) into a clean 100 mL Schott bottle and made up to 100 g with Milli-Q (18.2 MΩ). The solution was then sonicated for 15 min, with gentle mixing every 5 min. The amount of Na₂CO₃ to be added to seawater was calculated so that a similar maximum Ω_A would be reached, i.e. ∼ 7.7, as in the previous experiments with the highest addition of CaO and Ca(OH)₂. This required about twice the alkalinity increase as before (Table 1) because Na₂CO₃ additions concomitantly increase DIC when dissociating in two sodium ions and one CO${}_{\mathrm{3}}^{\mathrm{2}-}$ ion, making the Ω_A increase smaller. All carbonate chemistry calculations were performed in CO2SYS (see below).

In another experiment similar to the Na₂CO₃ addition, quartz powder was added after 2 d. Quartz powder was chosen as it does not dissolve on the timescales relevant for this study (Montserrat et al., 2017). The addition of quartz powder was similar to the sieved CaO and Ca(OH)₂ additions, i.e. through a 63 µm mesh. The mass of quartz particles added (in mg with 2 decimal places) was determined to provide the same mineral surface area as for the Ca(OH)₂ experiments with a TA increase of 500 µmol kg⁻¹. It was calculated using densities and masses of Ca(OH)₂ and quartz, assuming spherical particles with a diameter of 63 µm.

The third experiment followed the same experimental setup as described in Sect. 2.2.1. Here, Ca(OH)₂ was added to first increase TA by ∼ 500 µmol kg⁻¹ (Table 1). After 4 h of reaction, the entire content of the 2 L Schott beaker was filtered through a Nylon Captiva EconoFilter (25 mm) with a pore size of 0.45 µm into a clean 1 L Schott bottle using a peristaltic pump. The bottle was filled from bottom to top, with overflow to minimise gas exchange.

2.2.3 Dilution experiments

In a last set of experiments, alkalinity-enriched seawater was diluted with natural seawater to test if secondary precipitation could be avoided or stopped. Ca(OH)₂ powder was added to reach final alkalinity enrichments of 500 and 2000 µmol kg⁻¹, and dilutions were carried out at several time intervals.

For the experiment with a targeted TA increase of 500 µmol kg⁻¹, a larger quantity of TA-enriched seawater was required to perform all dilutions and sampling in comparison to the previous experiments. Therefore, two 5 L Schott bottles were filled with 5 kg of natural seawater and placed on a magnetic stirring platform. Calculated weighed-in masses of Ca(OH)₂ were added to the first bottle, as described in Sect. 2.2.1, using the 63 µm sieve, while the natural seawater in the second bottle was kept for subsequent dilutions. Both bottles were kept on the same bench under the same conditions, stirring at a rate of ∼ 200 rpm, for the duration of the experiment.

Following the Ca(OH)₂ addition, 1:1 dilutions (500 g TA-enriched seawater : 500 g natural seawater) were performed in clean 1 L Schott bottles that were kept in the dark and placed on a magnetic platform at a stirring rate of ∼ 200 rpm. After each sampling time, the bottles were exposed to UV light for at least 30 min. The second dilution experiment was set up like the first one, the only difference being that the targeted TA increase was 2000 µmol kg⁻¹. The dilution ratio was 1:7 to reduce the targeted TA increase again to 250 µmol kg⁻¹. All dilutions were performed 10 min, 1 h, 1 d and 1 week after Ca(OH)₂ addition, leading to two TA-enriched and eight diluted treatments.

2.3 Carbonate chemistry measurements

Samples for TA and DIC measurements were filtered through a Nylon Captiva EconoFilter (0.45 µm) using a peristaltic pump into 100 mL borosilicate 3.3 Schott DURAN glass stopper bottles. The bottles were gently filled from the bottom to top, using a 14-gauge needle as described in Schulz et al. (2017), with at least half of their volume allowed to overflow, corresponding to ∼ 150 mL of seawater sampled per time point. After filling, 50 µL of saturated mercuric chloride solution was added to each sample before being stored without headspace in the dark at 4 ^∘C.

TA was analysed in duplicate via potentiometric titrations by a Metrohm 848 Titrino plus coupled to an 869 Compact Sample Changer using 0.05 M HCl, with the ionic strength adjusted to 0.72 mol kg⁻¹ using NaCl, corresponding to a salinity of 35. Titrations and calculations followed the open-cell titration protocols by Dickson et al. (2007). DIC was measured in triplicate using an Automated Infra-Red Inorganic Carbon Analyzer (AIRICA, Marianda) coupled to a LI-COR LI-7000 infra-red detector as described in Gafar and Schulz (2018). Measured values of TA and DIC were corrected using an internal standard prepared as described in Dickson (2010), calibrated against certified reference materials, batch nos. 175 and 190.

The overall instrument uncertainty for TA and DIC was calculated as follows. For each measurement, a standard deviation was calculated, from duplicates of TA and triplicates of DIC. The samples and reference material standard deviations were averaged, and an error propagation on these values were used to estimate average measurement uncertainty, i.e. ± 1.0 µmol kg⁻¹ and DIC at ± 0.8 µmol kg⁻¹, for TA and DIC, respectively.

2.4 Particulate inorganic carbon and scanning electron microscopy (SEM)

In cases where TA and DIC decreases were observed, indicative of CaCO₃ precipitation, samples were taken at the end of the experiments for total particulate carbon (TPC), particulate organic carbon (POC) and scanning electron microscopy (SEM) analyses. TPC and POC samples were collected in duplicates on pre-combusted (450 ^∘C) GF/F filters and stored frozen until analysis. Before analysis, POC filters were fumed with HCl for 2 h before drying overnight at 60 ^∘C while TPC filters were dried untreated (Gafar and Schulz, 2018). The filters were wrapped in tin capsules and pressed into small 5 mm diameter balls. TPC and POC were quantified on a Thermo Fisher Flash Elemental Analyzer, coupled to a Delta V Plus isotope ratio mass spectrometer. Particulate inorganic carbon (PIC), or CaCO₃, was calculated based on the difference between TPC and POC. The results are reported in µmol kg⁻¹ of seawater with an uncertainty estimate by an error propagation of the square root of the sum of the squared standard deviations for TPC and POC.

For SEM analysis, 10 to 15 mL of the sample water was collected on polycarbonate Whatman Cyclopore filters with a 0.2 µm pore size and rinsed with 50 mL of Milli-Q. The filters were dried at 60 ^∘C overnight and kept in a desiccator until analysis on a tabletop Hitachi TM4000 Plus scanning electron microscope. The microscope was coupled to an energy-dispersive X-ray (EDX) analyser, allowing us to identify the CaCO₃ polymorph and elemental composition of precipitates. Finally, CaO and Ca(OH)₂ powders were analysed for their carbon content. This analysis aimed to identify the presence and estimate the amount of particulate carbon, most likely CaCO₃, in the respective mineral powders.

Figure 1 Changes in TA (a), DIC (b) and Ω_A (c) over time following two CaO additions.

Figure 2 Changes in TA (a), DIC (b) and Ω_A (c) of the samples over time following two Ca(OH)₂ additions.

2.5 Carbonate chemistry calculations

Measured DIC, TA, temperature and salinity were used to calculate the remaining carbonate chemistry parameters with the CO2SYS script for MATLAB^® (MathWorks) (Sharp et al., 2021). The borate-to-salinity relationship and boric acid dissociation constant from Uppstrom (1974) and the carbonic acid dissociation constants of Lueker et al. (2000) were used. With two measured carbonate chemistry parameters, i.e. DIC and TA, the others can be derived. An important difference in our experiments was that the dissolution of CaO and Ca(OH)₂ changed the calcium concentration, and hence the salinity-based Ω calculated by CO2SYS is underestimated. Ω is defined by the solubility product of CaCO₃ as

$$\begin{array}{}\text{(2)}& \mathrm{\Omega }={\displaystyle \frac{\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]\times \left[{\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}\right]}{K_{\mathrm{sp}}}},\end{array}$$

where [Ca²⁺] and [CO${}_{\mathrm{3}}^{\mathrm{2}-}$] denote seawater concentrations of Ca²⁺ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ and K_sp is the solubility product for calcite or aragonite at the appropriate salinity and temperature. To calculate saturation states, the correct calcium concentration [Ca²⁺]_Corr was estimated from measured salinity (Riley and Tongudai, 1967) and half the alkalinity concentration change, ΔTA, generated during CaO or Ca(OH)₂ dissolution or loss due to CaCO₃ precipitation:

$$\begin{array}{}\text{(3)}& {\left[{\mathrm{Ca}}^{\mathrm{2}+}\right]}_{\mathrm{Corr}}={\displaystyle \frac{\mathrm{0.01028}}{\mathrm{35}}}\times \mathrm{salinity}+{\displaystyle \frac{\mathrm{\Delta }\mathrm{TA}}{\mathrm{2}}},\end{array}$$

where 0.01028 is the molar Ca²⁺ concentration at a salinity of 35. K_sp was calculated from in situ temperature and salinity according to Mucci (1983). The correct Ω_C and Ω_A were then calculated according to Eq. (2). Please note that we have opted to report Ω_A rather than Ω_C since aragonite is more likely to be precipitated in natural modern seawater (Morse et al., 1997).

2.6 OAE simulations

CO2SYS and the results from the various dissolution experiments were used to simulate three OAE scenarios (Table 3). Three alkalinity additions were simulated, +250, +500 and +1000 µmol kg⁻¹. The starting parameters were TA = 2350 µmol kg⁻¹, DIC = 2100 µmol kg⁻¹, salinity = 35 and temperature = 19 ^∘C, using the same acid–base equilibrium constants as described in Sect. 2.5. In the first scenario, for all three additions, no CaCO₃ precipitation was assumed. We then estimated the amount of CO₂ taken up by the seawater after atmospheric re-equilibration, i.e. until a pCO₂ of ∼ 416 ppm. For the +500 and +1000 µmol kg⁻¹ TA increases, two additional simulations were performed. First, we assumed that as much CaCO₃ precipitated as TA was added; e.g. after increasing the TA by 500 µmol kg⁻¹, we assumed a loss of 500 µmol kg⁻¹ of TA and 250 µmol kg⁻¹ of DIC. We then simulated atmospheric re-equilibration until a pCO₂ of ∼ 416 ppm and recorded the changes in the carbonate chemistry parameters. Second, we assumed that CaCO₃ precipitated down to an Ω_A of ∼ 2 as observed in our experiments. After calculating full carbonate chemistry speciation in these various scenarios, the amount of CO₂ taken up after atmospheric re-equilibration was determined using the same approach as described above.

3 Results

3.1 Chemical composition of CaO and Ca(OH)₂

The bulk chemical compositions of the CaO and Ca(OH)₂ powders were analysed. These consisted primarily of calcium, with minor contributions of magnesium and silicon (see Table A2 for a more comprehensive list). Furthermore, CaO and Ca(OH)₂ contained about 9.4 ± 0.1 and 18.0 ± 0.2 mg g⁻¹ of particulate carbon, respectively, i.e. ∼ 0.9 % and ∼ 1.8 % by weight.

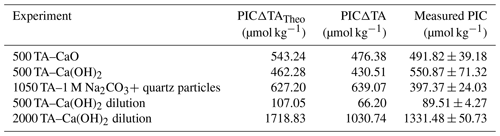
Table 2 Comparison between the estimated particulate inorganic carbon (PIC) based on half the TA change between the theoretical maximum TA increase upon full dissolution of the alkaline material added and the measured TA at the end of the experiment (Table 1), the estimated PIC based on half the TA changes between the measured maximum TA increase and the measured TA at the end of the experiment, and the measured PIC from the particulate carbon analysis.

3.2 CaO dissolution in filtered natural seawater

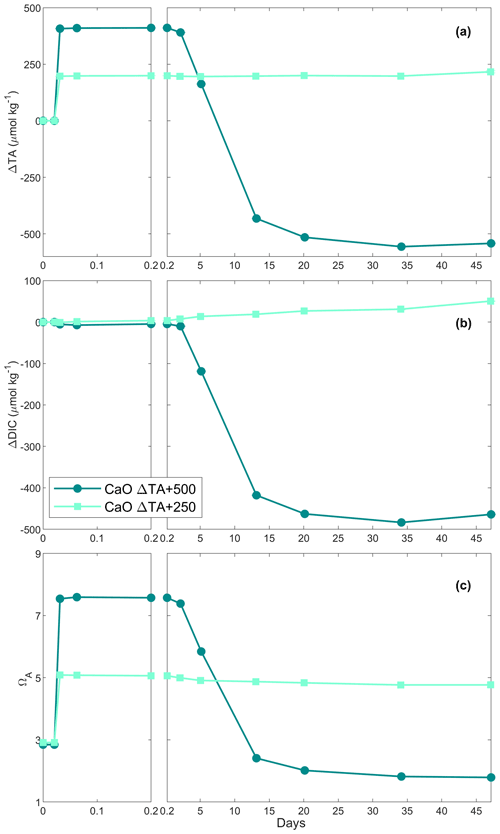
In the first CaO experiment with a targeted 250 µmol kg⁻¹ TA addition, TA increased by ∼ 200 µmol kg⁻¹ within the first 4 h (Fig. 1a). Following this increase, TA was stable over time. In contrast, DIC increased slowly, at about 1 µmol kg⁻¹ d⁻¹, reaching about +50 µmol kg⁻¹ on day 47 of the experiment (Fig. 1b). Ω_A reflected the trend observed for ΔTA, increasing from ∼ 2.9 to ∼ 5.1 within the first 4 h before slowly decreasing to 5.0 on day 47 (Fig. 1c).

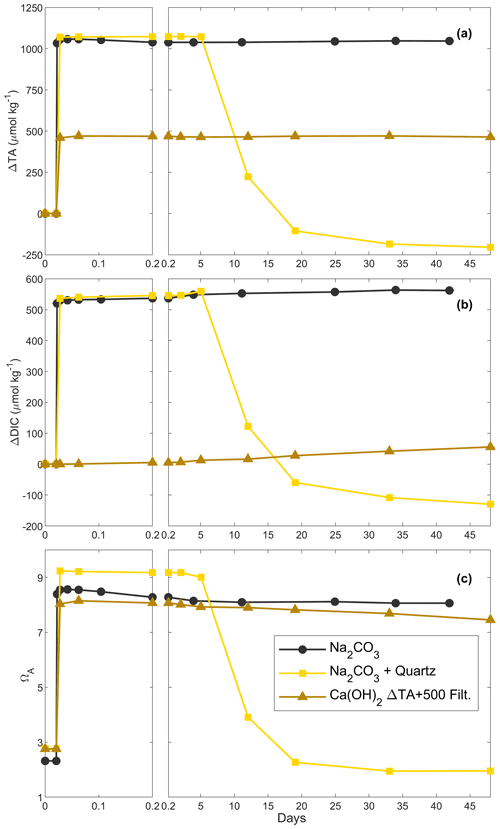
Figure 3 Changes in TA (a), DIC (b) and Ω_A (c) over time following additions of Na₂CO₃, Na₂CO₃ plus quartz particles and Ca(OH)₂ followed by a filtration step (see “Material and methods” for details).

In the second CaO experiment with a targeted 500 µmol kg⁻¹ TA addition, TA increased by ∼ 410 µmol kg⁻¹ within the first 4 h before slowly decreasing on day 3 (Fig. 1a). This was followed by a rapid decrease over the following week, eventually reaching a steady state on day 20 at a final ΔTA of about −540 µmol kg⁻¹. This corresponds to a total loss of TA of ∼ 950 µmol kg⁻¹, between the maximum measured TA and the final recorded TA. A small decrease in DIC of ∼ 10 µmol kg⁻¹ was observed over the first 2 d before a more significant reduction in the following week. Finally, ΔDIC levelled off at about −465 µmol kg⁻¹ (Fig. 1b). Ω_A rapidly increased during the first 4 h of the experiment from 2.8 up to 7.6 (Fig. 1c). Following this quick increase, Ω_A decreased by 0.3 units by day 3. Afterwards, Ω_A dropped quickly to 2.4 on day 13, and reached ∼ 1.8 on day 47, corresponding to a reduction of 1.0 compared to the starting seawater value.

3.3 Ca(OH)₂ dissolution in filtered natural seawater

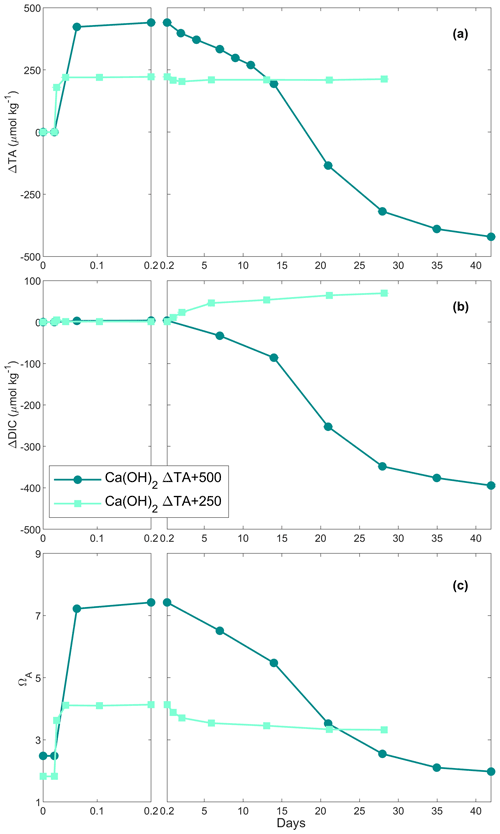
In the first Ca(OH)₂ experiment with a targeted TA addition of 250 µmol kg⁻¹, TA increased by ∼ 220 µmol kg⁻¹ after 4 h of reaction, before stabilising at a ΔTA of ∼ 210 µmol kg⁻¹ for the rest of the experiment (Fig. 2a). The DIC concentration increased quickly over the first 6 d after the TA addition before slowing down, reaching about +70 µmol kg⁻¹ by the end of the experiment (Fig. 2b). Finally, Ω_A reached ∼ 4.1 after 4 h, slightly decreasing over time, reaching 3.3 on day 28 (Fig. 2c).

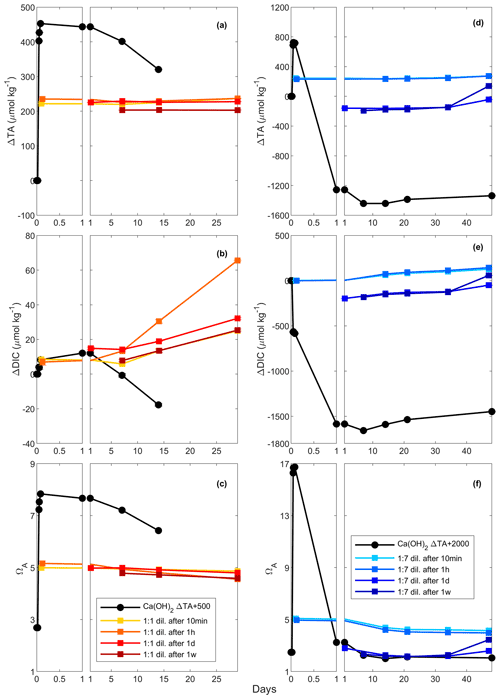
Figure 4 Changes in TA (a and d), DIC (b and e) and Ω_A (c and f) following a TA addition of 500 and 2000 µmol kg⁻¹, respectively, by Ca(OH)₂ (black line), as well as following a 1:1 dilution for the 500 µmol kg⁻¹ TA addition (red and yellow lines) and a 1:7 dilution for the 2000 µmol kg⁻¹ TA addition (blue lines). The dilutions were performed after 10 min, 1 h, 1 d and 1 week, and earlier dilutions are represented by lighter colours.

In the second Ca(OH)₂ experiment with a targeted TA addition of 500 µmol kg⁻¹, TA increased by ∼ 440 µmol kg⁻¹ within the first 4 h (Fig. 2a). This was followed by a steady decrease of ∼ 18 µmol kg⁻¹ d⁻¹ over the next 2 weeks, after which the decrease accelerated to ∼ 28 µmol kg⁻¹ d⁻¹ until day 35. Then, it levelled off at a ΔTA of about −420 µmol kg⁻¹ towards the end of the experiment. Overall, ∼ 860 µmol kg⁻¹ of TA was lost compared to the highest TA recorded. The overall DIC concentration decreased in a similar fashion to TA, reaching a ΔDIC of about −395 µmol kg⁻¹ compared to the initial DIC concentration (Fig. 2b). Ω_A increased from 2.5 to 7.4 in the first 4 h before decreasing, similarly to TA and DIC, reaching ∼ 2.0 on day 42 (Fig. 2c).

3.4 Na₂CO₃, particle addition and filtration

Three experiments assessed the influence of particles on CaCO₃ precipitation. In the first one, ∼ 1050 µmol kg⁻¹ of TA was added using a 1 M Na₂CO₃ solution, designed to obtain a similar maximum Ω_A to the previous experiments when TA decreased (Table 1). Upon addition, TA increased by ∼ 1060 µmol kg⁻¹ and DIC by ∼ 530 µmol kg⁻¹ within minutes. For the remainder of the experiment, ΔTA was fairly constant between 1060 and 1040 µmol kg⁻¹ (Fig. 3a). In contrast, DIC slightly increased over 42 d from a ΔDIC of ∼ 530 µmol kg⁻¹ on day 1 to ∼ 560 µmol kg⁻¹ on day 42 (Fig. 3b). Ω_A increased from ∼ 2.3 to ∼ 8.5 within minutes of the Na₂CO₃ addition and slightly decreased to ∼ 8.1 after 42 d of the experiment (Fig. 3c).

In the second experiment, the addition of 1 M Na₂CO₃ solution (Table 1) increased TA by 1070 µmol kg⁻¹, while DIC increased by ∼ 540 µmol kg⁻¹ within minutes and remained stable (Fig. 3a, b). After 2 d, quartz particles were added. Whereas ΔTA and ΔDIC remained invariant after 1 d, ΔTA decreased to ∼ 220 µmol kg⁻¹ and ΔDIC dropped to ∼ 120 µmol kg⁻¹ between day 5 and 12 (Fig. 3a, b). Over the next month, ΔTA and ΔDIC continued to decrease, although at a slowing rate, reaching about −200 and −110 µmol kg⁻¹, respectively, on day 42. Ω_A followed a similar trend, with an increase from ∼ 2.8 up to ∼ 9.2 within the first 1.5 h and a significant decline to ∼ 3.9 between day 5 and day 12, before stabilising at around ∼ 2.0 at the end of the experiment on day 48.

In the last experiment, Ca(OH)₂ was added, aiming for a TA increase of 500 µmol kg⁻¹ (Table 1), a level at which a significant TA decrease had been observed previously (Fig. 2a). In contrast to the previous experiment, after reaching ∼ 470 µmol kg⁻¹ at the 4 h mark, the content of the bottle was filtered and ΔTA remained relatively constant between 465 and 470 µmol kg⁻¹ over the following 48 d of the experiment (Fig. 3a). Meanwhile, ΔDIC increased from ∼ 5 to 55 µmol kg⁻¹ after filtration (Fig. 3b). Ω_A increased from ∼ 2.8 to ∼ 8.2 within the first 1.5 h after Ca(OH)₂ addition and then slightly decreased to ∼ 7.5 over the 48 d of the experiment (Fig. 3c).

3.5 Dilution experiments

3.5.1 The 500 µmol kg⁻¹ addition

In these experiments with a targeted TA increase of 500 µmol kg⁻¹ by Ca(OH)₂ addition, ΔTA increased to ∼ 450 µmol kg⁻¹ after 2 h (Fig. 4). These changes in TA were followed by a decline to ∼ 320 µmol kg⁻¹ after 14 d, although the latter was a slightly slower decrease than previously (Figs. 2, 4a). After a first increase in ΔDIC by ∼ 10 µmol kg⁻¹ on day 1, ΔDIC steadily decreased to about −20 µmol kg⁻¹ after 2 weeks (Fig. 4b). Finally, Ω_A increased from ∼ 2.7 to ∼ 7.8 after 2 h, before steadily decreasing to ∼ 6.4 on day 14 (Fig. 4c).

In the diluted treatments, ΔTA remained relatively stable over time, until the end of the experiments on day 29, regardless of dilution time (Fig. 4a). Upon dilution, ΔTA was reduced, values of which were similar for the 10 min, 1 h and 1 d dilutions. Overall, in the 1-week dilution, ΔTA was slightly lower, i.e. ∼ 205 µmol kg⁻¹ instead of ∼ 230 µmol kg⁻¹ on average. In all dilutions, ΔDIC increased over time, ranging between ∼ 20 and ∼ 60 µmol kg⁻¹, independently of dilution timing. Finally, Ω_A showed similar trends to ΔTA, reaching between ∼ 4.8 and ∼ 5.2 and slightly decreasing over time until the end of the experiment.

3.5.2 The 2000 µmol kg⁻¹ addition

This set of experiments aimed for a TA increase of 2000 µmol kg⁻¹ by Ca(OH)₂ addition. However, TA only increased to approximately one-third of the targeted value, i.e. ∼ 725 µmol kg⁻¹ within the first 2 h (Fig. 4d). Following this increase, TA rapidly decreased during the first day, reaching a ΔTA of about −1260 and then −1440 µmol kg⁻¹ in the following week (Fig. 4d). Over the second week of the experiment, TA appeared to stabilise before increasing until day 21. In contrast, ΔDIC decreased by ∼ 580 µmol kg⁻¹ within the first 2 h, before rapidly dropping to about −1590 µmol kg⁻¹ on day 1 and −1660 µmol kg⁻¹ after 7 d (Fig. 4e). Over the remaining 41 d, ΔDIC increased by ∼ 210 µmol kg⁻¹, remaining ∼ 1450 µmol kg⁻¹ below the starting DIC concentration. Ω_A increased to ∼ 16.7 after 2 h, followed by a rapid drop to ∼ 3.2 on day 1 and ∼ 2.0 on day 14 and slightly increasing over the following 34 d, varying between 2.0 and 2.1 (Fig. 4f).

With respect to ΔTA, ΔDIC and Ω_A, the 10 min and 1 h dilutions showed similar responses, as did the 1 d and 1-week dilutions. Upon dilution, ΔTA reached values of ∼ 240 µmol kg⁻¹ after the 10 min and 1 h dilutions and about −160 to −190 µmol kg⁻¹ after the 1 d and 1-week dilutions. With the exception of one data point in the 1-week dilution data, ΔTA remained relatively constant throughout all dilution experiments (Fig. 4d). DIC changes were similar to the TA changes, slowly increasing over time between 0.6 and 2.5 µmol kg⁻¹ d⁻¹, with very similar values reached for the 10 min and 1 h dilutions, as opposed to the 1 d and 1-week dilutions (Fig. 4e). Finally, Ω_A dropped from ∼ 5.0–5.1 to ∼ 4.0–4.1 over time in the 10 min and 1 h dilutions, while it decreased from ∼ 2.3–2.8 to ∼ 2.1–2.2 until day 21 in the 1 d and 1-week dilutions before increasing to ∼ 2.6–3.4 towards the end of the experiments (Fig. 4f).

3.6 Particulate inorganic carbon

With the exception of the ∼ 1050 µmol kg⁻¹ TA addition by Na₂CO₃ and quartz particles, measured PIC in experiments was always higher than estimates from measured ΔTA (Table 2). Furthermore, PIC estimated from the theoretical maximum TA increase upon full mineral dissolution, ΔTA_Theo, was always higher than estimated PIC from ΔTA, by about 7 % to 14 % in the ∼ 500 µmol kg⁻¹ TA additions with Ca(OH)₂ and CaO, respectively, and up to 67 % in the experiment with ∼ 2000 µmol kg⁻¹ TA additions.

4 Discussion

This study presents the first results investigating the dissolution of CaO and Ca(OH)₂ in natural seawater in the context of OAE. In experiments with at least 500 µmol kg⁻¹ TA increase, secondary precipitation was detected through observed TA and DIC decreases, as well as PIC increases. More specifically, at TA additions leading to an Ω_A higher than 7 (in the +500 and +1000 µmol kg⁻¹ TA treatments), “runaway CaCO₃ precipitation” was observed, meaning that not only was the added TA completely removed but significant portions of residual seawater TA were as well, until a new steady state was reached. This vastly reduces the desired CO₂ removal potential by OAE and should therefore be avoided. In a subsequent set of experiments, we simulated ocean mixing to estimate the timescales required to avoid and/or stop secondary CaCO₃ precipitation for applications that initially have TA additions above the critical threshold.

4.1 Identifying CaCO₃ precipitation, the problem of unmeasured precipitation, CO₂ gas exchange

CaCO₃ precipitation can occur via three pathways, i.e. heterogeneous, homogeneous and pseudo-homogeneous nucleation and precipitation (Chen et al., 2005; Marion et al., 2009; Wolf et al., 2008). Heterogeneous precipitation relies on the presence of existing solid mineral surfaces. This differs from homogeneous precipitation, characterised by the formation of CaCO₃ crystals from Ca²⁺ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ ions in the absence of any nucleation surfaces (Chen et al., 2005; Wolf et al., 2008). Finally, the last type of precipitation, termed pseudo-homogeneous, is similar to homogeneous nucleation, but it occurs on nuclei other than solid minerals such as colloids, organic particles or glassware in a laboratory setting (Marion et al., 2009). Concerning the Ω thresholds above which CaCO₃ precipitation is expected, the lowest threshold would be for heterogeneous and the highest for homogeneous, with pseudo-homogeneous nucleation in between. This is because nucleation sites effectively lower the activation energy required for CaCO₃ precipitation (Morse et al., 2007).

When 1 mol of CaCO₃ is precipitated, the TA of the solution decreases by 2 mol due to the removal of 1 mol of CO${}_{\mathrm{3}}^{\mathrm{2}-}$ ions, accounting for 2 mol of TA (Zeebe and Wolf-Gladrow, 2001). Simultaneously, the loss of 1 mol of CO${}_{\mathrm{3}}^{\mathrm{2}-}$ ions decreases the DIC concentration by 1 mol. Hence, any loss of TA and DIC following a 2:1 ratio can be linked to CaCO₃ precipitation (Zeebe and Wolf-Gladrow, 2001). Additionally, when CaCO₃ precipitation was suspected in our experiments, SEM and particulate inorganic carbon samples were taken to confirm the presence of CaCO₃ and to identify which polymorphs were predominant. In the +250 µmol kg⁻¹ TA additions by CaO and Ca(OH)₂, both appeared to fully dissolve without inducing CaCO₃ precipitation as TA and Ω_A quickly increased within minutes, similarly to what has been described in the literature (Chave and Suess, 1970; Rushdi et al., 1992), until reaching their respective maxima after about a day and remaining stable over weeks (Figs. 1a and c, 2a and c). A slight increase in DIC was observed over time as expected since atmospheric CO₂ was absorbed from the bottle headspace, created when 150 to 200 mL of solution was withdrawn at each sampling point. The measured TA increase was slightly below the theoretically expected increase, which is assumed to be due to a combination of impurities present (in the case of CaO, a significant fraction could be hydrated) and any loss of the finely ground material during the process of weighing and sieving. On average, ∼ 23 % of alkalinity added was not detected in the experiments with CaO and about 14 % for the experiments using Ca(OH)₂ (Table 1, Figs. 1 and 2).

In contrast, in the +500 µmol kg⁻¹ TA additions by CaO and Ca(OH)₂, TA started decreasing after about 1 d following the observed initial increase. If this TA loss was through CaCO₃ precipitation, DIC should be reduced by half this amount. The measured TA and DIC losses were very close to this 2:1 ratio for both the CaO and the Ca(OH)₂ experiments with a TA addition of 500 µmol kg⁻¹ (950:465 and 860:395 for CaO and Ca(OH)₂, respectively). This suggests that TA precipitated in the form of CaCO₃. The slight offset can be explained by ingassing of CO₂ from the headspace which lowers the TA : DIC ratio, becoming visible only when precipitation ceases towards the end (Fig. 1b). Another caveat is that the maximum increase in TA from full dissolution of CaO or Ca(OH)₂ cannot be measured in the presence of concurrent CaCO₃ precipitation. This is mostly evident in the +2000 µmol kg⁻¹ TA addition (Fig. 4), where DIC decreases due to CaCO₃ precipitation yet TA increases due to higher Ca(OH)₂ dissolution rates. This also explains why estimated PIC calculated from measured TA changes is generally smaller than measured PIC concentrations (Table 2). In the experiment with 1 M Na₂CO₃ and quartz particles, the measured TA-based PIC estimates were larger than the measured PIC. This difference is difficult to explain and could be possibly linked to the observed white layer on the bottle walls, indicative of CaCO₃ precipitation. In any case, while being a laboratory artefact, this has no practical consequences as in a natural setting the TA would eventually precipitate in the water column. In summary, trying to estimate CaCO₃ precipitation from measured changes in TA, without knowing how much TA was actually generated by full mineral dissolution or actual PIC measurements, might underestimate total precipitation.

4.2 The presence of mineral phases triggers runaway CaCO₃ precipitation

An important finding in our experiments was that whenever CaCO₃ precipitation was observed, it continued even if the solution dropped below an Ω_A of ∼ 4–5, levels at which no precipitation was observed in the +250 µmol kg⁻¹ TA addition experiments. Furthermore, in all these experiments, precipitation decreased and seemingly ceased at an Ω_A of ∼ 1.8–2.0. Therefore, it appears that when CaCO₃ is initially precipitated, CaCO₃ continues to precipitate in a runaway fashion, even if Ω_A drops below levels where precipitation would not be initiated in natural seawater. This is to be expected as CaCO₃ precipitates onto CaCO₃ mineral surfaces at any saturation state above 1, and the initial precipitation at high-saturation states provides new nucleation sites (Morse et al., 2003, 2007; Zhong and Mucci, 1989). The precipitation rate is directly proportional to Ω, decreasing exponentially until reaching zero at an Ω value of 1 (Fig. A4). However, the question of why precipitation occurred at a much lower Ω than anticipated, i.e. Ω∼ 7.5 vs. ∼ 12.3, remains (Marion et al., 2009).

It is known that the presence of particles in suspension can initiate and accelerate CaCO₃ precipitation (Millero et al., 2001; Morse et al., 2003; Wurgaft et al., 2021). It is unlikely that the presence of CaCO₃ impurities in CaO (less than 1 % carbon) and Ca(OH)₂ (less than 2 % carbon) from imperfect calcination would have caused precipitation as the presence of CaCO₃ mineral phases should have caused precipitation at any saturation state above 1, i.e. also in the +250 µmol kg⁻¹ TA addition experiments. Furthermore, modelling precipitation using experimentally determined Ω_A and surface-area-dependent aragonite precipitation rates onto CaCO₃ mineral phases (Zhong and Mucci, 1989) suggests that once precipitation becomes analytically detectable, it should proceed very rapidly before levelling off (Fig. A5). Furthermore, while we expected CaCO₃ precipitation to stop at Ω_A ∼ 1, we observed it to stop at Ω_A ∼ 2. The presence of dissolved organic carbon and soluble reactive phosphate could have slowed down if not stopped CaCO₃ precipitation at an Ω_A higher than 1 (Chave and Suess, 1970; Pan et al., 2021). We also observed that the bulk of precipitation occurred over a period of at least a week, after which an equilibration was reached with apparent differences between the different dissolving minerals (i.e. CaO, Ca(OH)₂ and quartz, although it is acknowledged that the experiments were not replicated).

Table 3 Simulations of the changes in TA, DIC, Ω_A, pCO₂ and pH_T (total scale) after TA increases of 250, 500 and 1000 µmol kg⁻¹, assuming complete mineral dissolution without precipitation, a complete dissolution followed by as much CaCO₃ precipitated as the amount of TA added and a complete dissolution followed by CaCO₃ precipitation until reaching an Ω_A of 2.0, before CO₂ re-equilibration to initial pCO₂. For each scenario, the number of moles of CO₂ absorbed per mole of TA added has been calculated for comparison. The 500 µmol kg⁻¹ TA addition simulation is shown in Fig. A3 in the Appendix.

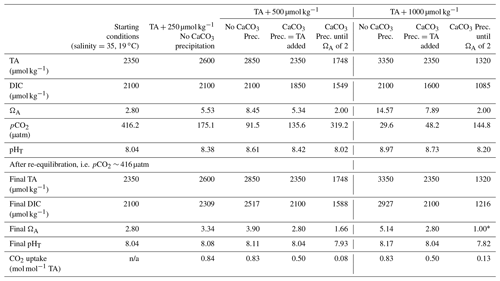
^* Note the value for Ω_A is rounded to 1.00 but calculated at 0.997. n/a: not applicable.

Another explanation for CaCO₃ precipitation is heterogeneous precipitation on not-yet-dissolved CaO and Ca(OH)₂ particles (or other impurities), leading to CaCO₃ crystal formation and initiating runaway precipitation. The Ω_A threshold for this process would depend on lattice compatibility of the mineral phases (Tang et al., 2020). For instance, CaCO₃ precipitation has been observed at any saturation state above 1 when introducing CaCO₃ seed particles. In contrast, Lioliou et al. (2007) did not report CaCO₃ precipitation onto quartz particles at an Ω_A lower than 3.5, and in order to trigger CaCO₃ precipitation onto quartz particles, Ω_A would need to be further increased. Here, we observed CaCO₃ precipitation on quartz particles at an Ω_A of ∼ 9.2 (Fig. 3). The reason for initially slower but then more rapid precipitation could be a combination of exponentially increasing CaCO₃ surface area while increasing lattice compatibility (Lioliou et al., 2007; Pan et al., 2021). The filtration of TA-enriched seawater supports this idea since not-yet-dissolved mineral phases that could facilitate early nucleation were removed, preventing runaway CaCO₃ precipitation (Fig. 3).

Needle-shaped aragonite precipitation onto quartz particles (Fig. 5c and d) was observed by SEM imaging. EDX analyses identified the larger mineral to be rich in silicon, a key characteristic of quartz, and the needle-shaped particles were composed of carbon, oxygen and calcium, indicative of CaCO₃ (Chang et al., 2017; Ni and Ratner, 2008; Pan et al., 2021). In contrast, direct aragonite precipitation onto not-yet-dissolved CaO and Ca(OH)₂ in the +500 µmol kg⁻¹ TA addition is difficult to prove as EDX analyses revealed the presence of Ca and O in both the mineral feedstocks and aragonite (Fig. 5a and b). Finally, in some situations (Fig. 5b), round crystals were also observed, suggesting the presence of vaterite (Chang et al., 2017). Nevertheless, aragonite crystals represented the majority of CaCO₃ observed by SEM.

Figure 5 SEM images from experiments with an increase in TA of ∼ 500 µmol kg⁻¹ by CaO (a) and Ca(OH)₂ (b) and with a TA increase of ∼ 1050 µmol kg⁻¹ by 1 M Na₂CO₃, followed by quartz particles addition (c and d).

4.3 Impacts of CaCO₃ precipitation on OAE potential

From an OAE perspective, CaCO₃ precipitation is an important chemical reaction that needs to be avoided. During CaCO₃ precipitation, dissolved [CO${}_{\mathrm{3}}^{\mathrm{2}-}$] and Ω decrease and [CO₂] increases, which reduces the ocean's uptake capacity for atmospheric CO₂, hence impacting the OAE potential. Considering typical open-ocean TA and DIC concentrations of 2350 and 2100 µmol kg⁻¹, respectively, at a salinity of 35 and a temperature of 19 ^∘C, this water mass would have a pCO₂ close to atmospheric equilibrium of 416 µatm, a pH_T value (total scale) of 8.04 and an Ω_A of 2.80. Without CaCO₃ precipitation, an addition of 500 µmol kg⁻¹ TA would lower pCO₂ to ∼ 92 µatm while increasing pH_T and Ω_A to about 8.61 and 8.45, respectively. If fully re-equilibrated with the atmosphere, DIC would increase by about 420 µmol kg⁻¹, leading to a pH_T and Ω_A 0.07 and 1.10 higher, respectively, than prior to the addition (Table 3). The resulting OAE efficiency would be 0.83 mol of atmospheric CO₂ absorbed per mole of TA added, very similar to estimates by Köhler et al. (2010). Considering that CaCO₃ is the source material for CaO and Ca(OH)₂ and that 2 mol of TA is produced per mole of CaO or Ca(OH)₂ mineral dissolution, ∼ 0.7 t of CO₂ could be captured per tonne of source material, assuming CO₂ capture during the calcination process. At a global scale, using all available ship capacity and assuming a slow discharge of 1.7 to 4.0 Gt of Ca(OH)₂ per year (Caserini et al., 2021), between 1.2 and 2.8 Gt of CO₂ per year could be absorbed by the ocean. Including direct coastal TA discharge at a constant addition of Ca(OH)₂ of 10 Gt yr⁻¹ (Feng et al., 2016), we could expect to absorb an additional 7 Gt of CO₂ per year. To put these model-derived numbers into perspective, the global cement industry currently produces about 4.1 Gt of cement per year (Statista, 2021). Depending on whether hydraulic (4CaO ⋅ Al₂O₃⋅ Fe₂O₃) or non-hydraulic (Ca(OH)₂) cement is being produced and assuming a molar Ca²⁺-to-CO₂ sequestration potential of 1.6, up to 3.9 Gt of atmospheric CO₂ could be captured per year. This is within the range required over the next 30 years to keep global warming below the 2 ^∘C target, as in the Representative Concentration Pathway (RCP) 2.6 scenario (Huppmann et al., 2018).

The above numbers can only be achieved if CaO or Ca(OH)₂ dissolution is complete without CaCO₃ precipitation. Hypothetically, when as much CaCO₃ precipitates as TA is added, i.e. 100 µmol kg⁻¹ of CaCO₃ precipitates after a TA increase of 100 µmol kg⁻¹, only 1 instead of 1.6 mol of DIC can be absorbed per 2 mol of TA, after equilibration with atmospheric pCO₂ (Table 3). This represents a decrease by nearly 40 % in OAE potential. Similarly, runaway CaCO₃ precipitation until an Ω_A of 2.0, as observed here, decreases the OAE potential further by almost 90 %. Consequently, only ∼ 0.1 mol of DIC would be absorbed per mole of TA added (Table 3). Furthermore, secondary CaCO₃ precipitation higher than TA addition will lead to pH_T and Ω levels lower than the initial ones. For instance, runaway precipitation for a TA addition of 500 µmol kg⁻¹ will see pH_T drop by about 0.1 from 8.04 to 7.93 and Ω_A from 2.80 to 1.66, significantly enhancing ongoing ocean acidification (Table 3). Runaway CaCO₃ precipitation for a TA addition of 1000 µmol kg⁻¹ (assumed to cease at an Ω_A of 2 as observed here) would see a further drop in Ω_A, i.e. to below 1, upon CO₂ re-equilibration with the atmosphere (Table 3). Under such conditions, aragonite would start to dissolve, impacting various marine organisms, especially carbonate-secreting organisms, e.g. sessile corals, benthic molluscs and planktonic pteropods (Riebesell et al., 2011; Zeebe and Wolf-Gladrow, 2001). In summary, runaway CaCO₃ precipitation in OAE must be avoided as it will not only reduce CO₂ uptake efficiency significantly but also enhance ocean acidification. Keeping track of OAE efficiency from changes in TA concentrations can be challenging as CaCO₃ precipitation can be underestimated as described earlier, requiring new and clever monitoring strategies.

4.4 Avoiding CaCO₃ precipitation by dilution and other TA addition strategies

An important aspect when it comes to avoiding CaCO₃ precipitation is the dilution that would occur in the wake of ships releasing TA in the ocean or by natural mixing of TA-enriched water with surrounding seawater (Caserini et al., 2021; Feng et al., 2017; Mongin et al., 2021). In our experiments, a 1:1 dilution appeared to seemingly inhibit CaCO₃ precipitation in seawater, even if performed only after 1 week for the +500 µmol kg⁻¹ TA addition. At a first glance, this comes as a surprise since precipitation nuclei would only be diluted by half, reducing surface area and precipitation rates by a factor of 2. However, as Ω_A is simultaneously reduced, precipitation rates are further reduced by a factor of 10 (see Fig. A4). Hence, the overall precipitation rate would see a reduction by a factor of 20. This should slow down precipitation initiated upon the alkalinity addition if on CaCO₃ particles but not completely inhibit it (Zhong and Mucci, 1989). A possible explanation could be that dilution lowers Ω_A below the critical threshold, overcoming the lattice mismatch, as most of the aragonite precipitation appears to be on the original seed mineral itself rather than on the newly formed aragonite (compare Fig. 5c and d).

Overall, CaCO₃ precipitation can be avoided if the TA + 500 µmol kg⁻¹ enriched seawater is diluted 1:1, reaching an Ω_A of ∼ 5.0. The more quickly dilution takes place, the less CaCO₃ would precipitate prior to dilution. Similar results were found for a TA addition of +2000 µmol kg⁻¹, i.e. the ability to stop precipitation at an Ω_A of ∼ 5.0, after a 1:7 dilution. However, only the 10 min and 1 h dilutions seem to be suitable in an OAE context as rapid aragonite precipitation at a higher initial Ω_A of about 16.7 would significantly reduce the CO₂ uptake efficiency. Furthermore, the difficulty in monitoring precipitation from simple TA measurements (as described above) would also mean that quantification of CO₂ removal is not straightforward. Therefore, in order to assign carbon credits, TA additions have to be done in a way that rule out or at least minimise secondary CaCO₃ precipitation. This is true for any type of TA addition and is not specific to additions of quick and hydrated lime.

Adding TA from land, as modelled by Feng et al. (2017), shows that as more TA is added, higher coastal Ω_A would be reached. By staying well below the Ω_A threshold identified here, i.e. limiting coastal Ω_A to only 3.2, up to ∼ 550 Gt of carbon in the form of CO₂ could be removed from the atmosphere between 2020 and 2100, corresponding to a reduction by about 260 ppm (Feng et al., 2017). The critical Ω_A threshold beyond which secondary CaCO₃ precipitation occurs could be higher for other alkaline minerals of interest for OAE, theoretically allowing for higher TA additions. However, it has to be kept in mind that in waters with high sediment load, often found in coastal settings, CaCO₃ could precipitate onto mineral particles other than those added to increase TA. This has been observed in river plumes (Wurgaft et al., 2021), on resuspended sediments of the Bahama Banks (Bustos-Serrano et al., 2009), and in the Red Sea following flash flood deposition of resuspended sediments and particles (Wurgaft et al., 2016). Even with minerals allowing for higher TA additions, an Ω_A threshold of 5 might be safer to adopt. Atmospheric CO₂ removal could be increased if TA were also added to the open ocean, e.g. on ships of opportunity. Here, additions could be much higher as ship movement and rapid mixing within a ship's wake would significantly dilute added TA as opposed to coastal point sources (Caserini et al., 2021; Köhler et al., 2013).

Finally, another option to increase atmospheric CO₂ uptake would be to keep the seawater equilibrated with air or CO₂-enriched flue gases, during mineral dissolution. Firstly, an Ω_A of 3.3 would be reached as opposed to 5 in the +250 µmol kg⁻¹ TA scenario (Table 3), when equilibration occurs during instead of after the dissolution process. Secondly, when reaching an Ω_A of 5 with CO₂ equilibration, nearly 1000 instead of 250 µmol kg⁻¹ of TA could be added, allowing for almost 4 times the amount of atmospheric CO₂ to be removed (this number is highly sensitive to temperature and ranges between ∼ 3 and ∼ 6 between 30 and 5 ^∘C). Unfortunately, this requires an extra step, which appears to be far more time-consuming and costly than a simple mineral addition. It should also be kept in mind that for the same Ω_A threshold, the amount of TA that can be added will increase at lower temperatures because of higher CO₂ solubility and, hence, naturally lower Ω_A in colder waters. Based on our Ω_A threshold of 5, at a salinity of 35 and at 5 ^∘C, about 3 times as much TA can be dissolved than at 30 ^∘C.

5 Conclusions

OAE is a negative-emission technology with large potential for atmospheric CO₂ removal (Caserini et al., 2021; Feng et al., 2016; Köhler et al., 2010). In order to maximise CO₂ uptake efficiency, secondary CaCO₃ precipitation has to be avoided. Here we show that an increase in TA by 500 µmol kg⁻¹ led to aragonite precipitation, reducing the CO₂ uptake potential from about 0.8 mol mol⁻¹ of TA added to nearly 0.1 mol. Precipitation most likely occurred on the CaO and Ca(OH)₂ mineral surfaces prior to their full dissolution. In contrast, an addition of 250 µmol kg⁻¹ of TA did not result in CaCO₃ precipitation, suggesting that an Ω_A of about 5 is a safe limit. This is probably the case for other minerals with even lower lattice compatibility for CaCO₃ since CaCO₃ could precipitate onto naturally present mineral phases in coastal settings, such as resuspended sediments. Safely increasing the amount of TA that could be added to the ocean could be achieved by (1) allowing for major mixing and dilution of enriched seawater by coastal tides or in the wake of ships, (2) equilibrating the seawater to atmospheric CO₂ levels prior to the addition during mineral dissolution, and/or (3) targeting low- rather than high-temperature regions.

Appendix A

Table A1 Seawater salinity in each experiment and phosphate concentrations in one of the batches.

n/a: not applicable.

Table A2 Main chemical composition of the CaO and Ca(OH)₂ feedstocks used for the TA increase experiments determined by ICP-MS analysis (expressed in mg g⁻¹, with the corresponding standard deviation, SD).

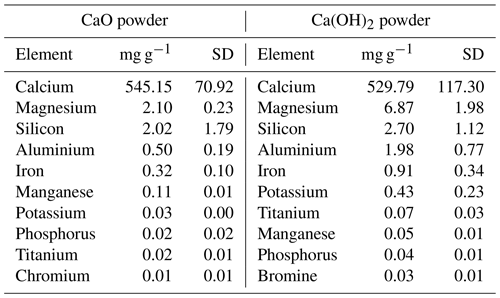
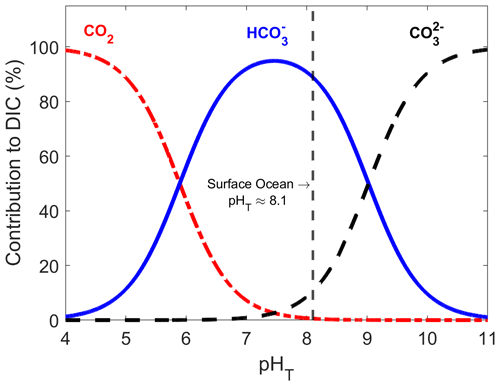
Figure A1 Relative contribution of dissolved CO₂, HCO${}_{\mathrm{3}}^{-}$ and CO${}_{\mathrm{3}}^{\mathrm{2}-}$ to total dissolved inorganic carbon in seawater as a function of pH_T (total scale), also known as a Bjerrum plot (based on the carbonic acid equilibrium constant from Mehrbach et al., 1973, and refitted by Dickson and Millero, 1987), at 25 ^∘C and a salinity of 35, with the current surface ocean pH average represented by the dashed vertical line (pH_T ∼ 8.1).

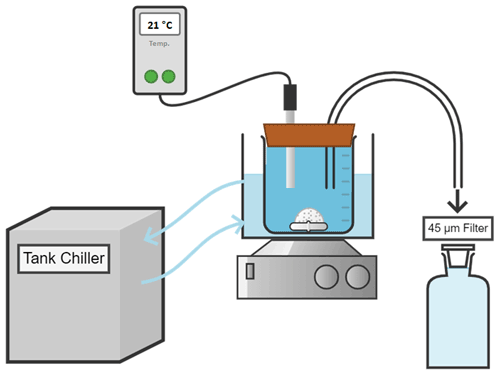
Figure A2 Conceptual diagram of the experimental setup used for the dissolution of alkaline minerals.

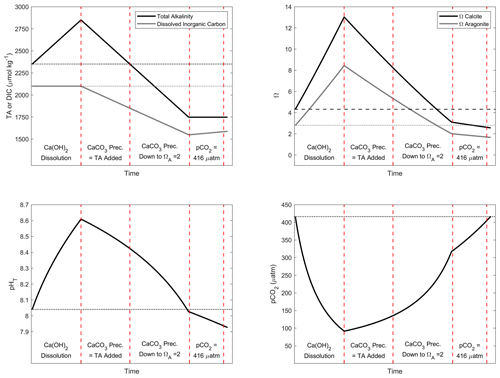
Figure A3 Simulation of the changes in TA, DIC, Ω_C, Ω_A, pCO₂ and pH_T after addition of 500 µmol kg⁻¹ of alkalinity. Four important steps are presented: first, assuming the complete Ca(OH)₂ dissolution without CaCO₃ precipitation; second, assuming as much CaCO₃ precipitation as the amount of TA added; third, assuming CaCO₃ precipitation happening until reaching an Ω_A of 2; and fourth, CO₂ uptake until equilibrium is reached between atmosphere and seawater at a pCO₂ of ∼ 416 µ atm.

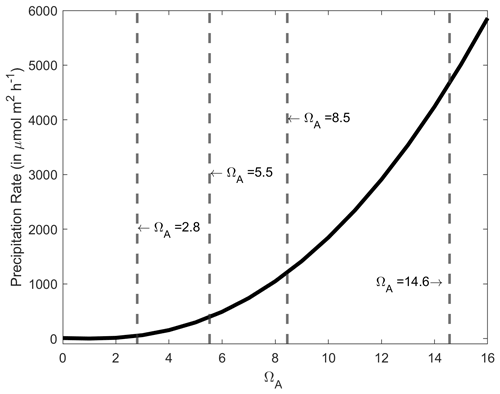
Figure A4 CaCO₃ precipitation rate onto aragonite seed crystals in µmol m⁻² h⁻¹ as a function of Ω_A, based on the measurements of Zhong and Mucci (1989) at 25 ^∘C and for a salinity of 35. The Ω_A values for the starting conditions and following a +250, +500 and +1000 µmol kg⁻¹ TA increase are presented by the dashed grey lines, i.e. 2.8, 5.5, 8.5 and 14.6, respectively.

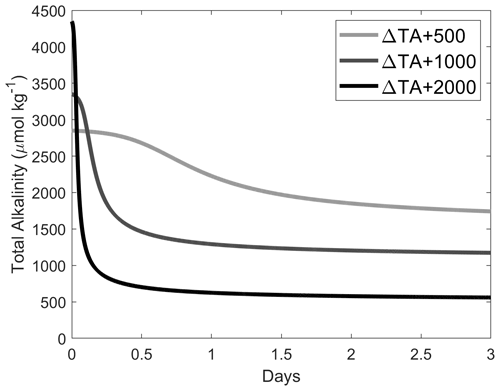
Figure A5 Simulations of TA loss due to aragonite precipitation after a TA addition of 500, 1000 and 2000 µmol kg⁻¹, based on Ω_A and surface-area-dependent precipitation rates shown in Fig. A4, assuming the initial presence of 2 % of CaCO₃ in our samples, i.e. ∼ 0.37, ∼ 0.74 and ∼ 1.48 mg kg⁻¹ for ΔTA + 500, ΔTA + 1000 and ΔTA + 2000 µmol kg⁻¹, respectively. CaCO₃ mass was converted to a surface area as described in Zhong and Mucci (1989). The starting conditions were TA = 2300 µmol kg⁻¹, DIC = 2100 µmol kg⁻¹, salinity = 35 and temperature = 21 ^∘C.