Intercomparison of methods to estimate gross primary production based on CO₂ and COS flux measurements

Separating the components of ecosystem-scale carbon exchange is crucial in order to develop better models and future predictions of the terrestrial carbon cycle. However, there are several uncertainties and unknowns related to current photosynthesis estimates. In this study, we evaluate four different methods for estimating photosynthesis at a boreal forest at the ecosystem scale, of which two are based on carbon dioxide (CO₂) flux measurements and two on carbonyl sulfide (COS) flux measurements. The CO₂-based methods use traditional flux partitioning and artificial neural networks to separate the net CO₂ flux into respiration and photosynthesis. The COS-based methods make use of a unique 5-year COS flux data set and involve two different approaches to determine the leaf-scale relative uptake ratio of COS and CO₂ (LRU), of which one (LRU_CAP) was developed in this study. LRU_CAP was based on a previously tested stomatal optimization theory (CAP), while LRU_PAR was based on an empirical relation to measured radiation.

For the measurement period 2013–2017, the artificial neural network method gave a GPP estimate very close to that of traditional flux partitioning at all timescales. On average, the COS-based methods gave higher GPP estimates than the CO₂-based estimates on daily (23 % and 7 % higher, using LRU_PAR and LRU_CAP, respectively) and monthly scales (20 % and 3 % higher), as well as a higher cumulative sum over 3 months in all years (on average 25 % and 3 % higher). LRU_CAP was higher than LRU estimated from chamber measurements at high radiation, leading to underestimation of midday GPP relative to other GPP methods. In general, however, use of LRU_CAP gave closer agreement with CO₂-based estimates of GPP than use of LRU_PAR. When extended to other sites, LRU_CAP may be more robust than LRU_PAR because it is based on a physiological model whose parameters can be estimated from simple measurements or obtained from the literature. In contrast, the empirical radiation relation in LRU_PAR may be more site-specific. However, this requires further testing at other measurement sites.

1 Introduction

Photosynthetic carbon uptake (or gross primary production, GPP) is a key component of the global carbon cycle, with the terrestrial ecosystems removing approximately 30 % of annual anthropogenic carbon dioxide (CO₂) emissions from the atmosphere (Luo et al., 2015; Friedlingstein et al., 2020). With the current climatic warming it has been suggested that both photosynthesis and respiration are increasing due to the CO₂ fertilization effect and rising temperatures providing more favourable conditions not only for photosynthesis but also for respiration (Dusenge et al., 2019). However, it is not known at which rate these two processes are changing and thus the extent to which they offset each other. In addition, their relative importance varies seasonally, with photosynthesis predicted to increase more than respiration in spring, leading to greater carbon uptake, while respiration is predicted to increase more than photosynthesis in autumn, leading to net carbon emission in northern terrestrial ecosystems (Piao et al., 2008). Methods to measure and study photosynthesis and respiration individually are thus crucial for future carbon cycle predictions.

Eddy covariance (EC) is widely used to measure the biosphere–atmosphere exchange of CO₂ at the ecosystem scale. However, EC only measures net ecosystem CO₂ flux (NEE), which includes contributions from both CO₂ uptake by photosynthesis (GPP) and ecosystem respiration (R). Traditionally, NEE partitioning into GPP and respiration uses the method of Reichstein et al. (2005), in which temperature response curves are fitted to nighttime CO₂ flux data (respiration). However, this method relies on nighttime EC flux measurements, which are uncertain and often filtered out due to low-turbulence conditions and possible advective gas transport (Aubinet, 2008). To address this problem, partitioning methods have been developed based on a combination of nighttime temperature responses of respiration (as in nighttime method) and daytime radiation responses of GPP (daytime method) (Lasslop et al., 2010; Kulmala et al., 2019). However, both the nighttime method and the daytime method assume that respiratory processes operate in the same way during the day and night and have uncertainties due to assumptions of functional relationships (Tramontana et al., 2020). These assumptions lead to uncertainties in partitioning because different biomass compartments (soil organic matter, roots, stems, branches, foliage) could have different drivers and respiration responses even within the same ecosystem (Kolari et al., 2009; Keenan et al., 2019). Leaf respiration during the day may be inhibited by radiation, the so-called Kok effect (Kok, 1949; Wohlfahrt et al., 2005; Heskel et al., 2013; Yin et al., 2020), and Keenan et al. (2019) and Wehr et al. (2016) suggest that, as a result, global GPP based on the nighttime method has been overestimated. On the other hand, photorespiration, which is an oxidation process competing with carboxylation under radiation, might offset inhibition by the Kok effect (Heskel et al., 2013).

One way to address these uncertainties in flux partitioning is to use machine learning methods, such as artificial neural networks, to separate NEE into respiration and GPP (Tramontana et al., 2020). The advantage of this method is that it makes no a priori assumptions about responses to environmental drivers but determines these based only on data. In a pioneering study, Desai et al. (2008) attempted to use an artificial neural network to emulate the nighttime partitioning method but obtained no significant improvements. More recently, Tramontana et al. (2020) proposed a new approach (NN_C-part) involving novel methods for implementing the network's structure and of inferring GPP and R signals from NEE. Both nighttime and daytime NEE are used for network training, so the dynamics of biophysical processes are accounted for in a comprehensive way.

Yet another approach to addressing uncertainties in GPP estimates is to use proxies for photosynthetic CO₂ uptake. One such proxy is carbonyl sulfide (COS), which is a sulfur compound with a tropospheric mixing ratio of approximately 500 ppt (parts per trillion) (Montzka et al., 2007). While the use of different CO₂-based partitioning methods is primarily aimed at more accurate GPP estimation, in contrast the use of COS as a proxy for GPP is aimed at a better process understanding of GPP. COS is mainly produced by oceans and anthropogenic sources (Kettle et al., 2002; Berry et al., 2013; Launois et al., 2015; Whelan et al., 2018), while vegetation is the largest sink (Sandoval-Soto et al., 2005; Blonquist et al., 2011). COS has been proposed as a proxy for GPP because it is taken up by plants through the same diffusive pathway as CO₂ and transported to the chloroplast surface. There it is destroyed by a hydrolysis reaction catalysed by the enzyme carbonic anhydrase (CA, also located within the cytoplasm; Polishchuk, 2021), while CO₂ continues its journey inside the chloroplast, where it is assimilated in the Calvin cycle (Wohlfahrt et al., 2012). It is assumed that COS is completely removed by hydrolysis so that there is no back-flux from the leaf to the atmosphere (Protoschill-Krebs et al., 1996). Estimates of GPP from COS flux measurements use the leaf relative uptake ratio (LRU), that is, the ratio of COS and CO₂ deposition rates at the leaf scale. While LRU has been treated either as a global or plant-specific constant (Asaf et al., 2013; Stimler et al., 2012), recent studies have shown that LRU is a function of solar radiation because CO₂ uptake is highly radiation dependent, while COS uptake is not (Stimler et al., 2010; Yang et al., 2018; Kooijmans et al., 2019; Spielmann et al., 2019) and may also vary with vapour pressure deficit (Sun et al., 2018b; Kooijmans et al., 2019). In addition to uncertainties related to variation in LRU, COS-based GPP estimates are uncertain because ecosystem-scale COS flux measurements typically have a low signal-to-noise ratio and high random uncertainty at a 30 min timescale, although this is reduced when fluxes are averaged over longer time periods (Kohonen et al., 2020).

In this study, we compare the annual, seasonal, daily, and sub-daily variation of (i) a traditional GPP estimate (GPP_NLR, NLR referring to non-linear regression) based on a combination of daytime and nighttime methods, (ii) a neural network GPP estimate based on NEE and NN_C-part (GPP_ANN), (iii) a GPP estimate based on COS flux measurements using the radiation-dependent LRU function from Kooijmans et al. (2019) (GPP_COS,PAR), and (iv) a GPP estimate based on COS flux measurements using a previously published stomatal optimization model (CAP) to calculate LRU (GPP_COS,CAP) in a boreal evergreen needle–leaf forest during the years 2013–2017. Our aim is to study potential inconsistencies in diel or seasonal patterns of GPP that may arise from extrapolating nighttime temperature responses to daytime ones, as well as to discuss the limitations and uncertainties of all four methods. We also make recommendations for improving COS-based GPP estimates.

2 Materials and methods

2.1 Site description

Measurements were conducted at the Hyytiälä forest Station for Measuring Ecosystem Atmosphere Relations (SMEAR) II measurement site ($\mathrm{61}{}^{\circ }{\mathrm{51}}^{\prime }$ N, $\mathrm{24}{}^{\circ }{\mathrm{17}}^{\prime }$ E), where the forest stand is already more than 50 years old (Hari and Kulmala, 2005). The stand is dominated by Scots Pine (Pinus Sylvestris L.) with some Norway spruce (Picea abies L. Karst.) and deciduous trees (e.g. Betula sp., Populus tremula, Sorbus aucuparia). The daytime flux footprint covers a ca. 50 ha area of the forest. The canopy height increased from approximately 18 to 20 m during the measurement period (2013–2017), and the all-sided leaf area index (LAI) was ca. 8 m² m⁻².

2.2 Measurements

Eddy covariance fluxes and environmental measurements

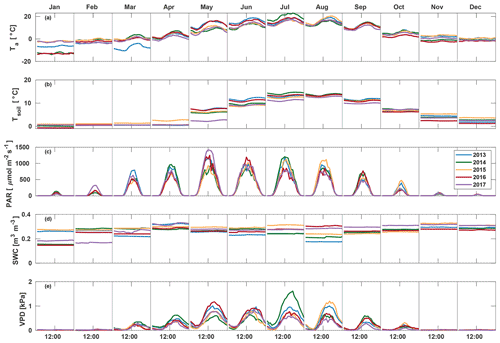
EC measurements were made on a 23 m high tower. The set-up consisted of a Gill HS (Gill Instruments Ltd., England, UK) sonic anemometer measuring horizontal and vertical wind velocities and sonic temperature, as well as a quantum cascade laser (QCL; Aerodyne Research Inc., Billerica, MA, USA) for measuring COS, CO₂ and H₂O mixing ratios at 10 Hz frequency. The set-up is described in more detail in Kohonen et al. (2020), and flux data are presented in Vesala et al. (2022). Flux processing was done using EddyUH software (Mammarella et al., 2016) following the methods presented by Kohonen et al. (2020). Fluxes were corrected for storage change and filtered according to friction velocity. Storage change fluxes of COS were calculated from the COS profile measurements in 2015–2017 and from concentration measurements at one height in other years, as described in Kohonen et al. (2020); CO₂ storage change fluxes were calculated from CO₂ concentration profile measurements. The friction velocity threshold was determined from CO₂ fluxes (Papale et al., 2006), and a threshold of 0.3 m s⁻¹ was applied to the entire data set to exclude periods of low turbulence. COS flux processing was done similarly to CO₂ processing, but time lag and spectral corrections were determined from CO₂ measurements and applied to COS as recommended by Kohonen et al. (2020). Gap-filling of the COS flux was done using empirical formulas based on photosynthetically active radiation (PAR) and vapour pressure deficit (VPD), as described by Kohonen et al. (2020). CO₂ fluxes were gap-filled and partitioned using a procedure to be explained in more detail in Sect. 2.3.1.

Environmental measurements used in the study include air temperature (T_a) at 16.8 m (measured with a Pt100 temperature sensor inside a ventilated custom shield), PAR above the canopy (Li-190SZ quantum sensor, LI-COR, Lincoln, NE, USA), relative humidity (RH) at 16.8 m height (Rotronic MP102H, Rotronic Instrument Corp., NY, USA), soil temperature (T_soil) at 2–5 cm depth (KTY81-110 temperature sensor, Philips, the Netherlands) as a mean of five locations, and soil water content (SWC) in the humus layer (Delta-T ML2 soil moisture sensor, Delta-T Devices, Cambridge, UK).

2.3 GPP calculations

This section describes each of the four methods for estimating GPP. Daily average GPP was only calculated if more than 50 % of the measured 30 min flux data were available for each day, and monthly averages were calculated from the daily means. In Vesala et al. (2022), COS fluxes were found to have 52 % data availability on average. While setting a 50 % threshold is somewhat subjective, it ensures that the analysed daily estimates of GPPs reflect measured fluxes rather than the gap-filling procedure. Gap-filled flux data were used in estimating diurnal variation and cumulative GPP. All comparisons between the methods used measured (non-gap-filled) data only, when both CO₂ and COS flux data were available.

2.3.1 GPP from traditional CO₂ flux partitioning

NEE was partitioned into respiration (R) and GPP_NLR as

$$\begin{array}{}\text{(1)}& \text{NEE}=R-{\text{GPP}}_{\text{NLR}},\end{array}$$

where R was estimated as in the nighttime method,

$$\begin{array}{}\text{(2)}& R=R_{\mathrm{C}}{Q}_{\mathrm{10}}^{T_{\text{sa}}/\mathrm{10}},\end{array}$$

where R_C is the respiration at a reference temperature (T=0 ^∘C), Q₁₀ is the temperature sensitivity of R, and T_sa is the arithmetic mean between the air temperature at 16.8 m height and soil temperature at 5 cm depth. Previous studies have shown T_sa to be a good choice of respiration driver at Hyytiälä forest (Kolari et al., 2009; Lasslop et al., 2012).

When NEE measurements were not available, the GPP model followed the formula

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& {\text{GPP}}_{\text{NLR}}=\\ & \left(\mathit{\alpha }\text{PAR}+P_{\text{max}}-\sqrt{(\mathit{\alpha }\text{PAR}+P_{\text{max}}{)}^{\mathrm{2}}-\mathrm{4}\mathrm{\Theta }\text{PAR}{P}_{\text{max}}}\right){\displaystyle \frac{f\left(T_{\text{a}}\right)}{\mathrm{2}\mathrm{\Theta }}}\end{array},\end{array}$$

where α, P_max, and Θ are fitting parameters, and f(T_a) is an instantaneous temperature response that brings GPP gradually towards zero at freezing temperatures, given by

$$\begin{array}{}\text{(4)}& f\left(T_{\mathrm{a}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+e^{\left(\mathrm{2}\right(T_{\mathrm{0}}-T_{\mathrm{a}}\left)\right)}}},\end{array}$$

where $T_{\mathrm{0}}=-\mathrm{2}$ ^∘C is the inflection point (Kolari et al., 2014).

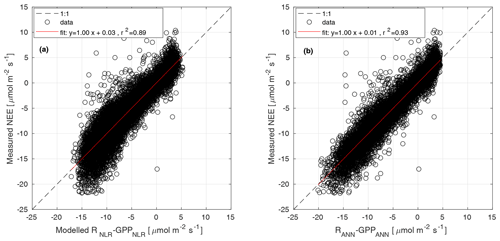
Parameters α, P_max, and R_C were estimated for 15 d periods, while Q₁₀ was estimated from the weighted mean of monthly Q₁₀ values from June to August over several years. Weights were the inverse of the confidence interval of each Q₁₀ estimate. Θ was determined as the value that gave the best model fit when the partitioning was run during summer months (June–August) over several years (Kulmala et al., 2019). The parameters of Eq. (3) were estimated from GPP partitioned with the nighttime method in Eq. (1). The modelled NEE from Eqs. (3) and (2) was compared with the measured NEE in Fig. B1a.

2.3.2 GPP from artificial neural networks

GPP_ANN from the data-driven model was estimated by applying the NN_C-part algorithm (Tramontana et al., 2020). NN_C-part is a customized neural network that emulates the bio-physical processes driving both GPP and R at ecosystem scale and has been applied to several vegetation types distributed globally. The network consists of two subnetworks, which simulate GPP and R. The two subnetworks are connected in the last node of the overall structure, in which the GPP and R signals are combined to calculate NEE. The GPP subnetwork consists of three layers and estimates the ecosystem-level gross photosynthesis using a light-use efficiency (LUE) approach; in particular, instantaneous LUE is estimated by the first two layers, while GPP is calculated as the product between LUE and incoming shortwave radiation in the third layer. NN_C-part has a hybrid nature, and gross photosynthesis is partially constrained by emulating the LUE concept.

Each subnetwork relies on specific predictors. Distinguishing features of this model are that (a) GPP and R derived by other models are not used, (b) functional relationships are derived directly from the data, and (c) the network's weights are tuned by training the machine learning only on NEE measurements. In this experiment we used the same predictors (VPD, incoming shortwave radiation, potential incoming radiation, T_a, T_soil, SWC, wind speed, and wind direction) and network structure as applied by Tramontana et al. (2020). However, to ensure the viability of this method, which is limited by the availability of both predictors and NEE measurements, we set lower requirements for the minimum percentage of measured data for both predictors and half hourly NEE. Moreover, data from all available years were pooled for use in a unique multi-year training process. In particular, we applied the following setting: for each year, less than 55 % of predictors were gap-filled, and at least 365 half-hourly NEEs should be measured for both nighttime and daytime. Despite the high percentage of missing data in observations, gaps had generally short duration with limited effects on the uncertainty of predicted outputs. The final GPP_ANN products were derived by applying trained networks on meteorological inputs and thus do not include NEE data after network training. The modelled NEE from NN_C-part was compared with the measured NEE in Fig. B1b.

2.3.3 GPP from COS flux measurements and an empirical LRU radiation relation

Based on previous soil chamber measurements at Hyytiälä forest it is known that the soil COS flux was −2.7 $\mathrm{pmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ on average with a variation of only 1 $\mathrm{pmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ during the growing season and a negligible diurnal variation (Kooijmans et al., 2017; Sun et al., 2018a). The average soil flux was thus first subtracted from the quality-filtered and gap-filled COS EC fluxes in order to derive the vegetation contribution to the ecosystem COS exchange. GPP was then calculated from the canopy COS fluxes (FCOS) using the formula (Sandoval-Soto et al., 2005; Blonquist et al., 2011)

$$\begin{array}{}\text{(5)}& {\text{GPP}}_{\text{COS}}={\displaystyle \frac{-\text{FCOS}}{\text{LRU}}}{\displaystyle \frac{[{\text{CO}}_{\mathrm{2}}{]}_{\mathrm{a}}}{[\text{COS}{]}_{\mathrm{a}}}},\end{array}$$

where [CO₂]_a and [COS]_a denote the atmospheric concentrations of CO₂ and COS (in mol m⁻³), respectively, at the EC measurement height, measured by the QCL.

LRU was calculated as a function of PAR (LRU_PAR) as described by the empirical equation of Kooijmans et al. (2019):

$$\begin{array}{}\text{(6)}& {\text{LRU}}_{\text{PAR}}={\displaystyle \frac{\mathrm{607.26}}{\text{PAR}}}+\mathrm{0.57}.\end{array}$$

This LRU equation was derived from field chamber measurements (LRU_ch) of pine branch CO₂ and COS fluxes with two chambers placed at the top of the canopy in 2017 at the same site and thus being independent from the EC flux measurements (Kooijmans et al., 2019).

2.3.4 GPP from COS flux measurements and LRU from stomatal optimization model

Finally, we estimated GPP from Eq. (5) using a new theoretical expression for LRU (LRU_CAP) derived from the stomatal optimization model CAP (Dewar et al., 2018). Full details of the derivation are given in Appendix A. The LRU_CAP formulation was based on the following general expression for LRU given by Eqs. (10)–(11) of Wohlfahrt et al. (2012):

$$\begin{array}{}\text{(7)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}}{\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{1.21}}+\frac{\mathrm{1}}{\mathrm{1.14}}\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{b}}^{\text{COS}}}}{\mathrm{1}+\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{b}}^{\text{COS}}}+\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{m}}^{\text{COS}}}}},\end{array}$$

where $g_x^{\text{COS}}(x=\mathrm{b},\mathrm{s},\mathrm{m})$ are, respectively, the boundary layer, stomatal, and mesophyll conductances for COS, c_a is the atmospheric CO₂ molar mixing ratio (mol mol⁻¹), c_i is the leaf intercellular CO₂ molar mixing ratio (mol mol⁻¹), and the numerical factors 1.21 and 1.14 are the ratios of the conductances of CO₂ to COS for stomata and the boundary layer (Wohlfahrt et al., 2012). If it is assumed that the boundary layer and mesophyll conductances are infinite (as done by Dewar et al., 2018), Eq. (7) reduces to

$$\begin{array}{}\text{(8)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}\right)}^{-\mathrm{1}}.\end{array}$$

An analytical expression for c_i was derived from the stomatal optimization model CAP by Dewar et al. (2018), according to which stomatal conductance maximize leaf photosynthesis, reflecting a trade-off between stomatal limitations to CO₂ diffusion and non-stomatal limitations (NSLs) to carboxylation capacity. The CAP model predicts the value of c_i as an analytical function of various environmental and physiological factors. Inserting this function into Eq. (8), LRU_CAP can then be expressed as

$$\begin{array}{}\text{(9)}& {\mathrm{\text{LRU}}}_{\text{CAP}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\displaystyle \frac{c_{\mathrm{a}}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}\left(\mathrm{1}+\sqrt{{\displaystyle \frac{K_{\text{sl}}\left|{\mathit{\psi }}_{\mathrm{c}}\right|}{\mathrm{1.6}{g}_{\mathrm{c}}\text{VPD}}}}\sqrt{\mathrm{1}+{\displaystyle \frac{\mathrm{2}{\mathrm{\Gamma }}^{*}{g}_{\mathrm{c}}}{\mathit{\alpha }\text{PAR}}}}\right),\end{array}$$

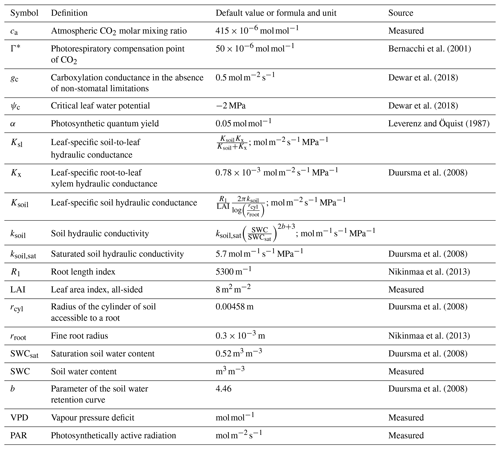
where Γ^* is the CO₂ photorespiratory compensation point (mol mol⁻¹), K_sl the soil-to-leaf hydraulic conductance ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{MPa}}^{-\mathrm{1}}$), ψ_c is the assumed critical leaf water potential (MPa) at which NSLs reduce photosynthesis to zero, g_c is the carboxylation conductance in the absence of NSLs ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) and α is the photosynthetic quantum yield (mol mol⁻¹) in the absence of NSLs (Duursma et al., 2008; Dewar et al., 2018). While Γ^*, and α vary seasonally with temperature, for simplicity we used fixed values representing the growing season averages of $\mathrm{50}\times {\mathrm{10}}^{-\mathrm{6}}$ and 0.05 mol mol⁻¹, respectively (Bernacchi et al., 2001; Leverenz and Öquist, 1987; Mäkelä et al., 2008). In addition to PAR ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) and VPD measurements (mol mol⁻¹), LRU_CAP requires soil moisture measurements through its dependence on the soil component of K_sl. All parameter definitions and values are listed in Table 1.

Bernacchi et al. (2001)Dewar et al. (2018)Dewar et al. (2018)Leverenz and Öquist (1987)Duursma et al. (2008)Duursma et al. (2008)Nikinmaa et al. (2013)Duursma et al. (2008)Nikinmaa et al. (2013)Duursma et al. (2008)Duursma et al. (2008)

Table 1 Explanations, literature values, and sources of the parameters used in the LRU_CAP formulation for Hyytiälä forest. c_a was derived from the measurements in Kooijmans et al. (2019), and SWC, PAR, and VPD from measurements done in this study. Soil-related values (K_soil,sat, r_cyl, SWC_sat, and b) are for soil horizon B (which was considered to be representative of the rooting zone), where the SWC measurements were also made.

LRU_CAP is based on a generic physiological model of stomatal function whose predictions have been successfully tested previously (e.g. Lintunen et al., 2020; Salmon et al., 2020; Dewar et al., 2021; Gimeno et al., 2019). The model parameters are all physiologically meaningful and can be measured independently or obtained from the literature. This formulation therefore represents a clear advance on previous COS-based methods based on empirical fitting (LRU_PAR) because it provides a physiological explanation for variations in LRU that may be more robust when extrapolating to other sites.

In addition, LRU_CAP was calculated using a combination of literature values and fitted parameters by fitting the parameter combinations $X=\left|{\mathit{\psi }}_{\mathrm{c}}\right|/\left(\mathrm{1.6}{g}_{\mathrm{c}}\right)$ (MPa m² s mol⁻¹) and $Y=\mathrm{2}{\mathrm{\Gamma }}^{*}{g}_{\mathrm{c}}/\mathit{\alpha }$ ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) to Eq. (9). This analysis was aimed at assessing the parameter sensitivity of LRU_CAP. While the literature-based parameter values gave X=2.5 and Y=0.001, the fitting values were X=2.64 and Y=0.0033 and gave a slightly better agreement of LRU_CAP with LRU_ch (RMSE=1.89, while without fitting RMSE=2.01, Fig. B2). However, we emphasize that this fitting procedure was conducted purely in order to assess the model performance and is not a requirement for applying LRU_CAP in practice when literature-based parameter values are available. Moreover, the results presented in this article are not based on fitted parameter values but on literature values only.

3 Results and discussion

3.1 Environmental conditions

March 2013 was colder than other years (average −7.0 ^∘C) and also had the highest average PAR (207.3 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) and lowest soil moisture (0.23 m³ m⁻³) (Fig. 1). A clear increase in VPD and decrease in soil moisture were seen in August 2013, with soil moisture decreasing from 0.24 in July to 0.19 m³ m⁻³ in August and afternoon median VPD increasing to 1.00 kPa. July 2014 was warmer (19.0 ^∘C) and dryer (VPD 0.88 kPa) than other years, but soil moisture remained high at 0.25 m³ m⁻³. In 2015, VPD increased from 0.44 in July to 0.62 kPa in August, and soil moisture decreased from 0.31 in July to 0.24 m³ m⁻³ in August. May 2017 had high amounts of radiation (monthly average PAR of 478.4 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$), and soil temperature was low (3.4 ^∘C), while soil moisture and VPD were at a normal level at 0.28 m³ m⁻³ and 0.47 kPa, respectively. Soil moisture in September–December in 2017 was 10 % higher than other years, while no significant differences between years were found in other environmental variables in late autumn.

Figure 1 Median diurnal variation of T_a, T_soil, PAR, SWC, and VPD in different months during the measurement period 2013–2017.

3.2 GPP comparison from sub-daily to seasonal scales

Midday GPP_ANN was on average 12 % higher than midday GPP_NLR during the summer months (May–July) in 2014 and 2017 (Figs. 2, 3, and 4a), opposite to the result found by Tramontana et al. (2020) in a comparison of GPP_ANN with standard FLUXNET partitioning during summer months at multiple sites. The difference between GPP_NLR and GPP_ANN during other months was negligible. We compared the more common use of air temperature as the respiration driver, GPP_airT (instead of the average of soil and air temperatures), against GPP_NLR and found that the two methods agreed very well with each other at all timescales (Fig. B3). The small differences in the diurnal variations of GPP_NLR and GPP_ANN are thus not due to the choice of temperature measurement as respiration driver. During the measurement period 2013–2017, 30 min, daily, and monthly GPP_ANN did not differ statistically from GPP_NLR (tested with the ANOVA test; Figs. B4–B6). However, on 30 min timescale the GPP_ANN was on average 15 % lower than GPP_NLR. The lower agreement of 30 min GPP_ANN and GPP_NLR than on longer timescales may have resulted from the NN_C-part method restricting GPP_ANN to only positive values, while GPP_NLR may take on negative values due to random noise in the NEE measurements. The relative and absolute differences of GPP_ANN to GPP_NLR are, however, very small when averaging over longer time periods (relative difference 2 % on average during summer months, Fig. 5).

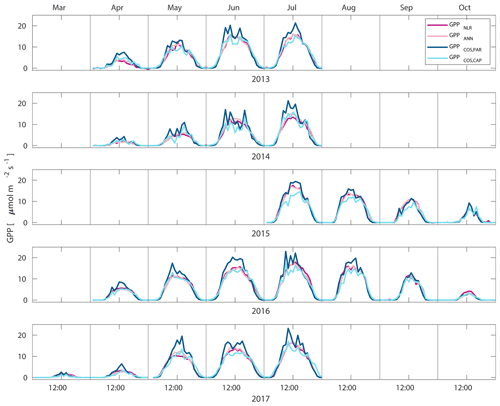
Figure 2 Median diurnal variation of GPP partitioned using a combined nighttime–daytime method (GPP_NLR, purple line), GPP from artificial neural networks (GPP_ANN, pink line), GPP from COS flux measurements with LRU determined according to Kooijmans et al. (2019) (GPP_COS,PAR, dark blue line), and GPP from COS flux measurements using a new approach for LRU (Sect. 2.3.4, GPP_COS,CAP, light blue line) in different months during the measurement period 2013–2017. Averaging was done to the same data points, and only months with more than 55 % of data coverage were included.

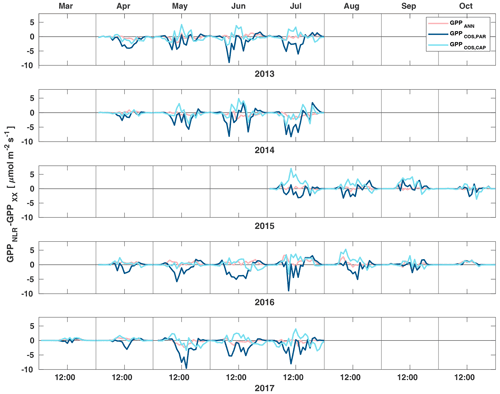
Figure 3 Diurnal variation of the difference of GPP_ANN (pink), GPP_COS,PAR (dark blue) and GPP_COS,CAP (light blue) to the reference GPP_NLR in different months during the measurement period 2013–2017. Averaging was done to the same data points and only months with more than 55 % of data coverage were included.

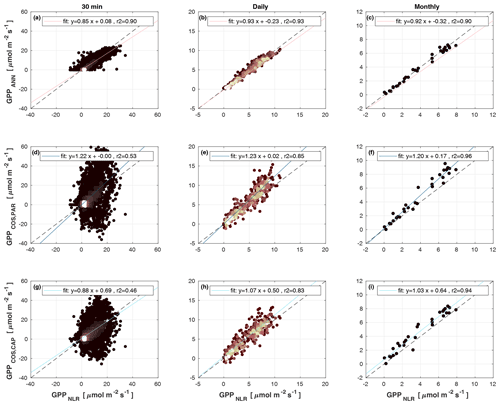
Figure 4 Scatter plots of GPP_ANN, GPP_COS,PAR, and GPP_COS,CAP against GPP_NLR in 30 min, daily, and monthly timescales. The colour of data points in 30 min and daily scatter plots indicates the data density, lighter colours indicating higher point density than dark ones.

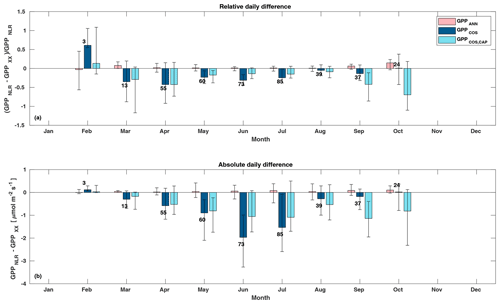
Figure 5 Relative (a) and absolute (b) difference of daily GPP_ANN (pink), GPP_COS,PAR (dark blue), and GPP_COS,CAP (light blue) to GPP_NLR in different months, averaged over the whole measurement period 2013–2017. Bars represent the median difference, and whiskers show the 25th and 75th percentiles. Numbers on top of the bars indicate how many daily flux data points have been used for calculating the medians. Median differences have been calculated using the same number of data points for each method in each month.

GPP_COS,PAR was very similar to GPP_NLR especially during morning and early evening (Figs. 2 and 3) but showed higher midday values than GPP_NLR, especially during summer months (May–August) in all years. At the daily scale, GPP_COS,PAR was on average 23 % higher than GPP_NLR (Figs. 4e and 5) and also differed from GPP_NLR and GPP_ANN statistically (p<0.01) on 30 min and daily scales (ANOVA test). At monthly scale, there was no statistical difference to any of the other GPP methods.

Based on the CAP stomatal optimization model, LRU_CAP requires PAR, SWC, and VPD, as well as ecosystem-specific literature values, for some parameters as input variables. In contrast, LRU_PAR by Kooijmans et al. (2019) only uses PAR. LRU_CAP therefore takes into account additional effects of drought and air humidity on LRU. In spring, the diurnal variation of GPP_COS,CAP closely follows that of GPP_NLR and GPP_ANN until June (Figs. 2 and 3). Especially in June and July GPP_COS,CAP is lower than the other GPP estimates. At 30 min timescale GPP_COS,CAP is on average 12 % lower than GPP_NLR, but there is large scatter due to noisy FCOS measurements, like for GPP_COS,PAR. However, there is less scatter in GPP_COS,CAP than GPP_COS,PAR (Fig. 4d and g), indicating that some of the scatter is due to LRU estimation. At daily scales GPP_COS,CAP is 7 % higher than GPP_NLR, and at monthly scales the difference decreases to 3 %. However, there is no statistically significant difference between the 30 min and monthly values of GPP_NLR and GPP_COS,CAP (ANOVA test). The relative and absolute difference between GPP_COS,CAP and GPP_NLR is also generally smaller than between GPP_COS,PAR and GPP_NLR throughout the year (Fig. 5). In addition, GPP_COS,CAP reproduces the same two distinctive probability density function peaks as GPP_NLR and GPP_ANN at 1.7 and 6.6 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, while GPP_COS,PAR finds weaker peaks at 2.4 and 7.4 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ (Fig. 6). In summary, GPP_COS,CAP gives better agreement with traditional GPP_NLR partitioning than GPP_COS,PAR. However, LRU_CAP was higher than LRU_ch and LRU_PAR at high radiation (PAR>1000 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, Fig. B7a). This may reflect intrinsic differences in the dependence of LRU_PAR and LRU_CAP on environmental drivers (PAR, VPD, SWC) as both estimates of LRU are based on conditions at the top of the canopy.

LRU_CAP was also calculated based on a combination of literature values and the fitted parameters X and Y (Sects. 2.3.4 and A1) in order to assess the sensitivity to parameter values. While literature values gave X=2.5 MPa m² s mol⁻¹ and Y=0.001 $\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, fitting gave X=2.64 MPa m² s mol⁻¹ and Y=0.0033 $\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ and a slightly better agreement of LRU_CAP with measured LRU (RMSE=1.89, while without fitting RMSE=2.01). Thus, while X was close to its literature value, Y was estimated to be 3 times higher. This mismatch suggests there may be scope for further model improvement, such as the inclusion of dark respiration and/or finite mesophyll and boundary layer conductances in the LRU_CAP model. However, as the difference between fitted LRU_CAP and literature-based LRU_CAP (statistical significance tested with Student's t test, p<0.01) was not large, with a median difference of 4 %, and the applicability of the model without fitting is better, we decided to use the literature-based parameterization of LRU_CAP in this study, without fitting to LRU_ch.

LRU_CAP was also calculated assuming finite mesophyll conductance as a further comparison (Sect. A2). The agreement of this method was better than assuming infinite mesophyll conductance at high PAR but worse at low PAR (Fig. B7d), very similar to the results from Maignan et al. (2021), who modelled LRU at Hyytiälä using the ORCHIDEE model. This version of LRU_CAP was also fitted to measured LRU in terms of parameters X and Y (Sect. A2) to make the low PAR LRU_CAP better, which resulted in X=3.45 and Y=0.0057, both higher than their expected literature values. We thus concluded that the assumption of infinite g_m gives an estimate that is closest to LRU_ch, although the assumption in itself is physiologically unrealistic. Kooijmans et al. (2019) found that internal conductance (a combination of mesophyll conductance and biochemical reactions) might limit leaf-scale FCOS during daytime. We find a better agreement of LRU_CAP with LRU_ch if g_m is assumed to be infinite, but there is a mismatch at high PAR, supporting the possibility that g_m might indeed be a limiting factor under high radiation. In CAP, infinite or finite g_m represents two contrasting hypotheses, in which NSLs act either entirely on photosynthetic capacity or entirely on g_m, respectively. In reality, NSLs may act on both photosynthetic capacity and g_m, with one or the other effect being dominant depending on environmental conditions. The contrasting abilities of each hypothesis to explain LRU_ch at low vs. high light might be explained by a shift in the action of NSLs from the photosynthetic capacity to g_m as light increases. However, verifying this possibility lies beyond the scope of the present study.

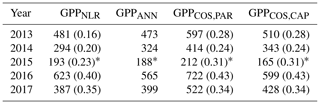
We calculated the cumulative GPP estimates over May–July, 13 weeks around the peak growing season for each year (Table 2). Cumulative GPP_COS,PAR was on average 25 % higher than cumulative GPP_NLR in all studied years. This is higher than the 4.3 % difference reported in Spielmann et al. (2019) and 3.5 % agreement reported in Commane et al. (2015). In contrast, cumulative GPP_COS,CAP varied from 17 % higher in 2014 to 15 % lower in 2015, and on average it was only 3 % higher than cumulative GPP_NLR. Cumulative GPP_ANN varied from 10 % higher in 2014 to 9 % lower in 2016 than GPP_NLR, and on average it was 0.1 % lower than GPP_NLR. As stated above, overall GPP_ANN was closest to GPP_NLR out of the three other GPP estimates. GPP_COS,CAP was closer to both of the CO₂-based GPP estimates than GPP_COS,PAR. However, at high PAR, LRU_COS,CAP was higher than chamber-based measurements, leading to a lower GPP. Nevertheless, no firm conclusions can be drawn here as the LRU observations only cover measurements at the top of the canopy and may not reflect LRU over the whole canopy.

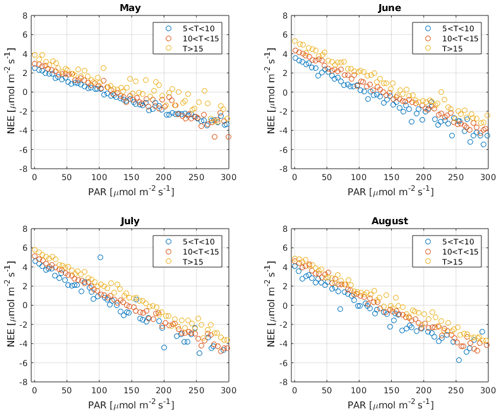
It has been suggested that, due to the Kok effect, leaf respiration is inhibited under radiation (Kok, 1949). This inhibition has been estimated to be approximately 13 % in the evergreen needle–leaf forests during summer (Keenan et al., 2019). Measurements of CO₂ isotope fluxes support the conclusion that, due to the Kok effect, GPP from traditional CO₂ flux partitioning using the nighttime method is overestimated (Wehr et al., 2016). However, ecosystem respiration at the Hyytiälä forest site is dominated by soil respiration (Ilvesniemi et al., 2009) so that the Kok effect may be of limited importance in this ecosystem (Keenan et al., 2019; Yin et al., 2020). Reduced leaf respiration under radiation would be visible as a break point around the compensation point with a change in the slope of NEE against radiation. However, such a break point was not detected in our observations, as is demonstrated in Fig. B8. While it is possible that less radiated needles experience less inhibition than well radiated ones that cancel out at the ecosystem scale (Wohlfahrt et al., 2005), this test provides some insight into the problem. It is thus not expected that independent GPP estimates in Hyytiälä would necessarily result in lower GPP than the traditional methods. Moreover, Tramontana et al. (2020) showed that uncertainties and biases in NEE (and COS flux) measurements exceed those resulting from the possible Kok effect.

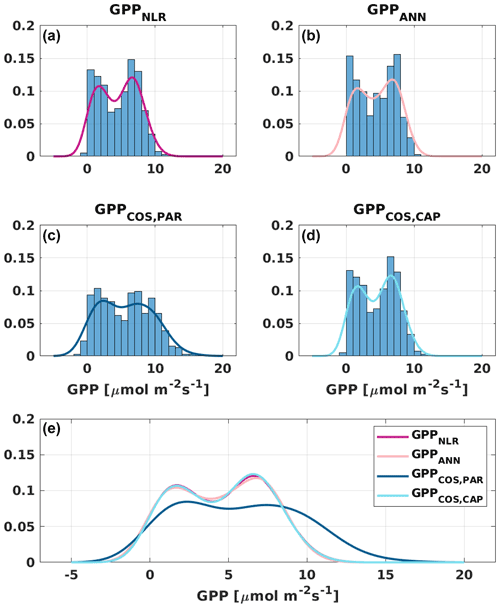
Figure 6 Distribution (bars) and probability density functions (lines) of daily average (a) GPP_NLR, (b) GPP_ANN, (c) GPP_COS,PAR, and (d) GPP_COS,CAP. All probability density functions are combined in (e) for better comparison.

Table 2 Cumulative GPP (g C m⁻²) over May–July with different GPP estimates. All sums are calculated from the same data coverage, and the fraction of gap-filled flux data (CO₂ flux for GPP_NLR, COS flux for GPP_COS,PAR and GPP_COS,CAP) is presented in parentheses. GPP_ANN does not include gap-filled NEE data since it is based on meteorological variables. ^* In 2015, the cumulative sum covers only July.

3.3 GPP responses to environmental conditions

All four GPP estimates responded similarly to environmental forcing (PAR, T_a, VPD) both in spring and summer (Fig. 7). In spring, all GPP estimates increased with increasing radiation levels, while in summer a saturation point was found at PAR>500 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$ that could be linked to VPD limitation on stomatal conductance in the afternoon (Kooijmans et al., 2019). GPP_COS,PAR was higher than GPP_COS,CAP at PAR>400 $\mathrm{\mu }\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, while at low PAR values they agreed well with each other both in spring and summer, as well as with GPP_NLR and GPP_ANN. GPP_COS,PAR thus has a stronger radiation response than the other GPP estimates due to a lower empirical LRU estimate than LRU_CAP at high PAR (Fig. B7). A similar PAR response was found in Spielmann et al. (2019), who studied GPP_COS,PAR with a traditional GPP partitioning method at four different sites in Europe. Although GPP_COS,CAP agrees well with both GPP_NLR and GPP_ANN at high PAR, it is likely underestimated due to high LRU_CAP at high PAR (Fig. B7).

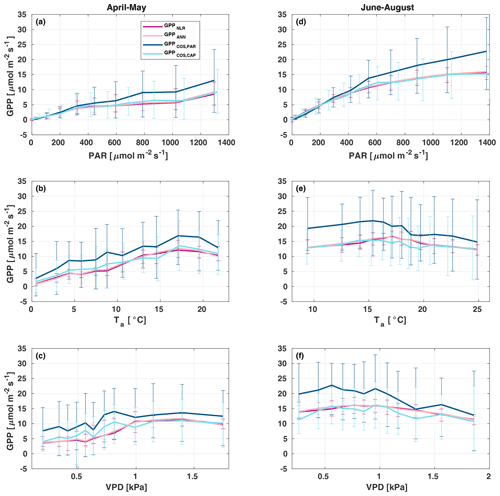
Figure 7 Responses of the different GPP estimates (GPP_NLR (purple), GPP_ANN (pink), GPP_COS,PAR (dark blue), and GPP_COS,CAP, light blue) to environmental parameters – photosynthetically active radiation (a, d), air temperature (b, e), and vapour pressure deficit (c, f) – in spring (a–c) and summer (d–f). Data are binned to 12 equally sized bins (same number of data points in each bin), and all GPPs have the same data coverage. Only measured (non-gap-filled) 30 min flux data were used, and GPP was filtered to include only PAR>700 µmol m² s⁻¹ in responses to T_a and VPD to avoid simultaneous correlation with PAR.

In spring, increasing air temperature increased all GPP estimates similarly until T_a reached 17 ^∘C. However, again GPP_COS,PAR was higher than other GPP estimates. In summer, air temperature did not have a notable effect on any GPP estimate. Responses to VPD were similar for each GPP estimates both in spring and summer. In spring, decreasing air humidity (increasing VPD) was associated with increased GPP until VPD>0.7 kPa, after which VPD had little or no effect. The apparent increase in GPP with VPD in spring may be caused by the correlation of T_a with VPD, coinciding with the start of the growing season as the trees are not water-limited after snowmelt. In summer, dryness started to limit GPP at VPD>1 kPa. We found that similar to PAR and T_a responses, GPP_COS,PAR was higher than other GPP estimates at low VPD values but decreased to similar levels at high VPD (1 kPa) both in spring and summer. GPP_COS,PAR gives higher GPP at low VPD than the CO₂-based methods, as does GPP_COS,CAP in spring (Fig. 7). This may indicate that some factor is limiting the photosynthesis reaction (e.g. biochemical limitations in CO₂ assimilation) even though the diffusion into the leaf is not limited.

3.4 Uncertainties and limitations of the GPP methods

Because ANN fitting is purely based on the provided examples, GPP_ANN could be more sensitive to the uncertainty of (training) data with respect to the parametric partitioning methods. Moreover, it is sensitive to missing data especially in the case of long data gaps (Tramontana et al., 2020). The method also requires large data sets for training NN_C-part, which may not be available at all measurement sites. However, GPP_ANN does not require prescribed relationships of GPP to environmental data, making it an attractive method for sites with good data availability.

GPP_COS,PAR uses an empirical PAR relation that is based on measurements at Hyytiälä forest. This PAR relation is site-specific and different compared to the one found by Yang et al. (2018). For this reason it is not known if and how it can be used at other sites, where it is suggested to retrieve it directly from observations. The choice of the empirical LRU–PAR relation at any given site is to some extent arbitrary. While the LRU_PAR function is simple and thereby attractive, it does not take into account the different light conditions inside the canopy, stomatal regulation during drought, or the effects of non-stomatal limitations on photosynthesis. Moreover, being an empirical model, it does not provide a process-based understanding for LRU. While the results of GPP_COS,PAR are promising, we found a 25 % difference in midday GPP during summer, similar to that found by Kooijmans et al. (2019). We did not find as good an agreement with CO₂-based GPP estimates as Asaf et al. (2013), who found an agreement within 15 % using a constant LRU of 1.6 in Mediterranean pine forests and crop fields. However, they also reported higher GPP_COS assumed to be related to soil COS uptake, which was not measured or taken into account in their GPP calculations. In our study, we subtracted an average measured soil flux (Sun et al., 2018a) from the ecosystem COS uptake. As the diurnal variation in soil COS exchange was small (less than 1 $\mathrm{pmol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) throughout the season, averaging did not make a large difference, and thus soil does not explain the differences found here. However, as soil COS flux measurements are not necessarily available at all sites, this may be one source of uncertainty in wider applications. Yang et al. (2018) studied COS flux components and GPP_COS in a Mediterranean citrus orchard and found GPP_COS to be on average 7 % lower than traditionally partitioned GPP. They also presented a light-dependent and seasonally varying LRU which, however, could not be applied to Hyytiälä COS fluxes due to the very different ecosystem types studied, indicating that the PAR responses may differ between ecosystems.

GPP_COS,CAP may be more applicable at other sites than GPP_COS,PAR because it is based on a generic physiological model of stomatal behaviour, which requires only literature-based parameter values and simple meteorological variables as inputs. However, as for LRU_PAR, LRU_CAP should also be tested at other sites against measured LRU to verify its applicability to other ecosystems. The version of LRU_CAP assuming infinite mesophyll conductance, while giving reasonable results in comparison with LRU_ch, is clearly physiologically unrealistic. The formulation of LRU_CAP with finite g_m did not compare as well with LRU_ch at Hyytiälä forest (RMSE=2.58, median difference to LRU_ch 22 %), especially during low light conditions, but may compare better at other measurement sites.

One source of uncertainty in GPP estimates based on LRU_CAP and LRU_PAR is that both LRU predictions are calculated from radiation measurements at the top of the canopy, where there is no shading by foliage, although the theoretical dependence of LRU_CAP on radiation is more generally applicable throughout the canopy. The branch chamber measurements (on which the empirical LRU_PAR function is based) were also made at the top of the canopy. The measured needles were thus well-adjusted to high radiation conditions. Therefore, we did not take into account light penetration and scattering through the canopy. However, the needles and leaves within the canopy are also well adjusted to low light conditions and may be more efficient with their stomatal control in varying light conditions than needles on top of the canopy. Thus, this may not be a large source of uncertainty. However, it is also possible that LRU varies throughout the canopy due to different light conditions.

4 Conclusions

Daily GPP_ANN and GPP_NLR did not differ significantly, and differences were also small at sub-daily and seasonal timescales. GPP_COS,PAR was higher than GPP_NLR at all timescales studied, including the estimate of 3-month cumulative GPP during the peak growing season. In contrast, GPP_COS,CAP, a new method based on stomatal optimization theory, gave better agreement with GPP_NLR at all timescales and was also less scattered than GPP_COS,PAR at a 30 min timescale.

The LRU_CAP function provides a new theoretical underpinning for COS-based GPP estimates that can be used at other measurement sites, potentially without requiring additional branch chamber measurements. LRU_CAP represents a significant improvement on previous LRU functions based on site-specific empirical regressions. However, LRU_CAP overestimated LRU at high radiation when compared to LRU observations at the top of the canopy, leading to a lower midday GPP_COS,CAP, especially in summer. This discrepancy may result from the assumption of infinite mesophyll conductance, or the absence of dark respiration, in the underlying stomatal optimization model. LRU_CAP would benefit from further testing at other measurement sites with COS and CO₂ branch flux measurements, including measurements inside the canopy for better canopy-integrated LRU estimates.

Although COS flux measurements are noisier, more expensive, and more difficult than those of CO₂, they provide an opportunity for better process-based understanding of photosynthesis in comparison to more traditional CO₂-based estimates of GPP. In addition to COS, other proxies such as solar-induced fluorescence and isotopic flux measurements should be tested simultaneously to properly investigate their deficiencies and advantages in estimating GPP and processes underlying photosynthesis.

The establishment of large long-term ecosystem research infrastructures (e.g. ICOS, NEON, TERN; see Papale, 2020) – involving sites equipped with eddy covariance systems that could potentially also host COS, SIF (solar-induced fluorescence), and isotope sensors – together with the planned launch of the FLEX satellite in 2025 (https://earth.esa.int/eogateway/missions/flex, last access: 28 June 2022) that will provide global vegetation fluorescence measurements, opens up a new phase in monitoring and understanding plant photosynthesis. Our results also underline the important role of small-scale ecophysiological measurements and models in underpinning these larger-scale initiatives.

Appendix A: LRU predicted by the CAP stomatal optimization model

A1 LRU_CAP assuming infinite mesophyll conductance

The general expression for the leaf relative uptake ratio (LRU) derived from the diffusion laws for COS and CO₂ (Wohlfahrt et al., 2012) is

$$\begin{array}{}\text{(A1)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}}{\displaystyle \frac{\frac{\mathrm{1}}{\mathrm{1.21}}+\frac{\mathrm{1}}{\mathrm{1.14}}\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{b}}^{\text{COS}}}}{\mathrm{1}+\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{b}}^{\text{COS}}}+\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{m}}^{\text{COS}}}}},\end{array}$$

where $g_x^{\text{COS}}(x=\mathrm{b},\mathrm{s},\mathrm{m})$ are the boundary layer, stomatal and mesophyll conductances for COS, respectively, c_a and c_i are the atmospheric and leaf intercellular CO₂ molar mixing ratios (mol mol⁻¹), respectively, and the numerical factors 1.21 and 1.14 are the ratios of the conductances of CO₂ to COS for stomata and the boundary layer, respectively.

If it is assumed that boundary layer and mesophyll conductances are infinite, Eq. (A1) reduces to

$$\begin{array}{}\text{(A2)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}\right)}^{-\mathrm{1}}.\end{array}$$

We derived c_i from the CAP stomatal optimization model (Dewar et al., 2018), according to which stomatal conductance adjusts to maximize the rate of leaf photosynthesis (A) through a trade-off between stomatal and non-stomatal limitations. Our photosynthesis model is based on that of Thornley and Johnson (1990) (their Eq. 9.12i), modified to include non-stomatal limitations (NSLs):

$$\begin{array}{}\text{(A3)}& A=\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\psi }}_{\text{leaf}}}{{\mathit{\psi }}_{\mathrm{c}}}}\right){\displaystyle \frac{\mathit{\alpha }Q{g}_{\mathrm{c}}(c_{\mathrm{i}}-{\mathrm{\Gamma }}^{*})}{\mathit{\alpha }Q+g_{\mathrm{c}}(c_{\mathrm{i}}+{\mathrm{\Gamma }}^{*})}},\end{array}$$

where α is the photosynthetic quantum yield (mol mol⁻¹) in the absence of NSLs, Q ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) is photosynthetically active radiation (PAR), g_c ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) is the initial slope of the A–c_i response curve in the absence of NSLs, Γ^* (mol mol⁻¹) is the photorespiratory CO₂ compensation point, ψ_leaf (MPa) is the leaf water potential, and ψ_c (MPa) is the critical leaf water potential at which NSLs reduce photosynthesis to zero. In Eq. (A3), NSLs are represented as an apparent downregulation of the A−c_i response curve by a factor that decreases with decreasing leaf water potential, as has been observed in numerous experiments (e.g. Lintunen et al., 2020; Salmon et al., 2020). Consequently, as stomatal conductance increases there is a trade-off between increased CO₂ supply and increased NSLs such that A has a maximum at some optimal value of stomatal conductance.

We used Eq. (A3) rather than the Farquhar photosynthesis model (Farquhar et al., 1980) because, in the latter, the abrupt switch from RuBisCo to electron transport limitation introduces artificial discontinuities in the CAP solution for optimal stomatal conductance (Dewar et al., 2018), whereas in Eq. (A3) there is a smooth transition from CO₂ limitation to light limitation, and no such discontinuities occur. The parameter g_c is equivalent to $V_{\text{cmax}}/(k_{\mathrm{m}}+{\mathrm{\Gamma }}^{*})$ in the Farquhar model.

The CAP solution for optimal stomatal conductance (Dewar et al., 2018) predicts that

$$\begin{array}{}\text{(A4)}& {\displaystyle \frac{c_{\mathrm{i}}-{\mathrm{\Gamma }}^{*}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\mathit{\beta }}},\end{array}$$

where

$$\begin{array}{}\text{(A5)}& \mathit{\beta }=\sqrt{{\displaystyle \frac{\mathrm{1.6}D}{K_{\text{sl}}\left|{\mathit{\psi }}_{\mathrm{c}}\right|}}{\left({\displaystyle \frac{\mathrm{1}}{g_{\mathrm{c}}}}+{\displaystyle \frac{\mathrm{2}{\mathrm{\Gamma }}^{*}}{\mathit{\alpha }Q}}\right)}^{-\mathrm{1}}},\end{array}$$

in which D is vapour pressure deficit (VPD; mol mol⁻¹), and K_sl is the leaf-specific soil-to-leaf hydraulic conductance ($\mathrm{mol}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}{\mathrm{MPa}}^{-\mathrm{1}}$). Writing Eq. (A2) in the equivalent form

$$\begin{array}{}\text{(A6)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\displaystyle \frac{c_{\mathrm{a}}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}{\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{i}}-{\mathrm{\Gamma }}^{*}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}\right)}^{-\mathrm{1}}\end{array}$$

and substituting the CAP prediction from Eqs. (A4) and (A5) then give

$$\begin{array}{}\text{(A7)}& \begin{array}{rl}& {\text{LRU}}_{\text{CAP}}=\\ & {\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\displaystyle \frac{c_{\mathrm{a}}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}\left(\mathrm{1}+\sqrt{{\displaystyle \frac{K_{\text{sl}}\left|{\mathit{\psi }}_{\mathrm{c}}\right|}{\mathrm{1.6}D{g}_{\mathrm{c}}}}}\sqrt{\mathrm{1}+{\displaystyle \frac{\mathrm{2}{\mathrm{\Gamma }}^{*}{g}_{\mathrm{c}}}{\mathit{\alpha }Q}}}\right).\end{array}\end{array}$$

In Eq. (A7) all the parameters are physiologically meaningful and can be measured independently or obtained from the literature because the underlying CAP model is based entirely on such parameters. This contrasts with the use of the stomatal optimization model of Medlyn et al. (2011), for example, which contains an undetermined parameter (λ, interpreted as the marginal water cost of carbon gain) that must be empirically fitted.

Nevertheless, to assess the performance of LRU_CAP obtained from literature-based parameter values, we compared it with LRU_CAP obtained by fitting the two key parameter combinations $X=\left|{\mathit{\psi }}_{\mathrm{c}}\right|/\left(\mathrm{1.6}{g}_{\mathrm{c}}\right)$ and $Y=\mathrm{2}{\mathrm{\Gamma }}^{*}{g}_{\mathrm{c}}/\mathit{\alpha }$ , in terms of which Eq. (A7) may be written as

$$\begin{array}{}\text{(A8)}& {\text{LRU}}_{\text{CAP}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\displaystyle \frac{c_{\mathrm{a}}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}\left(\mathrm{1}+\sqrt{{\displaystyle \frac{K_{\text{sl}}X}{D}}}\sqrt{\mathrm{1}+{\displaystyle \frac{Y}{Q}}}\right).\end{array}$$

Parameters X and Y were optimized to minimize the RMSE of log (LRU_CAP) to measured log (LRU), due to the logarithmic nature of LRU, with MATLAB's fminsearch function. However, we emphasize that this fitting procedure was conducted purely in order to assess the model performance and is not a requirement for applying LRU_CAP in practice when literature-based parameter values are available. Moreover, the results presented in this study are not based on the optimized values but on literature values only.

A2 LRU_CAP assuming finite mesophyll conductance

In the case that mesophyll conductance is not assumed to be infinite (but boundary layer conductance is infinite), Eq. (A1) becomes

$$\begin{array}{}\text{(A9)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{m}}^{\text{COS}}}}}{\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}}\right)}^{-\mathrm{1}}.\end{array}$$

If we further assume that the ratios of stomatal to mesophyll conductances are the same for CO₂ and COS, then from $g_{\mathrm{s}}^{{\mathrm{CO}}_{\mathrm{2}}}(c_{\mathrm{a}}-c_{\mathrm{i}})=g_{\mathrm{m}}^{{\mathrm{CO}}_{\mathrm{2}}}(c_{\mathrm{i}}-c_{\mathrm{c}})$, where c_c is the chloroplast CO₂ molar mixing ratio (mol mol⁻¹), we can make the substitution

$$\begin{array}{}\text{(A10)}& {\displaystyle \frac{g_{\mathrm{s}}^{\text{COS}}}{g_{\mathrm{m}}^{\text{COS}}}}={\displaystyle \frac{g_{\mathrm{s}}^{{\mathrm{CO}}_{\mathrm{2}}}}{g_{\mathrm{m}}^{{\mathrm{CO}}_{\mathrm{2}}}}}={\displaystyle \frac{c_{\mathrm{i}}-c_{\mathrm{c}}}{c_{\mathrm{a}}-c_{\mathrm{i}}}}\end{array}$$

in Eq. (A9) to obtain

$$\begin{array}{}\text{(A11)}& \text{LRU}={\displaystyle \frac{\mathrm{1}}{\mathrm{1.21}}}{\left(\mathrm{1}-{\displaystyle \frac{c_{\mathrm{c}}}{c_{\mathrm{a}}}}\right)}^{-\mathrm{1}},\end{array}$$

which reduces to Eq. (A2) when mesophyll conductance is infinite (since then c_c=c_i). As noted above, CAP represents NSLs in terms of an apparent downregulation of the A−c_i response curve (Eq. A3). This empirical observation may be interpreted in various ways: as a downregulation of photosynthetic efficiencies (α and g_c) in the chloroplast, a downregulation of mesophyll conductance ($g_{\mathrm{m}}^{{\mathrm{CO}}_{\mathrm{2}}}$), or some combination of the two. In the case when NSLs act entirely on $g_{\mathrm{m}}^{\text{COS}}$ with no effect on the biochemical efficiencies, A is given as a function of the chloroplast CO₂ concentration by (cf. Eq. A3)

$$\begin{array}{}\text{(A12)}& A={\displaystyle \frac{\mathit{\alpha }Q{g}_{\mathrm{c}}(c_{\mathrm{c}}-{\mathrm{\Gamma }}^{*})}{\mathit{\alpha }Q+g_{\mathrm{c}}(c_{\mathrm{c}}+{\mathrm{\Gamma }}^{*})}}.\end{array}$$

In this case, since Eq. (A3) still holds, we obtain the same optimal CAP solution for stomatal conductance and c_i (Eq. A4) as before but now with an additional prediction for the finite (but variable) mesophyll conductance as implied by Eq. (A12), which links the chloroplast CO₂ concentration (c_c) to the CAP solution of A. From Eq. (A12),

$$\begin{array}{}\text{(A13)}& c_{\mathrm{c}}-{\mathrm{\Gamma }}^{*}={\displaystyle \frac{\left(\frac{\mathit{\alpha }Q}{g_{\mathrm{c}}}+\mathrm{2}{\mathrm{\Gamma }}^{*}\right)A}{\mathit{\alpha }Q-A}}.\end{array}$$

The CAP solution for stomatal conductance is given by (Dewar et al., 2018)

$$\begin{array}{}\text{(A14)}& g_{\mathrm{s}}={\displaystyle \frac{\mathit{\alpha }Q}{\frac{\mathit{\alpha }Q}{g_{\mathrm{c}}}+\mathrm{2}{\mathrm{\Gamma }}^{*}}}{\displaystyle \frac{x\mathit{\theta }}{x{\mathit{\beta }}^{\mathrm{2}}+(\mathrm{1}-x)(xw+\mathrm{1})}},\end{array}$$

where

$$\begin{array}{}\text{(A15)}& {\displaystyle }\mathit{\theta }& {\displaystyle }=\mathrm{1}-{\displaystyle \frac{{\mathit{\psi }}_{\text{soil}}}{{\mathit{\psi }}_{\mathrm{c}}}},\text{(A16)}& {\displaystyle }w& {\displaystyle }={\displaystyle \frac{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}{\frac{\mathit{\alpha }Q}{g_{\mathrm{c}}}+\mathrm{2}{\mathrm{\Gamma }}^{*}}},\text{(A17)}& {\displaystyle }x& {\displaystyle }={\displaystyle \frac{c_{\mathrm{i}}-{\mathrm{\Gamma }}^{*}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\mathit{\beta }}},\end{array}$$

in which ψ_soil (MPa) is the soil water potential. Substituting x as a function of β into Eq. (A14) and simplifying give

$$\begin{array}{}\text{(A18)}& g_{\mathrm{s}}={\displaystyle \frac{\mathit{\alpha }Q}{\frac{\mathit{\alpha }Q}{g_{\mathrm{c}}}+\mathrm{2}{\mathrm{\Gamma }}^{*}}}{\displaystyle \frac{\mathit{\theta }}{\mathit{\beta }(\mathrm{1}+\mathit{\beta }+\frac{w}{\mathrm{1}+\mathit{\beta }})}}.\end{array}$$

We then find the CAP solution for A as follows:

$$\begin{array}{}\text{(A19)}& \begin{array}{rl}A& =g_{\mathrm{s}}(c_{\mathrm{a}}-c_{\mathrm{i}})\\ & =g_{\mathrm{s}}(c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*})(\mathrm{1}-x)\\ & =g_{\mathrm{s}}(c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}){\displaystyle \frac{\mathit{\beta }}{\mathrm{1}+\mathit{\beta }}}\\ & ={\displaystyle \frac{\mathit{\alpha }Q(c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*})}{\frac{\mathit{\alpha }Q}{g_{\mathrm{c}}}+\mathrm{2}{\mathrm{\Gamma }}^{*}}}{\displaystyle \frac{\mathit{\theta }}{(\mathrm{1}+\mathit{\beta }{)}^{\mathrm{2}}+w}}.\end{array}\end{array}$$

Substituting this into Eq. (A13) and simplifying then give

$$\begin{array}{}\text{(A20)}& \begin{array}{rl}{\displaystyle \frac{c_{\mathrm{c}}-{\mathrm{\Gamma }}^{*}}{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}}& ={\displaystyle \frac{\mathit{\theta }}{(\mathrm{1}+\mathit{\beta }{)}^{\mathrm{2}}+(\mathrm{1}-\mathit{\theta })w}}\\ & ={\displaystyle \frac{\mathit{\theta }}{(\mathrm{1}+\mathit{\beta }{)}^{\mathrm{2}}+(\mathrm{1}-\mathit{\theta })\frac{g_{\mathrm{c}}(c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*})}{\mathit{\alpha }Q+\mathrm{2}{\mathrm{\Gamma }}^{*}{g}_{\mathrm{c}}}}},\end{array}\end{array}$$

which can be combined with Eq. (A11) to give the solution of LRU_CAP with finite mesophyll conductance.

As for LRU_CAP with infinite mesophyll conductance, we also fitted this version with respect to parameters X and Y in order to compare it with the performance of the model using literature-based values. For this procedure, β and w were expressed in terms of X and Y,

$$\begin{array}{}\text{(A21)}& \mathit{\beta }={\displaystyle \frac{\mathrm{1}}{\sqrt{\frac{K_{\text{sl}}X}{D}(\mathrm{1}+\frac{Y}{Q})}}}\end{array}$$

and

$$\begin{array}{}\text{(A22)}& w={\displaystyle \frac{c_{\mathrm{a}}-{\mathrm{\Gamma }}^{*}}{\mathrm{2}{\mathrm{\Gamma }}^{*}}}{\displaystyle \frac{\mathrm{1}}{\frac{Q}{Y}+\mathrm{1}}},\end{array}$$

and then substituted into Eq. (A20). However, as for the infinite g_m solution, this fitting procedure was conducted purely in order to assess the model performance and is not a requirement for applying LRU_CAP in practice when literature-based parameter values are available.

Appendix B: Additional figures

Figure B1 Modelled against measured NEE using (a) NLR and (b) ANN models for modelling NEE.

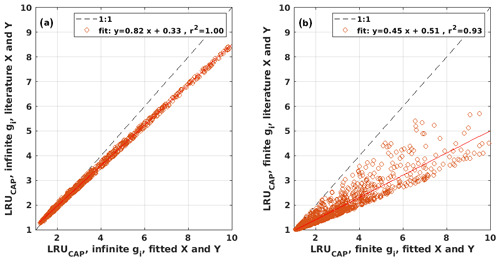
Figure B2 Scatter plots of LRU_CAP using the literature values against LRU_CAP using the optimized parameter values when assuming (a) infinite or (b) finite mesophyll conductance.

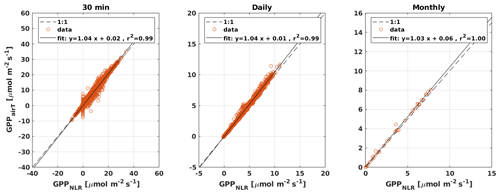
Figure B3 Scatter plots of GPP_airT that uses only air temperature as the driver for respiration against GPP_NLR that uses an average of air and soil temperatures as the respiration driver at 30 min, daily, and monthly timescales. The solid black line is the least-squares linear fit to the data.

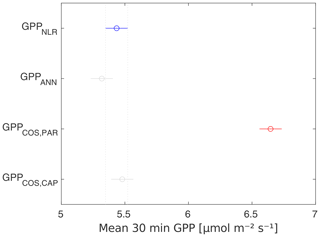
Figure B4 ANOVA test results for 30 min GPP data. Gray bars indicate no difference to the reference (blue), and red bars indicate statistical difference to the reference. The results show that only GPP_COS,PAR differs statistically from GPP_NLR at 30 min timescale.

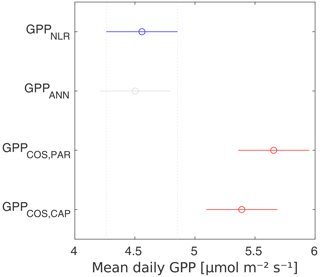
Figure B5 ANOVA test results for daily GPP data. Gray bars indicate no difference to the reference (blue), and red bars indicate statistical difference to the reference. The results show that both GPP_COS,PAR and GPP_COS,CAP differ statistically from both GPP_NLR and GPP_ANN at daily scale. GPP_COS,PAR and GPP_COS,CAP do not differ from each other.

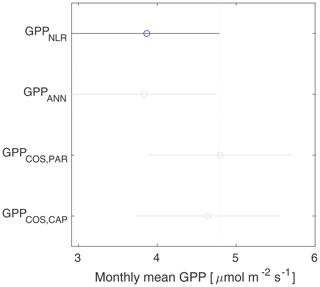
Figure B6 ANOVA test results for monthly GPP data. Gray bars indicate no difference to the reference (blue), and red bars indicate statistical difference to the reference. The results show that all GPPs are statistically the same at monthly scale.

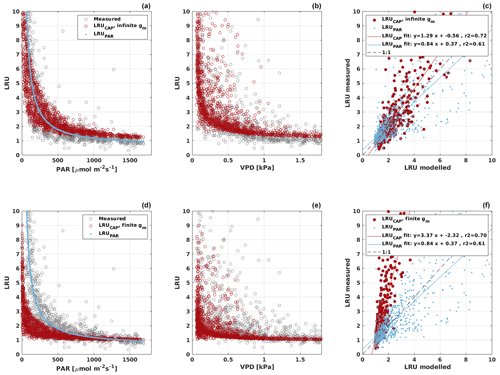
Figure B7 LRU derived from chamber measurements (gray) and modelled LRU_PAR (blue) and LRU_CAP (red) assuming infinite (a–c) or finite (d–f) mesophyll conductance (g_m) in LRU_CAP against PAR and VPD. Subplots (c) and (d) compare the chamber-measured LRU against modelled LRU_PAR and LRU_CAP.

Figure B8 Net ecosystem exchange (NEE) against photosynthetically active radiation (PAR) close to the compensation point during May, June, July, and August. Data are binned to different air temperature classes: $\mathrm{5}{}^{\circ }\mathrm{C}<T_{\mathrm{a}}<\mathrm{10}$ ^∘C (blue), $\mathrm{10}{}^{\circ }\mathrm{C}<T_{\mathrm{a}}<\mathrm{15}$ ^∘C (orange), and T_a>15 ^∘C (yellow).