the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of negative and positive CO2 emissions on global warming metrics using an ensemble of Earth system model simulations
Negar Vakilifard
Richard G. Williams
Philip B. Holden
Katherine Turner
Neil R. Edwards
David J. Beerling
The benefits of implementing negative emission technologies in the global warming response to cumulative carbon emissions until the year 2420 are assessed following the shared socioeconomic pathway (SSP) 1-2.6, the sustainable development scenario, with a comprehensive set of intermediate-complexity Earth system model integrations. Model integrations include 86 different model realisations covering a wide range of plausible climate states. The global warming response is assessed in terms of two key climate metrics: the effective transient climate response to cumulative CO2 emissions (eTCRE), measuring the surface warming response to cumulative carbon emissions and associated non-CO2 forcing, and the effective zero emissions commitment (eZEC), measuring the extent of any continued warming after net-zero CO2 emissions are reached. The transient climate response to cumulative CO2 emissions (TCRE) is estimated as 2.2 K EgC−1 (median value) with a 10 %–90 % range of 1.75 to 3.13 K EgC−1 in 2100, approximated from the eTCRE by removing the contribution of non-CO2 forcing. During the positive emission phase, the eTCRE decreases from 2.71 (2.0 to 3.65) to 2.61 (1.91 to 3.62) K EgC−1 due to a weakening in the dependence of radiative forcing on atmospheric carbon, which is partly opposed by an increasing fraction of the radiative forcing warming the surface as the ocean stratifies. During the net negative and zero emission phases, a progressive reduction in the eTCRE to 2.0 (1.39 to 2.96) K EgC−1 is driven by the reducing airborne fraction as atmospheric CO2 is drawn down mainly by the ocean. The model uncertainty in the slopes of warming versus cumulative CO2 emissions varies from being controlled by the radiative feedback parameter during positive emissions to being affected by carbon-cycle parameters during net negative emissions, consistent with the drivers of uncertainty diagnosed from the coefficient of variation of the contributions in the eTCRE framework. The continued warming after CO2 emissions cease and remain at zero gives a model mean eZEC of −0.03 K after 25 years, which decreases in time to −0.21 K at 90 years after emissions cease. However, there is a spread in the ensemble with a temperature overshoot occurring in 20 % of the ensemble members at 25 years after cessation of emissions. If net negative emissions are included, there is a reduction in atmospheric CO2 and there is a decrease in temperature overshoot so that the eZEC is positive in only 5 % of the ensemble members. Hence, incorporating negative emissions enhances the ability to meet climate targets and avoid risk of continued warming after net zero is reached.
- Article
(5302 KB) - Full-text XML
-
Supplement
(13683 KB) - BibTeX
- EndNote
There is an increasing need to adopt negative emission technologies (Luderer et al., 2013; Rogelj et al., 2015; Beerling et al., 2020) to enhance the chance of meeting the Paris climate agreement target (UNFCCC, 2015) to hold global warming well below 2 ∘C with an ambition of 1.5 ∘C given the ongoing growth in greenhouse gas concentrations (Boucher et al., 2012; Jeltsch-Thömmes et al., 2020). For a 1.5 ∘C target, there is a 66 % chance of meeting this target only if post-2019 cumulative carbon emissions are limited to less than ∼ 400 GtCO2 (IPCC, 2021). Two climate metrics of transient climate response to cumulative CO2 emissions (TCRE) and zero emissions commitment (ZEC) are essential to determine how much carbon may be emitted while remaining within the warming target.
The remaining carbon budget is inversely proportional to the TCRE, the increase in the global mean surface air temperature relative to cumulative CO2 emissions (Matthews et al., 2009; Zickfeld et al., 2012; IPCC, 2013; Gillett et al., 2013; Zickfeld et al., 2013; Friedlingstein et al., 2014; Matthews et al., 2017). Climate model projections reveal a simple near-linear relationship between the global surface air temperature change and cumulative CO2 emissions between 0 and ∼ 2000 PgC (MacDougall, 2016). However, despite a similar linear dependence, there is a wide inter-model range in TCRE values (Williams et al., 2017a; Spafford and MacDougall, 2020), varying from 1.4 to 2.5 K EgC−1 in intermediate-complexity Earth system models (Eby et al., 2013), 0.8 to 2.4 K EgC−1 in full-complexity Earth system models (Matthews et al., 2018) and 0.7 to 2.0 K EgC−1 (90 % confidence interval) in observationally constrained TCRE estimates from a 15-member Coupled Model Intercomparison Project (CMIP) 5 ensemble (Gillett et al., 2013).
For the case of radiative forcing exclusively from atmospheric CO2, the TCRE can be related to the dependence of the global mean temperature on the radiative forcing, the dependence of the radiative forcing on the atmospheric CO2 and the airborne fraction (Sect. 2; Williams et al., 2016; Ehlert et al., 2017; Katavouta et al., 2018; Williams et al., 2020). Applying this framework to seven CMIP5 and nine CMIP6 models following a 1 % annual increase in atmospheric CO2, the TCRE is affected by a large inter-model spread in the climate feedback parameter for CMIP6 (Williams et al., 2020) as well as by a larger inter-model spread in the land carbon system for CMIP5 (Jones and Friedlingstein, 2020). The inclusion of non-CO2 radiative forcing alters the relationship between emissions and surface warming through both direct warming and carbon feedback effects (Tokarska et al., 2018). For the more realistic case including non-CO2 radiative-forcing contributions, the TCRE may be estimated by approximately removing the warming linked to non-CO2 radiative forcing (Matthews et al., 2021). Alternatively, an effective TCRE (eTCRE) may be defined to include non-CO2 warming and the non-CO2 radiative forcing (Williams et al., 2016, 2017a).
The climate response after net-zero emissions is an important climate metric, encapsulated in the zero emissions commitment (ZEC) given by the mean surface air temperature change after CO2 emissions cease (Hare and Meinshausen, 2006; Matthews and Caldeira, 2008; Froelicher and Paynter, 2015; MacDougall et al., 2020). Quantification of the ZEC is critical for calculating the remaining carbon budget. Whether there is continued surface warming depends on competition between a cooling effect from the reduction in the radiative forcing from atmospheric CO2 as carbon is taken up by the ocean and terrestrial biosphere and a surface warming effect from a decline in the heat uptake by the ocean interior (Williams et al., 2017b). In an analysis of Earth system model responses to idealised CO2-only forcing, MacDougall et al. (2020) found a multi-model mean ZEC close to zero, with a wide spread in continued warming and cooling responses from individual models. Matthews and Zickfeld (2012) previously analysed the ZEC in the context of a realistic scenario by including contributions from non-CO2 forcings, but these authors did not address uncertainty. We address this gap by applying a perturbed physics ensemble to an experiment which includes non-CO2 forcing within the framework of a strong-mitigation scenario as is most appropriate for negative emissions.
Here we examine these two climate metrics, the TCRE and the ZEC, following the shared socioeconomic pathway (SSP) 1-2.6 scenario, which combines realistic socioeconomic conditions for sustainable development with the high-mitigation Representative Concentration Pathway (RCP) 2.6 scenario assuming large-scale employment of a range of greenhouse gas mitigation technologies and strategies. Our analysis is based on simulations with the intermediate-complexity Earth system model, Grid-ENabled Integrated Earth system model (GENIE-1). The use of intermediate complexity enables us to (i) quantify uncertainties through an ensemble consisting of 86 members that provide a wide range of plausible climate states and (ii) explore long timescales, in both historical and future periods. The pre-industrial baseline is chosen as 850 CE (Eby et al., 2013) rather than 1850 CE to account for both land use change and fossil fuel CO2 emissions occurring before 1850 CE. The reconstructions of land use change emissions for the periods prior to about 1800 have been based on prior estimates of population, mortality rate and land use assumptions and hold large uncertainties (Koch et al., 2019). The model was spun up to a pre-industrial climate and integrated from years 850 to 2420 CE, extending several centuries after the emissions cease to reveal whether there is continued warming and to quantify the effectiveness of negative emission applications. The TCRE analysis follows an eTCRE framework (Williams et al., 2016; Ehlert et al., 2017; Katavouta et al., 2018; Williams et al., 2020) and is compared with a correlation analysis between the varied model parameters and the slopes of change in temperature versus cumulative emissions. The effective ZEC (eZEC) analysis addresses the response of the ensemble during periods of net-zero carbon emissions but continued non-CO2 forcing following the SSP1-2.6 scenario.
In this study, the theoretical framework used to interpret the TCRE is set out including defining its thermal, radiative and carbon contributions (Sect. 2). The model methodology using the intermediate-complexity Earth system model GENIE-1 (Sect. 3) and the model responses including the spread in ensemble responses (Sect. 4) are described. The controls of the climate responses as defined by the two climate metrics, the effective TCRE and effective ZEC, are explored, including outlining the asymmetrical response to positive and negative emissions (Sect. 5). Finally, the implications of the study are summarised, including the benefits of implementing negative emissions (Sect. 6).
We first introduce the framework under the assumption of only CO2 forcing. A climate metric TCRE (in K EgC−1) is defined as the surface warming response to cumulative CO2 emissions:
where Δ is the change since year 850 CE, ΔT(t) is the global mean change in surface air temperature (in K), and Iem(t) is the cumulative CO2 emissions (in PgC) from the sum of fossil fuel emissions and land use changes.
The TCRE may be viewed as a product of two terms, the change in global mean air temperature divided by the change in the atmospheric carbon inventory, , and the airborne fraction, , given by the change in the atmospheric carbon inventory (in PgC) divided by the cumulative CO2 emissions (Matthews et al., 2009; Solomon et al., 2009; Gillett et al., 2013; MacDougall, 2016), such that
where is related to the transient climate response, defined by the temperature change at the time of doubling of atmospheric CO2 (Matthews et al., 2009). The TCRE is defined in terms of this surface warming response to CO2 forcing, usually following a 1 % annual rise in atmospheric CO2.
Alternatively, the TCRE may be linked to an identity involving a thermal dependence on radiative forcing, defined by the change in temperature divided by the change in radiative forcing, ΔF(t) (in W m−2), and the radiative-forcing dependence on CO2 emissions, defined by the change in radiative forcing divided by the cumulative CO2 emissions (Goodwin et al., 2015; Williams et al., 2016, 2017a), such that
These two viewpoints can be rationalised by rewriting the radiative-forcing dependence on CO2 emissions in Eq. (3) in terms of the radiative-forcing dependence on atmospheric CO2 and the airborne fraction (Ehlert et al., 2017; Katavouta et al., 2018; Williams et al., 2020).
The TCRE is then defined by the product of the thermal dependence, the radiative dependence between radiative forcing and atmospheric carbon, and the carbon dependence involving the airborne fraction:
The thermal response may be further understood from an empirical global radiative balance (Gregory et al., 2004; Forster et al., 2013). The increase in radiative forcing, ΔF(t), drives an increase in planetary heat uptake, N(t) (in W m−2), plus a radiative response, which is assumed to be equivalent to the product of the increase in global mean surface air temperature, ΔT(t), and the climate feedback parameter, λ(t) (in W m−2 K−1):
The thermal dependence in Eq. (4) given by the dependence of surface warming on radiative forcing, , is then given by the product of the inverse of the climate feedback, λ−1(t), and the planetary heat uptake divided by the radiative forcing, :
where represents the fraction of the radiative forcing that is lost to space and may be viewed as effectively equivalent to the fraction of the radiative forcing that warms the surface rather than the ocean interior.
The carbon dependence in Eq. (4) involving the airborne fraction, , is related to the changes in the ocean-borne, land-borne and sediment-borne fractions (Jones et al., 2013):
where the changes in the ocean, land and sediment inventories are denoted by ΔIocean(t), ΔIland(t) and ΔIsediment(t) (in PgC), respectively.
The TCRE is formally defined in terms of the climate response to cumulative CO2 emissions following a 1 % annual rise in atmospheric CO2 (Matthews et al., 2009). As the rise in anthropogenic radiative forcing is currently dominated by the radiative forcing from atmospheric CO2, the TCRE is a useful climate metric to understand future climate projections. However, in the more realistic framework we apply here, the warming response includes contributions from non-CO2 forcing. In such experiments, Matthews et al. (2021) advocate estimating the TCRE by approximately removing the warming due to the non-CO2 radiative forcing by multiplying by a non-dimensional factor (1−fnc), now explicitly acknowledging that ΔT(t) is not solely driven by Iem(t):
Matthews et al. (2021) interpret the non-dimensional factor (1−fnc) as representing the non-CO2 fraction of total anthropogenic forcing where . This estimation of the TCRE from general forcing scenarios assumes that the time – and scenario – independence of the TCRE translates to a general response independence from radiative-forcing elements.
In order to allow for possible changes in the thermal and carbon responses from the non-CO2 forcing, we prefer to define an eTCRE including the effect of the radiative forcing from non-CO2 and CO2 radiative components using a series of mathematical identities (Williams et al., 2016, 2017a), where
By including the effect of the non-CO2 radiative forcing, the eTCRE in Eq. (9) is larger than the TCRE with non-CO2 radiative forcing removed in Eq. (8) whenever the positive radiative effect of non-CO2 greenhouse gases exceeds the negative effect from aerosols. Our subsequent model diagnostics focus on evaluating the eTCRE and the thermal, radiative and carbon dependencies using Eq. (9).
Our analysis is based on Earth system model simulations for SSP1-2.6, the scenario with the fewest socioeconomic challenges to adaptation and mitigation of climate change (O'Neill et al., 2017; Riahi et al., 2017), which allows large-scale deployment of negative emission technologies (NETs). Here, we investigate the implications of NETs for atmospheric CO2 removal over 400 years by applying the net negative emissions of ∼ 156 PgC between the years 2077 and 2250 (Fig. 1a–b).
We employed the global intermediate-complexity Earth system model, GENIE-1 (release 2.7.7) (Holden et al., 2013a), consisting of the 3-D frictional geostrophic ocean model (GOLDSTEIN) ( resolution with 16 depth levels in the ocean) coupled to the 2-D energy moisture balance model of the atmosphere (EMBM) and a thermodynamic–dynamic sea-ice model (Edwards and Marsh, 2005). The land surface module is the dynamic model of terrestrial carbon and land use change ENTSML (Holden et al., 2013a). Ocean biochemistry, deep-sea sediments and rock weathering are modelled by BIOGEM (Ridgwell et al., 2007), SEDGEM ( resolution) and RoKGeM (Colbourn et al., 2013) modules, respectively.
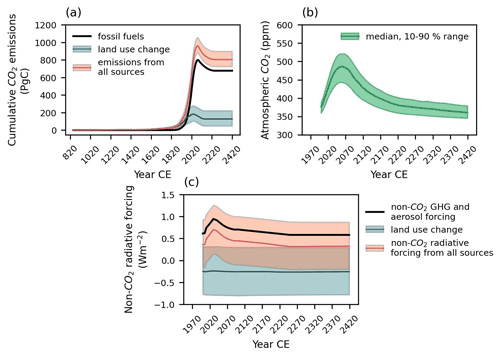
Figure 1(a) The cumulative CO2 emissions from 850 CE till the end of the model integration at year 2420; (b) the evolution of the atmospheric CO2; (c) non-CO2 radiative forcing from all sources (non-CO2 greenhouse gas (GHG) and aerosol forcing and land use change) from the year 2000 for the SSP1-2.6 scenario. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles.
Simulations start from pre-industrial spin-ups (Holden et al., 2013b) and follow historical transient forcing from 850 to 2005 CE (Eby et al., 2013). In this setting, the land use change emissions start from 850 CE and emissions from other sources including fossil fuels are introduced from 1750 CE. The historical forcing includes CO2 emissions, non-CO2 radiative forcings and land use changes, including both anthropogenic and natural sources (volcanic eruptions and solar variability). In order to meld the spin using RCP2.6 at year 2005 with the projected scenario SSP1-2.6, a constant adjustment of 0.446 W m−2 was added to the non-CO2 radiative forcing. This adjustment can be viewed as representing contributions from land use change albedo (explicitly modelled in GENIE-1, Fig. 1c) and from non-anthropogenic forcings, which were modelled in the historical spin-up (Eby et al., 2013), comprising volcanic forcing of 0.184 W m−2 and solar forcing of 0.059 W m−2 in 2005.
The future forcing scenario (2005 to 2420) follows SSP1-2.6 (Riahi et al., 2017) to the year 2100 and is extended to 2420. Negative emissions are applied as a reduction in anthropogenic CO2 emissions from the late 2020s, giving net negative emissions from 2077. To extend the SSP1-2.6 from 2100, we follow a similar protocol to Meinshausen et al. (2020). Land use change CO2 emissions are reduced to zero by 2150 with non-CO2 land use emissions held fixed from 2100. Fossil fuel emissions, including non-CO2 greenhouse gases, and negative CO2 emissions are all brought to zero by 2250 (Fig. 1a and c). This protocol differs slightly from Meinshausen et al. (2020), who reduce negative emissions to zero by 2200; we prefer to avoid a second period of positive emissions from 2200 to 2250. Therefore, we have three CO2 emission phases: positive emissions from 2020 to 2077, net negative emissions from 2077 to 2250 and zero emissions from 2250 to 2420 (Fig. 1a).
We assume that the carbon removed through negative emissions leaves the system permanently, which is the representation of NETs with long-lived and permanent carbon storage such as carbon capture and storage. This assumption also approximates enhanced rock weathering, although the chemical effects of weathering products are neglected, such as the effect of bicarbonate changes on ocean biogeochemistry which drive co-benefits for the ocean and marine ecosystems (Vakilifard et al., 2021).
To quantify the uncertainty in climate and carbon-cycle responses, we used an 86-member ensemble, a subset of a calibrated 471-member ensemble varying 28 model parameters (Holden et al., 2013a). The selection of 24 of these parameters (Holden et al., 2013b) covers oceanic, atmospheric, sea-ice, ocean biogeochemistry and terrestrial vegetation processes that are thought to contribute to variability in atmospheric CO2 on glacial–interglacial timescales (Kohfeld and Ridgwell, 2009). The remaining 4 parameters are relevant to the modern state of the climate carbon cycle, describing uncertainties in soil under land management, crop albedo, climate sensitivity and CO2 fertilisation. The 86 ensemble members are perturbed to cover uncertainty in the 28 parameters and are all constrained to simulate plausible pre-industrial values of global temperature, Atlantic overturning circulation, sea-ice coverage, vegetative and soil carbon, sedimentary calcium carbonate, and dissolved ocean oxygen (Holden et al., 2013b). They additionally simulate reasonable values of atmospheric CO2 at snapshots (1620, 1770, 1850, 1970 and 2005 CE) through the historical transient period (Foley et al., 2016). The varied parameters are summarised in the Supplement in Table S4 and are fully detailed, along with the ensemble design methodology, in Holden et al. (2013a, b).
The GENIE-1 model responses are next described in terms of the spread of ensemble responses and the essentials of the carbon and thermal responses.
4.1 Characterising the model ensemble
There are a wide range of responses within the ensemble members making up the model projections following the future forcing scenario SSP1-2.6. At the end of the positive emission phase at the year 2077, the increase in surface air temperature ranges from 1.5 to 4.2 K, the Atlantic meridional overturning circulation change from −12.3 to 0.6 Sv, the land carbon change from a loss of 78 PgC to a gain of 488 PgC and the ocean carbon uptake from a gain of 247 to 586 PgC (Fig. 2).
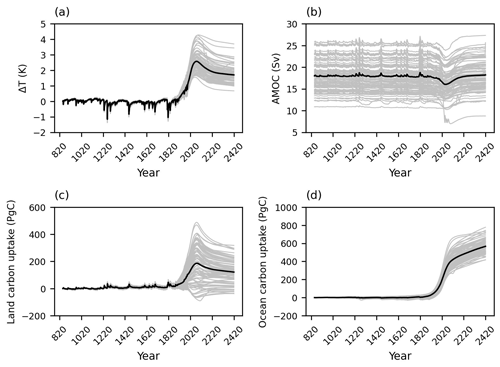
Figure 2Inter-model spread of 86-member ensemble for change in (a) the surface air temperature, (b) Atlantic meridional overturning circulation (AMOC), (c) the land carbon pool and (d) the ocean carbon pool from the year 850 CE until the year 2420 following the SSP1-2.6 scenario. Black lines show the mean values.
4.2 Carbon response
The distribution of carbon between carbon inventories is diagnosed (Fig. 3), and carbon conservation ensures that at all times the sum of the change in the carbon content of the atmosphere, ΔIatmos(t); ocean, ΔIocean(t); land, ΔIland(t); and ocean sediment, ΔIsediment(t), equals the cumulative CO2 emissions from both land use change and fossil fuels, Iem(t), with all inventories in petagrams of carbon (PgC):
Aside from the ocean sediments, which lose carbon, there is an increase in the carbon content of all inventories between the years 2020 and 2077, the positive emission phase (Fig. 3). During this emission phase, the carbon release from the sediment reservoir is ∼ 14 PgC on average, equivalent to a sedimentary CaCO3 dissolution flux of ∼ 21 TmolC yr−1 and consistent with Archer (1996), Ridgwell and Hargreaves (2007), and Sulpis et al. (2018). The application of carbon capture and storage from the year 2077 decreases the total carbon inventory until the year 2250. During the zero emission phase, the increase in ocean storage is associated with a decrease in carbon content in the atmosphere, land and sediment.
4.3 Thermal response
For the thermal analysis, a global energy balance (Eq. 5) is diagnosed, , in which the energy balance is expressed as the relationship between radiative forcing, ΔF(t) (W m−2); planetary heat uptake, N(t) (W m−2); and radiative response, λ(t)ΔT(t) (W m−2).
The radiative forcing, ΔF(t), is the sum of non-CO2 radiative forcing (including land use change albedo) and CO2 radiative forcing. The non-CO2 radiative forcing, (W m−2), is a prescribed model forcing input, besides land use change, which is diagnosed as the change in reflected surface insolation under land use change relative to that with natural vegetation, averaged annually across all grid cells. The land use change maps were also fixed from the year 2005, and these were associated with a global forcing of −0.53 to 0.05 W m−2 (25th- to 75th-percentile range) and mean and median values of −0.23 and −0.26 W m−2, respectively, across the ensemble. The uncertainty is driven primarily by crop albedo, which varies between 0.12 and 0.18 across the ensemble (Holden et al., 2013a). The CO2 radiative forcing, (W m−2), was calculated individually for each simulation based on the atmospheric CO2 concentration (C(t) (ppm)) as outlined in IPCC (2001):
where α is a constant equal to 5.35 W m−2 and C(t0) equals 278 ppm.
The ocean heat uptake is used to represent the planetary heat uptake as the model ocean is the principal energy sink and the model does not take into account the energy stored in the lithosphere or consumed in the melting of the ice sheets. In comparison, in the real world, the ocean is responsible for storing over 90 % of the Earth's total energy increase (Church et al., 2011). The climate feedback parameter, λ(t) (W m−2 K−1), is diagnosed from the ocean heat uptake and the change in global mean surface air temperature (Eq. 5). Most of the radiative forcing drives a radiative response involving a rise in surface air temperature, rather than an increase in ocean heat uptake (Fig. 4).
The climate response of the GENIE-1 model projections for positive and negative emissions is next assessed in terms of the response of two climate metrics, the effective transient climate response to cumulative CO2 emissions (eTCRE) and the effective zero emissions commitment (eZEC), as well as in terms of identifying the asymmetrical response to positive and negative emissions.
The results of GENIE-1 simulations show a linear relationship between the change in the surface air temperature and cumulative CO2 emissions over the positive emission phases (Fig. 5), with the slopes of this relationship varying between ∼ 1.62 and 3.42 K EgC−1 (based on the 10th- and 90th-percentile values). The range of slopes of the ΔT-versus-Iem curve, calculated by linear regression, over the net negative emission phase is larger than in the positive emission phase by a factor of ∼ 2 due to a decrease in non-CO2 radiative forcing leading to additional cooling during this period. Over this emission phase, the warming relationship is not linear in all ensemble members and exhibits a hysteresis behaviour, as previously identified in Zickfeld et al. (2016), Jeltsch-Thömmes et al. (2020) and Koven et al. (2022). Differences in the rates of surface air temperature change over the net negative emission phase are mainly due to the terrestrial carbon uncertainty (discussed in Sect. 4.2.2).
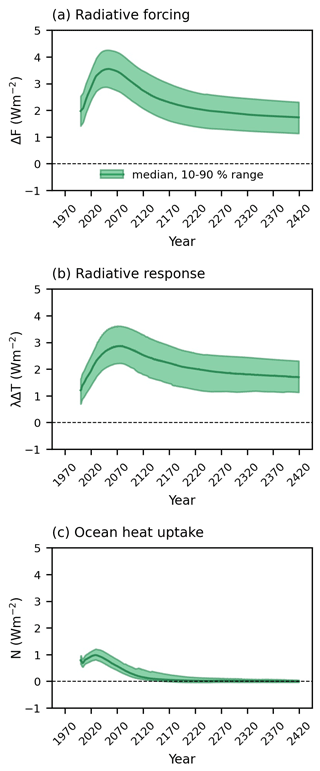
Figure 4The evolution of (a) radiative forcing, (b) radiative response and (c) ocean heat uptake in the SSP1-2.6 scenario from the year 2000. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles.
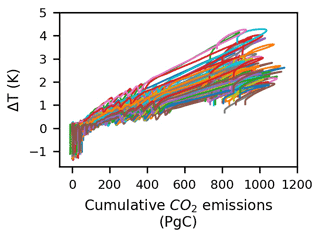
Figure 5Change in the surface air temperature versus cumulative CO2 emissions from 850 CE until the year 2420 in the SSP1-2.6 scenario.
5.1 Drivers of the effective transient climate response to cumulative CO2 emissions
Following Sect. 2, the effective transient climate response to cumulative CO2 emissions (eTCRE) is evaluated in terms of the product of (i) the dependence of surface warming on the radiative forcing, referred to as the thermal dependence, ; (ii) the dependence of the radiative forcing on the cumulative CO2 emissions, referred to as a radiative dependence, ; and (iii) the airborne fraction, , referred to as a carbon dependence (Eq. 9):
The model ensemble reveals a decrease in the eTCRE from the median value of 2.71 K EgC−1 in the year 2020 to 2.0 K EgC−1 in the year 2420 (with 10 %–90 % ranges of 2.0 to 3.65 and 1.39 to 2.96 K EgC−1, respectively) (Fig. 6a). During the positive emission phase (to the year 2077) this reduction is driven by a weakening in the radiative forcing with an increase in atmospheric carbon (Fig. 6b), which dominates over the increase in the thermal dependence (Fig. 6d). During the net negative and zero emission phases (from the year 2077), the eTCRE reduction is driven by the reducing airborne fraction as CO2 is drawn down by the ocean (Fig. 6e).
The eTCRE is scenario dependent and varies with both CO2 and non-CO2 portions of the radiative forcing. Following the analysis of Matthews et al. (2021), we quantify the spread of the non-CO2 fraction of total anthropogenic forcing, fnc (from Eq. 8), between 2020 and 2100 (Table S1) to investigate the extent of scenario dependency of the eTCRE. The results show that the fnc range varies from ∼ 10 % to ∼ 26 % (25th- to 75th-percentile values) in 2020 to ∼ 5 % to ∼ 21 % in 2100, corresponding to a ∼ 6 % decrease (mean value) over the course of 80 years. The TCRE diagnosed by removing the non-CO2 warming factor (from Eq. 8) remains constant at ∼ 2.2 K EgC−1 (median values) over the entire period. However, the uncertainty increases towards the end of the century, varying from 1.75 to 2.82 K EgC−1 (10th- to 90th-percentile values) in 2020 to up to ∼ 3.13 K EgC−1 in 2100 (Fig. S1).
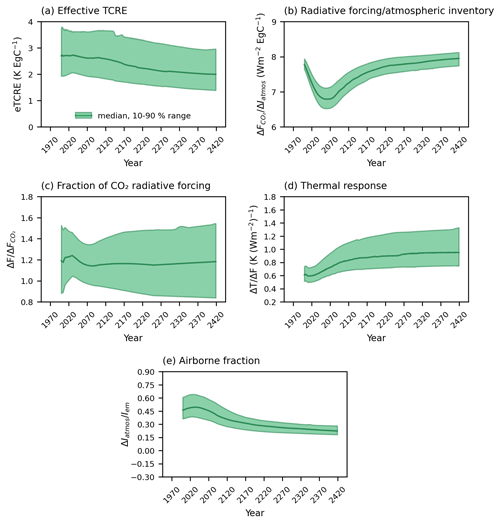
Figure 6Effective transient climate response to cumulative CO2 emissions (eTCRE) and its components for the SSP1-2.6 scenario from the year 2000: (a) eTCRE, (b) dependence of the radiative forcing on atmospheric CO2, (c) fractional radiative-forcing contribution from atmospheric CO2, (d) thermal dependence and (e) airborne fraction. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles.
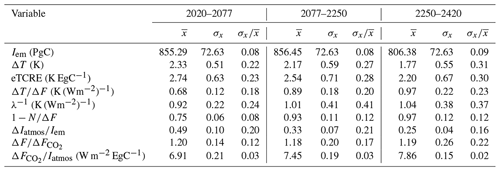
The uncertainty in the eTCRE, as well as its dependencies for the model ensemble, is assessed based on the non-dimensional coefficient of variation, given by the inter-model standard deviation divided by the ensemble mean (Williams et al., 2020). The uncertainty in the eTCRE varies from 0.23 to 0.3 over the course of the model integrations and is larger by 0.05 for the net negative emission phase compared to the positive emission phase (Table 1).
During the positive and net negative emissions, the coefficients of variation for the thermal dependence (∼ 0.18 to ∼ 0.2) and airborne fraction (∼ 0.2) provide the dominant contributions to the eTCRE uncertainty (Table 1). During the zero emission phase, however, the coefficient of variation for the fractional radiative-forcing contribution from atmospheric CO2, (∼ 0.22), is larger than the contribution from the airborne fraction (∼ 0.16). In all emission phases, the dependence of the radiative forcing on atmospheric CO2, , has the least contribution to the eTCRE uncertainty (∼ 0.02).
Table 1Effective transient climate response to cumulative CO2 emissions (eTCRE) and its components for the different emission phases in the SSP1-2.6 scenario. The coefficient of variation ( is defined by the inter-model standard deviation (σx) divided by the inter-model mean (.
5.1.1 Carbon dependence for the effective transient climate response to cumulative CO2 emissions
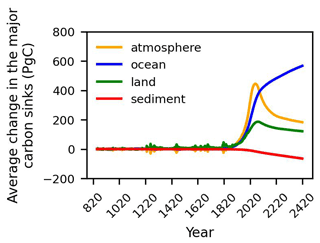
The fraction of emitted CO2 that remains in each carbon inventory (based on Eq. 7) varies over the course of the integrations. The carbon dependence for the eTCRE is given by the airborne fraction of carbon emissions, . By the year 2077, the end of the positive emission phase, the atmosphere is the largest carbon sink with an airborne fraction of ∼ 49 % (mean value) (Fig. 7a and Table S2). After the year 2077, during the net negative and zero emission phases, the ocean becomes the dominant carbon sink with an increase in the ocean-borne fraction, , up to ∼ 67 % (mean value) by 2420 (Fig. 7b and Table S2). The land-borne fraction, , decreases from ∼ 19 % (mean value) in 2020 to the minimum value of ∼ 15 % in 2420 (Fig. 7c and Table S2). The sediment-borne fraction, , remains negative at ∼ −0.04 (mean value) over the entire period (Fig. 7d and Table S2) and therefore acts as a weak carbon source.
The coefficient of variation is the largest for the land-borne fraction (∼ 0.7), followed by the sediment-borne fraction (∼ −0.5) and then the airborne and ocean-borne fractions, decreasing from ∼ 0.2 over the positive emission phase to ∼ 0.15 during the zero emission phase (Table S2). The main contribution to the model ensemble spread is, therefore, the land carbon system.
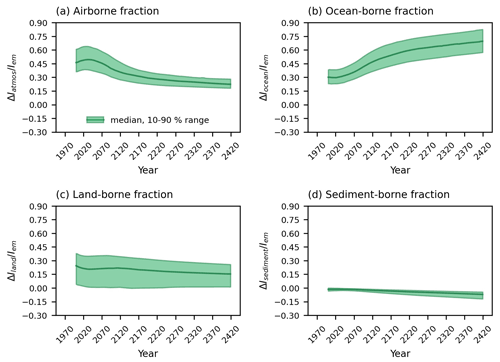
Figure 7The evolution of the (a) airborne fraction, (b) ocean-borne fraction, (c) land-borne fraction and (d) sediment-borne fraction in the SSP1-2.6 scenario. Note that the y axis shows the cumulative fraction of CO2 which remains in each carbon inventory. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles from the year 2000.
5.1.2 Radiative-forcing dependence for the effective transient climate response to cumulative CO2 emissions
By the end of the positive emissions at year 2077, the radiative-forcing dependence on atmospheric CO2 emissions, , weakens due to a saturation in the radiative forcing with an increase in atmospheric CO2 (Gillett et al., 2013; William et al., 2020) (Figs. 1b and 8b). During the net negative emissions and zero emission phases over the next few centuries from the year 2077 onwards, rises again due to a decrease in atmospheric CO2 associated with the decrease in the airborne fraction (Fig. 8c).
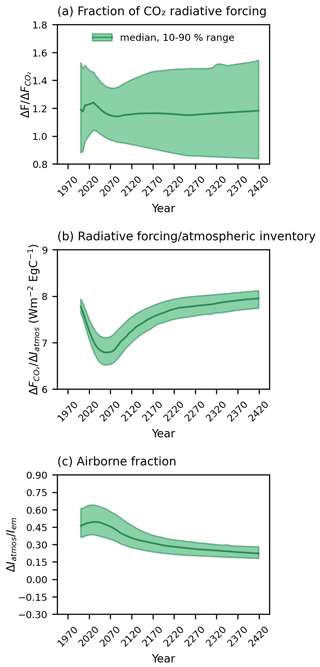
Figure 8Radiative-forcing dependence for the effective TCRE and its components in the SSP1-2.6 scenario from the year 2000. (a) Fractional radiative-forcing contribution from atmospheric CO2; (b) dependence of the radiative forcing on atmospheric CO2; (c) airborne fraction. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles.
5.1.3 Thermal dependence for the effective transient climate response to CO2 emissions
The thermal dependence of the eTCRE, involving the dependence of the surface warming on the radiative forcing, , increases in all emission phases (Fig. 9a) due to the reinforcing contributions of the inverse of the climate feedback parameter, λ(t)−1 (Fig. 9b), and the fraction of the radiative forcing warming the surface, (Fig. 9c). The increase in λ(t)−1 is equivalent to a slight decrease in the climate feedback λ(t). The temporal evolution of the climate feedback parameter is mirrored in other climate model studies as climate feedbacks evolve on different timescales according to the nature of the controlling processes (Gregory et al., 2004; Armour et al., 2013; Knutti and Rugenstein, 2015; Goodwin, 2018). The fraction of the radiative forcing warming the surface increases by ∼ 22 % (based on the mean values, Table 1) from the year 2020 to the year 2420 with a corresponding reduction in the heat transfer into the deep ocean; by the year 2420, nearly all the radiative forcing is warming the surface with the ratio reaching 0.97 (mean values, Table 1) (Fig. 9c–d). This response is probably due to an increase in ocean stratification from the rise in surface ocean temperature (Figs. S2–S4) from the increased radiative forcing.
The coefficient of variation for the thermal dependence remains ∼ 0.2 over the entire period (Table 1). Within the thermal dependence, the term relating to the climate feedback parameter λ(t)−1 has a coefficient of variation more than ∼ 3 times that of the fraction of the radiative forcing warming the surface (Table 1). As the thermal-dependence terms, λ(t)−1 and , are strongly anti-correlated (Fig. S5), the relative spread in the thermal response is thus mitigated by the feedback between the climate feedback parameter and the fraction of the radiative forcing warming the surface.
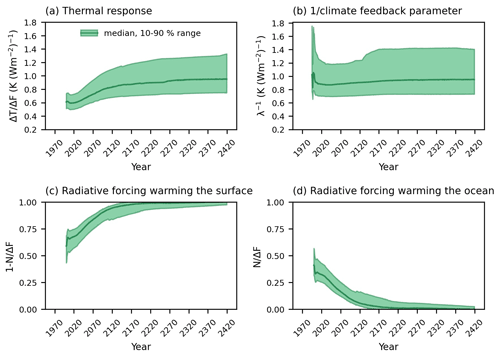
Figure 9The evolution of (a) thermal dependence for the effective TCRE given by the dependence of the surface warming on the radiative forcing, , and the contributions from (b) the inverse of the climate feedback, (c) the fraction of the radiative forcing warming the surface and (d) the fraction of the radiative forcing warming the ocean interior in the SSP1-2.6 scenario from the year 2000. Solid lines show the median values, and shaded areas indicate the values between the 10th and 90th percentiles.
5.2 The asymmetry of the Earth system response to positive and negative emissions
5.2.1 Hysteresis
The relationship between the surface air temperature and atmospheric CO2 exhibits hysteresis behaviour in most ensemble members, consistent with climate change reversibility studies (Fig. 10a) (Tokarska and Zickfeld, 2015; Jeltsch-Thömmes et al., 2020). The temperature remains at high levels after high atmospheric CO2, concurrently with a decrease in the ocean heat uptake, N(t) (Fig. 10b). The ability of the ocean interior to take up heat diminishes in time, probably due to increasing stratification and weakening ventilation. The fraction of the radiative forcing warming the ocean interior, (Fig. 10c), then continues to decrease after the peak in atmospheric CO2, leading to higher surface air temperatures even after the lower CO2 concentrations are restored.
The atmospheric CO2 declines during the net negative emission phase from the year 2077 (Fig. 1b) associated with the cumulative CO2 emissions of ∼ 960.4 PgC (median value) (Figs. 1a and 10d). After the cessation of the emissions, the atmospheric CO2 continues to decrease (Fig. 10d) mainly due to uptake by the ocean and to a lesser extent the land (Fig. 10e–f). The ocean carbon uptake is governed by the air–sea flux of CO2 and thermocline ventilation, with uncertainties dominated by ventilation processes transferring carbon from the surface ocean to the main thermocline and deep ocean (Holden et al., 2013b; Goodwin et al., 2015; Zickfeld et al., 2016; Jeltsch-Thömmes et al., 2020). The ocean continues to take up carbon after the peak in atmospheric CO2 as there is continuing long-term adjustment and ventilation of the deep ocean (Fig. 10e). The complex responses of land carbon (Fig. 10f) are driven by a range of competing processes, most notably carbon uptake through CO2 fertilisation and the carbon release through historical land use changes and accelerated respiration under warming.
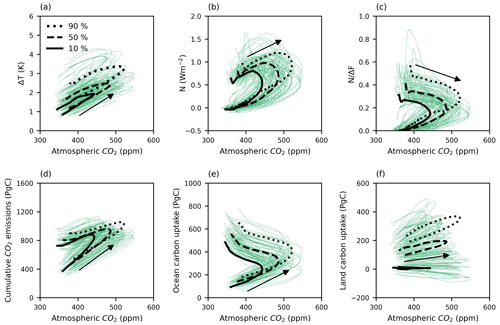
Figure 10The thermal (upper row) and carbon (lower row) variables versus atmospheric CO2 in the SSP1-2.6 scenario from the year 2000. (a) Change in surface air temperature; (b) ocean heat uptake; (c) fraction of the radiative forcing warming the ocean interior; (d) cumulative CO2 emissions; (e) change in the ocean carbon pool; (f) change in the land carbon pool. In each panel the black lines show the median and 10th- and 90th-percentile values of the atmospheric CO2 versus the median and 10th- and 90th-percentile values of the thermal and carbon variables.
5.2.2 Correlation between the model parameters and the slope of the change in surface air temperature versus cumulative CO2 emissions (
We calculated the coefficients of determination (R2) between and the 28 model parameters across the ensemble during both positive and net negative emission phases. For this purpose, 4 of the 86 simulations were omitted as outliers because they were undergoing substantial re-organisation of ocean circulation during the period of net negative emissions (Fig. S6), significantly perturbing ocean heat uptake.
During the positive emission phase, uncertainty in is dominated by the radiative feedback parameter (OL1) (R2 ∼ 61 %) (Table 2), which perturbs outgoing longwave radiation proportionally to ΔT (Matthews and Caldeira, 2007). This parameter is primarily designed to capture unmodelled cloud responses to global average temperature change, and it has previously been shown to drive 81 % of the variance in GENIE-1 climate sensitivity (Holden et al., 2010). The parameter links to the climate feedback parameter in the eTCRE framework (Sect. 4.1), which was shown to be the dominant driver of uncertainty in the thermal response and therefore eTCRE values.
Although radiative-forcing uncertainty dominates, carbon-cycle parameters also drive variance via the land use change soil carbon parameter (KC) (R2 ∼ 12 %) through its control on soil carbon losses under land use change. The fractional vegetation parameter (VFC) (R2 ∼ 11 %) drives additional carbon-cycle uncertainty through its control on terrestrial carbon surface density. The results are associated with the airborne fraction in the eTCRE framework, diagnosed as another factor controlling the uncertainty in the eTCRE during this emission phase (Sect. 4.1).
During net negative emissions (2077–2250), uncertainty in is affected mainly by the CO2 fertilisation (VPC) (R2 ∼ 35 %), which is a major source of terrestrial carbon uncertainty, and to a lesser extent the parameter that controls the rate of carbon loss from soils under land use change (KC, ∼ 11 %). The effect of the carbon contribution in the uncertainty is expressed through the airborne fraction in the eTCRE framework, which was revealed to be the main reason behind the large spread of the eTCRE over the net negative emission phase (Sect. 4.1), consistent with MacDougall et al. (2017).
5.3 The effective zero emissions commitment
The zero emissions commitment (ZEC) is now assessed, given by the mean surface air temperature change after CO2 emissions cease (Hare and Meinshausen, 2006; Matthews and Caldeira, 2008; Froelicher and Paynter, 2015; MacDougall et al., 2020). Whether there is continued surface warming depends on competition between a cooling effect from reduction in atmospheric CO2 due to the ocean and land sequestration of carbon and a surface warming effect from a decline in the heat uptake by the ocean interior (Williams et al., 2017b).
In our analysis, we define the effective ZEC (eZEC), which assesses the continued surface warming after the cessation of CO2 emissions while the non-CO2 greenhouse gas and aerosol forcings evolve. Our reference scenario applies SSP1-2.6 CO2 emissions until the year 2077 and zero emissions thereafter, with cumulative emissions of ∼ 961 PgC (median value) (Fig. S7). Following the analysis of MacDougall et al. (2020), we define eZEC25, eZEC50 and eZEC90 as the mean surface air temperature anomalies at the 25th, 50th and 90th years after the cessation of emissions to account for the implications of the eZEC over a range of multi-decadal timescales relevant to climate policy.
Diagnosed eZEC values are illustrated in Fig. 11 (the reference plotted as orange bars). In the reference scenario, the distribution of the eZEC displays an uncertain sign. There is a temperature overshoot in 20 % of eZEC25 values (10 %–90 % range from −0.08 to 0.02 K) and in 11 % of eZEC50 values (range from −0.17 to 0.01 K) and 5 % of eZEC90 values (range from −0.31 to −0.05 K). The ensemble means of eZEC25, eZEC50 and eZEC90 are −0.03, −0.10 and −0.21 K, respectively, and compare to values of −0.01, −0.07 and −0.12 K in the 1000 PgC experiment of MacDougall et al. (2020) (grey bars). The additional cooling is in part due to ongoing reductions in non-CO2 forcing from 0.728 W m−2 in 2077 to 0.648 W m−2 in 2167 (Fig. 1c), noting that MacDougall et al. (2020) performed an idealised experiment that only considered CO2 emissions forcing. We realise that our uncertainties are lower than those of MacDougall et al. (2020), which at least in part reflects the absence of internal (decadal) variability in the EMBM of GENIE-1, noting that inter-annual, although not decadal, variability was removed from MacDougall et al. (2020) through 20-year averaging.
In contrast to the reference scenario, surface temperatures decrease in all the ensemble members after cessation of positive emissions in the SSP1-2.6 scenario. We consider two alternative interpretations of the eZEC, the warming after the cessation of positive emissions (in 2077) and the warming after the cessation of net negative emissions (in 2250). The former may be more relevant from a policy perspective (as the time of likely peak warming), while the latter is theoretically useful to quantify committed warming when emissions are precisely zero.
The blue bars in Fig. 11 illustrate the eZEC results for the SSP1-2.6 scenario calculated relative to 2250. There is a temperature overshoot in 5 % of the eZEC25 values; however, the values remain at or below zero within the 10 %–90 % range (−0.06 to 0 K). The values of eZEC25 and eZEC90 are robustly negative, ranging from −0.1 to −0.01 K and −0.16 to −0.03 K (10th- to 90th-percentile range), respectively. Ensemble means are −0.03 K for eZEC25, −0.06 K for eZEC50 and −0.09 K for eZEC90.
The green bars in Fig. 11 illustrate the eZEC values from 2077 (which includes the period of ongoing net negative emissions). The average values of the eZEC are significantly lower than from 2250, being −0.1, −0.26 and −0.47 K, due to the additional cooling driven by net negative emissions. All eZEC values are again robustly negative, varying between −0.14 and −0.05 for eZEC25, −0.34 and −0.16 for eZEC50, and −0.61 and −0.31 for eZEC90 (10th- to 90th-percentile values), confirming that no ensemble member exhibits a temperature overshoot after the cessation of positive emissions.
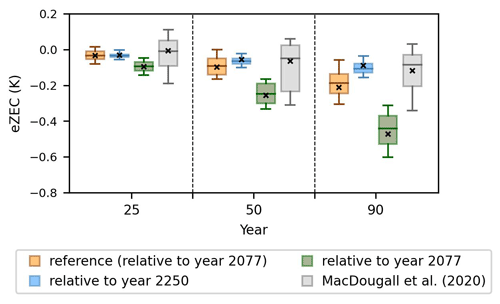
Figure 11The distribution of the effective zero emissions commitment (eZEC) in the reference scenario at the 25th, 50th and 90th years relative to the year 2077 (orange bars) and in SSP1-2.6 relative to the year 2250 (blue bars) and relative to the year 2077 (green bars) versus the zero emissions commitment results of MacDougall et al. (2020) (grey bars). The mean values are shown with cross marks. Note that the year 2077 is the end of the positive emission phase and the year 2250 is the end of the net negative emission phase.
There is an increasing need to develop and implement carbon capture and sequestration techniques to meet the Paris Agreement 1.5 and 2 ∘C temperature targets (UNFCCC, 2015). However, it is unclear how these negative emissions affect the climate response, as represented by two key climate metrics: the effective transient climate response to cumulative CO2 emissions (eTCRE), defining the relationship between surface warming and cumulative CO2 emissions, and the effective zero emissions commitment (eZEC), defining the anticipated warming after the cessation of CO2 emissions and continued non-CO2 greenhouse gas and aerosol forcings. The effect of negative emissions is assessed here using a GENIE-1 ensemble, following SSP1-2.6 with the net negative CO2 emissions of ∼ 156 PgC over 173 years. The model responses include 86 members that span a wide range of climate and carbon-cycle feedback strengths. The ensemble analysis is enabled by employing low resolution and intermediate complexity, with the most notable simplifications being of the fixed wind-field energy–moisture balance atmosphere, neglecting dynamic atmosphere–ocean feedbacks, and the simple model of terrestrial carbon, which neglects nutrient limitation, does not represent permafrost (or methane) and has a one-level description of soil carbon.
The eTCRE decreases in time due to a combination of the weakening in the radiative forcing with an increase in atmospheric carbon during positive emissions and a reduction in the airborne fraction after emissions cease, which together outweigh the strengthening thermal dependence.
The comparison of the coefficient of variation for the eTCRE and its dependencies shows that the thermal dependence and airborne fraction almost equally contribute to the uncertainty in the eTCRE during the positive emission phase. The results are consistent with those from the model parameter correlation analysis in which different slopes of the change in surface air temperature versus emissions are due to primarily the uncertainty in radiative feedbacks and to a lesser extent carbon-cycle feedbacks. Our results differ from the analyses of CIMIP5 and CMIP6 ensembles in which the radiative-forcing response and thermal response were the main contributors to the uncertainty in the TCRE, respectively (Williams et al., 2020). During the net negative emission phase, both analyses show that the carbon dependence causes the main uncertainty in the values of the eTCRE.
The relationship between thermal and carbon feedbacks with an increase in atmospheric CO2 exhibits hysteresis behaviour. The fraction of the radiative forcing warming the surface continues to increase after peak atmospheric CO2 as the ocean is stratified, leading to higher surface air temperatures after lower atmospheric CO2 values are restored. The increase in the ocean storage after the peak in atmospheric CO2 is associated with the long-term adjustment and ventilation of the deep ocean, while the reason for the continued terrestrial carbon storage relates to competing processes such as carbon uptake through CO2 fertilisation and carbon release through historical land use changes and accelerated respiration under warming.
The eZEC is close to zero. In the model mean of the integrations that exclude carbon capture and storage, the eZEC is −0.03 K at 25 years and decreases to −0.21 K at 90 years after emissions cease. However, even assisted by gradual reductions in non-CO2 forcing as in this scenario, the distribution of the eZEC after 25 years from the cessation of emissions shows continued warming in ∼ 20 % of ensemble members. Including carbon capture and storage reduces the probability of continued warming after net zero, with 95 % ensemble members exhibiting an eZEC close to or below zero. Hence, implementing negative emissions is required to reduce the risk of overshoot and continued warming after net zero is reached and increase the probability of meeting the Paris targets. Negative emissions technologies with naturally long CO2 removal lifetimes, such as enhanced rock weathering (Beerling et al., 2020), may be especially well suited for this purpose as the legacy effects of the repeated application of this technology increase the rate of carbon drawdown per unit area for years after implementation at no incremental cost (Beerling et al., 2020; Vakilifard et al., 2021).
The data that support the findings of this study are available from Zenodo, https://doi.org/10.5281/zenodo.7040612 (Vakilifard et al., 2022).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-19-4249-2022-supplement.
NV undertook model experimental design and all simulations and analyses. All authors were involved in the design of the model experiments, led by NV and RGW. All authors contributed to writing, led by NV and RGW.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has been supported by the Leverhulme Trust (grant no. RC-2015-029). Richard G. Williams is supported by the UK Natural Environment Research Council (grant no. NE/T007788/1).
This paper was edited by Ben Bond-Lamberty and reviewed by two anonymous referees.
Archer, D.: A data-driven model of the global calcite lysocline, Global Biogeochem. Cy., 10, 511–526, https://doi.org/10.1029/96GB01521, 1996.
Armour, K. C., Bitz, C. M., and Roe, G. H.: Time-varying climate sensitivity from regional feedbacks, J. Clim., 26, 4518–4534, https://doi.org/10.1175/JCLI-D-12-00544.1, 2013.
Beerling, D. J., Kantzas, E. P., Lomas, M. R., Wade, P., Eufrasio, R. M., Renforth, P., Sarkar, B., Andrews, M. G., James, R. H., Pearce, C. R., Mercure, J. F, Pollitt, H., Holden, P. B., Edwards, N. R., Khanna, M., Koh, L., Quegan, S., Pidgeon, N. F., Janssens, I. A., Hansen, J., and Banwart, S. A.: Potential for large-scale CO2 removal via enhanced rock weathering with croplands, Nature, 583, 242–248, https://doi.org/10.1038/s41586-020-2448-9, 2020.
Boucher, O., Halloran, P. R., Bruke, E. J., Doutriaux-Boucher, M., Jones, C. D., Lowe, J., Ringer, M. A., Robertson, E., and Wu, P.: Reversibility in an Earth System model in response to CO2 concentration changes, Environ. Res. Lett., 7, 024013, https://doi.org/10.1088/1748-9326/7/2/024013, 2012.
Church, J. A., White, N. J., Konikow, L. F., Domingues, C. M., Cogley, J. G., Rignot, E., Gregory, J. M., van den Broeke, M. R., Monaghan, A. J., and Velicogna, I.: Revisiting the Earth's sea-level and energy budgets from 1961 to 2008, Geophys. Res. Lett., 38, L18601, https://doi.org/10.1029/2011GL048794, 2011.
Colbourn, G., Ridgwell, A., and Lenton, T. M.: The Rock Geochemical Model (RokGeM) v0.9, Geosci. Model Dev., 6, 1543–1573, https://doi.org/10.5194/gmd-6-1543-2013, 2013.
Eby, M., Weaver, A. J., Alexander, K., Zickfeld, K., Abe-Ouchi, A., Cimatoribus, A. A., Crespin, E., Drijfhout, S. S., Edwards, N. R., Eliseev, A. V., Feulner, G., Fichefet, T., Forest, C. E., Goosse, H., Holden, P. B., Joos, F., Kawamiya, M., Kicklighter, D., Kienert, H., Matsumoto, K., Mokhov, I. I., Monier, E., Olsen, S. M., Pedersen, J. O. P., Perrette, M., Philippon-Berthier, G., Ridgwell, A., Schlosser, A., Schneider von Deimling, T., Shaffer, G., Smith, R. S., Spahni, R., Sokolov, A. P., Steinacher, M., Tachiiri, K., Tokos, K., Yoshimori, M., Zeng, N., and Zhao, F.: Historical and idealized climate model experiments: an intercomparison of Earth system models of intermediate complexity, Clim. Past, 9, 1111–1140, https://doi.org/10.5194/cp-9-1111-2013, 2013.
Edwards N. R. and Marsh R.: Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model, Clim. Dynam., 24, 415–433, https://doi.org/10.1007/s00382-004-0508-8, 2005.
Ehlert, D., Zickfeld, K., Eby, M., and Gillett, N.: The sensitivity of the proportionality between temperature change and cumulative CO2 emissions to ocean mixing, J. Clim., 30, 2921–2935, https://doi.org/10.1175/JCLI-D-16-0247.1, 2017.
Foley, A. M., Holden, P. B., Edwards, N. R., Mercure, J.-F., Salas, P., Pollitt, H., and Chewpreecha, U.: Climate model emulation in an integrated assessment framework: a case study for mitigation policies in the electricity sector, Earth Syst. Dynam., 7, 119–132, https://doi.org/10.5194/esd-7-119-2016, 2016.
Forster, P. M., Andrews, T., Good, P., Gregory, J. M., Jackson, L. S., and Zelinka, M.: Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models, J. Geophys. Res.-Atmos., 118, 1139–1150, https://doi.org/10.1002/jgrd.50174, 2013.
Froelicher, T. L. and Paynter, D. J.: Extending the relationship between global warming and cumulative carbon emissions to multi-millennial timescales, Environ. Res. Lett., 10, 075002, https://doi.org/10.1088/1748-9326/10/7/075002, 2015.
Friedlingstein, P., Andrew, R. M., Rogelj, J., Peters, G. P., Canadell, J. G., Knutti, R., Luderer, G., Raupach, M. R., Schaeffer, M., van Vuuren, D. P., and Le Quéré, C.: Persistent growth of CO2 emissions and implications for reaching climate targets, Nat.Geosci., 7, 709–715, https://doi.org/10.1038/ngeo2248, 2014.
Gillett, N. P., Arora, V. K., Matthews, D., and Allen, M. R.: Constraining the ratio of global warming to cumulative carbon emissions using CMIP5 simulations, J. Clim., 26, 6844–6858, https://doi.org/10.1175/JCLI-D-12-00476.1, 2013.
Goodwin, P., Williams, R. G., and Ridgwell, A.: Sensitivity of climate to cumulative carbon emissions due to compensation of ocean heat and carbon uptake, Nat. Geosci., 8, 29–34, https://doi.org/10.1038/ngeo2304, 2015.
Goodwin, P.: On the time evolution of climate sensitivity and future warming, Earth's Fut., 6, 1336–1348, https://doi.org/10.1029/2018EF000889, 2018.
Gregory, J. M., Ingram, W. J., Palmer, M. A., Jones, G. S., Stott, P. A., Thorpe, R. B., Lowe, J. A., Johns, T. C., and Williams, K. D.: A new method for diagnosing radiative forcing and climate sensitivity, Geophys. Res. Lett., 31, L03205, https://doi.org/10.1029/2003GL018747, 2004.
Hare, B. and Meinshausen, M.: How much warming are we committed to and how much can be avoided?, Climatic Change, 75, 111–149, https://doi.org/10.1007/s10584-005-9027-9, 2006.
Holden, P. B., Edwards, N. R., Oliver, K. I. C., Lenton, T. M., and Wilkinson, R. D.: A probabilistic calibration of climate sensitivity and terrestrial carbon change in GENIE-1, Clim. Dynam., 35, 785–806, https://doi.org/10.1007/s00382-009-0630-8, 2010.
Holden, P. B., Edwards, N. R., Gerten, D., and Schaphoff, S.: A model-based constraint on CO2 fertilisation, Biogeosciences, 10, 339–355, https://doi.org/10.5194/bg-10-339-2013, 2013a.
Holden, P. B., Edwards, N. R., Müller, S. A., Oliver, K. I. C., Death, R. M., and Ridgwell, A.: Controls on the spatial distribution of oceanic δ13CDIC, Biogeosciences, 10, 1815–1833, https://doi.org/10.5194/bg-10-1815-2013, 2013b.
IPCC (Intergovernment Panel on Climate Change): Climate change 2001: The scientific basis, Cambridge, UK, Cambridge University Press, ISBN 0521 80767 0, ISBN 0521 01495 6, 2001.
IPCC (Intergovernment Panel on Climate Change): Climate change 2013: The physical science basis, Cambridge, UK, Cambridge University Press, ISBN 978-1-107-05799-1, ISBN 978-1-107-66182-0, 2013.
IPCC (Intergovernment Panel on Climate Change): Climate change 2021: The scientific basis, Cambridge, UK, Cambridge University Press, ISBN 978-92-9169-158-6, 2021.
Jeltsch-Thömmes, A., Stocker, T. F., and Joos, F.: Hysteresis of the Earth system under positive and negative CO2 emissions, Environ. Res. Lett., 15, 124026, https://doi.org/10.1088/1748-9326/abc4af, 2020.
Jones, C., Robertson, E., Arora, V., Friedlingstein, P., Shevliakova, E., Bopp, L., Brovkin, V., Hajima, T., Kato, E., Kawamiya, M., Liddicoat, S., Lindsay, K., Reick, C. H., Roelandt, C., Segschneider, J., and Tjiputra, J.: Twenty-first-century compatible CO2 emissions and airborne fraction simulated by CMIP5 Earth system models under four representative concentration pathways, J. Clim., 26, 4398–4413, https://doi.org/10.1175/JCLI-D-12-00554.1, 2013.
Jones, C. D. and Friedlingstein, P.: Quantifying process-level uncertainty contributions to TCRE and carbon budgets for meeting Paris Agreement climate targets, Environ. Res. Lett., 15, 074019, https://doi.org/10.1088/1748-9326/ab858a, 2020.
Katavouta, A., Williams, R. G., Goodwin, P., and Roussenov, V.: Reconciling atmospheric and oceanic views of the transient climate response to emissions, Geophys. Res. Lett. 45, 6205–6214, https://doi.org/10.1029/2018GL077849, 2018.
Knutti, R. and Rugenstein, M. A. A.: Feedbacks, climate sensitivity and the limits of linear models, Phil. Trans. R. Soc. A, 373, 20150146, https://doi.org/10.1098/rsta.2015.0146, 2015.
Koch, A., Brierley, C., Maslin, M. M., and Lewis, S. L.: Earth system impacts of the European arrival and Great Dying in the Americas after 1492, Quaternary Sci. Rev., 207, 13–36, https://doi.org/10.1016/j.quascirev.2018.12.004, 2019.
Kohfeld, K. E. and Ridgwell, A.: Glacial-interglacial variability in atmospheric pCO2, in Surface Ocean-Lower Atmosphere Processes, Geophys. Res. Ser., 187, 251–286, https://doi.org/10.1029/2008GM000845, 2009.
Koven, C. D., Arora, V. K., Cadule, P., Fisher, R. A., Jones, C. D., Lawrence, D. M., Lewis, J., Lindsay, K., Mathesius, S., Meinshausen, M., Mills, M., Nicholls, Z., Sanderson, B. M., Séférian, R., Swart, N. C., Wieder, W. R., and Zickfeld, K.: Multi-century dynamics of the climate and carbon cycle under both high and net negative emissions scenarios, Earth Syst. Dynam., 13, 885–909, https://doi.org/10.5194/esd-13-885-2022, 2022.
Luderer, G., Pietzcker, R. C., Bertram, C., Kriegler, E., Meinshausen, M., and Edenhofer, O.: Economic mitigation challenges: how further delay closes the door for achieving climate targets, Environ. Res. Lett., 8, 034033, https://doi.org/10.1088/1748-9326/8/3/034033, 2013.
MacDougall, A. H: The transient response to cumulative CO2 emissions: a review, Curr. Clim. Change Rep., 2, 39–47, https://doi.org/10.1007/s40641-015-0030-6, 2016.
MacDougall, A. H., Swart, N. C., and Knutti, R.: The uncertainty in the transient climate response to cumulative CO2 emissions arising from the uncertainty in physical climate parameters, J. Clim., 30, 813–827, https://doi.org/10.1175/JCLI-D-16-0205.1, 2017.
MacDougall, A. H., Frölicher, T. L., Jones, C. D., Rogelj, J., Matthews, H. D., Zickfeld, K., Arora, V. K., Barrett, N. J., Brovkin, V., Burger, F. A., Eby, M., Eliseev, A. V., Hajima, T., Holden, P. B., Jeltsch-Thömmes, A., Koven, C., Mengis, N., Menviel, L., Michou, M., Mokhov, I. I., Oka, A., Schwinger, J., Séférian, R., Shaffer, G., Sokolov, A., Tachiiri, K., Tjiputra, J., Wiltshire, A., and Ziehn, T.: Is there warming in the pipeline? A multi-model analysis of the Zero Emissions Commitment from CO2, Biogeosciences, 17, 2987–3016, https://doi.org/10.5194/bg-17-2987-2020, 2020.
Matthews, H. D. and Caldeira, K.: Transient climate–carbon simulations of planetary geoengineering, P. Natl Acad. Sci. USA, 104, 9949–9954, https://doi.org/10.1073/pnas.0700419104, 2007.
Matthews, H. D. and Caldeira, K.: Stabilizing climate requires near–zero emissions, Geophys. Res. Lett., 35, L04705, https://doi.org/10.1029/2007GL032388, 2008.
Matthews, H. D. and Zickfeld, K.: Climate response to zeroed emissions of greenhouse gases and aerosols, Nat. Clim. Change, 2, 338–341, https://doi.org/10.1038/nclimate1424, 2012.
Matthews, H. D., Gillett, N. P., Stott, P. A., and Zickfeld, K.: The proportionality of global warming to cumulative carbon emissions, Nature, 459, 829–832, https://doi.org/10.1038/nature08047, 2009.
Matthews, H. D., Landry, J. S., Partanen, A. I., Allen, M., Eby, M., Forster, P. M., Friedlingstein, P., and Zickfeld, K.: Estimating carbon budgets for ambitious climate targets, Curr. Clim. Change Rep., 3, 69–77, https://doi.org/10.1007/s40641-017-0055-0, 2017.
Matthews, H. D., Zickfeld, K., Knutti, R., and Allen, M. R.: Focus on cumulative emissions, global carbon budgets and the implications for climate mitigation targets, Environ. Res. Lett., 13, 010201, https://doi.org/10.1088/1748-9326/aa98c9, 2018.
Matthews, H. D., Tokarska, K. B., Rogelj, J., Smith, C., MacDougall, A. H., Haustein, K., Mengis, N., Sippel, S., Forster, P. M., and Knutti, R.: An integrated approach to quantifying uncertainties in the remaining carbon budget, Commun. Earth Environ., 2, 7, https://doi.org/10.1038/s43247-020-00064-9, 2021.
Meinshausen, M., Nicholls, Z. R. J., Lewis, J., Gidden, M. J., Vogel, E., Freund, M., Beyerle, U., Gessner, C., Nauels, A., Bauer, N., Canadell, J. G., Daniel, J. S., John, A., Krummel, P. B., Luderer, G., Meinshausen, N., Montzka, S. A., Rayner, P. J., Reimann, S., Smith, S. J., van den Berg, M., Velders, G. J. M., Vollmer, M. K., and Wang, R. H. J.: The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500, Geosci. Model Dev., 13, 3571–3605, https://doi.org/10.5194/gmd-13-3571-2020, 2020.
O'Neill, B. C., Kriegler, E., Ebi, K. L., Kemp-Benedict, E., Riahi, K., Rothman, D. S., van Ruijven, B. J., van Vuuren, D. P., Birkmann, J., Kok, K., and Levy, M.: The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century, Global Environ. Chang., 42, 169–180, https://doi.org/10.1016/j.gloenvcha.2015.01.004, 2017.
Riahi, K., van Vuuren, D. P., Kriegler, E., Edmonds, J., O'Neill, B. C., Fujimori, S., Bauer, N., Calvin, K., Dellink, R., Fricko, O., Lutz, W., Popp, A., Cuaresma, J. C., Samir, K.C., Leimbach, M., Jiang, L., Kram, T., Rao, S., Emmerling, J., Ebi, K., Hasegawa, T., Havlík, P., Humpenöder, F., Da Silva, L. A., Smith, S., Stehfest, E., Bosetti, V., Eom, J., Gernaat, D., Masui, T., Rogelj, J., Strefler, J., Drouet, L., Krey, V., Luderer, G., Harmsen, M., Takahashi, K., Baumstark, L., Doelman, J. C., Kainuma, M., Klimont, Z., Marangoni, G., Lotze-Campen, H., Obersteiner, M., Tabeau, A., and Tavoni. M.: The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview, Global Environ. Chang., 42, 153–168, https://doi.org/10.1016/j.gloenvcha.2016.05.009, 2017.
Ridgwell, A. and Hargreaves, J. C.: Regulation of atmospheric CO2 by deep-sea sediments in an Earth system model, Global Biogeochem. Cy., 21, GB2008, https://doi.org/10.1029/2006GB002764, 2007.
Ridgwell, A., Hargreaves, J. C., Edwards, N. R., Annan, J. D., Lenton, T. M., Marsh, R., Yool, A., and Watson, A.: Marine geochemical data assimilation in an efficient Earth System Model of global biogeochemical cycling, Biogeosciences, 4, 87–104, https://doi.org/10.5194/bg-4-87-2007, 2007.
Rogelj, J., Luderer, G., Pietzcker, R. C., Kriegler, E., Schaeffer, M., Krey, V., and Riahi, K.: Energy system transformations for limiting end-of-century warming to below 1.5 ∘C, Nat. Clim. Change, 5, 519–27, https://doi.org/10.1038/nclimate2572, 2015.
Solomon, S., Plattner, G. K., Knutti, R., and Friedlingstein, P.: Irreversible climate change due to carbon dioxide emissions, P. Natl. Acad. Sci. USA, 106, 1704–1709, https://doi.org/10.1073/pnas.0812721106, 2009.
Spafford, L. and MacDougall, A. H.: Quantifying the probability distribution function of the transient climate response to cumulative CO2 emissions, Environ. Res. Lett., 15, 034044, https://doi.org/10.1088/1748-9326/ab6d7b, 2020.
Sulpis, O., Boudreau, B. P., Mucci, A., Jenkins, C., Trossman, D. S., Arbic, B. K., and Key, R. M.: Current CaCO3 dissolution at the seafloor caused by anthropogenic CO2, P. Natl. Acad. Sci. USA, 115, 11700–11705, https://doi.org/10.1073/pnas.1804250115, 2018.
Tokarska, K. B. and Zickfeld, K.: The effectiveness of net negative carbon dioxide emissions in reversing anthropogenic climate change, Environ. Res. Lett., 10, 094013, https://doi.org/10.1088/1748-9326/10/9/094013, 2015.
Tokarska, K. B., Gillet, N. P., Arora, V. K., Lee, W. G., and Zickfeld, K.: The influence of non-CO2 forcings on cumulative carbon emissions budgets, Environ. Res. Lett., 13, 034039, https://doi.org/10.1088/1748-9326/aaafdd, 2018.
UNFCCC (United Nations Framework Convention on Climate Change): Adoption of the Paris Agreement, 21st Conference of the Parties, United Nations, Paris, GE.15-21932(E), 2015.
Vakilifard, N., Kantzas, E. P., Holden, P. B., Edwards, N. R., and Beerling, D. J.: The role of enhanced rock weathering deployment with agriculture in limiting future warming and protecting coral reefs, Environ. Res. Lett., 16, 094005, https://doi.org/10.1088/1748-9326/ac1818, 2021.
Vakilifard, N., Williams, R. G., Holden, P. B., Turner, K., Edwards, N. R., and Beerling, D. J.: Impact of negative and positive CO2 emissions on global warming metrics using an ensemble of Earth system model simulations, Zenodo [data set], https://doi.org/10.5281/zenodo.7040612, 2022.
Williams, R. G., Goodwin, P., Roussenov, V. M., and Bopp, L.: A framework to understand the transient climate response to emissions, Environ. Res. Lett., 11, 015003, https://doi.org/10.1088/1748-9326/11/1/015003, 2016.
Williams, R. G., Roussenov, V., Goodwin, P., Resplandy, L., and Bopp, L.: Sensitivity of global warming to carbon emissions: effects of heat and carbon uptake in a suite of Earth system models, J. Clim., 30, 9343–9363, https://doi.org/10.1175/JCLI-D-16-0468.1, 2017a.
Williams, R. G., Roussenov, V., Frölicher,T. L., and Goodwin, P.: Drivers of continued surface warming after cessation of carbon emissions, Geophys. Res. Lett., 44, 10633–10642, https://doi.org/10.1002/2017GL075080, 2017b.
Williams, R. G., Ceppi, P., and Katavouta, A.: Controls of the transient climate response to emissions by physical feedbacks, heat uptake and carbon cycling, Environ. Res. Lett., 15, 0940c1, https://doi.org/10.1088/1748-9326/ab97c9, 2020.
Zickfeld, K., Arora, V. K., and Gillett, N. P.: Is the climate response to CO2 emissions path dependent?, Geophys. Res. Lett., 39, L05703, https://doi.org/10.1029/2011GL050205, 2012.
Zickfeld, K., Eby, M., Weaver, A. J., Alexander, K., Crespin, E., Edwards, N. R., Eliseev, A. V., Feulner, G., Fichefet, T., Forest, C. E., Friedlingstein, P., Goosse, H., Holden, P. B., Joos, F., Kawamiya, M., Kicklighter, D., Kienert, H., Matsumoto, K., Mokhov, I., Monier, E., Olsen, A. M., Pedersen, J. O. P., Perrette, M., Philippon-Berthier, G., Ridgwell, A., Schlosser, A., Schneider Von Deimling, T., Shaffer, G., Sokolov, A., Spahni, R., Steinacher, M., Tachiiri, K., Tokos, K. S., Yoshimori, M., Zeng, N., and Zhao, F.: Long-term climate change commitment and reversibility: An EMIC intercomparison, J. Clim., 26, 5782–5809, https://doi.org/10.1175/JCLI-D-12-00584.1, 2013.
Zickfeld, K., MacDougall, A. H., and Matthews, H. D.: On the proportionality between global temperature change and cumulative CO2 emissions during periods of net negative CO2 emissions, Environ. Res. Lett., 11, 055006, https://doi.org/10.1088/1748-9326/11/5/055006, 2016.