the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Reconstruction of global surface ocean pCO2 using region-specific predictors based on a stepwise FFNN regression algorithm
Guorong Zhong
Xuegang Li
Jinming Song
Baoxiao Qu
Fan Wang
Yanjun Wang
Bin Zhang
Xiaoxia Sun
Wuchang Zhang
Zhenyan Wang
Jun Ma
Huamao Yuan
Liqin Duan
Various machine learning methods were attempted in the global mapping of surface ocean partial pressure of CO2 (pCO2) to reduce the uncertainty of the global ocean CO2 sink estimate due to undersampling of pCO2. In previous research, the predictors of pCO2 were usually selected empirically based on theoretic drivers of surface ocean pCO2, and the same combination of predictors was applied in all areas except where there was a lack of coverage. However, the differences between the drivers of surface ocean pCO2 in different regions were not considered. In this work, we combined the stepwise regression algorithm and a feed-forward neural network (FFNN) to select predictors of pCO2 based on the mean absolute error in each of the 11 biogeochemical provinces defined by the self-organizing map (SOM) method. Based on the predictors selected, a monthly global 1∘ × 1∘ surface ocean pCO2 product from January 1992 to August 2019 was constructed. Validation of different combinations of predictors based on the Surface Ocean CO2 Atlas (SOCAT) dataset version 2020 and independent observations from time series stations was carried out. The prediction of pCO2 based on region-specific predictors selected by the stepwise FFNN algorithm was more precise than that based on predictors from previous research. Applying the FFNN size-improving algorithm in each province decreased the mean absolute error (MAE) of the global estimate to 11.32 µatm and the root mean square error (RMSE) to 17.99 µatm. The script file of the stepwise FFNN algorithm and pCO2 product are distributed through the Institute of Oceanology of the Chinese Academy of Sciences Marine Science Data Center (IOCAS, https://doi.org/10.12157/iocas.2021.0022, Zhong, 2021.
- Article
(8235 KB) -
Supplement
(611 KB) - BibTeX
- EndNote
As a net sink for atmospheric CO2, global oceans have removed about one-third of anthropogenic CO2 since the beginning of the industrial revolution (Sabine et al., 2004; Friedlingstein et al., 2019). However, the global ocean sea–air CO2 flux averaged between 2001–2015 varies from −1.55 to −1.74 Pg C yr−1 with a maximum difference in individual years of nearly 0.6 Pg C yr−1, depending on the surface ocean partial pressure of the CO2 (pCO2) product. These differences largely stem from differences in pCO2 estimates across the products (Rödenbeck et al., 2014; Iida et al., 2015; Landschützer et al., 2014; Denvil-Sommer et al., 2019). The magnitude and direction of the flux are primarily set by the air–sea pCO2 difference. Surface water pCO2 greater than the overlying air indicates CO2 is released from the ocean to the air. Conversely, absorption of CO2 by oceans happens when the pCO2 of the surface water is lower than the overlying air. The ocean in these two scenarios is known as the oceanic carbon source and oceanic carbon sink, respectively.
Sparse and uneven observations of surface ocean pCO2 in time and space have severely limited the understanding of interannual variability of oceanic carbon sink, and research based on different methods were carried out to break this barrier. In earlier studies, traditional unitary and multiple regression methods between surface ocean pCO2 and its drivers were attempted in the mapping of surface ocean pCO2, which were limited in specific regions and sometimes even in particular seasons with a relatively high root mean square error (RMSE; Sarma et al., 2006; Takahashi et al., 2006; Shadwick et al., 2010; Chen et al., 2011; Marrec et al., 2015). Advances in artificial neural networks and other machine learning algorithms, such as the feed-forward neural network (FFNN) method (Zeng et al., 2014, 2015; Moussa et al., 2016; Denvil-Sommer et al., 2019) and self-organization mapping (SOM) method (Friedrich and Oschlies, 2009; Telszewski et al., 2009; Hales et al., 2012; Nakaoka et al., 2013), significantly reduced the bias in interpolation based on relationships between surface ocean pCO2 and its drivers. In addition, finding better predictors or combining SOM with other neural networks was also attempted to decrease the pCO2 predicting error further (Hales et al., 2012; Nakaoka et al., 2013; Landschützer et al., 2014; Chen et al., 2019; Denvil-Sommer et al., 2019; Zhong et al., 2020; Wang et al., 2021). However, the selection of predictors in the surface ocean pCO2 mapping was more empirical, focusing on the theoretical drivers of the pCO2 and its variation. Sea surface temperature and salinity, related to the solubility of CO2 in seawater, are considered as the most important and used in almost all related studies (Landschützer et al., 2013; Nakaoka et al., 2013; Moussa et al., 2016; Laruelle et al., 2017; Zeng et al., 2017; Denvil-Sommer et al., 2019). Similarly, the chlorophyll a concentration, which is related to the phytoplankton uptake of CO2, is also widely used (Nakaoka et al., 2013; Landschützer et al., 2014; Laruelle et al., 2017; Zeng et al., 2017; Denvil-Sommer et al., 2019). One more predictor, mixed layer depth, frequently appears in associated studies as a proxy related to the vertical transport of dissolved carbon (Telszewski et al., 2009; Nakaoka et al., 2013; Landschützer et al., 2014; Zeng et al., 2017; Denvil-Sommer et al., 2019). In addition, sampling information, such as latitude and longitude (Friedrich and Oschlies, 2009; Jo et al., 2012; Zeng et al., 2015, 2017; Denvil-Sommer et al., 2019; Gregor et al., 2019) and sampling time (Friedrich and Oschlies, 2009; Zeng et al., 2015), has been used as a predictor. In recent research, the dry air mixing ratio of atmospheric CO2 (xCO2), related to the CO2 level in the air, was also used to predict surface ocean pCO2 (Landschützer et al., 2014; Denvil-Sommer et al., 2019). The sea surface height, which was considered effective in improving the spatial pattern and the accuracy of surface ocean pCO2 mapping at the basin and regional scales, and the monthly anomalies of the most widely used predictors mentioned above, were used by Denvil-Sommer et al. (2019). In research focusing on the surface ocean pCO2 mapping of coastal areas, bathymetry, sea ice, and wind speed were also used as predictors (Laruelle et al., 2017). In each of these research studies, the same combination of predictors was applied in all global ocean areas, although the global ocean was divided into several biogeochemical provinces in some of the research. However, the predictor that plays a vital role in the surface ocean pCO2 reconstruction at one region may not be a good predictor of surface ocean pCO2 in the other regions due to complex and variable drivers. Nevertheless, no widely recognized methods for judging the importance of each predictor in the surface ocean pCO2 mapping are available yet. Thus, we attempted to construct a stepwise FFNN algorithm to rank the importance of predictors and figure out the optimal combination in each biogeochemical province defined by SOM for decreasing the prediction errors in the surface ocean pCO2 mapping.
2.1 Data
The surface ocean fugacity of CO2 (fCO2) observation data from the Surface Ocean CO2 Atlas fCO2 dataset version 2020 (SOCATv2020; Bakker et al., 2016) was used to construct the non-linear relationship between surface ocean pCO2 and predictors. The conversion between fCO2 and pCO2 followed the formula (Körtzinger, 1999)
where fCO2 and pCO2 are in micro-atmospheres (µatm), P is the total atmospheric surface pressure (Pa) using the National Centers for Environmental Prediction (NCEP) monthly mean sea level pressure product (Dee et al., 2011), and T is the absolute temperature (K). R is the gas constant (8.314 ). Parameters B (m3 mol−1) and δ (m3 mol−1) are both viral coefficients (Weiss, 1974).
Table 1Predictors and corresponding data products.
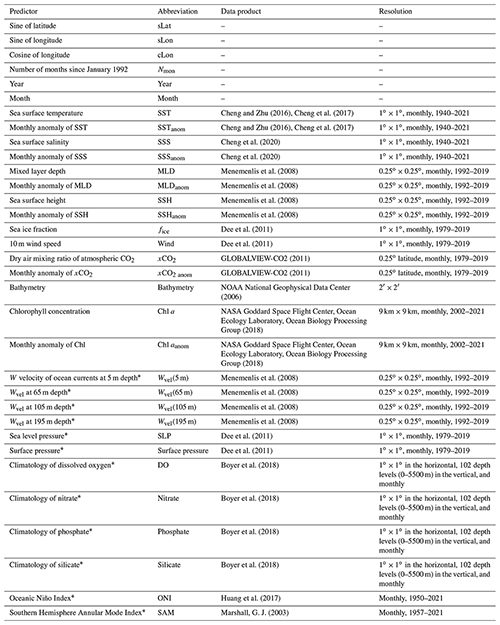
Predictors with the ∗ label were here for the first time included in the pCO2 mapping. All data products retrieved at resolutions higher than 1∘ × 1∘ were downscaled to 1∘ × 1∘ resolution.
In this work, 33 predictors were used (Table 1), where 21 were chosen from previous research of surface ocean pCO2 reconstruction based on machine learning methods. In addition, 12 predictors that were only used in similar previous research focused on the mapping of total alkalinity or dissolved inorganic carbon (Broullón et al., 2019; Broullón et al., 2020), or were possibly related to the driver of surface ocean pCO2 and its variability, were selected for testing (predictors labeled with * in Table 1). Most of these products were retrieved at 1∘ × 1∘ resolution. Some products retrieved at higher resolution were downscaled to 1∘ × 1∘ resolution by taking the average of all values in each 1∘ × 1∘ grid.
2.2 Biogeochemical provinces defined by the self-organizing map
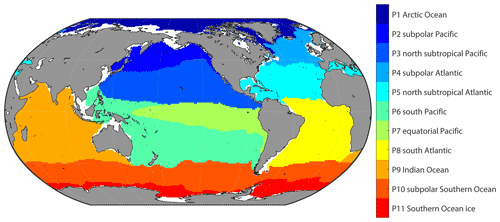
For applying a different combination of predictors in regions based on the differences in the dominated drivers of pCO2 and its variability, the global ocean was divided into a set of biogeochemical provinces using a self-organizing map (SOM) method. The monthly climatology of temperature, salinity, mixed layer depth, sea surface height, nitrate, phosphate, silicate, and dissolved oxygen and pCO2 climatology from Landschützer et al. (2020) were put into a 3-by-4 SOM network to generate 12 biogeochemical provinces, where the monthly climatology data in all 12 months were put into one SOM network to generate one discrete set of biogeochemical provinces. Provinces with less than 10 pixels and less than 1000 SOCAT observations were defined as discrete small “island” provinces and then merged with nearest provinces. The provinces covering areas separated by land were further divided artificially. For example, the province covering the northern subtropical Pacific and the province covering the northern subtropical Atlantic was set as one province in the original output of SOM, but it was mainly separated by the North American continent. So, we divided the province into two new provinces. The final version includes 11 biogeochemical provinces. In this study, the coastal area was not involved, and the boundary was defined as 200 m depth. In addition, the pCO2 mapping based on SOM-defined provinces tends to be less smooth near the border of different biogeochemical provinces, with an obvious borderline appearing. However, applying different predictors may make this problem worse. To obtain a smoother distribution, we defined the area within five 1 × 1 grids of province boundaries as a “boundary area”. Samples in the boundary area will be used as training samples in all adjacent provinces (Fig. S1 in the Supplement). However, this definition does not change the actual spatial coverage of each province, only bringing more training samples near the province boundary.
2.3 Stepwise FFNN algorithm
For finding a better combination of pCO2 predictors, a stepwise FFNN algorithm was constructed. The FFNN comprises four parts: input, hidden, summation, and output layers (Fig. 1). The input layer is designed to pass the inputs to the hidden layer, and the number of neurons is equal to the dimensions of the input matrix p. The hidden layer includes 25 neurons in the FFNN model, with a tan-sigmoid function as the transfer function. The input p is multiplied by a matrix of weights (w1 in Fig. 1), and the inner product between the result and a bias matrix (b1 in Fig. 1) is calculated as the input of the transfer function in the first hidden layer. In the summation layer, the transfer function f2 is a linear function. The output of the hidden layer is multiplied by another matrix of weights and summed. All bias and weights matrixes were randomly assigned at the beginning of FFNN training. The randomly assigned bias and weights matrixes, the number of training samples, and the sort order of training samples in the input matrix p define where the FFNN starts training in errors space. The practice of FFNN changes when these conditions change. Here we fixed the training samples and set one constant random number stream in MATLAB to ensure that the difference between the MAE based on different predictors entirely stems from the predictor differences. The random number was randomly chosen. When using different random number streams, several predictors at the end of the output list of the stepwise FFNN algorithm differed. However, the leading predictors were consistent, and the different predictors were also related. The fixed random number makes all networks using different predictors start training from the same point in the error space when comparing the performance of each predictor.
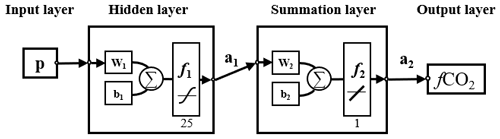
Figure 1Structure of the feed-forward neural network. w: weighted matrix; b: bias matrix; ∑: sum; f1: tan-sigmoid transfer function; f2: linear function; a: output matrix.
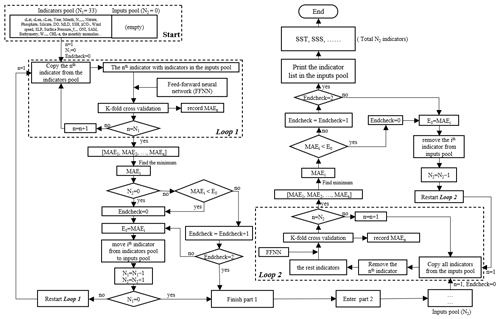
Figure 2The procedure of the stepwise FFNN algorithm. The flowchart follows an order of top left–bottom left–bottom right–top right. The meaning of Predictors pool: store all predictors waiting to be tested; Inputs pool: store predictors that were temporally considered as good predictors; Loop 1 and Loop 2: calculate the MAE when each predictor was added or removed; Selection step: add good predictors to the Inputs pool; Removal step: remove predictors from the Inputs pool if removing leads to MAE decrease; Determine step: check if the process reaches end condition. N1 and N2: number of predictors in the Predictors pool and Inputs pool, respectively; E0: lowest MAE in the last iteration of Loop 1 or Loop 2; Endcheck: the number of iterations that E0 continuously increased.
In the stepwise part, predictors of pCO2 are going to be added and removed one by one, and which predictors will be finally used in pCO2 predicting is determined according to the real-time change of predicting error. The mean absolute error (MAE), calculated using a K-fold cross validation method, was used to estimate the performance of each predictor in the FFNN predicting. Although the RMSE was widely used for the validation of machine learning methods, compared to the MAE, the RMSE was more sensitive to a few extreme samples, which generally deviated far from the FFNN predicting values, resulting in a considerable discrepancy between the FFNN outputs and pCO2 observations by sometimes up to hundreds of micro-atmospheres. A higher weight might be put on these few extreme samples than other samples in the predictor selection if the performance of each predictor was estimated by RMSE in the stepwise FFNN algorithm. To avoid the higher weight on these few extreme samples, the MAE was used instead for the internal performance loss function in the stepwise FFNN algorithm. The basic principle of the stepwise FFNN algorithm was adding each predictor from a set of predictors into the inputs of FFNN and removing each redundant predictor from the inputs successively to reduce the MAE in the fastest way, until no decrease in the MAE appeared (Fig. 2), and where the predictor having no contribution to the reducing of prediction error was considered as redundant.
At the beginning of the stepwise FFNN algorithm, all available predictors were put into a matrix, referred to as the Predictors pool (Start in Fig. 2). Each row represents one predictor, and each column represents one SOCAT sample. In this work, we collected 33 predictors for the test, that is, the Predictors pool matrix has 33 rows. Meanwhile, a matrix referred to as Inputs pool (Start in Fig. 2) was set up to store predictors with good performance, where good performance means that adding these predictors can significantly decrease the MAE between SOCAT pCO2 measurements and FFNN pCO2 predictions. Then a loop of K-fold validation test ran out to calculate the MAE when predicting pCO2 by each predictor in the Predictors pool in the first step (Loop 1 in Fig. 2). Thus 33 MAE values were obtained in total, and the minimum was recorded as E0. The predictor corresponding to the minimum MAE value was moved from the Predictors pool to the Inputs pool (Selection step in Fig. 2). After that, the Loop 1 restarted, i.e., the second step started with one predictor removed to the inputs pool and the remaining 32 predictors waiting to be tested. Then, the pCO2 was predicted using each of the rest 32 predictors in the predictors pool with the addition of all predictors in the inputs pool, and 32 MAE values were calculated out. If the MAE in the lowest situation, represented by the MAEi, decreased compared to the E0, the ith predictor was considered a good predictor and moved from the predictors pool to the inputs pool. Then the value of E0 was replaced by the MAEi (Selection step in Fig. 2). Part 1, including Loop 1, Selection step, and Determine step 1 in Fig. 2, was repeated until no predictor was left in the Predictors pool or no decrease of E0 could be found regardless of which two predictors were added in the next two steps. At this time, part 1 of the stepwise FFNN algorithm finished, and all predictors left in the Predictors pool were considered redundant. The second part ran in the opposite way in that the predictors were removed from the Inputs pool one by one to decrease E0 the fastest (Loop 2 in Fig. 2). The second part was used to remove the predictor that could be represented by other predictors in the inputs pool (Removal step in Fig. 2) and finished in the similar condition that no significant decrease could be found regardless of which predictor was removed in the next two steps (Determine step 2 in Fig. 2).
2.4 pCO2 product
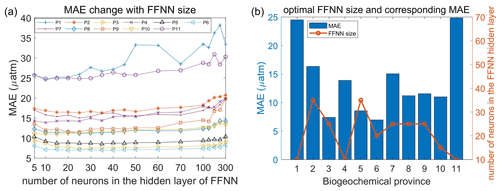
The dataset of predictors, except for chl a, start in 1992 or earlier, while the chl a data range from August 2002 to the present. In each province, the stepwise FFNN algorithm was run once, first based on all samples covered by the chl a data; secondly, the algorithm was run based on samples and all predictors except chl a and chl aanom in the year that chl a gridded data were not available. The pCO2 mapping in the year that chl a gridded data were not available was carried out based on the predictors selected in the second run. Then the final product was built based on two FFNNs: one trained for the period from August 2002 to August 2019 using one predictor set including chl a or chl aanom, and the second one for the period from January 1992 to July 2002 using the second predictor set without chl a and chl aanom. Although the performance may improve with the number of neurons increasing, the influence of the number of neurons on the performance of FFNN pCO2 prediction remains unclear. To further decrease the predicting error between FFNN outputs and SOCAT measurements, the number of neurons was improved by an error test in each province. The number of neurons increased from 5 to 300 (the increment was five during 5–50 and ten during 50–100 and fifty during 100–300). Then the corresponding MAE values of each size were recorded, and the number of neurons with the lowest MAE was applied. This test avoided the appearance of insufficient learning capacity for complex nonlinear relationships due to too few neurons and the overfitting problem due to too many neurons. Finally, based on the predictors selected by the stepwise FFNN algorithm and improved FFNN size, a monthly global 1∘ × 1∘ surface ocean pCO2 product from January 1992 to August 2019 was constructed.
Table 2Validation group using different predictors.
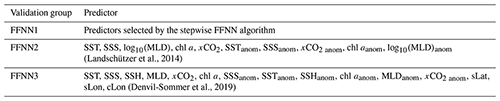
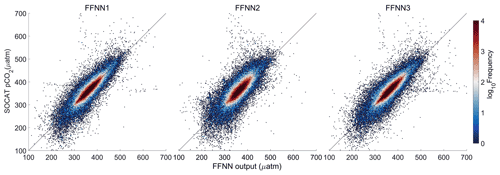
The FFNN performance of three groups with different predictors of pCO2 were compared to test the result of stepwise FFNN algorithm. Predictors in group FFNN1 were selected using the stepwise FFNN algorithm, and predictors in group FFNN2 were selected from Landschützer et al. (2014), and in group FFNN3 from Denvil-Sommer et al. (2019).
2.5 Validation
To better estimate the predicting error of FFNN, the MAE and the RMSE, which were widely used in previous research, were calculated using a K-fold cross validation method. To avoid overfitting caused by a lack of independence between the training and testing samples, we put the SOCAT samples in chronological order and then divided them into the group of years (Fig. 1; Gregor et al., 2019). In this paper, the value of K was set as 4. Thus, among every four neighboring years, three group samples were used to train the FFNN model, and the rest were used for testing. A total of four iterations were carried out, where the testing year changed in each iteration. After the four iterations finished, all samples were used for testing only once, and the MAE and RMSE between FFNN output and the testing samples were calculated. The performance of the predictor selection algorithm was estimated by comparing the MAE and RMSE results of the FFNN based on predictors selected by the stepwise FFNN algorithm with the result based on predictors used in previous research in each biogeochemical province (Table 2). All validation groups were applied with the same FFNN and same samples from SOCAT, with the only differences being in the predictors. The same K-fold validation procedure was applied for three validation groups based on different pCO2 predictors. Thus, three results were generated to estimate whether the stepwise FFNN algorithm can effectively find a better combination of pCO2 predictors. Finally, the pCO2 data generated in all validation groups were further compared with the completely independent observations from the Hawaii Ocean Time-series (HOT, 22∘45′ N, 158∘00′ W, since October 1988; Dore et al., 2009), Bermuda Atlantic Time-series Study (BATS, 31∘50′ N, 64∘10′ W, since October 1988; Bates, 2007) and The European Station for Time Series in the Ocean Canary Islands (ESTOC, 29∘10′ N, 15∘30′ W, from 1995 to 2009; González-Dávila and Santana-Casiano, 2012) stations. The pCO2 at HOT and BATS were estimated from total alkalinity (TA) and dissolved inorganic carbon (DIC), and pCO2 at ESTOC was directly measured. These observations were not included in the SOCAT dataset.
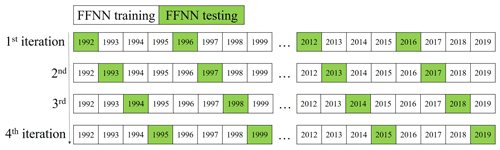
Figure 3The K-fold validation procedure. (The K value was set as 4, so iterations were repeated 4 times until all samples were set as having tested samples once. In each iteration, samples in 7 years were set as testing samples (green cells) and in the rest 21 years were set as training samples (white cells) to increase independence.)
Table 3Predictors in each biogeochemical province.
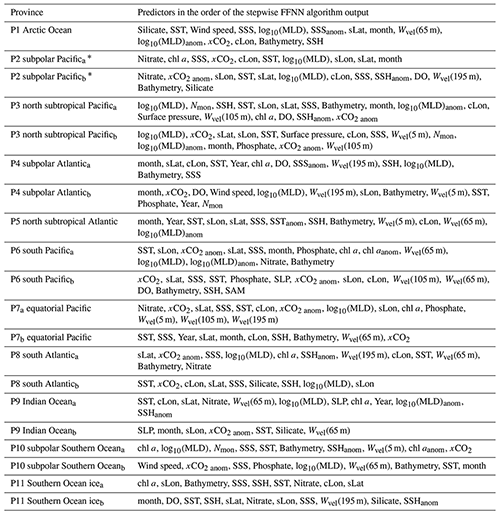
∗: Due to insufficient coverage of chl a data in the polar areas and during the period before 2002, in provinces that chl a or chl aanom were selected as predictors, the pCO2 data were divided into two periods. The period with available chl a data was represented by the subscript ”a”, such as P2a, including global grids from 2002 to 2019 except polar grids in winter. The period with unavailable chl a data was represented by the subscript ”b”, such as P2b, including global grids from 1992 to 2001 and some polar grids in winter from 1992 to 2019.
3.1 Biogeochemical provinces and corresponding predictors of pCO2
11 biogeochemical provinces generated from the SOM method after the separated small “island” was removed and the province separated by lands was divided manually (Fig. 4). The results of the stepwise FFNN algorithm in each province are shown in Table 3. The predictors were listed in the order that the stepwise FFNN algorithm printed recommended predictors out. The predictor printed earlier was relatively more highly recommended and played an important role in predicting pCO2 based on FFNN. Applying these predictors effectively decreased the predicting error between the FFNN outputs and pCO2 values from validation samples. Thus it is reasonable to consider that these predictors were highly related to the drivers of pCO2 and its variability. Predictors representing sampling positions were also listed as recommended predictors in some provinces, including latitude, longitude, and sampling time, suggesting that relatively steady spatial or temporal variability patterns of surface ocean pCO2 existed in these biogeochemical provinces. For example, the predictor month was considered recommended in most provinces, especially P4 subpolar Atlantic and P5 north subtropical Atlantic, while pCO2 in these areas regularly peaked and bottomed out in summer and winter (Takahashi et al., 2009; Landschützer et al., 2016, 2020). Similarly, the sine of latitude and the sine and cosine of longitude were listed as recommended predictors of pCO2 in most provinces, suggesting a meridional or zonal uniformly varying spatial distribution pattern of pCO2, which was not learned sufficiently by the FFNN model from existing measured predictors, and the predictors related to the spatial position were applied as supplementary.
As basic predictors highly related to the ocean environment, temperature and salinity were considered as parts of the most important predictors of surface ocean pCO2 and were applied in the pCO2 prediction in almost all previous related research based on various methods (Jo et al., 2012; Signorini et al., 2013; Landschützer et al., 2014; Marrec et al., 2015; Chen et al., 2016, 2017; S. Chen et al., 2019; Moussa et al., 2016; Laruelle et al., 2017; Zeng et al., 2017; Denvil-Sommer et al., 2019). The results of the stepwise FFNN algorithm also supported this. The temperature was listed as a recommended predictor in all biogeochemical provinces, suggesting that temperature was one of the most critical drivers of pCO2 and its variability in these provinces. Similarly, results from the stepwise FFNN algorithm provide evidence for the importance of salinity in predicting pCO2, which was also listed as a predictor in most provinces. The dry air mixing ratio of atmospheric CO2 (xCO2) and the monthly anomaly of xCO2 were also recommended predictors in most biogeochemical provinces, suggesting that the exchange of CO2 across the sea–air interface was also an important driver of surface ocean pCO2. As a widely used predictor in pCO2 prediction, the chlorophyll a concentration (chl a) played an essential role in fitting the influence of biological activities on pCO2 in previous research (Landschützer et al., 2014; Zeng et al., 2017; Laruelle et al., 2017; Denvil-Sommer et al., 2019). Especially in the province P10 subpolar Southern Ocean and P11 Southern Ocean ice, chl a was listed as the most recommended predictor in the result of the stepwise FFNN algorithm, while in some other provinces (P1 Arctic Ocean and P5 north subtropical Atlantic), chl a was considered redundant in that no effective decrease of MAE between FFNN outputs and pCO2 measurements appeared when the chl a data were used. Similar to the period where chl a was not available (represented by the subscript “b”), phosphate, nitrate, silicate, or dissolved oxygen were recommended instead. In the province P1 Arctic Ocean, silicate concentration and temperature were considered the most crucial predictors of pCO2.
3.2 pCO2 product
Based on the predictors given by the stepwise FFNN algorithm in each biogeochemical province, an FFNN size (representing the number of neurons in the hidden layer) improving validation was applied to decrease the prediction error further. The MAE values based on the same samples and FFNN model with a different number of neurons were calculated, then the number of neurons corresponding to the lowest MAE was applied (Fig. 5a). The MAE in most provinces tends to decrease first and then increase when the number of neurons in the hidden layer of the FFNN model increased from 5 to 300. Based on the variation of MAE with the number of neurons in the FFNN hidden layer, the optimal FFNN size in each province was considered as the number of neurons when the MAE was lowest. The result and corresponding MAE are shown in Fig. 5b. After applying optimal FFNN size in each province, the MAE and RMSE of global estimates between predicted pCO2 and measurements from SOCAT v2020 further decreased to 11.32 and 17.99 µatm, respectively.
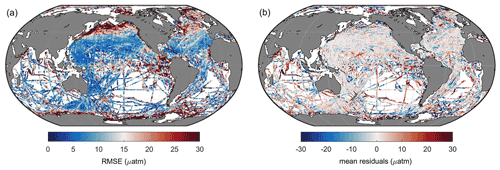
Figure 6Global maps of (a) RMSE and (b) mean residuals between predicted pCO2 and SOCAT observations.
Then the RMSE and mean residuals in each grid were calculated based on the K-fold cross validation method. In most grids, the RMSE was lower than 10 µatm, and the mean residuals were close to zero (Fig. 6). However, the prediction error in the north subpolar Pacific, the eastern equatorial Pacific, and the Southern Ocean near the Antarctic continent was significantly higher than in other areas. Also, the distribution of mean residuals suggested that surface ocean pCO2 in the Indian Ocean tends to be overestimated by the FFNN models, while in other regions, the distribution of mean residuals was more discrete, and no obvious pattern was found.
3.3 Validation of the stepwise FFNN algorithm based on SOCAT samples
Validation based on the K-fold cross validation method suggested that most FFNN outputs were quite close to the pCO2 values from SOCAT v2020 samples (Fig. 7). Comparing the results based on a different combination of predictors, the results of FFNN1 (based on stepwise FFNN algorithm, this paper) and FFNN3 (based on 15 predictors from Denvil-Sommer et al. 2019) were more precise than those of FFNN2 (based on 10 predictors from Landschützer et al. 2014). The plots in the result of FFNN1 were most concentrated along the y=x line, suggesting extremely close FFNN outputs with the measured pCO2 values from SOCAT, with the RMSE of 17.99 µatm in the global open oceans. The RMSE of FFNN1 was lower than that of FFNN2 (22.95 µatm) and FFNN3 (19.17 µatm).
Table 4Performance of pCO2 prediction based on different predictors.
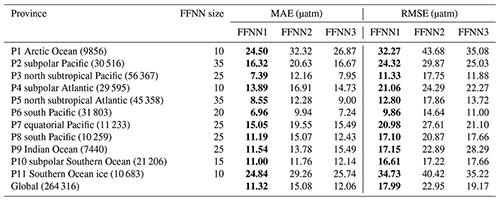
FFNN1 was based on predictors selected by the stepwise FFNN algorithm. FFNN2 and FFNN3 were based on predictors from Landschützer et al. (2014) and Denvil-Sommer et al. (2019), respectively. The lowest MAE and RMSE between different validation groups was shown in bold. The number in parentheses after the province name is the number of SOCAT monthly mean samples for that province.
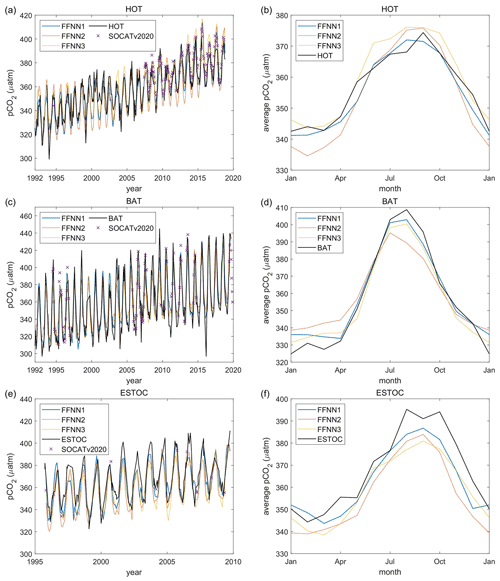
Figure 8Validation based on independent observation from time series stations: (a, b) the Hawaii Ocean Time-series (HOT; Dore et al., 2009); (c, d) the Bermuda Atlantic Time-series Study (BATS; Bates, 2007); (e, f) the European Station for Time Series in the Ocean Canary Islands (ESTOC; González-Dávila and Santana-Casiano, 2012). FFNN1 was based on predictors selected by the stepwise FFNN algorithm. FFNN2 and FFNN3 were based on predictors from Landschützer et al., 2014 and Denvil-Sommer et al., 2019, respectively. SOCATv2020 represents the monthly mean pCO2 of SOCAT observations in the corresponding grids of each time series station.
For specific comparison of accuracy in each province, the MAE of FFNN1 was lower in most provinces (Table 4), except for the relatively close results between the FFNN1 and FFNN3 in parts of the provinces. The MAE of FFNN1 in the province P9 Indian Ocean was significantly lower than that of the other validation groups, suggesting a better combination of predictors highly related to the drivers of surface ocean pCO2 and its variability in the Indian Ocean. Compared with FFNN2 and FFNN3, the predictors of FFNN1 added surface pressure and W velocity of ocean currents and abandoned the monthly anomalies of other predictors in the province P9 Indian Ocean. The low relevance between pCO2 and part of the monthly anomalies, such as SSSanom and SSTanom, may be responsible for the significantly lower MAE of FFNN1. Adding redundant predictors may cause misleading information in the learning of the FFNN model on the contrary. The MAE and RMSE differences between FFNN1 and FFNN3 in some provinces were relatively small. The reason for the higher MAE and RMSE of FFNN2 may be applying latitudes and longitudes as predictors in both FFNN1 and FFNN3 but not in FFNN2. In the province P10 subpolar Southern Ocean, latitudes and longitudes were considered not good predictors by the stepwise FFNN algorithm, and the results of three validation groups were extremely close.
3.4 Validation based on independent observations
The FFNN outputs based on a different combination of predictors were compared with independent observations from HOT (Dore et al., 2009), BATS (Bates, 2007), and ESTOC (González-Dávila and Santana-Casiano, 2012; Fig. 8). Compared with the independent observations from the HOT station, the three validation groups all show close results, which were also similar in the seasonal and interannual variability of pCO2. From 1992 to 2019, the RMSE between FFNN1 outputs and HOT observations was only 9.29 µatm, lower than the 10.85 µatm of FFNN2 and the 10.70 µatm of FFNN3. The monthly mean pCO2 of FFNN2 during winter was lower than the HOT observations and pCO2 values of other validation groups, while the FFNN1 and FFNN3 outputs were closer to the HOT observations. The MAE between predicted pCO2 and HOT observations was also lower in the validation group FFNN1, which was only 7.17 µatm, compared to the 8.61 µatm of FFNN2 and the 8.44 µatm of FFNN3. Higher bias was generated in the winter bottom and summer peak, shown more obviously in the monthly average of pCO2 (Fig. 8b). Compared with other validation groups, the result of FFNN1 was closer to the monthly average values of the HOT observations. The same conclusion can be obtained for the ESTOC and BATS station located in the province P5 north subtropical Atlantic. The RMSE between FFNN1 outputs and independent observations was 13.03 µatm for the BATS station and 11.35 µatm for the ESTOC station, lower than other validation groups. The RMSE between FFNN2 outputs and independent observations was 16.15 µatm for the BATS station and 14.51 µatm for the ESTOC station. For the group FFNN3, the RMSE was 13.09 µatm for the BATS station and 13.01 µatm for the ESTOC station. All results were extremely close to the independent observations, but the RMSE and MAE of FFNN1 were lower. Similar to the situation in the HOT station, FFNN1 was closest and FFNN3 second-closest. Based on the better performance of FFNN1, in which the predictors selected by the stepwise FFNN algorithm were used, we may conclude that the stepwise FFNN algorithm can effectively find a better combination of predictors to fit the driver of surface ocean pCO2 and obtain a lower error.
3.5 Climatological spatial distribution
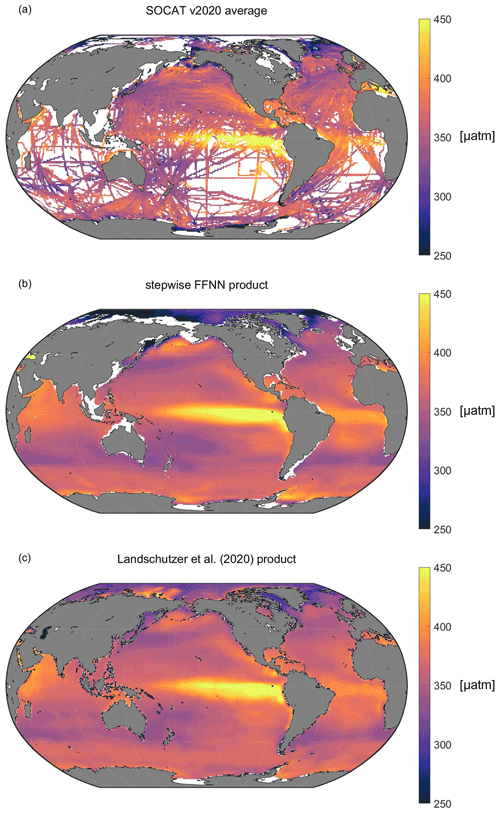
The climatological average distribution of pCO2 suggested significant spatial variability (Fig. 9), consistent with the average distribution of SOCAT observations. In the Pacific Ocean, the high pCO2 areas shown by the stepwise FFNN product (Fig. 9b), including the equatorial areas, east temperate areas, and north subpolar areas, were highly consistent with the SOCAT datasets (Fig. 9a). Similarly, the distribution of pCO2 in the Atlantic Ocean was also close. However, the stepwise FFNN product suggested lower pCO2 average values in the Arctic and higher values in the Southern Ocean near the Antarctic continent. Compared with the previous climatology product (Landschützer et al., 2020), the stepwise FFNN product has similar spatial patterns with high pCO2 in the eastern equatorial Pacific and equatorial Atlantic: an inconsistent spatial distribution also existed in the Arctic and parts of the Southern Ocean near the Antarctic continent. The differences between the stepwise FFNN product and the previous climatology product may be caused by differences in methods or SOCAT dataset versions used. In comparison, lower average values of the SOCAT dataset in the Southern Ocean may be caused by the undersampling in winter. The global spatial distribution pattern of the stepwise FFNN pCO2 product was basically well consistent with the previous climatology product and SOCAT dataset, suggesting that pCO2 predicting based on regional specific predictors selected by the stepwise FFNN algorithm was better than that based on the globally same predictors.
A stepwise FFNN algorithm was constructed to decrease the predicting error in the surface ocean pCO2 mapping by finding better combinations of pCO2 predictors in each biogeochemical province defined by the SOM method, based on which a monthly 1∘ × 1∘ gridded global open-oceanic surface ocean pCO2 product from January 1992 to August 2019 was constructed. Our work provided a statistical method for predictor selection for all research based on relationship fitting by machine learning methods. The validation based on the SOCAT dataset and independent observations shows that using regional-specific predictors selected by the stepwise FFNN algorithm retrieved a lower predicting error than globally similar predictors. This stepwise FFNN algorithm can also be used in pCO2 mapping research for higher resolution and coastal regions, and in other data mapping research using SOM or other region dividing methods. The preparation work consisted only of collecting as many predictors as possible that might be related to the target data, and they need to be sufficiently available in time and space. However, high predicting error in particular regions, such as polar regions and the equatorial Pacific, still needs to be improved. Since the stepwise FFNN algorithm's result largely depends on how biogeochemical provinces are divided, improving the SOM step is still necessary. In addition, the FFNN can be replaced by any suitable type of neural network. A possible way to improve the performance of the stepwise FFNN algorithm is to modify the structure of the FFNN or to use networks with more sophisticated architecture and to use different learning algorithms. In future work, the stepwise FFNN algorithm with possible improvement will be attempted for the mapping of other products, such as total alkalinity and pH in order to provide sufficient data support for studies on ocean acidification and carbon cycling.
The stepwise FFNN algorithm (as a .m file for MATLAB) and the global 1∘ × 1∘ gridded surface ocean pCO2 product since from January 1992 to August 2019 (as a NetCDF file) generated during this study are available from the Institute of Oceanology of the Chinese Academy of Sciences Marine Science Data Center at https://doi.org/10.12157/iocas.2021.0022 (Zhong, 2021) or directly at http://english.casodc.com/data/metadata-special-detail?id=1418424272359075841 (last access: 21 August 2021).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-19-845-2022-supplement.
JM, HY, and LD collected the dataset of pCO2 predictors, and BQ and YW contributed to the synthesis of datasets. GZ, XL, and JS designed the predictor selection algorithm and performed the reconstruction of pCO2 product. FW, BZ, XS, WZ, and ZW contributed to its further improvement. GZ prepared the manuscript with contributions from all co-authors.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank SOCAT for sharing the fCO2 observation data. The Surface Ocean CO2 Atlas (SOCAT) is an international effort, endorsed by the International Ocean Carbon Coordination Project (IOCCP), the Surface Ocean Lower Atmosphere Study (SOLAS), and the Integrated Marine Biosphere Research (IMBeR) program, to deliver a uniformly quality-controlled surface ocean CO2 database. The many researchers and funding agencies responsible for the collection of data and quality control are thanked for their contributions to SOCAT. We thank the NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group for sharing the chlorophyll concentration data.
This research has been supported by the National Key Research and Development Program of China (grant no. 2017YFA0603204), the Major Program of the Pilot National Laboratory for Marine Science and Technology (Qingdao) in the “14th 5-year Plan”, the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDA19060401), the National Natural Science Foundation of China (grant nos. 91958103, 42176200, and 41806133, and the Natural Science Foundation of Shandong Province (grant no. ZR2020YQ28).
This paper was edited by Peter Landschützer and reviewed by Anna Denvil-Sommer and two anonymous referees.
Bakker, D. C. E., Pfeil, B., Landa, C. S., Metzl, N., O'Brien, K. M., Olsen, A., Smith, K., Cosca, C., Harasawa, S., Jones, S. D., Nakaoka, S., Nojiri, Y., Schuster, U., Steinhoff, T., Sweeney, C., Takahashi, T., Tilbrook, B., Wada, C., Wanninkhof, R., Alin, S. R., Balestrini, C. F., Barbero, L., Bates, N. R., Bianchi, A. A., Bonou, F., Boutin, J., Bozec, Y., Burger, E. F., Cai, W.-J., Castle, R. D., Chen, L., Chierici, M., Currie, K., Evans, W., Featherstone, C., Feely, R. A., Fransson, A., Goyet, C., Greenwood, N., Gregor, L., Hankin, S., Hardman-Mountford, N. J., Harlay, J., Hauck, J., Hoppema, M., Humphreys, M. P., Hunt, C. W., Huss, B., Ibánhez, J. S. P., Johannessen, T., Keeling, R., Kitidis, V., Körtzinger, A., Kozyr, A., Krasakopoulou, E., Kuwata, A., Landschützer, P., Lauvset, S. K., Lefèvre, N., Lo Monaco, C., Manke, A., Mathis, J. T., Merlivat, L., Millero, F. J., Monteiro, P. M. S., Munro, D. R., Murata, A., Newberger, T., Omar, A. M., Ono, T., Paterson, K., Pearce, D., Pierrot, D., Robbins, L. L., Saito, S., Salisbury, J., Schlitzer, R., Schneider, B., Schweitzer, R., Sieger, R., Skjelvan, I., Sullivan, K. F., Sutherland, S. C., Sutton, A. J., Tadokoro, K., Telszewski, M., Tuma, M., van Heuven, S. M. A. C., Vandemark, D., Ward, B., Watson, A. J., and Xu, S.: A multi-decade record of high-quality fCO2 data in version 3 of the Surface Ocean CO2 Atlas (SOCAT), Earth Syst. Sci. Data, 8, 383–413, https://doi.org/10.5194/essd-8-383-2016, 2016.
Bates, N. R.: Interannual variability of the oceanic CO2 sink in the subtropical gyre of the North Atlantic Ocean over the last 2 decades, J. Geophys. Res.-Oceans, 112, C09013, https://doi.org/10.1029/2006JC003759, 2007.
Boyer, T. P., Garcia, H. E., Locarnini, R. A., Zweng, M. M., Mishonov, A. V., Reagan, J. R., Weathers, K. A., Baranova, O. K., Seidov, D., and Smolyar, I. V.: World Ocean Atlas 2018 [Dissolved Inorganic Nutrients and Dissolved Oxygen], NOAA National Centers for Environmental Information [data set], https://accession.nodc.noaa.gov/NCEI-WOA18 (last access: 4 August 2020), 2018.
Broullón, D., Pérez, F. F., Velo, A., Hoppema, M., Olsen, A., Takahashi, T., Key, R. M., Tanhua, T., González-Dávila, M., Jeansson, E., Kozyr, A., and van Heuven, S. M. A. C.: A global monthly climatology of total alkalinity: a neural network approach, Earth Syst. Sci. Data, 11, 1109–1127, https://doi.org/10.5194/essd-11-1109-2019, 2019.
Broullón, D., Pérez, F. F., Velo, A., Hoppema, M., Olsen, A., Takahashi, T., Key, R. M., Tanhua, T., Santana-Casiano, J. M., and Kozyr, A.: A global monthly climatology of oceanic total dissolved inorganic carbon: a neural network approach, Earth Syst. Sci. Data, 12, 1725–1743, https://doi.org/10.5194/essd-12-1725-2020, 2020.
Chen, L. Q., Xu, S. Q., Gao, Z. Y., Chen, H. Y., Zhang, Y. H., Zhan, J. Q., and Li, W.: Estimation of monthly air–sea CO2 flux in the southern Atlantic and Indian Ocean using in-situ and remotely sensed data, Remote Sens. Environ., 115, 1935–1941, https://doi.org/10.1016/j.rse.2011.03.016, 2011.
Chen, S., Hu, C., Barnes, B. B., Wanninkhof, R., Cai, W.-J., Barbero, L., and Pierrot, D.: A machine learning approach to estimate surface ocean pCO2 from satellite measurements, Remote Sens. Environ., 228, 203–226, https://doi.org/10.1016/j.rse.2019.04.019, 2019.
Chen, S. L., Hu, C. M., Byrne, R. H., Robbins, L. L., and Yang, B.: Remote estimation of surface pCO2 on the West Florida Shelf, Cont. Shelf Res., 128, 10–25, https://doi.org/10.1016/j.csr.2016.09.004, 2016.
Chen, S. L., Hu, C. M., Cai, W. J., and Yang, B.: Estimating surface pCO2 in the northern Gulf of Mexico: Which remote sensing model to use?, Cont. Shelf Res., 151, 94–110, https://doi.org/10.1016/j.csr.2017.10.013, 2017.
Cheng, L. and Zhu, J.: Benefits of CMIP5 multimodel ensemble in reconstructing historical ocean subsurface temperature variation, J. Climate, 29, 5393–5416, https://doi.org/10.1175/JCLI-D-15-0730.1, 2016.
Cheng, L., Trenberth, K., Fasullo, J., Boyer, T., Abraham, J., and Zhu, J.: Improved estimates of ocean heat content from 1960 to 2015, Sci. Adv., 3, 3, https://doi.org/10.1126/sciadv.1601545, 2017.
Cheng, L., Trenberth, K. E., Gruber, N., Abraham, J. P., Fasullo, J., Li, G., Mann, M. E., Zhao, X., and Zhu, J.: Improved estimates of changes in upper ocean salinity and the hydrological cycle, J. Climate, 33, 10357–10381, https://doi.org/10.1175/JCLI-D-20-0366.1, 2020.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thepaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Denvil-Sommer, A., Gehlen, M., Vrac, M., and Mejia, C.: LSCE-FFNN-v1: a two-step neural network model for the reconstruction of surface ocean pCO2 over the global ocean, Geosci. Model Dev., 12, 2091–2105, https://doi.org/10.5194/gmd-12-2091-2019, 2019.
Dore, J. E., Lukas, R., Sadler, D. W., Church, M. J., and Karl, D. M.: Physical and biogeochemical modulation of ocean acidification in the central North Pacific, P. Natl. Acad. Sci. USA, 106, 12235–12240, 2009.
Friedlingstein, P., Jones, M. W., O'Sullivan, M., Andrew, R. M., Hauck, J., Peters, G. P., Peters, W., Pongratz, J., Sitch, S., Le Quéré, C., Bakker, D. C. E., Canadell, J. G., Ciais, P., Jackson, R. B., Anthoni, P., Barbero, L., Bastos, A., Bastrikov, V., Becker, M., Bopp, L., Buitenhuis, E., Chandra, N., Chevallier, F., Chini, L. P., Currie, K. I., Feely, R. A., Gehlen, M., Gilfillan, D., Gkritzalis, T., Goll, D. S., Gruber, N., Gutekunst, S., Harris, I., Haverd, V., Houghton, R. A., Hurtt, G., Ilyina, T., Jain, A. K., Joetzjer, E., Kaplan, J. O., Kato, E., Klein Goldewijk, K., Korsbakken, J. I., Landschützer, P., Lauvset, S. K., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Marland, G., McGuire, P. C., Melton, J. R., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Neill, C., Omar, A. M., Ono, T., Peregon, A., Pierrot, D., Poulter, B., Rehder, G., Resplandy, L., Robertson, E., Rödenbeck, C., Séférian, R., Schwinger, J., Smith, N., Tans, P. P., Tian, H., Tilbrook, B., Tubiello, F. N., van der Werf, G. R., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2019, Earth Syst. Sci. Data, 11, 1783–1838, https://doi.org/10.5194/essd-11-1783-2019, 2019.
Friedrich, T. and Oschlies, A.: Neural network-based estimates of North Atlantic surface pCO2 from satellite data: A methodological study, J. Geophys. Res.-Oceans, 114, C03020, https://doi.org/10.1029/2007jc004646, 2009.
GLOBALVIEW-CO2: Cooperative Atmospheric Data Integration Project – Carbon Dioxide CD-ROM, NOAA ESRL, Boulder, Colorado, available via anonymous FTP to ftp://ftp.cmdl.noaa.gov, Path: ccg/co2/GLOBALVIEW (last access: 5 January 2013), 2011.
González-Dávila, M. and Santana-Casiano, J. M.: Carbon dioxide, temperature, salinity and other variables collected via time series monitoring from METEOR, POSEIDON and others in the North Atlantic Ocean from 1995-10-02 to 2009-11-25 (NCEI Accession 0100064), NOAA National Centers for Environmental Information [data set], https://doi.org/10.3334/cdiac/otg.tsm_estoc, 2012.
Gregor, L., Lebehot, A. D., Kok, S., and Scheel Monteiro, P. M.: A comparative assessment of the uncertainties of global surface ocean CO2 estimates using a machine-learning ensemble (CSIR-ML6 version 2019a) – have we hit the wall?, Geosci. Model Dev., 12, 5113–5136, https://doi.org/10.5194/gmd-12-5113-2019, 2019.
Hales, B., Strutton, P. G., Saraceno, M., Letelier, R., Takahashi, T., Feely, R., Sabine, C., and Chavez, F.: Satellite-based prediction of pCO2 in coastal waters of the eastern North Pacific, Prog. Oceanogr., 103, 1–15, https://doi.org/10.1016/j.pocean.2012.03.001, 2012.
Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., Menne, M. J., Smith, T. M., Vose, R. S., and Zhang, H.-M.: Extended reconstructed sea surface temperature, version 5 (ERSSTv5): upgrades, validations, and intercomparisons, J. Climate, 30, 8179–8205, 2017.
Iida, Y., Kojima, A., Takatani, Y., Nakano, T., Midorikawa, T., and Ishii, M.: Trends in pCO2 and sea-air CO2 flux over the global open oceans for the last two decades, J. Oceanogr., 71, 637–661, https://doi.org/10.1007/s10872-015-0306-4, 2015.
Jo, Y. H., Dai, M. H., Zhai, W. D., Yan, X. H., and Shang, S. L.: On the variations of sea surface pCO2 in the northern South China Sea: A remote sensing based neural network approach, J. Geophys. Res.-Oceans, 117, C08022, https://doi.org/10.1029/2011jc007745, 2012.
Körtzinger, A.: Determination of carbon dioxide partial pressure (pCO2), in: Methods of Seawater Analysis, 3rd Edn., edited by: Grasshoff, K., Kremling, K., and Ehrhardt, M., Wiley-VCH Verlag GmbH, Weinheim, Germany, https://doi.org/10.1002/9783527613984.ch9, 1999.
Landschützer, P., Gruber, N., Bakker, D. C. E., Schuster, U., Nakaoka, S., Payne, M. R., Sasse, T. P., and Zeng, J.: A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink, Biogeosciences, 10, 7793–7815, https://doi.org/10.5194/bg-10-7793-2013, 2013.
Landschützer, P., Gruber, N., Bakker, D. C. E., and Schuster, U.: Recent variability of the global ocean carbon sink, Global Biogeochem. Cy., 28, 927–949, https://doi.org/10.1002/2014gb004853, 2014.
Landschützer, P., Gruber, N., and Bakker, D. C. E.: Decadal variations and trends of the global ocean carbon sink, Global Biogeochem. Cy., 30, 1396–1417, https://doi.org/10.1002/2015gb005359, 2016.
Landschützer, P., Laruelle, G. G., Roobaert, A., and Regnier, P.: A uniform pCO2 climatology combining open and coastal oceans, Earth Syst. Sci. Data, 12, 2537–2553, https://doi.org/10.5194/essd-12-2537-2020, 2020.
Laruelle, G. G., Landschützer, P., Gruber, N., Tison, J.-L., Delille, B., and Regnier, P.: Global high-resolution monthly pCO2 climatology for the coastal ocean derived from neural network interpolation, Biogeosciences, 14, 4545–4561, https://doi.org/10.5194/bg-14-4545-2017, 2017.
Marrec, P., Cariou, T., Macé, E., Morin, P., Salt, L. A., Vernet, M., Taylor, B., Paxman, K., and Bozec, Y.: Dynamics of air–sea CO2 fluxes in the northwestern European shelf based on voluntary observing ship and satellite observations, Biogeosciences, 12, 5371–5391, https://doi.org/10.5194/bg-12-5371-2015, 2015.
Marshall, G. J.: Trends in the Southern Annular Mode from observations and reanalyses, J. Climate, 16, 4134–4143, https://doi.org/10.1175/1520-0442(2003)016<4134:TITSAM>2.0.CO;2, 2003.
Menemenlis, D., Campin, J., Heimbach, P., Hill, C., Lee, T., Nguyen, A., Schodlok, M., and Zhang, H.: ECCO2: High resolution global ocean and sea ice data synthesis, Mercator Ocean Quarterly Newsletter, 31, 13–21, 2008.
Moussa, H., Benallal, M. A., Goyet, C., and Lefevre, N.: Satellite-derived CO2 fugacity in surface seawater of the tropical Atlantic Ocean using a feedforward neural network, Int. J. Remote Sens., 37, 580–598, https://doi.org/10.1080/01431161.2015.1131872, 2016.
Nakaoka, S., Telszewski, M., Nojiri, Y., Yasunaka, S., Miyazaki, C., Mukai, H., and Usui, N.: Estimating temporal and spatial variation of ocean surface pCO2 in the North Pacific using a self-organizing map neural network technique, Biogeosciences, 10, 6093–6106, https://doi.org/10.5194/bg-10-6093-2013, 2013.
NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Moderate-resolution Imaging Spectroradiometer (MODIS) Aqua Chlorophyll Data, 2018 Reprocessing, NASA OB.DAAC, Greenbelt, MD, USA, https://doi.org/10.5067/AQUA/MODIS/L3M/CHL/2018, 2018.
NOAA National Geophysical Data Center: 2-minute Gridded Global Relief Data (ETOPO2) v2, NOAA National Centers for Environmental Information [data set], https://doi.org/10.7289/V5J1012Q, 2006.
Rödenbeck, C., Bakker, D. C. E., Metzl, N., Olsen, A., Sabine, C., Cassar, N., Reum, F., Keeling, R. F., and Heimann, M.: Interannual sea–air CO2 flux variability from an observation-driven ocean mixed-layer scheme, Biogeosciences, 11, 4599–4613, https://doi.org/10.5194/bg-11-4599-2014, 2014.
Sabine, C. L., Feely, R. A., Gruber, N., Key, R. M., Lee, K., Bullister, J. L., Wanninkhof, R., Wong, C. S., Wallace, D. W. R., Tilbrook, B., Millero, F. J., Peng, T. H., Kozyr, A., Ono, T., and Rios, A. F.: The oceanic sink for anthropogenic CO2, Science, 305, 367–371, https://doi.org/10.1126/science.1097403, 2004.
Sarma, V. V. S. S., Saino, T., Sasaoka, K., Nojiri, Y., Ono, T., Ishii, M., Inoue, H. Y., and Matsumoto, K.: Basin-scale pCO2 distribution using satellite sea surface temperature, Chl a, and climatological salinity in the North Pacific in spring and summer, Global Biogeochem. Cy., 20, Gb3005, https://doi.org/10.1029/2005gb002594, 2006.
Shadwick, E. H., Thomas, H., Comeau, A., Craig, S. E., Hunt, C. W., and Salisbury, J. E.: Air-Sea CO2 fluxes on the Scotian Shelf: seasonal to multi-annual variability, Biogeosciences, 7, 3851–3867, https://doi.org/10.5194/bg-7-3851-2010, 2010.
Signorini, S. R., Mannino, A., Najjar, R. G., Friedrichs, M. A. M., Cai, W. J., Salisbury, J., Wang, Z. A., Thomas, H., and Shadwick, E.: Surface ocean pCO2 seasonality and sea-air CO2 flux estimates for the North American east coast, J. Geophys. Res.-Oceans, 118, 5439–5460, https://doi.org/10.1002/jgrc.20369, 2013.
Takahashi, T., Sutherland, S. C., Feely, R. A., and Wanninkhof, R.: Decadal change of the surface water pCO2 in the North Pacific: A synthesis of 35 years of observations, J. Geophys. Res.-Oceans, 111, C07s05, https://doi.org/10.1029/2005jc003074, 2006.
Takahashi, T., Sutherland, S. C., Wanninkhof, R., Sweeney, C., Feely, R. A., Chipman, D. W., Hales, B., Friederich, G., Chavez, F., Sabine, C., Watson, A., Bakker, D. C. E., Schuster, U., Metzl, N., Yoshikawa-Inoue, H., Ishii, M., Midorikawa, T., Nojiri, Y., Kortzinger, A., Steinhoff, T., Hoppema, M., Olafsson, J., Arnarson, T. S., Tilbrook, B., Johannessen, T., Olsen, A., Bellerby, R., Wong, C. S., Delille, B., Bates, N. R., and de Baar, H. J. W.: Climatological mean and decadal change in surface ocean pCO2, and net sea–air CO2 flux over the global oceans, Deep-Sea Res. Pt. II, 56, 554–577, https://doi.org/10.1016/j.dsr2.2008.12.009, 2009.
Telszewski, M., Chazottes, A., Schuster, U., Watson, A. J., Moulin, C., Bakker, D. C. E., González-Dávila, M., Johannessen, T., Körtzinger, A., Lüger, H., Olsen, A., Omar, A., Padin, X. A., Ríos, A. F., Steinhoff, T., Santana-Casiano, M., Wallace, D. W. R., and Wanninkhof, R.: Estimating the monthly pCO2 distribution in the North Atlantic using a self-organizing neural network, Biogeosciences, 6, 1405–1421, https://doi.org/10.5194/bg-6-1405-2009, 2009.
Wang, Y., Li, X., Song, J., Zhong, G., and Zhang, B.: Carbon Sinks and Variations of pCO2 in the Southern Ocean From 1998 to 2018 Based on a Deep Learning Approach, IEEE J. Sel. Top. Appl., 14, 3495–3503, https://doi.org/10.1109/JSTARS.2021.3066552, 2021.
Weiss, R. F.: Carbon dioxide in water and seawater: the solubility of a non-ideal gas, Mar. Chem., 2, 203–215, 1974.
Zeng, J., Nojiri, Y., Landschützer, P., Telszewski, M., and Nakaoka, S.: A Global Surface Ocean fCO2 Climatology Based on a Feed-Forward Neural Network, J. Atmos. Ocean. Tech., 31, 1838–1849, https://doi.org/10.1175/jtech-d-13-00137.1, 2014.
Zeng, J., Matsunaga, T., Saigusa, N., Shirai, T., Nakaoka, S., and Tan, Z.-H.: Technical note: Evaluation of three machine learning models for surface ocean CO2 mapping, Ocean Sci., 13, 303–313, https://doi.org/10.5194/os-13-303-2017, 2017.
Zeng, J. Y., Nojiri, Y., Nakaoka, S., Nakajima, H., and Shirai, T.: Surface ocean CO2 in 1990–2011 modelled using a feed-forward neural network, Geosci. Data J., 2, 47–51, https://doi.org/10.1002/gdj3.26, 2015.
Zhong, G.: Global surface ocean pCO2 product based on a stepwise FFNN algorithm, Chinese Academy of Sciences Marine Science Data Center [data set, code], https://doi.org/10.12157/iocas.2021.0022, 2021.
Zhong, G., Li, X., Qu, B., Wang, Y., Yuan, H, and Song, J.: A General Regression Neural Network approach to reconstruct global 1∘ × 1∘ resolution sea surface pCO2, Acta Oceanol Sin., 10, 70–79, 2020.