the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Physical and stoichiometric controls on stream respiration in a headwater stream
Jancoba Dorley
Joel Singley
Tim Covino
Kamini Singha
Michael Gooseff
David Van Horn
Many studies in ecohydrology focusing on hydrologic transport argue that longer residence times across a stream ecosystem should consistently result in higher biological uptake of carbon, nutrients, and oxygen. This consideration does not incorporate the potential for biologically mediated reactions to be limited by stoichiometric imbalances. Based on the relevance and co-dependences between hydrologic exchange, stoichiometry, and biological uptake and acknowledging the limited amount of field studies available to determine their net effects on the retention and export of resources, we quantified how microbial respiration is controlled by the interactions between and the supply of essential nutrients (C, N, and P) in a headwater stream in Colorado, USA. For this, we conducted two rounds of nutrient experiments, each consisting of four sets of continuous injections of Cl− as a conservative tracer, resazurin as a proxy for aerobic respiration, and one of the following nutrient treatments: (a) N, (b) N+C, (c) N+P, or (d) C+N+P. Nutrient treatments were considered to be known system modifications that alter metabolism, and statistical tests helped identify the relationships between reach-scale hydrologic transport and respiration metrics. We found that as discharge changed significantly between rounds and across stoichiometric treatments, (a) transient storage mainly occurred in pools lateral to the main channel and was proportional to discharge, and (b) microbial respiration remained similar between rounds and across stoichiometric treatments. Our results contradict the notion that hydrologic transport alone is a dominant control on biogeochemical processing and suggest that complex interactions between hydrology, resource supply, and biological community function are responsible for driving in-stream respiration.
- Article
(2672 KB) -
Supplement
(948 KB) - BibTeX
- EndNote
High biochemical processing rates in streams and rivers occur at locations and times where the dynamic interconnections among hydrologic exchange, residence time, nutrient supply, and microbial biomass combine to form optimum conditions for metabolic activity (i.e., the transformation of nutrients, carbon, and oxygen or another electron acceptor into energy and biomass). The exchange of water between the main channel and transient-storage zones, where most microbes exist, is the primary mechanism supplying carbon, nutrients, and oxygen to metabolically active zones (Covino et al., 2010b, 2011; Gooseff et al., 2004; Gootman et al., 2020; Knapp et al., 2017). The extent of water exchange controls the residence time of solutes (Drummond et al., 2012; Gomez et al., 2012; Patil et al., 2013), their chemical signatures (Covino and McGlynn, 2007), and their microbial composition and metabolic functioning (Blume et al., 2002; Navel et al., 2011; Li et al., 2020). Exchange patterns are influenced by geomorphologic conditions (Cardenas et al., 2004; Gooseff et al., 2005; Kasahara and Wondzell, 2003; Emanuelson et al., 2022), hydrologic conditions (i.e., discharge and surrounding water table configuration) (Gooseff et al., 2005; Ward and Packman, 2019; Ward et al., 2013; Wondzell, 2006), and biofilm growth (Battin et al., 2003; Wen and Li, 2018). The spatiotemporal variability in exchange processes and resource availability (e.g., seasonal variations in nutrient loads) create heterogeneous hydrologic and biogeochemical gradients across space and time, within which ecosystem metabolism occurs (Mulholland et al., 1985; Mulholland and Hill, 1997).
To date, studies with a focus on hydrologic transport argue that longer residence times across a stream ecosystem should consistently result in higher biological demand for carbon, nutrients, and oxygen (Valett et al., 1996; Gooseff et al., 2005; Wondzell, 2006; Gomez et al., 2012; Zarnetske et al., 2012; Ward et al., 2013; Li et al., 2021), not fully incorporating the potential for biologically mediated reactions to be limited by stoichiometric imbalances. Ecological stoichiometry is the notion that biota balance the consumption of nutrients with energy requirements. Redfield (1934) noted that marine phytoplankton generally contained a ratio of of in their biomass, and these ratios are similar to those available in their environment. This Redfield ratio suggests that an ecosystem requires an optimal ratio of available nutrients to flourish and has been used as a guide for many other environmental stoichiometry studies. In a study of streams across eight biomes, Dodds et al. (2004) noted that N consumption depends in part on the C:N ratio of organic matter in streams and suggested that shifts in these state ratios likely influence N retention.
The net effect of supply and demand of resources can be explored at the reach scale with the non-dimensional Damköhler number, Da (Harvey et al., 2013; Pinay et al., 2015; Krause et al., 2017; Ocampo et al., 2006), which quantifies the ratio of transport (i.e., supply) to biological uptake (i.e., demand) timescales along flow paths (Oldham et al., 2013; Liu et al., 2022). Similarly to any other non-dimensional number, Da offers simplicity and objectivity for inter-site and intra-site comparisons. Da has been used to provide insight into the factors limiting the supply and demand of resources (Harvey et al., 2005) as values of Da∼1 define a balance between transport and uptake timescales, which theoretically results in maximal resource retention. Accordingly, where or when Da≪1, i.e., where or when the uptake timescale is much greater than the transport timescale, uptake is suboptimal, and it is referred to as reaction limited because even though resources became available through hydrologic exchange, they were not fully taken up (i.e., assimilated). Conversely, where or when Da≫1, i.e., where or when the transport timescale is much greater than the uptake timescale, resources become scarce or transport limited, and biologically inactive subregions start to develop (González-Pinzón and Haggerty, 2013; Harvey et al., 2013; Gootman et al., 2020). While Da captures essential components of the potential interactions between the supply and demand of ecologically relevant resources, it does not explicitly capture the role of stoichiometric limitations in relation to the supply (i.e., ratios in water fluxes) and demand ( biomass composition and needs) of resources (Tromboni et al., 2018). This is because Da numbers are estimated from solute-specific mass balances, which inform transport and reaction timescales for one resource at a time (e.g., only N) in isolation of other stoichiometrically relevant resources that can become limiting factors (e.g., C and P).
Based on the relevance and co-dependences between hydrologic exchange, stoichiometry, and biological uptake and the limited amount of field studies available to determine their net effects on the retention and export of resources, we sought to quantify how metabolic activity is controlled by the interactions between and the supply of essential nutrients (C, N, P) at the reach scale. More specifically, we tested if variations in stoichiometric conditions can induce metabolic limitations at which residence time alone becomes a weak predictor of stream respiration. We addressed the following research question: How is microbial respiration controlled by hydrologic exchange vs. stoichiometric conditions (i.e., supply of C, N, and P)? We hypothesized that aerobic respiration would be maximized when nutrient supply and demand were nearly balanced for a given hydrologic condition. To test this, we conducted a repeated set of stream tracer injections in Como Creek, a mountain stream in Colorado, USA, varying stream C (acetate; sensu Baker et al., 1999), N (NaNO3), and P (KH2PO4) concentrations to manipulate stoichiometry and nutrient supply. We repeated experiments under different flow conditions to quantify the tradeoffs between supply (transport and delivery of nutrients) and demand (microbial respiration). We tested for statistical relationships between hydrologic transport metrics and respiration metrics using the resazurin–resorufin tracer system (González-Pinzón et al., 2012; Knapp et al., 2018) and contextualized our findings within the framework of the Damköhler number.
2.1 Site description
Our research experiments were conducted in Como Creek, a forested pool and riffle stream in Colorado, USA. Como Creek is a tributary to Boulder Creek, with land cover consisting of approximately 20 % alpine meadow tundra and 80 % conifer forest. The study reach drains a 5.4 km2 catchment, with elevations ranging from 2895 to 3557 m and a mean average precipitation of 883 mm yr−1 (Ries III et al., 2017; Emanuelson et al., 2022). Como Creek has a snowmelt-driven hydrograph with stream discharges ranging from 1 to 98 L s−1 and features short-lived increases in discharge during the monsoon season between July and August (Fig. 1). The study reach is a multi-thread channel with substrates ranging from small gravel to bedrock. Additionally, the channel has an average width-to-depth ratio of 11.5, a sinuosity of 1.1, and an average longitudinal slope of 21 % (Natural Resources Conservation Service, 2022).
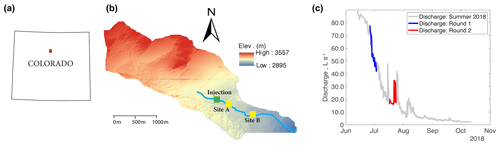
Figure 1(a) Location of Como Creek watershed in Colorado, (b) detailed map of the watershed where sites A and B are 50 and 350 m downstream from the injection location, and (c) hydrograph and timing of experimental work; each round of experiments consisted of four treatments featuring N, N+C, N+P, or C+N+P nutrient additions.
2.2 Stream tracer injection experiments
We conducted two rounds of experiments, each consisting of four sets of continuous injections (lasting ∼ 4–7 h) of Cl− as a conservative tracer, resazurin (referred to as Raz hereafter) as a proxy for aerobic respiration, and one of the following nutrient treatments: (a) N, (b) N+C, (c) N+P, or (d) C+N+P. In our study, the nutrient treatments are treated as known system modifications (control variables) for altering metabolism. Also, we use the transformation of Raz, which occurred at the same spatiotemporal scales as the nutrient additions, to calculate how changes in stoichiometric conditions and discharge affect respiration. Briefly, the reactive tracer Raz (blue in color) is irreversibly reduced to resorufin (Rru, red) under aerobic respiration, and the relationship between Raz transformation and oxygen consumption is linear (González-Pinzón et al., 2012, 2014, 2016; Knapp et al., 2018; Dallan et al., 2020).
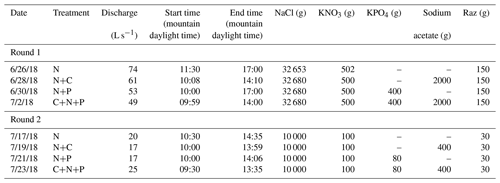
Before each tracer injection, we used the Tracer Injection Planning Tool (TIPT) (González-Pinzón et al., 2022) to estimate the amount of tracer mass needed to reach steady-state conditions at the downstream site and to estimate the duration of the tracer breakthrough curves. From our field sampling, ambient concentrations of nitrate averaged 0.035 (±0.002) mg L−1. We corroborated this value with a study by Smith et al. (2003), who generated estimates of background total nitrogen (TN) and total phosphorous (TP) yield and concentrations throughout the stream–river network in 14 ecoregions of the conterminous US. That study found 75th-quartile TN = 0.21 (±0.05) mg L−1 and TP = 0.02 (±0.005), which indicates relatively low nutrient concentrations compared to agricultural streams in the US Midwest featuring ambient concentrations up to 2 orders of magnitude higher. Based on estimated discharges and reach lengths, we targeted a maximum concentration of 2 mg L−1 for Cl− and 100 µg L−1 of resazurin at the most downstream locations. The concentrations for nitrogen, phosphorus, and carbon were based on the expected detection limit of phosphate (i.e., 0.1 mg L−1) for common ion chromatographs. From that minimum phosphate concentration expected, we scaled the masses of nitrogen and carbon using the Redfield ratio (Redfield, 1934). Table 1 shows the masses injected and the discharges observed during the studies. Note that we allowed the stream to return to ambient concentrations for 1 d after each set of injections.
We collected 20 mL aliquots in each tracer injection 50 and 350 m downstream of the injection site (labeled sites A and B, Fig. 1) to generate tracer breakthrough curves (BTCs) for Raz. All samples were filtered immediately after being collected using a 0.7 µm GF/F filter (Sigma-Aldrich) and kept on dry ice during transport until they were frozen at −4 ∘C for laboratory analysis for Raz concentrations. All analyses took place within a week after the end of each round of injections. At the laboratory, each sample was buffered to a pH of 8.5 (1:10 buffer-to-sample ratio) following Knapp et al. (2018). The fluorescence signals were measured with a Cary Eclipse fluorescence spectrophotometer (Agilent Technologies) using excitation/emission wavelengths of nm for Raz and nm for Rru and were converted to concentrations based on an eight-point calibration curve (R2=0.99).
We monitored specific conductivity (SC) and temperature using Campbell Scientific CS547A sensors connected to Campbell Scientific CR 1000 data loggers, which recorded and stored those measurements every 10 min. From the grab samples, we measured chloride using a Dionex ICS-1000 Ion Chromatograph with AS23/AG23 analytical and guard columns. Cl− data were augmented with background-corrected SC data to model conservative transport.
We monitored changes in stream stage every 10 min at the end of the study reach using pressure transducers (Campbell Scientific CS420) connected to a data logger (Campbell Scientific CR 1000). We used established stage–discharge relationships specific to the study site, as provided by the site managers. The discharge values reported in Table 1 represent mean values observed during a given experiment.
2.3 Conservative transport modeling and metrics
We calibrated the conservative transport parameters of the transient-storage model presented in Eqs. (1) and (2) using Cl− and stream water electrical conductivity data observed at sites A and B. For this, we used the MATLAB (The Mathworks Inc., Natick, Massachusetts) script from Knapp et al. (2018), which features a joint calibration of conservative and reactive solutes through a non-linear, least-squares optimization routine.
In the above equations, c [ML−3] and cts [ML−3] are the concentrations in the main channel and aggregate transient-storage zone; x [L] is the distance of the study reach; t [T] is time; u [L T−1] and D [L2 T−1] are parameters representing advective flow velocity and dispersion coefficient, respectively; qin [T−1] is a volumetric flux parameter accounting for lateral inputs; k[T−1] is the first-order mass transfer rate coefficient parameter between the main channel and the aggregate transient-storage zone; is the capacity ratio parameter representing the relative contribution of transient-storage-dominated to advection-dominated compartments in the stream, represented as areas along the reach; and λmc and λts [T−1] are processing-rate coefficients in the main channel and transient-storage zones (equaling zero for a conservative tracer).
We completed the parameter estimation using the differential evolution adaptive Metropolis (DREAM [ZS]) algorithm (Vrugt et al., 2009). We jointly fit Cl− and Raz data in a first step of 100 000 model generations. We assessed model convergence using Gelman and Rubin statistics (Gelman and Rubin, 1992). The goodness of fit between measured and simulated BTCs was quantified through the calculation of the residual sum of squares, (nRSS) (–), normalized by the squared theoretical peak tracer concentrations of each tracer BTC of the respective tracer at the given location. The medians of the best 1000 model simulations were used to assess the agreement between our final model fits and a subset of possible curve fits. The details on the model calibration procedure that we use in this work were presented in the supporting information of Gootman et al. (2020). Examples of observed and fitted breakthrough curves can be found in Figs. S1–S3 in the Supplement.
We estimated conservative transport timescales from the transport parameters to describe the transient-storage timescale, [T], and the mean travel time between sites A and B, τ [T], which was computed as follows:
where m0,cl and m1,cl are the zeroth and first-centralized temporal moments of the Cl− BTCs from each sampling site, i is a time index, and r is the total number of samples available in a BTC.
2.4 Estimating the transformation of Raz as a proxy for microbial respiration
We used the net transformation rate coefficients of Raz, λRaz [T−1], as a proxy for microbial respiration. λRaz incorporates transformation in the main channel and in transient-storage zones and was estimated following the work by González-Pinzón and Haggerty (2013), who derived algebraic relationships with analytical solutions to calculate processing-rate coefficients from the transient-storage model presented in Eqs. (1) and (2):
where is the zeroth temporal moment of Raz at the injection site [M L−3 T−1]; MRaz is the mass of Raz added to the injectate; Q is the stream discharge [L3 T−1]; is the dilution-corrected zeroth temporal moment of Raz estimated with BTC data from a sampling site; and is the Peclet number [–], which describes the relative importance of advection and dispersion in the system. As noted by González-Pinzón and Haggerty (2013), when Pe≫10, which is the case in advection-dominated systems such as open channel flow, the dispersion term Φ is negligible, and .
Since we can only get one transformation rate coefficient from every observed BTC available from Eq. (5) or from the direct calibration of the transient-storage model, we used the tracer addition for spiraling curve characterization (TASCC) framework (Covino et al., 2010b) to characterize uptake kinetics over the range of experimental concentrations observed. In TASCC, the ratio of reactive to conservative solute concentrations for every independent sample across the tracer BTCs is compared to the ratio of the concentrations of the injection solution to determine uptake metrics. If the added solutes are non-reactive, they will transport conservatively, and the ratio of the reactive to conservative solute concentrations will remain constant. Alternatively, if the added solutes are limiting, co-limiting, or reactive, they will not transport conservatively, and the ratio of the reactive to conservative solute concentrations will change over time as a function of reactivity. TASCC-based transformation rate coefficients for Raz were estimated using the following equation:
From each transformation rate coefficient λRaz and λRaz, sample, we also estimated an uptake (or mass transfer) velocity of Raz, or , where h is the mean depth of the stream. Following Ensign and Doyle (2006), uptake velocities represent the vertical velocity of solute molecules through the water column towards the benthos and are typically used in stream ecology to normalize processing-rate coefficients by the influence of contrasting discharge magnitudes to facilitate the comparison of results from small streams and large rivers. As demonstrated in Covino et al. (2010b), the range of λRaz, sample and values encompass the λRaz and values obtained from processing rates derived from temporal-moment analyses (e.g., Eq. 5).
Finally, reach-scale Damköhler numbers, Da [–], were calculated using the following equation:
2.5 Statistical tests
We calculated standard deviations (SDs) based on repeated measures of the distribution of the transport parameters of Eqs. (1) and (2) to create upper and lower boundaries of the uncertainties in our measurements (i.e., mean ± SD). Because our data were not normally distributed, we used the Mann–Whitney U nonparametric statistical test to determine if there were statistically significant differences between nutrient treatments across rounds (e.g., N vs. N in rounds 1 and 2), following a similar procedure as that in Ensign and Doyle (2006). For the Mann–Whitney U test, we set our significance level (α, alpha) to be equal to 0.05.
We explored the Pearson correlation coefficient (r) matrix between the transport parameters of Eqs. (1) and (2) and associated metrics to establish direct (r>0.1), inverse (r<−0.1), and non-existent correlations (−0.1<r<0.1) (Bowley, 2008). We classified the strength of the correlations as uncorrelated (), weakly correlated (), moderately correlated (), or strongly correlated () and included p values for each correlation.
Lastly, we tested differences in the mean values of the transport parameters of Eqs. (1) and (2) and associated metrics between nutrient treatments within each experimental round (e.g., N vs. N+C vs. N+P vs. C+N+P in round 1) using Student's t test based on deviation from the group's mean value (Blair et al., 1980).
3.1 Conservative transport and metrics of physical controls
Between experimental rounds 1 and 2, stream depth (h) and discharge (Q) decreased, causing significant differences in stream velocity (u), dispersion (D), mass transfer rate coefficients (k), transient-storage timescales (τTS), and mean travel times (τ) (Fig. 2). The only parameter that did not show significant differences was the relative contribution of the main channel to storage zone areas, .
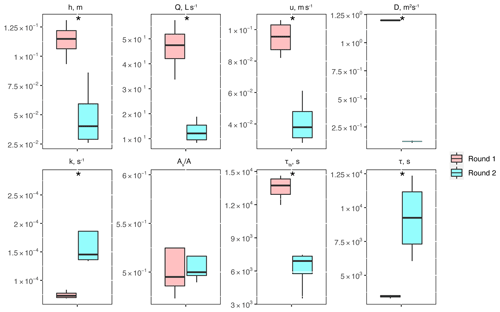
Figure 2Conservative transport parameters and metrics of physical controls estimated for the two experimental rounds: stream depth (h), stream velocity (u), dispersion (D), mass transfer rate coefficients (k), the ratio of transient-storage-dominated to advection-dominated compartments , transient-storage timescales (τTS), and mean travel times (τ). Asterisks represent statistical differences in magnitude for rounds 1 and 2 with p<0.05 (*) based on the Mann–Whitney U nonparametric statistical test.
The correlation matrix between parameters and metrics (Fig. 3) shows that Q (and interrelated quantities h and u), D, and τts were all directly correlated (moderately to strongly). Mean travel times between sites, τ, were directly and weakly correlated with k and the ratio and were inversely correlated (weakly to strongly) with the rest of the conservative transport parameters and metrics. Finally, the ratio was generally uncorrelated or weakly correlated with other quantities. Even though the correlations of some interdependent quantities are known to be spurious, e.g., Q vs. u and λRaz vs. (González-Pinzón et al., 2015), we included all relevant measured and modeled quantities in Fig. 3 to allow readers to explore different data pairs. For clarity, we differentiate with brackets all known spurious correlations. Note that we did not flag the correlation between and Q (and their interrelated quantities h and u) as spurious because the ratio of areas is an indicator of the relative volume-based contribution from advection-dominated to transient-storage-dominated compartments instead of an actual estimate of cross-sectional areas (Kelleher et al., 2013; González-Pinzón et al., 2013; Knapp and Kelleher, 2020).
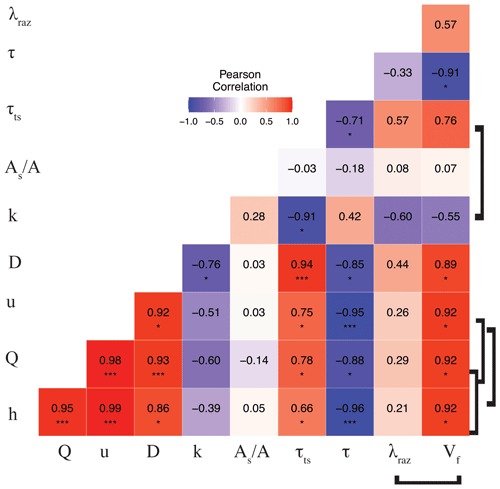
Figure 3Pearson correlation coefficient (r) heat map for the mean values of the transport parameters and metrics for each stoichiometric treatment during rounds 1 and 2. Brackets link known spurious correlations. Asterisks represent significant differences in magnitude between parameters with p<0.05 (*) and p<0.001 (***) based on the Pearson correlation.
One of the metrics of interest in stream reactive-transport modeling is the transient-storage timescale (, which quantifies the exposure that solutes have to biological communities in metabolically active transient-storage zones. In our study site, τts decreased by 1 order of magnitude from round 1 to round 2 and were comparable to the range of values observed in other studies involving forested mountain streams (Valett et al., 1996; Hall et al., 2002). Due to the geomorphology of the stream, which is characterized by pool and riffle sequences but steep longitudinal and valley slopes and shallow bedrock, transient storage was expected to occur mainly in the main channel (Fields and Dethier, 2019; Barnhart et al., 2021; Emanuelson et al., 2022). As flow receded from round 1 to round 2, we observed the disconnection of in-stream pools contributing to transient storage, which explains the direct correlation between discharge and transient-storage timescales. Another indication of the dominant contribution of in-stream pools to total transient storage is the lack of change in with discharge. Since A is expected to vary proportionally with discharge (i.e., , a constant suggests that the contribution of transient-storage-dominated (i.e., As) compartments (i.e., A) also varied proportionally with discharge.
3.2 Raz transformation (a proxy for respiration) as a function of physical controls
Our results indicate that the mean values of the transformation rate coefficient of Raz (λRaz) were directly and moderately correlated with the transient-storage timescale (τts), as other studies on reactive transport have shown (Valett et al., 1996; Hall et al., 2002; Gomez et al., 2012; Zarnetske et al., 2012; Kiel and Bayani Cardenas, 2014; Gootman et al., 2020). Mean λRaz values were directly and weakly correlated with discharge (Q) (also depths h and velocities u) and dispersion (D) and were directly and moderately correlated with τts. Mean λRaz values were inversely and weakly correlated with mean travel times (τ) and were inversely and moderately correlated with mass transfer rate coefficients (k) (Fig. 3). Raz uptake velocities () showed spurious, direct, and strong correlations with discharge (Q) (also h and u), strong correlations with dispersion (D) and transient-storage timescales (τts), and strong indirect correlations with mean travel times (τ) and k (moderate). Finally, both λRaz and were uncorrelated with . Unlike studies where an increased transient-storage timescale (τts) is mainly associated with slower hyporheic flows due to lower discharges (Q) (Zarnetske et al., 2007; Schmid et al., 2010), τts in our study site increased with Q because the geomorphology of the channel and the valley favored in-stream transient storage in lateral pools (Jackson et al., 2012, 2013, 2015). Similar declines in transient storage with falling discharge have been observed in other streams with comparable geomorphic characteristics (Covino et al., 2010a; Emanuelson et al., 2022); however, the absence of concurrent declines in respiration suggest biological control by some other mechanism.
3.3 Raz transformation (a proxy for respiration) as a function of physical and stoichiometric controls
Our results suggest no significant changes in respiration despite significant differences in discharge (Q), temperature, and nutrient treatments. Between experimental rounds, the mean values of Q (and h and u by extension) and temperature (except for N+C) were statistically different for each treatment comparison (Fig. 4a). For λRaz,sample, we only found statistical differences between rounds for the C+N+P treatments (Fig. 4c). Due to the large influence of Q on the uptake velocity of Raz () through stream depth (h), the statistical differences between rounds seen for Q were also seen for (Fig. 4d).
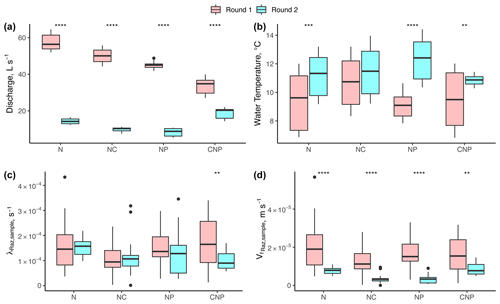
Figure 4Comparison of (a) stream discharge values recorded at the gaging station, (b) stream water temperatures, (c) transformation rate coefficients of resazurin (λRaz,sample) resulting from Eq. (6), and (d) associated uptake velocities of resazurin ( estimated for each experimental nutrient treatment addition during rounds 1 and 2. Due to the large influence of Q on the uptake velocity of Raz () through stream depth (h), most of the statistical differences between rounds seen for Q were also seen for . Asterisks represent significant differences in magnitude between rounds, with p<0.01 (**) and p∼0 (****) based on the Mann–Whitney U nonparametric statistical test.
When looking at the data collected from each round, we found that mean Q values were statistically different across nutrient treatments (Fig. 5a and d). For mean λRaz,sample values, the only treatments with statistical differences were the N+C and C+N+P from round 1 (Fig. 5b and e). Finally, mean values were only statistically different for the N vs. N+C treatments for round 1 and for all but the N+C vs. N+P and N vs. C+N+P treatments for round 2 (Fig. 5c and f).
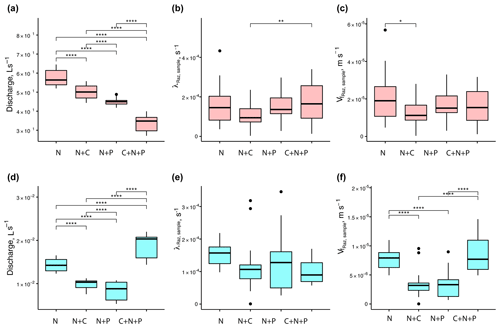
Figure 5Comparison of stream discharges (a, d), transformation rate coefficients of resazurin (λRaz,sample) resulting from Eq. (6) (b, e), and associated uptake velocities of resazurin () (c, f) across treatments for round 1 (a–c) and 2 (d–f). Due to the large influence of Q on the uptake velocity of Raz () through stream depth (h), most of the statistical differences between rounds seen for Q were also seen for . Asterisks represent significant differences in magnitude for treatments N, N+C, N+P, and C+N+P, with p<0.05 (*), p<0.01 (**), and p∼0 (****) based on the Mann–Whitney U nonparametric statistical test.
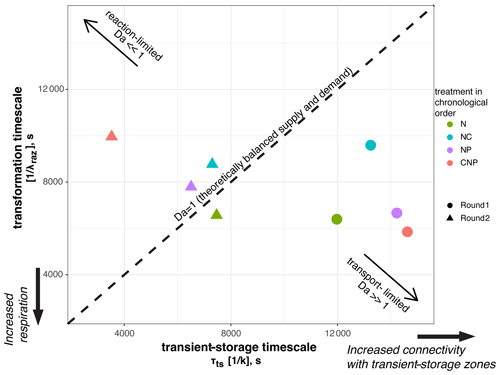
For each of the eight nutrient injections, we related the mean transient-storage timescales at the reach scale, τts, which indicate exposure times between solutes and microbial communities, and the mean transformation timescales of Raz at the reach scale, , which indicate respiration (Fig. 6). This Damköhler-based analysis allows us to visualize the interplay between physical, biological, and stoichiometric controls in the stream. We found that the range of variation of the mean transient-storage timescales was 3 times greater than that of the mean transformation timescales. In round 1, all the stoichiometric treatments resulted in transport-limited conditions due to the high values of τts; i.e., the average particle of Raz that entered a metabolically active compartment underwent transformation, and more Raz could have been transformed if it had been available. Thus, in round 1, respiration was high relative to the supply of solutes to the metabolically active transient-storage zones. In round 2, all stoichiometric treatments, except N, resulted in reaction-limited conditions; i.e., the average particle of Raz entering a metabolically active compartment left it without undergoing transformation. Thus, in round 2, respiration was slow relative to the exposure of solutes to microbial communities.
3.4 How is microbial respiration controlled by hydrologic exchange vs. stoichiometric conditions (i.e., supply of C, N, and P)?
We characterized reach-scale microbial respiration with the transformation timescale of Raz, ; the extent of hydrologic exchanges along the reach with the transient-storage timescale, τTS, and the relative size of the main channel and transient-storage areas, ; and stoichiometric conditions with our controlled nutrient additions (i.e., N, N+C, N+P, and C+N+P treatments). The most salient findings indicate that (a) discharge (Q) changed significantly between rounds (Fig. 4a) and across stoichiometric treatments (Fig. 5a, d) and was directly and moderately correlated with τTS and uncorrelated with (Fig. 3), suggesting that most transient storage occurred in lateral pools in the channel, which increased in quantity and extent proportionally with Q; and (b) the respiration activity indicated by λRaz remained similar between rounds with significantly different Q (Fig. 4b) and across controlled stoichiometric treatments also featuring different Q (Fig. 5b, e). Thus, we observed that respiration remained largely unchanged or constant with varying physical and stoichiometric conditions.
Several hypotheses may explain the invariant reach-scale respiration observed between experimental rounds and treatments. First, tradeoffs in metabolic rates may have occurred as the stream shifted from high to low flows. At high flows during late June and early July, lateral pools in the main channel were inundated, and transient-storage timescales likely associated with these pools were high. Under these conditions, the observed respiration was probably supported by low levels of processing in the hyporheic zone due to the prevalence of bedrock substrate and relatively low respiration from benthic biomass due to scour from high flows (Francoeur and Biggs, 2006; Katz et al., 2018). However, the combination of longer transient-storage timescales and an expanded total surface area resulted in moderate total respiration. In contrast, during the low flows seen in the second round of injections, surface area and transient-storage timescales were decreased due to the contraction of the channel. Under these conditions, biomass increased, likely due to decreased scour and increased stability (Francoeur and Biggs, 2006; Katz et al., 2018; Cargill et al., 2021), increased water temperatures (Perkins et al., 2012), and increased processing of autochthonous carbon (Wagner et al., 2017) (Fig. S4). This may have supported elevated areal metabolic rates in benthic biofilms (Battin et al., 2016), maintaining relatively constant respiration levels with respect to the first round of injections.
An alternative hypothesis to explain the consistency of the observed respiration values is that some other factor constrains respiration values within a narrow range. For example, the limitation of a key nutrient or metabolic resource may constrain respiration. While we designed the experiments to relieve stoichiometric constraints, it is possible that the quantities of C, N, and P in the injectate we were logistically able to introduce to the stream were insufficient to overcome demand. Also, the form of the resources may not have been readily available to communities adapted to these locals as stream microbial communities most efficiently process the forms and diversity of dissolved organic matter found in their native habitats, and they express extracellular enzymes in ratios appropriate to acquiring limiting nutrients (Hill et al., 2012; Lane et al., 2012; Wilhelm et al., 2015; Logue et al., 2016).
In previous studies, transient storage and nutrient uptake have presented contradictory relationships, which we summarize below.
Inconclusive relationships. Martí et al. (1997) did not find correlations between NH3 uptake length and in a desert stream using data from eight tracer injections. Webster et al. (2003) did not find statistically significant relationships between NH4 uptake and using the 11-stream LINX-I dataset that included arctic to tropical streams. From 37 injections conducted in 13 streams at Hubbard Brook Experimental Forest (HBEF), Hall et al. (2002) found weak correlations (R2=0.14–0.35) between transient-storage parameters and NH4 demand. Using data from seven streams in New Zealand, Niyogi et al. (2004) did not find significant correlations between soluble reactive phosphorous (P-SRP), NO3 uptake velocities, and . Bukaveckas (2007) reported an indefinite relationship between transient storage and NO3 and P-SRP retention efficiencies from tracer injections in a reference (N=13 injections), channelized (N=14 injections), and restored (N=17 injections) stream reach in the midwestern US. Lastly, the LINX-II dataset from 15N–NO3 injections in 72 streams located in eight regions of the US showed no relationship between NO3 uptake and the fraction of median travel time due to transient storage () (Hall et al., 2009).
Weak to moderate relationships. Thomas et al. (2003) showed that transient storage accounted for 44 % to 49 % of NO3 retention measured by 15N in a small headwater stream in North Carolina. Mulholland et al. (1997) found larger PO4 uptake rates in a stream with higher transient storage when they compared two forested streams. Ensign and Doyle (2005) found an increase in and the uptake velocities for NH4 and PO4 after the addition of flow baffles to two streams. Lautz and Siegel (2007) found a modest correlation (R2=0.44) between NO3 retention efficiency and transient storage in the Red Canyon Creek watershed, WY.
Strong relationships. Valett et al. (1996) found a strong correlation (R2=0.77) between transient storage and NO3 retention in three first-order streams in New Mexico. From nine tracer injections in two urban streams in the eastern US, Ryan et al. (2007) found strong relationships between P-SRP retention and transient-storage metrics (; R2>0.84) when the variables were measured in different seasons. Sheibley et al. (2014) observed that the retention of NO3 in seven agricultural streams in the US was positively correlated with and the average water flux through the storage zone per unit length of stream (qs=kA) and negatively correlated with the transient-storage timescale (τts). However, they found no significant correlation between NH and SRP retention and transient-storage metrics.
The studies referenced above were performed in streams with contrasting physical, chemical, and biological conditions. Together, they offer a broader perspective on the inconsistent relationship between transient-storage metrics and metabolic processing. Those studies do not feature co-injections of C, N, and P macronutrients (e.g., N+C, N+P, and N+C+P), even while some tracked ambient processing rates of more than one nutrient. Therefore, they generally represent solute-specific analyses, where the uptake of one nutrient at a time was analyzed and, thus, did not account for stoichiometric controls on nutrient uptake (however, see Tromboni et al. (2018) for an example of recent trend changes in this research area). By combining both transport and stoichiometric analyses, our study offers evidence that stoichiometric controls have an ambiguous relationship to reach-scale metabolic activities and that further investigations should be conducted using greater quantities and types of resources.
We conducted two rounds of four stoichiometric treatments (i.e., N, C+N, N+P, and C+N+P) in a headwater stream in Colorado to quantify reach-scale changes to stream respiration during flow recession and to answer the following question: How is respiration controlled by hydrologic exchange vs. stoichiometric conditions (i.e., supply of C, N, and P)? We found that discharge changed significantly between rounds and across stoichiometric treatments and that it was directly and moderately correlated with transient-storage timescales but uncorrelated with the ratio of contributions from advection-dominated to transient-storage-dominated compartments (i.e., ). This suggests that most transient storage occurred in lateral pools within the main channel, which increased in quantity and extent proportionally with discharge. We also found that respiration remained similar despite significant changes in discharge and stoichiometric treatments. Our results contradict the notion that hydrologic transport alone is a dominant control on biogeochemical processing and suggest that complex interactions between hydrology, resource supply, and biological community function are responsible for driving in-stream respiration.
The data used in this article can be found in the Consortium of Universities for the Advancement of Hydrologic Science (CUAHSI) HydroShare repository at http://www.hydroshare.org/resource/50ae3c59bebe4cb383e31408a0c10012 (Gonzalez-Pinzon, 2022).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-20-3353-2023-supplement.
RGP, TC, KS, and MG secured the funding for this research. All the co-authors designed and carried out the experiments. JD and RGP processed Raz samples, performed solute transport simulations and statistical analyses, and prepared the paper with input from all the co-authors. DVH supported the contextualization of hydrological and ecological interactions. All the co-authors approved the final version of the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Karin Emanuelson, Jackie Randell, Erin Jenkins, Tristan Weiss, and Melissa Pinzon for their field and laboratory assistance.
This research has been supported by the National Science Foundation (grant nos. 1642399, 1642368, 1642402, 1642403, and 1914490).
This paper was edited by Gabriel Singer and reviewed by three anonymous referees.
Baker, M. A., Dahm, C. N., and Valett, H. M.: Acetate retention and metabolism in the hyporheic zone of a mountain stream, Limnol. Oceanogr., 44, 1530–1539, https://doi.org/10.4319/lo.1999.44.6.1530, 1999.
Barnhart, T. B., Vukomanovic, J., Bourgeron, P., and Molotch, N. P.: Future land cover and climate may drive decreases in snow wind-scour and transpiration, increasing streamflow at a Colorado, USA headwater catchment, Hydrol. Process., 35, e14416, https://doi.org/10.1002/hyp.14416, 2021.
Battin, T. J., Kaplan, L. A., Newbold, J. D., and Hansen, C. M. E.: Contributions of microbial biofilms to ecosystem processes in stream mesocosms, Nature, 426, 439–442, https://doi.org/10.1038/nature02152, 2003.
Battin, T. J., Besemer, K., Bengtsson, M. M., Romani, A. M., and Packmann, A. I.: The ecology and biogeochemistry of stream biofilms, Nat. Rev. Microbiol., 14, 251–263, https://doi.org/10.1038/nrmicro.2016.15, 2016.
Blair, R. C., Higgins, J. J., Journal, S., and Winter, N.: A Comparison of the Power of Wilcoxon's Rank-Sum Statistic to That of Student's t Statistic under Various Nonnormal Distributions, American Educational Research Association and American Statistical Association Stable, J. Educat. Stat., 5, 309–35, https://doi.org/10.2307/1164905, 1980.
Blume, E., Bischoff, M., Reichert, J. M., Moorman, T., Konopka, A., and Turco, R. F.: Surface and subsurface microbial biomass, community structure and metabolic activity as a function of soil depth and season, Appl. Soil Ecol., 20, 171–181, https://doi.org/10.1016/S0929-1393(02)00025-2, 2002.
Bowley, A. L.: The Standard Deviation of the Correlation Coefficient, J. Am. Stat. Assoc., 23, 31–34, 2008.
Bukaveckas, P. A.: Effects of Channel Restoration on Water Velocity, Transient Storage, and Nutrient Uptake in a Channelized Stream, Environ. Sci. Technol., 41, 1570–1576, https://doi.org/10.1021/es061618x, 2007.
Cardenas, M. B., Wilson, J. L., and Zlotnik, V. A.: Impact of heterogeneity, bed forms, and stream curvature on subchannel hyporheic exchange, Water Resour. Res., 40, 1–14, https://doi.org/10.1029/2004WR003008, 2004.
Cargill, S. K., Segura, C., Villamizar, S. R., and Warren, D. R.: The influence of lithology on stream metabolism in headwater systems, Ecohydrology, 14, e2284, https://doi.org/10.1002/eco.2284, 2021.
Covino, T. P. and McGlynn, B. L.: Stream gains and losses across a mountain-to-valley transition: Impacts on watershed hydrology and stream water chemistry, Water Resour. Res., 43, 1–14, https://doi.org/10.1029/2006WR005544, 2007.
Covino, T. P., McGlynn, B., and Baker, M.: Separating physical and biological nutrient retention and quantifying uptake kinetics from ambient to saturation in successive mountain stream reaches, J. Geophys. Res.-Biogeosc., 115, 1–17, https://doi.org/10.1029/2009JG001263, 2010a.
Covino, T. P., Mcglynn, B. L., and Mcnamara, R. A.: Tracer Additions for Spiraling Curve Characterization (TASCC): Quantifying stream nutrient uptake kinetics from ambient to saturation, Limnol. Oceanogr. Methods, 8, 484–498, https://doi.org/10.4319/lom.2010.8.484, 2010b.
Covino, T. P., McGlynn, B., and Mallard, J.: Stream-groundwater exchange and hydrologic turnover at the network scale, Water Resour. Res., 47, 1–11, https://doi.org/10.1029/2011WR010942, 2011.
Dallan, E., Regier, P., Marion, A., and González-Pinzón, R.: Does the Mass Balance of the Reactive Tracers Resazurin and Resorufin Close at the Microbial Scale?, J. Geophys. Res.-Biogeosc., 125, 1–10, https://doi.org/10.1029/2019JG005435, 2020.
Dodds, W. K., Martí, E., Tank, J. L., Pontius, J., Hamilton, S. K., Grimm, N. B., Bowden, W. B., McDowell, W. H., Peterson, B. J., Valett, H. M., Webster, J. R., and Gregory, S.: Carbon and nitrogen stoichiometry and nitrogen cycling rates in streams, Oecologia, 140, 458–467, https://doi.org/10.1007/s00442-004-1599-y, 2004.
Drummond, J. D., Covino, T. P., Aubeneau, A. F., Leong, D., Patil, S., Schumer, R., and Packman, A. I.: Effects of solute breakthrough curve tail truncation on residence time estimates: A synthesis of solute tracer injection studies, J. Geophys. Res., 117, G00N08, https://doi.org/10.1029/2012JG002019, 2012.
Emanuelson, K., Covino, T. P., Ward, A. S., Dorley, J., and Gooseff, M. N.: Conservative solute transport processes and associated transient storage mechanisms: Comparing streams with contrasting channel morphologies, land use and land cover, Hydrol. Process., 36, e14564, https://doi.org/10.1002/hyp.14564, 2022.
Ensign, S. H. and Doyle, M. W.: In-channel transient storage and associated nutrient retention: Evidence from experimental manipulations, Limnol. Oceanogr., 50, 1740–1751, https://doi.org/10.4319/lo.2005.50.6.1740, 2005.
Ensign, S. H. and Doyle, M. W.: Nutrient spiraling in streams and river networks, J. Geophys. Res., 111, G04009, https://doi.org/10.1029/2005jg000114, 2006.
Fields, J. F. and Dethier, D. P.: From on high: Geochemistry of alpine springs, Niwot Ridge, Colorado Front Range, USA, Hydrol. Process., 33, 1756–1774, https://doi.org/10.1002/hyp.13436, 2019.
Francoeur, S. N. and Biggs, B. J. F.: Short-term Effects of Elevated Velocity and Sediment Abrasion on Benthic Algal Communities, Hydrobiologia, 561, 59–69, https://doi.org/10.1007/s10750-005-1604-4, 2006.
Gelman, A. and Rubin, D. B.: Inference from Iterative Simulation Using Multiple Sequences, Stat. Sci., 7, 457–472, https://doi.org/10.1214/ss/1177011136, 1992.
Gomez, J. D., Wilson, J. L., and Cardenas, M. B.: Residence time distributions in sinuosity-driven hyporheic zones and their biogeochemical effects, Water Resour. Res., 48, 1–17, https://doi.org/10.1029/2012WR012180, 2012.
Gonzalez-Pinzon, R.: Resazurin tracer data from experiments in Colorado (2018) and Iowa (2019), HydroShare [data set], http://www.hydroshare.org/resource/50ae3c59bebe4cb383e31408a0c10012, 2022.
González-Pinzón, R. and Haggerty, R.: An efficient method to estimate processing rates in streams, Water Resour. Res., 49, 6096–6099, https://doi.org/10.1002/wrcr.20446, 2013.
González-Pinzón, R., Haggerty, R., and Myrold, D. D.: Measuring aerobic respiration in stream ecosystems using the resazurin-resorufin system, J. Geophys. Res.-Biogeosc., 117, 1–10, https://doi.org/10.1029/2012JG001965, 2012.
González-Pinzón, R., Haggerty, R., and Dentz, M.: Scaling and predicting solute transport processes in streams, Water Resour. Res., 49, 4071–4088, https://doi.org/10.1002/wrcr.20280, 2013.
González-Pinzón, R., Haggerty, R., and Argerich, A.: Quantifying spatial differences in metabolism in headwater streams, Freshw. Sci., 33, 798–811, https://doi.org/10.1086/677555, 2014.
González-Pinzón, R., Mortensen, J., and Van Horn, D.: Comment on “Solute-specific scaling of inorganic nitrogen and phosphorus uptake in streams” by Hall et al. (2013), Biogeosciences, 12, 5365–5369, https://doi.org/10.5194/bg-12-5365-2015, 2015.
González-Pinzón, R., Peipoch, M., Haggerty, R., Martí, E., and Fleckenstein, J. H.: Nighttime and daytime respiration in a headwater stream, Ecohydrology, 9, 93–100, https://doi.org/10.1002/eco.1615, 2016.
González-Pinzón, R., Dorley, J., Singley, J., Singha, K., Gooseff, M., and Covino, T.: TIPT: The Tracer Injection Planning Tool, Environ. Model. Softw., 156, 105504, https://doi.org/10.1016/j.envsoft.2022.105504, 2022.
Gooseff, M. N., McKnight, D. M., Runkel, R. L., and Duff, J. H.: Denitrification and hydrologic transient storage in a glacial meltwater stream, McMurdo Dry Valleys, Antarctica, Limnol. Oceanogr., 49, 1884–1895, https://doi.org/10.4319/lo.2004.49.5.1884, 2004.
Gooseff, M. N., Bencala, K. E., Scott, D. T., Runkel, R. L., and McKnight, D. M.: Sensitivity analysis of conservative and reactive stream transient storage models applied to field data from multiple-reach experiments, Adv. Water Resour., 28, 479–492, https://doi.org/10.1016/j.advwatres.2004.11.012, 2005.
Gootman, K. S., Pinzón, R. G., Knapp, J. L. A., Garayburu-Caruso, V., and Cable, J.: Spatiotemporal Variability in Transport and Reactive Processes Across a First – to Fifth – Order Fluvial Network, Water Resour. Res., 56, e2019WR026303, https://doi.org/10.1029/2019WR026303, 2020.
Hall, R. J. O., Bernhardt, E. S., and Likens, G. E.: Relating nutrient uptake with transient storage in forested mountain streams, Limnol. Oceanogr., 47, 255–265, https://doi.org/10.4319/lo.2002.47.1.0255, 2002.
Hall, R. O., Tank, J. L., Sobota, D. J., Mulholland, P. J., O'Brien, J. M., Dodds, W. K., Webster, J. R., Valett, H. M., Poole, G. C., Peterson, B. J., Meyer, J. L., McDowell, W. H., Johnson, S. L., Hamilton, S. K., Grimm, N. B., Gregory, S. V., Dahm, C. N., Cooper, L. W., Ashkenas, L. R., Thomas, S. M., Sheibley, R. W., Potter, J. D., Niederlehner, B. R., Johnson, L. T., Helton, A. M., Crenshaw, C. M., Burgin, A. J., Bernot, M. J., Beaulieu, J. J., and Arangob, C. P.: Nitrate removal in stream ecosystems measured by 15N addition experiments: Total uptake, Limnol. Oceanogr., 54, 653–665, https://doi.org/10.4319/lo.2009.54.3.0653, 2009.
Harvey, J. W., Saiers, J. E., and Newlin, J. T.: Solute transport and storage mechanisms in wetlands of the Everglades, south Florida, Water Resour. Res., 41, W05009, https://doi.org/10.1029/2004WR003507, 2005.
Harvey, J. W., Böhlke, J. K., Voytek, M. A., Scott, D., and Tobias, C. R.: Hyporheic zone denitrification: Controls on effective reaction depth and contribution to whole-stream mass balance, Water Resour. Res., 49, 6298–6316, https://doi.org/10.1002/wrcr.20492, 2013.
Hill, B. H., Elonen, C. M., Seifert, L. R., May, A. A., and Tarquinio, E.: Microbial enzyme stoichiometry and nutrient limitation in US streams and rivers, Ecol. Indic., 18, 540–551, https://doi.org/10.1016/j.ecolind.2012.01.007, 2012.
Jackson, T. R., Haggerty, R., Apte, S. V., Coleman, A., and Drost, K. J.: Defining and measuring the mean residence time of lateral surface transient storage zones in small streams, Water Resour. Res., 48, W10501, https://doi.org/10.1029/2012WR012096, 2012.
Jackson, T. R., Haggerty, R., Apte, S. V., and O'Connor, B. L.: A mean residence time relationship for lateral cavities in gravel-bed rivers and streams: Incorporating streambed roughness and cavity shape, Water Resour. Res., 49, 3642–3650, https://doi.org/10.1002/wrcr.20272, 2013.
Jackson, T. R., Apte, S. V., Haggerty, R., and Budwig, R.: Flow structure and mean residence times of lateral cavities in open channel flows: influence of bed roughness and shape, Environ. Fluid Mech., 15, 1069–1100, https://doi.org/10.1007/s10652-015-9407-2, 2015.
Kasahara, T. and Wondzell, S. M.: Geomorphic controls on hyporheic exchange flow in mountain streams, Water Resour. Res., 39, 1005, https://doi.org/10.1029/2002wr001386, 2003.
Katz, S. B., Segura, C., and Warren, D. R.: The influence of channel bed disturbance on benthic Chlorophyll a: A high resolution perspective, Geomorphology, 305, 141–153, https://doi.org/10.1016/j.geomorph.2017.11.010, 2018.
Kelleher, C., Wagener, T., McGlynn, B., Ward, A. S., Gooseff, M. N., and Payn, R. A.: Identifiability of transient storage model parameters along a mountain stream, Water Resour. Res., 49, 5290–5306, https://doi.org/10.1002/wrcr.20413, 2013.
Kiel, B. A. and Bayani Cardenas, M.: Lateral hyporheic exchange throughout the Mississippi River network, Nat. Geosci., 7, 413–417, https://doi.org/10.1038/ngeo2157, 2014.
Knapp, J. L. A. and Kelleher, C.: A Perspective on the Future of Transient Storage Modeling: Let's Stop Chasing Our Tails, Water Resour. Res., 56, e2019WR026257, https://doi.org/10.1029/2019WR026257, 2020.
Knapp, J. L. A., González-Pinzón, R., Drummond, J. D., Larsen, L. G., Cirpka, O. A., and Harvey, J. W.: Tracer-based characterization of hyporheic exchange and benthic biolayers in streams, Water Resour. Res., 53, 1575–1594, https://doi.org/10.1002/2016WR019393, 2017.
Knapp, J. L. A., González-Pinzón, R., and Haggerty, R.: The Resazurin-Resorufin System: Insights From a Decade of “Smart” Tracer Development for Hydrologic Applications, Water Resour. Res., 54, 6877–6889, https://doi.org/10.1029/2018WR023103, 2018.
Krause, S., Lewandowski, J., Grimm, N. B., Hannah, D. M., Pinay, G., McDonald, K., Martí, E., Argerich, A., Pfister, L., Klaus, J., Battin, T., Larned, S. T., Schelker, J., Fleckenstein, J., Schmidt, C., Rivett, M. O., Watts, G., Sabater, F., Sorolla, A., and Turk, V.: Ecohydrological interfaces as hot spots of ecosystem processes: ECOHYDROLOGICAL INTERFACES AS HOT SPOTS, Water Resour. Res., 53, 6359–6376, https://doi.org/10.1002/2016WR019516, 2017.
Lane, C. S., Lyon, D. R., and Ziegler, S. E.: Cycling of two carbon substrates of contrasting lability by heterotrophic biofilms across a nutrient gradient of headwater streams, Aquat. Sci., 75, 235–250, https://doi.org/10.1007/s00027-012-0269-0, 2012.
Lautz, L. K. and Siegel, D. I.: The effect of transient storage on nitrate uptake lengths in streams: an inter-site comparison, Hydrol. Process., 21, 3533–3548, https://doi.org/10.1002/hyp.6569, 2007.
Li, L., Sullivan, P. L., Benettin, P., Cirpka, O. A., Bishop, K., Brantley, S. L., Knapp, J. L. A., van Meerveld, I., Rinaldo, A., Seibert, J., Wen, H., and Kirchner, J. W.: Toward catchment hydro-biogeochemical theories, Wiley Interdiscip. Rev. Water, 8, 1–31, https://doi.org/10.1002/wat2.1495, 2021.
Li, Z., Zeng, Z., Tian, D., Wang, J., Fu, Z., Wang, B., Tang, Z., Chen, W., Chen, H. Y. H., Wang, C., Yi, C., and Niu, S.: The stoichiometry of soil microbial biomass determines metabolic quotient of nitrogen mineralization, Environ. Res. Lett., 15, 034005, https://doi.org/10.1088/1748-9326/ab6a26, 2020.
Liu, S., Maavara, T., Brinkerhoff, C. B., and Raymond, P. A.: Global Controls on DOC Reaction Versus Export in Watersheds: A Damköhler Number Analysis, Global Biogeochem. Cy., 36, e2021GB007278, https://doi.org/10.1029/2021GB007278, 2022.
Logue, J. B., Stedmon, C. A., Kellerman, A. M., Nielsen, N. J., Andersson, A. F., Laudon, H., Lindström, E. S., and Kritzberg, E. S.: Experimental insights into the importance of aquatic bacterial community composition to the degradation of dissolved organic matter, ISME J., 10, 533–545, https://doi.org/10.1038/ismej.2015.131, 2016.
Martí, E., Grimm, N. B., and Fisher, S. G.: Pre- and Post-Flood Retention Efficiency of Nitrogen in a Sonoran Desert Stream, J. North Am. Benthol. Soc., 16, 805–819, https://doi.org/10.2307/1468173, 1997.
Mulholland, P. J. and Hill, W. R.: Seasonal patterns in streamwater nutrient and dissolved organic carbon concentrations: Separating catchment flow path and in-stream effects, Water Resour. Res., 33, 1297–1306, https://doi.org/10.1029/97wr00490, 1997.
Natural Resources Conservation Service: U.S. Department of Agriculture, 2006, Natural Resources Conservation Services, Web soil survey, http://websoilsurvey.nrcs.usda.gov/app/, last access: 1 July 2022.
Navel, S., Mermillod-Blondin, F., Montuelle, B., Chauvet, E., Simon, L., and Marmonier, P.: Water-Sediment Exchanges Control Microbial Processes Associated with Leaf Litter Degradation in the Hyporheic Zone: A Microcosm Study, Microb. Ecol., 61, 968–979, https://doi.org/10.1007/s00248-010-9774-7, 2011.
Niyogi, D. K., Simon, K. S., and Townsend, C. R.: Land use and stream ecosystem functioning: nutrient uptake in streams that contrast in agricultural development, Arch. Für Hydrobiol., 160, 471–486, https://doi.org/10.1127/0003-9136/2004/0160-0471, 2004.
Ocampo, C. J., Oldham, C. E., and Sivapalan, M.: Nitrate attenuation in agricultural catchments: Shifting balances between transport and reaction, Water Resour. Res., 42, W01408, https://doi.org/10.1029/2004WR003773, 2006.
Oldham, C. E., Farrow, D. E., and Peiffer, S.: A generalized Damköhler number for classifying material processing in hydrological systems, Hydrol. Earth Syst. Sci., 17, 1133–1148, https://doi.org/10.5194/hess-17-1133-2013, 2013.
Patil, S., Covino, T. P., Packman, A. I., McGlynn, B. L., Drummond, J. D., Payn, R. A., and Schumer, R.: Intrastream variability in solute transport: Hydrologic and geomorphic controls on solute retention, J. Geophys. Res.-Earth, 118, 413–422, https://doi.org/10.1029/2012JF002455, 2013.
Perkins, D. M., Yvon-Durocher, G., Demars, B. O. L., Reiss, J., Pichler, D. E., Friberg, N., Trimmer, M., and Woodward, G.: Consistent temperature dependence of respiration across ecosystems contrasting in thermal history, Glob. Change Biol., 18, 1300–1311, https://doi.org/10.1111/j.1365-2486.2011.02597.x, 2012.
Pinay, G., Peiffer, S., De Dreuzy, J.-R., Krause, S., Hannah, D. M., Fleckenstein, J. H., Sebilo, M., Bishop, K., and Hubert-Moy, L.: Upscaling Nitrogen Removal Capacity from Local Hotspots to Low Stream Orders' Drainage Basins, Ecosystems, 18, 1101–1120, https://doi.org/10.1007/s10021-015-9878-5, 2015.
Redfield, A. C.: On the Proportions of Organic Derivatives in Sea Water and Their Relation to the Composition of Plankton, James Johnstone Memorial Volume, University Press of Liverpool, 176–192, 1934.
Ries III, K. G., Newson, J. K., Smith, M. J., Guthrie, J. D., Steeves, P. A., Haluska, T., Kolb, K. R., Thompson, R. F., Santoro, R. D., and Vraga, H. W.: StreamStats, version 4, Fact Sheet, Reston, VA, https://doi.org/10.3133/fs20173046, 2017.
Ryan, R. J., Packman, A. I., and Kilham, S. S.: Relating phosphorus uptake to changes in transient storage and streambed sediment characteristics in headwater tributaries of Valley Creek, an urbanizing watershed, J. Hydrol., 336, 444–457, https://doi.org/10.1016/j.jhydrol.2007.01.021, 2007.
Schmid, B. H., Innocenti, I., and Sanfilippo, U.: Characterizing solute transport with transient storage across a range of flow rates: The evidence of repeated tracer experiments in Austrian and Italian streams, Adv. Water Resour., 33, 1340–1346, https://doi.org/10.1016/j.advwatres.2010.06.001, 2010.
Sheibley, R. W., Duff, J. H., and Tesoriero, A. J.: Low Transient Storage and Uptake Efficiencies in Seven Agricultural Streams: Implications for Nutrient Demand, J. Environ. Qual., 43, 1980–1990, https://doi.org/10.2134/jeq2014.01.0034, 2014.
Smith, R. A., Alexander, R. B., and Schwarz, G. E.: Natural background concentrations of nutrients in streams and rivers of the conterminous United States, Environ. Sci. Technol., 37, 3039–3047, https://doi.org/10.1021/es020663b, 2003.
Thomas, S. A., Maurice Valett, H., Webster, J. R., and Mulholland, P. J.: A regression approach to estimating reactive solute uptake in advective and transient storage zones of stream ecosystems, Adv. Water Resour., 26, 965–976, https://doi.org/10.1016/S0309-1708(03)00083-6, 2003.
Tromboni, F., Thomas, S. A., Gücker, B., Neres-Lima, V., Lourenço-Amorim, C., Moulton, T. P., Silva-Junior, E. F., Feijó-Lima, R., Boëchat, I. G., and Zandonà, E.: Nutrient Limitation and the Stoichiometry of Nutrient Uptake in a Tropical Rain Forest Stream, J. Geophys. Res.-Biogeosc., 123, 2154–2167, https://doi.org/10.1029/2018JG004538, 2018.
Valett, H. M., Morrice, J. A., Dahm, C. N., and Campana, M. E.: Parent lithology, surface-groundwater exchange, and nitrate retention in headwater streams, Limnol. Oceanogr., 41, 333–345, https://doi.org/10.4319/lo.1996.41.2.0333, 1996.
Vrugt, J. A., Ter Braak, C. J. F., Diks, C. G. H., Robinson, B. A., Hyman, J. M., and Higdon, D.: Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling, Int. J. Nonlinear Sci. Numer. Simul., 10, 273–290, https://doi.org/10.1515/IJNSNS.2009.10.3.273, 2009.
Wagner, K., Bengtsson, M. M., Findlay, R. H., Battin, T. J., and Ulseth, A. J.: High light intensity mediates a shift from allochthonous to autochthonous carbon use in phototrophic stream biofilms, J. Geophys. Res.-Biogeosc., 122, 1806–1820, https://doi.org/10.1002/2016JG003727, 2017.
Ward, A. S. and Packman, A. I.: Advancing our predictive understanding of river corridor exchange, Wiley Interdiscip. Rev. Water, 6, e1327, https://doi.org/10.1002/wat2.1327, 2019.
Ward, A. S., Payn, R. A., Gooseff, M. N., McGlynn, B. L., Bencala, K. E., Kelleher, C. A., Wondzell, S. M., and Wagener, T.: Variations in surface water-ground water interactions along a headwater mountain stream: Comparisons between transient storage and water balance analyses, Water Resour. Res., 49, 3359–3374, https://doi.org/10.1002/wrcr.20148, 2013.
Webster, J. R., Mulholland, P. J., Tank, J. L., Valett, H. M., Dodds, W. K., Peterson, B. J., Bowden, W. B., Dahm, C. N., Findlay, S., Gregory, S. V., Grimm, N. B., Hamilton, S. K., Johnson, S. L., Marti, E., Mcdowell, W. H., Meyer, J. L., Morrall, D. D., Thomas, S. A., and Wollheim, W. M.: Factors affecting ammonium uptake in streams – an inter-biome perspective, Freshw. Biol., 48, 1329–1352, https://doi.org/10.1046/j.1365-2427.2003.01094.x, 2003.
Wen, H. and Li, L.: An upscaled rate law for mineral dissolution in heterogeneous media: The role of time and length scales, Geochim. Cosmochim. Acta, 235, 1–20, https://doi.org/10.1016/j.gca.2018.04.024, 2018.
Wilhelm, L., Besemer, K., Fragner, L., Peter, H., Weckwerth, W., and Battin, T. J.: Altitudinal patterns of diversity and functional traits of metabolically active microorganisms in stream biofilms, ISME J., 9, 2454–2464, https://doi.org/10.1038/ismej.2015.56, 2015.
Wondzell, S. M.: Effect of morphology and discharge on hyporheic exchange flows in two small streams in the Cascade Mountains of Oregon, USA, Hydrol. Process., 20, 267–287, https://doi.org/10.1002/hyp.5902, 2006.
Zarnetske, J. P., Gooseff, M. N., Brosten, T. R., Bradford, J. H., McNamara, J. P., and Bowden, W. B.: Transient storage as a function of geomorphology, discharge, and permafrost active layer conditions in Arctic tundra streams, Water Resour. Res., 43, 7410, https://doi.org/10.1029/2005WR004816, 2007.
Zarnetske, J. P., Haggerty, R., Wondzell, S. M., Bokil, V. A., and González-Pinzón, R.: Coupled transport and reaction kinetics control the nitrate source-sink function of hyporheic zones, Water Resour. Res., 48, W11508, https://doi.org/10.1029/2012wr011894, 2012.