Characterizing the marine iodine cycle and its relationship to ocean deoxygenation in an Earth system model

Iodine (I) abundance in marine carbonates (measured as an elemental ratio with calcium, I $/$ Ca) is of broad interest as a proxy for local/regional ocean redox. This connection arises because the speciation of iodine in seawater, the balance between iodate (IO${}_{\mathrm{3}}^{-}$) and iodide (I⁻), is sensitive to the prevalence of oxic vs. anoxic conditions. However, although I $/$ Ca ratios are increasingly commonly being measured in ancient carbonate samples, a fully quantitative interpretation of this proxy requires the availability of a mechanistic interpretative framework for the marine iodine cycle that can account for the extent and intensity of ocean deoxygenation in the past. Here we present and evaluate a representation of marine iodine cycling embedded in an Earth system model (“cGENIE”) against both modern and paleo-observations. In this framework, we account for IO${}_{\mathrm{3}}^{-}$ uptake and release of I⁻ through the biological pump, the reduction in ambient IO${}_{\mathrm{3}}^{-}$ to I⁻ in the water column, and the re-oxidation of I⁻ to IO${}_{\mathrm{3}}^{-}$. We develop and test a variety of different plausible mechanisms for iodine reduction and oxidation transformation and contrast model projections against an updated compilation of observed dissolved IO${}_{\mathrm{3}}^{-}$ and I⁻ concentrations in the present-day ocean.

By optimizing the parameters controlling previously proposed mechanisms involved in marine iodine cycling, we find that we can obtain broad matches to observed iodine speciation gradients in zonal surface distribution, depth profiles, and oxygen-deficient zones (ODZs). However, we also identify alternative, equally well performing mechanisms which assume a more explicit mechanistic link between iodine transformation and environment – an ambiguity that highlights the need for more process-based studies on modern marine iodine cycling. Finally, to help distinguish between competing representations of the marine iodine cycle and because our ultimate motivation is to further our ability to reconstruct ocean oxygenation in the geological past, we conducted “plausibility tests” of different model schemes against available I $/$ Ca measurements made on Cretaceous carbonates – a time of substantially depleted ocean oxygen availability compared to modern and hence a strong test of our model. Overall, the simultaneous broad match we can achieve between modeled iodine speciation and modern observations, and between forward proxy modeled I $/$ Ca and geological elemental ratios, supports the application of our Earth system modeling in simulating the marine iodine cycle to help interpret and constrain the redox evolution of past oceans.

1 Introduction

Dissolved iodine (I) in seawater is redox sensitive and, as such, is a potential invaluable delineator of past ocean deoxygenation. This arises directly from (1) observations that the oxidized form of iodine (iodate, IO${}_{\mathrm{3}}^{-}$) is reduced to iodide (I⁻) under low-oxygen conditions, and (2) observations that IO${}_{\mathrm{3}}^{-}$ in seawater is incorporated into carbonate lattice during precipitation in proportion to its seawater abundance (whilst I⁻ is not) (Lu et al., 2010; Podder et al., 2017; Kerisit et al., 2018; Zhang et al., 2013; Hashim et al., 2022). As a result, past ocean IO${}_{\mathrm{3}}^{-}$ concentrations can be recorded in coeval carbonates as I $/$ Ca ratios, with the potential for carbonate I $/$ Ca to reflect the redox variation in the ancient seawater (Lu et al., 2010). Indeed, the I $/$ Ca ratio in marine carbonates is already being applied widely as a paleoredox proxy, with studies employing it to explore variations in the dissolved oxygen ([O₂]) concentration of seawater throughout much of Earth's history, from the Archean and through the Cenozoic (Lu et al., 2010; Hardisty et al., 2014; Zhou et al., 2015; Lu et al., 2016, 2018; Edwards et al., 2018; Bowman et al., 2020; Pohl et al., 2021; Wei et al., 2021; Ding et al., 2022; Shang et al., 2019; Liu et al., 2020; Fang et al., 2022; Uahengo et al., 2020; Yu et al., 2022; Tang et al., 2023). However, realizing the full potential for I $/$ Ca to provide critical insights into how the oxygenation of the ocean has evolved through time, and the causes and biological/ecological consequences of this, requires that we have an adequate understanding not only of carbonate IO${}_{\mathrm{3}}^{-}$ incorporation but of the dynamics of the marine iodine cycle in general.

Considerable progress has been made over the past few decades towards the goal of understanding the marine iodine cycle. Iodine has a relatively long residence time in the ocean (∼300 kyr; Broecker and Peng, 1983), leading to its concentration being relatively constant throughout the global ocean (at around 500 nM) (Elderfield and Truesdale, 1980; Truesdale et al., 2000; Chance et al., 2014). However, although the total concentration of dissolved iodine is relatively invariant, the two most abundant species of dissolved iodine in the ocean, IO${}_{\mathrm{3}}^{-}$ and I⁻, vary relative to each other depending on the environment. Today, IO${}_{\mathrm{3}}^{-}$ is generally the dominant iodine species in oxygenated regions of the ocean, where it represents total iodine nearly quantitatively below the euphotic zone. Within the euphotic zone, the concentration of I⁻ generally increases in association with release during phytoplankton growth and senescence (Hepach et al., 2020). Within oxygen-deficient zones (ODZs), IO${}_{\mathrm{3}}^{-}$ is reduced to I⁻, but not always quantitatively so, and is hence present only at relatively low concentrations, while I⁻ is abundant (Truesdale et al., 2000; Rue et al., 1997; Cutter et al., 2018; Moriyasu et al., 2020; Farrenkopf and Luther, 2002; Wong and Brewer, 1977; Truesdale et al., 2013; Rapp et al., 2020, 2019).

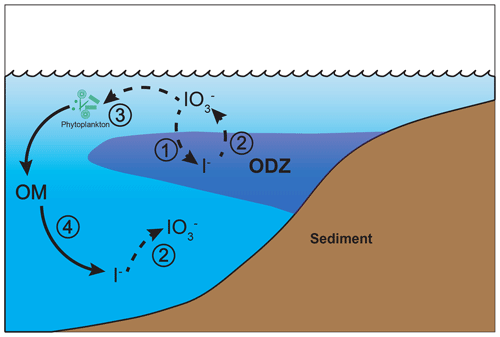
Figure 1 The iodine cycle in marine oxygen-deficient zones (ODZs) in cGENIE, including (1) IO${}_{\mathrm{3}}^{-}$ reduction to I⁻, (2) re-oxidation of I⁻ to IO${}_{\mathrm{3}}^{-}$, (3) photosynthetic IO${}_{\mathrm{3}}^{-}$ update by phytoplankton, and (4) I⁻ release from organic matter (OM) through remineralization. The detailed oxidation–reduction options are described in Sect. 2.2 and Table 1. Dashed arrows indicate variable processes during ensemble simulations.

Although IO${}_{\mathrm{3}}^{-}$ is generally depleted in low-[O₂] settings, the relationship between seawater [O₂] and [IO${}_{\mathrm{3}}^{-}$] is not simple and is not currently well understood. Recently published observations from ODZs in the ocean reveal that the relationship between dissolved [O₂] and [IO${}_{\mathrm{3}}^{-}$] is not linear; instead, it is possible that there is a certain [O₂] or related redox threshold associated with triggering IO${}_{\mathrm{3}}^{-}$ reduction (Cutter et al., 2018; Moriyasu et al., 2020; Farrenkopf and Luther, 2002; Rue et al., 1997; Chapman, 1983). Dissimilatory IO${}_{\mathrm{3}}^{-}$-reducing bacteria, along with an abiotic reduction with sulfide and dissolved Fe, have been identified within ODZs (Farrenkopf et al., 1997; Councell et al., 1997; Jiang et al., 2023). In addition, slow oxidation–reduction kinetics (Tsunogai, 1971; Hardisty et al., 2020; Schnur et al., 2024) imply the likelihood that in situ iodine signals could be integrated across large-scale physical oceanography processes, including ocean currents and mixing between water masses (Hardisty et al., 2021), meaning that iodine speciation reflects regional rather than strictly in situ redox conditions (Lu et al., 2020b). Non-redox-related processes, such as phytoplankton-mediated IO${}_{\mathrm{3}}^{-}$ reduction and organic matter (OM) remineralization, also exert controls on iodine speciation in the water column (Fig. 1; Elderfield and Truesdale, 1980; Wong et al., 1985; Luther and Campbell, 1991; Hepach et al., 2020). Therefore, it is difficult to infer water column redox simply based on iodine speciation without considering these interacting physical and biological effects.

Aside from the uncertainties associated with IO${}_{\mathrm{3}}^{-}$ reduction, it is notable that the oxidants responsible for IO${}_{\mathrm{3}}^{-}$ formation during I⁻ re-oxidation are currently unknown, only that it is unlikely to be free O₂, which is not thermodynamically favorable to oxidize I⁻ (Luther et al., 1995). A recent thermodynamic review indicates that reactive oxygen species (ROS), such as hydrogen peroxide and OH radicals, can fully oxidize I⁻ to IO${}_{\mathrm{3}}^{-}$. Iodide oxidation to IO${}_{\mathrm{3}}^{-}$ is a six-electron transfer, and other ROS, such as superoxide, are only thermodynamically favorable to catalyze partial oxidation to intermediates (Luther, 2023). These ROS have heterogenous distributions and ambient ocean concentrations that are typically relatively low compared to iodine, supporting the likelihood of temporally or spatially isolated high I⁻ oxidation rates despite overall extremely slow rates (Schnur et al., 2024). Additional support for spatially or temporally heterogenous I⁻ oxidation rates comes from recent experimental observations of IO${}_{\mathrm{3}}^{-}$ production from I⁻ in nitrifying cultures (Hughes et al., 2021). Nitrification (oxidation of NH${}_{\mathrm{4}}^{+}$ to NO${}_{\mathrm{2}}^{-}$ (and NO${}_{\mathrm{3}}^{-}$)) rates vary globally, with the highest values occurring in ODZs and the deep chlorophyll maximum (summarized in Table 2 of Hughes et al., 2021). Regardless, nitrification or other specific mechanisms have yet to be linked directly to I⁻ oxidation under normal marine conditions, leaving open the question of rates and locations of I⁻ oxidation.

Despite a growing understanding of I $/$ Ca variations through geologic time, it remains challenging to determine the mechanisms responsible for controlling the spatiotemporal patterns of marine [IO${}_{\mathrm{3}}^{-}$] and how these are linked to seawater oxygen, and there have only been a few attempts to date to model the marine iodine cycle. In a recent publication, a model was developed to simulate modern ocean surface I⁻ distributions, with the aim of being able to improve tropospheric ozone models (Wadley et al., 2020). This particular model was based around a relatively high horizontal ocean resolution (1° grid size) with a three-layer vertical upper water column. Iodine biogeochemical cycling was coupled with the nitrogen cycle, with the surface I⁻ distribution sensitive to biological and hydrological factors, including primary productivity, I : C ratio, oxidation, mixed-layer depth, advection, and freshwater flux. Because the Wadley et al. (2020) model was specifically focused on near-surface processes within the upper 500 m, it did not consider processes occurring within ODZs and is hence not directly applicable to questions concerning the controls on I $/$ Ca ratios. In contrast, a second model-based study deliberately targeted paleoceanographic questions and incorporated an iodine cycle including redox-controlled biogeochemical reactions into the “cGENIE” Earth system model (Lu et al., 2018). The advantage for paleo-studies afforded by this particular approach is that the cGENIE model can take into account different continental configurations, non-modern atmospheric composition (pO₂, pCO₂), and other boundary conditions that may have differed on ancient Earth relative to today (Ridgwell et al., 2007; Reinhard et al., 2016; Boscolo-Galazzo et al., 2021; Remmelzwaal et al., 2019; Pohl et al., 2022; Reinhard and Planavsky, 2022).

Here, we calibrate the iodine cycle within the cGENIE Earth system model to provide a mechanistic framework for interpreting ancient I $/$ Ca variations. In this study, we build on the work of Lu et al. (2018) and further develop and test a series of new potential parameterizations for water column iodine oxidation and reduction (in addition to reduction and transport associated with the biological pump). We also developed three criteria for assessing the model: (1) statistical evaluation using the “model skill score” (M-score) (Watterson, 1996), a non-dimensional measure calculated using location-dependent comparisons between the model and an iodine ocean observation data compilation; (2) graphical comparison of modeled and observed iodine across three illustrative iodine speciation gradients (depth profiles from multiple ocean basins, latitudinal transects of surface waters, and across transects of the Eastern Tropical North Pacific (ETNP) oxygen minimum zone (Moriyasu et al., 2020)); and (3) model applicability to ancient settings by comparing (also using the M-score) projections of ocean surface I $/$ Ca with published I $/$ Ca data from the Cretaceous (Zhou et al., 2015).

2 Model description

2.1 The cGENIE Earth system modeling framework

cGENIE is a class of model known as an “Earth system model with intermediate complexity” (EMIC), a global climate–carbon cycle model that simplifies one or more (typically physical climate) components of the Earth system. In the case of cGENIE, ocean circulation is solved for on a relatively low-resolution grid (here, an equal-area 36×36 grid, which equates to 10° in longitude and latitude increments from 3° near the Equator to 20° near the poles and to 16 non-equally spaced vertical levels). This is coupled to a 2D energy–moisture balance model (EMBM) and a 2D dynamic–thermodynamic sea-ice model. The physics are described in Marsh et al. (2011) and Edwards and Marsh (2005).

Representation of the primary factors controlling the oceanic iodine cycle – specifically, biological productivity, remineralization, and water column redox – follows Crichton et al. (2021). In this configuration, the rate of organic matter export from the ocean surface is calculated based on just a single nutrient (phosphate) control (together with modifiers reflecting ambient light, sea-ice cover, and temperature) and assumes a Redfield ratio stoichiometry (1:106) with carbon (Fig. 1). Organic matter is partitioned into particulate organic matter (POM) (33 % of total export) and dissolved organic matter (DOM) (67 %), with the former sinking down through the water column, where it is progressively remineralized at a rate scaling with ambient temperature (described in Crichton et al., 2021, and Boscolo-Galazzo et al., 2021). When dissolved oxygen nears depletion, sulfate (SO${}_{\mathrm{4}}^{\mathrm{2}-}$) is assumed to be consumed as an electron acceptor to support the remineralization of organic matter (both POM and DOM). The rate of POM remineralization in the water column is governed only by ambient temperature, which, in conjunction with a prescribed sinking rate, determines the vertical distribution of solute release and oxidant consumption. The relative availability of dissolved O₂ vs. SO${}_{\mathrm{4}}^{\mathrm{2}-}$ determines the proportion of organic matter degraded by each electron acceptor. In this, the relative consumption of SO${}_{\mathrm{4}}^{\mathrm{2}-}$ is governed by an SO${}_{\mathrm{4}}^{\mathrm{2}-}$ half-saturation limitation term as well as a dissolved oxygen (O₂) inhibition term, while oxic respiration of organic matter is restricted by an [O₂] half-saturation limitation term (described in Reinhard et al., 2020). Sulfate can hence be consumed even before dissolved oxygen can become fully depleted. For DOM, a decay constant (here, 0.5 years) determines the total fraction that is remineralized per unit time. It should be noted that, currently, there is no published nitrogen cycle in the cGENIE model framework and that we do not regard nitrate reduction as part of the redox cascade here.

2.2 Marine iodine cycling in cGENIE

In the cGENIE model, iodine is present in three reservoirs: IO${}_{\mathrm{3}}^{-}$ and I⁻ in the water column and I⁻ incorporated in POM (and DOM). We then consider four processes that transfer iodine between these reservoirs (summarized in Fig. 1): (1) IO${}_{\mathrm{3}}^{-}$ reduction in the water column, (2) I⁻ oxidation (also in the water column), (3) photosynthetic IO${}_{\mathrm{3}}^{-}$ uptake (and assumed intercellular reduction to I⁻), and (4) I⁻ release to seawater during the remineralization of POM (and DOM). As dissolved species, IO${}_{\mathrm{3}}^{-}$ and I⁻ are physically transported and mixed through ocean circulation (as I is incorporated into DOM), whereas iodine in POM settles vertically through the water column. This is the same overall framework used by Lu et al. (2018). In this paper, we re-assess this framework against an updated compilation of observed iodine speciation in the modern ocean and develop and test alternative representations of IO${}_{\mathrm{3}}^{-}$ reduction (process (1): “threshold”, “inhibition”, and “reminSO4lifetime”) and I⁻ re-oxidation (process (2): “lifetime”, “Fennel', and “reminO2lifetime”). Although we describe all five different parameterizations below for completeness and a number of different permutations of three IO${}_{\mathrm{3}}^{-}$ reduction and three I⁻ re-oxidation processes (presented in Table S1 in the Supplement), in this paper we will focus primarily on a single reduction parameterization (“threshold”) in combination with the three different re-oxidation schemes.

2.2.1 IO${}_{\mathrm{3}}^{-}$ reduction schemes

Threshold. In the numerical scheme of Lu et al. (2018), when [O₂] falls below a set concentration threshold, IO${}_{\mathrm{3}}^{-}$ is immediately and quantitatively reduced to I⁻ (thereafter, we term this IO${}_{\mathrm{3}}^{-}$ reduction parameterization “threshold”).

Inhibition. The “inhibition” scheme links the IO${}_{\mathrm{3}}^{-}$ reduction rate with the ambient O₂ concentration. Following the formulation for the rate of SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduction in Reinhard et al. (2020), we apply an oxygen inhibition term governed by a half-saturation constant. In devising this scheme, we note that, while IO${}_{\mathrm{3}}^{-}$ reduction rates have been determined experimentally, the quantitative relationship with [O₂] (or other parameters) is unknown. The IO${}_{\mathrm{3}}^{-}$ reduction under “inhibition” is mathematically described as

$$\begin{array}{}\text{(1)}& \mathrm{d}\left[{\mathrm{IO}}_{\mathrm{3}}^{-}\right]/\mathrm{d}t=\left[{\mathrm{IO}}_{\mathrm{3}}^{-}\right]\times k_{\mathrm{red}}\times {\displaystyle \frac{k_{{\mathrm{O}}_{\mathrm{2}}}}{k_{{\mathrm{O}}_{\mathrm{2}}}+\left[{\mathrm{O}}_{\mathrm{2}}\right]}},\end{array}$$

in which k_red is the maximum first-order reduction rate of IO${}_{\mathrm{3}}^{-}$ and $k_{{\mathrm{O}}_{\mathrm{2}}}$ is the half-saturation constant of O₂.

ReminSO4lifetime. Reduced sulfur (e.g., sulfides) is also suspected to play an important role in IO${}_{\mathrm{3}}^{-}$ reduction in seawater, especially in the sulfidic zones (Jia-zhong and Whitfield, 1986; Luther and Campbell, 1991; Wong and Brewer, 1977; Truesdale et al., 2013). We therefore devise a scheme (“reminSO4lifetime”) that scales a nominal “lifetime” for IO${}_{\mathrm{3}}^{-}$ with the rate of SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduction in the model. This has the effect of increasing the rate of IO${}_{\mathrm{3}}^{-}$ reduction (a shorter lifetime) under conditions of higher sulfate reduction rates and hence lower ambient oxygen concentrations and/or higher rates of organic matter degradation:

$$\begin{array}{}\text{(2)}& \mathrm{d}\left[{\mathrm{IO}}_{\mathrm{3}}^{-}\right]/\mathrm{d}t=\left[{\mathrm{IO}}_{\mathrm{3}}^{-}\right]\times {\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{sul}}}}\times \mathrm{d}\left[{\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}\right]/\mathrm{d}t,\end{array}$$

in which τ_sul defines the rate constant parameter linking the IO${}_{\mathrm{3}}^{-}$ and SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduction, while the d[SO${}_{\mathrm{4}}^{\mathrm{2}-}$] is the amount of SO${}_{\mathrm{4}}^{\mathrm{2}-}$ reduced during each model time step.

2.2.2 I⁻ oxidation schemes

Lifetime. In Lu et al. (2018), I⁻ is oxidized to IO${}_{\mathrm{3}}^{-}$ following first-order kinetics regardless of ambient O₂ (scheme “lifetime”). In this scheme, I⁻ oxidation follows the first-order reaction kinetics:

$$\begin{array}{}\text{(3)}& \mathrm{d}\left[{\mathrm{I}}^{-}\right]/\mathrm{d}t=\left[{\mathrm{I}}^{-}\right]\times {\displaystyle \frac{\mathrm{1}}{\mathit{\tau }}},\end{array}$$

where τ is the lifetime of I⁻ in seawater.

Fennel. Given the overlapping redox potential between I and N (e.g., Rue et al., 1997; Cutter et al., 2018), we explore the potential for a link between areas of I⁻ and nitrification. To simulate this, we devise an alternative “Fennel” scheme, in which I⁻ oxidation rates vary as a function of ambient O₂, increasing with ambient O₂ concentrations towards some hypothetical maximum value following Michaelis–Menten kinetics (Fennel et al., 2005). In Fennel et al. (2005), this parameterization was originally devised for ammonia re-oxidation. The form of this response is defined by the maximum reaction rate and O₂ half-saturation constant (Fennel et al., 2005):

$$\begin{array}{}\text{(4)}& \mathrm{d}\left[{\mathrm{I}}^{-}\right]/\mathrm{d}t=\left[{\mathrm{I}}^{-}\right]\times k_{\mathrm{ox}}\times {\displaystyle \frac{\left[{\mathrm{O}}_{\mathrm{2}}\right]}{k_{\mathrm{fenn}}+\left[{\mathrm{O}}_{\mathrm{2}}\right]}},\end{array}$$

in which k_ox defines the maximum rate constant of I⁻ oxidation, while k_fenn is the O₂ half-saturation constant.

ReminO2lifetime. Finally, in “reminO2lifetime”, we associate I⁻ oxidation with O₂ consumption during remineralization. The logic behind this parameterization is the recent observation of I⁻ oxidation to IO${}_{\mathrm{3}}^{-}$ catalyzed by bacteria, perhaps in association with ammonia oxidation (Hughes et al., 2021). Although the nitrogen cycle is not currently included in cGENIE, the NH${}_{\mathrm{4}}^{+}$ oxidation can be scaled to OM remineralization (Martin et al., 2019) and hence to O₂ consumption during remineralization. Under “reminO2lifetime”, the lifetime of I⁻ oxidation is inversely linked to O₂ consumption so that faster remineralization, which in the ocean leads to more intensive NH${}_{\mathrm{4}}^{+}$ oxidation, enhances I⁻ oxidation. This I⁻ oxidation scheme follows the equation

$$\begin{array}{}\text{(5)}& \mathrm{d}\left[{\mathrm{I}}^{-}\right]/\mathrm{d}t=\left[{\mathrm{I}}^{-}\right]\times {\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{2}}}}}\times \mathrm{d}\left[{\mathrm{O}}_{\mathrm{2}}\right]/\mathrm{d}t,\end{array}$$

where ${\mathit{\tau }}_{{\mathrm{O}}_{\mathrm{2}}}$ is the rate constant parameter and d[O₂] is the O₂ consumption during remineralization during a single time step in the model.

2.2.3 Biological reduction pump

The final pair of coupled processes in the marine iodine cycle framework concerns the processing of iodine directly through the biological pump. Phytoplankton-absorbed iodine is stored in the cell as IO${}_{\mathrm{3}}^{-}$, I⁻, or other forms, followed by release during senescence (Hepach et al., 2020). While there is some uncertainty as to whether IO${}_{\mathrm{3}}^{-}$ reduction is assimilatory or dissimilatory (Hepach et al., 2020), we adopt a comparable approach to nitrogen cycling (sequence: NO${}_{\mathrm{3}}^{-}$ uptake, N incorporation into organic matter, remineralization, and release as the reduced NH${}_{\mathrm{4}}^{+}$ form). We assume that IO${}_{\mathrm{3}}^{-}$ is assimilated by phytoplankton and incorporated into POM during photosynthesis (Elderfield and Truesdale, 1980) and released as I⁻ during remineralization and/or cell senescence (Wong et al., 2002, 1985; Hepach et al., 2020). cGENIE simulates these processes via an assumed Redfield ratio of iodine to carbon (I : C ratio) in OM. We note that, while the value of I : C can be adjusted in the model, it is currently assumed fixed in value throughout the ocean. We discuss the merits of an optimized and uniform I : C compared to variable I : C (e.g., Wadley et al., 2020) in more detail in the Discussion.

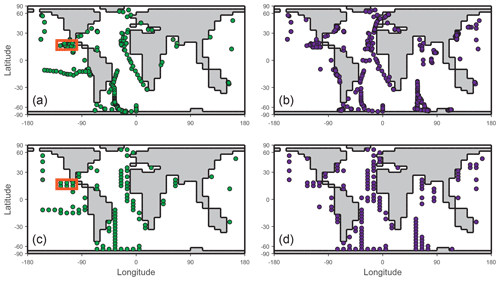
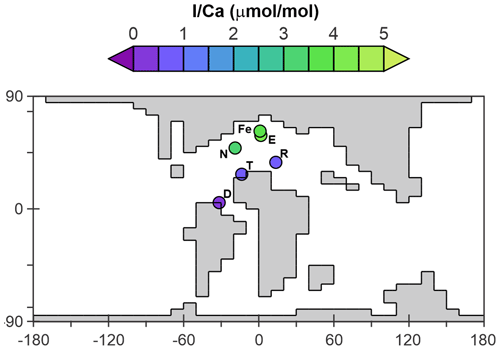
Figure 2 Ocean surface (uppermost ∼81 m corresponding to the depth of the surface layer in the cGENIE model) sampling locations of IO${}_{\mathrm{3}}^{-}$ (a) and I⁻ (b) field observations after data filtration for freshwater and sediment fluxes. The filtered observations were then gridded according to the cGENIE $\mathrm{36}\times \mathrm{36}\times \mathrm{16}$ framework for model–data comparison of IO${}_{\mathrm{3}}^{-}$ (c) and I⁻ (d). The orange boxes in panels (a) and (c) highlight the grids of the oxygen-deficient zone transect shown in Fig. 7.

2.3 Model–data evaluation

For evaluating the marine iodine cycle in the cGENIE model, we compiled oceanic iodine observation data from the literature (Fig. 2, Table S4). Our dataset builds on the compilation of Chance et al. (2019), which was used to calibrate the Wadley et al. (2020) model, but includes more recent publications (referenced in Table S4) and is also expanded to include the deep ocean and ODZ data. To avoid the influence of freshwater dilution and recycled iodine from the sedimentary flux, we applied a filter which only keeps the measurements with total iodine (or IO${}_{\mathrm{3}}^{-}$ plus I⁻) between 450 and 550 nM in the dataset. Note that the I⁻ measurements from the GP16 cruise in the ETSP are not included for the comparison because of potential method considerations (see Cutter et al., 2018, and Moriyasu et al., 2023). After filtering, the data were gridded to the cGENIE model grid (provided as .nc files in the Supplement).

We used the model skill measure (M-score) (Watterson, 1996) to assess the performance of the marine iodine cycle in cGENIE compared to the gridded data. For each iodine speciation (hereby IO${}_{\mathrm{3}}^{-}$ and I⁻), an M-score value is calculated through comparing gridded observations versus model results in each corresponding grid (Fig. 2). The synthesized M-score for iodine of each model experiment is calculated through averaging those for both I⁻ and IO${}_{\mathrm{3}}^{-}$. The higher the M-score value, the better the model–data performance.

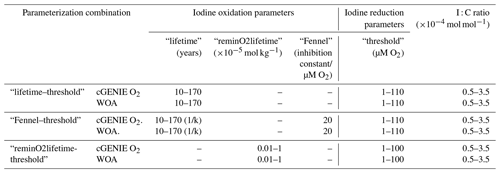
Table 1 The cGENIE iodine redox options and the associated range of parameters of these options. The detailed introduction of each parameter is described in Sect. 2.2.2, and the plausibility of these parameter ranges is discussed in Sect. 4.1.1. Note that the oxidation rate constant k in “Fennel” is in units of yr⁻¹ in the model configuration, which is the reciprocal of the “lifetime”. A detailed table containing all considered parameterization ranges can be found in Table S1.

Figure 3 The continental setting during the Cretaceous OAE2 (Cenomanian–Turonian) in cGENIE. The colored dots represent averaged pre-OAE2 I $/$ Ca measurements from each of the sections. D: Demerara Rise; E: Eastbourne; Fe: South Ferriby; N: Newfoundland; R: Raia del Pedale; T: Tarfaya.

2.4 Sensitivity analyses and model implementation

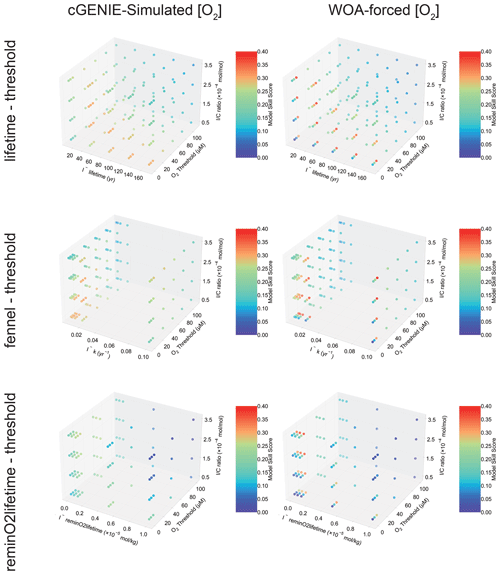
Because the relative roles of IO${}_{\mathrm{3}}^{-}$ reduction, I⁻ oxidation, and the shuttling of iodine through the biological pump are uncertain, we calibrate the parameters controlling these processes in cGENIE by creating an ensemble of different parameter value combinations controlling IO${}_{\mathrm{3}}^{-}$ reduction and I⁻ oxidation in a 2D regularly spaced grid and then repeat the same 2D parameter ensemble for different assumptions regarding the biological pump (I : C) (Table 1, Fig. 4). We focus on parameter ensembles testing the three different parameterizations for I⁻ oxidation (but only “threshold” as the IO${}_{\mathrm{3}}^{-}$ reduction parameterization): “lifetime–threshold”, “Fennel–threshold”, and “reminO2lifetime–threshold” (the results of two additional parameterization combinations, “lifetime–reminSO4lifetime” and “lifetime–inhibition”, are given in Table S1). We discuss the reasons for selecting these specific parameterization combinations in the Discussion. Finally, to explore whether the cGENIE model-simulated dissolved oxygen distribution imparts any particular bias to the tuned iodine cycle, we repeated the model ensembles for each of the three parameterization combinations but continually restored the 3D pattern of [O₂] in the model to that of the World Ocean Atlas 2018 (WOA18) climatology (Garcia et al., 2018). The model ensembles are summarized in Table 1.

Figure 4 The three-dimensional model skill score array of the experiment ensembles.

Each ensemble member was run for a total of 2000 years, and each starts from the same initial state, which was an experiment run for 10 000 years to equilibrium using a random set of iodine parameters within the ranges in Table 1. Running each ensemble member for 2000 years minimizes the CPU time but was also found to be more than sufficient to allow iodine inventories to equilibrate to new steady states. The output of each ensemble member is then statistically compared to our observational database.

2.5 Evaluation against geological observations

Parameter tuning, and the ability to reproduce modern observations, does not in itself offer any guarantee that spatial patterns are being simulated for the “correct” mechanistic reason. This is even more pertinent in the context of the application of a modern-tuned model to paleoredox reconstruction. To quantify to what degree the calibrated parameterization combinations for the modern marine iodine cycle have predictive power in the geological past, we carried out a deep-time plausibility test.

For the paleo-plausibility test, we adopted the Cretaceous pre-OAE2 (ca. 93 Ma) configuration (continental arrangement and ocean bathymetry, wind stress and velocity, and zonal average planetary albedo boundary conditions) of Monteiro et al. (2012). We choose this particular geological interval because the controls on ocean redox have previously been evaluated using the cGENIE model (Monteiro et al., 2012; Hülse et al., 2019), the oceanic conditions are much more extensively dysoxic and anoxic than in the present day and hence represent a relatively severe test of the model iodine cycle, and a number of I $/$ Ca proxy measurements are available (Zhou et al., 2015). In order to evaluate the same configuration of the iodine cycle as optimized in this study, we also substituted the temperature-independent representation of biological export production and fixed remineralization profile of POM in the water column (i.e., Ridgwell et al., 2007) for the temperature-dependent scheme of Crichton et al. (2021) used in our modern calibration. However, in substituting the biological pump scheme in the model, we alter the ocean redox landscape compared with Monteiro et al. (2012). We therefore explore a range of different assumptions regarding the ocean PO₄ inventory at the time as a means of generating a range of different plausible states of ocean oxygenation. In this, we test 0.2, 0.4, 0.6, 0.8, 1.0, and 1.5 times the mean modern concentration (2.15 µM). We run the model with each of the best-fit (highest M-score) sets of parameter values associated with the main three different parameterization combinations (two additional parameterization combinations were run and are presented in the Supplement), for each of the varying PO₄ inventory assumptions, and for 10 000 years to steady state. Major cation concentrations were adjusted to a value more representative of the earlier Cenozoic (18.2 mM [Ca²⁺], 29.9 mM [Mg²⁺]) (Panchuk et al., 2008), although that does not affect the calculation of carbonate I $/$ Ca values. In the absence of independent constraints on the Cretaceous total dissolved iodine inventory, we assumed this to be modern (500 nM mean concentration).

The I $/$ Ca data used for comparison with the model come from six sections (Zhou et al., 2015, Fig. 3, listed in Table S3). The pre-OAE2 I $/$ Ca baseline value from each section is estimated through averaging the pre-CIE I $/$ Ca measurements from Table S1 of Zhou et al. (2015). Diagenesis of carbonate-hosted I $/$ Ca tends to lower the primary values (Hardisty et al., 2017). However, such an offset is hard to quantitatively predict based on our current knowledge. In addition, according to Zhou et al. (2015), from whom we adopted the I $/$ Ca data, most of the sections only suffered minor diagenesis. To simplify the Cretaceous I $/$ Ca to IO₃ conversion, we regard the measured I $/$ Ca as primary and acknowledge there is potential uncertainty. For quantitative comparison between the model and the I $/$ Ca data, we create an empirically derived forward proxy model for I $/$ Ca. In this, we took the simulated concentration of IO${}_{\mathrm{3}}^{-}$ and Ca²⁺ in the ocean surface layer of the model at every ocean grid point and applied the temperature-dependent linear incorporation relationship derived from the inorganic calcite synthesis experiment of Zhou et al. (2014) to estimate I $/$ Ca. Specifically, the distribution coefficient (K_D) between I $/$ Ca and [IO₃] (K_D= (I $/$ Ca)/ [IO₃]) shows linear dependency with temperature (Fig. S3 in Zhou et al., 2014). For our Cretaceous model calibration, we apply the K_D based on local temperature (at each grid point associated with a sampling section) simulated by cGENIE. Beyond temperature, we acknowledge that IO${}_{\mathrm{3}}^{-}$ incorporation into carbonate lattice through substitution, IO${}_{\mathrm{3}}^{-}+$ Na${}^{+}\leftrightarrow$ CO${}_{\mathrm{3}}^{\mathrm{2}-}+$ Ca²⁺, is controlled by [Na⁺], [CO${}_{\mathrm{3}}^{\mathrm{2}-}$], and [Ca²⁺] (Podder et al., 2017). However, either quantifying these ions during the Cretaceous seawater or quantitative calculation of ion substitution dynamics requires further constraints. Although uncertainties are inevitable, we assume our temperature-controlled [IO${}_{\mathrm{3}}^{-}$] to I $/$ Ca conversion based on current quantitative knowledge meets the requirement for Cretaceous model–data comparison. We extracted simulated I $/$ Ca values from the model grid points corresponding to the sections reported by Zhou et al. (2015) and calculated the M-score.

3 Results

In this section, we start by summarizing the overall statistical outcome of the tuning then present a series of spatial analysis comparisons for each of the highest M-score ensemble members. The spatial analyses progressively reduce in scale, moving from global surface distributions (Sect. 3.2) to global and basin-specific water column profiles (Sect. 3.3) and finally to spatial comparisons for a specific ODZ region (Sect. 3.4). Our final set of results (Sect. 3.5) are of the modeled Cretaceous scenarios using the best parameterizations from the modern, which are then compared to carbonate I $/$ Ca values measured in the rock record.

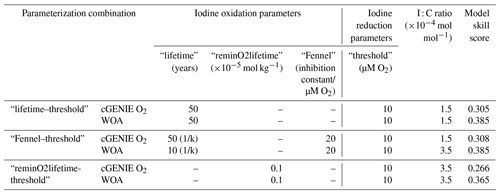
Table 2 The performance of the cGENIE iodine simulations and associated parameterization when the model reaches the best global M-score. Note that the oxidation rate constant k in “Fennel” is in units of yr⁻¹ in the model configuration, which is also the reciprocal of the “lifetime”. The full model performance is summarized in Table S2.

3.1 Model skill score

The M-score values achieved across the complete ensemble for each of the three main parameterization combinations are shown in Fig. 4 and illustrate how the statistical fit is M-score-sensitive to all three of the main parameters. Higher model skill scores are usually reached when “threshold” is tuned to 10 µM [O₂] for all the ensembles, including both model-simulated [O₂] and WOA-forced [O₂]. For the ensembles, “lifetime–threshold” and “Fennel–threshold”, the highest M-scores, are similar: 0.305 and 0.308, respectively (Table 2). Both these ensembles have the highest performance when “threshold”, “lifetime”, and I : C ratio are tuned to 10 µM [O₂], 50 years, and $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹, respectively, which is generally consistent with observations (Lu et al., 2016, 2020b; Tsunogai, 1971; Elderfield and Truesdale, 1980) (discussed in more detail later). The model performance of “reminO2lifetime–threshold” is not as good as the other two combinations, with the best M-score of 0.266 when “threshold”, “reminO2lifetime”, and I : C ratio are tuned to 10 µM O₂, $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}$ mol kg⁻¹, and $\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹, respectively (Table 2, Fig. 4). We note that, for each parameterization combination, the highest possible M-score achievable by tuning improves when [O₂] is forced to that of the World Ocean Atlas 2018 (WOA18) climatology (Garcia et al., 2018).

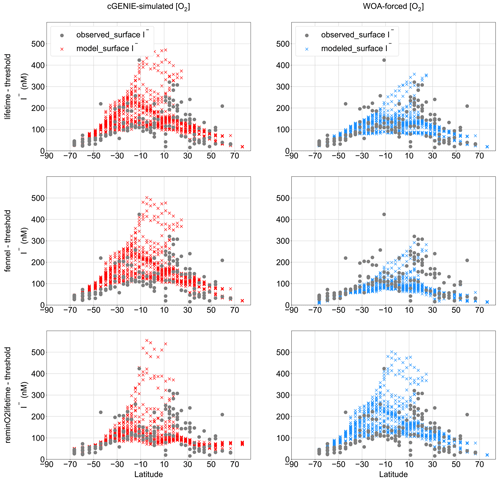
Figure 5 Modeled latitudinal surface iodide distribution compared to observation with the cGENIE-simulated [O₂] and the [O₂]-restoring forcing. The elevated [I⁻] observed and modeled in low latitudes is the result of phytoplankton reduction in the surface ocean. Note that the I⁻ distributions simulated by “lifetime–threshold” and “Fennel–threshold” are close but not identical.

3.2 Meridional surface I⁻ distribution

Figure 5 shows a comparison between the observed latitudinal distribution of [I⁻] at the surface and as simulated by the model for each parameterization combination (for the respective best M-score ensemble member). Note that the observations (Sect. 2.3) are binned to the corresponding model grid cells and, as such, reflect averages over the uppermost 80 m of the water column. This represents a reduction from 1338 to 141 surface-ocean data points. We find that the surface-ocean [I⁻] in the model shows a trend of increasing values towards low latitudes, broadly consistent with observations (Chance et al., 2014) (Fig. 5). The “lifetime–threshold” and “Fennel–threshold” show similar latitudinal trends but both overestimate the surface I⁻ in the mid- to low latitudes in the Southern Hemisphere. The “reminO2lifetime–threshold” ensemble produces a better estimation of the meridional surface [I⁻] trend, although it overestimates [I⁻] in the tropical surface ocean compared to the other two ensembles (Fig. 5).

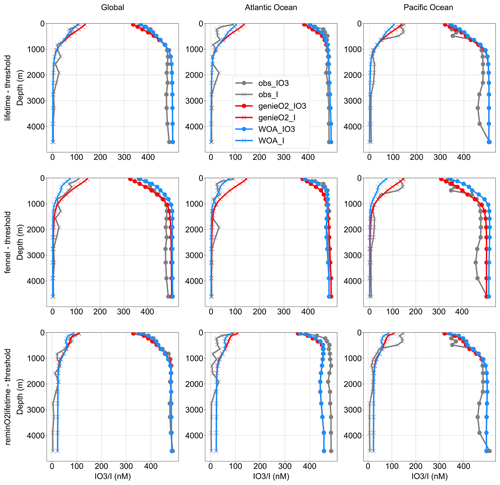
Figure 6 Modeled averaged iodine (including iodate and iodide) depth profile among the global ocean, the Pacific, and the Atlantic compared with observations. The surface I⁻ enrichment among the ocean basins is caused by phytoplankton reduction. The subsurface (∼500 m) I⁻ enrichment is the result of sampling bias, since most of the observations are from the ETNP and ETSP ODZs (see main text for details).

3.3 Global and basin-specific iodine depth distributions

Comparisons between the observed distributions of I⁻ and IO${}_{\mathrm{3}}^{-}$ seawater concentrations among the global ocean and the Atlantic and Pacific oceans are presented in Fig. 6. Again, we gridded the iodine observations (see Sect. 2.4) and selected subsets of the data that lay in either the Atlantic Basin or the Pacific Basin, contrasting with the corresponding model values at those locations. We find only relatively minor differences between the best M-score ensemble member of each of all three parameterization combinations, and all show increased [IO${}_{\mathrm{3}}^{-}$] and decreased [I⁻] with increased depth below the euphotic zone in the Atlantic and Pacific basins, as well as globally (Fig. 6). The modeled depth profile broadly matches with observations in the Atlantic and deep Pacific oceans, except the underestimated subsurface peak of [I⁻] observed in the Pacific and overestimated [IO${}_{\mathrm{3}}^{-}$] in the deep Pacific (Fig. 6). This mismatch of subsurface I⁻ peak is probably the result of sampling bias, with most of the Pacific iodine observations from ODZs in the Eastern Tropical North Pacific (ETNP) and the Eastern Tropical South Pacific (ETSP). For example, in model depth profiles masked to only include grid points with corresponding observations, the modeled Pacific depth profiles show a clear mid-depth ODZ feature (Fig. S9).

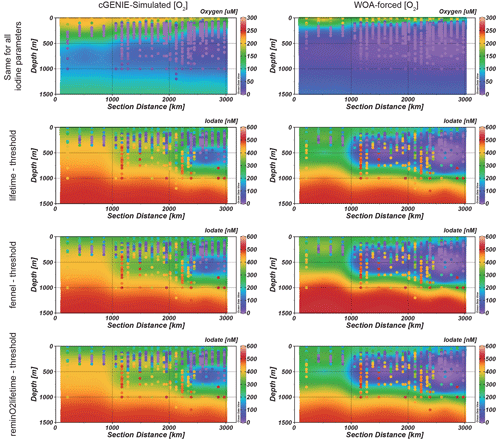
Figure 7 Modeled (contour) and observed (colored dots) west-to-east transect (location shown in Fig. 1) of O₂ (top row) and IO${}_{\mathrm{3}}^{-}$ (bottom rows) in the ETNP. Note that the WOA-forced [O₂] models simulate a larger extent of IO${}_{\mathrm{3}}^{-}$ anomaly, which better matches the observation. The left-hand panel contours are model results based on cGENIE-simulated [O₂], while contours on the right are model results from WOA-forced [O₂].

3.4 Iodine distribution within ODZs

To assess the model's ability to simulate iodine cycling in marine low-oxygen environments, we compared distributions of oxygen and iodine species in the ETNP (Fig. 7). The O₂ transects amongst all model simulations are the same because we only changed the parameterizations of the iodine cycle between ensembles and ensemble members (i.e., they all simulate the same biological pump in the ocean). All three best-performance experiments chosen show similar iodine anomalies (IO${}_{\mathrm{3}}^{-}$ depletion) in the ETNP, fitting the general feature of the observations. Other parameterizations did not replicate the ODZ (Fig. S4). However, even under the “best-fitting” parameters, compared to the observations, the ODZ feature in the model is underestimated both in intensity and in areal extent compared to the observations (Fig. 7). Notably, compared to [O₂] measured in the ETNP transect, the model underestimates the extent of the ODZ. Severe deoxygenation below 50 µM [O₂] was observed in relatively shallow depths between 100–200 m in the ETNP, and this ODZ extends for more than 3000 km towards offshore from the Mexican coast (Fig. 7). Although cGENIE simulates the O₂-deficient pattern in the ETNP, the extent of the ODZ is underestimated. The simulated oxycline is ∼200 m deeper than the observations, and the [O₂] variation is gradual. The ODZ below 20 µM [O₂] in the model is limited to a small spatial extent within 1000 km offshore, which is much smaller than that in the observations (Fig. 7).

We also ran model ensembles forcing cGENIE to restore the modern ocean [O₂] annual average climatology to that of the WOA18 (Garcia et al., 2018) (Fig. 7). Under these conditions, the subsurface IO${}_{\mathrm{3}}^{-}$-depletion zone in the ETNP ODZ in all three ensembles extends ∼2000 km offshore and spans across 100–1000 m in depth (Fig. 7). The shallow and extended ODZ iodine distribution in the ETNP better matches the observations compared to non-O₂ restoration simulations.

Figure 8 The model skill scores of modeled and measured I $/$ Ca during the pre-OAE2. The iodine cycling parameters are derived from modern simulations with cGENIE-simulated [O₂] and WOA-forced [O₂], respectively.

3.5 Evaluation against geological observations

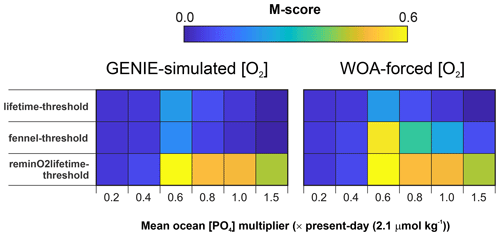
The statistical results of the pre-OAE2 evaluation are illustrated in Fig. 8 for the three main parameterization combinations and for parameter calibrations derived from internally and WOA-forced dissolved oxygen distributions (and in Fig. S10 for the full set of parameterization combinations tested). Most of the parameterization combinations reach their highest M-scores under the assumption of 0.6–0.8× modern [PO₄] (Fig. S10). Previous analysis using the same climatological configuration of the cGENIE model indicated a PO₄ inventory of 1.0× modern, which was most consistent with geological redox-related observations prior to OAE2 (Monteiro et al., 2012). However, our assumption here of temperature-dependent POM export and remineralization leads to higher export and shallower, more intense ODZs compared to the temperature-invariant biological scheme (see: Crichton et al., 2021). Hence, for a similar degree of ocean anoxia, we would expect the need for a slightly lower nutrient inventory, as we indeed find.

In terms of the I $/$ Ca M-score, we find the parameterization combinations “reminO2lifetime–threshold” and “Fennel–threshold” better replicate the geological observations compared to the “lifetime–threshold”. For “Fennel–threshold”, the WOA-derived parameter set values differ from those derived from cGENIE [O₂] (Table 2) and perform better. The performance of the scheme “reminO2lifetime–threshold” is largely independent of the ocean PO₄ inventory assumption for values of 0.6× modern and higher.

4 Discussion

In summary, we presented the results of cGENIE Earth system model ensembles (both with internally calculated and WOA-imposed [O₂] distribution) for three parameterization combinations of iodine cycling that showed the best performance (but we summarize a total of five different parameterization combinations in Table S2). We analyzed the performance of the ensembles via (1) M-score for the model–data match of both [I⁻] and [IO${}_{\mathrm{3}}^{-}$] across the entire ocean, (2) qualitative model–observation comparison of latitudinal surface-ocean distributions of [I⁻], (3) inspection of averaged depth profiles in global and individual ocean basins for both [I⁻] and [IO${}_{\mathrm{3}}^{-}$], (4) inspection of iodine transects across the across the Eastern Tropical North Pacific (ETNP) ODZ, and (5) M-score for model and carbonate I $/$ Ca observations (Zhou et al., 2015) for the Cretaceous.

4.1 Overall model skill score comparison

Two broad observations emerge from the M-score comparison. Firstly, the first-order ensembles associated with kinetic iodine oxidation (“lifetime–threshold” and “Fennel–threshold”) have the highest M-scores (Table 2), under both cGENIE-simulated [O₂] and WOA-forced [O₂]. This is consistent with previous observations of first-order kinetics for I⁻ oxidation (Tsunogai, 1971). Secondly, the simulations with WOA-forced [O₂] produce significantly higher M-scores than those of the cGENIE-simulated [O₂] field (at least ∼0.08 of improvement; Table 2). Despite a first-order non-O₂-dependent oxidation mechanism providing the highest M-scores, the WOA- vs. internally model-generated dissolved oxygen distribution comparison highlights the O₂ and related redox dependency of the iodine cycle from the perspective of IO${}_{\mathrm{3}}^{-}$ reduction. Each of these factors is discussed in Sect. 4.1.1.

4.1.1 Parameter value plausibility

A credible representation of the marine iodine cycle requires not only that observations can be replicated but that, in achieving a fit to observations, tuned parameter values fall within real-world ranges. In this section, we discuss the plausibility of our best-fit (maximized M-score) parameter values. For the iodine cycle, these parameters are the O₂ threshold, the parameter (depending on the specific parameterization combination) controlling the I⁻ oxidation rate, and the cellular I : C ratio.

Our model M-score is highest, with an [O₂] reduction threshold of 10 µM (Fig. 4 and Table 2). Although it is generally well accepted that IO${}_{\mathrm{3}}^{-}$ is reduced in low-oxygen settings (Luther, 1991; Rue et al., 1997; Wong et al., 1985; Wong and Brewer, 1977; Farrenkopf and Luther, 2002), the degree of O₂ depletion that triggers IO${}_{\mathrm{3}}^{-}$ reduction is still unclear. A relatively high threshold for triggering IO${}_{\mathrm{3}}^{-}$ reduction has been proposed based on comparison between planktic and benthic foraminiferal I $/$ Ca and ambient [O₂] (20–70 µM O₂; Lu et al., 2016, 2020a). These [O₂] thresholds are similar to those determined in a previous cGENIE-based iodine cycle study (30 µM) (Lu et al., 2018), but it is difficult to directly compare these to our results because of differences in the model representation of the ocean biological pump, the iodine observational dataset, and the model–data comparison methods utilized.

Many of the studies suggesting a relatively high [O₂] threshold are based on the relationship of [IO${}_{\mathrm{3}}^{-}$] and [O₂] within the upper chemocline of ODZs; however, evaluation of [O₂] and [IO${}_{\mathrm{3}}^{-}$] from ODZs throughout the entire water column suggests the potential for IO${}_{\mathrm{3}}^{-}$ persistence within the low-oxygen cores of ODZs. Specifically, IO${}_{\mathrm{3}}^{-}$ accumulation is observed within the ETNP and ETSP at depths where [O₂] is close to or below the detection limit of the sensors, which is reported near 1 µM (Hardisty et al., 2021). In addition, it is worth noting that the kinetics of IO${}_{\mathrm{3}}^{-}$ reduction is heterogeneous both within and between ODZs. For example, a transect evaluating IO${}_{\mathrm{3}}^{-}$ reduction rates in the ETNP observed rapid rates in the upper oxycline, where [O₂] was near ∼12 µM, but the potential for sluggish rates in the ODZ cores, where [O₂] was below detection. In an early study of the Arabian Sea, IO${}_{\mathrm{3}}^{-}$ was reduced rapidly within the ODZ core. Together, these suggest IO${}_{\mathrm{3}}^{-}$ reduction may be controlled by factors beyond O₂ (Hardisty et al., 2021; Farrenkopf and Luther, 2002). For example, IO${}_{\mathrm{3}}^{-}$ is likely formed in high-[O₂], non-ODZ water masses but can be sustained upon transport or mixing within oligotrophic offshore ODZ regions, where organic supplies are more limited (Hardisty et al., 2021). A comparison to the N cycle would also indicate a low [O₂] threshold; for example, denitrification has a sub-µM [O₂] threshold and has a similar redox potential with IO${}_{\mathrm{3}}^{-}$ reduction (Dalsgaard et al., 2014; Thamdrup et al., 2012). A sub-µM [O₂] threshold for IO${}_{\mathrm{3}}^{-}$ reduction could explain the [IO${}_{\mathrm{3}}^{-}$] variations observed in ODZ cores with [O₂] below the µM detection limits of sensors; however, iodine speciation has yet to be analyzed alongside [O₂] measurements via sensors with sub-µM detection limits, such as STOX sensors. Regardless, our 10 µM [O₂] threshold based on maximizing the M-score reflects a global average value and clearly falls within the ranges of oceanographic observations.

For both our study and that of Lu et al. (2018), an I⁻ lifetime of 50 years maximizes model performance. However, Lu et al. (2018) chose to implement a slightly lower value of 40 years for their paleo-application because it reflected the slowest rate observed in the literature at that time (Tsunogai, 1971). Notably, though IO${}_{\mathrm{3}}^{-}$ is the most abundant marine iodine species, its production from I⁻ has never been unambiguously observed under normal marine conditions. This has acted as a major hinderance to providing direct constraints. That said, our model-based estimate is consistent with a multitude of other constraints that indicate that I⁻ oxidation to IO${}_{\mathrm{3}}^{-}$ undergoes extremely slow kinetics. The I⁻ oxidation rates calculated through indirect methods, including mass balance and seasonal iodine speciation changes (Tsunogai, 1971; Campos et al., 1996; Truesdale et al., 2001; He et al., 2013; Edwards and Truesdale, 1997; Žic et al., 2013; Moriyasu et al., 2023), or through radiogenic-tracer-spiked incubations (Hardisty et al., 2020; Schnur et al., 2024; Ştreangã et al., 2024) have a wide range of variation from 1.5 to 670 nM yr⁻¹. The lifetime in cGENIE is 50 years, which can be approximately converted to the zeroth-order rate of <9 nM yr⁻¹, falling in the lower end of the previous studies.

Our best-fit I : C ratio is $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹, which is in agreement with plankton measurements and mass balance calculations (Chance et al., 2010; Elderfield and Truesdale, 1980). In the euphotic zone, IO${}_{\mathrm{3}}^{-}$ is taken up by phytoplankton and incorporated into their cellular structures followed by subsequent conversion into I⁻ (Hepach et al., 2020). Due to this, it is assumed that IO${}_{\mathrm{3}}^{-}$ removal in the surface layer of the ocean is a function of organic carbon fixation during primary productivity according to Redfield-like ratios (Campos et al., 1996; Chance et al., 2010). Of the parameters incorporated into the model, in theory, I : C should probably be the best constrained. However, published I : C ratios based on field and laboratory measurements vary over several orders of magnitude (10⁻⁵ to 10⁻³) (Elderfield and Truesdale, 1980; Campos et al., 1996; Hepach et al., 2020; Chance et al., 2010). To limit the number of model simulations and size of the ensembles, we only varied I : C between $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹ (in increments of $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}$), which covers the range indicated by previous studies (Elderfield and Truesdale, 1980).

It is unlikely that the I : C value is constant across the global ocean, due to differences in phytoplankton composition and other factors, such as temperature (Wadley et al., 2020). In cGENIE, most of the elevated (>200 nM) surface [I⁻] values occur in the ETSP and the northern Indian Ocean, representing the effect of high primary productivity and transformation of IO${}_{\mathrm{3}}^{-}$ to I⁻ via the rapid-recycling DOM “loss term” in the representation of biological export in the model (Fig. S6). The overestimation of tropical I⁻ within the model probably hints that the I : C ratio is not constant in the ocean, which is also hypothesized by Wadley et al. (2020), although in the absence of an explicit representation of primary productivity in the model and spatially variable f-ratios (Laws et al., 2000) (implicitly, the f-ratio can be considered to be 0.33 everywhere in cGENIE). In testing a fixed, spatially uniform I : C, Wadley et al. (2020) underestimated surface [I⁻] in low latitudes and overestimated concentrations in mid-latitudes. Based on their model–observation comparison, they hypothesized that the I : C ratio decreases systematically with sea surface temperature (SST) (Wadley et al., 2020). Until more constraints are developed on spatial variability and associated driving factors for I : C, a generalized approach of a globally uniform I : C remains the most parsimonious assumption, especially considering cGENIE's intended extrapolation to ancient settings.

4.1.2 Comparing alternative iodide oxidation parameterizations in cGENIE

Due to similarity in redox potentials, iodine cycling in the ocean has been hypothesized to be linked to the cycling of nitrogen (Rue et al., 1997). Nitrification promoting I⁻ oxidation to IO${}_{\mathrm{3}}^{-}$ has been inferred from field studies (Truesdale et al., 2001; Žic et al., 2013) and has more recently been linked via observation of I⁻ oxidation to IO${}_{\mathrm{3}}^{-}$ by ammonia-oxidizing bacteria in laboratory environments (Hughes et al., 2021). We further note that Wadley et al. (2020) explicitly link I⁻ oxidation to NH${}_{\mathrm{4}}^{+}$ oxidation in their surface-ocean iodine cycle model.

As an alternative to the first-order lifetime oxidation parameterization used here and in Lu et al. (2018) and in the current absence of a full nitrogen cycle (and hence explicit NH${}_{\mathrm{4}}^{+}$ oxidation) in cGENIE, we also applied a strategy (“reminO2lifetime”) which links I⁻ oxidation to organic carbon remineralization and the consumption rate of dissolved oxygen. The reasoning behind this is that the O₂ consumption rate in the model implicitly reflects bacterial oxidizing activity in the water column and hence the potential for I⁻ to be oxidized to IO${}_{\mathrm{3}}^{-}$. We find that the overall model performance involved with the “reminO2lifetime” is lower than other experiments, where I⁻ oxidation is ubiquitously oxidized according to a parameterized lifetime or “lifetime–threshold” (maximum M-score 0.266 vs. 0.305/0.308 under cGENIE-simulated [O₂]) (Fig. 4 and Table 2). However, despite slightly lower M-scores, the “reminO2lifetime” scheme generally replicates the latitudinal surface [I⁻] trend, the depth profiles in the ocean basins, and the ODZ transect (Figs. 4–6).

Under the default “lifetime” scheme, I⁻ will oxidize in the whole ocean regardless of the concentration (or even presence/absence) of ambient O₂. Hence, this scenario might not perform well in replicating the ocean iodine cycling at intervals during the Phanerozoic when ODZs were highly expanded, as it does not account for the possibility of slower I⁻ oxidation at low O₂ but above the IO${}_{\mathrm{3}}^{-}$-reduction O₂ threshold. Ideally, for application in paleoceanographic studies, I⁻ oxidation should be linked to ambient [O₂] in some way. Although thermodynamics theory suggests O₂ does not directly drive I⁻ oxidation (Luther et al., 1995), field studies in ODZs indeed observed that low [O₂] inhibits this process (Farrenkopf and Luther, 2002; Moriyasu et al., 2020). We hence developed and tested variable I⁻ oxidation kinetics, with the ambient dissolved O₂ providing an inhibition of the rate of oxidation based on the enzymatic nitrification scheme of Fennel et al. (2005).

Since most of the ocean is fully oxygenated today, there is little difference in M-scores between “lifetime” and “Fennel” oxidation parameterizations (0.305 vs. 0.308; Table 2). Despite the very close M-scores, “Fennel” oxidation under WOA forcing has a higher optimal I : C ratio ($\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹) and faster saturated I⁻ oxidation kinetics (0.1 yr⁻¹ vs. 0.02 yr⁻¹ in other ensembles). Such parameter differences between “Fennel” WOA and other ensembles reflect compensation between faster oxidation rate (process (2) in Fig. 1) and increased I⁻ production through the higher biotic uptake rate (process (3) in Fig. 1). The pre-OAE2 simulations are particularly illustrative of this tradeoff and are discussed in more detail in Sect. 4.3.

In summary, all three parameterization combinations produce high and comparable M-scores and similar parameters (oxidation, reduction, and I : C) associated with these M-scores (Table 2). Although direct field-based evidence to evaluate the controlling parameters of “reminO2lifetime” is absent, the parameters controlling the other model scheme are consistent with previous studies.

4.2 Beyond the M-score: model–data comparison across iodine gradients

As applied here, the M-score provides a quantitative measure that describes the overall model global performance and allows us to directly compare the implications of parameter value and parameterization choices. However, an M-score based on a global dataset can obscure regional gradients that may be important for both paleo- and modern oceanographic research. Indeed, amongst all the various ensembles we ran as part of this study (Table S1), only “lifetime–threshold”, “lifetime–Fennel”, and “reminO2lifetime–threshold” performed sufficiently well in replicating the modern oceanic iodine gradients (Figs. S2–S4 in the Supplement), and we thus decided to focus only on these three parameterization combinations. We discuss this in more detail below.

4.2.1 Meridional surface [I⁻] gradient

All three main parameterization combinations summarized in Table 2, along with the observations, show enrichment of I⁻ in the surface ocean at low latitudes (Fig. 5). The pathway of transforming IO${}_{\mathrm{3}}^{-}$ into I⁻ in these oxidized waters is through primary productivity in the euphotic zone, which results in I⁻ accumulation within the mixed layer (Chance et al., 2014). In the low-latitudinal surface ocean, weaker vertical mixing resulting from warmer surface temperatures allows I⁻ accumulation in the shallow mixed layer (Chance et al., 2014; Moriyaus et al., 2023). Therefore, the IO${}_{\mathrm{3}}^{-}$ flux from deep waters through seasonal mixing may be an important balance to the in situ IO${}_{\mathrm{3}}^{-}$ reduction rate by primary producers in the high latitudes (Chance et al., 2014; Moriyasu et al., 2023). Importantly, this temperature stratification and related vertical mixing trend is also simulated by cGENIE (Fig. S7). The cGENIE model generates the general pattern of latitudinal surface I⁻ distribution pattern, as well; however, overestimation may exist, especially in low latitudes and especially in the tropical surface, where [I⁻] is close to 500 nM among all the cGENIE-O₂ models (Fig. 5).

The cGENIE (internally generated oxygen distributions) vs. WOA (imposed distributions) O₂ comparison provides evidence that I⁻ generated in low-[O₂] settings may broadly enhance [I⁻] in oxygenated euphotic waters, with [I⁻] values lower and closer to observations in the WOA tunings (Fig. 5). This includes “lifetime–threshold”, where O₂ only impacts the reductive portion of the iodine cycle, but also the “Fennel” and “reminO2lifetime”, where rates of I⁻ oxidation are also [O₂] dependent. More specifically, most of the elevated (>200 nM) surface [I⁻] in cGENIE occurs in the ETSP and the northern Indian Ocean and corresponds to locations of high primary productivity (Fig. S6). Since the surface-ocean [O₂] in the model is never below 200 µM, O₂-dependent IO${}_{\mathrm{3}}^{-}$ reduction at the ocean surface is unlikely. Instead, ex situ transport from proximal regions of subsurface anoxia is the most probable source of elevated I⁻. Indeed, the most prominent regions of I⁻ enrichment in the model occur near the Peruvian coast and in the Arabian Sea, where ODZs lie below the surface (Fig. S6). More detailed data–model comparison among these two areas is limited because the observation data are few (e.g., Farrenkopf and Luther, 2002 and Rapp et al., 2020). In contrast, the meridional trend of I⁻ in the surface Atlantic Ocean, where ODZs are less developed, exhibits better agreement with both the observation and the Wadley et al. (2020) model (Fig. S6). The overestimation of tropical ocean surface [I⁻] by cGENIE is hence likely to be associated with deficiencies in the simulation of ODZ oxygenation.

That said, modeled overestimations of surface-ocean [I⁻] may be difficult to verify given current observational data densities. In comparing observational data to model latitudinal trends which have been masked to only include model grid points with corresponding observations, although the same broad trend of increasing [I⁻] in the low latitudes exists, there are fewer incidents of apparent model overestimation (Fig. S8). More observations in surface-ocean [I⁻] from low latitudes are needed to better assess the validity of elevated modeled surface-ocean [I⁻] in some regions.

4.2.2 Global and basin-specific iodine depth profiles

All the iodine cycle schemes (both cGENIE [O₂] and WOA-forced) generate a decrease in [I⁻] and an increase in [IO${}_{\mathrm{3}}^{-}$] from the euphotic zone down to the deep abyssal zone across ocean basins, matching the pattern driven by primary production (Fig. 6). As discussed in the previous section, this surface maximum of [I⁻] in the oxygenated water column is the result of biologically mediated reduction or release during cell senescence of phytoplankton. Below the euphotic zone, [I⁻] is close to zero and IO${}_{\mathrm{3}}^{-}$ becomes the dominant species. The deep ocean is mostly oxygenated and has longer water residence times (several millennia; Matsumoto, 2007) compared to the I⁻ lifetime (<40 years; Tsunogai, 1971), thus facilitating I⁻ oxidation in the absence of IO${}_{\mathrm{3}}^{-}$ reduction in ODZs.

We note that there are multiple general discrepancies between observations and model output and differences between the results of WOA vs. cGENIE [O₂] parameter tuning. In general, all models better reproduce the global average, relative to the basin-specific profiles. We suggest that the global averaged profiles are a better test of the cGENIE simulations because of sampling biases associated with individual basins. For example, the discrepancy between the model and observations is prominent in the Pacific (Fig. 6). The observed Pacific subsurface [I⁻] peak mirrors the [IO${}_{\mathrm{3}}^{-}$] minimum that occurs at depths where ODZs are present. This ODZ feature in the averaged Pacific observation profile is likely the result of sampling bias, since most of the observations from the Pacific are from the ETNP (Rue et al., 1997; Moriyasu et al., 2020) and thus do not reflect the overall iodine distribution in the Pacific Ocean (Fig. S9). This conclusion is supported by depth profiles masked to only include modeled grid points with corresponding observation data. For example, there is a clear mid-depth ODZ feature in the masked model Pacific depth profiles due to extensive ODZ studies in this region (Fig. S9). All this said, while the general features of iodine speciation with depth are generally similar, our data compilation indicates the potential for some basin-specific variations which require further research to validate and mechanistically understand.

4.2.3 Iodine distribution within ODZs

One of the major goals of calibrating the iodine cycle in cGENIE is to be able to simulate the iodine behavior associated with ancient low-oxygen settings. To assess this potential, we analyzed model performance for the ETNP (Rue et al., 1997; Moriyasu et al., 2020), where observational data are abundant and the areal extent of the ODZ is sufficiently large to be reflected in the model grid (Fig. 6). The simulated reduction in IO${}_{\mathrm{3}}^{-}$ to I⁻ generally overlaps with the extent of the ODZ (Fig. 6), which provides support for the use of cGENIE to understand the broad distribution of ancient [IO${}_{\mathrm{3}}^{-}$] and [O₂]. Non-threshold model parameterization combinations (not discussed here but shown in Fig. S4) did not replicate the ODZ feature in iodine speciation.

In all model configurations assuming cGENIE [O₂], the most prominent discrepancy is an underestimation of the spatial extent and intensity of the IO${}_{\mathrm{3}}^{-}$-depletion zone in the ETNP (Fig. 6) – a consequence of the simulated subsurface O₂-deficient area being notably narrower than WOA climatology (Figs. 6, S5). This is principally a consequence of relatively weak continental margin upwelling and equatorial divergence, itself a consequence of the low-resolution (both horizontally and vertically) model grid that the 3D ocean circulation component is implemented on together with its simplified physics (Marsh et al., 2011). Another consequence of the low-resolution nature of the cGENIE model grid is that the extent of the ETNP is on the order of the size of an individual grid box and that the entire ETNP only covers the longitude range of three grids in the model framework (Fig. 1). Meanwhile, the depth resolution is ca. 100–200 m per layer in the upper ocean, which also limits the finer simulation of ODZ features. Awareness of these limitations highlights the importance of focusing use of the model on regional and global oxygenation features as opposed to over-interpreting local features.

Other data–model misfits may be due to IO${}_{\mathrm{3}}^{-}$-reduction dependencies not explicitly accounted for in the model. As discussed above, shipboard incubation and radiogenic-tracer-spiked rate calculation suggest that IO${}_{\mathrm{3}}^{-}$ reduction is slow in the offshore ETNP ODZ (Hardisty et al., 2021). This could explain why measurable IO${}_{\mathrm{3}}^{-}$ is present in the core of the ETNP ODZ (Fig. 6). This is further exacerbated in the Eastern Tropical South Pacific ODZ, where [IO${}_{\mathrm{3}}^{-}$] remains above 250 nM in some studies (Cutter et al., 2018) but near detection limits in others (Rapp et al., 2020), suggesting extreme spatiotemporal variability related to currently unconstrained factors. Furthermore, while the capability of microbes using IO${}_{\mathrm{3}}^{-}$ as an electron acceptor for oxidizing organic matter has been confirmed in laboratory culture experiments (Councell et al., 1997; Reyes-Umana et al., 2021; Yamazaki et al., 2020; Amachi et al., 2007; Farrenkopf et al., 1997), no study to date has demonstrated non-O₂-dependent controls driving variable IO${}_{\mathrm{3}}^{-}$ reduction rates.

An important factor contributing to elevated [I⁻] in ODZs is benthic fluxes and reduction occurring within the uppermost layers of marine sediments (akin to denitrification). To help account for this in our M-score and model calibration (see the “Model description” section), “excess” iodine (>500 nM total iodine) was filtered from our observational dataset. The excess iodine originating from the sediment flux has been observed in ODZ water columns contacting anoxic sediments (Chapman, 1983; Farrenkopf and Luther, 2002; Cutter et al., 2018; Moriyasu et al., 2020; Scholz et al., 2024). We note that excess iodine occurs explicitly as I⁻, reflecting the limited oxygen or lack of oxygen within the ODZ, and is a local–regional phenomenon not yet observed to persist beyond ODZ settings. Future work can focus on understanding the degree, if any, to which excess I⁻ is oxidized to IO${}_{\mathrm{3}}^{-}$ and hence impacts the I $/$ Ca paleoredox proxy.

Figure 9 The pre-OAE2 I $/$ Ca field derived from cGENIE [IO${}_{\mathrm{3}}^{-}$] simulations and the comparison between modeled and observed I $/$ Ca from sections.

4.3 Applicability of the cGENIE marine iodine cycle to paleoredox reconstruction

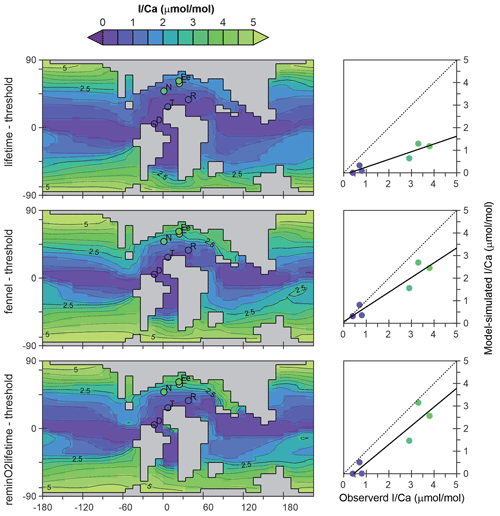
The pre-OAE2 comparison is revealing because the observations encapsulate a strong gradient between high and very low I $/$ Ca (Fig. 3), reflecting, respectively, high and low surface-ocean concentrations of IO${}_{\mathrm{3}}^{-}$ in the model. All three of the parameterization combinations (just focusing on WOA-derived parameter values) are capable of reproducing low I $/$ Ca values in the lower-latitudinal sections (Demerara Rise, Tarfaya, and Raia del Pedale; Fig. 9), although with a tendency to slightly overestimate seawater IO${}_{\mathrm{3}}^{-}$ depletion (cross-plots in Fig. 9). Low ocean-surface [IO${}_{\mathrm{3}}^{-}$] occurs in the model as a result of the existence of a circum-equatorial band of intense subsurface anoxia and short transport time to the surface (and hence limited oxidation). In the higher-latitudinal sections, including Newfoundland, Eastbourne, and South Ferriby, I $/$ Ca values tend to be underestimated to varying degrees (Fig. 9). However, compared to the “lifetime” parameterization, both “reminO2lifetime” and “Fennel” oxidation simulate the I $/$ Ca values in these high-latitudinal sections rather better, with the regression closer to the 1:1 line (dotted in Fig. 9). We find this relationship instructional for understanding controls in the modern iodine cycle.

We first note that both “lifetime” and “Fennel” iodine oxidation parameterizations, in conjunction with a threshold of IO${}_{\mathrm{3}}^{-}$ reduction and internally generated GENIE [O₂], give rise to identical parameter values (Table 2). We infer that this is because the modern ocean is predominately well-oxygenated; hence there is little inhibition of I⁻ oxidation in practice. In the Cretaceous environment, although I⁻ oxidation inhibition should be widespread, the M-scores are similar (Fig. 8). The rate of I⁻ oxidation in well-oxygenated seawater is likely then critical in explaining elevated I $/$ Ca values at higher Cretaceous latitudes. However, simply decreasing the lifetime in the modern ocean would result in an underestimation of surface-ocean [I⁻]. The “Fennel–threshold” combination under WOA [O₂] reveals a tradeoff that solves this: a decreased I⁻ lifetime compensated for by increased rates of I⁻ release to the ocean interior directly through the biological pump and elevated cellular I : C ($\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹ vs. $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ mol mol⁻¹). In the Cretaceous ocean, this combination allows both sharper latitudinal gradients in [IO${}_{\mathrm{3}}^{-}$] (and hence I $/$ Ca) and steeper vertical gradients to develop, which allow non-zero I $/$ Ca values at low latitudes to be captured (cross-plot in Fig. 9). This slight enhancement of the upper-ocean [IO${}_{\mathrm{3}}^{-}$] gradient is also apparent in the present-day analysis (Fig. 6). The combination of “reminO2lifetime” with a reduction threshold works similarly: a shorter lifetime for I⁻ under oxic conditions offset in the modern ocean by elevated cellular I : C (Table 2). However, in this case, our gridded parameter search identifies the tradeoff as producing the highest M-score for both modeled and WOA oxygen distributions.

What we learn from this is that the cGENIE iodine cycle tuned to modern observations has predictive power under a very different state of ocean oxygenation (and circulation and operation of biological pump). However, this is not true for every choice of parameterization, and the simple “lifetime–threshold” combination (which, when calibrated, was statistically almost the best representation of the iodine cycle) was unable to reproduce the latitudinal I $/$ Ca gradients in the Cretaceous ocean. Shortening the lifetime (and adding an inhibition term), together with increasing the assumed cellular I : C, maintains fidelity in simulating the modern ocean whilst capturing Cretaceous I $/$ Ca much better. That even better representations of Cretaceous I $/$ Ca were possible but at the expense of reproducing modern observations adequately hints that improvements in our mechanistic understanding are needed, although all of the above assumes that the simulation of the Cretaceous redox landscape is plausible.

One caveat to our paleo-comparison is that, because the residence time of iodine in the ocean is only around 300 kyr, the dissolved iodine inventory of the Cretaceous ocean could have deviated substantially from the modern seawater value that we assume here (500 nM). One possible explanation for the overall underestimation of I $/$ Ca by cGENIE might then be that the Cretaceous iodine inventory was higher than the modern (Zhou et al., 2015; Lu et al., 2018). Even a moderate increase (ca. 20 %–40 %) in the ocean iodine inventory (which we did not test here) would presumably act to increase the slope of the regression lines for the parameterization combinations “Fennel–threshold” and “reminO2lifetime–threshold” and bring them close to the 1:1 line (Fig. 9). Another uncertainty concerns the potential impact on carbonate I $/$ Ca ratios of dissolved calcium concentrations in the Cretaceous ocean that are different from the modern. The calcite crystal growth experiments of Zhou et al. (2014) on which we base our model-simulated I $/$ Ca values were carried out in synthetic solutions and not seawater. The partition coefficient K_D was calculated as [I $/$ Ca]/[IO${}_{\mathrm{3}}^{-}$], and, as a result, our model formulation is independent of the ambient Ca²⁺ concentration. New I $/$ Ca carbonate precipitation experiments that explicitly account for the geological range in seawater composition would help increase confidence in the model-simulated I $/$ Ca values and hence improve the possible model simulation comparison with geological observations.

4.4 Choice of marine iodine cycle representation in cGENIE

The risk in tuning model parameters to fit some data target is always that the processes being tuned are distorted to accommodate an underlying structural error with the model. In this paper, we illustrated how sub-regional-scale ocean oxygenation features, such as the Eastern Tropical North Pacific ODZ (Fig. 7), are poorly represented at the resolution of the cGENIE Earth system model and how this can lead to deficiencies in the simulation of the marine iodine cycle in these regions. Indeed, we found an improved statistical fit to observed iodine speciation data when we imposed a dissolved oxygen climatology to the model grid rather than using the internally generated model [O₂] fields (Table 2). In the case of the “Fennel” parameterization combination, we end up with two different sets of parameter values – one associated with the best fit to iodine speciation data under cGENIE-projected [O₂] and one under WOA-imposed [O₂]. Selecting this particular scheme for paleo-applications would appear to create a conundrum – whether to (a) choose the cGENIE [O₂]-derived parameter value set and accept that model deficiencies were being implicitly corrected for in simulating marine iodine cycling and hence imposing a potential bias on paleo-I $/$ Ca or (b) accept WOA [O₂]-derived parameter values. The choice would arguably be to accept the less potentially biased parameter value set (b), particularly as the relatively small-scale ODZ features of the modern ocean may be expanded to the regional to global scale in deeper-time oceans; hence the redox features driving iodate reduction would become much more tractable for a model of the resolution of cGENIE.

However, we note that this choice does not exist for the parameterization combinations “lifetime–threshold” and “reminO2lifetime–threshold”. In both cases, the sets of optimal parameter values are the same, whether derived from cGENIE-projected [O₂] or WOA-imposed [O₂] (Table 2). This gives us confidence that both these schemes are relatively agnostic to the details of how the modern oxygen cycle is simulated and that errors in the simulation of sub-regional-scale ocean oxygenation features are not critical (we note that iodine speciation data are still fitted better under WOA-imposed [O₂]). The choice of how best to represent the marine iodine cycle in cGENIE is then a choice between “lifetime–threshold”, which has been used in a similar form previously (Lu et al., 2018) and is capable of the best fit to modern observations, and “reminO2lifetime–threshold”. While “lifetime–threshold” might be preferable for more recent geological time and ocean ODZs similar to the present day, it fails to account for I $/$ Ca contrasts under more extreme redox gradients (Fig. 9). Although more difficult to interpret mechanistically, in suppressing the rate of I⁻ oxidation under low ambient [O₂], “reminO2lifetime–threshold” appears to be the more appropriate paleo-choice. We note that, to achieve improved simulation of sub-regional-scale features of the ocean redox landscape, future paleo-cGENIE model I $/$ Ca applications could make use of the coupled GENIE-PLASIM climate configuration (Holden et al., 2016). In this, the ocean circulation model is implemented on a higher-resolution grid (64 ×32 with 32 vertical levels) and includes a coupled atmospheric GCM component (hence enabling interannual variability). It is also capable of being configured with different continental configurations for paleoclimate questions (e.g., Keery et al., 2018).

5 Conclusions

Using the cGENIE Earth system model, we performed a series of ensemble experiments to determine suitable parameterizations to represent the marine iodine cycle and identified the best-performing combinations of parameter values in each case. We found that the optimized parameter values associated with water column IO${}_{\mathrm{3}}^{-}$ reduction and I⁻ oxidation, plus IO${}_{\mathrm{3}}^{-}$ planktonic uptake (and subsequence I⁻ release during remineralization), all fell within the range of field and experiment observations and hence could be considered plausible. Three iodine cycling parameterization combinations, “lifetime–threshold”, “reminO2lifetime–threshold”, and “Fennel–threshold”, were regarded as viable candidates following our tests of the global ocean model M-score and model–data comparisons made across specific iodine gradients (euphotic latitudinal distribution, depth distribution, and ODZ distribution). We further evaluated the plausibility of our parameterizations and their paleo- and ocean deoxygenation applicability by contrasting forward proxy model-generated I $/$ Ca values against observations, taking the (pre-OAE2) Cretaceous redox landscape as a case study. While we highlighted the importance of improving the simulation of dissolved oxygen distributions in models, we also found that our conclusions regarding preferred parameterizations and even specific parameter values were not overly dependent on the specific details of the simulated modern ODZs. Overall, while some model–data discrepancies emerge for both modern and paleo, these highlight that future observational and/or experimental work is necessary to better constrain modern iodine cycling mechanisms and related spatiotemporal heterogeneities but that representations of the marine iodine cycle in an Earth system model based on modern observations and mechanistic knowledge appear transferrable to interpreting the geological record of the I $/$ Ca oxygenation proxy.