Global satellite-driven estimates of heterotrophic respiration

While heterotrophic respiration (R_h) makes up about a quarter of gross global terrestrial carbon fluxes, it remains among the least-observed carbon fluxes, particularly outside the midlatitudes. In situ measurements collected in the Soil Respiration Database (SRDB) number only a few hundred worldwide. Similarly, only a single data-driven wall-to-wall estimate of annual average heterotrophic respiration exists, based on bottom-up upscaling of SRDB measurements using an assumed functional form to account for climate variability. In this study, we exploit recent advances in remote sensing of terrestrial carbon fluxes to estimate global variations in heterotrophic respiration in a top-down fashion at monthly temporal resolution and $\mathrm{4}{}^{\circ }\times \mathrm{5}{}^{\circ }$ spatial resolution. We combine net ecosystem productivity estimates from atmospheric inversions of the NASA Carbon Monitoring System-Flux (CMS-Flux) with an optimally scaled gross primary productivity dataset based on satellite-observed solar-induced fluorescence variations to estimate total ecosystem respiration as a residual of the terrestrial carbon balance. The ecosystem respiration is then separated into autotrophic and heterotrophic components based on a spatially varying carbon use efficiency retrieved in a model–data fusion framework (the CARbon DAta MOdel fraMework, CARDAMOM). The resulting dataset is independent of any assumptions about how heterotrophic respiration responds to climate or substrate variations. It estimates an annual average global average heterotrophic respiration flux of 43.6±19.3 Pg C yr⁻¹. Sensitivity and uncertainty analyses showed that the top-down R_h are more sensitive to the choice of input gross primary productivity (GPP) and net ecosystem productivity (NEP) datasets than to the assumption of a static carbon use efficiency (CUE) value, with the possible exception of the wet tropics. These top-down estimates are compared to bottom-up estimates of annual heterotrophic respiration, using new uncertainty estimates that partially account for sampling and model errors. Top-down heterotrophic respiration estimates are higher than those from bottom-up upscaling everywhere except at high latitudes and are 30 % greater overall (43.6 Pg C yr⁻¹ vs. 33.4 Pg C yr⁻¹). The uncertainty ranges of both methods are comparable, except poleward of 45^∘ N, where bottom-up uncertainties are greater. The ratio of top-down heterotrophic to total ecosystem respiration varies seasonally by as much as 0.6 depending on season and climate, illustrating the importance of studying the drivers of autotrophic and heterotrophic respiration separately, and thus the importance of data-driven estimates of R_h such as those estimated here.

1 Introduction

The terrestrial carbon-cycle–climate feedback (together with atmospheric processes) is a dominant contributor to the uncertainty of temperature projections in 2100 (Booth et al., 2012). The future effect of carbon–climate feedbacks depends on the climate sensitivity of net terrestrial carbon fluxes, which are a close balance of net primary productivity, disturbance-related fluxes, and heterotrophic respiration (R_h). The overall sensitivity of the terrestrial carbon uptake is thus dependent on the climatic response of these fluxes. Model-based estimates of global R_h vary by almost 50 % and are highly uncertain (Shao et al., 2013), especially in the tropics (Tian et al., 2015). The climatic sensitivity of R_h is also the primary driver of the large divergence across modeled global soil carbon pools (Tian et al., 2015; Todd-Brown et al., 2013), which make up the largest terrestrial carbon pool (Jobbágy and Jackson, 2000).

Few in situ measurements exist to constrain R_h, particularly in the tropics (Xu et al., 2016). For example, the international Soil Respiration DataBase (SRDB), which aims to compile data from all published studies of soil and heterotrophic respiration (Bond-Lamberty and Thomson, 2010), includes only 21 sites with R_h information in Central and South America and only 2 in Africa. The highly limited number of R_h data is likely affected by the relative difficulty and uncertainty of methods for partitioning total soil respiration (R_s) fluxes – which can be easily measured using respiration chambers – into autotrophic and heterotrophic components. Performing this partitioning requires isotopic measurements or destructive techniques such as girdling or trenching (Ryan and Law, 2005). Like R_s, total ecosystem respiration R_eco is also often considered a counterpart to photosynthetic fluxes but is rarely partitioned further. However, because most carbon cycle and ecosystem models represent autotrophic and heterotrophic components separately and because the climatic and soil sensitivities of the autotrophic and heterotrophic components of soil respiration differ (Metcalfe et al., 2010; Scott-Denton et al., 2006), it is challenging to translate soil or ecosystem respiration data to improvements of model representations for R_h. Although meta-analyses using data such as the SRDB have been used to understand the sources of spatial variability in soil respiration (Hursh et al., 2016) and heterotrophic respiration (Shao et al., 2013) rates, such studies are limited (by data availability) to consideration of annual respiration fluxes and sparse, discrete points in space. Thus, while gross primary productivity (GPP) is highly uncertain (Anav et al., 2015), GPP and R_eco are far more constrained by observations than R_h, which must be considered among the most uncertain fluxes in the carbon cycle. Temporally variable and spatially extensive estimates of R_h are therefore needed to better understand its drivers.

Starting several decades ago with Raich and Schlesinger (1992), several authors have tried to upscale sparse measurements to estimate global R_s. Most commonly, this is performed using a spatially explicit exponential model of the relationship between R_s and temperature, modified by land cover (Adachi et al., 2017), soil property (Chen et al., 2013), or soil moisture (Xu et al., 2016) limitations. Recent papers have also used machine learning methods to upscale the relationship between R_s and climate and biogeophysical properties, including random forest models (Jian et al., 2018) and artificial neural networks (Zhao et al., 2017). However, no similar effort has been made for estimating global R_h. Only Hashimoto et al. (2015) have extended a rigorous estimate of global, upscaled R_s to an estimate of global R_h. This was achieved by employing a previously noted apparent relationship between annual R_s and R_h at a given site (Bond-Lamberty et al., 2004). However, the approach of Hashimoto et al. (2015) assumes a specific functional form for the relationship between climate and R_s (and thus R_h), so that investigations of climatic sensitivities of R_h with this dataset are potentially circular. Furthermore, the approach assumes that base respiration rates and sensitivity parameters for temperature and precipitation to soil moisture are constant across the globe. This approach therefore cannot account for known dependencies of heterotrophic respiration on microbial biomass and composition (Johnston and Sibly, 2018; Walker et al., 2018; Wieder et al., 2013; Zhou et al., 2011) and substrate type (Cornwell et al., 2008). Modeling R_h as a function of precipitation alone is also inconsistent with theoretical, laboratory, and field studies that have found R_h to be a function of soil water potential (Manzoni et al., 2012; Moyano et al., 2012, 2013), which is nonlinearly related to precipitation depending on soil properties, vegetation cover, topography, and more.

In this paper, we introduce an alternative approach for estimating R_h at global or regional scales using remote sensing. Rather than a bottom-up approach for aggregating sparse point-based measurements, we propose a “top-down” method that naturally captures average values over large scales. The method derives R_h as the residual of satellite-constrained estimates of the carbon balance: net ecosystem productivity (NEP), gross primary productivity (GPP) and R_a. The NEP (the net difference between photosynthetic and respiration fluxes: $\mathrm{NEP}=\mathrm{GPP}-R_{\mathrm{a}}-R_{\mathrm{h}}$) is based on atmospheric inversions of satellite observations of column xCO₂ and xCO, and GPP is based on upscaling solar-induced fluorescence (SIF). The R_a is calculated based on GPP and carbon use efficiency estimates from a remote-sensing constrained model–data fusion framework. The top-down approach is applied to the period 2010–2012. Coarse-resolution R_h estimates are difficult to validate using in situ measurements because of representativeness errors. Instead, we rigorously compare the top-down method and its uncertainties to those of bottom-up R_h estimation, in this case as performed by Hashimoto et al. (2015).

2 Methods

2.1 Top-down estimates

2.1.1 Top-down approach

As summarized in Fig. 1, the top-down R_h at grid scale is calculated as the residual of observationally constrained estimates of the carbon balance:

$$\begin{array}{}\text{(1)}& {\displaystyle }{R}_{\mathrm{h}}=\mathrm{GPP}-\mathrm{NEP}-R_{\mathrm{a}}.\end{array}$$

The combination of NEP and GPP allows calculation of the ecosystem respiration R_eco, but an estimate of R_a is required to separate R_eco into R_a and R_h components. The R_a is calculated based on the GPP and on carbon use efficiency (CUE). Specifically, the autotrophic respiration R_a is assumed to be proportional to GPP according to a spatially variable but temporally constant CUE, where CUE is defined as the ratio of net primary production (NPP) to GPP. Thus, $\mathrm{CUE}=\mathrm{1}-R_{\mathrm{a}}/\mathrm{GPP}$. Equation (1) then becomes

$$\begin{array}{}\text{(2)}& {\displaystyle }{R}_{\mathrm{h}}=\mathrm{GPP}-\mathrm{NEP}-\left(\mathrm{1}-\mathrm{CUE}\right)\mathrm{GPP}.\end{array}$$

The CUE is commonly assumed to be constant at a given location (Gifford, 2003; McCree and Troughton, 1966) but has been found to vary depending on ecosystem type, stand age, and forest management (Collalti et al., 2018; Gifford, 2003; De Lucia et al., 2007). Note that by calculating autotrophic respiration as proportional to GPP, we classify the release of CO₂ from decomposition of root exudates by mycorrhizal fungi (Trumbore, 2006) as autotrophic rather than heterotrophic respiration. This is arguably a misclassification but is consistent with most in situ methods for measuring heterotrophic respiration (e.g., girdling, trenching, or isotopic measurements) (Ryan and Law, 2005).

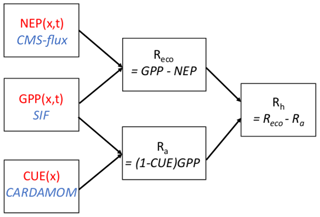
Figure 1 Schematic diagram of process used to calculate heterotrophic respiration R_he. Input datasets are outlined in red, and data sources are described in blue italics. Arrows indicate one flux is used to calculate another. Data sources are described in detail in Sect. 2.1.2.

The use of this method to calculate spatiotemporal variations in R_h is enabled by the fact that estimates of each of NEP, GPP, and CUE are available that are based on remote sensing and data assimilation. These datasets are further discussed in the following section.

2.1.2 Datasets used and implementation

The NEP is determined from an atmospheric inversion of remotely sensed columnar carbon dioxide and carbon monoxide observations in the NASA Carbon Monitoring System-Flux (CMS-Flux) system. It is described in detail in Bowman et al. (2017) and Liu et al. (2017) but summarized here for convenience. It has been validated using methods introduced in Liu and Bowman (2016). CMS-Flux estimates carbon fluxes through a 4-D variational inversion approach that ingests columnar xCO₂ observations from the Greenhouse gases Observing Satellite (GOSAT) and CO observations from the Measurement of Pollution in the Troposphere Instrument (MOPITT) (Worden et al., 2010) into the GEOS-Chem atmospheric transport model and its adjoint (Bey et al., 2001; Henze et al., 2007; Nassar et al., 2010; Suntharalingam et al., 2004). The net fluxes are further decomposed into biomass burning, oceanographic, fossil fuel, and chemical sources (including shipping, aviation, and others), as well as NEP components. The biomass burning emissions are constrained by the MOPITT CO observations and published CO∕CO₂ ratios. Anthropogenic and oceanographic priors for the fluxes come from the Fossil Fuel Land Data Assimilation System (Asefi-Najafabady et al., 2014; Rayner et al., 2010) and ECCO2-Darwin oceanographic model (Brix et al., 2015), respectively, and NEP flux priors come from the Carnegie–Ames–Stanford Approach (CASA) model simulations. As shown in Fig. S1 in the Supplement, the posterior and prior fluxes of NEP differ significantly almost everywhere: 42 % of pixels have a normalized root-mean-square difference between the prior and posterior fluxes greater than 1, consistent with a previous observing system simulation experiment for the CMS-Flux system (Liu et al., 2014). The total global NEP averages to 5±13 Pg C yr⁻¹ across 2010–2012, and the uncertainty of the NEP estimates is assumed to be normally distributed with a spatially and temporally varying standard deviation estimated in the atmospheric inversion via a Monte Carlo approach (Bousserez et al., 2015).

The GPP is determined based on an optimal rescaling of SIF observations. SIF is a by-product of photosynthesis and therefore provides direct information about the magnitude of GPP (Porcar-Castell et al., 2014). The information content of SIF for photosynthesis has been demonstrated using field-scale measurements (Yang et al., 2015) and by comparing satellite-based data to eddy-covariance towers (Guanter et al., 2014; Joiner et al., 2014; Sun et al., 2017; Wood et al., 2017; Zuromski et al., 2018), carbon dioxide mole fractions in Amazonia (Parazoo et al., 2013), and machine-learning-based estimates of GPP (Alemohammad et al., 2017). Despite the abundance of evidence that SIF carries information about GPP, the linear constant of proportionality between SIF and GPP depends on the light use efficiency of the vegetation in question, as well as the satellite efficiency for capturing photons, and is difficult to estimate a priori. Here, we use GPP estimates from Parazoo et al. (2014), who used a Bayesian approach to determine an optimal seasonally and spatially varying scaling parameter between SIF and prior GPP along with explicit uncertainty estimates. Monthly GPP at each grid point is inferred from a precision-weighted minimization of SIF, which is regressed against biome-specific GPP from upscaled flux tower data (Frankenberg et al., 2011; Jung et al., 2011) and prior GPP from eight terrestrial ecosystem models in the TRENDY project (Sitch et al., 2015). This approach has been used to examine regional GPP responses to climate variability and drought and has been extensively validated against flux tower data (Bowman et al., 2017; Liu et al., 2017; Parazoo et al., 2014, 2015), though it remains uncertain. The average global GPP across 2010–2012 is 114±41 Pg C yr⁻¹, and the uncertainty of the GPP estimates is determined as in Parazoo et al. (2014) and assumed to follow a normal distribution.

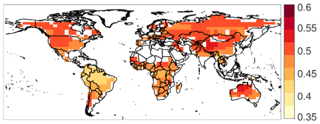
The CUE is determined from a 10-year (2001–2010) run of CARDAMOM (CARbon DAta MOdel fraMework) (Bloom and Williams, 2015; Bloom et al., 2016), in which uncertainties are explicitly represented as probability density functions computed from an ensemble. CARDAMOM is a model–data fusion system that uses a Bayesian framework to determine global ecological parameter combinations that minimize the mismatch with observations while still satisfying a set of ecological realism and dynamic stability constraints to regularize the inversion. CARDAMOM is built on the underlying Data Assimilation Linked Ecosystem Carbon model version 2, DALEC2 model (Bloom and Williams, 2015; Williams et al., 2005), with assimilation of observations of leaf area index (LAI), burned area, tropical biomass, and soil carbon (Bloom et al., 2016). Within CARDAMOM, a constant fraction f_a of photosynthetic carbon gain is assumed to be allocated to autotrophic respiration (note that $f_a=\mathrm{1}-\mathrm{CUE}$). The fraction f_a is directly linked to the allocation fractions of photosynthetic carbon to other pools (labile, wood, foliar, and fine root carbon) through conservation of mass. The allocation fractions directly influence the observed quantities used for CARDAMOM parameterization (e.g., LAI, tropical biomass, and soil carbon) and are subject to several ecological realism constraints. The resulting range of global CUE (between 0.35 and 0.6, shown in Fig. 2) is consistent with results found from meta-analyses (Gifford, 2003; De Lucia et al., 2007) and is also supported by theoretical considerations based on conservation of mass (Van Oijen et al., 2010) and plant carbon dynamics (Dewar et al., 1998). Average values of CARDAMOM CUE are generally lowest in the tropics, consistent with previous site-specific observations (Amthor, 2000; Chambers et al., 2004; De Lucia et al., 2007; Piao et al., 2010). The zonal mean variation in CARDAMOM CUE (not shown) also compares favorably with that of a recently produced random forest-derived global upscaling of in situ CUE measurements, decreasing at low latitudes and increasing at high latitudes to similar ranges (Tang et al., 2019), across a similar range (0.43 to 0.52 for CARDAMOM and 0.42 to 0.58 for the estimates of Tang et al., 2019).

Figure 2 Global variations in mean carbon use efficiency from CARDAMOM.

Autotrophic respiration may depend on stored supplies of carbon, causing a decoupling between the seasonality of GPP and R_a and thus temporal variation in CUE. This is particularly common in deciduous trees at midlatitudes and high latitudes (Epron et al., 2012; Kuptz et al., 2011). Less is known about seasonal variations in CUE in the tropics. Although small variations in CUE (e.g., $<=\mathrm{0.05}$) have been observed in both highland and lowland Amazonian sites, these variations were found to be small relative to seasonal variations in allocation rates to non-respiratory carbon pools (Doughty et al., 2015; Rowland et al., 2014). Nevertheless, the assumption of constant CUE likely adds error to the top-down estimates of R_h. This error is partially accounted for by the wide uncertainty range used for CUE. We further performed a sensitivity analysis in which the R_h derived using an assumption of constant CUE was compared to the R_h with a systematic seasonal variability in CUE. Although little is known about the true temporal variation in CUE across the globe, here we assumed a seasonal cycle of CUE proportional to that of GPP but renormalized to have a mean equal to the constant CARDAMOM CUE and a standard deviation of 0.1 at each pixel. That is,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{CUE}(x,y,t)={\mathrm{CUE}}_{\mathrm{CARD}}\left(x,y\right)+\\ \text{(3)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\mathrm{0.1}}{{\mathrm{SD}}_t\left(\mathrm{GPP}(x,y,t)-\stackrel{\mathrm{‾}}{\mathrm{GPP}}\right)}}\left(\mathrm{GPP}(x,y,t)-\stackrel{\mathrm{‾}}{\mathrm{GPP}}\right),\end{array}$$

where (x,y) determines pixel location in space, t is the monthly time vector, CUE_CARD(x,y) is the constant CUE determined from CARDAMOM, SD refers to standard deviation, and the overbar denotes a time average over the entire period. The use of a CUE proportional to GPP is chosen so as to provide a structure to the temporal variability of CUE that is potentially realistic for each pixel (i.e., not completely random), even if little is known about the overall controls on temporal variability in CUE. The 0.1 standard deviation magnitude is fairly conservative unless true temporal variation in CUE is much larger than spatial variation – the spatial standard deviation of CARDAMOM CUE across all global land surfaces is 0.06.

Additional sensitivity analyses were also performed to test the sensitivity of R_h to errors in the GPP and NEP datasets. To test the sensitivity to GPP, we compared R_h with an alternative set of R_h estimates calculated using GPP from FLUXCOM (Tramontana et al., 2016). FLUXCOM estimates of GPP are derived as the median value across an ensemble of estimates from 11 different machine learning models applied to meteorological drivers from reanalysis and remote sensing and trained on eddy-covariance observations. The uncertainty of the FLUXCOM GPP is calculated based on the standard deviation across the different machine learning methods. Note that FLUXCOM is a bottom-up method and thus carries many of the same uncertainties as other bottom-up methods (see Sect. 4.1), particularly in globally under-sampled regions. For example, only 17 of 225 eddy-covariance tower sites used to train the machine learning models are in the Southern Hemisphere. Furthermore, the FLUXCOM data are sensitive to the quality of the GPP partitioning of the observed tower NEP. Nevertheless, we use the FLUXCOM dataset here to study the sensitivity of R_h to GPP because it is widely used, well-regarded, and cross-validated against withheld parts of the eddy-covariance record. While FLUXCOM also estimates NEP, its NEP predictions are of lower quality than those of other fluxes (Tramontana et al., 2016). Furthermore, it shows significant bias (Exbrayat et al., 2019). Instead, taking advantage of the low magnitude of NEP, we test the sensitivity to NEP data quality by computing R_h assuming NEP is zero everywhere across the globe and across the time series. Because an uncertainty in NEP still needs to be assumed, we simply use the same uncertainties from the CMS-Flux product.

When calculating R_h in either the main or sensitivity analyses, all datasets are averaged to the same monthly temporal and 4^∘ latitude × 5^∘ longitude spatial resolution, the native resolution of flux estimates from CMS-Flux. We use NEP and GPP data over the period 2010–2012, when the CMS-Flux data have been validated in the most detail. However, even at 4^∘ by 5^∘ resolution, the precision of CMS-Flux data can still be poor. To reduce the random component of the error, all visual maps are presented after applying a 3 pixel by 3 pixel moving average smoother, as in Liu et al. (2018). When calculating R_h, a 4000-member ensemble is used for explicit simulation of the uncertainty distributions of each of the input variables. Additionally, a constraint on the signs of R_h, R_a, and GPP is used to ensure the estimated R_h is physically realistic (Bloom and Williams, 2015; Parazoo et al., 2018) – each of these three fluxes is required to be positive. A simple accept–reject sampling scheme is used that rejects ensemble members that violate this criterion. For each of these ensemble members, new samples of the uncertainty distribution of NEP, GPP, and CUE are drawn until each of R_h, R_a, and GPP for that ensemble member are positive. Using such a constraint is equivalent to using a Bayesian scheme with prior distributions for R_h, R_a, and GPP that are 0 for negative values and 1 otherwise.

The uncertainty of the resultant R_h is a combination of the uncertainty in the three input datasets: NEP, GPP, and CUE. There is some nonlinearity to this combination because the positive flux constraints limit what uncertainty combinations are considered to lead to acceptable R_h. To estimate how much each of these datasets contributes to the overall R_h uncertainty, R_h is reestimated three times, but in each case only one of the input datasets is given nonzero uncertainty. The resultant magnitude of the uncertainty in R_h is then compared.

2.2 Bottom-up estimates

2.2.1 Approach

To the best of our knowledge, only Hashimoto et al. (2015) have previously estimated R_h based on upscaling in situ measurements. Their method is based primarily on estimating R_s, for which a simple functional form adapted from Raich et al. (2002) is used:

$$\begin{array}{}\text{(4)}& R_{\mathrm{s}}=F\times e^{aT-b{T}^{\mathrm{2}}}\times {\displaystyle \frac{\mathit{\alpha }{P}_t+\left(\mathrm{1}-\mathit{\alpha }\right)P_{t-\mathrm{1}}}{K+\mathit{\alpha }{P}_t+\left(\mathrm{1}-\mathit{\alpha }\right)P_{t-\mathrm{1}}}},\end{array}$$

where F (gC m⁻² d⁻¹) is a base rate and a (^∘C⁻¹) and b (^∘C⁻²) control the sensitivity to temperature T (^∘C). The R_s also depends on the current-month precipitation P_t (cm month⁻¹) and the previous-month precipitation P_t−1 (cm month⁻¹), with the relative weight of each determined by a (–). The K (cm month⁻¹) parameter also controls the influence of precipitation. For lack of more information, all parameters are assumed to be globally constant, so that the only spatial variation is provided by variations in the climatic drivers. Hashimoto et al. (2015) used temperature and precipitation from the Climate Research (CRU) 3.21 (Harris et al., 2014) and fit the above function to observations from the SRDB using a Bayesian Markov Chain Monte Carlo scheme. To determine the annual average R_h at a location based on annual R_s, Hashimoto et al. (2015) employed a previously determined relationship between annual soil and heterotrophic respiration (Bond-Lamberty et al., 2004):

$$\begin{array}{}\text{(5)}& \ln \left(R_{\mathrm{h}}\right)=c+d\ln \left(R_{\mathrm{s}}\right),\end{array}$$

where c=1.22 and d=0.73. While it is in theory possible to apply Eq. (5) to any number of recent bottom-up R_s estimation approaches, we apply it here only to the estimates from Hashimoto et al. (2015) in Eq. (4), both for consistency with the literature and since the data from Hashimoto et al. (2015) are among the most commonly used bottom-up R_s estimates.

2.2.2 Parametrization and implementation

We implemented Eq. (4) using climate data from the CRU 4.01 and using the maximum a posteriori parameter values from Hashimoto et al. (2015) (that is, F=1.68 gC m⁻² d⁻¹, a=0.0528 ^∘C⁻¹, b=0.000628 ^∘C⁻², α=0.98, and K=1.20 cm month⁻¹) to determine monthly resolution estimates of R_s. The R_s estimates were then temporally aggregated to determine annual R_h using Eq. (5). These are referred to as the bottom-up estimates below.

Extrapolating from a limited sample of parameters with multiple fitted parameters carries the risk of overfitting. Fortunately, several measurements of R_s and R_h have been added to the SRDB since the Hashimoto et al. (2015) study; the number of R_s measurements has increased by 20 %, from 1638 to 1979. Similarly, the number of measurements of heterotrophic respiration has increased from 53 measurements when Bond-Lamberty et al. (2004) originally derived Eq. (4) to 362 measurements in the most recent SRDB version. To test the applicability of the original parameters, we also implemented the bottom-up approach at the increased number of SRDB location-years available since Hashimoto et al. (2015), i.e., all datapoints in SRDB v20180126. Consistent with the original study, for SRDB experiments for which the observed annual average was determined over a range of years, we only used the middle year in the range. We compared simulated to observed annual R_s and R_h for both the case of the maximum a posteriori parameters from the original Hashimoto et al. (2015) study and for a set of updated model parameters determined by a nonlinear least-squares fit. For the updated parameters, the coefficients of the R_h–R_s relationship are also optimized. Because the updated parameters did not perform significantly better (see Sect. 3.2), the original parameters were used in the rest of this study.

No uncertainty was considered in Hashimoto et al. (2015). To determine the uncertainty of the bottom-up estimates, we tested them against SRDB observations. Measurements in the SRDB are highly concentrated in the midlatitudes: 74 % of R_h measurements and 78 % of R_s measurements were made at a latitude greater than 30^∘ N. The uncertainty of the bottom-up estimates is therefore likely to exhibit significant spatial and temporal variability due to sampling error alone, on top of errors related to the imposed functional form and its parameterization. To find one or more covariates between the expected uncertainty of R_h and other factors, the errors associated with bottom-up implementations at the SRDB sites were linearly regressed against the following possible predictors: latitude, longitude, mean and standard deviation of precipitation, mean and standard deviation of temperature, and mean predicted R_h. Several nonlinear functions of latitude were also tested. Of these, the mean predicted R_h and latitude were chosen as predictors because they had the greatest explanatory power (R=0.23 when used in combination). Adding more predictor variables does not further increase the adjusted R².

In order to determine a spatiotemporally variable uncertainty range we calculated the 25th and 75th percentile of all 362 R_h errors associated with using the bottom-up model. These formed a baseline globally averaged confidence interval δ_base that was then modified linearly based on the modeled R_h and latitude (consistent with the linear regression tests mentioned above):

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}_i={\mathit{\delta }}_{\mathrm{base},i}\left({\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{1}}+{\mathit{\gamma }}_{\mathrm{2}}{R}_{\mathrm{h}}^{\mathrm{bu}}+{\mathit{\gamma }}_{\mathrm{3}}\mathrm{lat}}{{\mathit{\gamma }}_{\mathrm{4}}}}\right),\end{array}$$

where i denotes either the 25th or 75th percent confidence interval, $R_{\mathrm{h}}^{\mathrm{bu}}$ is the predicted mean bottom-up heterotrophic respiration rate, lat is the pixel latitude, γ₁₋₃ are regression parameters, and γ₄ is the mean error of the bottom-up method across the SRDB dataset. Although the amount of variability in error captured using this method (R=0.23) is still extremely low, no alternative ways of capturing the expected spatiotemporal variability in bottom-up R_h uncertainty exist, and poorly accounting for this variability is still expected to be more useful than not accounting for it at all.

2.3 Comparison analyses

We compared the mean and uncertainty estimates of the top-down and bottom-up annual R_h across latitudes. Because no bottom-up estimates of the seasonal cycle of R_h are available, we further compared the seasonality of R_h in different regions to the seasonality of R_s from bottom-up estimates and R_eco from the top-down estimates. Pixels are seasonally aggregated for simplicity and plotting and to reduce noise from the propagation of atmospheric inversion uncertainty. In particular, we consider high-latitude regions (latitudes greater than 55^∘ N/S), midlatitudes (latitudes between 30 and 55^∘ N/S), dry tropics (latitudes <30^∘ N/S and mean annual precipitation less than 1500 mm yr⁻¹), and wet tropics (latitudes <30^∘ N/S and mean annual precipitation greater than 1500 mm yr⁻¹). To calculate the uncertainty of the bottom-up R_s estimates, a method analogous to that used for determining the 25th–75th confidence interval of bottom-up R_h was used.

3 Results

3.1 Annual average R_h from top-down and bottom-up estimates

3.1.1 Top-down R_h

The annual mean tropical R_h is 450±200 gC m⁻² yr⁻¹. The spatial pattern of mean annual R_h is similar to that of GPP, (Fig. 3a, R²=0.97, p<0.001), as expected. More complex dynamics are revealed by considering the coefficient of variation (CV) of R_h (e.g., temporal standard deviation divided by mean per grid cell, Fig. 3b). The CV does not closely follow known spatial patterns in biomes, GPP, turnover times, or other carbon parameters (e.g., Anav et al., 2015; Bloom et al., 2016; Carvalhais et al., 2014; FAO/IIASA/ISRIC/ISS-CAS/JRC, 2009), as it reflects a combination of all these factors. More information about the temporal variability of substrate availability (e.g., litter and soil organic matter) is needed to disentangle the climatic and biogeophysical controls on R_h dynamics. This is left for a future investigation. Note that the high CV values in semiarid regions are likely due to the near-zero mean R_h there.

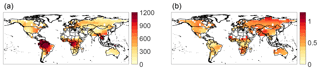
Figure 3 Spatial variability in top-down R_h. Maps of (a) mean R_h (gC m² yr⁻¹) and (b) temporal coefficient of variation in top-down R_h, calculated based on monthly data over 2010–2012.

Figure 4 shows the results of sensitivity analyses for each of GPP (by comparing the R_h estimates with those derived using GPP from FLUXCOM), NEP (by comparing with R_h estimates derived assuming zero NEP), and CUE (by comparing with R_h estimates derived assuming a seasonally varying CUE, as described in Sect. 2.1). When the GPP data source is changed to FLUXCOM (Fig. 4a–b), the temporal dynamics of R_h are most varied in the central American Great Plains, Australia, and in the tropics, especially in the Amazon. However, other hot spots for a mean difference exist, such as in Central Canada and Eastern Europe. Changing to using zero value NEP (Fig. 4c–d) most significantly introduces a mean difference in the southern Amazon and in Central Africa, though, interestingly, the signs of the resulting difference are opposite between the continents. The temporal dynamics of these regions is also the most sensitive to inclusion of actual NEP estimates in the R_h calculation. Despite the fact that NEP's global mean value is more than an order of magnitude smaller than that of GPP, neglecting NEP causes large changes to the estimated R_h over much of the globe, showing the value of including NEP estimates in the top-down R_h calculation. Note, however, that the mean deviation in R_h for either the NEP or GPP sensitivity analyses is still smaller than the mean difference between the top-down and bottom-up R_h over most of the world. The only exception to this is in the high latitudes where all differences between estimates are of a similar magnitude.

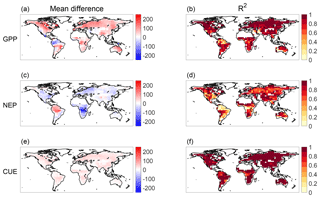
Figure 4 Results of sensitivity analyses for three input datasets. (a, c, e) Mean difference (gC m² yr⁻¹) between baseline top-down R_h and alternate-input top-down R_h and (b, d, f) R² between baseline top-down R_h and alternate-input top-down R_h. Sensitivity analyses performed include using FLUXCOM GPP (a, b), assuming uniformly zero values of NEP (c, d) and that CUE varies temporally in a manner proportional to GPP (e, f).

Lastly, Fig. 4e and f show the results of the sensitivity analysis assuming a temporally variable CUE. Overall, this sensitivity analysis leads to far smaller changes to R_h than those for GPP and NEP. The magnitude of the R_h change resulting from a change in CUE depends on whether the seasonality of GPP aligns with R_h and whether the changed CUE causes unrealistic flux combinations across any of the ensemble members. The difference in time-averaged R_h is relatively small – no more than 50 g C m⁻² yr⁻¹ for any pixel. Despite the change in seasonality of CUE, the temporal dynamics of the 36 months of estimated R_h also remain relatively similar in the sensitivity analysis. More than 90 % of pixels have an R² between the R_h from constant CUE and the R_h from seasonally variable CUE that are greater than 0.8. The largest difference in R_h seasonality occurs in the wet tropics. In these regions, the average GPP is largest, and a change in CUE seasonality corresponds to the greatest absolute change in R_a.

Figure 5 maps the relative contributions of uncertainty in NEP, GPP, and CUE to R_h, as calculated by consecutively recalculating R_h, assuming in each case that all but one of the three datasets have zero uncertainty. The uncertainty in GPP is the dominant source of uncertainty in R_h across most of the globe, except in parts of the Amazon. Consistent with the CUE sensitivity analysis (Fig. 4e and f), the contribution of CUE to the R_h uncertainty is greatest in the tropics. In many high-latitude regions, NEP also contributes significantly to the overall R_h uncertainty. This contrasts with the results of the zero-NEP sensitivity analysis (Fig. 4c–d) in which NEP effects were no greater in the high latitudes than elsewhere in the world because the CMS-Flux NEP is close to zero in mean magnitude in the high latitudes but nevertheless relatively uncertain there. Overall, future efforts to improve top-down approaches for R_h estimation would likely benefit most from reduced uncertainty in remotely-sensed GPP and NEP estimates.

Figure 5 RGB map of relative contributions to R_h uncertainty in each of the input datasets, NEP (red), CUE (blue), and GPP (green). Note that a yellow color signifies similarly sized uncertainties for GPP and NEP, which are much larger than the uncertainty for CUE.

3.1.2 Bottom-up R_h

The performance of the bottom-up approach at SRDB sites for both R_s and R_h is shown in Fig. 6. The influence of latitude on modeled R_h is stronger than on observed R_h (since the color patterns in Fig. 6 are largely horizontal). The uncertainties of the bottom-up method are high. Indeed, for both the bottom-up R_s and R_h, the root-mean-square error (RMSE) (421 g C m⁻² yr⁻¹ for R_s, 306 g C m⁻² yr⁻¹ for R_h) is only less than 15 % lower than the RMSE for a model that simply predicted the average observed respiration value everywhere (RMSE = 488 g C m⁻² yr⁻¹ for R_s, 333 g C m⁻² yr⁻¹ for R_h). The R_s RMSE = 421 g C m⁻² yr⁻¹ is also higher than the 376 g C m⁻² yr⁻¹ RMSE value reported by Hashimoto et al. (2015) when their equation was applied to a smaller subset of the current SRDB dataset. The performance of the bottom-up model may be even worse on a cross-validation dataset that is entirely independent.

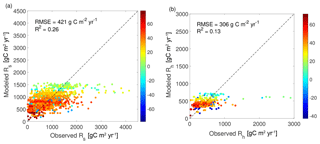
Figure 6 Comparison of observed annual respiration terms at SRDB sites vs. bottom-up estimates at the same sites for (a) 1979 soil respiration sites and (b) 362 heterotrophic respiration sites. Each point denotes a single experiment and is colored by the experiment's latitude.

To test whether the bottom-up model can be improved, its parameters were optimized using a nonlinear least-squares fit. The resulting values (F=1.30 gC m⁻² d⁻¹, a=0.0565 ^∘C⁻¹, b=0 ^∘C⁻², α=9.8, K=0.0008 cm month⁻¹, c=0.92, and d=0.75) were of a similar magnitude as the original parameters (F=1.68 gC m⁻² d⁻¹, a=0.0528 ^∘C⁻¹, b=0.000628 ^∘C⁻², α=0.98, K=1.20 cm month⁻¹, c=1.22, and d=0.73) for all values except K and α, the two parameters controlling the relationship between precipitation and R_h. This suggests that precipitation is among the most uncertain controls of R_h, consistent with the fact that moisture limitations on R_h are mediated by soil water potential rather than precipitation. However, because using the optimized parameters led to only a 3 % reduction in RMSE (from 306 to 294 g C m⁻² yr⁻¹, Fig. S2), the original parameters were used elsewhere in the paper. Several constraints and alternative initial conditions were tested for fitting, but these did not lead to a better-performing fit (not shown). Some compensation between parameters is likely occurring when fitting to observations, reducing the quality of the fit.

In the absence of additional information about the bottom-up model uncertainty, the SRDB implementation and the associated errors were also used to determine a model for the uncertainty of the global bottom-up estimates. As shown in Fig. 7, the R_h experiments in the SRDB overrepresent midlatitudes but underrepresent low and high latitudes relative to the distribution of global land area. This can also be seen visually in a map of the experimental locations (Fig. S3). As a result, pixels with low R_h (which are typical in the high-latitudes) are underrepresented in the SRDB, such that the bottom-up model has greater uncertainty there. These factors are accounted for by the dynamic uncertainty model in Eq. (5).

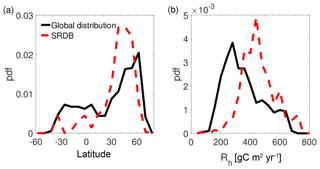
Figure 7 Distribution of all SRDB experiments (dashed red lines) and global land points where top-down retrievals were possible in terms of (a) latitude and (b) bottom-up modeled R_h. Modeled R_h rather than observed R_h were used for the SRDB data in the comparison to isolate the differences due to the representativeness of the SRDB experiments relative to the entire global land area and to remove any possible effects of biases in modeled global values and observed SRDB values.

3.1.3 Comparison

The top-down and bottom-up estimates and their uncertainties are compared in Fig. 8. Global maps of the two R_h estimates are also shown in Fig. S4. Except in boreal regions and in Australia, the top-down estimates are greater than the bottom-up estimates. This is reflected in their global averages, with mean R_h rates of 452 g C m⁻² yr⁻¹ for top-down vs. 353 g C m⁻² yr⁻¹ for bottom-up estimates (43.6 and 33.4 Pg C yr⁻¹, respectively, summed across the globe). The highest-magnitude fluxes are in the low-latitude tropics, consistent with findings for R_s by Zhao et al. (2017) and the monotonic R_h–R_s relationship in Eq. (5). The difference between the two estimates is also largest in this region – top-down estimates are an average of 281 g C m⁻² yr⁻¹ larger than bottom-up ones between 30 ^∘S and 30 ^∘N but are only 10 g C m⁻² yr⁻¹ larger than bottom-up estimates between 30 and 45^∘ N/S. When compared against SRDB observations (Fig. 6b), the bottom-up estimates were 500–2000 g C m⁻² yr⁻¹ or more lower than observations at several low-latitude sites, suggesting the bottom-up estimates may be underrepresenting R_h across the region. The tropics is also the region where the relative uncertainties in both top-down (57 % median relative 25th–75th confidence interval width) and bottom-up (76 % median relative 25th–75th confidence interval width) estimates are highest. For the bottom-up estimation, this is due to a lack of representative in situ observations, while for the top-down estimates this is likely driven by uncertainties in NEP from atmospheric diffusion and satellite sampling in the atmospheric inversions (Liu et al., 2014) and GPP (Parazoo et al., 2014). Remarkably, although uncertainty estimates for both the bottom-up and top-down approaches were conservative, the two estimates are so different at low latitudes that there is almost no overlap in their uncertainty ranges.

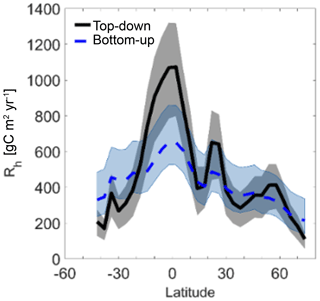
Figure 8 Longitudinally averaged R_h as estimated from top-down (black solid line) and bottom-up (dashed blue line) estimates, respectively. Shaded areas represent the average 25th–75th uncertainty bars at each latitude.

The greatest overlap between the two datasets and their uncertainty ranges occurs between 30 and 50^∘ N, where more than 48 % of SRDB observations fall and the bottom-up estimates are likely the most reliable. At high latitudes (above 55^∘ N), the top-down uncertainty narrows but the bottom-up uncertainty does not. In this region, bottom-up uncertainties are about 30 % greater than the uncertainties of the top-down R_h.

3.2 Seasonal cycle of respiration components

The bottom-up estimates only provide R_h at annual timescales. To gain insight into the realism of the seasonal cycle of the top-down R_h estimates, they are compared to the seasonal cycle of bottom-up R_s and top-down R_eco in several regions in Fig. 9. Consistent with the low values of bottom-up R_s (Sect. 3.1.3), the top-down R_s are not much lower than R_h. There is significant overlap between the uncertainty ranges of both in many region–month combinations, despite the fact that true R_h is always lower than (or equal to) R_s due to the occurrence of belowground autotrophic respiration. Indeed, the bottom-up R_s and top-down R_h nearly overlap in the January–March period in the wet tropics. Remarkably, during boreal winter at high latitudes, the top-down R_eco, R_s, and R_h all agree. This is likely because the constant CUE assumption assumes that R_a is near-zero in boreal winter when GPP shuts down, which may not be realistic. Previous studies have found that wintertime R_s can provide as much as 20 % or more of total boreal soil CO₂ fluxes (see overview in Hobbie et al., 2000), but here only 5.2 % of bottom-up estimated R_s and 8.8 % of top-down estimated R_h occurs between December and February. In the dry tropics, the seasonal cycle of top-down R_h is remarkably flat and flatter than that of bottom-up R_s. This could be explained by the fact that temperature, moisture, and substrate variabilities do not vary the same way across the seasons and may partially compensate for one another. However, more research is needed to determine what controls dry tropical variations in R_h and a detailed investigation of this issue is beyond the scope of this paper.

The ratio of estimated R_h to R_eco spans between close to 1 in high-latitude winters and 0.4 in the wet tropics. Similarly, the ratio of R_h to R_s varies from 0.75 to 0.94 for different month–region combinations.

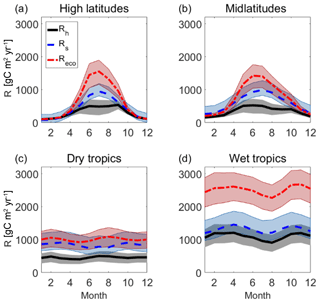
Figure 9 Comparison between the regionally and temporally averaged seasonal cycle of different respiration components: top-down R_h (black solid line and area), bottom-up R_s (dashed blue line and blue area), and top-down R_eco (dashed–dotted red line and area). Shaded areas represent the average 25th–75th uncertainty bars at each latitude. (a) High latitudes (latitude >55^∘ N/S) (b) midlatitudes (30^∘ N/S < latitude < 55^∘ N/S), (c) dry tropics (latitude <30^∘ N/S and mean annual precipitation <1500 mm yr⁻¹), and (d) wet tropics (latitude <30^∘ N/S and mean annual precipitation >1500 mm yr⁻¹).

4 Discussion

4.1 Top-down and bottom-up approaches are both uncertain

Top-down estimates of R_h are 30 % higher, on average, than bottom-up estimates. At low-latitudes, the top-down estimates of R_h are so much larger than the bottom-up ones that there is almost no overlap between their respective 25th–75th uncertainty intervals, despite efforts to create conservative uncertainty intervals in each case. Consistent with these results, the bottom-up R_h were previously shown to be biased low relative to models from the Climate Model Intercomparison Project 5 (CMIP5) (Taylor et al., 2012) in the low latitudes, though it is unclear whether this is because CMIP5 models are biased high or because the bottom-up estimates are biased low relative to true R_h (Hashimoto et al., 2015, Fig. 10). Zhou et al. (2009) found that attributing a globally uniform Q₁₀ value decreases model-simulated average R_h by 40 %, and a similar dynamic may be causing the bottom-up R_h estimates to be too low. It should also be noted that the global average R_s estimates of the bottom-up approach are 10–20 Pg lower than the six other estimates of global R_s published in the last decade (Bond-Lamberty, 2018) and that a lower bottom-up R_s leads to a lower bottom-up R_h (Eq. 5).

The top-down and bottom-up approaches to estimation of R_h have complementary strengths and weakness, as detailed in Table 1. Top-down estimates are indirect, and errors and uncertainties in any of the source datasets can propagate to errors and uncertainties in the retrieved R_h. These include the assumption of a temporally constant CUE, which, among other factors, can lead to unrealistically low R_h in boreal winters. Additional uncertainties also include, for example, choices made in the atmospheric inversion (Peylin et al., 2013) or the retrieval of SIF and its scaling to GPP (e.g., whether a constant set of values is used, or whether this scaling is dynamic as in the Parazoo et al., 2014, data used here). GPP is the most uncertain of the input fluxes (Fig. 5). Despite their uncertainties, the top-down estimates are globally representative. By contrast, bottom-up upscaling starts with more accurate, direct observations of R_h but suffers from a lack of representativeness: direct observations are often temporal snapshots covering only a single year or a few years at a given site, with the time period observed varying dramatically between sites. More importantly, they underrepresent boreal and tropical regions and may over- or under-sample disturbed sites in different regions. While the uncertainties of the remote-sensing datasets used for top-down estimation show some variations across different parts of the globe, remote-sensing-based estimates of vegetation properties such as photosynthesis and biomass have previously been argued to contain significantly lower representativeness error than bottom-up estimates (Saatchi et al., 2015; Schimel et al., 2015). A similar dynamic is at play for R_h.

Table 1 Advantages and disadvantages of top-down vs. bottom-up estimation methods.

The top-down approach introduced here is dependent on the quality of the input datasets used. Among the sensitivity analyses performed, NEP and GPP generally had a greater effect on the resulting R_h than the assumed values of CUE. The primary GPP and NEP datasets used here (those from Parazoo et al. (2014) and CMS-Flux, respectively) are sensitive to both observational error (e.g., due to cloud cover) and uncertainties in the retrieval algorithms (including, but not limited to, uncertainties in the relationship between SIF and GPP and, for NEP, in the inversion of atmospheric transport models). As shown in Fig. 4, uncertainties in top-down GPP and NEP can have significant effects on the mean and temporal variability of estimated R_h. Nevertheless, the sensitivity of R_h to alternative GPP and NEP assumptions was still lower than the difference between the top-down and bottom-up R_h estimates everywhere outside the high latitudes. Thus, despite the large sensitivity of the top-down R_h to the quality of the input datasets (and to a lesser degree, to the assumption of constant CUE), our new approach still provides meaningful new constraints on R_h not available from bottom-up estimation alone.

For the bottom-up approach, the errors associated with sampling bias are likely also exacerbated by the uncertainty in parameterizing a single functional model and the difficulty of parameter optimization. When the model parameters were refit on a version of the SRDB that was slightly expanded from that used in Hashimoto et al. (2015), the precipitation-sensitivity parameterization changed dramatically, while the error statistics remained similar, suggesting possible overfitting. Furthermore, even comparing against an SRDB dataset that was similar to that used to derive the original parameters, the bottom-up approach barely had improved error statistics (RMSE of 306 g C m⁻² yr⁻¹) relative to a model that simply ignores spatial variations and everywhere assigns the same value (RMSE of 333 g C m⁻² yr⁻¹). Such results suggest a structural problem with the underlying modeling approach (no good parameters exist) but also call into question whether currently used parameters are truly optimal given the model structure. In a recent study, machine-learning-based approaches for estimating R_s were able to explain 60 %–70 % of the R_s variability (Zhao et al., 2017), considerably more than the 35 % variability explained in this study using the Hashimoto et al. (2015) approach. If the robustness of machine-learning-based bottom-up upscaling methods can be further established, they may form a path forward for improved fidelity of bottom-up estimation of R_h and for allowing estimation of R_h at a temporal resolution finer than the current annual timescales. However, the number of R_h observations in the SRDB – and presumably the literature as a whole – is 5 times smaller than the number of R_s sites. Thus, additional measurements of R_h are needed for this approach, and they must include under-sampled areas. This is unlikely to be possible in the foreseeable future.

Despite the complementary sources of uncertainties in both top-down and bottom-up R_h estimates, the strong overlap between the two estimates and their uncertainty ranges in the latitude range 30–50^∘ N (the same latitude range where SRDB observations are most common, Fig. 7) is encouraging. Indeed, if the uncertainty of top-down estimates can be reduced, they could be used to constrain or help parameterize bottom-up models similar to those compared to here, allowing creation of a longer record than may be possible with top-down observational data alone.

4.2 General applicability of the carbon balance inversion method

This paper introduced a new method for top-down estimation of R_h by calculating it as the residual of the carbon balance. The propagation of uncertainty under realism constraints (in the form of the correct sign on each of the respiration components and GPP) is key to avoiding large errors in this approach. In this paper, we used large-scale, regionally available estimates for the carbon balance components, including recently developed atmospheric inversion-based net biome exchange (NBE) and NEP estimates from CMS-Flux. However, the approach could also be applied at finer resolutions, for example using regional-scale atmospheric inversions. If the local carbon use efficiency can be determined (Tang et al., 2019), the method could also be applied at smaller spatial and temporal scales, such as to data from eddy-covariance towers. For example, constraints based on estimates of R_h from a carbon balance inversion could be useful in upscaling chamber-based soil respiration measurements to the tower scale, which could help explain inconsistencies between tower and chamber measurements of respiration fluxes (Barba et al., 2017; Phillips et al., 2016).

4.3 Implications for carbon–climate feedbacks

The response of terrestrial net carbon fluxes to climate change is likely to feed back to future climate (Bodman et al., 2013), but the sign and magnitude of this feedback is highly uncertain (Friedlingstein et al., 2014). The tropics likely form a dominant control on global carbon–climate feedbacks (Cox et al., 2000; Schimel et al., 2015). However, in the period 2010–2015, GPP explained less than one-third of variations in tropical NEP, suggesting an important role for R_a and R_h in controlling net terrestrial carbon uptake and its climate sensitivity (Sellers et al., 2018). A recent modeling study also suggested that R_h forms a dominant control on net biome production (NBP) at multi-decadal timescales (Zhang et al., 2018). Studies of climate-carbon feedbacks commonly consider either R_eco or R_s, but in doing so they conflate two separate respiration components (total R_a and R_h, or belowground R_a and R_h, respectively), which have different biogeophysical controls and responses to climate. The large spatial and temporal variations in the ratio of top-down heterotrophic to R_eco and R_s in Fig. 8 act as a reminder that heterotrophic respiration should be studied separately from other respiration fluxes in this context.

The recent launch of TROPOMI, which has daily coverage and approximately 7 km × 3.5 km pixel resolution, will greatly increase measurements of SIF, and hence will also greatly increase the number of estimates of GPP (Kohler et al., 2018), the largest source of uncertainty in the global R_h estimates (Fig. 5). Increased data density from OCO-2 (Crisp et al., 2004) and, in the future, GeoCarb (Polonsky et al., 2014) should also provide better regional estimates of NEP. With these and other improvements to remote-sensing-driven estimates of GPP and NEP, top-down estimation of R_h may be a promising avenue for creating a better understanding the role of R_h fluxes in carbon–climate feedbacks. However, because the temporal variability of the derived R_h varies depending on the quality of the GPP, NEP, and CUE datasets (as well as, to a lesser degree, the assumed constancy of the CUE assumptions), any studies using top-down R_h should carefully consider uncertainty propagation in any hypothesis testing. Nevertheless, with careful consideration of uncertainty, top-down estimation may be a promising approach for understanding or bounding the role of R_h in carbon–climate feedbacks.