Oxygen isotope composition of waters recorded in carbonates in strong clumped and oxygen isotopic disequilibrium

Paleoenvironmental reconstructions, which are mainly retrieved from oxygen isotope (δ¹⁸O) and clumped isotope (Δ₄₇) compositions of carbonate minerals, are compromised when carbonate precipitation occurs in isotopic disequilibrium. To date, knowledge of these common isotopic disequilibria, known as vital effects in biogenic carbonates, remains limited, and the potential information recorded by δ¹⁸O and Δ₄₇ offsets from isotopic equilibrium values is largely overlooked. Additionally, in carbonates formed in isotopic equilibrium, the use of the carbonate δ¹⁸O signature as a paleothermometer relies on our knowledge of the paleowaters' δ¹⁸O value, which is often assumed. Here, we report the largest Δ₄₇ offsets observed to date (as much as −0.270 ‰), measured on microbial carbonates that are strongly linked to carbonate δ¹⁸O offsets (−25 ‰) from equilibrium. These offsets are likely both related to the microorganism metabolic activity and yield identical erroneous temperature reconstructions. Unexpectedly, we show that the δ¹⁸O value of the water in which carbonates precipitated, as well as the water–carbonate δ¹⁸O fractionation dependence on temperature at equilibrium, can be retrieved from these paired δ¹⁸O and Δ₄₇ disequilibrium values measured in carbonates. The possibility to retrieve the δ¹⁸O value of paleowaters, sediments' interstitial waters or organisms' body water at the carbonate precipitation loci, even from carbonates formed in isotopic disequilibrium, opens long-awaited research avenues for both paleoenvironmental reconstructions and biomineralization studies.

1 Introduction

Oxygen isotope composition (δ¹⁸O) paired with clumped isotope composition (Δ₄₇) of carbonate minerals is increasingly used for reconstructing paleoenvironmental or diagenetic conditions (Ghosh et al., 2006; Henkes et al., 2018; Mangenot et al., 2018a, b). The δ¹⁸O of carbonates depends on both the δ¹⁸O value of the water in which the carbonate precipitated and the precipitation temperature (Urey et al., 1951). Its use to reconstruct paleoenvironments can be combined with the new carbonate C–O “clumped isotope” abundance (Δ₄₇) thermometer which depends only on the carbonate precipitation temperature (Ghosh et al., 2006). By combining the Δ₄₇-derived temperatures and the carbonate δ¹⁸O value (δ¹⁸O_carbonate), the δ¹⁸O value of the water (δ¹⁸O_water) in which the carbonate precipitated can be retrieved. However, this requires that solid carbonate and water reached isotopic equilibrium, which is often hard to prove. Conversely, carbonate precipitation in isotopic disequilibrium is commonly encountered (Affek et al., 2014; Loyd et al., 2016). Out of equilibrium, δ¹⁸O and Δ₄₇ values are particularly known to occur in biogenic carbonates (Thiagarajan et al., 2011; Bajnai et al., 2018) – the most abundant carbonates in the sedimentary record. To date, the reasons for these isotopic disequilibria in carbonates remain largely under-constrained. While Δ₄₇ compositions of carbonates seemed at first free of any biologically driven or mineral-specific fractionation known to affect δ¹⁸O_carbonate compositions (Eiler, 2011), recently identified disequilibrium Δ₄₇ values (Saenger et al., 2012; Affek, 2013; Tang et al., 2014; Burgener et al., 2018) shed new light on and help to unravel the mechanisms responsible for oxygen isotopic disequilibrium in carbonate minerals. Even though the identification of these vital effects does not prevent δ¹⁸O and Δ₄₇ tools from being powerful paleothermometers as empirical calibrations taking vital effects into account allow temperature reconstructions, it has become crucial to determine if the δ¹⁸O and Δ₄₇ disequilibria observed in carbonates as diverse as those found in coral reefs (Saenger et al., 2012), brachiopods (Bajnai et al., 2018), microbialites and methane seep carbonates (Loyd et al., 2016) along with speleothems (Affek et al., 2014) could be explained by oxygen isotope disequilibria occurring in dissolved inorganic carbon (DIC) involved in carbonate precipitation. In this case, δ¹⁸O and Δ₄₇ disequilibria in biogenic carbonates would record information, however unavailable yet, on the physiological characteristics of carbonate-forming organisms.

In previous experiments we produced microbial calcium carbonates (Millo et al., 2012; Thaler et al., 2017) that recorded the strongest oxygen isotope disequilibrium ever identified between DIC and precipitation water (i.e., −25 ‰ offset from δ¹⁸O_carbonate equilibrium values). We used carbonic anhydrase (CA), an enzyme able to accelerate oxygen isotope equilibration between DIC and water via fast CO₂ hydration and ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ dehydration. When CA was added to the precipitation water, the carbonate oxygen isotope compositions reached equilibrium with the precipitation water (Thaler et al., 2017). Here, we build on these experiments as they offer a unique opportunity to assess experimentally whether carbonates precipitated from DIC in disequilibrium with water also record Δ₄₇ disequilibrium values and the type of information that is actually carried by these paired disequilibria. We later show how and to what extent this can be applied to previously published cases of oxygen isotopic offsets from equilibrium values in both biogenic and abiotic carbonates.

2 Materials and methods

2.1 Precipitation of microbial carbonates

Carbonates were precipitated at 30±0.1 ^∘C using the procedure detailed in Millo et al. (2012) and Thaler et al. (2017) and summarized hereafter. The precipitation solution (initial pH = 6.0) was composed of ions added to Milli-Q^® water (resistivity = 18 MΩ cm) by dissolving salts in the following order: MgSO₄•7H₂O (16 mM), NaCl (80 mM), KCl (4 mM), urea (33.3 mM) and CaCl₂ (40 mM). The aim was to mimic the ionic composition of groundwater (Millo et al., 2012). In experiments with CA whose δ¹⁸O results (but not the Δ₄₇ ones) were recently published in Thaler et al. (2017), the precipitation solution was supplemented with CA at a concentration of 2 mg L⁻¹. The precipitation solution (with or without CA) was then mixed at a volumetric ratio of 1 : 1 with the ureolytic soil bacteria Sporosarcina pasteurii (Fig. 1) suspended in Milli-Q^® water, at a final optical density at 600 nm of 0.100±0.010. For this study, 16 gastight Exetainer^® vials were filled with the precipitation solution without CA in order to sacrifice them at regular time intervals (i.e., 30, 60, 120, 180 and 360 min and 24 h) and thus obtain information on the kinetics of the reaction, while reproducing the procedure followed for the experiment with CA (Thaler et al., 2017) consisting of 27 vials sacrificed every 10 to 30 min and after 24 h. The vials capped with rubber septa were filled up to the brim, i.e., without headspace, hence preventing any gaseous exchange with the atmosphere or headspace gases.

Figure 1 Scanning electron microscopy images of the bio-induced carbonates formed with CA (almost pure calcite and traces of vaterite and aragonite as determined using X-ray diffraction; Thaler et al., 2017). The fingerprints of Sporosarcina pasteurii cells are visible as black holes (a showing a cross section of carbonate) or as rods and indicated by white arrows.

Ureolysis corresponds to two types of hydrolysis: (i) the hydrolysis of urea into ammonia (NH₃) and carbamate (H₂N-COOH) (H₂N-CO-NH₂ + H₂O → NH₃ + H₂N-COOH), which is catalyzed by urease and is the rate-limiting step, and (ii) the rapid and spontaneous hydrolysis of carbamate into ammonia and CO_2(aq) (H₂N-COOH + H₂O → NH₃ + CO_2(aq) + H₂O) (Krebs and Roughton, 1948; Matsuzaki et al., 2013) or H₂CO₃ (H₂N-COOH + H₂O → NH₃ + H₂CO₃) (Mobley and Hausinger, 1989; Krajewska, 2009).

Ureolysis completion was followed by evaluating the production of dissolved inorganic nitrogen (DIN = NH₃ + ${\mathrm{NH}}_{\mathrm{4}}^{+}$). Determination of pH, DIN concentration and amount of precipitated carbonates (Fig. 2), as well as isotopic measurements, was performed for each vial to monitor their evolution as the ureolysis reaction progresses. The pH initially increased from 6.0 to 9.0 due to NH₃ production by ureolysis and consecutive alkalinization of the precipitation solution (Fig. 2a). The subsequent carbonate precipitation (Fig. 2b) lowered pH to 8.6 (without CA) and 8.4 (with CA) and was followed by a second pH increase to 8.8 (without CA) and 8.7 (with CA) when carbonate precipitation stopped while ureolysis continued. At ureolysis completion, all the calcium initially present in solution (i.e., the limiting reagent) had precipitated whereas 35 % to 45 % of the DIC produced by ureolysis remained in solution. Carbonate precipitates, formed at the bottom and on the wall of the vials, were immediately rinsed with a few drops of pure ethanol in order to dehydrate bacteria and prevent further ureolysis, carbonate formation and/or dissolution–reprecipitation processes. Ethanol was then removed, and, prior to their collection, carbonates were dried overnight at 40 ^∘C in the vials placed in a ventilated oven equipped with desiccating beads. The majority of the carbonates precipitated in this study were composed of calcite with minor amounts of aragonite (1 % to 4 %), vaterite (2 % to 4 %) and magnesian calcite with low Mg content (Mg_0.064, Ca_0.936)CO₃ (up to 8 %) (Thaler et al., 2017).

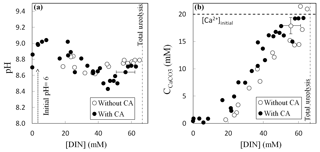
Figure 2 Evolution of pH (a) and amount of precipitated calcium carbonate $C_{{\mathrm{CaCO}}_{\mathrm{3}}}$ (b) as a function of the production of dissolved inorganic nitrogen DIN ($\mathrm{DIN}={\mathrm{NH}}_{\mathrm{3}}+{\mathrm{NH}}_{\mathrm{4}}^{+}$) by bacteria during ureolysis, without carbonic anhydrase (CA) (this study) and with CA (data from Thaler et al., 2017). Error bars account for 2 SD and are always smaller than symbols for pH values. The mineralogy of the carbonates precipitated with or without CA was determined by X-ray diffraction, indicating that solid carbonates are mostly composed of calcite (including up to 8 % of low-Mg calcite, (Mg_0.064, Ca_0.936)CO₃), vaterite (2 %–4 %) and aragonite (1 %–4 %) (Thaler et al., 2017). The influence of mineralogy on isotopic measurements and temperature estimates is discussed in the Supplement, Sect. S1.

All of the measured chemical parameters (pH, DIC, amount of solid carbonates, Ca²⁺ concentration, DIN) along with DIC and solid carbonate δ¹³C behave similarly with or without active CA (Thaler et al., 2017). It was not possible to measure Δ₄₇ for all the precipitated carbonates due to their low amount, particularly for the tubes sacrificed at the beginning of the experiments (Table S1 in the Supplement).

2.2 δ¹⁸O and Δ₄₇ measurements and associated uncertainties

All the isotopic analyses were made at Institut de physique du globe de Paris (IPGP, France). δ¹⁸O analyses were performed on carbonate powders of ca. 2 mg with a continuous-helium-flow isotope ratio mass spectrometer AP 2003 (Analytical Precision 2003, GV Instruments) coupled to a gas chromatograph column (GC-IRMS, Chrompac Column Type 99960), as described in Millo et al. (2012) and Thaler et al. (2017). External reproducibility on carbonate standards is ±0.1 ‰ (1 SD) and represents the uncertainty assigned to δ¹⁸O_carbonate data.

The analytical procedure used for clumped isotope Δ₄₇ measurements is only briefly presented here and detailed in Bonifacie et al. (2017). About 5 mg of carbonates was digested at 90 ^∘C for 20 min with 104 % phosphoric acid H₃PO₄ in a common acid bath. The produced gaseous CO₂ was purified with a manual vacuum line before introduction into a Thermo Scientific MAT 253 dual-inlet mass spectrometer. Each purified CO₂ gas was analyzed for its abundance in isotopologues with m∕z from 44 to 49 versus a working gas provided by Oztech Trading Corporation with ${\mathit{\delta }}^{\mathrm{13}}\mathrm{C}=-\mathrm{3.71}$ ‰ Vienna Pee Dee Belemnite (VPDB) and ${\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=+\mathrm{24.67}$ ‰ Vienna Standard Mean Ocean Water (VSMOW), as determined with the international reference material NBS19. One single Δ₄₇ measurement corresponds to 70 cycles of 26 s integration time each (total integration time = 1820 s). Conventional δ¹⁸O and δ¹³C data were also acquired simultaneously with Δ₄₇ measurements with this instrument (Tables S1 and S2). They are in excellent consistency with data obtained with the continuous-flow method on smaller samples (Table S1).

The Δ₄₇ is calculated as a function of the stochastic distribution of the CO₂ isotopologues, as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathrm{\Delta }}_{\mathrm{47}}& =\left[\left({\displaystyle \frac{R_{\mathrm{measured}}^{\mathrm{47}}}{R_{\mathrm{stochastic}}^{\mathrm{47}}}}-\mathrm{1}\right)-\left({\displaystyle \frac{R_{\mathrm{measured}}^{\mathrm{46}}}{R_{\mathrm{stochastic}}^{\mathrm{46}}}}-\mathrm{1}\right)\right.\\ & \left.-\left({\displaystyle \frac{R_{\mathrm{measured}}^{\mathrm{45}}}{R_{\mathrm{stochastic}}^{\mathrm{45}}}}-\mathrm{1}\right)\right]\times \mathrm{1000},\end{array}\end{array}$$

where Δ₄₇ is expressed in per mill (‰), and R⁴⁷, R⁴⁶ and R⁴⁵ are the abundance ratios of the masses 47, 46 and 45, respectively, relative to the mass 44 (¹²C¹⁶O¹⁶O). $R_{\mathrm{measured}}^X$ denotes measured ratios of the CO₂ sample. $R_{\mathrm{stochastic}}^X$ values are calculated from the measured 44, 45, 46 and 47 abundance ratios. The number of isotopologues of mass 47 (mainly ¹³C¹⁸O¹⁶O, but also ¹²C¹⁷O¹⁶O and ¹³C¹⁷O¹⁷O) measured within the CO₂ sample extracted from the acid digestion of the carbonates is linked to the number of isotopologues of mass 63 (mainly ¹³C¹⁸O¹⁶O¹⁶O) within the reacted carbonate mineral (Guo et al., 2009). For the correction from ¹⁷O interferences, we used the ¹⁷O correction parameters from Brand et al. (2010), as recently recommended (Daëron et al., 2016; Schauer et al., 2016). In order to transfer the obtained raw Δ₄₇ data into the absolute carbon dioxide equilibrium scale “CDES” (Δ_47 CDES90 being the Δ₄₇ values of carbonates reacted within acid at 90 ^∘C), standards of CO₂ gases equilibrated at 25 and 1000 ^∘C and with bulk isotopic compositions covering the range of measured carbonate samples (δ⁴⁷ values between −50 ‰ and +24 ‰) were analyzed interspaced with unknown samples (typically 15 equilibrated CO₂ gas analyses by discrete session of analysis, four analytical sessions in total; Table S5). For each analytical session, as recommended in Dennis et al. (2011), the Δ₄₇ data were finally corrected with a fixed equilibrated gas line slope (only slightly varying from 0.0048 to 0.0062 over our analytical sessions) and an empirical transfer function (slopes varying from 1.0859 to 1.1344) based on the equilibrated CO₂ standards. Finally, the accuracy of our whole dataset and processing procedure was validated on carbonate reference material (i.e., IPGP-Carrara and 102-GC-AZ01), typically analyzed every two unknown samples (Table S5). The Δ₄₇ values obtained at IPGP over the course of this study are ${\mathrm{\Delta }}_{\mathrm{47}\mathrm{CDES}\mathrm{90}}=\mathrm{0.316}\pm \mathrm{0.020}$ ‰ (1 SD, n=16) for IPGP-Carrara and ${\mathrm{\Delta }}_{\mathrm{47}\mathrm{CDES}\mathrm{90}}=\mathrm{0.620}\pm \mathrm{0.010}$ ‰ (1 SD, n=18) for 102-GC-AZ01. Those values are indistinguishable from the values obtained at IPGP over 4 years of analyses on the same instrument (n>300) or previously reported by other laboratories (Daëron et al., 2016).

2.3 Temperature estimates and associated uncertainties

Apparent temperatures obtained from oxygen isotope compositions were calculated based on the measured δ¹⁸O_carbonate values of both the precipitated carbonate and the precipitation water in each experimental vial (Table S1) and using the equation of oxygen isotopes' fractionation between calcite and water from Kim and O'Neil (1997). Apparent temperatures issued from clumped isotope compositions were calculated from Δ_47 CDES90 data using the composite universal Δ₄₇–T calibration (Eq. 3 from Bonifacie et al., 2017, with T, the temperature). It is noteworthy that our main observations and conclusions do not change if other calibrations to temperature are used for δ¹⁸O and/or Δ₄₇ (e.g., Coplen, 2007; Kelson et al., 2017) (see also Table S3). For both proxies, the uncertainties on temperature estimates reported here correspond to the standard deviation of the mean of replicated isotopic measurements of the same powder propagated in the calibration equation (but the actual errors on the calibration themselves are not considered). Note that the long-term external reproducibility on homogeneous calcite reference materials found in this study (i.e., ±0.020 ‰, 1 SD) is used for samples with only one measurement or with 1 SD lower than 0.020 ‰ (Tables S1 and S5, Sect. S1 in the Supplement).

For the temperature (T) derived from the Δ₄₇ data, we chose the calibration determined by Bonifacie et al. (2017) as it integrates a consequent number of data (n>300), whose statistical weight has been properly considered and covers a wide temperature range (from 1 to 350 ^∘C), three characteristics that were recently shown by several teams as governing the precision on Δ₄₇–T calibration equations (Bonifacie et al., 2017; Kelson et al., 2017; Fernandez et al., 2017). Importantly, this calibration covers the high apparent temperature ranges reported here (i.e., low Δ₄₇ values) allowing us to avoid loss of precision and accuracy when extrapolating to temperature ranges that have not been experimentally investigated. Finally the Bonifacie et al. (2017) calibration has been checked independently with other methods (Mangenot et al., 2017; Dassié et al., 2018) on the range of temperatures (∼30 to 96 ^∘C) where most available calibrations diverge and/or are not well constrained. Indeed, these studies report excellent consistencies: (i) between TΔ₄₇ and homogenization temperatures from fluid inclusion microthermometry (Mangenot et al., 2017) and (ii) between the δ¹⁸O_water values directly measured in fluid inclusions by cavity ring-down spectroscopy and those calculated from combined TΔ₄₇ and δ¹⁸O_carbonate of the host mineral (Dassié et al., 2018). Though we recognize that the normalization to carbonate standards presented in Bernasconi et al. (2018) might become commonly used by the community in the future (i.e., with the ongoing intercomparison InterCarb project), we preferred not to use this correction frame here because not enough of the four carbonate standards proposed by Bernasconi et al. (2018) were run together with our samples (n=14 runs in total of ETH1, ETH2, ETH3 and ETH4 standards; Table S5), and such a normalization method will then introduce larger uncertainty than the normalization we performed with the large number of equilibrated gases ran daily together with our unknowns (n=104 equilibrated gas; Table S5 – note also 33 secondary carbonate standards 102-GC-AZ01 and IPGP-Cararra, also run in other IPGP studies and some other laboratories). Also remarkably, Δ₄₇ values obtained here on the four ETH carbonate standards are all systematically higher than values reported in Bernasconi et al. (2018) (Table S4). Though the reason for this positive offset is still unclear, it is noteworthy that positive offsets are also observed when compiling other recent published values (Table S4; Daëron et al., 2016; Schauer et al., 2016; Fiebig et al., 2019).

3 Results and discussion

3.1 Δ₄₇ and δ¹⁸O compositions of microbial carbonates can present strongly correlated vital effects

We performed Δ₄₇ measurements on (i) microbial carbonates precipitated without CA by faithfully replicating the experiment detailed in Thaler et al. (2017) and (ii) microbial carbonates precipitated in the presence of CA remaining from these experiments. These calcium carbonates were precipitated as the result of microbially driven hydrolysis of urea into DIC and ammonia (Millo et al., 2012). They constitute a reliable model for carbonate precipitation triggered by enzymatic production or transport of DIC, as is the case for micro- and macro-skeletal carbonates common in the Phanerozoic and for microbially mediated carbonates since the Precambrian.

Without CA, the isotopic values of the very first carbonate precipitates present strong isotopic offsets from equilibrium values. The Δ₄₇ offset to equilibrium starts from −0.270 ‰ (the largest Δ₄₇ offset ever measured in solid carbonates), and the offset to equilibrium reaches −24.7 ‰ for δ¹⁸O_carbonate (Fig. 3 and Table S1). Both Δ₄₇ and δ¹⁸O_carbonate absolute values then increase as ureolysis progresses, reducing offsets from equilibrium values to −0.179 ‰ for Δ₄₇ and −15.7 ‰ for δ¹⁸O_carbonate. In the presence of CA, the trends observed for the Δ₄₇ and δ¹⁸O_carbonate values are similar, but the offsets from equilibrium are drastically reduced (down to −0.027 ‰ for Δ₄₇ and −1.4 ‰ for δ¹⁸O_carbonate at the end of the experiment; Fig. 3), hence attesting for ongoing isotopic equilibration of DIC with water by CA enzymatic activity prior to and during carbonate precipitation. The comparable behavior of Δ₄₇ and δ¹⁸O_carbonate values with respect to CA suggests that both disequilibria are inherited from the δ¹⁸O and Δ₄₇ signatures of the DIC generated by the biological activity.

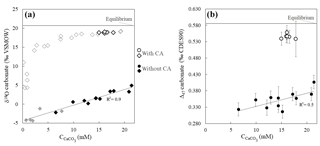
Figure 3 Strong δ¹⁸O and Δ₄₇ disequilibria recorded in microbial carbonates as shown by δ¹⁸O_carbonate (a) and Δ₄₇ (b) values of calcium carbonates (CaCO₃) precipitated during bacterial ureolysis at 30 ^∘C (with and without carbonic anhydrase, CA; open and solid symbols, respectively) as a function of carbonate accumulation ($C_{{\mathrm{CaCO}}_{\mathrm{3}}}$). Black symbols correspond to samples for which both Δ₄₇ and δ¹⁸O measurements were performed. The grey horizontal lines are equilibrium δ¹⁸O_carbonate and Δ₄₇ values at 30 ^∘C for calcite following Bonifacie et al. (2017) and Kim and O'Neil (1997) calibrations, respectively. Uncertainties (1 standard deviation, 1 SD) are smaller than the symbol for δ¹⁸O and $C_{{\mathrm{CaCO}}_{\mathrm{3}}}$ values (Table S1). Reported Δ₄₇ uncertainties are detailed in Sect. 2 and Sect. S1 in the Supplement.

3.2 Δ₄₇ and δ¹⁸O_carbonate disequilibrium originates from the metabolic production of DIC

Here, we discuss the potential processes known to generate δ¹⁸O and Δ₄₇ isotope fractionations during carbonate precipitation and we identify the main mechanism explaining our paired Δ₄₇ and δ¹⁸O_carbonate disequilibria. The relatively high precipitation rate (R) in our experiments ($\log R=-\mathrm{3.95}$ mol m⁻² s⁻¹; Thaler et al., 2017) can only account for an oxygen kinetic isotope fractionation (KIF) of about 1 ‰ to 2 ‰ for δ¹⁸O values (Watkins et al., 2013), while the oxygen isotope disequilibrium recorded in our carbonates reaches −24.7 ‰. Degassing of CO₂, known to fractionate DIC oxygen isotopes (Affek and Zaarur, 2014), can be ruled out as there is no gas phase in our experiments (see Sect. 2.1). Any potential kinetic fractionation due to DIC diffusion (Thiagarajan et al., 2011) is also unlikely as precipitation occurred on the bacterial DIC-producing cells, as highlighted by scanning electron microscopy showing bacterial cells trapped within and at the surface of carbonate crystals (Fig. 1). Accordingly, the large offsets from equilibrium values observed for both Δ₄₇ and δ¹⁸O in our microbial carbonates can only result from (i) a KIF induced by CO₂ hydration or hydroxylation into ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ (but only if ureolysis produces CO₂ rather than H₂CO₃, which has not been established yet; Matsuzaki et al., 2013) or (ii) a metabolic isotopic signature of the DIC produced by the bacteria, inherited from the initial isotopic composition of urea and/or due to a KIF introduced by the urease enzyme. CO₂ hydration and hydroxylation lead to the formation of ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, with two oxygen atoms coming from CO₂ and the third one from H₂O (hydration) or OH⁻ (hydroxylation). The δ¹⁸O${}_{{\mathrm{HCO}}_{\mathrm{3}}^{-}}$ value can then be estimated using a simple mass balance calculation (Létolle et al., 1990; Usdowski et al., 1991). The newly formed ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ is depleted in ¹⁸O compared to the reacting CO₂ because of the incorporation of oxygen coming from H₂O or OH⁻, both depleted in ¹⁸O relative to ¹⁶O in contrast to CO₂ (Green and Taube, 1963; Beck et al., 2005). Such a low δ¹⁸O${}_{{\mathrm{HCO}}_{\mathrm{3}}^{-}}$ value, several per mill lower than the equilibrium one, can then be preserved in the calcium carbonate if precipitation occurs shortly after CO₂ hydration and hydroxylation and before the full equilibration with water (Rollion-Bard et al., 2003). Regarding clumped isotopes, ab initio calculations predict that the fractionation associated with CO₂ hydration and hydroxylation increases the relative abundance of ¹³C–¹⁸O bonds and thus the Δ₄₇ value (Guo, 2009). Even though this predicted fractionation trend has previously been used to explain several datasets for which CO₂ hydroxylation was assumed to occur prior to carbonate precipitation (Tripati et al., 2015; Spooner et al., 2016), such a tendency can only be validated using data acquired on carbonates for which CO₂ hydration and hydroxylation are demonstrated. This is the case of (i) hyperalkaline travertines (Falk et al., 2016) even though part of the reported kinetic isotope fractionation can be interpreted as resulting from the CO₂ dissolution process (Clark et al., 1992) and (ii) two experimental samples (Tang et al., 2014) precipitated at high pH where CO₂ hydroxylation dominates. Both studies show, in agreement with the ab initio calculations (Guo, 2009), higher Δ₄₇ and lower δ¹⁸O_carbonate values compared to equilibrium. Thus, in a case where ureolysis would produce CO₂ in isotopic equilibrium with water, the Δ₄₇ values affected by CO₂ hydration and hydroxylation recorded in calcium carbonates should be higher than the equilibrium value, while our microbial carbonates show Δ₄₇ values lower than equilibrium. Thus, we conclude that our low Δ₄₇ values measured in carbonates can only be explained by a metabolic source effect. In our case it corresponds to the ureolytic production of DIC, either directly as H₂CO₃ or as CO₂, with a Δ₄₇ value low enough to compensate for any potentially succeeding increase due to the KIF associated with CO₂ hydration and hydroxylation. Nonetheless, the slow but continuous increase observed in our experiment without CA for both Δ₄₇ and δ¹⁸O_carbonate values more likely reflects ongoing equilibration of DIC oxygen isotopes with water at a slow rate.

Our results highlight that the isotope clumping proceeds continuously as C–O bonds are breaking and reforming in the DIC, allowing oxygen isotopes (¹⁶O, ¹⁷O and ¹⁸O) to be redistributed between H₂O, OH⁻, H₂CO₃, ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ species via ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{OH}}^{-}$ attachment to CO₂ and detachment from ${\mathrm{HCO}}_{\mathrm{3}}^{-}$. In the experiment with CA, both Δ₄₇ and δ¹⁸O_carbonate simultaneously reach values close to equilibrium, and without CA both Δ₄₇ and δ¹⁸O_carbonate values increase simultaneously. This coevolution corroborates former observations of comparable kinetics for clumped isotopes and δ¹⁸O equilibration between DIC and water or CO₂ and water once δ¹³C is equilibrated (Affek, 2013; Clog et al., 2015). This principle has been used to correct for the disequilibrium fractionation factor in speleothems (Affek et al., 2008).

3.3 Erroneous yet comparable temperatures reconstructed from disequilibrium Δ₄₇ and δ¹⁸O values in carbonates

Apparent temperatures were calculated from disequilibrium Δ₄₇ values obtained in the experiment without CA using the calibration of Bonifacie et al. (2017). Ranging from 198±21 to 115±8 ^∘C (Fig. 4), they are at odds with the actual precipitation temperature of 30±1 ^∘C (see Sect. 2.1). This shows that when carbonates precipitate from DIC in oxygen isotope disequilibrium with water, the abundance of ¹³C–¹⁸O bonds in carbonates does not correlate with precipitation water temperature. Conversely, the temperatures reconstructed from the Δ₄₇ values of carbonates precipitated in the presence of CA, ranging from 47±6 to 39±2 ^∘C, are much closer to the actual precipitation temperature. Interestingly, the apparent temperatures reconstructed using Kim and O'Neil (1997) calibration from the δ¹⁸O_carbonate and δ¹⁸O_water values of the same samples show comparable offsets from the actual temperature in both experiments without CA (from 218±2 to 139±1 ^∘C) and with CA (from 39±1 to 37±1 ^∘C) (Fig. 4). Practically, this implies that similar temperatures calculated from both carbonate Δ₄₇ and δ¹⁸O_carbonate values (in a case where the precipitation water δ¹⁸O can be determined) can neither constitute evidence against O isotope disequilibrium nor confirm that this is the true precipitation temperature.

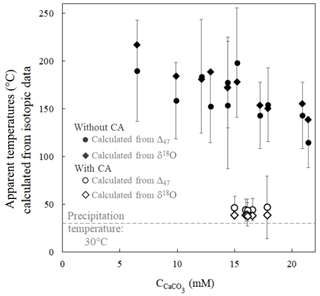
Figure 4 δ¹⁸O_carbonate and Δ₄₇ disequilibria in microbial carbonates induce comparable biased estimates of precipitation temperature as illustrated by apparent temperatures calculated from the carbonate δ¹⁸O_carbonate and Δ₄₇ signatures as a function of CaCO₃ accumulation. Open and solid symbols refer to the experiments with and without CA, respectively. The dashed grey line corresponds to the actual precipitation temperature. Apparent temperatures are respectively calculated from the δ¹⁸O_carbonate and Δ₄₇ calibrations to the temperature of Kim and O'Neil (1997) and Bonifacie et al. (2017). Reported uncertainties were calculated as the propagation of the 1 standard deviation (1 SD) error of the isotopic data in the calibration equations (Sect. 2 and Sect. S1 in the Supplement).

3.4 Δ₄₇ and δ¹⁸O_carbonate paired disequilibria record the δ¹⁸O of the water in which the carbonates precipitated

The fact that both Δ₄₇ and δ¹⁸O_carbonate values permit us to calculate similarly evolving apparent temperatures along the (dis)equilibration profile recorded in carbonates as the experiment proceeds indicates that the δ¹⁸O_carbonate, δ¹⁸O_water, Δ₄₇ and apparent temperature values are all together linked. In a diagram of Δ₄₇ versus δ¹⁸O_carbonate, all of our data align, irrespectively of the fact that they are in strong isotopic disequilibrium or close to equilibrium (Fig. 5). Their alignment is fitted with what would be expected for equilibrium Δ₄₇ and δ¹⁸O_carbonate values of calcite precipitated at various temperatures from water at a given δ¹⁸O_water value. This δ¹⁸O_water value can be calculated by combining, for the same temperature, the equations of Δ₄₇ and δ¹⁸O_carbonate temperature calibrations from Bonifacie et al. (2017) and Kim and O'Neil (1997), respectively (Eq. 2):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{water}}& =\exp \lfloor -{\displaystyle \frac{\mathrm{18.03}}{\sqrt{\frac{\mathrm{0.0422}\times {\mathrm{10}}^{\mathrm{6}}}{{\mathrm{\Delta }}_{\mathrm{47}\mathrm{CDES}\mathrm{90}}-\mathrm{0.1126}}}}}+\mathrm{32.42}\times {\mathrm{10}}^{-\mathrm{3}}\\ & +\ln ({{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{carbonate}}+\mathrm{1000})\rfloor -\mathrm{1000},\end{array}\end{array}$$

with δ¹⁸O_water and δ¹⁸O_carbonate values in the same isotopic reference (here VSMOW) and Δ₄₇ values reported on the absolute carbon dioxide equilibrated scale (Δ_47 CDES90). The calibration of Kim and O'Neil (1997) was preferred over more recent calibration equations (e.g., Watkins et al., 2013) because it provides the best consistency for temperatures reconstructed from both the carbonate δ¹⁸O and Δ₄₇ values at temperatures above 100 ^∘C. Note that Kim and O'Neil (1997) and Bonifacie et al. (2017) calibrations were developed independently, which prevents circular reasoning. Finally, as the calibration of Kim and O'Neil (1997) is the most used calcite calibration to date, it also allows for a broader comparison with previously published results.

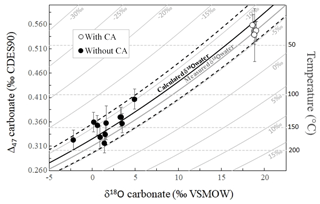
Figure 5 Combined δ¹⁸O_carbonate and Δ₄₇ disequilibria of microbial carbonates precipitated at 30 ^∘C allow reconstruction of the δ¹⁸O of the water (δ¹⁸O_water) in which they precipitate. Solid grey curves represent the calculated Δ₄₇ and δ¹⁸O_carbonate compositions of carbonates precipitated at oxygen isotope equilibrium from water with fixed δ¹⁸O_water values (indicated on each curve) and variable temperatures. Horizontal dashed grey lines are calculated for fixed temperatures and variable δ¹⁸O_water. The average δ¹⁸O_water value of $-\mathrm{6.6}\pm \mathrm{0.4}$ ‰ measured in our experiments is reported using the thick solid grey curve. The solid black curve was obtained using the δ¹⁸O_water calculated with Eq. (2) ($-\mathrm{8.0}\pm \mathrm{2.8}$ ‰) with its associated errors (dashed black curves).

Despite the fact that the data present a large range of offsets from equilibrium (Fig. 5), the mean δ¹⁸O_water value calculated using Eq. (2) for each combination of Δ₄₇ and δ¹⁸O_carbonate values measured for our carbonates is $-\mathrm{8.0}\pm \mathrm{2.8}$ ‰ (1 SD), indistinguishable (i.e., within errors) from the δ¹⁸O_water values measured in our experiments ($-\mathrm{6.4}\pm \mathrm{0.2}$ ‰ with CA and $-\mathrm{6.8}\pm \mathrm{0.2}$ ‰ without CA; Fig. 5). Note that such precision in δ¹⁸O_water values found in disequilibrium carbonates is remarkable considering that even for equilibrium carbonates at isotopic equilibrium for both δ¹³C and δ¹⁸O, δ¹⁸O_water can only be retrieved from paired Δ₄₇ and δ¹⁸O_carbonate values with a precision of ±1 ‰ at best (see Fig. S1 in the Supplement). This creates the promising opportunity to retrieve the δ¹⁸O value of the water in which carbonates precipitated out of equilibrium for both δ¹⁸O_carbonate and Δ₄₇.

In order to evaluate the applicability of such an approach to other types of carbonates, Fig. 6 compiles disequilibrium paired δ¹⁸O_carbonate and Δ₄₇ data from two previously published experimental studies (Tang et al., 2014; Staudigel and Swart, 2018). These studies were chosen to further evaluate the relevancy of our δ¹⁸O_carbonate–Δ₄₇ correlation because they are the only published dataset reporting full sets of measured (rather than calculated) δ¹⁸O_water, δ¹⁸O_carbonate and Δ₄₇ values, with one or both proxies showing disequilibrium, together with precipitation temperatures. A perfect knowledge (i.e., measurements and not estimates) of these four parameters is mandatory here to adequately test whether the use of our new δ¹⁸O_water proxy could be generalized to a large diversity of carbonates. This thus precludes plotting most published Δ₄₇ studies on both natural and experimental samples, in which δ¹⁸O_water and/or temperature were not directly measured, in Fig. 6. These two datasets are also recent enough to allow the conversion of their Δ₄₇ values to the currently used normalization method (i.e., the CDES absolute reference frame). It will then allow comparison with future studies, if measuring and reporting all these four parameters together becomes the rule rather than the exception in Δ₄₇ studies.

Figure 6a shows paired δ¹⁸O_carbonate and Δ₄₇ values of abiotic carbonates produced at 5, 25 and 40 ^∘C that are known to be affected by KIF due to fast precipitation and for at least two of them by KIF due to CO₂ hydration and hydroxylation prior to precipitation (Tang et al., 2014). Except for these two carbonate samples, the data align on a covariation curve of Δ₄₇ versus δ¹⁸O_carbonate that cannot be explained solely by temperature variation. As for our microbial carbonates obtained with or without CA, the average calculated δ¹⁸O_water (Eq. 2; $-\mathrm{11.2}\pm \mathrm{1.5}$ ‰) matches within error with the measured δ¹⁸O_water ($-\mathrm{9.6}\pm \mathrm{0.2}$ ‰) (Dietzel et al., 2009).

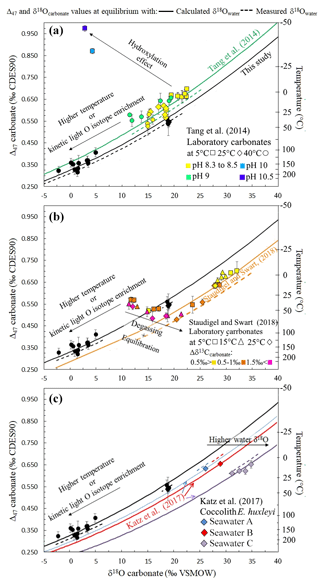
Figure 6 Δ₄₇ and δ¹⁸O_carbonate relationship to precipitation water δ¹⁸O_water for other solid carbonates presenting oxygen isotope disequilibria. In (a) to (c) the black data series (this study, performed at 30 ^∘C) shows how kinetic oxygen isotope fractionation in the DIC prior to carbonate precipitation can be mistaken for high-temperature isotopic equilibrium. Similarly to Fig. 5, the solid curves were obtained using the δ¹⁸O_water calculated with Eq. (2). (a) Abiotic carbonates from Tang et al. (2014) illustrating the effect of CO₂ hydroxylation on Δ₄₇ and δ¹⁸O_carbonate values (various pH values plotted with different colors, various temperatures plotted with different symbols). (b) Abiotic carbonates from Staudigel and Swart (2018) illustrating the effect of CO₂ degassing and DIC oxygen isotope equilibration with water on Δ₄₇ and δ¹⁸O_carbonate values. Δδ¹³C_carbonate stands for the difference between the δ¹³C value measured in carbonates and the final δ¹³C of the data series at the end of equilibration (various Δδ¹³C ranges plotted with different colors, various temperatures plotted with different symbols). (c) Coccolithophorid E. huxleyi grown at 7, 10, 15, 20 and 25 ^∘C from Katz et al. (2017) showing how coccoliths with equilibrium Δ₄₇ values record the equilibrium δ¹⁸O_water of their body water, which differs from that of the culture medium (i.e., artificial seawaters A, B and C plotted with different colors).

Figure 6b shows paired δ¹⁸O_carbonate and Δ₄₇ values of abiotic carbonates that were precipitated during an initial CO₂ degassing + DIC equilibration phase followed by solely equilibration with water at 5, 15 and 25 ^∘C (Staudigel and Swart, 2018). During the latter equilibration phase, even though the carbonates precipitated out of isotopic equilibrium, the paired δ¹⁸O_carbonate and Δ₄₇ values align on a covariation curve of the average calculated δ¹⁸O_water value (Eq. 2; $-\mathrm{3.0}\pm \mathrm{1.1}$ ‰) close to the measured δ¹⁸O_water (−0.65 ‰). As a major outcome of this study, we thus anticipate that reliable δ¹⁸O_water values of precipitation water can be retrieved from carbonates presenting Δ₄₇ and δ¹⁸O_carbonate values in strong disequilibrium.

Some data presented in Fig. 6 also permit us to evaluate the conditions of applicability of our approach. In Fig. 6a, the two data points deviating from the covariation curve of Δ₄₇ versus δ¹⁸O_carbonate correspond to carbonates precipitated at pH ∼10 and 5 ^∘C (while the others formed at pH and temperatures ranging from 8.3 to 9 and 5 to 40 ^∘C, respectively) that have recorded a KIF due to CO₂ hydration and hydroxylation prior to precipitation (Tang et al., 2014). At pH = 10, CO₂ reacts at 95 % with OH⁻, and at 5 ^∘C DIC isotopic equilibration with water takes days. To a lesser extent, the KIF induced by CO₂ hydroxylation also seems visible at pH = 9 (and 40 ^∘C), where CO₂ reacts at 82 % with OH⁻, but DIC isotopic equilibration with water at 40 ^∘C only takes about 15 h. As previously detailed, the direction of these isotopic offsets from equilibrium is compatible with ab initio calculations (Guo, 2009) and can be intuitively understood as follows: in carbonates derived from CO₂ hydroxylation, the $R_{\mathrm{stochastic}}^X$term used for the Δ₄₇ calculation (Eq. 1) should be strongly modified as the ¹⁸O concentration in OH⁻ and H₂O is lower than in CO₂, and the reaction does not add more ¹³C than what is present in CO₂. This might explain why in the case of disequilibria acquired through CO₂ hydroxylation, the correlation between paired δ¹⁸O and Δ₄₇ disequilibria and the precipitation water δ¹⁸O is not preserved, and δ¹⁸O_water cannot be reconstructed by the approach proposed here. The negative slope associated with this KIF on the Δ₄₇ and δ¹⁸O_carbonate diagram (Fig. 6a) is nevertheless a good tool to identify CO₂ hydroxylation reactions.

In Fig. 6b, during the CO₂ degassing phase of the precipitation experiment (Staudigel and Swart, 2018), the data also deviate from the covariation curve of δ¹⁸O versus Δ₄₇. This behavior was interpreted by the authors as a decoupling between Δ₄₇ and δ¹⁸O_carbonate values due to variable kinetics of ¹²C–O and ¹³C–O bonding. A known difference in equilibration kinetics takes place between C and O isotopes in the carbonate system as carbon isotopes equilibrate in seconds, while oxygen isotopes necessitate minutes to hours to equilibrate among the different oxygen-bearing species (i.e., CO₂, ${\mathrm{HCO}}_{\mathrm{3}}^{-}$, ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$, H₂O, OH⁻), depending on the pH, temperature and salinity of the solution (Zeebe and Wolf-Gladrow, 2001). However, note that in that experiment, the carbon isotope compositions evolved for several hours as a result of CO₂ degassing (Staudigel and Swart, 2018). We propose here that CO₂ degassing, because it affects both C and O isotopes, modifies the $R_{\mathrm{stochastic}}^X$ term (in Eq. 1), thus preventing Δ₄₇ and δ¹⁸O from varying with the proportionality that allows us to retrieve the δ¹⁸O_water value on a covariation plot of Δ₄₇ versus δ¹⁸O. Hence, as for CO₂ hydroxylation, in the case of a KIF induced by CO₂ degassing, δ¹⁸O_water cannot be reconstructed exclusively from disequilibrium δ¹⁸O_carbonate and Δ₄₇ values.

In summary, we conclude that mechanisms that can drastically change the $R_{\mathrm{stochastic}}^X$term in Δ₄₇ calculation (such as CO₂ hydroxylation and degassing) prevent δ¹⁸O_water reconstructions from paired disequilibrium Δ₄₇ and δ¹⁸O_carbonate values. Nevertheless, these mechanisms lead to peculiar types of carbonates (e.g., speleothems that form in caves from CO₂ degassing, and travertine that forms on lands where fluids and gas escape from subsurface reservoirs, for CO₂ hydroxylation) that represent only a small fraction of all the carbonates existing on Earth. We hypothesize that ureolysis, which consists in two successive steps of urea hydrolysis, an exchange reaction with the H₂O molecule from the aqueous medium, might give a DIC whose $R_{\mathrm{stochastic}}^X$ term in the Δ₄₇ calculation is already close to that of DIC under equilibration with the δ¹⁸O_water. This would explain why even our most extreme out-of-equilibrium carbonates still fall close to the covariation line of Δ₄₇ versus δ¹⁸O_carbonate corresponding to the real δ¹⁸O_water value.

3.5 Toward a better understanding of body water δ¹⁸O in biomineralizing organisms

The ability to reconstruct precipitation water δ¹⁸O_water from disequilibrium Δ₄₇ and δ¹⁸O_carbonate values further allows us to examine the origin of the vital effect observed in organisms for which (i) CO₂ degassing and hydration and hydroxylation KIF can be ruled out, and (ii) only small δ¹³C variations are observed, thus preserving the $R_{\mathrm{stochastic}}^X$ term in Δ₄₇ calculation. We hypothesize that such an approach could help to understand how Δ₄₇ and δ¹⁸O signals are affected by kinetic effects in most of the biogenic carbonates, provided that CO₂ hydroxylation or degassing does not occur prior to carbonate precipitation. This approach could thus be applied to the vast majority of sedimentary carbonates (Milliman, 1993) (i.e., microbialites, brachiopods, bryozoans, bivalves, foraminifera, coccoliths) and since deep time, even when δ¹⁸O_carbonate variations occur in the shell of the organism. Additionally, the data presented here stand as an experimental demonstration that the mechanisms controlling carbonate δ¹⁸O equilibration with water (i.e., DIC equilibration with water) also control solid carbonate Δ₄₇ equilibrium (Watkins and Hunt, 2015). This result can be used to recover information on biomineralization mechanisms. For example, in recent coccolithophorid Emiliania huxleyi culture experiments, the calcitic shell produced by the organism systematically yields a 2 ‰ positive δ¹⁸O offset from equilibrium values while its Δ₄₇ values seem to faithfully record precipitation temperature (Katz et al., 2017). These coccolithophorids were grown in waters with different δ¹⁸O_water compositions (i.e., measured at −6.14 ‰, −5.82 ‰ and 0.65 ‰ VSMOW that are respectively seawater A, B and C in Fig. 6c). Based on our results, which demonstrate that no δ¹⁸O disequilibrium should be recorded in solid carbonates if the associated Δ₄₇ is at equilibrium, we can assume that the coccoliths precipitated at oxygen isotope equilibrium. We also calculate the actual δ¹⁸O value of the water in which precipitation took place from Eq. (2) (respectively shifted by 1.0±0.2 ‰, 2.1±0.4 ‰ and 1.1±0.7 ‰ towards more positive values compared to the δ¹⁸O_water value measured for the culture medium water; Fig. 6c). This could reflect a biologically driven difference between the δ¹⁸O of body water at the precipitation site inside E. huxleyi and the δ¹⁸O of ambient water (i.e., the culture medium water). This hypothesis is supported by what is known about intracellular precipitation of coccoliths performed by coccolithophorids: each coccolith forms from the accumulation of coccolithosomes, which are vesicles containing up to approximately twelve 7 nm spherical calcium-rich granular units (Outka and Williams, 1971). Water in these ∼100 nm vesicles can be considered a finite reservoir whose isotopic composition could be modified through isotopic exchange with DIC affected by metabolic isotope fractionation. Another mechanism that could increase the δ¹⁸O value of a finite water reservoir by equilibrating it with a comparable reservoir of DIC would be the introduction of DIC systematically as CO₂. As ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ are enriched in ¹⁶O in comparison to CO₂, the CO₂ conversion to ${\mathrm{HCO}}_{\mathrm{3}}^{-}$ and ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ at equilibrium before precipitation would pump ¹⁶O from water.

In both case scenarios, a local change in water isotopic composition requires that the water molecules' turnover (i.e., external inputs) in these cellular organites is slow enough. Coccolithosomes are subunits of the Golgi complex, which is a system of flat stacked vesicles concentrating a lot of membranes in a small location (Outka and Williams, 1971). It is thus plausible that in a single-celled organism, living in seawater and performing intracellular biomineralization, specific osmolarity and water circulation regulation mechanisms are occurring. It is particularly plausible in the Golgi complex, whose water content is isolated from seawater by several membranes. We thus suggest that inside coccolithosomes, coccolith precursors precipitate in equilibrium with the body water for oxygen isotopes but that the body water has a different δ¹⁸O value than the seawater, which explains the observed δ¹⁸O apparent fractionation while the Δ₄₇ composition reflects culture temperature (Katz et al., 2017). It has already been highlighted through geochemical analysis of coccoliths that coccolithosome water has altered pH (Liu et al., 2018) and ion concentrations (Hermoso et al., 2017) in comparison to seawater. We hypothesize that the internal δ¹⁸O water would thus be another parameter controlled by the coccolithophore algae.

3.6 Ubiquity of the observed δ¹⁸O_carbonate–δ¹⁸O_water–Δ₄₇–temperature covariations in both equilibrium and disequilibrium carbonates

As shown above (Fig. 5), in a diagram of Δ₄₇ versus δ¹⁸O_carbonate, disequilibrium carbonates precipitated at fixed temperature plot on the theoretical line of equilibrium carbonates precipitated with a similar δ¹⁸O_water but at a different temperature. This is illustrated in Fig. 7 where the three disequilibrium data series studied in this paper (Fig. 5 for this study and Fig. 6a and b for datasets from Tang et al., 2014, and Staudigel and Swart, 2018) align with equilibrium data series. In other words, the values of the disequilibrium 1000ln α_{carbonate−water} for oxygen isotopes (with $\mathit{\alpha }=\frac{{{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{carbonate}}+\mathrm{1000}}{{{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}}_{\mathrm{water}}+\mathrm{1000}}$) are similar to the equilibrium 1000ln α_{carbonate-water} for any given, and independently determined, apparent Δ₄₇ temperature (Fig. 7). In detail, our closest-to-equilibrium data recording low apparent temperatures match better with the predicted equations from Coplen (2007) and Watkins et al. (2013), recently updated (Daëron et al., 2019). This last calibration is based on carbonates from two caves where calcite precipitates extremely slowly and is thus assumed to have precipitated at equilibrium. Note that the use of these two cave samples for determining the dependence on temperature of the equilibrium 1000ln α_{carbonate-water} relies on the assumption that constant environmental conditions, including temperature in the two caves (7.9 and 33.7 ^∘C) and the δ¹⁸O_water value of the precipitation water, prevailed over the whole period of carbonate precipitation (Coplen, 2007; Kluge et al., 2014). In Fig. 7, the disequilibrium data recording high apparent temperatures (above 100 ^∘C) match better with the predicted equation of Kim and O'Neil (1997). This 1000ln α_{carbonate-water} dependence on temperature was established on carbonates precipitated in the laboratory at well-known δ¹⁸O_water and temperatures (from 10 to 40 ^∘C) but was suspected to present a small KIF due to a high precipitation rate that lowers the value of the 1000ln α_{carbonate-water} (Watkins et al., 2013). Despite this, we used this equation to retrieve the δ¹⁸O_water from our experimental carbonates, because most of them are associated with high apparent Δ₄₇ temperatures. Coplen (2007) or Watkins et al. (2013) equations would have 2 ‰ lower values (ca. $-\mathrm{10}\pm \mathrm{2}$ ‰ compared to $-\mathrm{8}\pm \mathrm{3}$ ‰ calculated with the equation of Kim and O'Neil, 1997). From our results, due to our experimental conditions and the associated error in our dataset, it is not possible and not our intention to argue in favor of one of these calibrations. This however shows how crucial it is to improve knowledge on the equilibrium 1000ln α_{carbonate-water} at both high and low temperatures in order to improve the accuracy and precision of our new proxy for reconstructing the δ¹⁸O_water from which carbonates, even disequilibrium ones, precipitated.

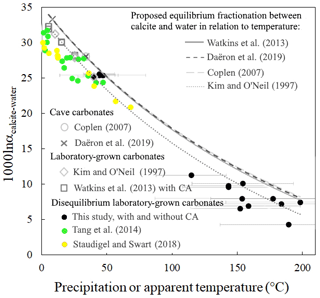
Figure 7 The relation to temperature of the equilibrium oxygen isotope fractionation factor between calcium carbonate and water (1000ln α_{calcite−water}) appears to be retrievable from solid carbonates (mainly calcites) in strong clumped and oxygen isotope disequilibrium such as our microbial carbonates (black dots, precipitated at 30 ^∘C) and two additional data series of laboratory-grown carbonates showing disequilibrium fractionation (Tang et al., 2014; Staudigel and Swart, 2018) (green and yellow dots, respectively). The data points affected by CO₂ hydroxylation (Tang et al., 2014) or CO₂ degassing (Staudigel and Swart, 2018) (see Fig. 6) are not included. Grey symbols correspond to cave carbonates precipitated at or near equilibrium (Coplen, 2007; Daëron et al., 2019) or laboratory experiments (Kim and O'Neil, 1997; Watkins et al., 2013). Those grey data series are usually considered representative of the equilibrium fractionation factor between calcium carbonate and water whose relations to temperature, extrapolated at high temperature, are illustrated by the different dashed curves. Plotted temperatures correspond to precipitation temperatures except for disequilibrium carbonates for which apparent temperatures have been calculated based on Δ₄₇ values. The x-axis errors for this study are included in the symbol size. The y-axis error for all the reconstructed temperatures is given on the figure.

Importantly, we here establish a new method to determine the equilibrium 1000ln α_{carbonate-water}, which consists in using the kinetics of Δ₄₇ and δ¹⁸O covariations during (dis)equilibration. Notably, because of the very large range of apparent temperatures recorded by disequilibrium carbonates (between ∼40 and 200 ^∘C; Fig. 7), this method could be particularly adapted to calibrate 1000ln α_{carbonate-water} at high temperatures for which the differences between the two most popular equations for 1000ln α_{carbonate-water} dependence on temperature (Kim and O'Neil, 1997; Coplen, 2007) appear larger (Fig. 7). Unfortunately, none of the three experimental setups having produced these disequilibrium carbonates (this study, as well as Tang et al., 2014, and Staudigel and Swart, 2018) were designed for the purpose of calibrating the equilibrium 1000ln α_{carbonate-water}. It is thus not possible, using these datasets, to propose a meaningful calibration. At least in our experiment, too many phenomena including the relatively high precipitation rate, variations in δ¹³C values (∼3 ‰) (Thaler et al., 2017) and presence of traces of aragonite and vaterite in our carbonates (Sect. 2.1 and Sect. S1 in the Supplement) lower the accuracy of the reconstructed equilibrium 1000ln α_{carbonate-water} values.

From a broader perspective, we anticipate that such an approach will help in determining critical equilibrium fractionation factors for other gaseous isotopic systems (such as isotopologues of molecules containing S–O bonds) or minerals of prime interest in biology and geology if clumped isotope measurements expand further beyond gaseous mass spectrometry (e.g., bonding between Fe–O, Fe–S, Ca–C).

4 Conclusions

Our experimental results show that the information held in disequilibrium (and apparent disequilibrium) carbonates is diverse and promising. First, a paired Δ₄₇ and δ¹⁸O_carbonate disequilibrium indicates that carbonates have precipitated in a dynamic environment where DIC and water did not reach isotopic equilibrium. In our microbial carbonate experiments, all the DIC is produced in isotopic disequilibrium with water and precipitates rapidly. Accordingly, the disequilibrium O isotope compositions recorded in those carbonates are maximized compared to what can be expected in nature where newly produced DIC is expected to be mixed with at least partly equilibrated ambient DIC before carbonates precipitate. Second, the combined use of clumped and traditional oxygen isotopic compositions allows the retrieval of the δ¹⁸O of the precipitation water, i.e., organism body water or environmental water, even for carbonates presenting δ¹⁸O and/or Δ₄₇ disequilibria or apparent disequilibria. Hence, except in the case of processes such as CO₂ degassing and CO₂ hydration and hydroxylation, which likely modify the $R_{\mathrm{stochastic}}^X$ term in Δ₄₇ calculation, paired Δ₄₇ and δ¹⁸O_carbonates disequilibria in carbonates can be used to reconstruct the oxygen isotope composition of both DIC and water at the precipitation loci even when precipitation occurred under disequilibrium conditions. Third, the (dis)equilibration trend in a covariation diagram of Δ₄₇ versus δ¹⁸O_carbonates can be used as a new method to determine the equilibrium fractionation factor between carbonate and water for a wide range of temperatures. Altogether, this opens up new avenues to better constrain not only past climate changes through improved paleoenvironmental reconstructions but also the physiology and habitat of sea life sensitive to ocean acidification.