the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimates of mean residence times of phosphorus in commonly considered inorganic soil phosphorus pools
Julian Helfenstein
Chiara Pistocchi
Astrid Oberson
Federica Tamburini
Daniel S. Goll
Emmanuel Frossard
Quantification of turnover of inorganic soil phosphorus (P) pools is essential to improve our understanding of P cycling in soil–plant systems and improve representations of the P cycle in land surface models. Turnover can be quantified using mean residence time (MRT); however, to date there is little information on MRT of P in soil P pools. We introduce an approach to quantify MRT of P in sequentially extracted inorganic soil P pools using data from isotope exchange kinetic experiments. Our analyses of 53 soil samples from the literature showed that MRT of labile P (resin- and bicarbonate-extractable P) was on the order of minutes to hours for most soils, MRT in NaOH-extractable P (NaOH-P) was in the range of days to months, and MRT in HCl-extractable P (HCl-P) was on the order of years to millennia. Multiple-regression models were able to capture 54 %–63 % of the variability in MRT among samples and showed that land use was the most important predictor of MRT of P in labile and NaOH pools. MRT of P in HCl-P was strongly dependent on pH, as high-pH soils tended to have longer MRTs. This was interpreted to be related to the composition of HCl-P. Under high pH, HCl-P contains mostly apatite, with a low solubility, whereas under low-pH conditions, HCl-P may contain more exchangeable P forms. These results suggest that current land surface models underestimate the dynamics of inorganic soil P pools and could be improved by reducing model MRTs of the labile and NaOH-P pools, considering soil-type-dependent MRTs rather than universal exchange rates and allowing for two-way exchange between HCl-P and the soil solution.
- Article
(1117 KB) -
Supplement
(691 KB) - BibTeX
- EndNote
Since only a small fraction (usually < 1 %) of soil phosphorus (P) is present as phosphate in the dissolved state where it can be taken up by plants and microbes, the rate at which this pool is replenished from other soil P pools is critical to assess the bioavailability of soil P (Syers et al., 2008). The extent and the timescale on which unavailable soil P forms can become gradually bioavailable are important factors affecting ecosystem productivity under increasing carbon dioxide concentrations (Sun et al., 2017). Estimates of P availability thus directly influence inferences on carbon sequestration. However, currently P availability is poorly constrained in land surface models, which hampers our ability to project future carbon sequestration rates (Goll et al., 2012). Modeling the rate of replenishment from different pools requires knowledge of the mean residence time of P in these pools. While there is growing information on concentrations of soil P pools in soils (Hou et al., 2018b), and how they react to drivers such as crop management, land use change, or changing climate (Feng et al., 2016; Negassa and Leinweber, 2009; von Sperber et al., 2017), little is known about the temporal dynamics of these pools (Hou et al., 2019). This knowledge gap not only limits linking data on soil P pools to P availability, it also slows the incorporation of P into global land surface models and hence estimating the effect of P cycling on long-term ecosystem functioning at large spatial and temporal scales (Reed et al., 2015).
Soil P pools are most commonly measured using sequential extraction, whereby soil P is extracted with increasingly strong reagents to yield experimentally defined P pools. While different variants of sequential extraction exist, the Hedley extraction and variants thereof are most widespread (Hedley et al., 1982). Here, we analyzed studies that used a resin extraction, followed by 0.5 M NaHCO3, 0.1 M NaOH, and finally 1 M HCl extractions. It is assumed that resin- and NaHCO3-extractable P represents loosely sorbed P, NaOH extracts P associated with Fe and Al (hydr)oxides, and HCl-extractable P (HCl-P) contains phosphates associated with Ca and soluble in acids, especially apatites (Moir and Tiessen, 1993). A precise characterization of P mineral forms present in these inorganic pools is difficult since there is a plethora of mixed compounds and not pure crystalline P forms in soils. However, spectroscopic techniques have been used to confirm that soils with more HCl-P tend to contain more calcium phosphate, and soils with relatively larger NaOH pools contain more P associated with Fe and Al (Frossard et al., 2002; Helfenstein et al., 2018a; Kar et al., 2011; Prietzel et al., 2016; Wu et al., 2014).
Mean residence time (MRT) of P has been quantified in the soil solution and in soil microbes; however, little is known about the mean residence time of P in Hedley pools. Mean residence time is defined here as the average time required to completely renew the content of a pool at steady state and is also called turnover time in other studies (Six and Jastrow, 2002). Radioisotopic labeling experiments have shown that the MRT of P in soil solution is on the order of milliseconds to minutes (Fardeau et al., 1991; Helfenstein et al., 2018b), while MRT of P in soil microbiota tends to be on the order of days to weeks (Gross and Angert, 2017; Oberson and Joner, 2005; Spohn and Widdig, 2017). Isotope exchange kinetic experiments, where the dilution of a radioisotopic tracer (33P or 32P) is traced in a soil–water suspension, allow measurement of the exchange of P by physicochemical processes as a function of time (Fardeau, 1996; Frossard et al., 2011). While the MRT of P in resin, NaOH, and HCl pools has recently been approximated in soils on a Hawaiian climatic gradient (Helfenstein et al., 2018a), it is not clear if these MRTs also pertain to nonvolcanic soils.
Land surface models describe the complex interactions governing the cycles of water, energy, and carbon, and they increasingly incorporate cycles of major soil nutrients (i.e., nitrogen and phosphorus) (e.g. Wang et al., 2010). The representations of inorganic soil phosphorus dynamics are currently very rudimentary in such models: soil inorganic phosphorus is commonly separated into different pools according to differences in residence times (fast, intermediate, and slow pools) (Wang et al., 2010). Although the structure, i.e., number of soil P pools and the connection among pools, differs among models, they commonly apply the same concept. In general, the residence time of P in the fastest pool is modeled as a function of multiple abiotic (chemical weathering, sorption) and biotic (mineralization, immobilization, plant uptake, phosphatase activity) processes (Lloyd et al., 2001), while more recalcitrant pools have prescribed globally uniform decay rates. The decay rates are either derived from calibration to achieve plausible total soil P stocks (Goll et al., 2012; Wang et al., 2010; Yang et al., 2014) or derived from temporal net changes in soil P fraction along a single soil chronosequence (Goll et al., 2017). Such calibration strategies are not able to capture gross exchanges among soil P pools, which do not result in net changes in pool size but are critical for the bioavailability of soil P. Hence, current model formulations of P cycling are likely underestimating inorganic soil P dynamics and overestimating inorganic P pool MRTs.
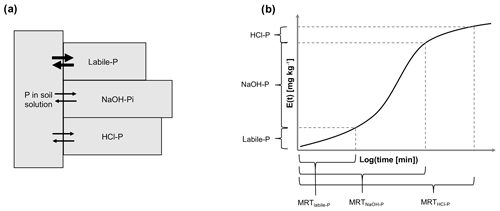
The objective of this work was to quantify the MRT of P in inorganic soil P pools in a wide range of soil types and provide much needed information to constrain soil P dynamics in global models. We limited our study to inorganic pools because the isotope exchange kinetic approach can only be used to study physicochemical exchange processes, whereas MRT of P in organic pools is controlled by biological processes. In our analysis, we assume that the time necessary to renew the total amount of P present in a Hedley pool (MRT) can be equated to the time necessary for phosphate ions in solution to exchange with all phosphate ions located in this pool (Fig. 1a). This allowed us to calculate MRT using the function for isotopically exchangeable P as determined in isotope exchange kinetic experiments. However, it also means that potentially important processes influencing P MRT, such as biological and solid-state P transformations, were neglected. The second objective of this work was to determine if variation in MRT among soils could be explained by soil properties and climatic variables. To meet these aims, we searched the literature for soil samples for which both P sequential extraction and kinetic isotope exchange data were available. We then used a function describing isotopically exchangeable P as a function of time to calculate MRT of P in resin P, labile P (resin and bicarbonate extractable), NaOH-extractable P (NaOH-P), and HCl-P.
2.1 Dataset
We found 53 soils for which both P sequential extraction and isotope exchange kinetic data were available. Twelve samples were from a Hawaiian climatic gradient (Helfenstein et al., 2018a), five from a long-term field trial in Switzerland (Keller et al., 2012), 11 from a study of different soils throughout New Zealand (Chen et al., 2003), 14 from a forested geosequence in Germany (Lang et al., 2017), seven from field experiments on highly weathered soil in Colombia (Buehler et al., 2003; Oberson et al., 1999), and four from an agricultural field trial on Fluvisols in Italy (Borda et al., 2014). Information on soil properties (pH, soil texture, organic C concentration), climate (mean annual temperature and mean annual precipitation), soil P pools (total P, resin-extractable P, NaHCO3-extractable inorganic P, NaOH-extractable inorganic P, HCl-extractable P), and P exchange properties (Pw, m, n, Pinorg; see Sect. 2.2) was retrieved from the original publications, from associated publications, or by contacting the authors (Table 1). One study used an ammonium chloride extraction instead of a resin extraction (Chen et al., 2003). We added the first two extractions (resin or ammonium chloride and NaHCO3) and called this the “labile pool”. For two studies (Borda et al., 2014; Helfenstein et al., 2018a) soil texture was not reported and had to be estimated from global gridded (250 m resolution) soil information (Hengl et al., 2017) based on geographic information of the sample site. For the full documentation of sources for the soil property information, please see Supplement Table S1. Four soils (“Himatangi”, “Hurundi”, “Okarito”, and “Temuka”; Chen et al., 2003) were excluded because, unlike the rest of the samples, the Hedley pools of these soils were much larger than the pools from isotope exchange kinetics. This yielded unreasonably high MRTs because of the asymptotic behavior of the E(t) equation. In the discussion, we briefly discuss how excluding these soils affected multiple-regression models.
Table 1Selected soil properties, climate conditions, soil phosphorus pools, and phosphorus exchange kinetic properties of soils used in this study.
Despite only encompassing 53 soils from 20 geographic sites, the dataset included samples from a wide set of climatic conditions (Supplement Fig. S1), and a variety of soil texture classes (Fig. S2). Eleven of the soil samples were from arable land use, 14 from forest, and 28 from grassland. The world reference base soil orders entailed were Acrisol (1), Andosols (17), Cambisols (19), Ferralsols (7), Fluvisols (4), and Luvisols (5) (IUSS Working Group WRB, 2015). While some of the soils are considered to be low in available P (Buehler et al., 2003; Lang et al., 2017; Oberson et al., 1999), the dataset also includes soils developed on P-rich parent materials (Helfenstein et al., 2018a; Lang et al., 2017) or soils that have been intensively fertilized (Borda et al., 2014).
2.2 Estimating mean residence times
Isotopically exchangeable P (E(t)) (mg kg−1) can be modeled as a function of time by Eq. (1) (Fardeau, 1996), where m and n are statistical parameters, Pw (mg kg−1) is water-extractable P, r(∞) is the radioactivity measured in solution after an infinite time, and R is the radioactivity (Bq) introduced at t=0.
The ratio is usually approximated as , where Pinorg is the total amount of inorganic P (mg kg−1) (Fardeau, 1993). The parameters m and n describe the rapid and slow physicochemical exchange processes, respectively, and are determined by fitting a nonlinear regression model to measurements of radioisotope concentration in solution from an isotope exchange kinetic experiment (for details see Fardeau et al., 1991; Frossard et al., 2011).
By plugging in different values of t (min), one can calculate the amount of P that is exchangeable within a given time frame. Likewise, it is possible to calculate the amount of P exchangeable between two time points, e.g. between 1 d and 3 months (Frossard et al., 2011). While isotope exchange kinetic experiments used to fit m and n only last for around 90 min, extrapolated E values have been shown to describe P exchange well over a time span of months, accurately describing P available to plants and being considered the gold standard for measuring P availability (Frossard et al., 1994; Hamon et al., 2002). Furthermore, E(1 min) has been shown to correlate with resin P, E(3 months) with NaOH-P, and E(>3 months) with HCl-P in sewage sludge (Frossard et al., 1996) and for soils from a Hawaiian climatic gradient (Helfenstein et al., 2018a).
To estimate mean residence times of sequential extraction pools, we plugged in P pool values as measured by sequential extraction (Ppool) for E(t) (Eq. 2), and then we solved for t to determine the amount of time necessary to exchange all the phosphate ions contained in that pool (Eq. 3).
In sequential extractions, P pools are sequentially removed from the soil, and this has to be accounted for in the calculation of MRT. MRT of resin P and labile P was calculated using Eq. (3) and plugging in resin P or labile P pool sizes for Ppool. However, for NaOH-P and HCl-P the previously removed P pools have to be formally “added back”. Hence, for NaOH-P and HCl-P the Ppool was set equal to the sum of labile P and NaOH-P or labile P, NaOH-P, and HCl-P respectively (Fig. 1b). Not accounting for the sequential nature of these pools and using NaOH-P or HCl-P for Ppool directly in Eq. (3) would underestimate MRT.
Estimating MRT using Eq. (3) required making several assumptions. Firstly, we assumed that the labile pool exchanges much faster than the NaOH-P pool, which again exchanges much faster than HCl-P. This assumption rests on the observation that radioisotope specific activity after labeling is higher in resin P ≫ NaOH-P ≫ HCl-P in a variety of soils (Buehler et al., 2002; Bünemann et al., 2004; Daroub et al., 2000; Pistocchi et al., 2018; Vu et al., 2010). Secondly, we assumed that all P transformations occur via the soil solution; i.e., we neglected potential exchange between pools in the solid phase (such as diffusive penetration, Fig. 1a) (Barrow and Debnath, 2014). For example, we did not consider exchange between NaOH-P and “occluded” soil P forms, considered in some modeling approaches (Hou et al., 2019), but which do not involve phosphate release to the soil solution.
Thirdly, our approach carries over all assumptions from an isotope exchange kinetic experiment (Frossard et al., 2011), including that biological activity does not markedly impact P exchange during the duration of an isotope exchange kinetic experiment (usually 90 min). The assumption that biological activity is negligible at this timescale can be tested by applying a microbial inhibitor to the soil suspension (Bünemann et al., 2012). If the microbial inhibitor does not significantly affect radioisotopic recovery compared to the control, biological processes have a negligible effect. Microbial inhibitors did not affect radioisotopic recovery of soils from the Hawaiian climatic gradient or soils from the forested geosequence (only extreme soils tested, including a very low P soil) used in this study (Bünemann et al., 2016; Helfenstein et al., 2018a). However, for the other studies analyzed here, no such tests were undertaken. Hence, our approach can only be used to estimate MRT of P in inorganic P pools turning over through physicochemical processes but does not account for biological processes. In our analysis, we also do not consider the residual P pool (P remaining in soil after the HCl extraction), assuming that this pool only plays a negligible role in P exchange.
2.3 Effect of soil properties on mean residence times
To determine the effect of soil properties on MRT, we performed multiple regressions, in which independent soil properties were the explanatory variables and MRTs the response variables. Multiple-regression models were fitted to the three response variables “t_labile”, “t_NaOH”, and “t_HCl”. For each response variable, we derived a maximum scope model including all numerical soil properties (pH, soil texture, and organic C) and climatic data as well as categorical explanatory variables “land use” and “extraction method”. Different studies used slightly different extraction methods; the effect of this on the variability was explored using the extraction method variable. Additionally, we tested the correlation of MRTs with oxalate or dithionite-extractable aluminum and iron as a simple regression for the samples (n=41–43) for which these data were available. The R function “step” (R Core Team, 2018) was then used for stepwise selection of explanatory variables by minimizing Akaike's information criterion (AIC) (Sakamoto et al., 1986). Model size was reduced to reduce collinearity between predictor variables, as assessed using the variance inflation factor (VIF), which was below 5 for each of the explanatory variables (Fox and Monette, 1992). Non-normally distributed variables were log-transformed to meet the assumption of normality.
3.1 P exchange as a function of time
P pools as defined by sequential extraction displayed highly significant correlations with P pools defined by exchangeability, with most points falling close to the 1:1 line (Fig. 2). Pearson's moment correlation between labile P and P exchangeable within 1 h was 0.84, between NaOH-P and P exchangeable between 1 h and 3 months was 0.94, and between HCl-P and P only exchangeable in time spans longer than 3 months was 0.87.
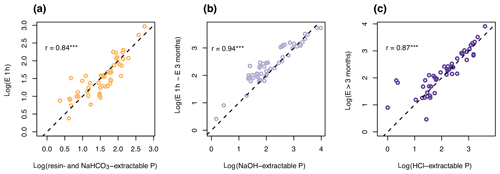
Figure 2Correlation between chemically extracted pools and isotopically exchangeable P. Resin- and NaHCO3-extractable P correlated with P exchangeable in 1 h (E1 h) (a), NaOH-extractable P with P exchangeable between 1 h and 3 months (b), and HCl-extractable P with P only exchangeable in over 3 months (c). Units of both axes are log(mg P kg−1). The dotted line shows the 1:1 line. Pearson's product–moment correlation (r value on plot) was highly significant (p<0.001) for all three correlations.
The soils showed a broad range of P exchange as a function of time. P that was exchangeable within 1 min (E1 min) ranged from 0.99 to 218 mg kg−1, and P that was exchangeable in 3 months ranged from 11.7 to 6311 mg kg−1 between the different soils (Table 1). Soils developed on P-rich basalt (Helfenstein et al., 2018a; Lang et al., 2017) had the highest E values, while Ferralsols had the lowest E values (Oberson et al., 1999). Half of the soils had < 5 mg P kg−1 exchangeable within 1 min, which is considered a threshold for low P availability (Gallet et al., 2003). Differences in P exchange behavior were due either to different levels of total inorganic P or to different P forms present in the soil (Fig. 3). For example, a soil with high amounts of inorganic P exchanged more within the same time interval than a soil with low amounts of inorganic P. Similarly, soils with large proportions of HCl-P tended to have lower slopes of E curves than soils with relatively more labile or NaOH-P. This variability is reflected in the proportion of E1 min to total P, which spanned from 0.04 % to 6 % of total soil P. Similarly, E3 months represented on average 25 % of total soil P, spanning from 4 % to 64 %.
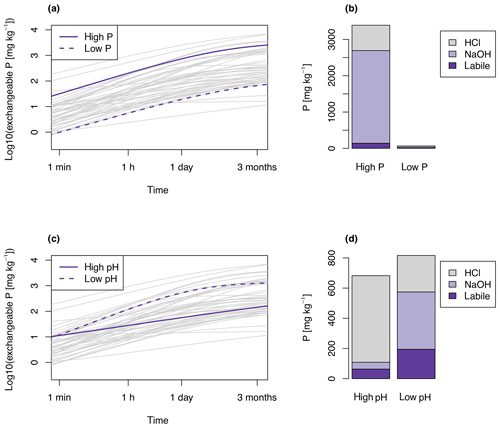
Figure 3Examples of exchangeable P as a function of time (E curves). Grey lines show E curves of each soil in the dataset. Panels (a) and (b) highlight two highly reactive soils, one with high amounts of P (an Andosol from Helfenstein et al., 2018a) and one with little P (a Ferralsol from Oberson et al., 1999). Panels (a) shows the E curves and (b) the corresponding sequential extraction (b). Panels (c) and (d) highlight two soils with similar amounts of total P, but different pH and P exchange behavior. For the high-pH Fluvisol (pH = 8.1, from Borda et al., 2014), P exchange is slow, compared to a Cambisol with much more exchange in the fast–intermediate term (pH = 3.8, from Lang et al., 2016) (c). In the high-pH soil most P is HCl extractable, whereas for the low-pH soil more P is found in the NaOH and labile pools (d).
3.2 Estimates of mean residence times
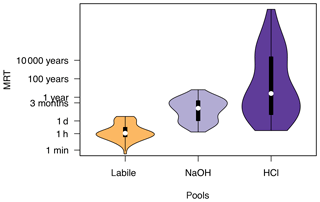
The median MRT of P in the labile pool was around 1 h (67 min), for NaOH-P around 1 month (3.4×104 min), and for HCl-P around 3 years (1.4×106 min). However, calculated MRTs of individual soils spanned many orders of magnitude. Mean residence time of P in labile P ranged from 0.4 to 4.4×103 min, with two frequency maxima, one around 1 h and one around 1 d (Fig. 4). Mean residence time of P in NaOH-P ranged from 91 to 3.4×106 min and also had two frequency maxima, one at around 1 d and one at around 3 months. Mean residence time of P in HCl-P had the widest spread, from 129 to 1.7×1015 min. While most soils had a MRT of P in HCl-P around 1 year, another frequency maximum occurred at around 10 000 years. The median MRT of P in resin P (n=42) was 19 min, with a range of 10−4 to 102 min.
3.3 Soil properties affecting mean residence times
Multiple-regression models were able to explain between 54 % and 63 % of the variability in MRT for each pool (Table 2). The MRT of P in labile P was best predicted by a model including clay and land use (adjusted R2=0.63, F statistic = 30.6, p<0.001). Land use was the most important predictor of t_labile. A model only including land use had an adjusted R2 of 0.52 (F statistic 29.6, p<0.001). While most forest and grassland soils had a MRT of P in labile P around 1 h, arable soils tended to have a longer MRT of around 1 d (Fig. 5a). The land use effect on MRT of P in labile P was not a pool size effect (Fig. 5b). In addition, MRT decreased with increasing clay content (adjusted R2=0.12, F statistic = 6.8, p=0.01) (Fig. S3).
Table 2Multiple-regression models for mean residence times of P in labile P, NaOH-extractable P, and HCl-P. Models were determined by a stepwise selection process that maximizes Akaike's information criterion.
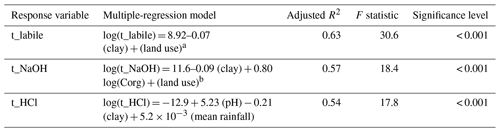
a For arable = 0; for forest = −3.08; for grassland = −3.78. b For arable = 0; for forest = −5.94; for grassland = −1.81
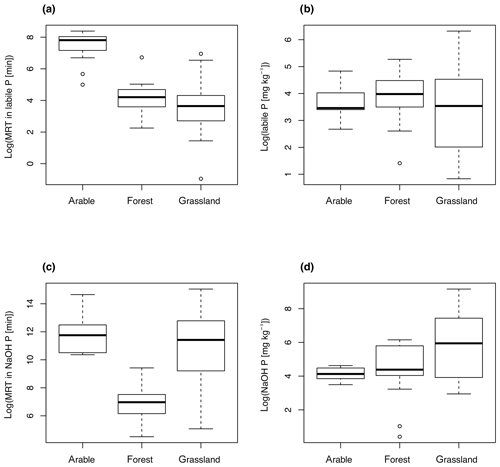
Figure 5Mean residence time (MRT) of P (a, c) and pool size (b, d) as a function of land use. MRT of both P in labile P (a) and NaOH-P (c) was significantly affected by land use.
The MRT of P in NaOH-P was best predicted by a model with clay, land use, and organic C (adjusted R2=0.57, F statistic = 18.4, p<0.001). Of those three explanatory variables, the relationship was again strongest with land use. A model only including land use had an adjusted R2 of 0.44 (F statistic 21.6, p<0.001). In general, forest soils had a shorter MRT of around 1 d and arable soils a longer MRT of around 3 months. Grassland soils spanned the full range of MRT of P in NaOH-P (Fig. 5c). As for MRT in labile P, the land use effect on MRT was not a pool size effect (Fig. 5d). MRT of P in NaOH-P also decreased with increasing clay content (adjusted R2=0.13, F statistic = 7.1, p<0.01) (Fig. S3). While organic C was also a significant predictor in the multiple-regression model, a simple regression between organic C and MRT of NaOH-P was not significant (Fig. S4).
The MRT of P in HCl-P was best predicted by a model with clay, pH, and mean annual rainfall (adjusted R2=0.54, F statistic = 17.8, p<0.001). The strongest of these predictors was pH (Fig. 6). MRT of P in HCl-P increased with increasing pH following Eq. (4):
where t_HCl is in minutes (adjusted R2=0.47, F statistic = 37.7, p<0.001). Like with the models for labile P and NaOH-P, predicted MRT also decreased with increasing clay concentration for MRT of HCl-P; however, this relationship was not significant as a simple regression (Fig. S3).
Sequential extraction is probably the most common method used to study P pool distribution in soils. However, the residence time of P in these pools and environmental controls remains poorly understood. While earlier works hypothesized that resin and bicarbonate P have a fast turnover, and NaOH and HCl a slow turnover, data on MRT of P in these pools for a wide range of soils were previously missing (Cross and Schlesinger, 1995; Tiessen et al., 1984). We found that on average resin P has a MRT in the range of several minutes, labile of 1 h (forest and grassland soils) or 1 d (arable soils), NaOH-P in the range of days (forest and some grassland soils) to months (arable soils), and HCl-P in the range of years to millennia, with a strong pH dependence. The large variability in MRTs could be partially explained by soil properties, especially pH and clay, or land use, but may also be due to unaccounted soil properties as well as methodological limitations of either our approach or the lab techniques used to produce the original data. For instance, some variability in the MRT estimation might be generated by the different methods used to measure total inorganic P. The accuracy in total inorganic P measurement might affect MRTs as results from Eq. (2).
As a predictor of MRTs of labile and NaOH-P, land use is likely a proxy for soil P balance (fertilizer inputs, outputs with harvest) and biological activity. Arable soils are more likely to receive P fertilizers. Long-term fertilizer inputs may lead to a decrease in surface charge resulting from diffusive penetration of P into the reacting materials and therefore to a lower phosphate buffering capacity (Barrow and Debnath, 2014). Hence, fertilizer application may lead to larger P pool sizes but longer MRT (Helfenstein et al., 2018b). Biological activity has been shown to accelerate P turnover in the labile pool through rapid uptake and release by the soil microbial community (Oehl et al., 2001; Pistocchi et al., 2018; Weiner et al., 2018). This holds especially true under grassland or forest and under low P availability. We consider the later explanation less likely, since microbial uptake–release tend to be negligible during the isotopic exchange kinetic experiments (Oehl et al., 2001), or it is suppressed using microbial inhibitors (Bünemann et al., 2012). However, we cannot completely rule out such an influence as in most soil samples included in our dataset this effect was not systematically tested.
The pH dependence of MRT in HCl-P is likely because the composition of the HCl pool varies strongly with pH. Under high pH, the HCl pool tends to contain apatites, calcium phosphate minerals which are highly stable (Moir and Tiessen, 1993; Nriagu, 1976). Our results predict that under such conditions, MRT of HCl-P may be on the order of millennia or longer, orders of magnitude longer than estimated MRTs of NaOH-P. In acidic soils on the other hand, apatite is much less stable (Guidry and Mackenzie, 2003), and the HCl pool may contain either carryover from the NaOH pool or other phosphates that are more reactive (Prietzel et al., 2016). Equation (4) predicts a MRT in HCl-P of three-fourths of a year for a soil with a pH of 4.5, a range into which MRT of many NaOH-P pools also falls. Hence, our results suggest that the exchange kinetics of NaOH and HCl pools are more similar under low-pH conditions, whereas under high-pH conditions, there seems to be a clear distinction between availability of NaOH-extractable P and HCl-extractable P. Nevertheless, even under neutral to alkaline conditions, the HCl-P pool may be involved in bidirectional exchange of phosphate involving precipitation of phosphate with Ca to form secondary Ca phosphates, without net change in pool size (Frossard et al., 1995), although at pedogenetic timescales this pool progressively decreases in size (Walker and Syers, 1976). Also, using stable oxygen isotopes in phosphate, it was shown that in 150 000-year-old soils from arid conditions and neutral pH, roughly half of the HCl-P pool contained secondary phosphates (Helfenstein et al., 2018a). The relationship of pH and other relationships, e.g. land use as a predictor for t_labile and t_NaOH, pertained if the outliers “Himatangi”, “Hurundi”, “Okarito”, and “Temuka” were included in the multiple-regression analyses; however, including the outliers reduced overall model adjusted R2 to around 0.4 for all three models.
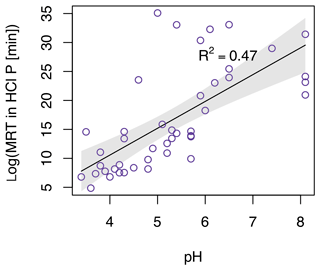
Figure 6Simple regression of calculated mean residence time of P in HCl-P with pH. F statistic = 37.7; p<0.001.
Clays are important binding sites for P (Gérard, 2016). Our data seem to show that the clay content influences residence times not only of labile P, but also of the NaOH and HCl pools. In our analysis, the clay variable includes not only clay minerals but also secondary minerals such Fe and Al oxyhydroxides, as it follows the particle size classification. Fe and Al oxyhydroxides are known to be key in inorganic P exchange behavior (Achat et al., 2016; Syers et al., 2008). For the samples where data on oxalate- and dithionite-extractable Al and Fe were available (n = 41–43), simple regression showed only weak correlations with MRTs and only significance for MRT of NaOH-P with oxalate-extractable Al, dithionite-extractable Fe, and the sum of dithionite-extractable Al and Fe as explanatory variables (adjusted R2≤0.16, p<0.05; data not shown). In general, soil properties controlling P sorption also control P exchangeability and therefore residence time. Indeed, high amounts of P sorbents might relate to more rapidly exchangeable P (Achat et al., 2016; Demaria et al., 2013). The variety of mechanisms involved in P binding on such soil surfaces (multilayer sorption, inner-sphere complexes, surface precipitation; see Gérard, 2016 and references therein) might explain why the effect of clay is significant for all residence times.
Data from long-term (weeks–months) radioisotope tracer incubation experiments, where both physicochemical and biological processes are considered, support our estimates of MRTs. While such studies have not reported estimates of MRTs, the time by which specific activity of 33P of the NaOH or HCl pool equilibrates with the specific activity of the labile P pool provides an estimate of MRT of the slowest pool, i.e., the time needed to exchange all the phosphate ions located in the slowest pool with the ones in the soil solution. According to this assumption and using the data published by Buehler et al. (2002) from the same Ferralsols also included in our dataset, we could estimate a MRT of the NaOH pool between 7 and 14 d (soils under savanna and pasture) or longer than 2 weeks (two soils under rice). These values are similar to MRTs from our study: 1 and 5 d for the soils under savanna and pasture, respectively, and 28 and 88 d for the soils under rice. Generally, specific activity of 33P in the HCl pool did not equilibrate during the duration of the experiment (2 weeks to 3 months, depending on the study), suggesting longer MRTs for this pool (Buehler et al., 2002; Bünemann et al., 2004; Pistocchi et al., 2018; Vu et al., 2010). Nevertheless, for stable pools such as the HCl-P, it is questionable whether our estimates of MRTs are realistic, as the extrapolation of E values (Eq. 1) has been tested only over time spans of days to months (Bünemann et al., 2007; Frossard et al., 1994) and is impossible to validate for longer time spans due to the short half-lives of both radioactive P isotopes.
Insights from stable oxygen isotope analysis support our estimates of MRT of HCl-P. At the beginning of soil development, all soil P has the parent material stable oxygen isotope value (δ18OP) (Roberts et al., 2015; Tamburini et al., 2012). With time, biological activity brings δ18OP into steady state with soil water (Blake et al., 2005). By analyzing δ18OP in sequentially extracted pools in soils of known age, it is possible to roughly constrain MRT of P in these pools. While δ18OP of bicarbonate- and NaOH-extractable P tends to be in the soil–water steady state (Helfenstein et al., 2018a; Roberts et al., 2015), HCl-P may retain parent material signature even in older soils. In a chronosequence on granitic parent material, it was shown that the HCl pool acquired the biological signature after several thousand years (Tamburini et al., 2012), whereas under more arid conditions, where apatite remains stable, HCl-P may not have turned over completely even after 150 000 years of soil development (Helfenstein et al., 2018a). This supports not only our long and variable estimates of MRTs of P in the HCl-P, but also their strong dependence on pH, the main driver of apatite stability.
Table 3Mean residence times of different soils calculated in this study compared to values used in land surface models. Mean residence times of the resin and labile (resin + bicarbonate) P pools are displayed in minutes, while mean residence times of the NaOH and HCl P pools are displayed in years. Residence times of the listed models were extracted from the literature or by contacting respective authors (Wang et al., 2010; Goll et al., 2012; Yang et al., 2014; Zhu et al., 2016; Goll et al., 2017).
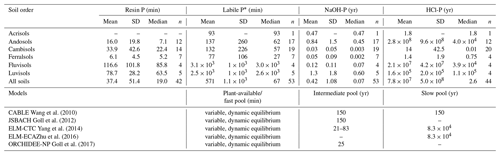
* Resin- and bicarbonate-extractable P.
4.1 Limitations
The main limitations of our study concern representativity of the soil samples used and uncertainty introduced due to assumptions taken to calculate MRTs. The 53 soil samples used in our study only came from a small number of studies, and some soils, like Andosols and Cambisols, were overrepresented in our study, while other important soils such as Vertisols, Podzols, or carbonate- or organic-matter-rich soil orders were not represented or underrepresented. In addition, soils with large amounts of NaOH- and HCl-P were overrepresented in our study compared to a larger global dataset (Fig. S5). However, our resin P values closely match resin P frequency distribution of a larger global dataset (Hou et al., 2018a). In terms of P exchange kinetics, our soils covered the full range of reported m and n values and can thus be considered to reflect the full range of P exchange kinetic properties observed in soils (Fig. S6) (Achat et al., 2016; Helfenstein et al., 2018b). Assumptions taken to calculate MRT of P in soil P pools required making several simplifications. Our approach only considers a simplified system of soil and water in steady-state conditions and excludes biological activity. In field conditions, P residence times may be different due to non-steady-state conditions, microbial interactions with abiotic processes, and plant uptake and alterations of the physical and chemical soil environment (Hinsinger, 2001). For example, intensive P uptake by plants may lead to net changes in soil P pools in addition to exchange fluxes (Guo et al., 2000). Also, it is likely that MRTs are affected by temperature and changes in soil moisture. Continued improvement of tracer experiments is paramount to provide empirical data on mean residence times and magnitudes of biological and physicochemical fluxes (Bünemann, 2015; Wanek et al., 2019). However, for the time being, our ad hoc approach provides preliminary estimates of mean residence times of commonly used P pools, with the potential to improve both interpretation of lab- and field-scale results as well as land surface modeling.
4.2 Implications for lab- and field-scale research
Mean residence times of P in inorganic soil P pools reported here are important for improved understanding of P dynamics in soil. Sequential extraction continues to be widely used to measure soil P status, for example to study effects of land use change and P inputs or environmental drivers on soil P cycling (Blake et al., 2003; Feng et al., 2016; von Sperber et al., 2017). Understanding the residence times of soil P pools will allow us to fine-tune hypotheses of expected changes and improve interpretation of observed changes in pool sizes. Furthermore, analysis of stable oxygen isotopes in phosphate, which is gaining importance as a tracer of phosphate transformation and indicator of biological vs. geochemical P cycling, is tightly linked to sequential extraction (Tamburini et al., 2018). Knowledge of mean residence times has the potential to improve interpretation of sequential extractions and derivate methods.
4.3 Implications for land surface modeling
Our study allows us to draw several conclusions important for land surface modeling. Firstly, we show that current land surface models (LSMs) largely overestimates MRTs of P in inorganic soil P pools. As models do not report all information needed to calculate MRT, we approximate modeled P pool MRT (in the following: MRT*) of the intermediate and slow pool as the inverse of the decay rate assuming the pool size and fluxes are in equilibrium (i.e., net losses are equal to net gains). Juxtaposing our estimates of MRTs of P in inorganic soil P pools with values used in existing land surface models shows that existing land surface models underestimate inorganic P turnover by several orders of magnitude (Table 3). While our estimates of the mean residence times of the NaOH pool are in the range of months to years, existing models run with MRTs of these pools of decades to centuries (Table 3). The discrepancy between our estimates and existing model values is so large and consistent among models that it is unlikely due to slightly different conceptualizations of the P cycle or the approximation of MRT in models by decay rates. Rather, the overestimation of the stability of inorganic P pools in existing LSM is likely due to the calibration of models using net changes to inorganic soil P pools (Goll et al., 2017; Hou et al., 2019). As the P exchange among two given pools is most often two-way, the calibration of residence times on the net exchange must lead to an underestimation of P turnover. The data provided here will allow us to better calibrate soil P dynamics and/or evaluate modeled MRT.
Secondly, we found that residence times of P in slow inorganic pools varies considerably between soils, suggesting that land surface models should account for existing knowledge of P pool stability under different soil and environment conditions, rather than assuming globally uniform mean residence times. We found variation over several orders of magnitude in mean residence times of the same pool between different soils, and this variation could partly be explained by secondary soil and environment variables.
Thirdly, land surface models should consider that the HCl-P pool may have two-way exchange of P. Current model formulations assume the HCl-P pool contains only primary apatite, and the flux between the HCl-P pool and the soil solution is one-way (only dissolution) (Hou et al., 2019; Yang et al., 2014; Yu et al., 2018). From empirical observations it is known that HCl-P does not only contain primary apatite but may also contain secondary P minerals (Helfenstein et al., 2018a; Tamburini et al., 2012). Under acidic conditions, this may be Fe- and Al-associated minerals, while under neutral and alkaline pH this may be precipitated Ca phosphates (Frossard et al., 1995). Also, P radioisotope transfer from the soil solution to the HCl-P pool is well-documented (Buehler et al., 2002; Pistocchi et al., 2018). To take this into account, future P model formulation should consider a two-way flux between the HCl-P pool and the soil solution, with an exchange rate dependent on pH (see Eq. 4). While this change is likely to have limited impact for the modeling of neutral to alkaline soils, where the HCl-P pool is stable, in more acidic soils the HCl-P pool tends to have similar dynamics to the NaOH-P pool, thus having a considerable impact on P cycling and P availability.
In conclusion, mean residence times for inorganic P pools proposed here and the lessons learned should help improve model formulation of P in land surface models. Our estimates of MRTs suggest that current land surface models overestimate P MRT in inorganic soil P pools and as a consequence might overestimate the importance of biological soil P transformation (e.g. via phosphatases). Also, the temporal dynamics of P pools was found to vary largely between different soil types, which is not captured by models. Finally, model formulations should refrain from equating HCl-P to primary P, as this pool often contains secondary P minerals and is relatively dynamic in low-pH soils. More empirical data on soil P pool mean residence times are needed, also from soil–plant systems and field experiments, but our data provide the basis to start building data-constrained soil P models.
All data are available in the Supplement CSV file “all_data.csv” except for isotope exchange kinetic data from the DOK experiment (five soils). These data have not yet been published and are in the process of being published by Astrid Oberson. For isotope exchange kinetic data from the DOK experiment please contact Astrid Oberson, ETH Zürich, Switzerland.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-17-441-2020-supplement.
Data collection, analysis, and preparation of the manuscript were carried out by JH and CP on equal terms, with contributions from EF, AO, DSG, and FT.
The authors declare that they have no conflict of interest.
The authors would like to thank all primary data producers whose data was re-used in this study. We are also very grateful to Enqing Hou, Lin You, Sebastian Doetterl, Peter Vitousek and an anonymous reviewer for providing valuable comments to improve the manuscript. Also, the authors are grateful to fruitful discussions with Janine Burren, Philippe Deleporte, Timothy McLaren, and Federico Cantini.
This research has been supported by the Swiss National Science Foundation (grant no. 200021_162422).
This paper was edited by Edzo Veldkamp and reviewed by Enqing Hou and two anonymous referees.
Achat, D. L., Pousse, N., Nicolas, M., Brédoire, F., and Augusto, L.: Soil properties controlling inorganic phosphorus availability: general results from a national forest network and a global compilation of the literature, Biogeochemistry, 127, 255–272, https://doi.org/10.1007/s10533-015-0178-0, 2016.
Barrow, N. J. and Debnath, A.: Effect of phosphate status on the sorption and desorption properties of some soils of northern India, Plant Soil, 378, 383–395, https://doi.org/10.1007/s11104-014-2042-8, 2014.
Blake, L., Johnston, A. E., Poulton, P. R., and Goulding, K. W. T.: Changes in soil phosphorus fractions following positive and negative phosphorus balances for long periods, Plant Soil, 254, 245–261, https://doi.org/10.1023/A:1025544817872, 2003.
Blake, R. E., O'Neil, J. R., and Surkov, A. V.: Biogeochemical cycling of phosphorus: Insights from oxygen isotope effects of phosphoenzymes, Am. J. Sci., 305, 596–620, https://doi.org/10.2475/ajs.305.6-8.596, 2005.
Borda, T., Celi, L., Bunemann, E. K., Oberson, A., Frossard, E., and Barberis, E.: Fertilization strategies affect phosphorus forms and release from soils and suspended solids, J. Environ. Qual., 43, 1024–1031, https://doi.org/10.2134/jeq2013.11.0436, 2014.
Buehler, S., Oberson, A., Rao, I. M., Friesen, D. K., and Frossard, E.: Sequential Phosphorus Extraction of a 33P-Labeled Oxisol under Contrasting Agricultural Systems, Soil Sci. Soc. Am. J., 66, 868–877, https://doi.org/10.2136/sssaj2002.8680, 2002.
Buehler, S., Oberson, A., Sinaj, S., Friesen, D. K., and Frossard, E.: Isotope methods for assessing plant available phosphorus in acid tropical soils, Eur. J. Soil Sci., 54, 605–616, https://doi.org/10.1046/j.1365-2389.2003.00542.x, 2003.
Bünemann, E., Marschner, P., McNeill, A., and McLaughlin, M.: Measuring rates of gross and net mineralisation of organic phosphorus in soils, Soil Biol. Biochem., 39, 900–913, https://doi.org/10.1016/j.soilbio.2006.10.009, 2007.
Bünemann, E. K.: Assessment of gross and net mineralization rates of soil organic phosphorus – A review, Soil Biol. Biochem., 89, 82–98, https://doi.org/10.1016/j.soilbio.2015.06.026, 2015.
Bünemann, E. K., Steinebrunner, F., Smithson, P. C., Frossard, E., and Oberson, A.: Phosphorus dynamics in a highly weathered soil as revealed by isotopic labeling techniques, Soil Sci. Soc. Am. J., 68, 1645–1655, https://doi.org/10.2136/sssaj2004.1645, 2004.
Bünemann, E. K., Oberson, A., Liebisch, F., Keller, F., Annaheim, K. E., Huguenin-Elie, O., and Frossard, E.: Rapid microbial phosphorus immobilization dominates gross phosphorus fluxes in a grassland soil with low inorganic phosphorus availability, Soil Biol. Biochem., 51, 84–95, https://doi.org/10.1016/j.soilbio.2012.04.012, 2012.
Bünemann, E. K., Augstburger, S., and Frossard, E.: Dominance of either physicochemical or biological phosphorus cycling processes in temperate forest soils of contrasting phosphate availability, Soil Biol. Biochem., 101, 85–95, https://doi.org/10.1016/j.soilbio.2016.07.005, 2016.
Chen, C. R., Sinaj, S., Condron, L. M., Frossard, E., Sherlock, R. R., and Davis, M. R.: Characterization of phosphorus availability in selected New Zealand grassland soils, Nutr. Cycl. Agroecosys., 65, 89–100, https://doi.org/10.1023/a:1021889207109, 2003.
Cross, A. F. and Schlesinger, W. H.: A literature review and evaluation of the Hedley fractionation: Applications to the biogeochemical cycle of soil phosphorus in natural ecosystems, Geoderma, 64, 197–214, https://doi.org/10.1016/0016-7061(94)00023-4, 1995.
Daroub, S. H., Pierce, F. J., and Ellis, B. G.: Phosphorus fractions and fate of phosphorus-33 in soils under plowing and no-tillage, Soil Sci. Soc. Am. J., 64, 170–176, https://doi.org/10.2136/sssaj2000.641170x, 2000.
Demaria, P., Sinaj, S., Flisch, R., and Frossard, E.: Soil properties and phosphorus isotopic exchangeability in cropped temperate soils, Commun. Soil Sci. Plant Anal., 44, 287–300, https://doi.org/10.1080/00103624.2013.741896, 2013.
Fardeau, J. C.: Le phosphore assimilable des sols?: sa représentation par un modèle fonctionnel à plusieurs compartiments, Agronomie, 13, 317–331, 1993.
Fardeau, J. C.: Dynamics of phosphate in soils. An isotopic outlook, Fertil. Res., 45, 91–100, https://doi.org/10.1007/bf00790658, 1996.
Fardeau, J.-C., Morel, C., and Boniface, R.: Phosphate ion transfer from soil to soil solution: kinetic parameters, Agronomie, 11, 787–797, 1991.
Feng, J., Turner, B. L., Lü, X., Chen, Z., Wei, K., Tian, J., Wang, C., Luo, W., and Chen, L.: Phosphorus transformations along a large-scale climosequence in arid and semiarid grasslands of northern China, Global Biogeochem. Cy., 30, 1264–1275, https://doi.org/10.1002/2015gb005331, 2016.
Fox, J. and Monette, G.: Generalized collinearity diagnostics, J. Am. Stat. Assoc., 87, 178–183, https://doi.org/10.1080/01621459.1992.10475190, 1992.
Frossard, E., Morel, J. L., Fardeau, J. C., and Brossard, M.: Soil isotopically exchangeable phosphorus: A comparison between E and L values, Soil Sci. Soc. Am. J., 58, 846–851, https://doi.org/10.2136/sssaj1994.03615995005800030031x, 1994.
Frossard, E., Brossard, M., Hedley, M. J., and Metherell, A.: Reactions controlling the cycling of P in soils, in: Phosphorus in the Global Environment: Transfers, Cycles, and Management, edited by: Tiessen, H., John Wiley & Sons, Ltd., 107–138, 1995.
Frossard, E., Sinaj, S., and Dufour, P.: Phosphorus in Urban Sewage Sludges as Assessed by Isotopic Exchange, Soil Sci. Soc. Am. J., 60, 179–182, https://doi.org/10.2136/sssaj1996.03615995006000010029x, 1996.
Frossard, E., Skrabal, P., Sinaj, S., Bangerter, F., and Traore, O.: Forms and exchangeability of inorganic phosphate in composted solid organic wastes, Nutr. Cycl. Agroecosys., 62, 103–113, https://doi.org/10.1023/A:1015596526088, 2002.
Frossard, E., Achat, D. L., Bernasconi, S. M., Fardeau, J., Jansa, J., Morel, C., Randriamanantsoa, L., Sinaj, S., and Oberson, A.: The use of tracers to investigate phosphate cycling in soil–plant systems, in: Phosphorus in Action, edited by: Bünemann, E. K., Springer, Heidelberg, 59–91, 2011.
Gallet, A., Flisch, R., Ryser, J.-P., Frossard, E., and Sinaj, S.: Effect of phosphate fertilization on crop yield and soil phosphorus status, J. Plant Nutr. Soil Sci., 166, 568–578, https://doi.org/10.1002/jpln.200321081, 2003.
Gérard, F.: Clay minerals, iron/aluminum oxides, and their contribution to phosphate sorption in soils – A myth revisited, Geoderma, 262, 213–226, https://doi.org/10.1016/j.geoderma.2015.08.036, 2016.
Goll, D. S., Brovkin, V., Parida, B. R., Reick, C. H., Kattge, J., Reich, P. B., van Bodegom, P. M., and Niinemets, Ü.: Nutrient limitation reduces land carbon uptake in simulations with a model of combined carbon, nitrogen and phosphorus cycling, Biogeosciences, 9, 3547–3569, https://doi.org/10.5194/bg-9-3547-2012, 2012.
Goll, D. S., Vuichard, N., Maignan, F., Jornet-Puig, A., Sardans, J., Violette, A., Peng, S. S., Sun, Y., Kvakic, M., Guimberteau, M., Guenet, B., Zaehle, S., Penuelas, J., Janssens, I., and Ciais, P.: A representation of the phosphorus cycle for ORCHIDEE (revision 4520), Geosci. Model Dev., 10, 3745–3770, https://doi.org/10.5194/gmd-10-3745-2017, 2017.
Gross, A. and Angert, A.: Use of 13C- and phosphate 18O-labeled substrate for studying phosphorus and carbon cycling in soils: a proof of concept, Rapid Commun. Mass Sp., 31, 969–977, https://doi.org/10.1002/rcm.7863, 2017.
Guidry, M. W. and Mackenzie, F. T.: Experimental study of igneous and sedimentary apatite dissolution: Control of pH, distance from equilibrium, and temperature on dissolution rates, Geochim. Cosmochim. Ac., 67, 2949–2963, https://doi.org/10.1016/S0016-7037(03)00265-5, 2003.
Guo, F., Yost, R. S., Hue, N. V., Evensen, C. I., and Silva, J. A.: Changes in phosphorus fractions in soils under intensive plant growth, Soil Sci. Soc. Am. J., 64, 1681–1689, https://doi.org/10.2136/sssaj2000.6451681x, 2000.
Hamon, R. E., Bertrand, I., and McLaughlin, M. J.: Use and abuse of isotopic exchange data in soil chemistry, Soil Res., 40, 1371–1381, https://doi.org/10.1071/SR02046, 2002.
Hedley, M. J., Stewart, J. W. B., and Chauhan, B. S.: Changes in inorganic and organic soil phosphorus fractions induced by cultivation practices and by laboratory incubations, Soil Sci. Soc. Am. J., 46, 970–976, https://doi.org/10.2136/sssaj1982.03615995004600050017x, 1982.
Helfenstein, J., Tamburini, F., von Sperber, C., Massey, M., Pistocchi, C., Chadwick, O., Vitousek, P., Kretzschmar, R., and Frossard, E.: Combining spectroscopic and isotopic techniques gives a dynamic view of phosphorus cycling in soil, Nat. Commun., 9, 3226, https://doi.org/10.1038/s41467-018-05731-2, 2018a.
Helfenstein, J., Jegminat, J., McLaren, T. I., and Frossard, E.: Soil solution phosphorus turnover: derivation, interpretation, and insights from a global compilation of isotope exchange kinetic studies, Biogeosciences, 15, 105–114, https://doi.org/10.5194/bg-15-105-2018, 2018b.
Hengl, T., Mendes de Jesus, J., Heuvelink, G. B., Ruiperez Gonzalez, M., Kilibarda, M., Blagotic, A., Shangguan, W., Wright, M. N., Geng, X., Bauer-Marschallinger, B., Guevara, M. A., Vargas, R., MacMillan, R. A., Batjes, N. H., Leenaars, J. G., Ribeiro, E., Wheeler, I., Mantel, S., and Kempen, B.: SoilGrids250m: Global gridded soil information based on machine learning, PLoS One, 12, e0169748, https://doi.org/10.1371/journal.pone.0169748, 2017.
Hinsinger, P.: Bioavailability of soil inorganic P in the rhizosphere as affected by root-induced chemical changes: a review, Plant Soil, 237, 173–195, https://doi.org/10.1023/a:1013351617532, 2001.
Hou, E., Tan, X., Heenan, M., and Wen, D.: A global dataset of plant available and unavailable phosphorus in natural soils derived by Hedley method, Sci. Data, 5, 180166, https://doi.org/10.1038/sdata.2018.166, 2018a.
Hou, E., Chen, C., Luo, Y., Zhou, G., Kuang, Y., Zhang, Y., Heenan, M., Lu, X., and Wen, D.: Effects of climate on soil phosphorus cycle and availability in natural terrestrial ecosystems, Glob. Change Biol., 24, 3344–3356, https://doi.org/10.1111/gcb.14093, 2018b.
Hou, E., Lu, X., Jiang, L., Wen, D., and Luo, Y.: Quantifying soil phosphorus dynamics: a data assimilation approach, J. Geophys. Res.-Biogeo., 124, 2159–2173, https://doi.org/10.1029/2018JG004903, 2019.
IUSS Working Group WRB: World reference base for soil resources 2014, update 2015: International soil classification system for naming soils and creating legends for soil maps, FAO, Rome, 144–181, 2015.
Kar, G., Hundal, L. S., Schoenau, J. J., and Peak, D.: Direct chemical speciation of P in sequential chemical extraction residues using P K-edge X-ray absorption near-edge structure spectroscopy, Soil Sci., 176, 589–595, https://doi.org/10.1097/SS.0b013e31823939a3, 2011.
Keller, M., Oberson, A., Annaheim, K. E., Tamburini, F., Mäder, P., Mayer, J., Frossard, E., and Bünemann, E. K.: Phosphorus forms and enzymatic hydrolyzability of organic phosphorus in soils after 30 years of organic and conventional farming, J. Plant Nutr. Soil Sci., 175, 385–393, https://doi.org/10.1002/jpln.201100177, 2012.
Lang, F., Krüger, J., Amelung, W., Willbold, S., Frossard, E., Bünemann, E. K., Bauhus, J., Nitschke, R., Kandeler, E., Marhan, S., Schulz, S., Bergkemper, F., Schloter, M., Luster, J., Guggisberg, F., Kaiser, K., Mikutta, R., Guggenberger, G., Polle, A., Pena, R., Prietzel, J., Rodionov, A., Talkner, U., Meesenburg, H., von Wilpert, K., Hölscher, A., Dietrich, H. P., and Chmara, I.: Soil phosphorus supply controls P nutrition strategies of beech forest ecosystems in Central Europe, Biogeochemistry, 136, 5–29, https://doi.org/10.1007/s10533-017-0375-0, 2017.
Lloyd, J., Bird, M., Veenendall, E., and Kruijt, B.: Should phosphorus availability be constraining moist tropical forest respones to increasing CO2 concentrations?, in: Global Biogeochemical Cycles in the Climate System, edited by: Schulze, E.-D., Heimann, M., Harrison, S., Holland, E., Lloyd, J., Prentice, I. C., and Schimel, D. S., Elsevier, New York, 95–114, 2001.
Moir, J. O. and Tiessen, H.: Characterization of Available P by Sequential Extraction, in: Soil Sampling and Methods of Analysis, edited by: Carter, M. R., CRC Press, Boca Raton, FL, 293–306, 1993.
Negassa, W. and Leinweber, P.: How does the Hedley sequential phosphorus fractionation reflect impacts of land use and management on soil phosphorus: A review, J. Plant Nutr. Soil Sci., 172, 305–325, https://doi.org/10.1002/jpln.200800223, 2009.
Nriagu, J. O.: Phosphate – clay mineral relations in soils and sediments, Can. J. Earth Sci., 13, 717–736, https://doi.org/10.1139/e76-077, 1976.
Oberson, A. and Joner, E. J.: Microbial turnover of phosphorus in soil, in: Organic phosphorus in the environment, edited by: Turner, B. L., Frossard, E., and Baldwin, D. S., CABI Publishing, p. 133, 2005.
Oberson, A., Friesen, D. K., Tiessen, H., Morel, C., and Stahel, W.: Phosphorus status and cycling in native savanna and improved pastures on an acid low-P Colombian Oxisol, Nutr. Cycl. Agroecosys., 55, 77–88, https://doi.org/10.1023/a:1009813008445, 1999.
Oehl, F., Oberson, A., Probst, M., Fliessbach, A., Roth, H.-R., and Frossard, E.: Kinetics of microbial phosphorus uptake in cultivated soils, Biol. Fert. Soils, 34, 31–41, https://doi.org/10.1007/s003740100362, 2001.
Pistocchi, C., Mészáros, É., Tamburini, F., Frossard, E., and Bünemann, E. K.: Biological processes dominate phosphorus dynamics under low phosphorus availability in organic horizons of temperate forest soils, Soil Biol. Biochem., 126, 64–75, https://doi.org/10.1016/j.soilbio.2018.08.013, 2018.
Prietzel, J., Klysubun, W., and Werner, F.: Speciation of phosphorus in temperate zone forest soils as assessed by combined wet-chemical fractionation and XANES spectroscopy, J. Plant Nutr. Soil Sci., 179, 168–185, https://doi.org/10.1002/jpln.201500472, 2016.
R Core Team: R: A language and environment for statistical computing, available at: http://www.r-project.org (last access: 12 May 2019), 2018.
Reed, S. C., Yang, X., and Thornton, P. E.: Incorporating phosphorus cycling into global modeling efforts: a worthwhile, tractable endeavor, New Phytol., 208, 324–329, https://doi.org/10.1111/nph.13521, 2015.
Roberts, K., Defforey, D., Turner, B. L., Condron, L. M., Peek, S., Silva, S., Kendall, C., and Paytan, A.: Oxygen isotopes of phosphate and soil phosphorus cycling across a 6500 year chronosequence under lowland temperate rainforest, Geoderma, 257/258, 14–21, https://doi.org/10.1016/j.geoderma.2015.04.010, 2015.
Sakamoto, Y., Ishiguro, M., and Kitagawa, G.: Akaike Information Criterion Statistics, KTK Scientific Publishers, Tokyo, 1–290 pp., 1986.
Six, J. and Jastrow, J. D.: Organic matter turnover, in: Encyclopedia of Soil Science, edited by: Lal, R., Marcel Dekker, Inc., New York, 936–942, 2002.
Spohn, M. and Widdig, M.: Turnover of carbon and phosphorus in the microbial biomass depending on phosphorus availability, Soil Biol. Biochem., 113, 53–59, https://doi.org/10.1016/j.soilbio.2017.05.017, 2017.
Sun, Y., Peng, S., Goll, D. S., Ciais, P., Guenet, B., Guimberteau, M., Hinsinger, P., Janssens, I. A., Peñuelas, J., Piao, S., Poulter, B., Violette, A., Yang, X., Yin, Y., and Zeng, H.: Diagnosing phosphorus limitations in natural terrestrial ecosystems in carbon cycle models, Earth's Futur., 5, 730–749, https://doi.org/10.1002/2016EF000472, 2017.
Syers, J. K., Johnston, A. E., and Curtin, D.: Efficiency of soil and fertilizer phosphorus use: Reconciling changing concepts of soil phosphorus behaviour with agronomic information, FAO, Rome, available at: http://www.fao.org/docrep/010/a1595e/a1595e00.htm (last access: 12 May 2019), 2008.
Tamburini, F., Pfahler, V., Bünemann, E. K., Guelland, K., Bernasconi, S. M., and Frossard, E.: Oxygen isotopes unravel the role of microorganisms in phosphate cycling in soils, Environ. Sci. Technol., 46, 5956–5962, https://doi.org/10.1021/es300311h, 2012.
Tamburini, F., Pistocchi, C., Helfenstein, J., and Frossard, E.: A method to analyse the isotopic composition of oxygen associated to organic phosphorus in soil and plant material, Eur. J. Soil Sci., 69, 816–826, https://doi.org/10.1111/ejss.12693, 2018.
Tiessen, H., Stewart, J. W. B., and Cole, C. V: Pathways of phosphorus transformations in soils of differing pedogenesis, Soil Sci. Soc. Am. J., 48, 853–858, https://doi.org/10.2136/sssaj1984.03615995004800040031x, 1984.
von Sperber, C., Stallforth, R., Du Preez, C., and Amelung, W.: Changes in soil phosphorus pools during prolonged arable cropping in semiarid grasslands, Eur. J. Soil Sci., 68, 462–471, https://doi.org/10.1111/ejss.12433, 2017.
Vu, D. T., Tang, C., and Armstrong, R. D.: Transformations and availability of phosphorus in three contrasting soil types from native and farming systems: A study using fractionation and isotopic labeling techniques, J. Soils Sediments, 10, 18–29, https://doi.org/10.1007/s11368-009-0068-y, 2010.
Walker, T. W. and Syers, J. K.: The fate of phosphorus during pedogenesis, Geoderma, 15, 1–19, https://doi.org/10.1016/0016-7061(76)90066-5, 1976.
Wanek, W., Zezula, D., Wasner, D., Mooshammer, M., and Prommer, J.: A novel isotope pool dilution approach to quantify gross rates of key abiotic and biological processes in the soil phosphorus cycle, Biogeosciences, 16, 3047–3068, https://doi.org/10.5194/bg-16-3047-2019, 2019.
Wang, Y. P., Law, R. M., and Pak, B.: A global model of carbon, nitrogen and phosphorus cycles for the terrestrial biosphere, Biogeosciences, 7, 2261–2282, https://doi.org/10.5194/bg-7-2261-2010, 2010.
Weiner, T., Gross, A., Moreno, G., Migliavacca, M., Schrumpf, M., Reichstein, M., Hilman, B., Carrara, A., and Angert, A.: Following the Turnover of Soil Bioavailable Phosphate in Mediterranean Savanna by Oxygen Stable Isotopes, J. Geophys. Res.-Biogeo., 123, 1850–1862, https://doi.org/10.1029/2017jg004086, 2018.
Wu, Y., Prietzel, J., Zhou, J., Bing, H., Luo, J., Yu, D., Sun, S., Liang, J., and Sun, H.: Soil phosphorus bioavailability assessed by XANES and Hedley sequential fractionation technique in a glacier foreland chronosequence in Gongga Mountain, Southwestern China, Sci. China Earth Sci., 57, 1860–1868, https://doi.org/10.1007/s11430-013-4741-z, 2014.
Yang, X., Thornton, P. E., Ricciuto, D. M., and Post, W. M.: The role of phosphorus dynamics in tropical forests – a modeling study using CLM-CNP, Biogeosciences, 11, 1667–1681, https://doi.org/10.5194/bg-11-1667-2014, 2014.
Yu, L., Zanchi, G., Akselsson, C., Wallander, H., and Belyazid, S.: Modeling the forest phosphorus nutrition in a southwestern Swedish forest site, Ecol. Modell., 369, 88–100, https://doi.org/10.1016/j.ecolmodel.2017.12.018, 2018.