Observation-constrained estimates of the global ocean carbon sink from Earth system models

The ocean slows global warming by currently taking up around one-quarter of all human-made CO₂ emissions. However, estimates of the ocean anthropogenic carbon uptake vary across various observation-based and model-based approaches. Here, we show that the global ocean anthropogenic carbon sink simulated by Earth system models can be constrained by two physical parameters, the present-day sea surface salinity in the subtropical–polar frontal zone in the Southern Ocean and the strength of the Atlantic Meridional Overturning Circulation, and one biogeochemical parameter, the Revelle factor of the global surface ocean. The Revelle factor quantifies the chemical capacity of seawater to take up carbon for a given increase in atmospheric CO₂. By exploiting this three-dimensional emergent constraint with observations, we provide a new model- and observation-based estimate of the past, present, and future global ocean anthropogenic carbon sink and show that the ocean carbon sink is 9 %–11 % larger than previously estimated. Furthermore, the constraint reduces uncertainties of the past and present global ocean anthropogenic carbon sink by 42 %–59 % and the future sink by 32 %–62 % depending on the scenario, allowing for a better understanding of the global carbon cycle and better-targeted climate and ocean policies. Our constrained results are in good agreement with the anthropogenic carbon air–sea flux estimates over the last three decades based on observations of the CO₂ partial pressure at the ocean surface in the Global Carbon Budget 2021, and they suggest that existing hindcast ocean-only model simulations underestimate the global ocean anthropogenic carbon sink. The key parameters identified here for the ocean anthropogenic carbon sink should be quantified when presenting simulated ocean anthropogenic carbon uptake as in the Global Carbon Budget and be used to adjust these simulated estimates if necessary. The larger ocean carbon sink results in enhanced ocean acidification over the 21st century, which further threatens marine ecosystems by reducing the water volume that is projected to be undersaturated towards aragonite by around 3.7×10⁶–7.4×10⁶ km³ more than originally projected.

1 Introduction

The emissions of anthropogenic carbon (C_ant) since the beginning of industrialization through fossil-fuel burning, cement production, and land-use change have altered the global carbon cycle and climate (Friedlingstein et al., 2022). Around 40 % of the additional carbon since 1850 has accumulated in the atmosphere, where it represents the main anthropogenic greenhouse gas (IPCC, 2021). More than half of the emitted C_ant has been taken up by the land biosphere (∼ 30 %) and the ocean (∼ 25 %) (Friedlingstein et al., 2022). The remaining ∼ 5 % is the budget imbalance, a mismatch between carbon emissions and sink estimates which cannot be explained yet (Friedlingstein et al., 2022). By each taking up around a quarter of the C_ant emissions, the land biosphere and ocean sinks slow down global warming and climate change.

The ocean C_ant sink is defined here as a combination of the uptake of newly emitted carbon and the change in the natural carbon inventory in the ocean due to changes in temperatures, winds, and the freshwater cycle caused by climate change (Joos et al., 1999; Frölicher and Joos, 2010; McNeil and Matear, 2013). The uptake rate of C_ant on sub-millennial timescales is mainly determined by the ocean circulation and carbonate chemistry and only partly by biology (Sarmiento et al., 1998; Joos et al., 1999; Caldeira and Duffy, 2000; Sabine et al., 2004) despite the overall importance of marine biology for natural carbon fluxes (Falkowski et al., 1998; Steinacher et al., 2010). The rate-limiting process of C_ant uptake is the circulation that transports surface waters with high C_ant concentrations into the deeper ocean and allows waters with low or no C_ant concentrations to upwell back to the ocean surface. The largest part of this ocean upwelling occurs in the Southern Ocean where strong westerlies drive northward Ekman transport of surface waters, which are then replaced by older, deeper water masses (Marshall and Speer, 2012; Talley, 2013; Morrison et al., 2015). These predominantly northward flowing waters take up C_ant from the atmosphere and are eventually transferred to mode and intermediate waters that sink back into the ocean interior (Marshall and Speer, 2012; Talley, 2013). This overturning makes the Southern Ocean the largest marine C_ant sink (∼ 40 % of global ocean C_ant uptake) (Caldeira and Duffy, 2000; Mikaloff Fletcher et al., 2006; Frölicher et al., 2015; Terhaar et al., 2021b). Another region of large uptake rates is the North Atlantic (Caldeira and Duffy, 2000; Mikaloff Fletcher et al., 2006), where the Atlantic Meridional Overturning Circulation (AMOC) transports surface waters with high C_ant (Pérez et al., 2013) and subsurface waters with low C_ant concentrations northward (Ridge and McKinley, 2020). The subsurface waters outcrop in the subpolar North Atlantic where they take up C_ant from the atmosphere (Ridge and McKinley, 2020). These high C_ant waters are then ventilated by the AMOC into the deep ocean where the C_ant is efficiently stored (Joos et al., 1999; Winton et al., 2013).

While the circulation determines the volume that is transported into the deeper ocean, the Revelle factor (Revelle and Suess, 1957; Sabine et al., 2004) determines the concentration of C_ant in these water masses. The Revelle factor describes the biogeochemical capacity of the ocean to take up C_ant. This biogeochemical capacity is strongly dependent on the amount of carbonate ions in the ocean that react with CO₂ and H₂O to form bicarbonate ions (Egleston et al., 2010; Goodwin et al., 2009; Revelle and Suess, 1957). The more CO₂ is transferred via this reaction to bicarbonate ions, the more CO₂ can be taken up again from the atmosphere. The available amount of carbonate ions for this reaction depends sensitively on the difference between ocean alkalinity and dissolved inorganic carbon (C_T) (Fig. A2 in Appendix A) (Egleston et al., 2010; Goodwin et al., 2009; Revelle and Suess, 1957), highlighting the importance of alkalinity for the global ocean carbon uptake (Middelburg et al., 2020). As the buffer factor influences the C_ant uptake, it also exerts a strong control on the transient climate response, i.e., the warming per cumulative CO₂ emissions (Katavouta et al., 2018; Rodgers et al., 2020).

In addition to slowing global warming, the C_ant uptake by the ocean also causes ocean acidification (Orr et al., 2005; Gattuso and Hansson, 2011; Kwiatkowski et al., 2020), i.e., a decline in ocean pH and carbonate ion concentrations. The decline in carbonate ion concentrations has negative effects on the growth and survival of many marine species, especially on calcifying organisms whose shells and skeletons are made up of calcium carbonate minerals (Orr et al., 2005; Fabry et al., 2008; Kroeker et al., 2010, 2013; Doney et al., 2020). Calcium carbonate minerals in the ocean exist mainly in the metastable forms of aragonite and high-magnesium calcite and the more stable form calcite. The stability of calcium carbonate minerals is described by their saturation states (Ω), which describe the product of the concentrations of calcium ([Ca²⁺]) and carbonate ions ([CO${}_{\mathrm{3}}^{\mathrm{2}-}$]) divided by their product in equilibrium. Reductions of saturation states of aragonite (Ω_arag) and calcite (Ω_calc) have been shown to negatively impact organisms and ecosystems (Langdon and Atkinson, 2005; Kroeker et al., 2010; Bednaršek et al., 2014; Albright et al., 2016). Once saturation states drop below one, the water is undersaturated and actively corrosive towards the respective mineral form.

Accurately quantifying the ocean anthropogenic carbon sink is thus of crucial importance for understanding and quantifying the carbon cycle, global warming, and climate change, as well as ocean acidification. A better knowledge of the size of the historical and future ocean carbon sink and reduced uncertainties will hence not only lead to an improved understanding of the overall carbon cycle and global climate change (IPCC, 2021) but also allow targeted climate and ocean policies (IPCC, 2022). One of the key tools to assess the past, present, and future ocean carbon sink is Earth system models (ESMs). However, the simulated ocean C_ant sink varies across the different ESMs (Frölicher et al., 2015; Wang et al., 2016; Bronselaer et al., 2017; Terhaar et al., 2021b), and the model differences grow over time; i.e., ESMs that simulate a small ocean C_ant uptake over the last decades also simulate a small uptake over the 21st century (Fig. 1b) (Wang et al., 2016). Therefore, a better knowledge of the ocean C_ant sink in the last decades would be one possibility to reduce uncertainties in the simulated ocean carbon from 1850 to 2100.

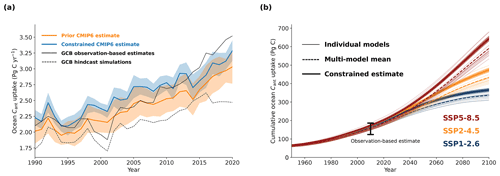
Figure 1 Simulated ocean anthropogenic carbon uptake from Earth system models. (a) Simulated annual mean air–sea C_ant fluxes from 17 CMIP6 Earth system models from 1990 to 2020 before (orange line) and after the constraint is applied (blue line). After 2014, results from SSP5-8.5 were chosen as this is the only SSP for which each model provided results, and differences in atmospheric CO₂ mixing ratios in SSP5-8.5 (Meinshausen et al., 2020) are small compared to observations until 2020 (maximum difference of 2.5 ppm in 2020) (NOAA/GML, 2022). In addition, mean air–sea C_ant fluxes based on multiple observation-based estimates (solid black line) and hindcast simulations (dashed black line) from the Global Carbon Budget 2021 (Friedlingstein et al., 2022) are shown. For readability, the uncertainties of these estimates (on average 0.24 Pg C yr⁻¹ for observation-based estimates and 0.28 Pg C yr⁻¹ for hindcast simulations) are not shown in the figure. (b) Simulated cumulative ocean C_ant uptake since 1765 for the historic period until 2014 (17 ESMs) and for the future from 2015 to 2100 under SSP1-2.6 (blue, 14 ESMs), SSP2-4.5 (orange, 16 ESMs), and SSP5-8.5 (red, 17 ESMs). Thin lines show the results from each individual ESM, the dashed lines the multi-model mean, the solid lines the constrained estimate, and the shading the uncertainty around the constrained estimate. Furthermore, the observation-based ocean C_ant inventory estimate in 2010 from Khatiwala et al. (2013) is shown. As ESM simulations in CMIP6 start in 1850, the air–sea C_ant fluxes were corrected upwards for the late starting date in the constrained estimate following Bronselaer et al. (2017) (see Appendix A, Sect. A1).

2 Quantifying the past ocean anthropogenic carbon sink with observations and hindcast simulations and existing uncertainties

The large background concentration of C_T in the ocean and the vast ocean volume make it difficult to directly observe the relatively small anthropogenic perturbations in the ocean interior. Therefore, different methods have been developed to estimate the accumulation of C_ant in the ocean (Khatiwala et al., 2013), such as the ΔC^* method (Gruber et al., 1996; Sabine et al., 2004) or the transient time distribution method (Hall et al., 2002) based on observations of inert tracers, like CFCs. These estimates result in an estimated ocean C_ant inventory in 2010 of 155 ± 31 Pg C (Khatiwala et al., 2013) (Fig. 1b, Table 1) but do not or only partly include climate-driven changes in C_T.

Further development of the ΔC^* method into the eMLR(C^*) method (Clement and Gruber, 2018) and more observations through new techniques, such as Biogeochemical-Argo (BGC-Argo) floats (Claustre et al., 2020), and more research cruises (Lauvset et al., 2021) will allow the increase in marine C_ant to be quantified on shorter timescales and with reduced uncertainty. The increase in C_ant from 1994 to 2007 by the eMLR(C^*) method is 34 ± 4 Pg C (12 % uncertainty, Table 1) (Gruber et al., 2019a), again not accounting for potential climate-driven changes in C_T. In addition to interior C_ant estimates, surface ocean observations of the partial pressure of CO₂ (pCO₂) and new statistical methods, such as neural networks (Landschützer et al., 2016), have led to a variety of observation-based estimates of the air–sea CO₂ flux (Rödenbeck et al., 2014; Zeng et al., 2014; Landschützer et al., 2016; Gregor et al., 2019; Watson et al., 2020; Iida et al., 2021; Gregor and Gruber, 2021; Chau et al., 2022). When subtracting the pre-industrial outflux of CO₂ due to riverine carbon fluxes (Sarmiento and Sundquist, 1992; Aumont et al., 2001; Jacobson et al., 2007; Resplandy et al., 2018; Lacroix et al., 2020; Regnier et al., 2022) from these air–sea CO₂ flux estimates, the global ocean C_ant uptake can be derived (Friedlingstein et al., 2022), resulting in an estimated ocean C_ant uptake from 1994 to 2007 of 29 ± 4 Pg C (14 % uncertainty, Table 1).

The difference of 5 Pg C between the interior and surface ocean mean estimates was attributed to outgassing of ocean CO₂ caused by a changing climate and climate variability (Gruber et al., 2019a). However, simulations from ESMs of the sixth phase of the Coupled Model Intercomparison Project (CMIP6) estimate the climate-driven and externally forced climate-variability-driven air–sea CO₂ flux from 1994 to 2007 to be only −1.6 ± 0.5 Pg C (Table A3). When averaging over an ensemble of ESMs, forced variability (e.g., due to the volcanic eruptions or varying emissions of CO₂ and other radiative agents) is still preserved. However, unforced interannual-to-decadal variability is largely removed when averaging over an ensemble of ESMs. Although comparisons suggest that the ocean C_ant uptake was low compared to atmospheric CO₂ in the 1990s and high in the 2000s (Rödenbeck et al., 2013, 2022), a comparison of different C_ant uptake estimates for different decadal-scale periods does not reveal any clear variability-related deviation for the 1994–2007 period (IPCC, 2021, AR6 WGI, chap. 5, Fig. 5.8; Canadell et al., 2021). Overall, uncertainties remain at present too large for any quantitative conclusions, but it seems unlikely that unforced variability causes an air–sea CO₂ flux of −3.4 Pg C (difference between −5 Pg C from Gruber et al. (2019a) and −1.6 Pg C from ESMs), twice as large as the simulated flux from forced variability and climate change. It hence remains a challenge to derive the total ocean C_ant sink from interior estimates that do not account for climate-driven changes in C_T.

An alternative way of estimating the strength of the ocean carbon sink is the use of global ocean biogeochemical models forced with atmospheric reanalysis data (Sarmiento et al., 1992; Friedlingstein et al., 2022). From 1994 to 2007, the ocean biogeochemical hindcast models that participated in the Global Carbon Budget 2021 (Friedlingstein et al., 2022) simulate a C_ant uptake of 26 ± 3 Pg C (Table 1). This estimate is 3 Pg C below the surface observation-based estimate, and the difference increases further after 2010 (Fig. 1a). Compared to the interior ocean C_ant estimate, the simulated uptake by these hindcast models is 3–6 Pg C (10 %–19 %) smaller depending on the correction term that is used for climate-change-induced outgassing of natural CO₂. Such differences between observation-based and simulated ocean C_ant uptake could be explained regionally by systematic biases in models (Goris et al., 2018; Terhaar et al., 2020a, 2021a, b), as well as data sparsity (Bushinsky et al., 2019; Gloege et al., 2021).

Overall, the difference between ocean hindcast models, observation-based CO₂ flux estimates, and interior ocean C_ant estimates, as well as the uncertainties in the climate-driven change in C_T and pre-industrial outgassing, indicate that uncertainties of the ocean C_ant sink over the last decades remain substantial. The uncertainty of the C_ant sink appears larger than the uncertainty typically given for an individual estimate of the C_ant sink from a specific data product.

Table 1 Global ocean air–sea C_ant flux estimates based on 17 ESMs from CMIP6 before and after being starting-date-corrected and constrained, as well as previous estimates over different time periods. Prior uncertainty is the multi-model standard deviation. The uncertainty of the starting-date-corrected values also includes the uncertainty from that correction. The constrained uncertainty is a combination of the starting date correction, the multi-model standard deviation after the constraint is applied, and the uncertainty from the correction itself (see Sects. 3.1 and A1). Uncertainties from the decadal variability on shorter timescales, e.g., for 1994–2007, are not included. The star indicates estimates that do not account for climate-driven changes in the ocean carbon sink.

3 Constraining the ocean anthropogenic carbon sink in Earth system models

Another way to constrain the past, present, and future global ocean anthropogenic carbon sink is the use of process-based emergent constraints (Orr, 2002) that identify a relationship across an ensemble of ESMs between a relatively uncertain variable, such as the C_ant uptake in the Southern Ocean, and a variable that can be observed with a relatively small uncertainty, such as the sea surface salinity in the subtropical–polar frontal zone in the Southern Ocean. The identified relationship is then combined with observations, in this example the sea surface salinity, to better estimate the uncertain variable, here the C_ant uptake in the Southern Ocean (Terhaar et al., 2021b). Such relationships must be explainable by an underlying mechanism (Hall et al., 2019); i.e., higher sea surface salinity in the frontal zone leads to denser sea surface waters and stronger mode and intermediate water formation, which enhances the transport of C_ant from the ocean surface to the ocean interior and allows hence for more C_ant uptake. In recent years, process-based emergent constraints have successfully reduced uncertainties in simulated processes across ensembles of ESMs (Orr, 2002; Matsumoto et al., 2004; Wenzel et al., 2014; Kwiatkowski et al., 2017; Goris et al., 2018; Eyring et al., 2019; Hall et al., 2019; Terhaar et al., 2020a, 2021a, b; Bourgeois et al., 2022). In the ocean, for example, a bias towards smaller C_ant uptake was identified in the Southern Ocean (Terhaar et al., 2021b). Similarly, ESMs from CMIP5 were shown to underestimate the future uptake of C_ant in the North Atlantic due to smaller than observed sequestration of C_ant into the deeper ocean (Goris et al., 2018). However, the relatively uncertain observation-based estimates of C_ant sequestration (see section above) did not allow Goris et al. (2018) to reduce uncertainties. Similarly, the C_ant uptake in the tropical Pacific Ocean across ESMs could be reduced with observations of the local surface ocean carbonate ion concentrations (Vaittinada Ayar et al., 2022), which is anti-correlated to the Revelle factor. Despite a better understanding of the regional C_ant uptake, uncertainties of the global ocean C_ant sink have not been reduced yet.

Here, we identify a mechanistic constraint for the global ocean C_ant sink across 17 ESMs from CMIP6 (Table A1 in Appendix A). We demonstrate that a linear combination of three observable quantities, (1) the sea surface salinity in the subtropical–polar frontal zone in the Southern Ocean, (2) the strength of the AMOC at 26.5^∘ N, and (3) the globally averaged surface ocean Revelle factor, can successfully predict the strength of the global ocean C_ant sink across the CMIP6 ESMs (r² of 0.87 for the global ocean C_ant uptake from 1994 to 2007). The sea surface salinity in the subtropical–polar frontal zone in the Southern Ocean and the AMOC determine the strength of the two most important regions of mode, intermediate, and deep-water formation (Goris et al., 2018, 2022; Terhaar et al., 2021b). In addition, the Revelle factor accounts for biases in the biogeochemical buffer capacity of the ocean, i.e., the relative increase in ocean C_T for a given relative increase in ocean pCO₂ (Revelle and Suess, 1957). As the Revelle factor quantifies relative increases in ocean C_T, the increase in surface ocean C_ant depends on the Revelle factor and the natural surface ocean C_T. Therefore, the Revelle factor in the ESMs was adjusted for model biases in natural surface ocean C_T (see Sect. A1). Compared to observations, CMIP6 models represent the observation-based average strength of the AMOC from 2004 to 2020 (16.91 ± 0.49 Sv) (McCarthy et al., 2020) right but have a large inter-model spread (16.91 ± 3.00 Sv), underestimate the observed inter-frontal sea surface salinity (34.07 ± 0.02) and have a large inter-model spread (33.89 ± 0.13), and overestimate the surface-averaged Revelle factor that was derived by GLODAPv2 (10.45 ± 0.01) by 0.24 (10.73 ± 0.24) with the largest Revelle factor biases in the main C_ant uptake regions (Fig. 2). The underestimation of the C_T-adjusted Revelle factor by the ESM ensemble is mainly due to a bias towards concentrations of surface ocean carbonate ion concentrations that are smaller than the observed concentrations (Sarmiento et al., 1995), caused by a simulated difference of surface ocean alkalinity and C_T that is smaller than the observed difference (Fig. A2).

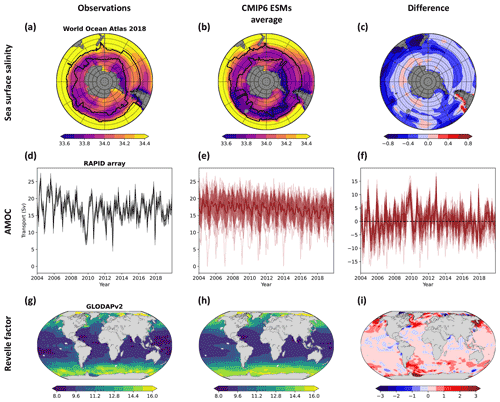
Figure 2 Sea surface salinity in the Southern Ocean, the Atlantic Meridional Overturning Circulation, and the Revelle factor at the ocean surface from observations and Earth system models. Annual mean sea surface salinity from the (a) World Ocean Atlas 2018 (Zweng et al., 2018; Locarnini et al., 2018), (b) 17 Earth system models from CMIP6 from 1995 to 2014, and (c) the difference between both. The black lines in (a, b) indicate the annual mean positions of the polar and subtropical fronts. The strength of the monthly-averaged Atlantic Meridional Overturning Circulation, here defined as the maximum of the streamfunction at 26.5^∘ N, from 2004 to 2020 (d) as observed by the RAPID array (McCarthy et al., 2020), (e) as simulated by 17 Earth system models from CMIP6, and (f) the difference between both. Each model simulation is shown in (e) and (f) as a thin red line, the multi-model average is shown as a thick red line, and the multi-model standard deviation is shown as red shading. The annual mean sea surface Revelle factor calculated with mocsy2.0 (Orr and Epitalon, 2015) from (g) gridded GLODAPv2 observations that are normalized to the year 2002 (Lauvset et al., 2016), from (h) output of 17 Earth system model simulations from CMIP6 in 2002 and adjusted for biases in the surface ocean C_T (see Sect. A1), and (i) their difference.

3.1 Applying the constraint and uncertainty estimation

For the three-dimensional emergent constraint, multi-linear regression was used. First, it was assumed that the ocean C_ant uptake for every model M ($C_{\mathrm{ant}}^M$) can be approximated by a linear combination of the inter-frontal sea surface salinity in the Southern Ocean in model M (SSS${}_{\mathrm{Southern}\mathrm{Ocean}}^M$), the AMOC strength in model M (AMOC^M), and the globally averaged surface ocean Revelle factor in model M (Revelle${}_{\mathrm{global}}^M$):

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{C}_{\mathrm{ant}}^M& =a\cdot {\mathrm{SSS}}_{\mathrm{Southern}\mathrm{Ocean}}^M+b\cdot {\mathrm{AMOC}}^M\\ & +c\cdot {\mathrm{Revelle}}_{\mathrm{global}}^M+d+\mathit{\epsilon }.\end{array}\end{array}$$

The parameters a, b, and c are scaling parameters of the three predictor variables, d is the y intercept, and ε describes the residual between the predicted C_ant flux by this multi-linear regression model and the simulated C_ant uptake by model M. The free parameters a, b, c, and d were fitted based on the simulated inter-frontal sea surface salinity in the Southern Ocean, AMOC, Revelle factor, and C_ant uptake. The three predictors are not statistically correlated (r²=0.00 for salinity and AMOC, r²=0.03 for Revelle factor and AMOC, and r²=0.10 for salinity and Revelle factor) and can hence be used in a multi-linear regression.

The constrained C_ant flux is estimated by replacing the simulated inter-frontal sea surface salinity in the Southern Ocean, AMOC, and Revelle factor by the observed ones and by setting ε to zero. As the Revelle factor describes the inverse of the ocean capacity to take up C_ant from the atmosphere, Eq. (1) should in principal be used with $\frac{\mathrm{1}}{{\mathrm{Revelle}}_{\mathrm{global}}^M}$. However, using ${\mathrm{Revelle}}_{\mathrm{global}}^M$ facilitates understanding and the presentation of the results and only introduces maximum errors of around 0.1 % for the Revelle factor adjustment for the models that simulate the largest deviations from the observed Revelle factor. To estimate the uncertainty, all model results were first corrected for their biases in the three predictor variables; i.e., if a model has a salinity that is 0.2 smaller than the observed salinity, the simulated C_ant uptake by this model is increased by a⋅0.2. The same correction is made for the other two predictor variables (Fig. 3). If the three predictor variables were predicting the C_ant flux perfectly, the bias-corrected C_ant uptake from all models would be the same. The remaining inter-model standard deviation therefore represents the uncertainty from the multi-linear regression model due to other factors that influence the ocean C_ant uptake. The second part of the uncertainty originates from the uncertainty in the observations of the predictor variables that influences the magnitude of the correction. This uncertainty ($\mathrm{\Delta }{C}_{\mathrm{ant}}^{\mathrm{obs}}$) is calculated as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathrm{\Delta }{C}_{\mathrm{ant}}^{\mathrm{obs}}& =\sqrt{{\left(a\cdot \mathrm{\Delta }{\mathrm{SSS}}_{\mathrm{Southern}\mathrm{Ocean}}^{\mathrm{obs}}\right)}^{\mathrm{2}}}\\ & \stackrel{\mathrm{‾}}{+{\left(b\cdot \mathrm{\Delta }{\mathrm{AMOC}}^{\mathrm{obs}}\right)}^{\mathrm{2}}+{\left(c\cdot \mathrm{\Delta }{\mathrm{Revelle}}_{\mathrm{global}}^{\mathrm{obs}}\right)}^{\mathrm{2}}},\end{array}\end{array}$$

with $\mathrm{\Delta }{\mathrm{SSS}}_{\mathrm{Southern}\mathrm{Ocean}}^{\mathrm{obs}}$, ΔAMOC^obs, and $\mathrm{\Delta }{\mathrm{Revelle}}_{\mathrm{global}}^{\mathrm{obs}}$ being the uncertainty of the three observed predictor variables. Eventually, the overall uncertainty of this constrained C_ant flux is estimated as the square root of the sum of the products of the square of both uncertainties.

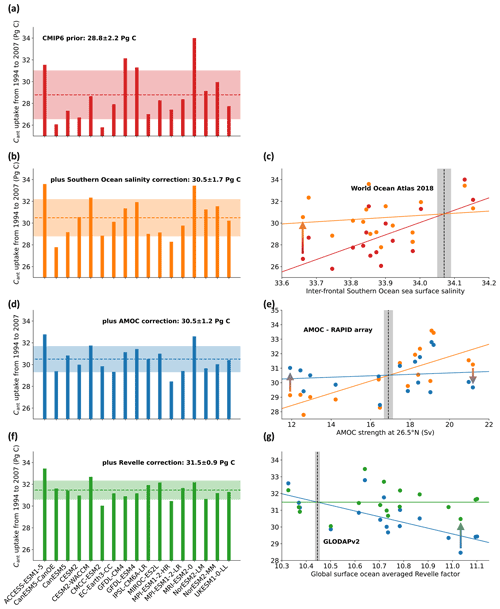
Figure 3 Global ocean anthropogenic carbon simulated by Earth system models from CMIP6 corrected for biases in sea surface salinity in the Southern Ocean, the Atlantic Meridional Overturning Circulation, and the Revelle factor. (a) Global ocean anthropogenic carbon (C_ant) uptake from 1994 to 2007 as simulated by 17 ESMs from CMIP6 and corrected for the late starting date (Bronselaer et al., 2017). For each ESM, one ensemble member was used, as the difference between ensemble members has been shown to be small compared to the inter-model differences (Terhaar et al., 2020a, 2021b). In the years 1994 and 2007, only half of the annual C_ant uptake was accounted for to make it comparable to interior ocean estimates that compare changes in C_ant from mid-1994 to mid-2007 and not from the start of 1994 to the end of 2007 (Gruber et al., 2019a). (b) C_ant uptake after correcting the simulated C_ant uptake from (a) for biases in the Southern Ocean sea surface salinity (Terhaar et al., 2021b) from (c). The dots in (c) represent individual models before (red) and after (orange) the sea surface salinity correction. (d) C_ant uptake after correcting sea-surface-salinity-corrected C_ant uptake from (b) for biases in the Atlantic Meridional Overturning Circulation from (e). The dots in (e) represent individual models before (orange) and after (blue) the Atlantic Meridional Overturning Circulation correction. (f) C_ant uptake after correcting the sea-surface-salinity- and AMOC-corrected C_ant uptake from (d) for biases in the global ocean surface Revelle factor from (g). The dots in (g) represent individual models before (blue) and after (green) the Revelle factor correction. The simulated Revelle factor by the ESMs was adjusted for biases in the surface ocean C_T (see Sect. A1). The dashed colored lines in (a), (b), (d), and (f) show the multi-model mean, and the shading shows the uncertainty, which is a combination of the multi-model standard deviation after correction and the uncertainty of the correction factor due to the uncertainty of the observational constraint (see Sect. A1). The dashed black lines in (c), (e), and (g) show the observations from the World Ocean Atlas 2018 (Zweng et al., 2018; Locarnini et al., 2018), the RAPID array (McCarthy et al., 2020), and GLODAPv2 (Lauvset et al., 2016) with their uncertainties as grey shading, the colored lines show linear fits, and the arrows illustrate the correction for individual models.

3.2 Exploiting the constraint with observations

By exploiting this multi-variable emergent constraint with observations, the simulated C_ant uptake by ESMs from 1994 to 2007 increases from 28.8 ± 2.2 to 31.5 ± 0.9 Pg C (Figs. 1 and 3, Tables 1 and A2). Biases in the Southern Ocean salinity are responsible for around 60 % of the bias in the global ocean C_ant uptake in the CMIP6 models, while the bias in the Revelle factor explains the remaining 40 % (Fig. 3). The AMOC, whose multi-model mean in ESMs is similar to observations, does not change the central C_ant uptake estimate but allows uncertainties (Fig. 3) to be reduced. The constrained C_ant uptake of 31.5 ± 0.9 Pg C is 0.9 Pg C smaller than the interior ocean C_ant estimate of 34 ± 4 Pg C based on observations (Gruber et al., 2019a) when subtracting the multi-model mean climate-driven CO₂ flux estimate from the CMIP6 models of 1.6 Pg C (Table A3). This difference of 0.9 Pg C is smaller than the uncertainties. Furthermore, the constrained C_ant uptake of 31.5 ± 0.9 Pg C is 2.5 Pg C larger than the observation-based air–sea C_ant flux estimates from 1994 to 2007 of 29 ± 4 Pg C from the Global Carbon Budget 2021 (Table 1), but both estimates agree within the uncertainties. When comparing a short period, for example the years after 2013, the observation-based air–sea C_ant flux estimates can deviate from the constrained CMIP6 ESM estimates (Fig. 1) due to unforced climate-variability-driven CO₂ flux. Thus, the small difference between observation-based ocean C_ant uptake estimates from 1994 to 2007 and the results provided here may not exist over a longer period of time and be caused by a different timing and magnitude of decadal variabilities in ESMs and the real world (Landschützer et al., 2016; Gruber et al., 2019b; Bennington et al., 2022), as well as uncertainties in the observation-based products (Bushinsky et al., 2019; Gloege et al., 2021, 2022). Indeed, when the entire period for which observation-based air–sea C_ant flux estimates from the Global Carbon Budget are available (1990–2020), the constrained estimate of the ocean C_ant sink based on ESMs (80.7 ± 2.5 Pg C) is very similar to the observation-based estimate from surface ocean pCO₂ observations (81 ± 7 Pg C) (Table 1).

The good agreement between the air–sea C_ant flux estimates from ESMs and surface ocean pCO₂ observations in combination with interior ocean C_ant of a similar magnitude suggests that the air–sea C_ant flux from hindcast simulations over the last three decades (68 ± 8 Pg C) and possibly also over the 1994–2007 period (26 ± 3 Pg C) underestimates the ocean C_ant uptake (Table 1). Therefore, the Global Carbon Budget 2021 estimate of the ocean C_ant uptake over the last decades, which is an average of the estimate of C_ant uptake from observation-based methods and hindcast models, should be corrected upwards. Reasons for this underestimation may be an underestimation of the AMOC or the Southern Ocean inter-frontal sea surface salinity, an overestimation of the Revelle factor, a small ensemble of models (8 models) that are biased towards low uptake models, very short spin-up times (Séférian et al., 2016), neglecting the water vapor pressure when calculating the local pCO₂ in each ocean grid cell (Hauck et al., 2020) as is done in CMIP models (Orr et al., 2017), or different pre-industrial atmospheric CO₂ mixing ratios (Bronselaer et al., 2017; Friedlingstein et al., 2022). However, even after correcting these hindcast simulations upwards by employing the emergent constraint identified here, their corrected estimate may remain below the CMIP-derived estimate for the period from 1994 to 2017 due to the historical decadal variations in the C_ant uptake that is not represented with the same phasing in fully coupled ESMs (Landschützer et al., 2016; Gruber et al., 2019b; Bennington et al., 2022). A detailed analysis by the individual modeling teams would be necessary to identify the reason for underestimation in the individual hindcast models, as the output is not openly available.

Over the historical period from 1850 to 2020, the constraint identified here increases the simulated ocean C_ant uptake by 15 Pg C (r²=0.80) from 174 ± 13 to 189 ± 7 Pg C (Table 1). The constrained estimate of the C_ant agrees within the uncertainties of the estimate from the Global Carbon Budget for the same period (170 ± 35 Pg C) (Friedlingstein et al., 2022), which is a combination of prognostic approaches until 1959 (Khatiwala et al., 2013; DeVries, 2014), and ocean hindcast simulations and observation-based CO₂ flux products from 1960 to 2020 (Friedlingstein et al., 2022). However, our new estimate is 19 Pg C larger and could explain around three-quarters of the budget imbalance (B_IM) between global CO₂ emissions and sinks over the period 1850 to 2020 (25 Pg C) (Friedlingstein et al., 2022) and contribute to answering an important outstanding question in the carbon cycle community.

Overall, this new estimate of the ocean C_ant uptake, based on ESMs and constrained by observations, presents an independent and new estimate of the past and present ocean C_ant uptake that is around 10 % larger and 42 %–59 % less uncertain than the multi-model average and its standard deviation, respectively. The lower bound of the uncertainty correction is for the past ocean C_ant uptake since 1765 in which the late starting date correction introduces an uncertainty that cannot be reduced without running the simulations from 1765 onwards. Towards the end of the 20th century, the uncertainty from this correction becomes smaller so that the emergent constraint can reduce uncertainties by almost 60 %.

3.2.1 Southern Ocean

While the constraints were applied globally, they are also applicable regionally as shown for the inter-frontal sea surface salinity in the Southern Ocean (Terhaar et al., 2021b). Here, we update the regional constraint in the Southern Ocean with the now additionally available ESMs and extend the constraint by adding the basin-wide-averaged Revelle factor in the Southern Ocean as a second variable. For the period from 1765 to 2005, the simulated multi-model mean air–sea C_ant flux that is adjusted for the late starting date is 63.5 ± 6.1 Pg C. Please note that the numbers here are for fluxes from 1765 to 2005 and are not the same as in Terhaar et al. (2021b), where fluxes from 1850 to 2005 were reported. The two-dimensional constraint shows a higher correlation coefficient (r²=0.70) than the one-dimensional constraint when only the inter-frontal sea surface salinity is used as a predictor (r²=0.62). Slight differences to Terhaar et al. (2021b) exist due to the additional ESMs that are by now available. When exploiting this relationship with observations of the Southern Ocean Revelle factor (12.19 ± 0.01) and the sea surface salinity, the best estimate of the cumulative air–sea C_ant flux from 1765 to 2005 in the Southern Ocean increases to 72.0 ± 3.4 Pg C. In comparison, observation-based estimates for the same period report 69.6 ± 12.4 Pg C (Mikaloff Fletcher et al., 2006) and 72.1 ± 12.6 Pg C (Gerber et al., 2009). The constraint thus reduces the uncertainty not only globally but also in the Southern Ocean by 44 %.

3.2.2 Atlantic Ocean

As for the Southern Ocean, we also apply a two-dimensional constraint to the Atlantic Ocean, using the AMOC and the basin-wide-averaged surface ocean Revelle factor in the North Atlantic as predictors. The unconstrained cumulative air–sea C_ant flux from 1765 to 2005 in the North Atlantic adjusted for the late starting date is 21.9 ± 3.3 Pg C. For this period, the two-dimensional constraint results in a relationship with a correlation coefficient of 0.57. If only the AMOC had been used, the correlation factor would have been 0.49. When exploiting this relationship with observations of the North Atlantic Revelle factor and AMOC, the best estimate of the cumulative air–sea C_ant flux from 1765 to 2005 in the Atlantic Ocean increases to 22.7 ± 2.2 Pg C. In comparison, observation-based estimates are 20.4 ± 4.9 Pg C (Mikaloff Fletcher et al., 2006) and 20.4 ± 6.5 Pg C (Gerber et al., 2009). The constrained and unconstrained estimates are both above the observation-based estimates but within the uncertainties. The constrained estimate is even higher than the unconstrained one but only by 0.8 Pg C, and its uncertainty is reduced by 33 %.

4 Consequences for projected ocean anthropogenic carbon uptake and acidification over the 21st century

As the present and future C_ant uptake are strongly correlated across ESMs, the relationship identified here can also be used to constrain future projections of the global ocean C_ant uptake. The global ocean C_ant uptake from 2020 to 2100 increases from 156 ± 11 to 173 ± 8 Pg C (r²=0.56) under the high-mitigation, low-emission Shared Socioeconomic Pathway 1-2.6 (SSP1-2.6) that likely allows us to keep global warming below 2 ^∘C (O'Neill et al., 2016; Riahi et al., 2017), from 251 ± 17 to 277 ± 9 Pg C (r²=0.74) under the middle-of-the-road SSP2-4.5, and from 407 ± 30 Pg C to 445 ± 12 Pg C (r²=0.87) under the high-emission, no-mitigation SSP5-8.5 (Fig. 1b). Overall, the future ocean C_ant uptake in CMIP6 models is thus 9 %–11 % larger than simulated by ESMs and 32 %–62 % less uncertain depending on the future scenario. The correlation coefficient and hence the uncertainty reduction reduces – but remains still large – when atmospheric CO₂ stops increasing (SSP1-2.6, SSP2-4.5). Larger uncertainties for stabilization than for near-exponential growth scenarios are expected, as the reversal of the atmospheric CO₂ growth rate will exert a stronger external impact on the magnitude of the ocean carbon sink (McKinley et al., 2020).

The increase in projected uptake of C_ant also increases the estimate of future ocean acidification rate. For ocean ecosystems, the threshold for water masses to become undersaturated towards specific calcium carbonate minerals (Ω=1) is of critical importance (Orr et al., 2005; Fabry et al., 2008; Doney et al., 2020), although negative effects for some calcifying organisms can already be observed at saturation states above one (Ries et al., 2009), and some calcifying organisms can even live in undersaturated waters (Lebrato et al., 2016). Over the 21st century, the volume of water masses in the global ocean that remain supersaturated towards the meta-stable calcium carbonate mineral aragonite is projected to decrease in CMIP6 from 283×10⁶ km³ in 2002 (based on GLODAPv2 observations; Lauvset et al., 2016) to 194×10⁶ ± 6×10⁶ km³ under SSP1-2.6, to 143×10⁶ ± 4×10⁶ km³ under SSP2-4.5, and to 97×10⁶ ± 4×10⁶ km³ under SSP5-8.5. The constraint reduces these estimates to 186×10⁶ ± 5×10⁶, 138×10⁶ ± 2×10⁶, and 93×10⁶ ± 2×10⁶ km³, respectively (r² = 0.31–0.69), resulting in an additional decrease in the available habitat for calcifying organisms of 3.7×10⁶–7.4×10⁶ km³ depending on the scenario. This additionally projected habitat loss is mainly located in the mesopelagic layer between 200 and 1000 m and thus affects organisms that live there permanently or temporarily during diel vertical migration (Behrenfeld et al., 2019). The additionally undersaturated volume corresponds to an area of 1.6–3.1 times the area of the Mediterranean Sea whose mesopelagic layer would be additionally undersaturated towards aragonite. However, the global character of the constraint and the uncertainty of the interior distribution of C_ant do not allow us to localize these areas.

5 Robustness of the emergent constraint and possible impact of changing riverine carbon input over time

Emergent constraints across large datasets such as an ensemble of ESMs with hundreds of variables can always be found and might not necessarily be reliable and robust (Caldwell et al., 2014; Brient, 2020; Sanderson et al., 2021; Williamson et al., 2021). To test the robustness of emergent constraints, three criteria were proposed (Hall et al., 2019). The constraint must be relying on a well-understood mechanism, that mechanism must be reliable, and the constraint must be validated in an independent model ensemble.

Here, the well-understood mechanisms are the fundamental ocean biogeochemical properties such as the Revelle factor (Revelle and Suess, 1957), as well as the Southern Ocean and North Atlantic large-scale ocean circulation features that are known to be the determining factors for the ocean ventilation (Marshall and Speer, 2012; Talley, 2013; Buckley and Marshall, 2016). For the Southern Ocean, the verification of the link between sea surface salinity and C_ant uptake was previously done by linking the sea surface salinity to the density and to the volume of intermediate and mode waters in each model. Furthermore, the robustness of the constraint was tested against changes in the definition of the inter-frontal zone (Terhaar et al., 2021b). In addition, other potential predictors were tested, such as the magnitude and seasonal cycle of sea-ice extent, wind curl, and the mixed layer depth, as well as upwelling strength of circumpolar deep waters. All these variables are known to influence air–sea gas exchange, freshwater fluxes, and circulation and, in turn, salinity and C_ant uptake. However, none of these factors alone explains biases in the surface salinity and C_ant uptake in the Southern Ocean. Therefore, the sea surface salinity that emerges as a result of all these individual processes represents, so far, the best variable in terms of mechanistic explanation and observational uncertainty to bias-correct models for Southern Ocean C_ant uptake. Further evidence for the underlying mechanism of the relationship between Southern Ocean sea surface salinity and C_ant uptake was provided by a later study that analyzed explicitly the stratification in the water column (Bourgeois et al., 2022). Here, we further showed that the Southern Ocean C_ant uptake constrained by the Revelle factor and the inter-frontal sea surface salinity compares much better to observation-based estimates than the unconstrained estimate, further corroborating the identified regional constraint and mechanism (Sect. 3.2.1).

Similarly, it was shown that the transport of C_ant by the AMOC is crucial for the C_ant uptake in the North Atlantic (Winton et al., 2013; Goris et al., 2018; Brown et al., 2021). As the AMOC is predominantly observed at 26.5^∘ N, a change to the definition is not possible. Instead, we replaced the AMOC as a predictor by another indicator for deep-water formation, namely the area of waters in the North Atlantic below which the water column is weakly stratified (see Sect. A1 and Table A4) (Hess, 2022). The results remain almost unchanged, indicating the robustness of the constraint and that the AMOC is indeed a good indicator for the stability of the water column in the North Atlantic and the associated deep-water formation. As for the Southern Ocean, we also made a regional two-dimensional constraint using the AMOC and the regional Revelle factor and compared it to observation-based C_ant flux estimates. The good relationship between the AMOC and the North Atlantic C_ant uptake improves the confidence in the AMOC as a valid predictor.

Eventually, we also tested the robustness of the biogeochemical predictor by varying the definition of the Revelle factor. First, the Revelle factor was only calculated north of 45^∘ N and south of 45^∘ S, assuming that the high-latitude regions are responsible for the largest C_ant uptake, and second, the global Revelle factor was calculated by weighting the Revelle factor in each cell by the multi-model mean cumulative C_ant uptake from 1850 to 2100 in that cell so that the Revelle factor in cells with larger uptake is more strongly weighted. Under both definitions, the results remain almost unchanged (Table A4). Furthermore, the Revelle factor has been shown here to improve the C_ant uptake in the Atlantic and Southern Ocean and has been earlier shown to determine the C_ant uptake in the tropical Pacific Ocean (Vaittinada Ayar et al., 2022), suggesting that the Revelle factor is a robust predictor of global and regional ocean C_ant uptake.

To provide further indication of the importance of the AMOC and the Southern Ocean surface salinity and the three-dimensional constraint in general, we have compared simulated CFC-11, provided by 10 ESMs from CMIP6, with observed CFC-11 from GLODAPv2.2021 (Lauvset et al., 2021) (Sect. A4) and also compared the interior ocean distribution of C_ant with observation-based estimates (Sabine et al., 2004; Gruber et al., 2019a) (Sect. A5). The comparison of CFCs demonstrates the importance of the AMOC for the ventilation of the North Atlantic, as ESMs with a low AMOC underestimate the observed subsurface CFC-11 concentrations in the North Atlantic. Similarly, ESMs with a small inter-frontal Southern Ocean surface salinity underestimate observed subsurface (below 200 m) CFC-11 concentrations in the Southern Hemisphere. In addition to the evaluation with observations of CFC, the comparison of the interior ocean C_ant distribution demonstrates first that the ESMs on average represent the observation-based distributions within the margins of error (Tables A5 and A6). Only in the Southern Hemisphere does the ESM average remain below, as expected due to the average ESM bias towards inter-frontal sea surface salinities that are too low compared to observed ones, less formation of mode and intermediate waters, and hence relatively little storage of C_ant in the Southern Hemisphere. When using the model that represents best the three predictors, GFDL-ESM4 (Geophysical Fluid Dynamics Laboratory ESM4; Dunne et al., 2020; Stock et al., 2020), the comparison to observation-based interior ocean C_ant distribution becomes almost identical (Tables A7 and A8), suggesting that a better representation of these parameters indeed improves the simulation of C_ant uptake and its distribution in the ocean interior.

To validate the constraint identified here in another model ensemble, we used all six ESMs of the CMIP5 ensemble that provided all necessary output variables (Table A1). As these six ESMs are not sufficient to robustly fit a function with four unknown parameters, we applied the predicted relationship by the CMIP6 models to the CMIP5 models and evaluated how well this relationship allows the simulated historical C_ant uptake to be predicted by these models. The CMIP6-derived relationship allows us to predict the simulated C_ant uptake with an accuracy of 3 % (± 5 Pg C) for the period from 1850 to 2014 and with an accuracy of 4 % (± 1.3 Pg C) for the period from 1994 to 2007 (Fig. A5). The largest uncertainty stems from the NorESM2-ME (Norwegian Earth System Model version 2) model, which simulates a historical AMOC strength of ∼ 30 Sv, almost twice as large as the observed AMOC strength and ∼ 9 Sv larger than all other CMIP6 ESMs over which the relationship was fitted. For such strong deviations from the observations and other ESMs, the linear relationship might not be applicable anymore. However, despite one out of six ESMs from CMIP5 having a particularly high AMOC, the relationship identified here still allows us to predict the simulated C_ant uptake with small uncertainties and hence confirms its applicability.

Despite this robustness, emergent constraints are, by definition, always relying on the existing ESMs and on the processes that are represented by these ESMs. If certain processes are not implemented or implemented in the same way across all ESMs, biases over the entire model ensemble can occur that cannot be corrected by an emergent constraint (Sanderson et al., 2021). Possible non-represented processes in our case are, among others, changing freshwater input from the Greenland and Antarctic ice sheet that may impact the freshwater cycle and circulation in the Southern Ocean or the AMOC, as well as changes in riverine input of carbon over time. However, the expected effect of ice melt on sea surface salinity in the Southern Ocean and on the AMOC is small compared to the model spread (Bakker et al., 2016; Terhaar et al., 2021b), at least on the timescales considered here. Changing riverine carbon fluxes could, however, have a larger effect. So far, only one CMIP6 ESM, the CNRM-ESM2-1 (Séférian et al., 2019), has dynamic carbon riverine delivery that changes with global warming. In this model, carbon riverine delivery increases over the 20th century so that the interior ocean change in C_ant in 2000 is around 19 Pg C smaller than the air–sea C_ant uptake (Fig. A4). The situation reverses at the beginning of the 21st century so that riverine carbon delivery increases, and the interior ocean change in C_ant becomes up to 60 Pg C larger than the air–sea C_ant uptake. As such, riverine carbon delivery has the potential to enhance or decrease the ocean C_ant inventory in addition to air–sea C_ant uptake. This would also question the comparability of C_ant inventory and air–sea C_ant uptake estimates. However, the present state of the ESMs does not allow a quantitative assessment of this process, and future research is needed.

In addition, parametrizations of non-represented processes such as mesoscale and sub-mesoscale circulation features like small-scale eddies may lead to biases in the model ensemble. For individual models, it has been shown that changes in horizontal resolution and hence a more explicitly simulated circulation change the model physics and biogeochemistry and hence also the ocean carbon and heat uptake (Lachkar et al., 2007, 2009; Dufour et al., 2015; Griffies et al., 2015). However, an increase in resolution does not necessarily lead to improved simulations, and the changes in oceanic C_ant uptake may be lower or higher, depending on the model applied. When increasing the NEMO (Nucleus for European Modelling of the Ocean) ocean model from a non-eddying version (2^∘ horizontal resolution) to an eddying version (0.5^∘), Lachkar et al. (2009) find a decrease in the sea surface salinity of around 0.1 at the Southern Ocean surface that brings the model further away from the observed salinity, a decrease in the volume of Antarctic intermediate water, and a decrease in the Southern Ocean uptake of CFC and hence likely also of C_ant. This example corroborates the underlying mechanism of the emergent constraint in the Southern Ocean that higher sea surface salinity directly affects the formation of Antarctic intermediate water and the uptake of C_ant. Another example can be found within the ESM ensemble of CMIP6. The MPI-ESM-1-2-HR and MPI-ESM-1-2-LR have a horizontal resolution of 0.4 and 1.5^∘, respectively, but the same underlying ocean model. The high-resolution version has an inter-frontal salinity of 33.98, a Southern Ocean surface Revelle factor of 12.82, and a Southern Ocean C_ant uptake from 1850 to 2005 of 56.4 Pg C. The coarser-resolution version has an inter-frontal sea surface salinity of 33.92, a Southern Ocean surface Revelle factor of 12.89, and a Southern Ocean C_ant uptake of 58.0 Pg C. These differences are much smaller than the inter-model differences (33.66–34.15 for salinity, 12.14–13.11 for the Revelle factor, and 48.8–71.1 Pg C for the Southern Ocean C_ant uptake) that result from different ocean circulation and biogeochemical models, sea-ice models, and atmospheric and land biosphere models, as well as the coupling between these models. These examples show that higher resolution does not necessarily lead to better results, affecting potentially the predictor and the predicted variable in the same way, and that differences in the underlying model components and spin-up and initialization strategies lead so far to much larger differences between ESMs than resolution does (Séférian et al., 2020). As long as simulations with higher resolution, which are also spun-up over hundreds of years (Séférian et al., 2016), are not yet available, and potentially important processes such as changing riverine fluxes and freshwater from land ice are not included, it remains speculative if higher resolution would lead to a reduction in inter-model uncertainty or even a better representation of the observations. Moreover, the relationships identified here that are based on the current understanding of physical and biogeochemical oceanography and that were tested for robustness in several ways may likely also exist across ensembles of eddy-resolving models.

6 Conclusion

The three-dimensional emergent constraint identified here reveals a bias towards an insufficient C_ant uptake by the CMIP6 ESM ensemble, reduces uncertainties of the global ocean C_ant sink, and leads to an enhanced process understanding of the C_ant uptake in ESMs. The constraint was tested for robustness in multiple ways and across different model ensembles. It was evaluated regionally and globally against CFC measurements, against estimates of the interior ocean C_ant accumulation, and against observation-based estimates of the air–sea CO₂ flux globally and regionally. The constraint demonstrates that the global ocean C_ant uptake can be estimated from three observable variables, the salinity in the subtropical–polar frontal zone in the Southern Ocean, the Atlantic Meridional Overturning Circulation, and the global surface ocean Revelle factor. The uncertainties of the regional ocean C_ant uptake estimates in the Atlantic and Southern Ocean can also be reduced with the respective regional predictors. Improved or continuing observations of these quantities (Lauvset et al., 2016; Zweng et al., 2018; Locarnini et al., 2018; Claustre et al., 2020; McCarthy et al., 2020) and their representation and evaluation in ESMs and ocean models should therefore be of priority in the next years and decades. Although biogeochemical variables were tuned or calibrated in more ESMs in CMIP6 than in CMIP5 (Séférian et al., 2020), this tuning does not seem to result in better results than in untuned ESMs yet (Fig. A3).

Moreover, biases in these quantities and corrections for the late starting date may well be the reason for offset between models and observations over the last 30 years (Hauck et al., 2020; Friedlingstein et al., 2022). Although the constraints identified here cannot correct for misrepresentation of the unforced decadal variability, such variability likely plays a minor role when averaging results over longer periods. Indeed, we find good agreement between our estimate and the observation-based estimate from the Global Carbon Budget 2021 for the period from 1990 to 2020. This agreement suggests that the hindcast models underestimate the ocean C_ant uptake. This underestimation is thus likely the explanation for the difference between models and the observation-based product in the Global Carbon Budget (Friedlingstein et al., 2022). However, the output of the Global Carbon Budget hindcast models is not publicly available for evaluating possible data–model differences for the inter-frontal sea surface salinity, the AMOC, and the Revelle factor.

Despite this step forward in the understanding of ESMs, a comprehensive research strategy that combines the measurements of important physical, biogeochemical, and biological parameters in the ocean with other data streams and modeling is needed. A comprehensive approach is necessary to improve our still incomplete understanding of the global carbon cycle and its functioning in the climate and Earth system over the past and under ongoing global warming.

The larger than previously estimated future ocean C_ant sink corresponds to around 2 to 4 years of present-day CO₂ emissions (∼ 10.5 Pg C yr⁻¹) depending on the emission pathway. The larger ocean C_ant sink thus increases the estimated remaining emission budget but only by a small amount. However, it also results in enhanced projected ocean acidification that may be harmful for large, unique ocean ecosystems (Fabry et al., 2008; Gruber et al., 2012; Kawaguchi et al., 2013; Kroeker et al., 2013; Doney et al., 2020; Hauri et al., 2021; Terhaar et al., 2021a).

This study follows recent approaches by the IPCC and climate science that suggest using the best available information about models instead of a multi-model mean to provide consistent and accurate information for climate science and policy (IPCC, 2021; Hausfather et al., 2022). The improved estimate provided here of the size of the global ocean carbon sink may help to close the carbon budget imbalance from 1850 onwards (Friedlingstein et al., 2022) and to improve the understanding of the overall carbon cycle and the global climate (IPCC, 2021). Eventually, a better understanding of the ocean carbon sink and the reduction of its uncertainties in the past and in the future will allow better-targeted climate and ocean policies (IPCC, 2022).

Appendix A

A1 Earth system models

Model outputs from 18 Earth system models from CMIP6 and 6 Earth system models from CMIP5 (Table A1) were used for the analyses.

Table A1 CMIP5 and CMIP6 models used in this study and the corresponding model groups.

^* CMIP5 models are written in italics.

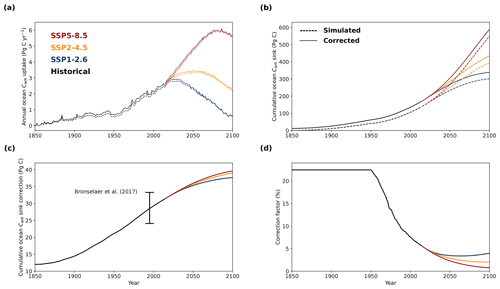
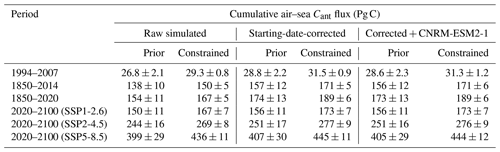
Figure A1 Correction of simulated anthropogenic carbon air–sea flux for the late starting date in Earth system models. (a) Multi-model annual mean anthropogenic carbon (C_ant) air–sea flux for 17 ESMs from CMIP6 before (dashed lines) and after (solid lines) the correction for the late starting date over the historical period from 1850 to 2014 (black) and for the future from 2015 to 2100 under SSP1-2.6 (blue), SSP2-4.5 (orange), and SSP5-8.5 (red). (b) Cumulative ocean C_ant uptake since 1765 (corrected simulated flux) and 1850 (raw simulated flux), (c) difference between cumulative ocean C_ant uptake between corrected and raw simulated flux, and (d) the correction factor that was applied. The C_ant correction that was estimated by Bronselaer et al. (2017) is shown in (c). The cumulative C_ant uptake from 1765 to 1850 was set to 12 Pg C as estimated by Bronselaer et al. (2017).

Table A2 Global ocean air–sea CO₂ flux estimates based on 17 ESMs from CMIP6 before and after constraint over different periods with corrected and uncorrected estimates and with and without CNRM-ESM2-1. Prior uncertainty is the multi-model standard deviation, and constrained uncertainty is a combination of the multi-model standard deviation after correction and the uncertainty from the correction itself (see Sect. 3.1).

The analyzed variables include the air–sea CO₂ flux (fgco2, name of the variable in standardized CMIP output), total dissolved inorganic carbon (dissic), total alkalinity (talk), total dissolved inorganic silicon (si), total dissolved inorganic phosphorus (po4), potential temperature (thetao), salinity (so), and the Atlantic meridional streamfunction (msftmz or msftyz). All ESMs were included for which the entire set of variables was available on the website of the Earth System Grid Federation at the start of the analysis. Based on these variables, all other presented variables were derived.

• The air–sea C_ant flux was calculated as the difference in air–sea CO₂ flux between the historical plus future (SSP for CMIP6 and RCP (Representative Concentration Pathway) for CMIP5) simulation and the corresponding pre-industrial control simulation on the native model grids (where possible). The air–sea C_ant fluxes were corrected for their late starting date in 1850 (and 1861 for GFDL-ESM2M) and the slightly higher atmospheric CO₂ mixing ratio in that year compared to the beginning of industrialization and the start of the CO₂ increase in 1765 (Bronselaer et al., 2017). To that end, we scaled the simulated air–sea C_ant flux with the anthropogenic change in the atmospheric partial pressure of CO₂ (pCO₂) with respect to pre-industrial conditions following previous studies (Mikaloff Fletcher et al., 2006; Gruber et al., 2009; Terhaar et al., 2021b):

  $$\begin{array}{}\text{(A1)}& C_{\mathrm{ant}}^{\mathrm{corr}}\left(t\right)=C_{\mathrm{ant}}\left(t\right){\displaystyle \frac{p{\mathrm{CO}}_{\mathrm{2}}\left(t\right)-p{\mathrm{CO}}_{\mathrm{2}}\left(\mathrm{1765}\right)}{p{\mathrm{CO}}_{\mathrm{2}}\left(t\right)-p{\mathrm{CO}}_{\mathrm{2}}\left(\mathrm{1850}\right)}},\end{array}$$

  with C_ant(t) being the simulated air–sea C_ant flux by the respective ESM in year t and $C_{\mathrm{ant}}^{\mathrm{corr}}\left(t\right)$ being the corrected air–sea C_ant flux. For GFDL-ESM2M, which starts in 1861, the correction was made with respect to pCO₂(1861). When pCO₂(t) is close to pCO₂(1850), their difference becomes unrealistically large, causing overly strong flux corrections. Therefore, we limited the flux correction in magnitude using the correction term in the year 1950 as an upper limit. By doing so, we do not only remove unrealistically high air–sea C_ant fluxes before 1950 but also reach excellent agreement with the previously estimated air–sea C_ant flux correction term of Bronselaer et al. (2017) (Fig. A1). When the cumulative C_ant fluxes since 1765 are shown, an additional amount of 12 Pg C (16 Pg C for GFDL-ESM2M) was added that was estimated to have entered the ocean before 1850 (Bronselaer et al., 2017). For comparison, we also calculated the constrained estimates for the ocean C_ant sink when no air–sea C_ant flux correction is applied (Table A2). Bronselaer et al. (2017) estimate the uncertainty of the correction to be ± 16 % for cumulative C_ant fluxes from 1765 to 1995. Although uncertainties reduce over time, we apply the 16 % from the past to all estimates and hence provide a conservative upper bound of this uncertainty.

• Accordingly, the change in ocean interior C_ant was calculated as the difference in total dissolved inorganic carbon between the historical plus future (SSP/RCP) simulation and the corresponding pre-industrial control simulation on the native model grids (where possible).

• The change in air–sea CO₂ flux that is caused by a changing climate was calculated as the difference in fgco2 in the historical simulation and the “bgc” simulation in which only atmospheric CO₂ changes but not the climate. These “bgc” simulations were available for five ESMs (Table A3).

• The surface ocean Revelle factor was calculated from sea surface total dissolved inorganic carbon (dissic), total alkalinity (talk), total dissolved inorganic silicon (si), total dissolved inorganic phosphorus (po4), potential temperature (thetao), and salinity (so) averaged around the year 2002 (from 1997 to 2007 for CMIP6 and 1999 to 2005 for CMIP5; 2005 is the last year of the historical simulation) using mocsy2.0 (Orr and Epitalon, 2015) with its default constants that are recommended for best practice (Dickson et al., 2007). The years were centered around 2002 to make the Revelle factor comparable to the one estimated based on GLODAPv2, which is normalized to the year 2002 (Lauvset et al., 2016). As the Revelle factor describes the relative change in C_T per relative change in pCO₂ (Revelle and Suess, 1957), the absolute uptake of C_T does not only depend on the Revelle factor but also on the natural C_T in the surface ocean. To calculate the buffer capacity for each ESM, the Revelle factor was therefore adjusted in each grid cell by multiplying it by the ratio of observed C_T and the simulated C_T in each ESM separately. Data from each ESM were regridded on a regular 1^∘ × 1^∘ grid to make them comparable to the gridded GLODAPv2 data. Furthermore, a mask was applied before the basin-wide-averaged Revelle factor was calculated so that only those values were used for which all ESMs and the gridded GLODAPv2 product had data. In addition, marginal seas (Mediterranean Sea, Hudson Bay, Baltic Sea) were excluded because global ESMs are not designed to accurately represent these small-scale seas. In addition, the surface ocean carbonate ion (CO${}_{\mathrm{3}}^{\mathrm{2}-}$) concentration was calculated so that the C_T-adjusted Revelle factor is mainly determined by the CO${}_{\mathrm{3}}^{\mathrm{2}-}$ concentrations, which itself can be approximated by the difference between surface ocean alkalinity and C_T (Fig. A2).

• The monthly AMOC strength was calculated as the maximum of the streamfunction below 500 m at the latitude in the respective model that is closest to 26.5^∘ N for each month from 2004 to 2020. After 2014, simulated outputs from SSP5-8.5 and RCP4.5 were used as all ESMs provided output for these pathways. For SSP5-8.5, the mole fraction of atmospheric CO₂ in SSP5-8.5 is 414.9 ppm in 2020 (Meinshausen et al., 2020), 2.5 ppm over the observed mole fraction of atmospheric CO₂ in 2020 (NOAA/GML, 2022). For RCP4.5, the mole fraction of atmospheric CO₂ is 412.4 ppm in 2020. Such small differences in the mole fraction of atmospheric CO₂ do not cause detectable changes in global warming or the AMOC (IPCC, 2021).

• Future saturation states of aragonite were calculated from simulated changes in total dissolved inorganic carbon (dissic), total alkalinity (talk), total dissolved inorganic silicon (si), total dissolved inorganic phosphorus (po4), potential temperature (thetao), and salinity (so) since 2002 that are added to the respective observed variables from the gridded GLODAPv2 product, which are normalized to 2002, using mocsy2.0 (Orr and Epitalon, 2015) with its default constants that are recommended for best practice (Dickson et al., 2007). By only adding simulated differences, model uncertainties in the initial state of the ocean biogeochemical system in the deeper ocean are removed (Orr et al., 2005; Terhaar et al., 2020a, 2021a, b). All variables were regridded before on a regular 1^∘ × 1^∘ grid so that they could be added to the gridded GLODAPv2 data. The same mask that was also used to compare the Revelle factor was applied to make all projections comparable.

• The annual average sea surface salinity between the polar and subtropical front in the Southern Ocean was derived from regridded (1^∘ × 1^∘ regular grid) monthly sea surface salinity and temperatures (for defining the fronts) following Terhaar et al. (2021b).

• The area of weakly stratified waters was calculated based on climatologies of the potential temperature and salinity from 1995 to 2014 (Hess, 2022). All data were regridded on a regular 1^∘ × 1^∘ grid with 33 depth levels before analysis. An area was defined as weakly stratified if the density gradient between the surface and the cell at 1000 m depth was smaller than 0.5 kg m⁻³ in a given month, assuming that such a small monthly mean gradient allows mixing of water into the lower limb of the AMOC at some time in that month. This predictor, as well as the different ways of calculating the Revelle factor predictor (see Sect. 5, “Robustness of the emergent constraint and possible impact of changing riverine carbon input over time”), was used to test the robustness of the emergent constraint identified here (Table A4).

The model CNRM-ESM2-1 was not used for the constraints because it includes dynamical riverine forcing that no other model includes (Fig. A4) and is not directly comparable. Instead, output from this ESM was prominently used in the section “Robustness of the emergent constraint and possible impact of changing riverine carbon input over time”. However, even if CNRM-ESM2-1 had been included, the results would change by less than 1 % (Table A2).

Table A3 Climate-driven changes in the air–sea CO₂ flux (Pg C yr⁻¹) as simulated by five Earth system models from CMIP6.

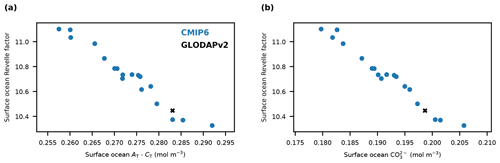
Figure A2 Surface ocean Revelle factor against the difference of surface alkalinity and dissolved inorganic carbon, as well as against surface carbonate ion concentrations. Basin-wide-averaged surface ocean Revelle factor as simulated by 18 ESMs from CMIP6 (blue dots) against the basin-wide-averaged surface ocean (a) difference between total alkalinity (A_T) and C_T and (b) carbonate ion (CO${}_{\mathrm{3}}^{\mathrm{2}-}$) concentrations. The observation-based estimates from GLODAPv2 are shown as black crosses. The Revelle factor in each ESM was adjusted for biases in the surface ocean C_T (see Sect. A1).

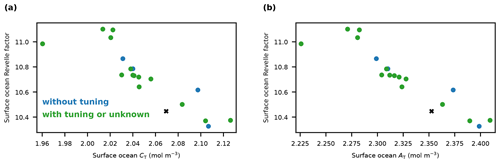
Figure A3 Surface ocean Revelle factor against the surface alkalinity and dissolved inorganic carbon. Basin-wide-averaged surface ocean Revelle factor as simulated by 18 ESMs from CMIP6 (blue dots) against the basin-wide-averaged surface ocean (a) total alkalinity (A_T) and (b) C_T. The observation-based estimates from GLODAPv2 are shown as black crosses. The Revelle factor in each ESM was adjusted for biases in the surface ocean C_T (see Sect. A1).

Table A4 Constrained global ocean air–sea CO₂ flux estimates based on 17 ESMs from CMIP6 with varying predictors.

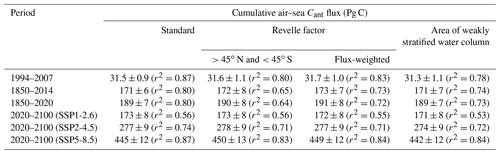
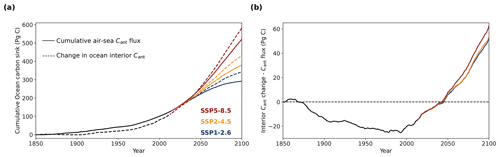
Figure A4 Anthropogenic carbon air–sea fluxes and inventory changes simulated by CNRM-ESM2-1. (a) Cumulative air–sea anthropogenic carbon (C_ant) fluxes (solid lines) and C_ant interior changes (dashed lines) as simulated by CNRM-ESM2-1 for the historic period until 2014 (black) and from 2015 to 2100 under SSP1-2.6 (blue), SSP2-4.5 (orange), and SSP5-8.5 (red), (b) as well as the difference of both quantities. The thin dashed black line in (b) indicates zero difference.

A2 Observations and observation-based products

Throughout this paper, three observation-based products are used to constrain the ESM output.

Monthly climatologies of sea surface salinity and sea surface temperatures from the World Ocean Atlas 2018 (Zweng et al., 2018; Locarnini et al., 2018) were used to derive annual averages and uncertainties of the sea surface salinity between the polar and subtropical fronts in the Southern Ocean following Terhaar et al. (2021b). Climatologies of the World Ocean Atlas 2018 were also used to calculate the area of weakly stratified surface waters.

Time series of the AMOC strength from the RAPID array (McCarthy et al., 2020) were used to calculate monthly means and uncertainties of the AMOC from 2004 to 2020.

The gridded observation-based estimates of total dissolved inorganic carbon, total alkalinity, total dissolved inorganic silicon, total dissolved inorganic phosphorus, in situ temperature, and salinity from GLODAPv2 (Lauvset et al., 2016) were used to calculate the Revelle factor and acted as a starting point for projected saturation states over the 21st century (see above).

A3 Validation of the identified constraint in CMIP5

The emergent constraint identified here was derived from an ensemble of 17 ESMs from CMIP6. To test the robustness of emergent constraints, these constraints should be validated in an independent ensemble of ESMs (Hall et al., 2019). Here, we used all six ESMs from CMIP5, which provided all necessary output variables for this analysis (see Sect. A1). For all these models, the C_ant uptake for the period from 1994 to 2007 and from 1850 to 2014 was predicted based on the simulated inter-frontal sea surface salinity in the Southern Ocean, the AMOC strength, and the global ocean basin-wide-averaged Revelle factor using the multi-linear relationship derived from the CMIP6 models (Fig. A5).

Figure A5 Global ocean anthropogenic carbon uptake simulated by Earth system models from CMIP5 against the predicted uptake based on simulated predictors from CMIP6 models. Global ocean anthropogenic carbon uptake simulated by six ESMs from CMIP5 (Table A1) (a) from 1994 to 2007 and (b) from 1850 to 2014 against the predicted anthropogenic carbon uptake based on the simulated CMIP6 predictors in each ESM: the inter-frontal annual mean sea surface salinity in the Southern Ocean, the Atlantic Meridional Overturning Circulation, and the Revelle factor adjusted for surface ocean C_T. Please note that two ESMs are at almost the same place in (a) with a predicted C_ant uptake of around 31 Pg C.

A4 Comparison between simulated and observed CFC-11 concentrations

Comparison between simulated and observed CFC-11 uptake can be used to estimate the ventilation of waters from the surface waters to the deeper ocean (Hall et al., 2002). Although CFCs can roughly evaluate the ventilation rate of the ocean, no perfect agreement between CFCs and C_ant can be expected as CFCs are not taken up at the same speed as C_ant (i.e., fast air–sea equilibration timescale for CFC), and their solubility has a different temperature dependency than the solubility of C_ant (warm waters can hold less CFCs but more C_ant due to their low Revelle factor, whereas cold waters hold more CFCs but less C_ant) (Revelle and Suess, 1957; Broecker and Peng, 1974; Weiss, 1974). These differences can lead to differences between uptake, storage, and distribution of CFCs and C_ant that can become especially large in high-latitude oceans (Matear et al., 2003; Terhaar et al., 2020b).

Here, we use simulated CFC-11 from ESMs and observed CFC-11 from GLODAPv2.2021 (Lauvset et al., 2021) to provide further evidence that the inter-frontal sea surface salinity in the Southern Ocean and the AMOC are good indicators of the ocean ventilation and that ESMs tend to underestimate the ventilation of surface waters to the deeper ocean. Out of the 18 ESMs from CMIP6, 10 provided simulated three-dimensional fields of CFC-11 (CanESM5, CESM2, CESM2-WACCM, EC-Earth-CC, GFDL-CM4, GFDL-ESM4, MRI-ESM2-0, NorESM2-LM, NorESM2-MM, UKESM1-0-LL). To compare these ESMs to the observed concentrations, all ESMs were sampled at the same time (month and year), the same latitude and longitude, and the same depth as the observations. To assess the ventilation below the mixed layer, we only used observations below 200 m. Furthermore, we limited our assessment to observations until 2004 as CFC-11 in the atmosphere peaked in 1994 (Bullister, 2017), and subducted waters since then might already re-emerge to the surface. Thus, 506 000 measurements remained. As these measurements are not equally distributed and strongly clustered in the Northern Hemisphere (Lauvset et al., 2021), we mapped all measurements on a regular 5^∘ × 5^∘ grid with 11 depth levels from 200 to 6000 m that increase with depth. In each cell on the grid the average bias was calculated. Afterwards, the volume-averaged bias was calculated for the Southern Hemisphere and the North Atlantic (limited by the Equator and 65^∘ N) (Fig. A6).

Figure A6 Biases in subsurface CFC-11 concentrations between observations against the Atlantic Meridional Overturning Circulation and the inter-frontal Southern Ocean salinity. Basin-wide-averaged biases in CFC-11 concentrations (observations minus simulated) below 200 m for all 10 ESMs that provided simulated CFC-11 (blue dots) (a) in the North Atlantic Ocean (north of the Equator and limited by the Fram Strait, the Barents Sea Opening, and Baffin Bay) and against the AMOC and (b) in the Southern Hemisphere (south of the Equator) against the inter-frontal annual mean sea surface salinity in the Southern Ocean. The observation-based estimates for the AMOC and the inter-frontal annual mean sea surface salinity in the Southern Ocean are shown as black crosses and with zero bias in CFC-11.

A5 Comparison between simulated and observation-based estimates of the interior ocean C_ant accumulation

Another way to test the emergent constraint identified here is the comparison to observation-based estimates of the interior ocean C_ant accumulation. Here, we compare model results against the estimate for interior ocean C_ant accumulation from 1800 to 1994 (Sabine et al., 2004) and from 1994 to 2007 (Gruber et al., 2019a), although different reconstruction methods yield different results (e.g., Khatiwala et al., 2013, their Fig. 4). While a good representation of the interior ocean C_ant distribution is not necessarily related to a correct estimate of the air–sea C_ant flux, it can provide an indication of the model performance and the robustness of the applied corrections. For both comparisons, we compare the multi-model mean and standard deviation and results from the ESM that represent best the three observational predictors (i.e., GFDL-ESM4). GFDL-ESM4 has a global ocean Revelle factor of 10.37, an inter-frontal sea surface salinity of 34.00, and an AMOC of 18.25. The biases that may exist in the multi-model mean, such as relatively little C_ant in the Southern Hemisphere due to a multi-model-averaged sea surface salinity that is too low compared to observed sea surface salinities, should be smaller for GFDL-ESM4.

The comparison to the observation-based estimate of C_ant accumulation from 1800 to 1994 (Sabine et al., 2004) demonstrates that the ESMs represent the distribution of C_ant in the ocean between the basins and different latitudinal regions well (Table A5). Small underestimations exist in the Indian and Atlantic tropical oceans, as well as in the southern subpolar Atlantic Ocean. The differences in the Indian Ocean may well be to observational uncertainties that are especially large in this relatively under-sampled ocean basin (Sabine et al., 2004; Gruber et al., 2019a). The underestimation in the Southern Atlantic and the Atlantic sector of the Southern Ocean are consistent with an underestimation of the formation of mode and intermediate waters in the Southern Ocean due to a sea surface salinity that is too low. This underestimation is strongly reduced in the GFDL-ESM4 model (Table A6), indicating that the better representation of the inter-frontal sea surface salinity in the Southern Ocean also improves the simulated distribution of C_ant in the ocean. Furthermore, GFDL-ESM4 also simulates slightly higher C_ant in the North Atlantic, consistent with its AMOC being slightly too high.

The comparison for the period from 1994 to 2007 also indicates that the ESMs on average simulate the C_ant interior storage pattern as estimated based on observations of Gruber et al. (2019a) (Table A7). The ESMs agree with the observation-based estimates with respect to the basin and hemispheric distribution. However, they underestimate on average the storage in the Southern Hemisphere in line with the underestimation of the formation of intermediate and mode waters in the Southern Ocean. When only considering GFDL-ESM4 (Table A8), this underestimation is reduced, and all other regions show very good agreement.

The remaining small difference in both comparisons may be also due to different alignments of the basin boundaries, an unknown distribution of the C_ant that entered the ocean before 1850 and has been advected 50 years longer in the ocean interior in the case of Sabine et al. (2004), a different decadal variability in GFDL-ESM4 than in the real world in the case of Gruber et al. (2019a), and uncertainties in the observation-based estimates. Despite all these potential pitfalls, the three-dimensional repartition of C_ant between observation-based products and ESMs agree, and the model that best simulates the three key predictors, GFDL-ESM4, is almost identical to the observation-based estimates.

Table A5 Distribution of C_ant inventories (in Pg C) by basin and latitude band for 1994. The first number in each cell is the multi-model mean and standard deviation across all 18 ESMs from CMIP6, and the second number is from Table S1 in Sabine et al. (2004).

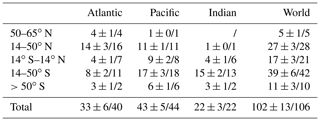
Table A6 Distribution of C_ant inventories (in Pg C) by basin and latitude band for 1994. The first number in each cell is derived from GFDL-ESM4, and the second number is from Table S1 in Sabine et al. (2004).

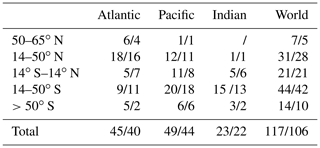
Table A7 Distribution of C_ant inventories (in Pg C) by basin and hemisphere from 1994 to 2007. The first number in each cell is the multi-model mean and standard deviation across all 18 ESMs from CMIP6, and the second number is from Table 1 in Gruber et al. (2019a).

Table A8 Distribution of C_ant inventories (in Pg C) by basin and hemisphere from 1994 to 2007. The first number in each cell is derived from GFDL-ESM4, and the second number is from Table 1 in Gruber et al. (2019a).