the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A Numerical reassessment of the Gulf of Mexico carbon system in connection with the Mississippi River and global ocean
Le Zhang
Coupled physical–biogeochemical models can fill the spatial and temporal gap in ocean carbon observations. Challenges of applying a coupled physical–biogeochemical model in the regional ocean include the reasonable prescription of carbon model boundary conditions, lack of in situ observations, and the oversimplification of certain biogeochemical processes. In this study, we applied a coupled physical–biogeochemical model (Regional Ocean Modelling System, ROMS) to the Gulf of Mexico (GoM) and achieved an unprecedented 20-year high-resolution (5 km, ) hindcast covering the period of 2000 to 2019. The biogeochemical model incorporated the dynamics of dissolved organic carbon (DOC) pools and the formation and dissolution of carbonate minerals. The biogeochemical boundaries were interpolated from NCAR's CESM2-WACCM-FV2 solution after evaluating the performance of 17 GCMs in the GoM waters. Model outputs included carbon system variables of wide interest, such as pCO2, pH, aragonite saturation state (ΩArag), calcite saturation state (ΩCalc), CO2 air–sea flux, and carbon burial rate. The model's robustness is evaluated via extensive model–data comparison against buoys, remote-sensing-based machine learning (ML) products, and ship-based measurements. A reassessment of air–sea CO2 flux with previous modeling and observational studies gives us confidence that our model provides a robust and updated CO2 flux estimation, and NGoM is a stronger carbon sink than previously reported. Model results reveal that the GoM water has been experiencing a ∼ 0.0016 yr−1 decrease in surface pH over the past 2 decades, accompanied by a ∼ 1.66 µatm yr−1 increase in sea surface pCO2. The air–sea CO2 exchange estimation confirms in accordance with several previous models and ocean surface pCO2 observations that the river-dominated northern GoM (NGoM) is a substantial carbon sink, and the open GoM is a carbon source during summer and a carbon sink for the rest of the year. Sensitivity experiments are conducted to evaluate the impacts of river inputs and the global ocean via model boundaries. The NGoM carbon system is directly modified by the enormous carbon inputs (∼ 15.5 Tg C yr−1 DIC and ∼ 2.3 Tg C yr−1 DOC) from the Mississippi–Atchafalaya River System (MARS). Additionally, nutrient-stimulated biological activities create a ∼ 105 times higher particulate organic matter burial rate in NGoM sediment than in the case without river-delivered nutrients. The carbon system condition of the open ocean is driven by inputs from the Caribbean Sea via the Yucatan Channel and is affected more by thermal effects than biological factors.
- Article
(6013 KB) -
Supplement
(1396 KB) - BibTeX
- EndNote
Carbon dioxide (CO2) concentration in the atmosphere increased approximately 150 % from 1750 to 2019 (Le Quéré et al., 2018), and the storage and transport of carbon in Earth's ecosystem under the context of climate change have been receiving incremental attention over the past decades (Anav et al., 2013; Lindsay et al., 2014; Jones et al., 2016). The direction and magnitude of ocean–atmosphere CO2 fluxes are subject to change with increasing atmospheric CO2 concentrations (Smith and Hollibaugh, 1993; Wollast and Mackenzie, 1989; Landschützer et al., 2018), incremental ocean dissolved inorganic carbon (DIC) level (Torres et al., 2011), modification of the coastal alkalinity generation process (Renforth and Henderson, 2017), changes in organic matter (OM) remineralization patterns (Buesseler et al., 2020), and river inputs (Yao and Hu, 2017). As an enormous reservoir, the ocean has taken up some 170 ± 20 PgC (Le Quéré et al., 2018) since the industrial revolution. This alleviates the CO2 accumulation rate in the atmosphere while inducing a consequent increase in ocean carbon level and a decrease in ocean pH and calcium mineral saturation state (Ω, Doney et al., 2009). Given the role it plays in shaping climate feedback in the long term and the risk for coastal ecosystems under acidification stress, carbon sink quantities and their trends have been studied and monitored by multiple studies (Maher and Eyre, 2012; Czerny et al., 2013; Najjar et al., 2018; Bushinsky et al., 2019).
Nevertheless, mismatches in carbon flux estimates among different studies and difficulties in describing the spatial and temporal pattern of pCO2 data collected from ship-based measurements have left many vital questions unanswered. Global Earth system models (ESMs) are essential tools for studying the linkage between the ocean carbon cycle and climate change. Extensive utilization of ESMs in hindcasting and coupled biogeochemistry provides pivotal information for understanding the carbon cycle on a global scale (Anav et al., 2013; Laurent et al., 2021; Lindsay et al., 2014; Jones et al., 2016; Todd-Brown et al., 2014). However, their relatively coarse spatial resolution is likely not appropriate to be directly compared with field measurements. It is imperative to apply high-resolution regional ocean models to understand carbon exchange and carbon budget at a regional scale. While high-resolution regional models have been developed to represent the complex patterns of ocean circulation and elemental fluxes on the continental shelves, the regional ocean carbon system is challenging to model and predict due to its high sensitivity to the boundary and initial conditions, uncertainties in the carbon pathway, and complex interactions between the atmosphere, ocean, and land (Hofmann et al., 2011).
The Gulf of Mexico (GoM) is a semi-closed marginal sea. The presence of the Mississippi–Atchafalaya River System (MARS) and the obstructions from the Florida Strait and Yucatan Channel mitigate the impact of the global ocean on the GoM regarding water acidity and carbon levels. Allochthonous nutrients from river input, upwelling, and boundaries shape the general pattern of the carbon cycling in the GoM (Cai et al., 2011; Chen et al., 2000; Delgado et al.,2019; Dzwonkowski et al., 2018; Laurent et al., 2017; Jiang et al., 2019; Sunda and Cai, 2012) and need to be properly included in carbon system modeling of the GoM. Fennel et al. (2011) performed a coupled physical–biological modeling of the northern GoM (NGoM) shelf with the nitrogen cycle to describe the phytoplankton variability under the influence of the MARS covering the period of 1990 to 2004. They found that biomass accumulation in the light-limited plume region near the Mississippi River delta was not primarily controlled bottom-up by nutrient stimulation because of the lack of nutrient limitation in the eutrophic zone. Xue et al. (2016) achieved a first GoM carbon budget and concluded that the export of carbon out of the gulf via the Loop Current is largely balanced by river inputs and influx from the air. Their regional carbon model used three sets of initial and open boundary conditions derived from empirical salinity–temperature–DIC–alkalinity relationships. Although this method of carbon system prescription leveraged the convenience of widely available physical variables and was feasible for regions with scarce DIC and alkalinity data, its reliability was questionable as temperature and salinity alone cannot fully describe the spatial and temporal pattern of these carbon variables. Laurent et al. (2017) presented a regional model study of the eutrophication-driven acidification and simulated the recurring development of extended and acidified bottom waters in summer on the NGoM shelf. They proved that the acidified waters were confined to a thin bottom boundary layer where the production of CO2 was dominated by benthic metabolic processes. Despite reduced Ω values being produced at the bottom due to acidification, these regions remain supersaturated with aragonite. Chen et al. (2019) presented a unified model to estimate surface pCO2 by applying machine learning (ML) methods to remote sensing data and cruise pCO2 measurements. Their ML model confirmed that the GoM was a carbon sink. Recently Gomez et al. (2020) performed another GoM carbon model study covering the period of 1981 to 2014. Their model initial and boundary conditions were derived from a downscaled Coupled Model Intercomparison Project 5 (CMIP5) Modular Ocean Model (25 km resolution, Liu et al., 2015). Their model results showed that the GoM was a sink for atmospheric CO2 during winter–spring and a source during summer-fall, producing a basin-wide mean CO2 uptake of 0.35 mol m−2 yr−1. Nevertheless, their model does not include the DOC pool or the calcification process, which are imperative to describe the dynamic of DIC and alkalinity in the ocean.
Despite the above carbon system regional modeling efforts, we notice that several processes that could contribute significantly to the carbon cycle in the GoM have not been investigated yet. The carbon cycle in the ocean is linked with the nutrient cycle through photosynthetic activities, calcification, and OM remineralization (Anav et al., 2013; Farmer et al., 2021; King et al., 2015). OM remineralization could be the most critical mechanism regulating the ocean carbon system, followed by the CaCO3 cycle (Lauvset et al., 2020), with the remineralization of small detritus accounting for over 40 % of the DIC production on the shelf (Laurent et al., 2017). Autochthonous nutrients from direct remineralization of OM determine the gradient of DIC in the euphotic layer (Boscolo-Galazzo et al., 2021; Boyd et al., 2019). During this process, the fast-sinking of OM and higher particulate to dissolved ratio foster a larger sedimentation rate and more significant DIC removal of the euphotic layers; on the contrary, the slower sinking and faster decomposition rate of OM favor nutrient and DIC retention in the euphotic layers (Davis et al., 2019; Mari et al., 2017; Turner, 2015). The remineralization of land-derived OM and CaCO3 precipitation are significant factors controlling air–sea CO2 flux (Mackenzie et al., 2004). Studies have revealed that the formation of marine CaCO3 (Burton and Walter, 1987; Inskeep and Bloom, 1985; Zhong and Mucci, 1989; Zuddas and Mucci, 1998) and the dissolution of marine CaCO3 mineral are Ω-dependent as well (Adkins et al., 2021). The Ω will be depressed as more CO2 dissolves in seawater and can be used as an indicator for the buffering capacity of the ocean carbonate system. Given that Ω influences the calcification rate of marine organisms and regulates the acidity of bottom waters, it should be considered in the CaCO3 cycle for a comprehensive carbon cycle assessment.
By using the biogeochemical boundaries from one of the latest CMIP6 products, our model inherited the climate perturbation signals (Liu et al., 2021) and the accumulative effect of carbon variables from the global solutions. Our regional model includes critical carbon cycle processes lacking in previous efforts, including the most up-to-date carbonate chemistry thermodynamic parameterization, phosphate cycling, formation and dissolution of CaCO3, and the inclusion of the DOC as a semi-labile carbon pool. The objective of this study is (1) to assess the feasibility and robustness of utilizing global model products to drive a regional coupled physical–biogeochemical model and (2) to examine the temporal trend of key variables of the carbon system (pCO2, pH, air–sea CO2 exchange, and Ω) of the surface ocean in the GoM. In addition, to evaluate the impact of MARS and the global ocean on GoM's carbon cycling, two perturbed experiments are designed. The following sections are organized: model setup is given in Sect. 2; in Sect. 3, we validate the model's performance against buoys, remote-sensing-based ML solution, and ship-based measurements. The trend of key carbon system variables over the past two decades and an assessment of the contribution of riverine inputs and the global ocean are presented in Sect. 4. An evaluation of our regional model's performance against existing regional models is given in Sect. 5, together with an outlook on future model development.
Model setup
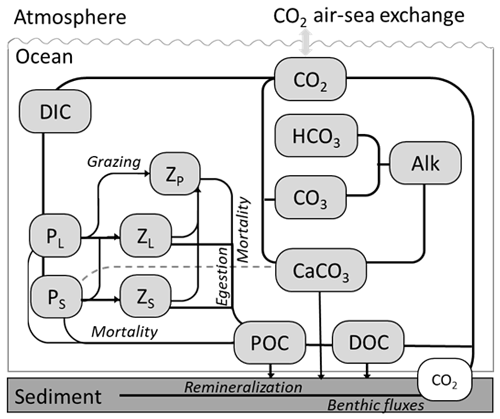
Our model is built on the platform of the Coupled Ocean–Atmosphere–Wave–Sediment Transport modeling system (COAWST; Warner et al., 2010). COAWST is an open-source community model which includes the Model Coupling Toolkit to allow data exchange among three state-of-the-art numerical models: Regional Ocean Modelling System (ROMS, svn 820, Haidvogel et al., 2008; Shchepetkin and McWilliams, 2005), the Weather Research and Forecasting model (WRF, Skamarock, et al., 2005), and the Simulating Waves Nearshore model (SWAN, Booij et al., 1999). The carbon model presented in this study is based on a well-validated coupled physical–biogeochemical model by Zang et al. (2019, 2020), which covers the entire GoM waters (Gulf-COAWST, Fig. 1). Gulf-COAWST has a horizontal grid resolution of ∼5 km and 36 sigma-coordinate (terrain-following) vertical levels. A third-order upstream horizontal advection and fourth-order centered vertical advection are used for momentum and tracer advection. The biogeochemical model is developed based mainly on the pelagic N-based biogeochemical model Pacific Ecosystem Model for Understanding Regional Oceanography (NEMURO, Kishi, et al., 2007, 2011). In this study, we extend the original 11 state variables of the NEMURO, including nutrients (Si(OH)4, NO3, NH4), plankton groups (ZP: predator zooplankton, ZL: large zooplankton, ZS: small zooplankton, PL: large phytoplankton, PS: small phytoplankton), dissolved organic nitrogen (DON), particulate organic nitrogen (PON), and opal (OPL), to 17, with added variables of phosphate (PO4), particulate inorganic carbon (CalC), dissolved organic carbon (DOC), oxygen (O2), dissolved inorganic carbon (DIC), and total alkalinity (TA). The stoichiometry between carbon and nitrogen in the OM production and remineralization is set to 6.625 following Fennel (2008).
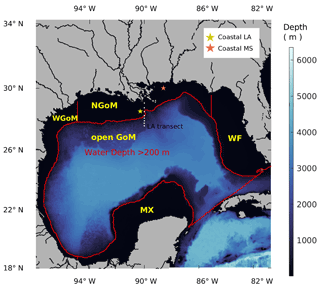
Figure 1Gulf-COAWST model domain with water depth in color (unit: m). Subregional definitions follow Xue et al. (2016), which are the Mexico shelf (MX), western Gulf of Mexico shelf (WGoM), northern Gulf of Mexico shelf (NGoM), western Florida shelf (WF), and open GoM.
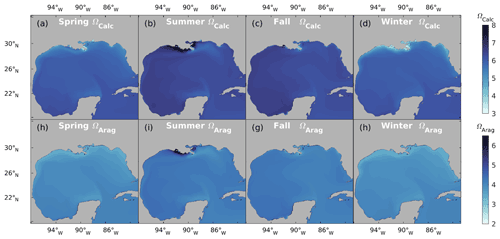
The revised biogeochemical model incorporates key processes regulating the carbon model, including primary production, river DIC, PON and DOC delivery, sediment carbon burial, CO2 air–sea flux, CaCO3 cycling, and OM remineralization (Fig. 2). Widely used carbon system variables, such as pCO2, pH, and Ω, are used as carbon system state indicators. The carbon module that takes in DIC, TA, PO4, Si (dissolved inorganic silicon), salt, and temperature for calculating pCO2, pH, ΩArag, and ΩCalc largely follows the recommended best practices (Dickson et al., 2007; Eyring et al., 2016; Orr et al., 2017; Zeebe and Wolf-Gladrow, 2001), with an updated parameter prescription for dissociation constants for carbonic acid (K1) and the bicarbonate ion (K2) (Millero, 2010), as well as solubility products for aragonite KA and calcite KC (Mucci, 1983) with a pressure effect (Millero, 1982, 2007).
The inorganic carbonate mineral (mainly CaCO3) forms during the photosynthetic activities of some phytoplankton species and fosters aggregation of detritus and their sinking. The rate of CaCO3 production follows a dynamic ratio regarding the primary production of small phytoplankton with low-temperature inhibition and enhancement during bloom conditions (Moore et al., 2004). The production and dissolution of CaCO3 are important processes for ocean acidity regulation, as its production (by 1 unit) nominally takes away a unit of [CO] from water, which reduces the alkalinity and DIC by 2 units and 1 unit, respectively. This process routinely happens during photosynthetic activities of some phytoplankton species (such as coccolithophores, parameterized implicitly as a portion of small phytoplankton in this model) and other marine calcifiers. Carbonate minerals produced in the euphotic zone could be treated as equivalent storage of alkalinity and are usually transported towards the ocean sediment through sinking. Aragonite and calcite are two common mineral phases of CaCO3 secured by marine organisms and are included in the model. ΩCalc and ΩArag are calculated as the equilibrium product of Ca2+ and CO. When Ω>1, calcification is thermodynamically favored, and when Ω<1, dissolution is thermodynamically favored. In Eq. (1), [Ca2+] and [CO ] are the concentrations of calcium and carbonate ions, respectively. [Ca2+] is determined through salinity (Millero, 1982, 1995), and [CO] is calculated through the carbon module. Ksp is the stoichiometric solubility product dependent on pressure, temperature, and salinity. Ksp is defined for aragonite and calcite as KA and calcite KC, respectively.
In our model, the sediment pool of sinking particles is a simplified representation of burial and benthic remineralization processes, whereby the flux of sinking materials out of the bottommost grid point is added to the sediment pool and enters the burial pool (remains inactive) with a dynamic ratio, the active sediment pools undergo enzyme-aided decomposition at rates regulated by temperature and oxygen and then release a corresponding influx of ammonium, DIC, and alkalinity at the sediment–water interface. Our model uses a CO2 production ratio of 0.138 between sediment aerobic respiration and denitrification (Fennel et al., 2006) and an alkalinity production ratio of 1.93 between pyrite burial and denitrification (Hu and Cai, 2011). Upon being sunk to acidified regions, the dissolution of CaCO3, regulated by Ω, can consume dissolved CO2 and neutralize the acid.
The bulk formula for air–sea gas exchange for CO2 is used following Wanninkhof (1992). Air–sea CO2 flux is calculated with a time step of 240 s and output in the form of a daily average. The gas transfer velocity coefficient of 0.31 cm h−1 is used in Eq. (2).
where is the air–sea CO2 flux (in mmol CO2 m−2 d−1), Sc is the Schmidt number (nondimensional) (calculated following Wanninkhof, 2014), s is the solubility of CO2 in seawater (in mol CO2 m−3 µatm−1) (calculated following Weiss, 1974), and ΔpCO2 is the air–sea pCO2 difference (in µatm). The term k660 is the quadratic gas transfer coefficient in cm h−1 (converted to m d−1). We calculated the air–sea CO2 flux using the relationships of gas exchange with wind speed at 10 m over the sea surface (U10), following Wanninkhof (1992). We used the ocean convention for the CO2 flux; i.e., a positive flux is defined as the ocean being a sink of atmospheric CO2. Air pCO2 level is prescribed using a fitted curve from the column-averaged dry-air mole fraction of atmospheric carbon dioxide from 2002 to the present derived from a satellite product (merged dataset from SCIAMACHY/ENVISAT, TANSO-FTS/GOSAT, and OCO-2, https://cds.climate.copernicus.eu/, last access: 24 May 2021; Dils et al., 2014).
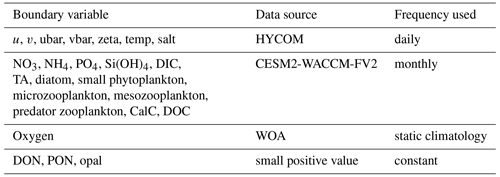
We performed a 20-year model hindcast covering the period of 1 January 2000 to 31 December 2019. The physical model setup was similar to that of Zang et al. (2020), with ocean physical initial and boundary conditions interpolated from the data-assimilated Hybrid Coordinate Ocean Model (HYCOM/NCODA, GLBu0.08/expt_19.1, expt_90.9, expt_91.0, expt_91.1, expt_91.2, and GLBv0.08/expt_93.0, https://www.hycom.org, last access: 27 September 2021; Chassignet et al., 2003, 2013). Physical boundary conditions are of daily frequency and include u, v, ubar, vbar, zeta, temperature, and salt. Atmospheric forcings with 6-hourly frequency include ground-level or sea surface downwelling shortwave and longwave radiation, ground-level or sea surface upwelling shortwave and longwave radiation, surface air pressure, surface air temperature, relative humidity, precipitation, wind at 10 m. They were extracted from the NCEP Climate Forecast System Reanalysis (CFSR) (Saha et al., 2010) and Climate Forecast System Version 2 (CFSv2) (Saha et al., 2011). See Table A2 for a list of model forcing frequencies.
The Coupled Model Intercomparison Project 6 (CMIP6) participating GCMs consume enormous research resources and generate unprecedented knowledge on global carbon system evolution with a whole-ecosystem conservation perspective (Bentsen et al., 2019; Bethke et al., 2019; Boucher et al., 2021, 2018; Danabasoglu, 2019a, b; Danabasoglu, 2019c, d; Guo et al., 2018; Jungclaus et al., 2019; Krasting et al., 2018; Lovato et al., 2021; Neubauer et al., 2019; Seland et al., 2019; Swart et al., 2019; Wieners et al., 2019; Ziehn et al., 2019). Utilizing GCMs results in a refined regional model that extends their research value, especially in bridging coarse GCM products with in situ field observations. With the interannual variation estimated by GCMs, the regional model could take advantage of global models by using dynamic boundaries that reflect climate oscillations and carbon accumulation in oceanic waters. In this study, we carefully evaluate various GCM products as candidates for initial and boundary conditions for the biogeochemical model. The two prognostic variables dissolved inorganic carbon (DIC) and total alkalinity (TA) are the essential data needed to drive a regional oceanic carbon model. There are no time-varying observational products or reanalysis of DIC and TA that have ideal three-dimensional coverage of the GoM. NCAR's CESM2-WACCM-FV2 solution was chosen to serve as the model boundary due to its relatively small bias in the carbonate variables in the GoM, relatively high horizontal resolution in the GoM compared with other GCMs, and availability of nutrients and carbon variables (see Table A1 for more details). Monthly boundary conditions of the biogeochemical variables (DIC, DOC, TA, NO3, PO4, Si, NH3) are extracted from CESM2-WACCM-FV2 solutions (historical, r1i1p1f1, nominal resolution 100 km, Danabasoglu, 2019b). As the global model simulation ended in December 2014, the biogeochemical boundary condition of 2014 was used repeatedly for the period from 2015 to 2019. The oxygen boundary condition is static without temporal changes since O2 is not available from the CESM2-WACCM-FV2 and is interpolated from the World Ocean Atlas 2018 (WOA18) product (Boyer et al., 2018; García et al., 2019). Freshwater and terrestrial nutrient inputs from 47 major rivers discharged to the GoM are applied as point sources with daily frequency. River discharge and water quality data for rivers in the US are collected from the US Geological Survey (USGS) stations (https://maps.waterdata.usgs.gov, last access: 25 August 2020). River DOC is prescribed following the values reported by Shen et al. (2012), with additional references from several other studies (Reiman and Xu, 2019; Stackpoole et al., 2017; Wang et al., 2013; Xu and DelDuco, 2017). Mexican river discharge data are collected from BANDAS (https://www.gob.mx/conagua, last access: 25 December 2019). Water quality data for Mexican rivers are prescribed as the average of that of the Mississippi and Atchafalaya rivers. River nutrient and carbon load are reconstructed from available USGS observations (see Fig. 3 for time series of river DIC and TA input). Missing river alkalinity values are interpolated from climatological values, and missing river DIC values are calculated from pH and alkalinity using the MATLAB program CO2SYS (Lewis and Wallace, 1998). Validations of the model's performance in physics, nutrient cycle, and primary production can be found in Zang et al. (2019, 2020). In this study, we focus on the model's performance in the carbon cycle, which is presented in the next section.
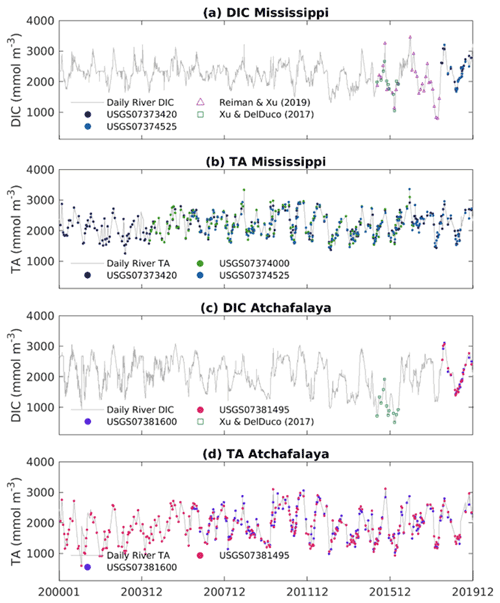
Figure 3River DIC and TA concentration prescribed in the model. Grey lines are the interpolated daily concentration values; colored data points are raw data collected from multiple sources.
Since the model-simulated DIC concentration in the water column is sensitive to initial conditions (Hofmann et al., 2011; Xue et al., 2016), using the initial condition from a snapshot (January 2000) of the global model result would be appropriate as the global model has been well stabilized up to the year 2000 from its “pre-industry” experiment. The regional model has the benefit of swift spin-up, with the biogeochemical model typically completing its spin-up in 1 year (e.g., Große et al., 2019; Laurent and Fennel, 2019; Laurent et al., 2021). We conducted a series of sensitivity tests and confirmed that a 1-year spin-up period (the year 2000) is sufficient for our current model setup. All results presented below are based on model outputs from 2001 to 2019 unless otherwise specified. To quantify the impact of river discharge and the global ocean on the carbon system in the GoM, in addition to the control experiment wherein the historical product of the CESM2-WACCM-FV2 experiment is applied as the boundary conditions (from here, experiment “His”), two perturbed experiments, “Bry” and “NoR”, are added. The Bry experiment has clamped DIC and TA conditions as those of the year 2000 for all following years while keeping all other experiment setups the same as that of the His. The NoR experiment eliminates the presence of all rivers in the model while keeping the rest of the experiment setup the same as that of the His. As most available observations are confined to the surface ocean, except for the GOMECC transects, for this study we focus on the surface ocean carbon condition in the NGoM and open GoM waters.
This section focuses on the validation of the model results via comparison against autonomous mooring systems with surface pCO2 measurements, ship-based measurements from the Gulf of Mexico Ecosystems and Carbon Cruise transects (GOMECC, Barbero et al., 2019; Wanninkhof et al., 2013, 2016), and pCO2 underway measurements (data downloaded from https://www.ncei.noaa.gov/access/oads/, last access: 15 August 2021). Direct observations of the GoM carbon system have been recognized as unbalanced among seasons due to fewer data points available in winter compared to other seasons. To overcome the sporadic direct measurement dataset, we also performed a model–data comparison against the remote-sensing-based ML product of sea surface pCO2 by Chen et al. (2019).
3.1 Model–buoy comparisons
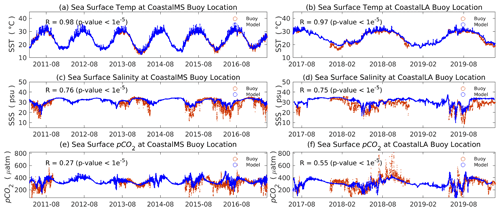
Temporal variability of sea surface pCO2 was recorded by the autonomous mooring system at two sites (CoastalMS and coastal LA) operated by the Atlantic Oceanographic and Meteorological Laboratory (AOML) of the National Oceanic and Atmospheric Administration (NOAA). The CoastalMS buoy site (for location see Fig. 1, data coverage: 14 January to 9 December 2009; 17 March 2011 to 4 August 2012; 10 July 2013 to 10 February 2014; 10 February to 3 May 2014; 12 December 2014 to 22 March 2015; 30 March 2015 to 22 September 2016; 23 September 2016 to 29 May 2017) is predominately impacted by the Mississippi River followed by the coastal ocean, whereas the CoastalLA buoy site (data coverage: 14 July to 7 November 2017; 14 December 2017 to 26 April 2019; 4 June 2019 to 12 August 2020; 12 August 2020 to 25 August 2021; 25 August to 29 November 2021) is mutually influenced by the Mississippi River and the coastal ocean. The high-frequency measurements provide a time-resolved picture of year-round changing pCO2 values. Temperature and salinity can influence the chemical equilibrium in the carbonate system, therefore shifting the pCO2 values. Validating the temperature and salinity at these two mooring sites is a prerequisite before looking into the surface pCO2 levels. In Fig. 4, the top four panels compare the sea surface temperature (SST) and salinity (SSS) between model and buoy measurements and show satisfying model–data agreements, with correlation coefficients larger than 0.75. At CoastalMS, the range for sea surface pCO2 is 150∼ 600 µatm. Sea surface pCO2 records are more volatile at CoastalLA with a maximum value >800 µatm and a minimum value around 150 µatm. Following the salinity drop, pCO2 at the CoastalMS site is simultaneously reduced, demonstrating the river's influence on both salinity and pCO2. At CoastalLA, however, the pCO2 level does not necessarily follow the trend of salinity, implying complex controlling factors in addition to the river inputs. The bottom two panels of Fig. 4 show acceptable agreement between measured and simulated sea surface pCO2, with a correlation coefficient of 0.27 between modeled and observed surface pCO2 at the CoastalMS buoy location and a correlation coefficient of 0.55 between modeled and observed surface pCO2 at the CoastalLA buoy location. We notice model–data discrepancies in April 2018 at CoastalLA and July 2011 at CoastalMS and ascribe such bias to the uncertainty in the riverine DIC input prescription and the limited model horizontal resolution (∼ 5 km).
3.2 Model–cruise comparisons
Cruise carbon measurements include underway water pCO2 data and conductivity–temperature–depth (CTD) bottle results. We compare the model result at the LA transect with the observations of GOMECC cruises conducted at the same location during GOMECC1 in 2007, GOMECC2 in 2012, and GOMECC3 in 2017. Measurements of TA during GOMECC cruises followed Dickson's definition (1981), wherein the TA is expressed as Eq. (3).
Equation (3) contains 14 variables, among which is explicitly modeled as an active tracer, , , [OH−], , [H+], [HF], [H3PO4], and are calculated by the carbon module, and [HS−], [HNO2], and [NH3] are unaccounted for. Figure 5 shows the vertical profiles of observed DIC, TA, and their ratio collected at the LA transects (−90∘ W, 27.5–29.1∘ N, shown in Fig. 1) overlaid with the model solution; the top 200 m depth is stretched three times to have a better view of the more densely sampled observational data, and a black dot is placed in the location of each observational data point, with the oversized colored dot representing the value of the measurement. All three transects were taken during July when nutrient supply from the MARS was high. Model-simulated profiles at the transects are taken from the closest date of the daily averaged output. The general trends in Fig. 5 for DIC, TA, and their ratio demonstrate a good match between the model result and the in situ CTD data. A relatively low surface DIC concentration (<2150 mmol m−3) above the 200 m isobath demonstrates the river's influence at the NGoM. The general increasing trend of DIC with depth confirms the presence of a biological pump, whereby inorganic carbon is utilized during photosynthesis in the euphotic layer. Subsequently, the generated OM sinks into deeper waters while being remineralized along the way. The TA profiles show more variation compared with DIC, for which a lower TA concentration (<2380 milliequivalents m−3) could generally be found at the surface as the direct dilution from river discharge, followed by a quick increase to ∼ 2380 milliequivalents m−3 in the euphotic layer due to photosynthetic activities, which generate alkalinity. Deeper, the TA profiles show a decreasing trend between 200 and 700 m, which could be explained by the water column respiration and nitrification. The TA profiles show a slow increase from 800 m and deeper, which coincides with the alkalinity generation processes in sediment and possibly dissolution of carbonate minerals, both adding to the bottom water TA. The TA DIC ratio has a maximum at the surface due to low DIC concentration and decreases with depth as DIC concentration increases. The last column in Fig. 5, namely (d), (h), and (l), quantifies the difference between the model solutions as well as the observations and the distribution of the difference. Figure 5d shows that 51.2 % of model–obs difference for DIC is within [] µmol kg−1. Similarly, Fig. 5h shows that 49.8 % of model–obs difference for TA is within [] µmol kg−1, and Fig. 5l shows that 91.6 % of model–obs difference for the TA DIC ratio is within [−0.02 0.02]. The model's root mean square error (RMSE) for DIC, TA, and the TA DIC ratio over the GOMECC (2007–2017) LA transect dataset is 30.97, 26.86, and 0.014, respectively.
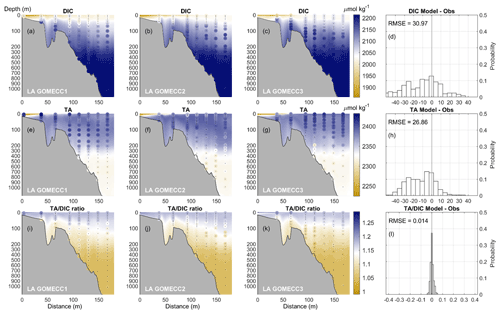
Figure 5Discrete measurement of DIC and TA along the LA transect during GOMECC1, GOMECC2, and GOMECC3 cruises shown as oversized scattered dots (with the little black dots indicating their locations) compared with model results in color contour, with the water depth shown on the left side of each figure in meters. The distributions of model bias and RMSE for DIC, TA, and the TA DIC ratio combining the three GOMECC cruises at the LA transect are shown in (d), (h), and (l), respectively.
3.3 Model–ML pCO2 product comparisons
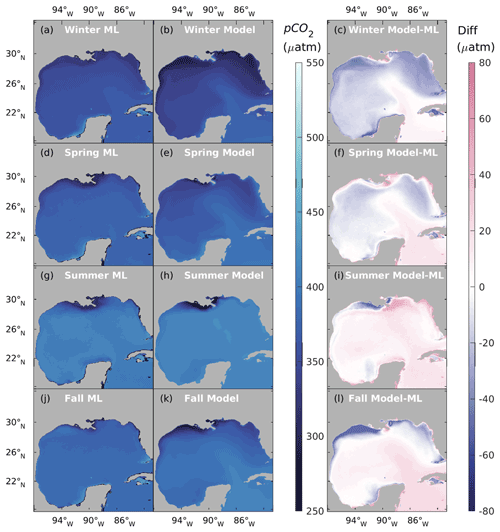
Direct comparison between cruise measurements of ocean surface pCO2 and daily averaged model results might suffer from systematic bias due to the sparsity of cruise data, both temporally and spatially. The ML model generates surface pCO2 from Chen et al. (2019) integrated >220 cruise surveys for 2002–2019 and MODIS ocean color product covering 2002–2017. The comparison between the two surface pCO2 products is shown in Fig. 6, where surface pCO2 results from Chen et al. (2019) are denoted as “ML” and results from this work are denoted as “Model” for the monthly climatology from July 2002 to December 2017. The two results exhibit a similar spatial distribution of surface pCO2, with our model result revealing more dominant features from the Loop Current in the open ocean. Compared with the ML model, our model produces lower pCO2 estimates over NGoM during winter and fall, higher pCO2 estimates over WF during summer, and a stronger influence from the Caribbean Sea. Chen et al. (2019) reported that no satellite data were found for pCO2<145 µatm or >550 µatm during their model development. This can also be a factor when considering the differences between the two products. Further comparison between our model and other products can be found in Sect. 5.1.
Besides buoy records, transects, and the ML products, we also perform an extensive model–data comparison using available ship-based underway pCO2 measurements from the Ocean Carbon and Acidification Dataset (https://www.ncei.noaa.gov/access/oads/, last access: 12 October 2021). These extensive model–data comparisons give us confidence that our model, driven by carbon boundary conditions from the global model, can reproduce temporal, spatial, and vertical variability of the CO2 dynamics in the GoM.
In this section, we present the spatial and temporal pattern of key carbon system variables, namely pCO2, pH, Ω, and air–sea CO2 flux simulated over the past 20 years in the GoM. In this study, we emphasize the surface carbon condition in two regions: NGoM and the open GoM, where most existing in situ data are distributed. We perform a linear fit of the time series of the key carbon system variables in each region and show the fitted relationships in Fig. 7. The slopes of the fitted linear plot give estimations of the change rate of each carbon variable over the past 2 decades.
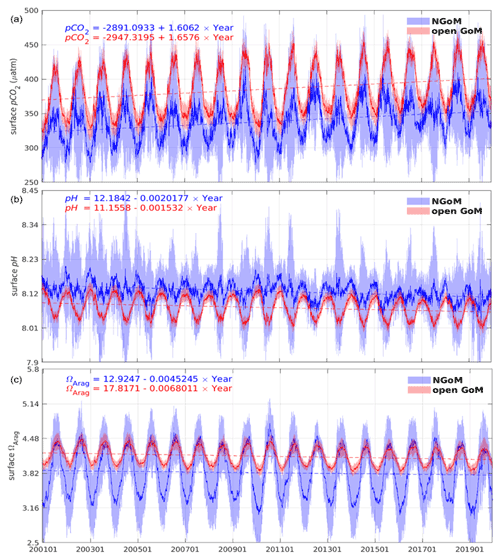
Figure 7Time series and trend analysis of sea surface (a) pCO2, (b) pH, and (c) ΩArag for the NGoM (blue) and open GoM (red). Solid lines depict the daily spatial mean value; shaded areas stand for 1 standard deviation, and dashed lines trace the linear fit of the time series.
4.1 pCO2
We simulate a generally increasing trend in surface pCO2 level for both NGoM and open GoM, with an increasing rate of 1.61 and 1.66 µatm yr−1, respectively (Fig. 7). Seasonal ocean surface pCO2 variation is primarily affected by temperature variations. To evaluate the pCO2 trend without temperature effects, we decouple the thermal and nonthermal components of pCO2 at the ocean surface using Eqs. (4) and (5) and further extract the pCO2 variation due to gross primary production and air–sea CO2 flux. The temperature sensitivity of CO2 of γT=4.23 % per degree Celsius, proposed by Takahashi et al. (1993), is used to perform the thermal decoupling in Eqs. (4) and (5). The thermal effect on pCO2 (pCO) is defined as the deviation between apparent pCO2 and the estimated pCO2 at the mean SST (denoted as < SST >). The nonthermal counterpart (pCO) is obtained by removing the thermal effect from the pCO2 time series using Eq. (5). Note that this definition of pCO is different from the original definition given by Takahashi et al. (2002). The new definition allows the thermal and nonthermal CO2 components to sum up to the apparent pCO2. pCO2 variations due to gross primary production are estimated from the carbon module based on the DIC consumed by gross primary production and denoted as pCO. pCO2 variations due to air–sea CO2 flux are calculated from the carbon module based on the DIC change from the air–sea exchange and denoted as pCO.
The contribution from gross primary production (GPP) is the process that directly affects the CO2 uptake, and GPP can be calculated by tracking the photosynthesis activity of diatoms and small phytoplankton (which is a function of solar radiation, temperature, nutrients, and phytoplankton concentrations). Respiration, on the other hand, is more complicated to quantify since it concerns both living biota (phytoplankton, zooplankton) and nonliving detritus (PON, DOC). Both respiration at the surface and respiration that happens in deeper water as detritus sinks modify DIC concentration and create concentration gradients. We leave the respiration in the end-member of the pCO components, which incorporated various mixing processes (e.g., river water and oceanic water mixing, vertical mixing of upwelled waters, horizontal-advection-induced lateral transport of tracers with concentration gradients, and entrainment of waters with different chemical nature – i.e., temperature, salt, DIC, TA, and detritus concentration). Remineralization and respiration are included in the term pCO due to the result of the two processes altering water chemical nature (DIC, TA, detritus concentration), and the impacts of water chemical nature on pCO2 are constantly being modified by (and as a result of) the mixing process.
Figure 8 shows the seasonal and spatial patterns of four decoupled pCO2 components, namely pCO, pCO, pCO, and pCO. The pCO patterns in the second row (e, f, g, h) of Fig. 8 reflect the fluctuation of pCO2 due to thermal effects. Over the four seasons, a general pattern of rising pCO from spring to summer and a gradual reduction from summer onwards can be observed. The NGoM shelf exhibits the lowest pCO values during winter, while WF shows elevated pCO values during summer. The higher pCO values in the southern part of the Yucatan shelf reveal the warm water flowing into the GoM from the Caribbean Sea. The top row (a, b, c, d) of Fig. 8 shows the nonthermal component of pCO2. The relatively high pCO during winter on the NGoM shelf, compared to that of the open GoM, shows the strong solvation effect of CO2 with low SST, contributing to a high DIC TA ratio and strong carbon uptake.
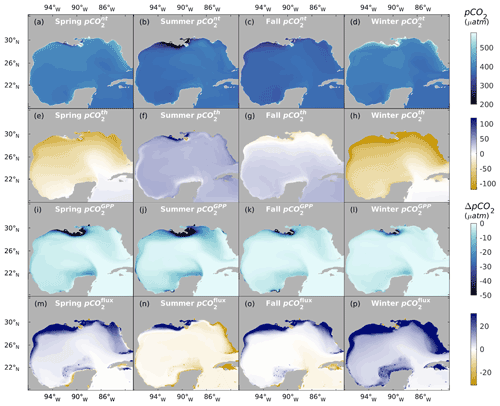
Figure 8Spatial distribution of sea surface pCO2 over four seasons. From the top to the bottom row: pCO (a through d), pCO (e through h), pCO (i through l), pCO (m through p; positive indicates the air–sea CO2 flux works in the direction of increasing sea surface pCO2).
The lower two rows of Fig. 8 show pCO2 changes due to the gross primary production and CO2 air–sea exchange, respectively. The pCO reflects the intensity of primary production in terms of pCO2 reduction. pCO has larger magnitudes in NGoM during spring and summer and is gradually attenuated during and after fall. The large magnitudes of pCO during summer in NGoM waters and the open GoM region following the extension of the MARS plume suggest strong biological CO2 removal in those regions. These results show that gross primary production has a stronger regulation on surface pCO2 during spring and summer in river-dominated waters and upwelling regions. At the same time, a minor contribution from gross primary production can be seen during winter, on the flat and shallow WF, and in the open GoM regions south of the Loop Current.
The pCO reflects the intensity of air–sea CO2 exchange attempting to mitigate the disequilibrium caused by local physical and biological processes. The relatively high value of pCO and low magnitude of pCO, as well as low river discharge (minimal river water mixing) in the WF during winter, indicate a strong CO2 uptake from the atmosphere due to low SST. This analysis agrees with the low pCO and high pCO values in the WF during winter, as shown in Fig. 8d and p. Situations during seasons other than winter are more complicated due to biological activities and mixing. The Mississippi delta region has a high pCO value during summer; however, combined with the effects of mixing and strong primary production (large magnitude of pCO), this region acts as a strong carbon sink that exhibits a high value of pCO compensated from the atmosphere. Figure 8 demonstrates that most of the time during the year, the surface pCO2 pattern is not dominated by a single factor but a combination of multiple controlling processes. The result of pCO2 decomposition agrees with the current view of the pCO2 dynamic and carbon uptake patterns in the GoM, which is strong carbon uptake during winter due to the thermal effect and high biological CO2 drawdown during spring and summer under the riverine influence.
4.2 pH
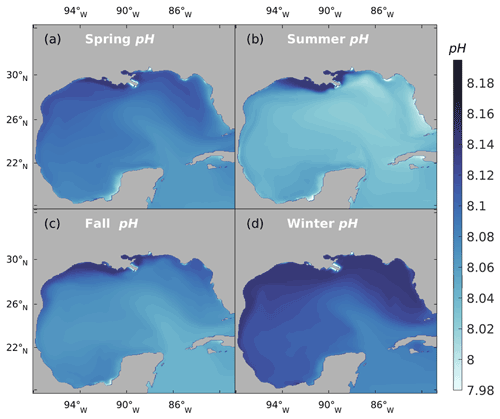
Ocean surface pH in the GoM shows a clear decreasing trend, with a 0.0020 yr−1 decrease over the NGoM region and a 0.0015 yr−1 decrease over the open GoM region. Figure 9 shows the seasonal pattern of ocean surface pH over the GoM. Spatial and seasonal pH patterns show larger variation over the NGoM, especially on the inner shelf (depth <50 m). The pH level in the surface water is closely associated with temperature, photosynthetic activities, and water mixing. The high pH value on the NGoM shelf reveals the strong influence of riverine alkalinity export and nutrient-stimulated primary production. The lower pH values on the WF shelf during summer and the generalized greater pH values over NGoM during winter demonstrate the high pH sensitivity to SST. The upwelling region along the western Yucatan shelf shows reduced pH values all year-round compared with its surrounding waters. The upwelling along the WGoM slope has a similar effect of reducing and maintaining a relatively low pH, effectively forming a pH boundary between the shelf water and the open GoM. The open GoM is largely dominated by the warmer and lower-pH water from the Caribbean Sea throughout the year.
4.3 Aragonite and calcite saturation state
Aragonite undersaturation occurs ([CO] <66 µmol kg2) before calcite undersaturation ([CO] <42 µmol kg2) (Feely et al., 2022, 2009). As a result, ΩCalc is approximately 50 % higher than ΩArag, and their spatial and seasonal variations are very similar, as shown in Fig. 10. Variations in temperature, alkalinity, and pCO2 impose important controls on ΩArag. The multiyear variability of ΩArag at the ocean surface is shown in Fig. 7c. The NGoM region shows a smaller decreasing trend in ΩArag (0.0045 yr−1) compared to that of the open GoM (0.0068 yr−1). Note that the data in Fig. 7 do not include water from the shallow shelf waters (water depth <10 m); therefore, the trend in NGoM does not incorporate the condition in coastal estuaries. The spatial distribution of ΩArag across the GoM depicts a healthy level of Ω and a low risk of ocean acidification (Fig. 10). While the coastal ocean generally has a relatively high Ω level, some coastal locations warrant special attention when evaluating their tendency towards calcium mineral dissolution. These locations include coastal regions that experience a large load of riverine OM inputs (e.g., the Mississippi River delta in summer) and the upwelling regions that receive relatively higher-acidity water from the bottom ocean (e.g., west of Yucatan). These regions show significant Ω reductions compared to the surrounding waters and are potential victims of ocean acidification. The influence of the river on Ω is complex. On one hand, a high nutrient level of river discharge could stimulate a high photosynthetic rate, which consumes DIC and increases Ω. On the other hand, photosynthesis favors calcification, which consumes carbonate ions and reduces Ω. Therefore, Ω is subject to increase with stronger photosynthesis and decrease with stronger calcification. Hence, the magnitude of the overall effect will depend upon photosynthetic rates and the calcification rate. In this work, two phytoplankton groups are modeled, diatoms (silicifying) and small phytoplankton (implicitly including the calcifying coccolithophores, foraminifera, and dinoflagellates), of which only the small phytoplankton group has the potential to conduct calcification (Raven and Giordano, 2009). Besides being regulated by temperature and small phytoplankton concentration, the calcification rate also depends on the composition of the phytoplankton population. The small phytoplankton group has a survival advantage at relatively low nitrogen concentrations and could be grazed by two zooplankton groups (mesozooplankton and microzooplankton), whereas diatoms are more nutrient-demanding and can be grazed by three zooplankton groups (predator zooplankton, mesozooplankton, and microzooplankton). The competitive phytoplankton evolution shapes the relative rates between photosynthesis and calcification on the NGoM shelf during summer. The reduced Ω to the east of the Mississippi River delta is a combined result of high-DIC water entrained by Loop Current eddies west of the delta and an increased ratio of small phytoplankton in offshore waters.
4.4 Air–sea CO2 flux
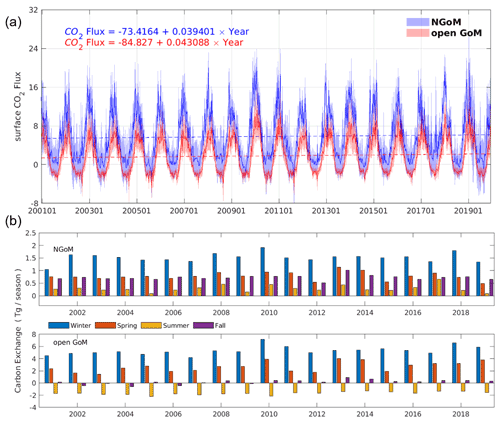
Air–sea CO2 flux is calculated from daily averaged model data from 2001–2019 (Table 3). The GoM overall is a CO2 sink with a mean flux rate of 0.62 mol C m−2 yr−1 (11.77 Tg C yr−1), which is commensurate with the reported value of 11.8 Tg C yr−1 by Coble et al. (2010). The greatest carbon uptake rate occurs in winter (1.97 mol C m−2 yr−1), while the weakest carbon uptake is present in fall (0.16 mol C m−2 yr−1). The strongest carbon efflux is simulated in summer (−0.57 C m−2 yr−1). On average, water in the NGoM acts as a sink throughout the year, and the water in the open GoM acts as a weak source during summer (and fall for 2002, 2004, 2006, and 2009) and a sink during the rest of the year. The direction and magnitude of the air–sea exchange can be seen in Fig. 11, where a positive number indicates that the ocean is a carbon sink. The NGoM is a very strong CO2 sink year-round, and the open GoM is a source of CO2 during summer but a sink in the rest of the year (except during fall in a few years), as shown in Fig. 11b. There are clear trends and patterns in multiyear CO2 air–sea flux, as shown in Fig. 11a, where a greater air–sea CO2 flux average could be seen at the end of 2019 than that of 2001, resulting in a stronger carbon influx in both regions. A significant anomaly in the middle part of the record (2009–2011) can be observed, which could result from the influence of a large negative North Atlantic Oscillation (NAO) index and El Niño in 2010 (Buchan et al., 2014). Similar observations in the Caribbean Sea are attributed to the single-year anomalies in the climate indices and the climate mode teleconnection (Wanninkhof et al., 2019).
4.5 Contribution from river and global ocean
In this section, we further diagnose river discharge and the global ocean's impacts on the GoM carbon system via a comparison between the control experiment (His) and the two perturbed experiments (Bry and NoR). In the Bry experiment the clamped boundary conditions that maintain the DIC and TA level as that of the year 2000, and in the NoR experiment the river forcing was removed to examine the impact of fluvial input on the coastal carbon system.
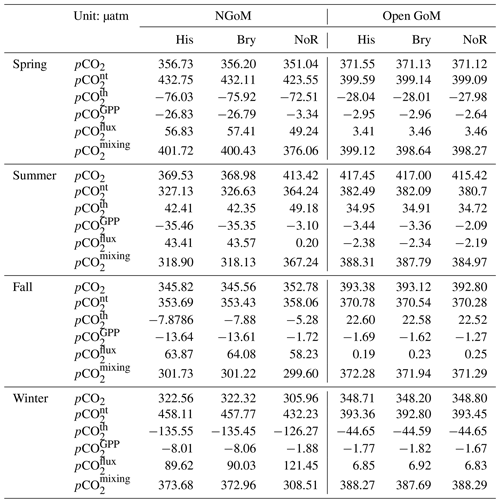
Figure 12 shows the multiyear mean levels of the four carbon variables (pCO2, pH, ΩArag, and CO2 flux) simulated by the three experiments. Table 1 summarizes the mean levels of pCO2 over the NGoM and open GoM. The definition of pCO, pCO, pCO, pCO, and pCO can be found in Sect. 4.1. The pCO is defined in Eq. (6), which reflects the pCO2 level due to the water mixing. It can also be considered the pCO2 level determined by the water with a multiyear mean temperature and without the influence of gross primary production or air–sea CO2 flux.
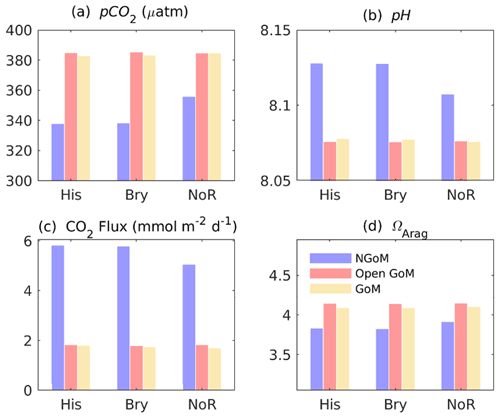
Figure 12Multiyear synoptic of sea surface pCO2, pH, CO2 air–sea flux, and ΩArag with His, Bry, and NoR experiments. Color bars show the corresponding mean level from 2001 to 2019. Color legend: blue – NGoM, red – open GoM, yellow – GoM-wide. The units for pCO2, pH, CO2 flux, and ΩArag are µatm, unitless (full scale), mmol m−2 d−1, and unitless, respectively (note that the CO2 air–sea flux used the ocean convention, with a positive value indicating transport from air to sea; i.e., the ocean is a sink).
The most salient difference among the three experiments is the significant elevation of the annual mean pCO2 level (in Fig. 12) in the NGoM by the NoR experiment, combined with a significantly reduced carbon sink during summer (in Fig. 13, from 0.287 to −0.093 Tg per season using His as a benchmark). The difference can be better resolved by the pCO2 decomposition results shown in Table 1, where a drastic change in the water carbon system emerges in the NGoM during the NoR experiment (compared to the other experiments with river input), evidenced by the large pCO value deviating from that of the His and Bry experiment in the NGoM region during spring, summer, and winter. The low values of pCO in NGoM during summer can be explained by a strong biological drawdown of CO2 associated with the high productivity fueled by the riverine nutrient supply. pCO components of −35.35 and −35.46 µatm, corresponding to the strong biological drawdown of CO2 in Bry and His experiments, are in sharp contrast to that of the NoR experiment, which is only −3.10 µatm. Consequently, distinct patterns of CO2 air–sea flux are shown in Fig. 13, and highly contrasting CO2 air–sea-flux-induced surface pCO2 changes are shown in Table 1 (pCO). The summer pCO component for NGoM of the two experiments with river inputs exhibits a relatively large value (∼ 43 µatm) compared with that of the NoR experiment (0.2 µatm), demonstrating a much smaller disequilibrium between oceanic and atmospheric pCO2 when rivers are absent. The changes introduced by removing the river showcase the dominating impact of river input on the NGoM carbon system in terms of gross primary production, surface pCO2 level, and air–sea CO2 exchange. Due to the different intensities of gross primary production, in the His experiment sediment PON concentration is 6 times that of the NoR experiment, and riverine nutrients in His fostered a ∼ 105 times higher PON burial rate in NGoM sediments than that of NoR.
Table 1 show a close resemblance in the magnitude and seasonal pattern between the Bry and His experiment in the open GoM region, with a small yet steady reduction in pCO by the Bry experiment among all seasons. The small reductions in pCO of the Bry experiment compared to that of His reflect the contribution from extraneous carbon accumulation from the global ocean that is included in the His experiment. As expected, slightly greater CO2 sink values are reported in Fig. 13 for Bry than His. Since the Bry experiment has a smaller carbon accumulation in the open GoM region compared to that of the His experiment, the ocean surface requires a slightly greater carbon uptake to reach equilibrium with the atmosphere. Since oceanic water is a natural buffer system and the ocean surface is under constant interaction with the atmosphere, it is reasonable that the His and Bry experiments do not show significant differences in surface carbon variables. However, this does not mean that the accumulative signal of DIC from the global ocean is neglectable. As shown in Fig. 14, the ocean water equilibrium witnessed migration over the 20-year simulation. Compared with the Bry experiment, the His experiment received accumulated carbon input from the global ocean and underwent a [CO] reduction as large as 15 % in some affected regions at the 100 m depth. Combining the results from the three experiments, we conclude that, in addition to elevated atmospheric CO2 levels, inputs from both MARS and global oceans contribute to the overall acidification trend in GoM, with the impacts from MARS mainly limited to the NGoM shelf region and the global ocean's impacts spanning the open GoM.
In this study, we demonstrate that the regional high-resolution carbon model can reproduce the spatial and seasonal patterns of ocean surface pCO2 in the GoM and generate reliable TA DIC profiles in the NGoM shelf. We detect a consistent acidification trend in the GoM over the past 2 decades. In this section, we present a side-by-side evaluation of the regional model with GCMs, global climatology products, and other regional models, followed by an envisioning of the future outlook and model development.
5.1 Model performance
In this section, we further evaluate the performance of our model via comparison against different global and regional models, as well as climatological products. The GoM region has limited observations of dissolved inorganic carbon (DIC) and total alkalinity (TA), and observational data covering different depths are even fewer. Due to lack of observations, global climatology products either have no coverage in the GoM region, e.g., mapped observation-based oceanic DIC monthly climatology from the Max Planck Institute for Meteorology (MOBO-DIC_MPIM) (NCEI Accession 0221526) (Keppler et al., 2020), or only contain surface carbon variables, e.g., the global gridded dataset of the surface ocean carbonate system called OceanSODA-ETHZ (v2021,NCEI Accession 0220059) (Gregor and Gruber, 2020), climatological distributions of pH, pCO2, total CO2, alkalinity, and CaCO3 saturation in the global surface ocean (NCEI Accession 0164568) (Takahashi et al., 2017), the partial pressure of carbon dioxide collected from surface underway observations in the worldwide oceans (NCEI Accession 0161129) (Bakker et al., 2017), an observation-based global monthly gridded sea surface pCO2 product (NCEI Accession 0160558) (Landschützer et al., 2017), and a global ocean pCO2 climatology combining open-ocean and coastal areas (NCEI Accession 0209633) (Landschützer et al., 2020). The most updated global monthly TA (NCEI Accession 0222470) (Broullón et al., 2020b) and DIC (NCEI Accession 0222469) (Broullón et al., 2020a) products offer a 12-month climatology with a spatial resolution and 102 vertical levels. Nevertheless, these products utilize a neural network approach to achieve three-dimensional coverage. Thus, one should be cautious that the generated monthly climatology products are not built solely from the interpolation of observations (Cervantes-Díaz et al., 2022). Rather, they are machine learning products with many untested assumptions. For instance, they use pCO2 from LDEOv2016 (Takahashi et al., 2017) and TA from Broullón et al. (2019) to compute surface DIC values to increase the spatial coverage in the training data used by the machine learning model (Broullón et al. 2020a, b). In contrast, GCMs are based on large-scale circulations that are coupled with biogeochemical processes. They utilize rigorous reasoning numerical methods with conservation schemes and should therefore have higher inherent consistency. In the following, we check the bias of several regional model products (see Fig. 15) using mean bias, RMSE, and R defined as follows:
where M stands for model output, O stands for observation, Cov refers to the covariance, and σ indicates the standard deviation. Further, we utilized the Taylor diagram to assess the model's ability to capture spatial patterns with regard to a given set of reference data (Babaousmail et al., 2021). The Taylor skill score (TSS) is defined by Eq. (10):
where σo and σm are the standard deviation of the observation and model, respectively. The value of TSS ranges from 0 to 1, with values close to 1 corresponding to better performance. R is the correlation coefficient between the observation and model, and Ro is the maximum correlation coefficient attainable (we use 0.999).
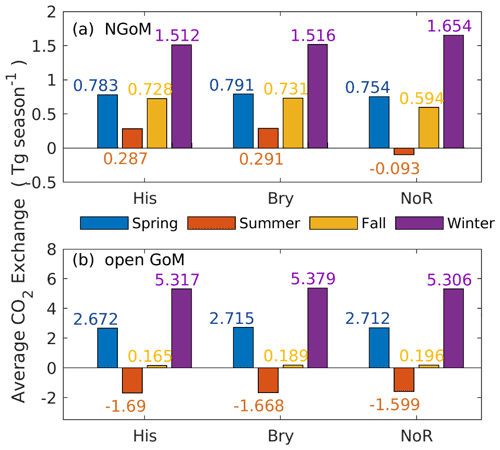
Figure 13Seasonal air–sea CO2 exchange at NGoM and the open GoM region among the His (historical), Bry (fixed boundary), and NoR (non-river) experiments.
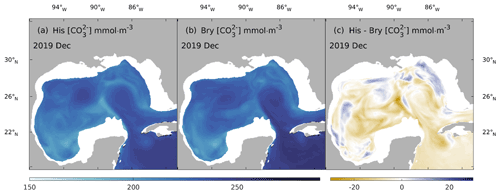
Figure 14Comparison of monthly averaged carbonate ion concentration ([CO]) between His and Bry at 100 m depth in 2019. (a) December mean [CO] of the His experiment, (b) December mean [CO] of the Bry experiment, and (c) difference between (a) and (b).
The nondimensional model skill defined in Eq. (10) can be used to quantify the improvement of the model to reproduce observed data with regard to the climatological value:
where di represents the available measurements, (di−ℑ[mi]) is the observation–model difference, and (di−ci) is the observation–climatology difference (Zhang et al., 2012). Usually, a skill of 0.25 means the model can reproduce 25 % more variance than those already described in climatology. By using the observation–model difference from this work and the observation–climatology difference from other models and climatology, we can evaluate the relative performance between this work as well as other models and climatology – a positive skill value ideally indicates improvement of the model in the numerator over the model and climatology in the denominator, while a negative skill value indicates the opposite. We use the other products as the reference to calculate the observation–product difference in the denominator, use our model to calculate the observation–model difference in the numerator, and list the corresponding skill value in Table 2, indicating the percentage improvement or deterioration gained by this work over the referenced product.
In Fig. 15, we interpolate regional model results to the nearest location of the underway surface pCO2 measurements. We limited the observational data from 1 January 2001 to 31 December 2014 to ensure the ideal coverage of most products. Model results by Xue et al. (2016) only had temporal coverage from 2005 to 2010. Surface DIC, TA, temperature, and salinity from Gomez et al. (2020) were downloaded from NCEI Accession 0242495 (Gomez et al., 2021) to derive the surface pCO2 patterns according to the method described in their paper. Underway pCO2 observation data are compared with model results of the nearest year in Fig. 15. The statistics of model–data comparison are listed in Table 2.
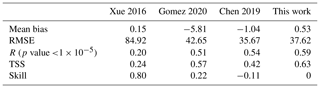
For regional models, the 12-month ML-based climatology product by Chen et al. (2019) has the best performance in terms of RMSE (35.67) and skill (−0.11) (Table 2). However, the 12-monthly climatology product suffers from a temporal disadvantage when compared with model products with smaller time frequency. For example, model Chen 2019 had an R value of 0.54, while the daily averaged model (this work) had an R value of 0.59. The multiyear monthly product by Xue et al. (2016) has the largest RMSE (84.92) among the tested products and overestimates shelf regions while underestimating pCO2 in the open-ocean region (especially the Loop Current). Overall, model Xue 2016 performs poorly in regard to surface pCO2 with a low R value of 0.20 and a low TSS of 0.24, and the model in this study can reproduce 80 % more variance than that already described in model Xue 2016 (the skill of this work over model Xue 2016 is 0.80). In addition, the TSS of this work is 0.63, which is higher than that of the model Xue 2016 (0.24), supporting one of the major findings of this work that the NGoM is a carbon sink instead of a source during summer. Likewise, the open ocean should not be as strong a carbon sink as Xue et al. (2016) suggested since their estimated pCO2 in the open ocean is significantly lower than the observations. Model results by Gomez et al. (2020) had a relatively low RMSE of 42.65 and a relatively high TSS of 0.57 among all models. When using model Gomez 2020 as the reference, this work generated a skill score of 0.22. Figure 15 reveals that model Gomez 2020 tends to overestimate pCO2 on the northwest shelf of the GoM and underestimate it in the open ocean, especially the southern GoM connected with the Caribbean seas.
In Fig. 16, we extracted the monthly surface pCO2 trend at two buoy locations from the regional models and climatology products to be compared with the monthly averaged buoy pCO2 measurements. Taylor diagrams are shown for an integrated evaluation of the standard deviation and correlation coefficient of each model and climatology product concerning observation at the two buoy locations. At the two buoy locations, most products tend to overestimate the summer pCO2, with model Xue 2016 yielding the largest overestimation. The coastal buoys recorded a typical low during the May, June, and July period, but most products failed to capture such a trend. Global models with coarse resolution and simplified, if any, river flux prescriptions generally perform poorly in the coastal region. Even for the relatively well-performing regional Gomez 2020 and the ML-based model Chen 2019, an overestimation as large as 100 µatm during May or June is found. Such an overestimation likely results in a reduced air–sea CO2 flux when the ocean is a carbon sink (for flux estimates see Table 3). As shown in Fig. 16, this work can capture the monthly climatology of surface pCO2 at two buoy locations relatively well. Such agreements result in relatively better correlation coefficients (with smaller p values) and standard deviation within the range of [25 50] for CoastalMS and [50 75] for CoastalLA in Fig16. Both the monthly time series and the Taylor diagrams in Fig. 16 reveal the benefits of this regional model as a good description of the coastal carbon system under the influence of the MARS.
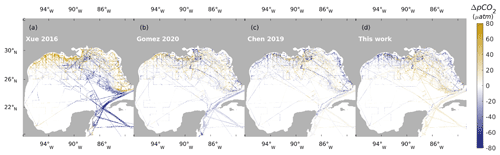
Figure 15Comparison of sea surface pCO2 between regional ocean model products (Xue 2016, Gomez 2020, Chen 2019, this work) and underway sea surface pCO2 measurements. A positive ΔpCO2 indicates that the product data overestimate sea surface pCO2. A negative ΔpCO2 suggests that the product data underestimate sea surface pCO2. A neutral ΔpCO2 indicates that the product data agree well with the observed sea surface pCO2. The white spaces between the cruise lines indicate that these regions do not have observational pCO2 data and do not indicate neutral bias.
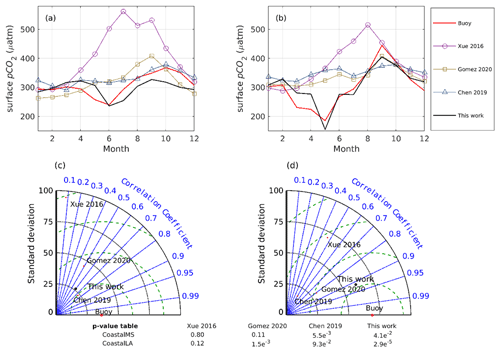
Figure 16Comparison of sea surface pCO2 among regional ocean model products (Xue 2016, Gomez 2020, Chen 2019, this work) at two buoy sites. Climatology at the two buoy locations of Gomez et al. (2020) is calculated by multiyear averaging from 2000–2014 model surface results. Climatology at the two buoy locations of Xue et al. (2016) is calculated by multiyear averaging from 2005–2010. Climatology at the two buoy locations of Chen et al. (2019) is calculated from their 12-monthly ML surface pCO2 product (from July 2002 to December 2017). Buoy raw observations have a frequency of ∼ 3 h, and monthly averages are used to be compared with monthly model estimates. The p value for each correlation coefficient is listed in the p-value table.
5.2 Air–sea flux
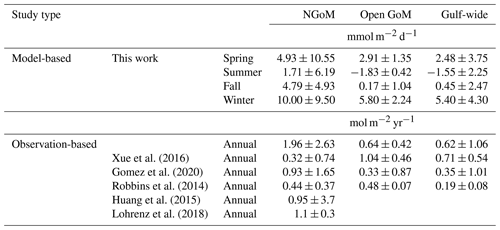
In Table 3, we compare the annual air–sea CO2 flux generated by this work with that reported by Xue et al. (2016) for 2005–2010, Gomez et al. (2020) for 2005–2014, Robbins et al. (2014) for 1996–2012, Huang et al. (2015) for 2004–2008, and Lohrenz et al. (2018) for 2006–2010. Using the same gas transfer velocity parameterization as this study, Xue et al. (2016) simulated a smaller carbon sink in the NGoM and a larger carbon sink estimation in the open GoM due to their overestimation of shelf pCO2 and underestimation of the open GoM pCO2, as shown in Fig. 15. The large bias of the open GoM carbon sink by Xue et al. (2016) likely results from the oversimplified prescription of the initial and boundary condition of DIC and TA (based on the empirical relationship with temperature and salinity), which led to an overestimation of carbon sink in the open GoM (1.6 times the value reported by this work and up to 3 times that reported by Gomez et al., 2020). To compare with the flux estimates of Gomez et al. (2020), we rescaled our estimates to the gas transfer velocity parameterization used in their work (based on Wanninkhof, 2014) and produced mean estimations of 1.59 ± 2.13, 0.52 ± 0.34, and 0.50 ± 0.86 mol m−2 yr−1 for the NGoM, open GoM, and gulf-wide, respectively. It is expected that this work estimated a larger carbon sink in the NGoM region compared with that of Xue et al. (2016) and Gomez et al. (2020), as revealed in Figs. 15a–b and 16a–b. Surface pCO2 in the coastal region simulated by Xue et al. (2016) is significantly overestimated, as shown in Figs. 15 and 16a–b. This model bias corresponds to the smallest NGoM carbon sink estimation in Table 3. Similarly, surface pCO2 in the coastal NGoM region and at the two buoy locations was overestimated by Gomez et al. (2020) (Figs. 15b, 16a, b). This pCO2 overestimation can be a reason for its smaller carbon sink estimation for the NGoM compared with that of Lohrenz et al. (2018), Huang et al. (2015), and this work. Additionally, the NGoM is a carbon source from June to October according to Gomez et al. (2020), which is different from what we simulated in this study (NGoM is a carbon sink all year-round). Combining information from Fig. 16, where Gomez et al. (2020) overestimate pCO2 by ∼ 50 µatm on average during June at the two coastal locations, we conclude that the NGoM air–sea CO2 sink by Gomez et al. (2020) is likely underestimated. The observation-based studies by Huang et al. (2015) yielded an annual sink of 0.96 ± 3.7 mol C m−2 yr−1 for NGoM based on wind data from the monthly satellite product QuikSCAT (12.5 km resolution). Lohrenz et al. (2018) estimated an annual sink of 1.1 ± 0.3 mol C m−2 yr−1 for NGoM using gas transfer velocities estimated for each 8 d period. To sum up, we conclude that the air–sea CO2 flux generated by this work is more robust in the NGoM region than that in previous model and climatology products. Nevertheless, a direct carbon flux comparison between model and observation-based studies needs to account for the differences in wind data and the gas transfer velocities.
5.3 Outlook and future model development
A likely warmer climate combined with heavier precipitation and greater river discharge is predicted in the following years for the MARS (Dai et al., 2020; Fischer and Knutti, 2015; Frei et al., 1998; Tao et al., 2014), although climate change might reduce precipitation for some low- and middle-latitude regions (Arora and Boer, 2001; Na et al., 2020). A warmer climate will reduce the momentum of the Loop Current, and less tropical water (reduced by about 20 %–25 %) will be introduced into the GoM from the Caribbean (Liu et al., 2012). As a consequence, the Loop Current might penetrate less into the NGoM and reduce the upwelling along the NGoM and WF slope. Stronger river discharge with nutrient loads will exacerbate the NGoM acidification in bottom water (Laurent et al., 2018) while increasing the surface water biological CO2 utilization and removal, creating larger river plume regions that exhibit a distinct carbon footprint compared to surrounding waters. Such predictions resemble the perturbation prescribed in the Bry and NoR experiments, wherein a reduced global ocean impact can be assessed by the difference between Bry and His experiments, and impacts from increased river discharge can be assessed by the difference between His and NoR experiments. We anticipate the open GoM to be a stronger carbon sink in the future under the projection of Loop Current weakening. And the NGoM will continue to be a strong carbon sink, with the sink region expanded in response to predicted greater river discharge and smaller momentum in the Loop Current.
Field samples of the carbon system give us synoptic knowledge of the carbon cycle in the ocean. However, carbon system attributes are subject to large fluctuation due to temperature, salinity, mixing, and biological activities; current observations of the carbon system at the sea surface or vertically along transects are far from enough to reveal the carbon system evolution in the GoM. As ship-based observations are limited by spatial coverage and temporal coverage, mooring observations have a high frequency (∼ 3 h) in time but only cover limited geological locations. The ML model derived from remote sensing and cruise data inherits the bias from satellite ocean color products and ship-based measurements, and, more importantly, it assumes that the training data contains all information that defines the system it is trying to predict, which is not necessarily the truth. One benefit of numerical models is to offer information to bridge fragmentary knowledge and fill in the gaps between observations and reality. However, the marine carbon cycle is admittedly a complex process. Several simplifications and parameterizations are needed to perform a numerical simulation. Nevertheless, specifications for some key processes may warrant further investigation and better parameterization. (1) The multiple alkalinity generation processes in the sediment pool (Fennel et al., 2008; Thomas et al., 2009) in current experiments are linked linearly with the aerobic decomposition of PON with a fixed ratio, which can potentially induce large bias during high PON concentrations. The anoxic zone chemistry component can be added to properly simulate the carbonate system in oxygen-deficient conditions (Raven et al., 2021), which can prevail in bottom boundary layer waters in coastal regions in NGoM, especially during summer. Adding in anoxic zone chemistry will also allow a more diversified prescription for TA generation, which plays a key role in the understanding of sediment pH dynamics (Gustafsson et al., 2019; Middelburg et al., 2020). (2) In our model, the density-related fragmentation or flocculation of detritus OM is simplified with one particulate and one dissolved pool, each with a fixed sinking rate. Coagulation and flocculation can transform DOC into particulate OM or subsequently form large aggregates, whose remineralization rate can be much faster (Ploug et al., 1999). The remineralization–sinking dynamic determines the fate of OM decomposition (and water column DIC profile) and should be allowed to have more degrees of freedom in future model development. (3) Calcification in this work can reflect the primary factors regulating marine calcification. However, important feedback from water acidity on the calcification is omitted due to the overall supersaturation with aragonite in GoM shelf waters. Therefore, the modeled CaCO3 PON ratio could not reflect the decreasing trends of the CaCO3 PON ratio under acidification (Zondervan et al., 2001). (4) Phytoplankton groups can play different roles in carbon cycling given their different sizes, sinking rates, and calcification rates, among others, and their relative ratio would be critical to the carbon dynamic (Le Moigne et al., 2015; Poulton et al., 2007). The interplay between zooplankton grazing and phytoplankton bloom in this work captured the seasonal dynamic but only had fixed modes toward nutrient levels. High nutrient concentration favors the success of diatoms, and a lower nutrient level gives small phytoplankton a competitive advantage in NGoM (Aké-Castillo and Vázquez, 2008; Chakraborty and Lohrenz, 2015; Qian et al., 2003; Strom and Strom, 1996). More phytoplankton groups and possible predation avoidance mechanisms could be added to the model to give the bloom pattern (and subsequently the carbon export) more variance (Liszka, 2018; Rost and Riebesell, 2004). (5) Adding the higher-trophic-level biology could be the next step to improving the model. Marine fishes are reported to produce precipitated carbonates within their intestines at high rates and contribute to TA increase in the top 1000 m of ocean waters (Wilson et al., 2009). (6) This model did not include sediment silicate weathering and carbon flux through atmospheric deposition, which can potentially be important sources and sinks of carbon to the ocean waters as well (Jurado et al., 2008; Wallmann et al., 2008).
This study presents a high-resolution regional carbon model for the GoM with fully coupled carbonate chemistry calculations and air–sea interaction. The model can reliably simulate the spatial and temporal pattern of the surface ocean carbon system. We show, for the first time, a solid validation of a regional carbon model via direct comparison against high-frequency CO2 buoys, TA DIC vertical profiles along the coastal transects, a remote-sensing-based ML model product, and underway pCO2 measurements (surface). We calculated the decadal trends of important carbon system variables such as pCO2, pH, air–sea CO2 exchange, and Ω over the NGoM and open GoM regions.
The GoM surface pCO2 values experience a steady increase from 2001 to 2019, with an increasing rate of 1.61 µatm yr−1 in NGoM and 1.66 µatm yr−1 in the open GoM, respectively. Correspondingly, the ocean surface pH is declining at a rate of 0.0020 and 0.0015 yr−1 for NGoM and open GoM, respectively. The surface Ω over the NGoM and open GoM region remains supersaturated with aragonite during the time span of the model but with a slightly decreasing trend. The carbon sink of both NGoM and open GoM regions exhibits increasing trends and will continue to increase at a faster pace in the coming years under the prospect of climate change with rising atmospheric pCO2.
We decouple the influence on surface pCO2 into thermal and nonthermal components and further analyze the surface pCO2 changes due to gross primary production and air–sea CO2 flux. We find that the low temperature during winter and the biological uptake during spring and summer are the primary drivers making GoM an overall CO2 sink. During the modeled period of 2001–2009, the GoM overall is a CO2 sink with a mean flux rate of 0.62 mol C m−2 yr−1 (11.77 Tg C yr−1). The NGoM region is a CO2 sink year-round and is very susceptible to changes in river forcing. The open GoM region is dominated by thermal effects and converts from a carbon sink to a source during summer.
The historical simulation (His) and perturbed tests (Bry, NoR) are performed to determine whether observed changes in the GoM carbon system are driven by secondary effects of carbon accumulation from the global ocean or local forcing, such as river inputs. The results show that, in addition to the increasing atmospheric pCO2 over the GoM, the spatial distribution and trend in carbon system variables could only be explained when the effects of carbon accumulation via boundary conditions and the impact from river discharge are included. Although eliminating carbon accumulation via boundary in the Bry experiment did not bring a significant difference in surface carbon variables compared with that of His, a clear chemical equilibrium shift between [CO] and [HCO] can be observed at subsurface depths under the perturbation of the accumulative boundary carbon concentrations. With a projected warming climate, we anticipate the GoM to be a stronger carbon sink due to elevated river discharge and reduced impact from the global ocean.
Table A1Summary of CMIP6 GCMs considered for boundaries conditions of the regional model.
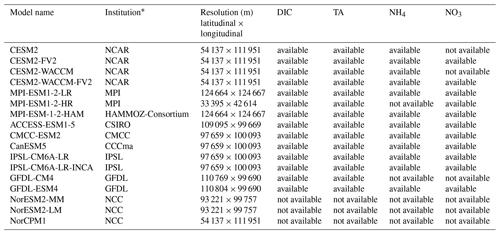
* Full names of institutions are as follows. CCCma: Canadian Centre for Climate Modelling and Analysis (Canada). CSIRO: Commonwealth Scientific and Industrial Research Organization and Bureau of Meteorology (Australia). CMCC: Centro Euro-Mediterraneo per I Cambiamenti Climatici (Italy). IPSL: L'Institut Pierre-Simon Laplace (France). MPI: Max Planck Institute for Meteorology (Germany). NCC: Norwegian Climate Centre (Norway). NCAR: National Center for Atmospheric Research (US). GFDL: Geophysical Fluid Dynamics Laboratory (US).
Code is publicly accessible by contacting the corresponding author.
Calculated CO2 flux data are available at the LSU mass storage system, and details are on the web page of the Coupled Ocean Modeling Group at LSU (http://coastandenvironment.lsu.edu/docs/faculty/xuelab/, last access: 1 September 2022). Data requests can be sent to the corresponding author via this web page.
The supplement related to this article is available online at: https://doi.org/10.5194/bg-19-4589-2022-supplement.
ZGX designed the experiments and LZ carried them out. LZ developed the model code and performed the simulations. LZ and ZGX prepared the paper.
The contact author has declared that neither of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are grateful to Chuanmin Hu (University of South Florida) and Fabian Gomez (NOAA) for kindly sharing their data as well as the constructive comments from the two anonymous reviewers.
Research support was provided through the National Science Foundation (award number OCE-1635837; EnvS 1903340; OCE-2049047; OCE-2054935), NASA (award number NNH17ZHA002C), the Louisiana Board of Regents (award number NASA/LEQSF (2018-20)-Phase3-11), and a NOAA Graduate Research Fellowship in Ocean, Coastal and Estuarine Acidification (OA R/CWQ-11). Computational support was provided by the High-Performance Computing Facility (clusters SuperMIC and QueenBee3) at Louisiana State University.
This paper was edited by Stefano Ciavatta and reviewed by two anonymous referees.
Adkins, J. F., Naviaux, J. D., Subhas, A. V., Dong, S., and Berelson, W. M.: The Dissolution Rate of CaCO3 in the Ocean, Ann. Rev. Mar. Sci., 13, 57–80, https://doi.org/10.1146/annurev-marine-041720-092514, 2021.
Aké-Castillo, J. A. and Vázquez, G.: Phytoplankton variation and its relation to nutrients and allochthonous organic matter in a coastal lagoon on the Gulf of Mexico, Estuar. Coast. Shelf Sci., 78, 705–714, https://doi.org/10.1016/j.ecss.2008.02.012, 2008.
Anav, A., Friedlingstein, P., Kidston, M., Bopp, L., Ciais, P., Cox, P., Jones, C., Jung, M., Myneni, R., and Zhu, Z.: Evaluating the land and ocean components of the global carbon cycle in the CMIP5 earth system models, J. Clim., 26, 6801–6843, https://doi.org/10.1175/JCLI-D-12-00417.1, 2013.
Arora, V. K. and Boer, G. J.: Effects of simulated climate change on the hydrology of major river basins, J. Geophys. Res.-Atmos., 106, 3335–3348, https://doi.org/10.1029/2000JD900620, 2001.
Babaousmail, H., Hou, R., Ayugi, B., Ojara, M., Ngoma, H., Karim, R., Rajasekar, A., and Ongoma, V.: Evaluation of the Performance of CMIP6 Models in Reproducing Rainfall Patterns over North Africa, Atmosphere, 12, 475, https://doi.org/10.3390/atmos12040475, 2021.
Bakker, D. C. E., Pfeil, B., Smith, K., Harasawa, S., Landa, C. S., Nakaoka, S., Nojiri, Y., Metzl, N., O'Brien, K. M., Olsen, A., Schuster, U., Tilbrook, B., Wanninkhof, R., Alin, S. R., Barbero, L., Bates, N., Bianchi, A. A., Bonou, F., Boutin, J., Bozec, Y., Burger, E. F., Castle, R. D., Chen, L., Chierici, M., Cosca, C. E., Currie, K. I., Evans, W., Featherstone, C., Feely, R. A., Fransson, A., Greenwood, N., Gregor, L., Hankin, S., Hardman-Mountford, N., Harlay, J., Hauck, J., Hoppema, M., Humphreys, M. P., Hunt, C. W., Johannessen, T., Jones, S. D., Keeling, R. F., Kitidis, V., Kozyr, A., Krasakopoulou, E., Kuwata, A., Lauvset, S. K., Lo Monaco, C., Manke, A. B., Mathis, J. T., Merlivat, L., Monteiro, P. M. S., Munro, D. R., Murata, A., Newberger, T., Omar, A. M., Ono, T., Paterson, K., Pierrot, D., Robbins, L. L., Sabine, C. L., Saito, S., Salisbury, J. E., Schneider, B., Schlitzer, R., Sieger, R., Skjelvan, I., Steinhoff, T., Sullivan, K. F., Sutherland, S. C., Sutton, A. J., Sweeney, C., Tadokoro, K., Takahashi, T., Telszewski, M., van Heuven, S. M. A. C., Vandemark, D., Wada, C., Ward, B., and Watson, A. J.: Partial pressure (or fugacity) of carbon dioxide, salinity and other variables collected from Surface underway observations using Carbon dioxide (CO2) gas analyzer and other instruments from unknown platforms in the world-wide oceans from 1968-11-16 to 2014-12-31 (NCEI Accession 0161129), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.3334/cdiac/otg.socat_v4_grid, 2017.
Barbero, L., Pierrot, D., Wanninkhof, R., Baringer, M. O., Byrne, R. H., Langdon, C., Zhang, J.-Z., and Stauffer, B. A.: Dissolved inorganic carbon, total alkalinity, nutrients, and other variables collected from CTD profile, discrete bottle, and surface underway observations using CTD, Niskin bottle, flow-through pump, and other instruments from NOAA Ship Ronald H. Brown in the Gulf of Mexico, Southeastern coast of the United States, and Mexican and Cuban coasts during the third Gulf of Mexico and East Coast Carbon (GOMECC-3) Cruise from 2017-07-18 to 2017-08-20 (NCEI Accession 0188978), NOAA Natl. Centers Environ. Information Dataset, https//doi.org/10.25921/yy5k-dw60, 2019.
Bentsen, M., Oliviè, D. J. L., Seland, Ø., Toniazzo, T., Gjermundsen, A., Graff, L. S., Debernard, J. B., Gupta, A. K., He, Y., Kirkevåg, A., Schwinger, J., Tjiputra, J., Aas, K. S., Bethke, I., Fan, Y., Griesfeller, J., Grini, A., Guo, C., Ilicak, M., Karset, I. H. H., Landgren, O. A., Liakka, J., Moseid, K. O., Nummelin, A., Spensberger, C., Tang, H., Zhang, Z., Heinze, C., Iversen, T., and Schulz, M.: NCC NorESM2-MM model output prepared for CMIP6 CMIP historical, Version 20191108, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.8040, 2019.
Bethke, I., Wang, Y., Counillon, F., Kimmritz, M., Fransner, F., Samuelsen, A., Langehaug, H. R., Chiu, P.-G., Bentsen, M., Guo, C., Tjiputra, J., Kirkevåg, A., Oliviè, D. J. L., Seland, Ø., Fan, Y., Lawrence, P., Eldevik, T., and Keenlyside, N.: NCC NorCPM1 model output prepared for CMIP6 CMIP historical. Version 20200724, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.10894, 2019.
Booij, N., Ris, R. C., and Holthuijsen, L. H.: A third-generation wave model for coastal regions: 1. Model description and validation, J. Geophys. Res.-Ocean., 104, 7649–7666, https://doi.org/10.1029/98JC02622, 1999.
Boscolo-Galazzo, Flavia, K. A., Crichton, A. R., Mawbey, E. M., Wade, B. S., and Pearson, P. N.: Temperature controls carbon cycling and biological evolution in the ocean twilight zone, Science, 371, 1148–1152, https://doi.org/10.1126/science.abb6643, 2021.
Boucher, O., Denvil, S., Levavasseur, G., Cozic, A., Caubel, A., Foujols, M.-A., Meurdesoif, Y., Cadule, P., Devilliers, M., Ghattas, J., Lebas, N., Lurton, T., Mellul, L., Musat, I., and Migno, F.: IPSL IPSL-CM6A-LR model output prepared for CMIP6 CMIP historical. Version 20180803, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.5195, 2018.
Boucher, O., Denvil, S., Levavasseur, G., Cozic, A., Caubel, A., Foujols, M.-A., Meurdesoif, Y., Balkanski, Y., Checa-Garcia, R., Hauglustaine, D., Bekki, S., and Marchand, M.: IPSL IPSL-CM6A-LR-INCA model output prepared for CMIP6 CMIP historical. Version 20210216, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.13601, 2021.
Boyd, P. W., Claustre, H., Levy, M., Siegel, D. A., and Weber, T.: Multi-faceted particle pumps drive carbon sequestration in the ocean, Nature, 568, 327–335, https://doi.org/10.1038/s41586-019-1098-2, 2019.
Boyer, T. P., García, H. E., Locarnini, R. A., Zweng, M. M., Mishonov, A. V., Reagan, J. R., Weathers, K. A. Baranova, O. K., Paver, C. R., Seidov, D., and Smolyar, I. V.: World Ocean Atlas 2018, [woa18_all_ o16_01.nc], Natl. Centers Environ. Information Dataset, https://www.ncei.noaa.gov/archive/accession/NCEI-W (last access: 15 January 2022), 2018.
Broullón, D., Pérez, F. F., Velo, A., Hoppema, M., Olsen, A., Takahashi, T., Key, R. M., Tanhua, T., González-Dávila, M., Jeansson, E., Kozyr, A., and van Heuven, S. M. A. C.: A global monthly climatology of total alkalinity: a neural network approach, Earth Syst. Sci. Data, 11, 1109–1127, https://doi.org/10.5194/essd-11-1109-2019, 2019.
Broullón, D., Pérez, F. F., Velo, A., Hoppema, M., Olsen, A., Takahashi, T., Key, R. M., Tanhua, T., Santana-Casiano, J. M., and Kozyr, A.: A global monthly climatology of oceanic total dissolved inorganic carbon (DIC): a neural network approach (NCEI Accession 0222469), NOAA Natl. Centers Environ. Inf., https://doi.org/10.25921/ndgj-jp24, 2020a.
Broullón, D., Pérez, F. F., Velo, A., Hoppema, M., Olsen, A., Takahashi, T., Key, R. M., Tanhua, T., González-Dávila, M., Jeansson, E., Kozyr, A., and van Heuven, S. M. A. C.: A global monthly climatology of total alkalinity (AT): a neural network approach (NCEI Accession 0222470), NOAA Natl. Centers Environ. Inf., https://doi.org/10.25921/5p69-y471, 2020b.
Buchan, J., Hirschi, J. J.-M., Blaker, A. T., and Sinha, B.: North Atlantic SST anomalies and the cold North European weather events of winter 2009/10 and December 2010, Mon. Weather Rev., 142, 922–932, https://doi.org/10.1175/MWR-D-13-00104.1, 2014.
Buesseler, K. O., Boyd, P. W., Black, E. E., and Siegel, D. A.: Metrics that matter for assessing the ocean biological carbon pump, P. Natl. Acad. Sci. USA, 117, 9679–9687, https://doi.org/10.1073/pnas.1918114117, 2020.
Burton, E. A. and Walter, L. M.: Relative precipitation rates of aragonite and Mg calcite from seawater: Temperature or carbonate ion control?, Geology, 15, 111–114, https://doi.org/10.1130/0091-7613(1987)15<111:RPROAA>2.0.CO;2, 1987.
Bushinsky, S. M., Landschützer, P., Rödenbeck, C., Gray, A. R., Baker, D., Mazloff, M. R., Resplandy, L., Johnson, K. S., and Sarmiento, J. L.: Reassessing Southern Ocean Air-Sea CO2 Flux Estimates With the Addition of Biogeochemical Float Observations, Global Biogeochem. Cy., 33, 1370–1388, https://doi.org/10.1029/2019GB006176, 2019.
Cai, W. J., Hu, X., Huang, W. J., Murrell, M. C., Lehrter, J. C., Lohrenz, S. E., Chou, W. C., Zhai, W., Hollibaugh, J. T., Wang, Y., Zhao, P., Guo, X., Gundersen, K., Dai, M., and Gong, G. C.: Acidification of subsurface coastal waters enhanced by eutrophication, Nat. Geosci., 4, 766–770, https://doi.org/10.1038/ngeo1297, 2011.
Cervantes-Díaz, G. Y., Hernández-Ayón, J. M., Zirino, A., Herzka, S. Z., Camacho-Ibar, V., Norzagaray, O., Barbero, L., Montes, I., Sudre, J., and Delgado, J. A.: Understanding upper water mass dynamics in the Gulf of Mexico by linking physical and biogeochemical features, J. Mar. Syst., 225, 103647, https://doi.org/10.1016/j.jmarsys.2021.103647, 2022.
Chakraborty, S. and Lohrenz, S. E.: Phytoplankton community structure in the river-influenced continental margin of the northern Gulf of Mexico, Mar. Ecol. Prog. Ser., 521, 31–47, https://doi.org/10.3354/meps11107, 2015.
Chassignet, E. P., Smith, L. T., Halliwell, G. R., and Bleck, R.: North Atlantic simulations with the Hybrid Coordinate Ocean Model (HYCOM): impact of the vertical coordinate choice, reference pressure, and thermobaricity, J. Phys. Oceanogr., 33, 2504–2526, https://doi.org/10.1175/1520-0485(2003)033<2504:NASWTH>2.0.CO;2, 2003.
Chassignet, E. P., Hurlburt, H. E., Smedstad, O. M., Halliwell, G. R., Hogan, P. J., Wallcraft, A. J., Baraille, R., and Bleck, R.: The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system, J. Mar. Syst., 65, 60–83, https://doi.org/10.1016/j.jmarsys.2005.09.016, 2007.
Chen, S., Hu, C., Barnes, B. B., Wanninkhof, R., Cai, W. J., Barbero, L., and Pierrot, D.: A machine learning approach to estimate surface ocean pCO2 from satellite measurements, Remote Sens. Environ., 228, 203–226, https://doi.org/10.1016/j.rse.2019.04.019, 2019.
Chen, X., Lohrenz, S. E., and Wiesenburg, D. A.: Distribution and controlling mechanisms of primary production on the Louisiana–Texas continental shelf, J. Mar. Syst., 25, 179–207, https://doi.org/10.1016/S0924-7963(00)00014-2, 2000.
Coble, P. G., Robbins, L. L., Daly, K. L., Cai, W.-J., Fennel, K., and Lorenz, S. E., A Preliminary Carbon Budget for the Gulf of Mexico, Marine Science Faculty Publications, Ocean Carbon and Biogeochemistry Newsletter, volume. 3, 1–4, 820, https://digitalcommons.usf.edu/msc_facpub/820 (last access: 5 November 2021), 2010.
Czerny, J., Schulz, K. G., Ludwig, A., and Riebesell, U.: Technical Note: A simple method for air–sea gas exchange measurements in mesocosms and its application in carbon budgeting, Biogeosciences, 10, 1379–1390, https://doi.org/10.5194/bg-10-1379-2013, 2013.
Dai, A., Rasmussen, R. M., Liu, C., Ikeda, K., and Prein, A. F.: A new mechanism for warm-season precipitation response to global warming based on convection-permitting simulations, Clim. Dynam., 55, 343–368, https://doi.org/10.1007/s00382-017-3787-6, 2020.
Danabasoglu, G.: NCAR CESM2-FV2 model output prepared for CMIP6 CMIP historical. Version 20191120, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.11297, 2019a.
Danabasoglu, G.: NCAR CESM2-WACCM-FV2 model output prepared for CMIP6 CMIP historical. Version 20191120, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.11298, 2019b.
Danabasoglu, G.: NCAR CESM2-WACCM model output prepared for CMIP6 CMIP historical, Version 20190917, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.10071, 2019c.
Danabasoglu, G.: NCAR CESM2 model output prepared for CMIP6 CMIP historical, Version 20191105, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.7627, 2019d.
Davis, C. E., Blackbird, S., Wolff, G., Woodward, M., and Mahaffey, C.: Seasonal organic matter dynamics in a temperate shelf sea, Prog. Oceanogr., 177, 101925, https://doi.org/10.1016/j.pocean.2018.02.021, 2019.
Delgado, J. A., Sudre, J., Tanahara, S., Montes, I., Hernández-Ayón, J. M., and Zirino, A.: Effect of Caribbean Water incursion into the Gulf of Mexico derived from absolute dynamic topography, satellite data, and remotely sensed chlorophyll a, Ocean Sci., 15, 1561–1578, https://doi.org/10.5194/os-15-1561-2019, 2019.
Dickson, A. G.: An exact definition of total alkalinity and a procedure for the estimation of alkalinity and total inorganic carbon from titration data, Deep-Sea Res. Pt. A, 28, 609–623, https://doi.org/10.1016/0198-0149(81)90121-7, 1981.
Dickson, A. G., Sabine, C. L., and Christian, J. R. (Eds): Guide to best practices for ocean CO2 measurement, Sidney, British Columbia, North Pacific Marine Science Organization, 191 pp, PICES Special Publication 3; IOCCP Report 8 https://doi.org/https://doi.org/10.25607/OBP-1342, 2007.
Dils, B., Buchwitz, M., Reuter, M., Schneising, O., Boesch, H., Parker, R., and Wunch, D.: The Greenhouse Gas Climate Change Initiative (GHG-CCI): comparative validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 retrieval algorithm products with measurements from the TCCON, Atmos. Meas. Tech., 7, 1723–1744, https://doi.org/10.5194/amt-7-1723-2014, 2014.
Doney, S. C., Fabry, V. J., Feely, R. A., and Kleypas, J. A.: Ocean acidification: The other CO2 problem, Ann. Rev. Mar. Sci., 1, 169–192, https://doi.org/10.1146/annurev.marine.010908.163834, 2009.
Dzwonkowski, B., Fournier, S., Reager, J. T., Milroy, S., Park, K., Shiller, A. M., Greer, A. T., Soto, I., Dykstra, S. L., and Sanial., V.: Tracking sea surface salinity and dissolved oxygen on a river-influenced, seasonally stratified shelf, Mississippi Bight, northern Gulf of Mexico, Cont. Shelf Res., 169, 25–33, https://doi.org/10.1016/j.csr.2018.09.009, 2018.
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., and Taylor, K. E.: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization, Geosci. Model Dev., 9, 1937–1958, https://doi.org/10.5194/gmd-9-1937-2016, 2016.
Farmer, J. R., Hertzberg, J. E., Cardinal, D., Fietz, S., Hendry, K., Jaccard, S. L., Paytan, A., and Al, E.: Assessment of C, N, and Si isotopes as tracers of past ocean nutrient and carbon cycling, Global Biogeochem. Cy., 35, e2020GB006775, https://doi.org/10.1029/2020GB006775, 2021.
Feely, R. A., Sabine, C. L., Lee, K., Millero, F. J., Lamb, M. F., Greeley, D., Bullister, J. L., Key, R. M., Peng, T.-H., Kozyr, A., Ono, T., and Wong, C. S.: In situ calcium carbonate dissolution in the Pacific Ocean, Global Biogeochem. Cy., 16, 1144, https://doi.org/10.1029/2002GB001866, 2002.
Feely, R. A., Doney, S. C., and Cooley, S. R.: Ocean acidification: Present conditions and future changes in a high-CO2 world, Oceanography, 22, 36–47, http://www.jstor.org/stable/24861022 (last access: 24 September 2021), 2009.
Fennel, K., Wilkin, J., Levin, J., Moisan, J., O'Reilly, J., and Haidvogel, D.: Nitrogen cycling in the Middle Atlantic Bight: Results from a three-dimensional model and implications for the North Atlantic nitrogen budget, Global Biogeochem. Cy., 20, 1–14, https://doi.org/10.1029/2005GB002456, 2006.
Fennel, K., Wilkin, J., Previdi, M., and Najjar, R.: Denitrification effects on air-sea CO2 flux in the coastal ocean: Simulations for the northwest North Atlantic, Geophys. Res. Lett., 35, 1–5, https://doi.org/10.1029/2008GL036147, 2008.
Fennel, K., Hetland, R., Feng, Y., and DiMarco, S.: A coupled physical-biological model of the Northern Gulf of Mexico shelf: model description, validation and analysis of phytoplankton variability, Biogeosciences, 8, 1881–1899, https://doi.org/10.5194/bg-8-1881-2011, 2011.
Fennel, W.: Towards bridging biogeochemical and fish-production models, J. Mar. Syst., 71, 171–194, https://doi.org/10.1016/j.jmarsys.2007.06.008, 2008.
Fischer, E. M. and Knutti, R.: Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes, Nat. Clim. Change, 5, 560–564, https://doi.org/10.1038/nclimate2617, 2015.
Frei, C., Schär, C., Lüthi, D., and Davies, H. C.: Heavy precipitation processes in a warmer climate, Geophys. Res. Lett., 25, 1431–1434, https://doi.org/10.1029/98GL51099, 1998.
García, H. E., Weathers, K. W., Paver, C. R., Smolyar, I., Boyer, T. P., Locarnini, M., Zweng, M. M., Mishonov, A. V, Baranova, O. K., and Seidov, D.: World Ocean Atlas 2018, Volume 3: Dissolved Oxygen, Apparent Oxygen Utilization, and Dissolved Oxygen Saturation, NOAA Atlas NESDIS 83, 38 pp. https://archimer.ifremer.fr/doc/00651/76337/ (last access: 28 January 2021), 2019.
Gomez, F. A., Wanninkhof, R., Barbero, L., Lee, S.-K., and Hernandez Jr., F. J.: Seasonal patterns of surface inorganic carbon system variables in the Gulf of Mexico inferred from a regional high-resolution ocean biogeochemical model, Biogeosciences, 17, 1685–1700, https://doi.org/10.5194/bg-17-1685-2020, 2020.
Gomez, F. A., Wanninkhof, R., Barbero, L., and Lee, S.-K.: Surface patterns of temperature, salinity, total alkalinity (TA), and dissolved inorganic carbon (DIC) across the Gulf of Mexico derived from the GoMBio model experiments from 1981-01-01 to 2014-12-31 (NCEI Accession 0242495), subset used: hindcast.surface.fields.nc, NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.25921/c34h-gb83, 2021.
Gregor, L. and Gruber, N.: OceanSODA-ETHZ: A global gridded data set of the surface ocean carbonate system for seasonal to decadal studies of ocean acidification (v2021) (NCEI Accession 0220059), NOAA Natl. Centers Environ. Information. Dataset, Version 2021, https://doi.org/10.25921/m5wx-ja34, 2020.
Große, F., Fennel, K., and Laurent, A.: Quantifying the relative importance of riverine and open-ocean nitrogen sources for hypoxia formation in the northern Gulf of Mexico, J. Geophys. Res.-Ocean., 124, 5451–5467, https://doi.org/10.1029/2019JC015230, 2019.
Guo, H., John, J. G., Blanton, C., McHugh, C., Nikonov, S., Radhakrishnan, A., Rand, K., Zadeh, N. T., Balaji, V., Durachta, J., Dupuis, C., Menzel, R., Robinson, T., Underwood, S., Vahlenkamp, H., and Bu, R.: NOAA-GFDL GFDL-CM4 model output historical, Version: 20180701, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.8594, 2018.
Gustafsson, E., Hagens, M., Sun, X., Reed, D. C., Humborg, C., Slomp, C. P., and Gustafsson, B. G.: Sedimentary alkalinity generation and long-term alkalinity development in the Baltic Sea, Biogeosciences, 16, 437–456, https://doi.org/10.5194/bg-16-437-2019, 2019.
Haidvogel, D. B., Arango, H., Budgell, W. P., Cornuelle, B. D., Curchitser, E., Di Lorenzo, E., Fennel, K., Geyer, W. R., Hermann, A. J., Lanerolle, L., Levin, J., McWilliams, J. C., Miller, A. J., Moore, A. M., Powell, T. M., Shchepetkin, A. F., Sherwood, C. R., Signell, R. P., Warner, J. C., and Wilkin, J.: Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System, J. Comput. Phys., 227, 3595–3624, https://doi.org/10.1016/j.jcp.2007.06.016, 2008.
Hofmann, E. E., Cahill, B., Fennel, K., Friedrichs, M. A. M., Hyde, K., Lee, C., Mannino, A., Najjar, R. G., O'Reilly, J. E., Wilkin, J., and Xue, J.: Modeling the dynamics of continental shelf carbon, Ann. Rev. Mar. Sci., 3, 93–122, https://doi.org/10.1146/annurev-marine-120709-142740, 2011.
Hu, X. and Cai, W. J.: An assessment of ocean margin anaerobic processes on oceanic alkalinity budget, Global Biogeochem. Cy., 25, 1–11, https://doi.org/10.1029/2010GB003859, 2011.
Huang, W. J., Cai, W. J., Wang, Y., Lohrenz, S. E., and Murrell, M. C.: The carbon dioxide system on the Mississippi River-dominated continental shelf in the northern Gulf of Mexico, J. Geophys. Res.-Ocean, 120, 1429–1445, https://doi.org/10.1002/2014JC010498, 2015.
Inskeep, W. P. and Bloom, P. R.: An evaluation of rate equations for calcite precipitation kinetics at pCO2 less than 0.01 atm and pH greater than 8, Geochim. Cosmochim. Ac., 49, 2165–2180, https://doi.org/10.1016/0016-7037(85)90074-2, 1985.
Jiang, Z. P., Cai, W. J., Chen, B., Wang, K., Han, C., Roberts, B. J., Hussain, N., and Li, Q.: Physical and Biogeochemical Controls on pH Dynamics in the Northern Gulf of Mexico During Summer Hypoxia, J. Geophys. Res.-Ocean., 124, 5979–5998, https://doi.org/10.1029/2019JC015140, 2019.
Jones, C. D., Arora, V., Friedlingstein, P., Bopp, L., Brovkin, V., Dunne, J., Graven, H., Hoffman, F., Ilyina, T., John, J. G., Jung, M., Kawamiya, M., Koven, C., Pongratz, J., Raddatz, T., Randerson, J. T., and Zaehle, S.: C4MIP-The Coupled Climate-Carbon Cycle Model Intercomparison Project: Experimental protocol for CMIP6, Geosci. Model Dev., 9, 2853–2880, https://doi.org/10.5194/gmd-9-2853-2016, 2016.
Jungclaus, J., Bittner, M., Wieners, K.-H., Wachsmann, F., Schupfner, M., Legutke, S., Giorgetta, M., Reick, C., Gayler, V., Haak, H., de Vrese, P., Raddatz, T., Esch, M., and Mauritsen, Thorst, E.: MPI-M MPI-ESM1.2-HR model output prepared for CMIP6 CMIP historical, Version 20190710, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.6594, 2019.
Jurado, E., Dachs, J., Duarte, C. M., and Simo, R.: Atmospheric deposition of organic and black carbon to the global oceans, Atmos. Environ., 42, 7931–7939, https://doi.org/10.1016/j.atmosenv.2008.07.029, 2008.
Keppler, L., Landschützer, P., Gruber, N., Lauvset, S. K., and Stemmler, I.: Mapped Observation-Based Oceanic Dissolved Inorganic Carbon (DIC), monthly climatology from January to December (based on observations between 2004 and 2017), from the Max-Planck-Institute for Meteorology (MOBO-DIC_MPIM) (NCEI Accession 0221526), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.25921/yvzj-zx46, 2020.
King, A. L., Jenkins, B. D., Wallace, J. R., Liu, Y., Wikfors, G. H., Milke, L. M., and Meseck, S. L.: Effects of CO2 on growth rate, C : N : P, and fatty acid composition of seven marine phytoplankton species, Mar. Ecol. Prog. Ser., 537, 59–69, https://doi.org/10.3354/meps11458, 2015.
Kishi, M. J., Kashiwai, M., Ware, D. M., Megrey, B. A., Eslinger, D. L., Werner, F. E., Noguchi-Aita, M., Azumaya, T., Fujii, M., Hashimoto, S., Huang, D., Iizumi, H., Ishida, Y., Kang, S., Kantakov, G. A., Kim, H. cheol, Komatsu, K., Navrotsky, V. V., Smith, S. L., Tadokoro, K., Tsuda, A., Yamamura, O., Yamanaka, Y., Yokouchi, K., Yoshie, N., Zhang, J., Zuenko, Y. I., and Zvalinsky, V. I.: NEMURO-a lower trophic level model for the North Pacific marine ecosystem, Ecol. Modell., 202, 12–25, https://doi.org/10.1016/j.ecolmodel.2006.08.021, 2007.
Kishi, M. J., Ito, S. I., Megrey, B. A., Rose, K. A., and Werner, F. E.: A review of the NEMURO and NEMURO, FISH models and their application to marine ecosystem investigations, J. Oceanogr., 67, 3–16, https://doi.org/10.1007/s10872-011-0009-4, 2011.
Krasting, J. P., John, J. G., Blanton, C., McHugh, C., Nikonov, S., Radhakrishnan, A., Rand, K., Zadeh, N. T., Balaji, V., Durachta, J., Dupuis, C., Menzel, R., Robinson, T., Underwood, S., Vahlenkamp, H., Dunne, K. A., Gauthier, P. P., Ginoux, P., Griffies, S. M., Hallberg, R., Harrison, M., Hurlin, W., Malyshev, S., Naik, V., Paulot, F., Paynter, D. J., Ploshay, J., Reichl, B. G., Schwarzkopf, D. M., Seman, C. J., Silvers, L., Wyman, B., Zeng, Y., Adcroft, A., Dunne, J. P., Dussin, R., Guo, H., He, J., Held, I. M., Horowitz, L. W., Lin, Pu; Milly, P. C., Shevliakova, E., Stock, C., Winton, M., Wittenberg, A. T., Xie, Y., and Zhao, M.: NOAA-GFDL GFDL-ESM4 model output prepared for CMIP6 CMIP historical, Version 20190726, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.8597, 2018.
Landschützer, P., Gruber, N., and Bakker, D. C. E.: An observation-based global monthly gridded sea surface pCO2 product from 1982 onward and its monthly climatology (NCEI Accession 0160558), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.7289/v5z899n6, 2017.
Landschützer, P., Gruber, N., Bakker, D. C. E., Stemmler, I., and Six, K. D.: Strengthening seasonal marine CO2 variations due to increasing atmospheric CO2, Nat. Clim. Change, 8, 146–150, https://doi.org/10.1038/s41558-017-0057-x, 2018.
Landschützer, P., Laruelle, G. G., Roobaert, A., and Regnier, P.: A combined global ocean pCO2 climatology combining open ocean and coastal areas (NCEI Accession 0209633), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.25921/qb25-f418, 2020.
Laurent, A. and Fennel, K.: Time-Evolving, Spatially Explicit Forecasts of the Northern Gulf of Mexico Hypoxic Zone, Environ. Sci. Technol., 53, 14449–14458, https://doi.org/10.1021/acs.est.9b05790, 2019.
Laurent, A., Fennel, K., Cai, W. J., Huang, W. J., Barbero, L., and Wanninkhof, R.: Eutrophication-induced acidification of coastal waters in the northern Gulf of Mexico: Insights into origin and processes from a coupled physical-biogeochemical model, Geophys. Res. Lett., 44, 946–956, https://doi.org/10.1002/2016GL071881, 2017.
Laurent, A., Fennel, K., Ko, D. S., and Lehrter, J.: Climate change projected to exacerbate impacts of coastal eutrophication in the northern Gulf of Mexico, J. Geophys. Res.-Ocean., 123, 3408–3426, https://doi.org/10.1002/2017JC013583, 2018.
Laurent, A., Fennel, K., and Kuhn, A.: An observation-based evaluation and ranking of historical Earth system model simulations in the northwest North Atlantic Ocean, Biogeosciences, 18, 1803–1822, https://doi.org/10.5194/bg-18-1803-2021, 2021.
Lauvset, S. K., Carter, B. R., Perez, F. F., Jiang, L. Q., Feely, R. A., Velo, A., and Olsen, A.: Processes Driving Global Interior Ocean pH Distribution, Global Biogeochem. Cy., 34, 1–17, https://doi.org/10.1029/2019GB006229, 2020.
Le Moigne, F. A. C., Poulton, A. J., Henson, S. A., Daniels, C. J., Fragoso, G. M., Mitchell, E., Richier, S., Russell, B. C., Smith, H. E. K., and Tarling, G. A.: Carbon export efficiency and phytoplankton community composition in the A tlantic sector of the Arctic Ocean, J. Geophys. Res.-Ocean, 120, 3896–3912, https://doi.org/10.1002/2015JC010700, 2015.
Le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Hauck, J., Pongratz, J., Pickers, P. A., Korsbakken, J. I., Peters, G. P., Canadell, J. G., Arneth, A., Arora, V. K., Barbero, L., Bastos, A., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Doney, S. C., Gkritzalis, T., Goll, D. S., Harris, I., Haverd, V., Hoffman, F. M., Hoppema, M., Houghton, R. A., Hurtt, G., Ilyina, T., Jain, A. K., Johannessen, T., Jones, C. D., Kato, E., Keeling, R. F., Goldewijk, K. K., Landschützer, P., Lefèvre, N., Lienert, S., Liu, Z., Lombardozzi, D., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S., Neill, C., Olsen, A., Ono, T., Patra, P., Peregon, A., Peters, W., Peylin, P., Pfeil, B., Pierrot, D., Poulter, B., Rehder, G., Resplandy, L., Robertson, E., Rocher, M., Rödenbeck, C., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Steinhoff, T., Sutton, A., Tans, P. P., Tian, H., Tilbrook, B., Tubiello, F. N., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., Wright, R., Zaehle, S., and Zheng, B.: Global Carbon Budget 2018, Earth Syst. Sci. Data, 10, 2141–2194, https://doi.org/10.5194/essd-10-2141-2018, 2018.
Lewis, E. and Wallace, D.: Program Developed for CO2 System Calculations ORNL/CDIAC-105, Carbon Dioxide Information Analysis Centre, https://doi.org/10.2172/639712, 1998.
Lindsay, K., Bonan, G. B., Doney, S. C., Hoffman, F. M., Lawrence, D. M., Long, M. C., Mahowald, N. M., Moore, J. K., Randerson, J. T., and Thornton, P. E.: Preindustrial-control and twentieth-century carbon cycle experiments with the Earth system model CESM1(BGC), J. Clim., 27, 8981–9005, https://doi.org/10.1175/JCLI-D-12-00565.1, 2014.
Liszka, C.: Zooplankton-mediated carbon flux in the Southern Ocean: influence of community structure, metabolism and behaviour, Ph.D. thesis, School of Environmental Sciences, University of East Anglia, England, 237 pp., https://ueaeprints.uea.ac.uk/id/eprint/69977 (last access: 15 September 2021, 2018.
Liu, Y., Lee, S. K., Muhling, B. A., Lamkin, J. T., and Enfield, D. B.: Significant reduction of the Loop Current in the 21st century and its impact on the Gulf of Mexico, J. Geophys. Res.-Ocean., 117, C05039, https://doi.org/10.1029/2011JC007555, 2012.
Liu, Y., Lee, S. K., Enfield, D. B., Muhling, B. A., Lamkin, J. T., Muller-Karger, F. E., and Roffer, M. A.: Potential impact of climate change on the Intra-Americas Sea: Part – 1. A dynamic downscaling of the CMIP5 model projections, J. Mar. Syst., 148, 56–69, https://doi.org/10.1016/j.jmarsys.2015.01.007, 2015.
Liu, M., Ren, H.-L., Zhang, R., Ineson, S., and Wang, R.: ENSO phase-locking behavior in climate models: from CMIP5 to CMIP6, Environ. Res. Commun., 3, 31004, https://doi.org/10.1088/2515-7620/abf295, 2021.
Lohrenz, S. E., Cai, W. J., Chakraborty, S., Huang, W. J., Guo, X., He, R., Xue, Z., Fennel, K., Howden, S., and Tian, H.: Satellite estimation of coastal pCO2 and air-sea flux of carbon dioxide in the northern Gulf of Mexico, Remote Sens. Environ., 207, 71–83, https://doi.org/10.1016/j.rse.2017.12.039, 2018.
Lovato, T., Peano, D., and Butenschön, M.: CMCC CMCC-ESM2 model output prepared for CMIP6 CMIP historical, Version 20210114, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.13195, 2021.
Mackenzie, F. T., Lerman, A., and Andersson, A. J.: Past and present of sediment and carbon biogeochemical cycling models, Biogeosciences, 1, 11–32, https://doi.org/10.5194/bg-1-11-2004, 2004.
Maher, D. T. and Eyre, B. D.: Carbon budgets for three autotrophic Australian estuaries: Implications for global estimates of the coastal air-water CO2 flux, Global Biogeochem. Cy., 26, GB1032, https://doi.org/10.1029/2011GB004075, 2012.
Mari, X., Passow, U., Migon, C., Burd, A. B., and Legendre, L.: Transparent exopolymer particles: Effects on carbon cycling in the ocean, Prog. Oceanogr., 151, 13–37, https://doi.org/10.1016/j.pocean.2016.11.002, 2017.
Middelburg, J. J., Soetaert, K., and Hagens, M.: Ocean alkalinity, buffering and biogeochemical processes, Rev. Geophys., 58, https://doi.org/10.1029/2019RG000681, e2019RG000681, 2020.
Millero, F. J.: The effect of pressure on the solubility of minerals in water and seawater, Geochim. Cosmochim. Ac., 46, 11–22, https://doi.org/10.1016/0016-7037(82)90286-1, 1982.
Millero, F. J.: Thermodynamics of the carbon dioxide system in the oceans, Geochim. Cosmochim. Ac., 59, 661–677, https://doi.org/10.1016/0016-7037(94)00354-O, 1995.
Millero, F. J.: The marine inorganic carbon cycle, Chem. Rev., 107, 308–341, https://doi.org/10.1021/cr0503557, 2007.
Millero, F. J.: Carbonate constants for estuarine waters, Mar. Freshw. Res., 61, 139–142, https://doi.org/10.1071/MF09254, 2010.
Moore, J. K., Doney, S. C., and Lindsay, K.: Upper ocean ecosystem dynamics and iron cycling in a global three-dimensional model, Global Biogeochem. Cy., 18, GB4028, https://doi.org/10.1029/2004GB002220, 2004.
Mucci, A.: The Solubility of Calcite and Aragonite in Seawater at Various Salinities, Temperatures and One Atmosphere Total Pressure, Am. J. Sci., 283, 780–799, https://doi.org/10.2475/ajs.283.7.780, 1983.
Na, Y., Fu, Q., and Kodama, C.: Precipitation probability and its future changes from a global cloud‐resolving model and CMIP6 simulations, J. Geophys. Res. Atmos., 125, e2019JD031926, https://doi.org/10.1029/2019JD031926, 2020.
Najjar, R. G., Herrmann, M., Alexander, R., Boyer, E. W., Burdige, D. J., Butman, D., Cai, W. J., Canuel, E. A., Chen, R. F., Friedrichs, M. A. M., Feagin, R. A., Griffith, P. C., Hinson, A. L., Holmquist, J. R., Hu, X., Kemp, W. M., Kroeger, K. D., Mannino, A., McCallister, S. L., McGillis, W. R., Mulholland, M. R., Pilskaln, C. H., Salisbury, J., Signorini, S. R., St-Laurent, P., Tian, H., Tzortziou, M., Vlahos, P., Wang, Z. A., and Zimmerman, R. C.: Carbon Budget of Tidal Wetlands, Estuaries, and Shelf Waters of Eastern North America, Global Biogeochem. Cy., 32, 389–416, https://doi.org/10.1002/2017GB005790, 2018.
Neubauer, D., Ferrachat, S., Siegenthaler-Le Drian, C., Stoll, J., Folini, D. S., Tegen, I., Wieners, K.-H., Mauritsen, T., Stemmler, I., Barthel, S., Bey, I., Daskalakis, N., Heinold, B., and Kokkola, H, U.: HAMMOZ-Consortium MPI-ESM1.2-HAM model output prepared for CMIP6 CMIP historical. Version 20190627, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.5016, 2019.
Orr, J. C., Najjar, R. G., Aumont, O., Bopp, L., Bullister, J. L., Danabasoglu, G., Doney, S. C., Dunne, J. P., Dutay, J. C., Graven, H., Griffies, S. M., John, J. G., Joos, F., Levin, I., Lindsay, K., Matear, R. J., McKinley, G. A., Mouchet, A., Oschlies, A., Romanou, A., Schlitzer, R., Tagliabue, A., Tanhua, T., and Yool, A.: Biogeochemical protocols and diagnostics for the CMIP6 Ocean Model Intercomparison Project (OMIP), Geosci. Model Dev., 10, 2169–2199, https://doi.org/10.5194/gmd-10-2169-2017, 2017.
Ploug, H., Grossart, H. P., Azam, F., and Jørgensen, B. B.: Photosynthesis, respiration, and carbon turnover in sinking marine snow from surface waters of Southern California Bight: implications for the carbon cycle in the ocean, Mar. Ecol. Prog. Ser., 179, 1–11, https://doi.org/10.3354/meps179001, 1999.
Poulton, A. J., Adey, T. R., Balch, W. M., and Holligan, P. M.: Relating coccolithophore calcification rates to phytoplankton community dynamics: Regional differences and implications for carbon export, Deep-Sea Res. Pt. II, 54, 538–557, https://doi.org/10.1016/j.dsr2.2006.12.003, 2007.
Qian, Y., Jochens, A. E., Kennicutt Ii, M. C., and Biggs, D. C.: Spatial and temporal variability of phytoplankton biomass and community structure over the continental margin of the northeast Gulf of Mexico based on pigment analysis, Cont. Shelf Res., 23, 1–17, https://doi.org/10.1016/S0278-4343(02)00173-5, 2003.
Raven, J. A. and Giordano, M.: Biomineralization by photosynthetic organisms: Evidence of coevolution of the organisms and their environment?, Geobiology, 7, 140–154, https://doi.org/10.1111/j.1472-4669.2008.00181.x, 2009.
Raven, M. R., Keil, R. G., and Webb, S. M.: Microbial sulfate reduction and organic sulfur formation in sinking marine particles, Science, 371, 178–181, https://doi.org/10.1126/science.abc6035, 2021.
Reiman, J. H. and Xu, Y. J.: Dissolved carbon export and CO2 outgassing from the lower Mississippi River – Implications of future river carbon fluxes, J. Hydrol., 578, 124093, https://doi.org/10.1016/j.jhydrol.2019.124093, 2019.
Renforth, P. and Henderson, G.: Assessing ocean alkalinity for carbon sequestration, Rev. Geophys., 55, 636–674, https://doi.org/10.1002/2016RG000533, 2017.
Robbins, L. L., Wanninkhof, R., Barbero, L., Hu, X., Mitra, S., Yvon-Lewis, S., Cai, W., Huang, W., and and Ryerson, T.: Air-sea exchange, Report of The US Gulf of Mexico Carbon Cycle Synthesis Workshop, U.S. Geol. Surv., St. Petersburg, FL. Ocean Carbon & Biogeochemistry, 67 pp., 2014.
Rost, B. and Riebesell, U.: Coccolithophores and the biological pump: responses to environmental changes, Coccolithophores, Springer, Berlin, Heidelberg, 99–125, https://doi.org/10.1007/978-3-662-06278-4_5, 2004.
Saha, S., Moorthi, S., Pan, H., Wu, X., Wang, J., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H., Stokes, D., Grumbine, R., Gayno, G., Wang, J., Hou, Y., Chuang, H., Juang, H. H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Delst, P. V., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H., Yang, R., Lord, S., van den Dool, H., Kumar, A., Wang, W., Long, C., Chelliah, M., Xue, Y., Huang, B., Schemm, J., Ebisuzaki, W., Lin, R., Xie, P., Chen, M., Zhou, S., Higgins, W., Zou, C., Liu, Q., Chen, Y., Han, Y., Cucurull, L., Reynolds, R. W., Rutledge, G., and Goldberg, M.: NCEP Climate Forecast System Reanalysis (CFSR) Selected Hourly Time-Series Products, January 1979 to December 2010, Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, https://doi.org/10.5065/D6513W89, 2010.
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y., Chuang, H., Iredell, M., Ek, M., Meng, J., Yang, R., Mendez, M. P., van den Dool, H., Zhang, Q., Wang, W., Chen, M., and Becker, E.: NCEP Climate Forecast System Version 2 (CFSv2) 6-hourly Products, Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, https://doi.org/10.5065/D61C1TXF, 2011.
Seland, Ø., Bentsen, M., Oliviè, D. J. L., Toniazzo, T., Gjermundsen, A., Graff, L. S., Debernard, J. B., Gupta, A. K., He, Y., Kirkevåg, A., Schwinger, J., Tjiputra, J., Aas, K. S., Bethke, I., Fan, Y., Griesfeller, J., Grini, A., Guo, C., Ilicak, M., Karset, I. H. H., Landgren, O. A., Liakka, J., Moseid, K. O., Nummelin, A., Spensberger, C., Tang, H., Zhang, Z., Heinze, C., Iversen, T., and Schulz, M.: NCC NorESM2-LM model output prepared for CMIP6 CMIP historical, Version 20190815, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.8036, 2019.
Shchepetkin, A. F. and McWilliams, J. C.: The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model, Ocean Model., 9, 347–404, https://doi.org/10.1016/j.ocemod.2004.08.002, 2005.
Shen, Y., Fichot, C. G., and Benner, R.: Floodplain influence on dissolved organic matter composition and export from the Mississippi – Atchafalaya River system to the Gulf of Mexico, Limnol. Oceanogr., 57, 1149–116, https://doi.org/10.4319/lo.2012.57.4.1149, 2012.
Skamarock, W. C., Klemp, J. B., Dudhi, J., Gill, D. O., Barker, D. M., Duda, M. G., Huang, X.-Y., Wang, W., and Powers, J. G.: A Description of the Advanced Research WRF Version 3, Tech. Rep., 113, https://doi.org/10.5065/D6DZ069T, 2005.
Smith, S. V. and Hollibaugh, J. T.: Coastal metabolism and the oceanic organic carbon balance, Rev. Geophys., 31, 75–89, https://doi.org/10.1029/92RG02584, 1993.
Stackpoole, S. M., Stets, E. G., Clow, D. W., Burns, D. A., Aiken, G. R., Aulenbach, B. T., Creed, I. F., Hirsch, R. M., Laudon, H., Pellerin, B. A., and Striegl, R. G.: Spatial and temporal patterns of dissolved organic matter quantity and quality in the Mississippi River Basin, 1997–2013, Hydrol. Process., 31, 902–915, https://doi.org/10.1002/hyp.11072, 2017.
Strom, S. L. and Strom, M. W.: Microplankton growth, grazing, and community structure in the northern Gulf of Mexico, Mar. Ecol. Prog. Ser., 130, 229–240, https://doi.org/10.3354/meps130229, 1996.
Sunda, W. G. and Cai, W. J.: Eutrophication induced CO2-acidification of subsurface coastal waters: Interactive effects of temperature, salinity, and atmospheric PCO2, Environ. Sci. Technol., 46, 10651–10659, https://doi.org/10.1021/es300626f, 2012.
Swart, N. C., Cole, J. N. S., Kharin, V. V., Lazare, M., Scinocca, J. F., Gillett, N. P., Anstey, J., Arora, V., Christian, J. R., Jiao, Y., Lee, W. G., Majaess, F., Saenko, O. A., Seiler, C., and Seinen, M.: CCCma CanESM5 model output prepared for CMIP6 CMIP historical, Version 20190429, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.3610, 2019.
Takahashi, T., Olafsson, J., Goddard, J. G., Chipman, D. W., and Sutherland, S. C.: Seasonal variation of CO2 and nutrients in the high-latitude surface oceans: A comparative study, Global Biogeochem. Cy., 7, 843–878, https://doi.org/10.1029/93GB02263, 1993.
Takahashi, T., Sutherland, S. C., Sweeney, C., Poisson, A., Metzl, N., Tilbrook, B., Bates, N., Wanninkhof, R., Feely, R. A., Sabine, C., Olafsson, J., and Nojiri, Y.: Global sea–air CO2 flux based on climatological surface ocean pCO2, and seasonal biological and temperature effects, Deep-Sea Res. Pt. II, 49, 1601–1622, https://doi.org/10.1016/S0967-0645(02)00003-6, 2002.
Takahashi, T., Sutherland, S. C., and Kozyr, A.: Global ocean surface water partial pressure of CO2 database: Measurements performed during 1957–2016 (version 2016), ORNL/CDIAC-161, NDP-088 (V2015), Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, US Department of Energy, Oak Ridge, Tennessee, Dataset, Document available at: https://www.nodc.noaa.gov/ocads/oceans/LDEO_Underway_Database/NDP-088_V2016.pdf, 2017.
Takahashi, T., Sutherland, S., Chipman, D. W., Goddard, J. G., Newberger, T., and Sweeney, C.: Climatological Distributions of pH, pCO2, Total CO2, Alkalinity, and CaCO3 Saturation in the Global Surface Ocean (NCEI Accession 0164568), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.3334/cdiac/otg.ndp094, 2017.
Tao, B., Tian, H., Ren, W., Yang, J., Yang, Q., He, R., Cai, W., and Lohrenz, S.: Increasing Mississippi river discharge throughout the 21st century influenced by changes in climate, land use, and atmospheric CO2, Geophys. Res. Lett., 41, 4978–4986, 2014.
Thomas, H., Schiettecatte, L.-S., Suykens, K., Koné, Y. J. M., Shadwick, E. H., Prowe, A. E. F., Bozec, Y., de Baar, H. J. W., and Borges, A. V.: Enhanced ocean carbon storage from anaerobic alkalinity generation in coastal sediments, Biogeosciences, 6, 267–274, https://doi.org/10.5194/bg-6-267-2009, 2009.
Todd-Brown, K. E. O., Randerson, J. T., Hopkins, F., Arora, V., Hajima, T., Jones, C., Shevliakova, E., Tjiputra, J., Volodin, E., Wu, T., Zhang, Q., and Allison, S. D.: Changes in soil organic carbon storage predicted by Earth system models during the 21st century, Biogeosciences, 11, 2341–2356, https://doi.org/10.5194/bg-11-2341-2014, 2014.
Torres, R., Pantoja, S., Harada, N., González, H. E., Daneri, G., Frangopulos, M., Rutllant, J. A., Duarte, C. M., Rúiz-Halpern, S., Mayol, E., and Fukasawa, M.: Air-sea CO2 fluxes along the coast of Chile: From CO2 outgassing in central northern upwelling waters to CO2 uptake in southern Patagonian fjords, J. Geophys. Res.-Ocean., 116, 1–17, https://doi.org/10.1029/2010JC006344, 2011.
Turner, J. T.: Zooplankton fecal pellets, marine snow, phytodetritus and the ocean's biological pump, Prog. Oceanogr., 130, 205–248, https://doi.org/10.1016/j.pocean.2014.08.005, 2015.
Wallmann, K., Aloisi, G., Haeckel, M., Tishchenko, P., Pavlova, G., Greinert, J., Kutterolf, S., and Eisenhauer, A.: Silicate weathering in anoxic marine sediments, Geochim. Cosmochim. Ac., 72, 2895–2918, https://doi.org/10.1016/j.gca.2008.03.026, 2008.
Wang, H., Hu, X., Cai, W. J., and Rabalais, N. N.: Comparison of fCO2 trends in river dominant and ocean dominant ocean margins, Am. Geophys. Union, 2016.
Wang, X., Cai, Y., Guo, L., and Dist, V.: Variations in abundance and size distribution of carbohydrates in the lower Mississippi River, Pearl River and Bay of St Louis, Estuar. Coast. Shelf Sci., 126, 61–69, https://doi.org/10.1016/j.ecss.2013.04.008, 2013.
Wanninkhof, R.: Relationship between wind speed and gas exchange over the ocean, J. Geophys. Res., 97, 7373–7382, https://doi.org/10.1029/92JC00188, 1992.
Wanninkhof, R.: Relationship between wind speed and gas exchange over the ocean revisited, Limnol. Oceanogr. Methods, 12, 351–362, https://doi.org/10.4319/lom.2014.12.351, 2014.
Wanninkhof, R., Zhang, J.-Z., Baringer, M. O., Langdon, C., Cai, W.-J., Salisbury, J. E., and Byrne, R. H.: Partial pressure (or fugacity) of carbon dioxide, dissolved inorganic carbon, alkalinity, temperature, salinity and other variables collected from Surface underway, discrete sample and profile observations using Alkalinity titrator, Barometric pressure sensor and other instruments from NOAA Ship RONALD H. BROWN in the Coastal Waters of Florida, Gray's Reef National Marine Sanctuary and others from 2007-05-11 to 2007-08-04 (NCEI Accession 0083633), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.3334/cdiac/otg.clivar_nacp_east_coast_cruise_2007, 2013.
Wanninkhof, R., Zhang, J.-Z., Baringer, M. O., Langdon, C., Cai, W.-J., Salisbury, J. E., and Byrne, R. H.: Partial pressure (or fugacity) of carbon dioxide, dissolved inorganic carbon, pH, alkalinity, temperature, salinity and other variables collected from discrete sample and profile observations using CTD, bottle and other instruments from NOAA Ship RONALD H. BROWN in the Gray's Reef National Marine Sanctuary, Gulf of Mexico and North Atlantic Ocean from 2012-07-21 to 2012-08-13 (NCEI Accession 0157619), NOAA Natl. Centers Environ. Information Dataset, https://doi.org/10.3334/cdiac/otg.coastal_gomecc2, 2016.
Wanninkhof, R., Triñanes, J., Park, G. H., Gledhill, D., and Olsen, A.: Large Decadal Changes in Air-Sea CO2 Fluxes in the Caribbean Sea, J. Geophys. Res.-Ocean., 124, 6960–6982, https://doi.org/10.1029/2019JC015366, 2019.
Warner, J. C., Armstrong, B., He, R., and Zambon, J. B.: Development of a Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) Modeling System, Ocean Model., 35, 230–244, https://doi.org/10.1016/j.ocemod.2010.07.010, 2010.
Weiss, R.: Carbon dioxide in water and seawater: the solubility of a non-ideal gas, Mar. Chem., 2, 203–215, https://doi.org/10.1016/0304-4203(74)90015-2, 1974.
Wieners, K.-H., Giorgetta, M., Jungclaus, J., Reick, C., Esch, M., Bittner, M., Legutke, S., Schupfner, M., Wachsmann, F., Gayler, V., Haak, H., de Vrese, P., Raddatz, T., and Mauritsen, Thorst, E.: MPI-M MPI-ESM1.2-LR model output prepared for CMIP6 CMIP historical. Version 20190710, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.6595, 2019.
Wilson, R. W., Millero, F. J., Taylor, J. R., Walsh, P. J., Christensen, V., Jennings, S., and Grosell, M.: Contribution of fish to the marine inorganic carbon cycle, Science, 323, 359–362, 2009.
Wollast, R. and Mackenzie, F. T.: Global biogeochemical cycles and climate, Clim. Geo-sciences, Springer, 453–473, https://doi.org/10.1007/978-94-009-2446-8_26, 1989.
Xu, Y. J. and DelDuco, E. M.: Unravelling the relative contribution of dissolved carbon by the Red River to the Atchafalaya River, Water, 9, 871, https://doi.org/10.3390/w9110871, 2017.
Xue, Z., He, R., Fennel, K., Cai, W.-J., Lohrenz, S., Huang, W.-J., Tian, H., Ren, W., and Zang, Z.: Modeling pCO2 variability in the Gulf of Mexico, Biogeosciences, 13, 4359–4377, https://doi.org/10.5194/bg-13-4359-2016, 2016.
Yao, H. and Hu, X.: Responses of carbonate system and CO2 flux to extended drought and intense flooding in a semiarid subtropical estuary, Limnol. Oceanogr., 62, S112–S130, https://doi.org/10.1002/lno.10646, 2017.
Zang, Z., Xue, Z. G., Xu, K., Bentley, S. J., Chen, Q., D’Sa, E. J., and Ge, Q.: A Two Decadal (1993–2012) Numerical Assessment of Sediment Dynamics in the Northern Gulf of Mexico, Water, 11, 938, https://doi.org/10.3390/w11050938, 2019.
Zang, Z., Xue, Z. G., Xu, K., Bentley, S. J., Chen, Q., D'Sa, E. J., Zhang, L., and Ou, Y.: The role of sediment-induced light attenuation on primary production during Hurricane Gustav (2008), Biogeosciences, 17, 5043–5055, https://doi.org/10.5194/bg-17-5043-2020, 2020.
Zeebe, R. and Wolf-Gladrow, D.: CO2 in Seawater: Equilibrium, Kinetics, Isotopes, Amsterdam, Elsevier Science, The Netherlands: Elsevier Elsevier Oceanography Book Series, 65, 346 pp, Amsterdam, http://113.160.249.209:8080/xmlui/handle/123456789/2912, 2001.
Zhang, X., Hetland, R. D., Marta-Almeida, M., and DiMarco, S. F.: A numerical investigation of the Mississippi and Atchafalaya freshwater transport, filling and flushing times on the Texas-Louisiana Shelf, J. Geophys. Res. Ocean., 117, C11009, https://doi.org/https://doi.org/10.1029/2012JC008108, 2012.
Ziehn, T., Chamberlain, M., Lenton, A., Law, R., Bodman, R., Dix, M., Wang, Y., Dobrohotoff, P., Srbinovsky, J., Stevens, L., Vohralik, P., Mackallah, C., Sullivan, A., O'Farrell, S., and Druken, K.: CSIRO ACCESS-ESM1.5 model output prepared for CMIP6 CMIP historical, Version 20191115, Earth Syst. Grid Fed., https://doi.org/10.22033/ESGF/CMIP6.4272, 2019.
Zhong, S. and Mucci, A.: Calcite and aragaonite precipitation from seawater solutions of various salinities : Precipitation rates and overgrowth compositions, Chem. Geol., 78, 283–299, https://doi.org/10.1016/0009-2541(89)90064-8, 1989.
Zondervan, I., Zeebe, R. E., Rost, B., and Riebesell, U.: Decreasing marine biogenic calcification: A negative feedback on rising atmospheric pCO2, Global Biogeochem. Cy., 15, 507–516, https://doi.org/10.1029/2000GB001321, 2001.
Zuddas, P. and Mucci, A.: Kinetics of calcite precipitation from seawater: II. The influence of the ionic strength, Geochim. Cosmochim. Ac., 62, 757–766, https://doi.org/10.1016/S0016-7037(98)00026-X, 1998.