A chemical kinetics theory for interpreting the non-monotonic temperature dependence of enzymatic reactions

One notable observation of enzymatic chemical reactions is that, for a given abundance of enzymes and substrates, temperature increases cause reaction rates to first increase consistent with the Arrhenius relationship, then plateau, and finally fall off quickly to zero at high temperatures. While many mathematical functions have been used to describe this pattern, we here propose a chemical kinetics theory which successfully replicates this observation and provides insights into the processes responsible for these dynamics. The chemical kinetics theory combines the law of mass action, von Smoluchowski's diffusion-limited chemical reaction theory, and Eyring's transition state theory. This new theory reveals that the thermally reversible enzyme denaturation ensured by the ceaseless thermal motion of molecules and ions in an enzyme solution explains the plateau and subsequent decrease in chemical reaction rates with increasing temperature. The temperature-dependent affinity parameter (K) that relates enzymes and substrates through their binding also affects the shape of the emergent temperature response. We demonstrate that with an increase in substrate availability, K shifts the optimal temperature, where reaction rates plateau, towards higher values. Further, we show that the chemical kinetics theory accurately represents 12 sets of published enzyme assay data and includes the popular mechanistic model by Ratkowsky et al. (2005) as a special case. Given its good performance and solid theoretical underpinning, we believe this new theory will facilitate the construction of more mechanistic-based environmental biogeochemical models.

1 Introduction

When an enzyme-catalyzed chemical reaction is monitored under a range of temperatures, one often observes that the reaction rate first increases with temperature in a manner following the Arrhenius function, peaks at some temperature, and then falls off quickly to zero when the temperature is too high for the enzyme to function (Sharpe and DeMichele, 1977; Peterson et al., 2004). As enzymes catalyze almost every chemical reaction relevant to life, this temperature response has also been observed for growth and respiration rates that emerge from the interactions among myriads of chemical reactions in an organism (Precht et al., 1973).

In order to describe this non-monotonic relationship between enzymatic reaction rates and temperature, many empirical and mechanistic-based functions have been proposed. Sharpe and DeMichele (1977) proposed a model that incorporates the empirical observation of thermally reversible enzyme denaturation (e.g., Sizer, 1943; Alexandrov, 1964) and the transition state theory (Eyring, 1935). They assumed that enzymes undergo reversible transitions between three states: a cold-induced inactive state, a heat-induced inactive state, and an active state capable of catalysis. By assuming reactions to be substrate unlimited, they obtained a model with five thermodynamic parameters that is able to almost perfectly fit published temperature-dependent growth rates of eight poikilothermic organisms (see their Figs. 5 and 6). We note that the applicability of the Sharpe–DeMichele model to growth rates of an organism is based on the assumed existence of control by master enzymes (Johnson and Lewin, 1946). Motivated by the success of Sharpe and DeMichele (1977) and the work on thermally reversible protein denaturation by Murphy et al. (1990), Ratkowsky et al. (2005) grouped the two inactive states into one and, again assuming no substrate limitation, derived a model with two thermodynamic parameters and two enzyme informatic parameters which was able to very accurately fit 35 sets of observed temperature-dependent bacterial growth rates. The model by Ratkowsky et al. (2005) was later used by Corkrey et al. (2012, 2014) to successfully interpret the temperature-dependent growth rates of many more poikilothermic organisms. Ghosh et al. (2016) extended the Ratkowsky et al. (2005) model by including the thermally reversible denaturation of many enzymes and proteins informed by proteomics and were able to satisfactorily interpret the measured temperature-dependent growth rates of mesophiles and thermophiles.

Recently, Hobbs et al. (2013) have argued that enzyme denaturation is not necessary to interpret the non-monotonic dependence of enzymatic reaction rates on temperature. Instead, they proposed the macromolecular rate theory (MMRT) which assumes that the change in heat capacity associated with enzyme catalysis and its consequent effect on the temperature dependence of the Gibbs free energy of activation can describe the temperature dependence of enzyme activity. Following the success of Hobbs et al. (2013) on modeling the temperature dependence of single-enzyme catalyzed reactions, Schipper et al. (2014) showed that MMRT fits measured relationships between soil biogeochemical rates and temperature better, including those for aerobic respiration, methane oxidation, nitrification, and denitrification, than Arrhenius-like or Q₁₀ functions. Later, Alster et al. (2016) demonstrated that MMRT was successful at capturing the temperature dependence of extracellular enzyme activities, including those of β-glucosidase, leucine aminopeptidase, and phosphatase. Following these studies, Liang et al. (2018) recommended that MMRT should be used for the improved description of the measured relationship between plant leaf respiration and temperature. Recently, Alster et al. (2020) advocated that MMRT should be used widely to represent the temperature dependence of many types of soil biogeochemical processes.

Besides the mechanistic-based models mentioned above, there are quite a number of empirical-based models described in the literature, e.g., the log-polynomial function (O'Sullivan et al., 2017), the four-parameter square root function (Ratkowsky et al., 1983), the Zwietering model (Zwietering et al., 1991), the cardinal temperature model with inflection ( Lobry et al., 1991), and others. More examples can be found in Grimaud et al. (2017) and Noll et al. (2020).

While the mechanistic-based and empirical-based models described above have been quite successful in fitting the relationship between measured rates and temperature, they do not account for the fact that the overall temperature response may be affected by substrate availability. This issue is acknowledged, for example, when Sharpe and DeMichele (1977) put forward their model and may be a barrier for developing biogeochemical models that strive to resolve the temperature dependence of biogeochemical rates mechanistically.

In the following, we develop the chemical kinetics model to deliver a comprehensive description of the non-monotonic relationship between temperature and enzymatic reaction rates. The model incorporates the observation that thermally reversible enzyme denaturation always occurs due to the thermal motion of molecules and ions in the solution of enzyme proteins (Finkelstein and Ptitsyn, 2016), as well as three well-established theories of chemical reactions: (1) the law of mass action (Koudriavtsev et al., 2001), (2) von Smoluchowski's diffusion-limited chemical reaction theory (von Smoluchowski, 1917), and (3) Eyring's transition state theory (Eyring, 1935). We evaluate the theory with 12 datasets of enzyme assays and then discuss how this new theory provides mechanistic explanations and accurate representations of the temperature dependence of biogeochemical reaction rates. We leave out the temperature-dependent irreversible enzyme denaturation but note that it needs to be included in a dynamic model (Tang and Riley, 2015; Alvarez et al., 2018).

2 Methods

2.1 The enzymatic reaction problem

We consider the simplest form of enzymatic reactions:

$$\begin{array}{}\text{(1)}& E_n+S\underset{k_{\mathrm{1}}^{-}}{\stackrel{k_{\mathrm{1}}^{+}}{\leftrightarrows }}{E}_{n}S\stackrel{v_{\max }}{⟶}{E}_n+P,\end{array}$$

where E_n is the concentration of free enzymes whose conformation structure is in the active state and able to carry out the catalysis; P is product concentration; S is substrate concentration; E_nS is enzyme–substrate complex concentration; and $k_{\mathrm{1}}^{+}$, $k_{\mathrm{1}}^{-}$, and v_max are temperature-dependent (T) kinetics parameters. Although it is not necessary for the validity of Michaelis–Menten kinetics (Briggs and Haldane, 1925), for scaling purposes, v_max (the maximum enzymatic catalysis rate) is often assumed to be much greater than $k_{\mathrm{1}}^{-}$ (Tang and Riley, 2017; Kooijman, 2009; Holling, 1959; Aksnes and Egge, 1991; Van Slyke and Cullen, 1914). Throughout this study, we take all variables to be in ISO units and provide a list of all variables and their explanations in the Appendix.

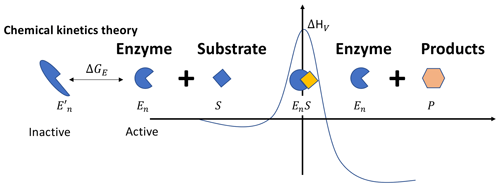
Figure 1 In the chemical kinetics theory, the Gibbs free energy of activation ΔG_V is a linear function of temperature, i.e., $\mathrm{\Delta }{G}_V=\mathrm{\Delta }{H}_V-T\mathrm{\Delta }{S}_V$, with the enthalpy of activation ΔH_V and the entropy of activation ΔS_V both being constant. This behavior of ΔG_V, along with the thermally reversible denaturation of the enzymes (as depicted by the inactive and active states here), leads to the non-monotonic temperature response of the catalysis rate. Other variables are defined in the main text.

By applying the law of mass action and the quasi-steady-state approximation (Borghans et al., 1996) to Eq. (1), i.e., $k_{\mathrm{1}}^{+}{E}_{n}S=\left(v_{\max }+k_{\mathrm{1}}^{-}\right)C$, with C being the concentration of enzyme–substrate complex E_nS, we obtain the Michaelis–Menten equation for the overall reaction rate F:

$$\begin{array}{}\text{(2)}& F=v_{\max }C=v_{\max }{\displaystyle \frac{E_{n\mathrm{t}}S}{K+S}},\end{array}$$

where $K=v_{\max }/k_{\mathrm{1}}^{+}$ is the half-saturation parameter (by taking the usual assumption $v_{\max }\gg k_{\mathrm{1}}^{-}$; Tang and Riley, 2017), and E_nt is the total concentration of enzymes that are able to form enzyme–substrate complexes, i.e., $E_{n\mathrm{t}}=E_n+C$.

We next describe how the chemical kinetics theory represents the temperature dependence of F.

2.2 The chemical kinetics theory

In studying proteins in an aqueous solution, it was observed that proteins may spontaneously unfold into inactive states, which for enzymes means losing their catalysis capability (Nojima et al., 1977; Finkelstein and Ptitsyn, 2016). By taking advantage of the thermal motion, the unfolded inactive enzyme proteins can also refold into their active state, regaining their catalysis capability (Oliveberg et al., 1995). Therefore, as thermal motion is ceaseless for all temperatures that are physiologically amenable to enzymatic reactions, it is safe to assert that at any time, even without irreversible denaturation, some enzymes are in inactive states not capable of catalyzing their specialized chemical reactions.

Chemical kinetics theory (Fig. 1) incorporates the observation of thermally reversible denaturation by considering that a fraction (1−f_E(T)) of the enzymes (E_t) are in the thermally reversible denatured inactive state (e.g., Finkelstein and Ptitsyn, 2016; Ghosh and Dill, 2009), so the catalytically active enzyme concentration E_nt is f_E(T)E_t. Further, by thermodynamics, Jin and Bethke (2003) showed that, in addition to enzyme catalysis, the chemical reaction is driven by a thermodynamic potential parameterized through a function f_R(T), which is a function of ΔG_R, the Gibbs free energy of the chemical reaction of converting the reactants into products. These turn Eq. (2) into

$$\begin{array}{}\text{(3)}& F={\displaystyle \frac{v_{\max }{f}_E\left(T\right)E_{\mathrm{t}}S}{K+S}}{f}_R\left(T\right),\end{array}$$

where

$$\begin{array}{}\text{(4)}& {\displaystyle }{v}_{\max }=v_{\max ,\mathrm{0}}{f}_v\left(T\right),\text{(5)}& {\displaystyle }K={\displaystyle \frac{v_{\max }}{k_{\mathrm{1}}^{+}}}=K_{\mathrm{0}}{f}_K\left(T\right),\text{(6)}& {\displaystyle }{f}_R\left(T\right)=\mathrm{1}-\exp \left(-{\displaystyle \frac{\mathrm{\Delta }{G}_{\mathrm{R}}}{RT}}\right),\end{array}$$

and v_max,0 and K₀ are values of v_max and K evaluated at temperature T₀, respectively.

For Eq. (6), f_R(T) can be computed following Jin and Bethke (2003), with ΔG_R dependent on its reference value at standard conditions and the reaction quotient of the chemical reaction under the given environmental condition (characterized by pressure, temperature, salinity, pH, etc.). However, except when there is significant product inhibition, f_R may be set to one, which is adopted in the remainder of this paper. We next derive expressions for f_v(T), f_K(T), and f_E(T).

For v_max, applying the transition state theory (Eyring, 1935), we have

$$\begin{array}{}\text{(7)}& f_v\left(T\right)=\left({\displaystyle \frac{T}{T_{\mathrm{0}}}}\right)\exp \left(-{\displaystyle \frac{\mathrm{\Delta }{H}_V}{RT}}\left(\mathrm{1}-{\displaystyle \frac{T}{T_{\mathrm{0}}}}\right)\right),\end{array}$$

where T₀ is the reference temperature when v_max equals v_max,0, and ΔH_V is the temperature-independent enthalpy of activation. In deriving Eq. (7), the Gibbs free energy ΔG_V of transition state theory is taken as a linear function of temperature, i.e., $\mathrm{\Delta }{G}_V=\mathrm{\Delta }{H}_V-T\mathrm{\Delta }{S}_V$, with entropy ΔS_V being constant, and incorporated into v_max,0.

To derive the temperature dependence f_K(T) for K, we follow the definition of K in Eq. (2) and adopt the assumption that v_max is much greater than $k_{\mathrm{1}}^{-}$ in Eq. (5). Applying the diffusion-limited chemical reaction model by von Smoluchowski (1917) indicates that $k_{\mathrm{1}}^{+}$ is proportional to diffusivity. Therefore, by using the Stokes–Einstein equation of diffusivity (Miller, 1924) and considering the Arrhenius-type temperature dependence of water's dynamic viscosity, $k_{\mathrm{1}}^{+}$ will have a similar functional form of temperature dependence as v_max (see Tang et al., 2021, for more details), resulting in

$$\begin{array}{}\text{(8)}& f_K\left(T\right)=\exp \left(-{\displaystyle \frac{\mathrm{\Delta }{H}_K}{RT}}\left(\mathrm{1}-{\displaystyle \frac{T}{T_{\mathrm{0}}}}\right)\right).\end{array}$$

In application, considering the activation enthalpy of self-diffusion of water as constant, e.g., 18 kJ mol⁻¹ (Konya and Nagy, 2018), one may compute $\mathrm{\Delta }{H}_K=\mathrm{\Delta }{H}_V-\mathrm{18}$.

A two-state model (e.g., Zwanzig, 1997) is used to formulate the temperature-dependent function f_E(T) as

$$\begin{array}{}\text{(9)}& f_E\left(T\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+\exp \left(-\frac{\mathrm{\Delta }{G}_{\mathrm{E}}}{RT}\right)}},\end{array}$$

with R being the universal gas constant, and protein-unfolding Gibbs free energy as

$$\begin{array}{}\text{(10)}& \begin{array}{rl}\mathrm{\Delta }{G}_{\mathrm{E}}& =\mathrm{\Delta }{H}_E-T\mathrm{\Delta }{S}_E=\mathrm{\Delta }{C}_{\mathrm{p}}\left(T-T_H\right)\\ & -T\mathrm{\Delta }{C}_{\mathrm{p}}\ln \left({\displaystyle \frac{T}{T_S}}\right).\end{array}\end{array}$$

Here ΔC_p is the heat capacity of protein unfolding (computed as $\partial \mathrm{\Delta }{H}_E/\partial T=T\partial \mathrm{\Delta }{S}_E/\partial T$), whose sign is opposite to that of the negative heat capacity of refolding measured by Oliveberg et al. (1995) and which is always positive due to protein's hydrophobicity (Silverstein, 2020). T_H is the temperature at which unfolding enthalpy ΔH_E is zero, and T_S is the temperature at which unfolding entropy ΔS_E is zero. ΔC_p, T_H, and T_S are all functions of protein chain length (Ghosh and Dill, 2009), and, usually, T_S is greater than T_H.

When Eqs. (3)–(8) are combined, we have

$$\begin{array}{}\text{(11)}& F=v_{\max ,\mathrm{0}}{\displaystyle \frac{f_v\left(T\right)f_E\left(T\right)E_{\mathrm{t}}S}{K_{\mathrm{0}}{f}_K\left(T\right)+S}},\end{array}$$

which describes the temperature dependence of biochemical reaction rates in the absence of significant product inhibition. When Eq. (11) is applied to represent the temperature dependence of an enzymatic reaction, once the reference temperature T₀ is chosen, one needs to estimate four parameters: T_H, T_S, ΔH_V, and ΔC_p.

In particular, by assuming that S is much larger than K₀f_K(T), we obtain the substrate-unlimited rate equation:

$$\begin{array}{}\text{(12)}& F_{\mathrm{\infty }}=v_{\max ,\mathrm{0}}{E}_{\mathrm{t}}{f}_v\left(T\right)f_E\left(T\right)=r_{\mathrm{0}}{f}_v\left(T\right)f_E\left(T\right),\end{array}$$

which is the four-parameter model proposed by Ratkowsky et al. (2005) to describe the temperature-dependent growth of various microorganisms (also see Corkrey et al., 2012, 2014). Since the Ratkowsky model has been successfully applied to hundreds of published datasets, the more generic chemical kinetics theory should be equally accurate under substrate-unlimited conditions and can provide further insights into the non-monotonic relationship between enzymatic reaction rates, temperature, and substrate availability.

To facilitate parametric fitting (as will be described in Sect. 2.3), taking the logarithm of Eq. (11) leads to

$$\begin{array}{}\text{(13)}& \begin{array}{rl}\ln F\left(T\right)& =\ln v_{\max ,\mathrm{0}}+\ln \left(\mathrm{1}+S/K_{\mathrm{0}}\right)\\ & +\ln \left({\displaystyle \frac{f_v\left(T\right)f_E\left(T\right)}{f_K\left(T\right)+S/K_{\mathrm{0}}}}\right).\end{array}\end{array}$$

2.3 Empirical data reanalysis

We extracted the assay data of all seven enzymes from Hobbs et al. (2013) and all five enzymes from Peterson et al. (2004) to evaluate the chemical kinetics theory. We did not try to analyze data from soils, as that would involve a more comprehensive model (considering both the production and destruction of enzymes), which is beyond the scope of this study. Since we were not able to extract the reaction rates directly from the figures in these studies or to obtain the original data, the rate for each enzyme was normalized with its own rate at a selected reference temperature T_r, based on the criterion that the data point at T_r is crossed by lines of their original numerical fitting (Hobbs et al., 2013, used MMRT and Peterson et al., 2004, used their equilibrium model). In the logarithm form (i.e., lnF(T)), this normalization ensures that the values of ln F(T)−ln F(T_r) used as observations at different temperatures are independent of the value of $\ln v_{\max ,\mathrm{0}}+\ln \left(\mathrm{1}+S/K_{\mathrm{0}}\right)$ at the reference temperature T₀ of the enzyme assay. We obtain the best-fit parameters by using the “fminsearch” function from MATLAB R2020b to minimize the summed difference between modeled and measured values of ln F(T)−ln F(T_r). In the process of parameter estimation, we found that fminsearch estimated the same parameter values corresponding to the global minimum of the cost function even when starting from differential initial guesses, indicating that the parametric fitting is robust. However, this robustness leads to some difficulty in estimating the uncertainty of the parameter fitting process. Specifically, because we were not able to digitally extract meaningful uncertainty of the observations from the figures either in Peterson et al. (2004) or in Hobbs et al. (2013), we could not apply the Monte Carlo method to compute uncertainties of the estimated parameters. We also tried using finite difference to approximate the Hessian matrix of the cost function at the best parameter estimates obtained by fminsearch. However, the ill condition of the approximated Hessian matrix prevents us from estimating the parametric uncertainty meaningfully. We could not apply the bootstrapping method because too few data points were available. Nonetheless, the excellent parametric fitting indicates that the results are robust.

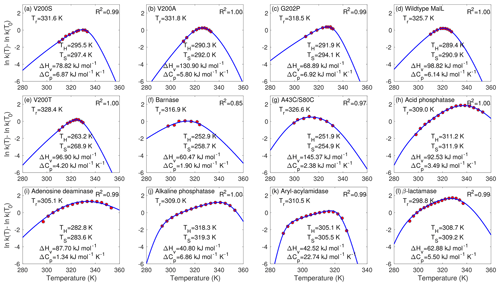
Figure 2 Fitting of the chemical kinetics theory (solid lines) to the enzyme assay data (red circles). Panels (a)–(g) are measurements from Hobbs et al. (2013), and panels (h)–(l) are from Peterson et al. (2004). T_r is the reference temperature used in the data extracted from published figures (and is different from the reference temperature T₀ that was actually involved in the enzyme assay experiments). R² is for the linear regression between the model predictions with best-fit parameters (blue lines) and measurements (in red circles). Following their original studies, parametric fitting for panels (f) and (g) used $S/K_{\mathrm{0}}=$2, while others used $S/K_{\mathrm{0}}=\mathrm{10}$.

3 Results

For the data of all 12 enzyme assays, the chemical kinetics theory obtained almost perfect model–data fitting with the fminsearch-computed best-fit parameters (Fig. 2). The R² values for the linear regression between model predictions and observations are above 0.97 for 11 cases and 0.85 for 1 case (barnase) (Fig. 2f). The best-fit heat capacity ΔC_p values of the thermodynamically reversible conversion between active and inactive conformation states of the enzymes are all positive, varying between 1.34 kJ mol⁻¹ K⁻¹ (for adenosine deaminase in Fig. 2i) and 22.74 kJ mol⁻¹ K⁻¹ (for aryl-acylamidase in Fig. 2k), in agreement with the range reported in Fig. 2c by Ghosh and Dill (2009).

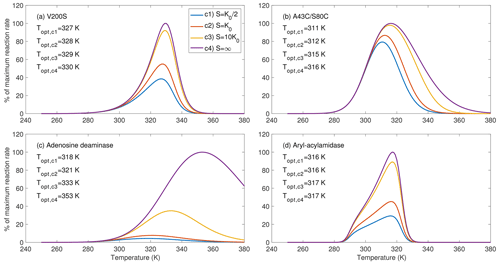
Figure 3 Substrate availability strongly affects the temperature sensitivity of the enzymatic reaction rates, as shown for four example enzymes chosen from parameters inferred in Fig. 2. For substrate level c4, the rate curve corresponds to f_v(T)f_E(T) from Eq. (12). The bulge in (d) is due to the special combination of the inferred parameters.

For the four example enzymes chosen from the estimated parameters from Fig. 2, we found the optimal temperature (i.e., where the reaction rate reaches its maximum) has varying dependence on substrate availability (Fig. 3). We show temperature response curves of the other eight enzymes in the Supplement and note that they show similar patterns to those in Fig. 3. All examples show that as substrate availability increases, the optimal temperature increases and the temperature response curve shifts towards higher temperatures. For enzyme aryl-acylamidase (Fig. 3d), the true physiological optimal temperature under the saturating substrate concentration (i.e., when S=∞, computed by Eq. 12) equals the emergent optimal temperature at a substrate concentration of 10K₀ and is 1 K higher than those at substrate concentrations of K₀ and $K_{\mathrm{0}}/\mathrm{2}$. For enzymes V200S and A43C/S80C, the optimal temperature at a substrate concentration of 10K₀ is 1 K lower than the physiological optimal temperature (Fig. 3a, b). However, this difference is 20 K for adenosine deaminase (Fig. 3c). These results clearly demonstrate that substrate availability plays a potentially important role in the emergent temperature response of biochemical reaction rates. Nevertheless, we note that this prediction of the substrate-abundance-induced shift in optimal temperature is appropriate for single enzyme reactions. As we discuss below, the relationship between optimal temperature and substrate abundance in real soils is much more complicated.

4 Discussion and conclusion

Our theoretical analysis suggests that, even for a single-substrate–single-enzyme reaction, its temperature response involves contributions from at least four processes: (1) the thermally reversible transition between active and inactive enzymes (which is ensured by the ceaseless thermal motions of molecules and ions in the enzyme solution), (2) the binding between active enzymes and substrates to form enzyme–substrate complexes, (3) the transition state activation of the enzyme–substrate complex, and (4) the thermodynamic feasibility for the biochemical reaction to generate product molecules. The chemical kinetics theory explicitly accounts for these four processes and can be extended to include more processes when more complex biochemical reactions are considered (e.g., as discussed in Tang et al., 2021). In particular, this theory demonstrates that substrate availability affects the functional relationship between biochemical rates and temperature (Eq. 11). Ignoring this effect may lead to the misinterpretation of observed optimal temperatures and confound analyses of, e.g., microbial thermal adaptation. Specifically, we find that higher optimal temperatures can be achieved under higher substrate availability for single-enzyme–single-substrate reactions. Such a shift in optimal temperature with substrate abundance also appears to align with the findings in Alvarez et al. (2018), although their interpretation attributes it to irreversible enzyme denaturation.

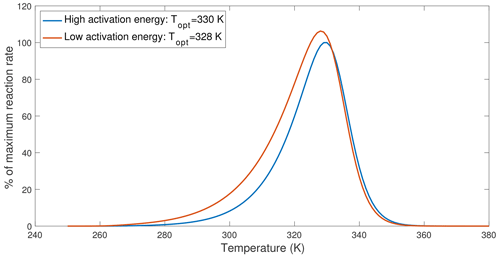
Figure 4 An example demonstrating that lower activation energy causes the optimal temperature to shift towards lower values. The curves are drawn based on Eq. (12), with the high-activation-energy case using parameters from V200S and the low-activation-energy case reduced ΔH_V from 78.82 to 58.82 kJ mol⁻¹.

Recently, Numa et al. (2021) and Robinson et al. (2020) observed that adding plant litter or glucose to soil incubation samples resulted in lower inferred optimal temperatures of soil respiration (when fitted with MMRT). Since adding more substrate most likely increased substrate concentrations, the lower optimal temperature appeared to contradict predictions by the chemical kinetics theory. However, applying the chemical kinetics theory to soils requires the consideration of interactions between substrates, microbes, and organo-mineral interactions. Since sorption interactions between organic matter and soil minerals tend to increase the overall activation energy or enthalpy of carbon use by microbes (Tang and Riley, 2015) and newly added substrates most likely have a lower activation energy than existing soil organic substrates, we expect a decrease in the optimal temperature of soil respiration. We explore this effect by computing temperature response curves for low- and high-activation-energy cases computed using Eq. (12) that assumes no substrate limitation. This example shows that lowering the activation energy reduced the optimal temperature by ∼2 K (Fig. 4). Therefore, what Numa et al. (2021) and Robinson et al. (2020) observed could have resulted from a shift in substrate type and availability, which should be modeled through the explicit representation of substrate competition and organo-mineral interactions (as discussed in Tang and Riley, 2013, 2015). In particular, we argue that the change in optimal temperature is not a simple indication of microbial physiological adaption but an emergent consequence due to interactions among many factors, including substrate availability; soil conditions; enzyme dynamics; and, among others, microbial physiology.

One important feature of the chemical kinetics theory is that it infers a positive heat capacity of protein unfolding (i.e., ΔC_p associated with thermally reversible enzyme denaturation) and a constant enthalpy of activation ΔH_V of the forward conversion of the enzyme–substrate complex. This positive ΔC_p is consistent with the negative heat capacity of enzyme refolding found by Oliveberg et al. (1995) and with many previous studies (Ghosh and Dill, 2009; Murphy et al., 1990; Finkelstein and Ptitsyn, 2016). Recently, using molecular dynamics simulations, Aqvist and Van der Ent (2022) inferred the heat capacity to be zero for both catalysis and binding processes for a designer enzyme 1A53-2.5, supporting a constant ΔH_V (note that heat capacity equals to $\partial H_V/\partial T)$. Moreover, Aqvist and Van der Ent (2022) and Aqvist (2022) suggested that the non-monotonic relationship between temperature and catalysis rate can be explained by the existence of an equilibrium between active enzyme substrate complex E_nS and inactive enzyme substrate complex ${E^{\prime }}_{n}S$. To some extent, the conceptual model by Aqvist and Van der Ent (2022) is equivalent to the chemical kinetics theory if the latter allows the inactive enzymes to form inactive enzyme–substrate complexes. The finding of zero heat capacity for both catalysis and binding processes has been debated in Lear et al. (2023) and Aqvist (2023), but they concluded that different kinetic models can fit the measured temperature-dependent catalysis rates equally well. In particular, Aqvist (2023) noted that a kinetic model considering thermally reversible enzyme denaturation fits the observations equally well. However, deducing a non-zero heat capacity for both catalysis and binding processes seems to require one to ignore the thermally reversible enzyme denaturation, which is inconsistent with the ceaseless thermal motion of molecules and ions in the enzyme solution.

Combining the transition state theory and the protein denaturation model by Lumry and Eyring (1954), Peterson et al. (2004) proposed an equilibrium model that includes both reversible and irreversible enzyme denaturation to explain their observed non-monotonic relationship between temperature and catalysis rates. However, because they assumed a constant enthalpy for the reversible enzyme denaturation, their Gibbs free energy of enzyme unfolding became a linear function of temperature. This linear function contrasts with the nonlinear function (i.e., Eq. 10) and the existence of multiple native protein states that are usually observed or inferred in studies of protein physics (Ghosh and Dill, 2009; Silverstein, 2020; Sheng and Pan, 2002; Finkelstein and Ptitsyn, 2016). Further, their model involves an explicit temporal dependence in the formulated catalysis rates, which introduces one more parameter (i.e., time) than the chemical kinetics model. Moreover, Peterson et al. (2004) also assumed their enzyme assays are substrate saturated, which is not always the case in real systems and can affect the temperature dependence of the substrate affinity parameter and thereby the overall reaction rate.

In summary, we show here that the chemical kinetics theory, by incorporating (1) the observed thermally reversible transitions of enzymes between their active and inactive states (which occurs even in the absence of substrate molecules due to the ceaseless thermal motion of molecules and ions in the enzyme solution) (Anfinsen, 1973; Finkelstein and Ptitsyn, 2016; Sizer, 1943; Oliveberg et al., 1995), (2) the law of mass action (Koudriavtsev et al., 2001), (3) the diffusion-limited chemical reaction theory by von Smoluchowski (1917), and (4) the transition state theory by Eyring (1935), can satisfactorily explain the non-monotonic relationship between temperature and catalysis rates and is a more comprehensive mechanistic representation of the temperature dependence of enzyme-catalyzed biochemical rates.

Can chemical kinetics theory be upscaled to an organism from the single-substrate–single-enzyme examples presented here? While it is likely impossible (and certainly beyond the scope of this paper) to demonstrate such a scaling analytically, Tang et al. (2021) showed, with an Ohm's law analogy, that the temperature dependence of the emergent kinetic parameters (i.e., the overall v_max and K) for chains of enzymes followed a similar form as described by the chemical kinetics theory. Indeed, some previous studies (e.g., Ratkowsky et al., 2005; Corkrey et al., 2012; Ghosh et al., 2016) have shown that even Eq. (12) (which excludes substrate dependence) is able to satisfactorily describe the temperature-dependent growth of many organisms. Particularly, the success in capturing the temperature-dependent bacterial growth rate in Ghosh et al. (2016), where they extended the thermally reversible enzyme denaturation in Eq. (12) to include all lethal proteins sampled from the proteome of mesophilic and thermophilic bacteria, suggests that the chemical kinetics theory may be scalable to organisms. Further work is required to evaluate whether the chemical kinetics theory has the potential to be applied directly to microbes, animals, and plants.

Finally, because almost every microbe, animal, and plant is able to respire on multiple substrates (Madigan et al., 2009; Cooper and Hausman, 2007) and the availability of those substrates fluctuates at multiple timescales, the chemical kinetics theory and the equilibrium chemistry approximation kinetics for substrate competition networks (Tang and Riley, 2013) together suggest that a given organism will be unlikely to have either a fixed temperature response curve or optimal temperature even with a fixed proteome distribution. Rather, the temperature response curve – and therefore the optimal temperature – is likely to be dynamic, motivating inclusion of these concepts in biogeochemical models.

Appendix A: Nomenclature

Symbol	Unit	Meaning
ΔCp	kJ mol−1 K−1	Heat capacity of protein unfolding.
ΔGR	kJ mol−1	Gibbs free energy of the chemical reaction.
ΔGE	kJ mol−1	Gibbs free energy of protein unfolding.
ΔHK	kJ mol−1	Enthalpy of activation of parameter K.
ΔHv	kJ mol−1	Enthalpy of activation of vmax.
ΔHE	kJ mol−1	Enthalpy of protein unfolding.
ΔSE	kJ mol−1	Entropy of protein unfolding.
C	mol m−3	Enzyme–substrate complex concentration.
En	mol m−3	Free-active-enzyme concentration.
Ent	mol m−3	Total active enzyme concentration.
Et	mol m−3	Total enzyme concentration.
F	mol m−3 s−1	Biochemical reaction rates.
F∞	mol m−3 s−1	Biochemical reaction rates when substrate
		is unlimited.
K0	mol m−3	Half-saturation parameter at reference
		temperature T0.
K	mol m−3	Half-saturation parameter at temperature T.
P	mol m−3	Product concentration.
R	J K−1	Universal gas constant.
S	mol m−3	Free-substrate concentration.
T	K	Thermodynamic temperature.
TH	K	Temperature when ΔHE is zero.
TS	K	Temperature when ΔSE is zero.
fK(T)	None	Temperature dependence of parameter K.
fR(T)	None	Thermodynamic potential of the chemical
		reaction at T.
fv(T)	None	Temperature dependence of vmax.
$k_{\mathrm{1}}^{+}$	m3 mol−1 s−1	Specific forward binding rate between active
		enzymes and substrates.
$k_{\mathrm{1}}^{-}$	s−1	Specific enzyme–substrate complex dissociation
		rate.
r0	mol m−3 s−1	Biochemical reaction rate at temperature T0.
vmax,0	s−1	Maximum specific catalysis rate at reference
		temperature T0.
vmax	s−1	Maximum specific catalysis rate at reference
		temperature T.