the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Global analysis of the controls on seawater dimethylsulfide spatial variability
Jane P. Mulcahy
Rafel Simó
Martí Galí
Anoop S. Mahajan
Shrivardhan Hulswar
Paul R. Halloran
Dimethylsulfide (DMS) emitted from the ocean makes a significant global contribution to natural marine aerosol and cloud condensation nuclei and, therefore, our planet's climate. Oceanic DMS concentrations show large spatiotemporal variability, but observations are sparse, so products describing global DMS distribution rely on interpolation or modelling. Understanding the mechanisms driving DMS variability, especially at local scales, is required to reduce uncertainty in large-scale DMS estimates. We present a study of mesoscale and submesoscale (< 100 km) seawater DMS variability that takes advantage of the recent expansion in high-frequency seawater DMS observations and uses all available data to investigate the typical distances over which DMS varies in all major ocean basins. These DMS spatial variability length scales (VLSs) are uncorrelated with DMS concentrations. The DMS concentrations and VLSs can therefore be used separately to help identify mechanisms underpinning DMS variability. When data are grouped by sampling campaigns, almost 80 % of the DMS VLS can be explained using the VLSs of sea surface height anomalies, density, and chlorophyll a. Our global analysis suggests that both physical and biogeochemical processes play an equally important role in controlling DMS variability, which is in contrast with previous results based on data from the low to mid-latitudes. The explanatory power of sea surface height anomalies indicates the importance of mesoscale eddies in driving DMS variability, previously unrecognised at a global scale and in agreement with recent regional studies. DMS VLS differs regionally, including surprisingly high-frequency variability in low-latitude waters. Our results independently confirm that relationships used in the literature to parameterise DMS at large scales appear to be considering the right variables. However, regional DMS VLS contrasts highlight that important driving mechanisms remain elusive. The role of submesoscale features should be resolved or accounted for in DMS process models and parameterisations. Future attempts to map DMS distributions should consider the length scale of variability.
- Article
(2196 KB) -
Supplement
(3689 KB) - BibTeX
- EndNote
Dimethylsulfide (DMS) is a volatile sulfur gas produced by surface ocean microbial food webs and emitted to the atmosphere (Bates et al., 1992). DMS emissions dominate atmospheric biogenic sulfur and form a significant component of natural marine aerosol loads (Simó, 2001; Sanchez et al., 2018; Quinn et al., 2017). Aerosols increase light scattering and modify cloud optical properties, thereby contributing to a radiative forcing of climate (Charlson et al., 1987; Carslaw et al., 2013; Galí et al., 2021). The amount, composition, and distribution of natural aerosol in the atmosphere determine the indirect radiative forcing effect of anthropogenic aerosols on climate, but these are poorly constrained by global climate models (Carslaw et al., 2013). DMS-derived sulfate aerosols are ephemeral (∼ 1 d residence time; Boucher et al., 2003) and of greater consequence for cloud modulation in remote pristine regions (Halloran et al., 2010). The distribution of natural marine aerosol sources should be represented at the resolution required to capture the frequency and magnitude of their variability. This is critical for reducing the large uncertainties associated with natural aerosol–cloud interactions.
Oceanic DMS production and consumption pathways are complex, and the controls on DMS spatial distribution in the global ocean are not fully resolved (Galí and Simó, 2015). The Global Surface Seawater DMS Database (GSSDD) contains measurements that show large-scale temporal and spatial variability in DMS concentrations (Lana et al., 2011; Hulswar et al., 2022). In situ DMS measurements are relatively sparse and limited with respect to global distribution, coverage, and spatiotemporal sampling frequency, rendering the majority of DMS observations insufficient to resolve local and submesoscale variability (Tortell et al., 2011; Belviso et al., 2004a; Lana et al., 2011). DMS sampling is globally biased towards spring–summer months (see Fig. S1, Supplement) and has disproportionally targeted biologically productive areas (e.g. northeastern Pacific and northwestern Atlantic, see Fig. 1), which can lead to an overrepresentation of high DMS concentrations within the database (Galí et al., 2018). Monthly and repeat interannual DMS measurements are rare and generally restricted to DMS productive areas (Galí et al., 2018; Tesdal et al., 2015). Sparse, infrequent, and seasonally and spatially biased observations of highly variable DMS concentrations create uncertainty because it is hard to quantify the representativeness of the measurements. Sampling uncertainties inevitably propagate through to DMS concentration and flux climatologies, parameterisations, and model outputs (Belviso et al., 2004b).
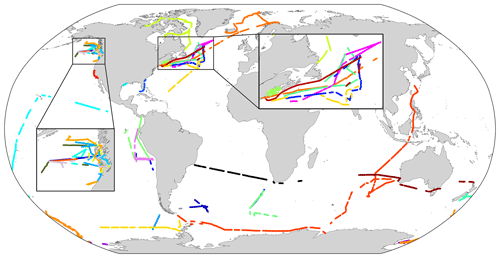
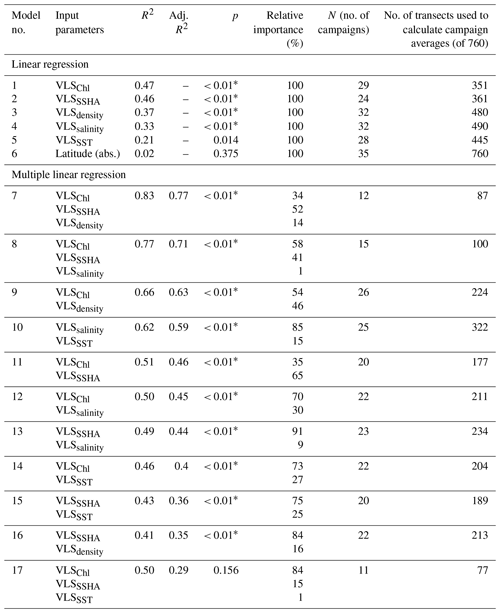
Figure 1Global extent of the 37 high-frequency DMS campaigns included in this analysis (coloured). Data are only shown for the underway transects used in the VLS analysis (see Sect. 2.3). Insets show detail for northeastern Pacific and northwestern Atlantic regions with multiple sampling campaigns (see Table S2 and Fig. S1 in the Supplement for metadata relating to each sampling campaign and the spatiotemporal distribution, respectively).
Relatively simple extrapolation methods have been used to fill the gaps between sparse observations to provide globally representative estimates of DMS (Lana et al., 2011; Kettle et al., 1999; Hulswar et al., 2022). Significant differences in these smoothed climatological estimates, and thus uncertainties, have been attributed to the gap-filling techniques used, specifically the appropriate interpolation/smoothing radius of influence (Hulswar et al., 2022). More complex algorithms have been generated at the basin or global scale using parameters such as chlorophyll, light, nutrients, surface temperature, and mixed layer depth (Simó and Dachs, 2002; Anderson et al., 2001; Aranami and Tsunogai, 2004; Halloran et al., 2010; Vallina and Simó, 2007; Aumont et al., 2002; Belviso et al., 2004a; Galí et al., 2015, 2018; Miles et al., 2009; Chu et al., 2003; Herr et al., 2019). More recently, global and regional climatologies have been generated using machine learning approaches (Wang et al., 2020; McNabb and Tortell, 2023, 2022; Humphries et al., 2012). The variation in different climatological DMS estimates highlights that the scientific community needs to better understand and map the processes controlling its oceanic distribution (Halloran et al., 2010; Belviso et al., 2004b). Modelled seasonal and regional aerosol–cloud interactions and radiative forcing are directly sensitive to the accuracy and choice of seawater DMS estimates (Woodhouse et al., 2013, 2010; Mahajan et al., 2015).
Recent studies have focussed on local and submesoscale DMS variability, taking advantage of improvements to seawater DMS concentration sampling resolution (e.g. Asher et al., 2011; Nemcek et al., 2008; Tortell, 2005a, b; Tortell and Long, 2009; Zindler et al., 2014). This study explores the potential mechanisms that appear to govern DMS variability at the < 100 km scale and investigates whether these align with the variables used within large-scale DMS parameterisations. An improved understanding of submesoscale DMS variability will aid the development of future climatological flux estimates and the appropriate radius of influence that sparse observations should be afforded when smoothing and interpolating in situ observations.
Variability length scale (VLS) analysis is a powerful tool for quantifying submesoscale variability. VLS analysis can be used to indicate the lowest sampling resolution necessary to capture most of the spatial variability (Royer et al., 2015). High-resolution measurements are required to assess small-scale variability. For example, observing variations within 10 km when the research ship is travelling at 8 m s−1 requires measurements every 20 min. Instruments that can observe variability at these high resolutions have been deployed in recent years and have substantially contributed to the global DMS database (Hulswar et al., 2022). A growing number of high-frequency DMS measurements offers the opportunity for a global analysis of the drivers of DMS variability at small scales.
VLS analysis for DMS has been applied in only a few studies, with most focusing on a specific region and/or a single sampling campaign (e.g. Ross Sea, Tortell and Long, 2009; Tortell et al., 2011; northeastern subarctic Pacific, Tortell, 2005b; Asher et al., 2011; Nemcek et al., 2008). A larger-scale VLS analysis was undertaken on the 7-month low- to mid-latitude global circumnavigation conducted during the Malaspina Expedition 2010 (M10; Royer et al., 2015). Royer et al. (2015) combined their VLS analysis with VLS values from three high-latitude studies (7–15 km; Asher et al., 2011; Nemcek et al., 2008; Tortell et al., 2011) and reported an inverse relationship between DMS VLS and latitude (R = −0.74, p < 0.005). Royer et al. (2015) also reported that biological variables dominate over physical variables as drivers of DMS VLS in low-latitude regions. While it is tempting to draw global conclusions from the similarities and differences between these studies, each study adopts a slightly different approach to the data treatment, measurement of interpolation error, and/or classification of VLS (see Table S1, Supplement).
This study applies a single, objective VLS analysis to high-frequency global DMS observations over the past 15 years (Figs. 1 and S1, Supplement). The dataset used includes all available data from previous VLS studies. Our study assesses whether the factors controlling DMS variability can be identified using a submesoscale variability analysis across all ocean basins. Section 2 describes the datasets used and the VLS methodology. Section 3 presents results including global VLS statistics, regional patterns of DMS variability, and drivers of DMS variability. Finally, the findings are discussed in Sect. 4, with conclusions made in Sect. 5.
2.1 Seawater DMS data
The majority of DMS data are sourced from the global surface seawater DMS database (GSSDD; see https://saga.pmel.noaa.gov/dms/, last access: 15 April 2022). Selection criteria are used to identify datasets suitable for submesoscale VLS analysis: a minimum of 100 data points in total and ≤ 1 h between measurements, which excludes all data with a spatial resolution of > 30 km. Applying these filters results in 37 eligible datasets (collected between 2004 and 2019). The filters broadly separate the DMS database by sampling method, highlighting the rapid shift during the early 2000s from discrete, low-frequency gas chromatography analytical systems to continuous, semi-automated high-frequency mass spectrometry (Bell et al., 2012; Saltzman et al., 2009). Additional data are from the Malaspina Expedition in 2010–2011 (M10; Royer et al., 2015), the North Atlantic Aerosol and Marine Ecosystem Study in 2015–2018 (NAAMES; Bell et al., 2021; Figs. 1 and S1, Table S2, Supplement, campaign numbers: 33 – blue, 34 – green, 35 – red, 36 – yellow), and the Southern oCean SeAsonaL Experiment in 2019 (SCALE; Manville and Bell, 2023; Figs. 1 and S1, Table S2, Supplement, campaign number: 37, green). The M10 circumnavigation data are split spatiotemporally into three datasets, each broadly covering different ocean basins (Figs. 1 and S1, Table S2, Supplement, campaign numbers: 30 – M10a, black; 31 – M10b, dark red; 32 – M10c, cyan).
2.2 Ancillary in situ and coincident satellite measurements
Ancillary in situ and remotely sensed data are used to explore the potential mechanisms driving DMS variability. In situ sea surface salinity (hereafter salinity) and sea surface temperature (SST) from each DMS dataset are used to derive sea surface density (hereafter density) (see Fernandes, 2014).
Satellite monthly mean chlorophyll a (Chl) and 5 d sea surface height anomaly (SSHA) data are matched to the average date of each DMS sampling cruise. Satellite data pixels are extracted along the coordinates of the DMS cruise track using the NASA SeaDAS software (version 7.5.3). NASA MEaSUREs level 4 (L4) 0.17∘ 5 d SSHA data are used to explore the role of eddies in driving DMS variability (Zlotnicki et al., 2019). NASA MODIS-Aqua level 3 (L3) 4 km monthly Chl is used as a proxy for plankton biomass and biological productivity (NASA Goddard Space Flight Center, 2018).
2.3 Data processing
Underway data are screened to only include data acquired when the ship speed was > 1 m s−1 to avoid measurements made when ships were sampling on station. Ship speed is calculated from distance and time between measurements. Each DMS dataset and all its ancillary data are divided into transects. Transects are defined as continuous data sections with a minimum sampling frequency of 1 h. Most observations (83 %) captured by the temporal filter are < 2.2 km apart. The minimum transect length is calculated in two stages: (1) the linear distance between the start and end of a continuous data section must be > 100 km to avoid campaigns that targeted a specific area multiple times (e.g. a productive bloom or mesoscale eddy); (2) each dataset is divided into equal length transects, with an along-track distance of at least 100 km. The initial data processing yields 1039 continuous transects from 37 DMS campaigns, with each transect 100–199 km in cumulative length (Fig. 1).
2.4 Variability length scale (VLS) analysis
Previous DMS VLS studies have not applied a standardised or consistent approach (Royer et al., 2015; Asher et al., 2011; Tortell et al., 2011; Tortell, 2005b; Tortell and Long, 2009; Nemcek et al., 2008). The analysis presented here adopts the method used to study the VLS of seawater CO2 (Hales and Takahashi, 2004), which was later applied to DMS by Tortell et al. (2011) and Nemcek et al. (2008).
The highest observational DMS sampling resolution in the datasets is typically between 0.2 and 2.2 km. Each data transect is subsampled repeatedly, starting from the first data point, at increasingly coarse spacings ranging from 2.2 km to half the length of the transect (the lowest possible resolution), increasing in 0.2 km increments. At each subsampling resolution, the first and last subsampled points of the data transect define the subsampling window. Subsampled data across the subsampling window are linearly interpolated to the resolution of the original data. Where the subsampling window matches the length of the data transect, the interpolation error associated with the subsampling resolution is calculated as the root mean squared error (RMSE) between the original and the interpolated values. Where the subsampling window is not equal to the length of the transect, the window is shifted along the transect, incrementing by one data point, and the transect is re-subsampled. Re-subsampled data are linearly interpolated across the shifted window, and the RMSE is re-calculated. The subsampling window is repeatedly shifted along the data transect and interpolation RMSE re-calculated until the subsampling ends on the last data point of the transect. The error associated with the subsampling resolution is taken as the average of all the RMSE values produced by sliding the window across the data transect at that resolution. The RMSE is calculated following Eq. (1):
The RMSE typically increases in proportion to the coarseness of the subsampling until a maximum error plateau, or asymptote, is reached. The maximum error plateau corresponds to the total variance of the dataset (Tortell et al., 2011; Belviso et al., 2004a). The trend in RMSE as a function of subsampling resolution is well described by a non-linear first-order inverse exponential rise function following Eq. (2):
where Ex is the interpolation error at subsampling resolution x, E∞ is the asymptotic maximum interpolation error at an infinite subsampling resolution, and VLS is the characteristic length scale of variability. The VLS is determined by the subsampling resolution (interpolation distance) where a tangent of the initial slope intersects with the maximum error (E∞, Fig. 2). The VLS also corresponds to the intersect on the curve (Ex) that is 63 % of E∞, i.e. Eq. (3):
Previous work suggested that a sudden change (or “breakpoint”) in the RMSE slope can be used to characterise the DMS VLS (Royer et al., 2015; Asher et al., 2011). However, this approach is unreliable because the data assessed in this study show that the breakpoint does not always occur, and its identification is subjective (see Table S1, Supplement).
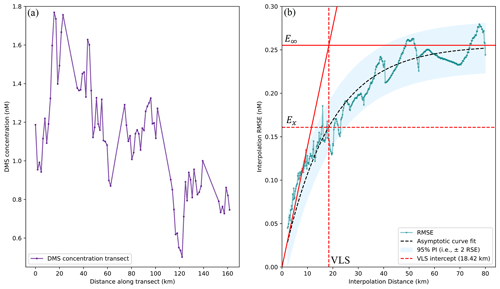
Figure 2(a) Example of seawater DMS concentration (nM) data transect (sampled from the northwestern Atlantic during the NAAMES1 (November 2015) campaign; see Bell et al., 2021), analysed to find the variability length scale (VLS). (b) Asymptotic error curve (dashed black) fitted to interpolation errors (RMSE, nM; dotted cyan) plotted as a function of increasingly coarse interpolation distance (km). The 95 % prediction intervals (PIs) of the non-linear regression fit, i.e. residual standard errors (RSE), are shaded blue. The VLS (km) is characterised as the intercept (dashed red) on the curve at 63 % of the asymptotically approached maximum interpolation error (nM). Method adapted from Hales and Takahashi (2004).
An inverse exponential rise function (Eqs. 2 and 3) is used here to objectively derive the VLS. The objective VLS method is applied to all 1039 transects and six variables: DMS, SST, salinity, density, Chl, and SSHA.
2.5 Quality assurance and VLS statistics
Two filters are used to identify viable data transects. The VLS is rejected if the distance is greater than the maximum subsampling/interpolation distance (equal to half the transect length), which only occurred in very noisy datasets. The second filter is the quality of fit to the data using the residual standard error (RSE) (Fig. 2b), which is defined as RSE , where n is the number of data points in the transect and ssres is the sum of the squares of the residuals, i.e. .
The RSE is normalised using the maximum RSE of the curve (i.e. (RSE RSE at the asymptote) × 100), and if the normalised RSE exceeds 10 %, the curve is deemed to inadequately describe the data and the transect is rejected. The two quality control filters reduce the initial 1039 transects to 763 “viable” transects.
The VLS distributions from the 763 transects are skewed for all parameters (Figs. 3 and S2, Supplement). The geometric mean and geometric standard deviation (GSD) are computed to assess central tendency and spread while accounting for skew in the data. Note that the geometric mean is regularly referred to as the “average” within this paper to aid readability. All significance testing uses the non-parametric Mann–Whitney U test. Transects are grouped and averaged by sampling campaign to assess underlying spatial and temporal (regional and seasonal) patterns of variability. Average VLS distances are calculated for each sampling campaign and for all variables (VLSDMS, VLSSST, VLSsalinity, VLSdensity, VLSChl, VLSSSHA). A minimum threshold of four transects was necessary before calculating a campaign-averaged VLS. Exclusion of campaigns with fewer than four transects reduced the total number of campaigns from 37 to 35.
Figure 3Frequency distribution of variability length scales (VLSs, km) for all DMS transects (grey bars). Vertical coloured lines correspond to the global geometric mean (and geometric standard deviation, GSD) from all transects for VLSDMS (dark blue), VLSSSHA (beige), VLSdensity (cyan), and VLSChl (magenta).
Correlation and multiple linear regression (MLR) are used to explore the global controls on VLSDMS (see Sect. 3.3.1 and 3.3.2). The campaign-averaged VLS used in each correlation and regression analysis only includes transects where coincident VLS can be calculated from the DMS and non-DMS variables. The MLR models with two input variables contain 20–26 datasets, and MLR models with three input variables contain 11–15 datasets. The relative importance of the input variables in each MLR model are calculated based on the incremental R2 used to determine interactional dominance (defined as the incremental R2 contribution of each predictor to the complete model; Azen and Budescu, 2003).
3.1 Global VLS statistics
The global average DMS concentration and geometric standard deviation (GSD) for the viable transects covered in this study are 2.23 nM (average) and 2.29 (GSD), which are similar to the global average and GSD from the GSSDD (2.66 nM (average), 2.88 (GSD); https://saga.pmel.noaa.gov/dms/, last access: 15 April 2022). The similarity between the two datasets suggests that the data used in this study are representative of global observations. The global average and GSD of VLSDMS from all 763 transects are 12.57 km and 2.33, respectively (Fig. 3). The global average VLSDMS is the smallest of the six variables tested, with VLSSSHA the most similar (15.76 km, 1.77 GSD) (Fig. 3). Global average VLSChl is slightly larger (20.89 km, 1.67 GSD) and similar to global average VLSdensity (20.21 km, 1.76 GSD) and its components VLSSST (21.23 km, 1.73 GSD) and VLSsalinity (19.52 km, 1.84 GSD) (Figs. 3 and S1, Supplement). Global average VLSDMS and VLSSSHA are significantly different (p < 0.01) from each other and the global average VLS of all other parameters. Global average VLSChl, VLSdensity, VLSSST, and VLSsalinity are not significantly different from one another.
All six variables have an average spatial variability that is tens of kilometres in all regions. The global average VLSSSHA is similar (within 4 km) to the global average VLSDMS. The global average VLSs for all other parameters are within 9 km of the global average VLSDMS. The campaign-averaged VLSDMS ranges from 2 to 30 km, which is the same order of magnitude as the range of 7–50 km reported by other DMS variability studies (Asher et al., 2011; Nemcek et al., 2008; Tortell, 2005b; Tortell et al., 2011; Royer et al., 2015). Note that a detailed comparison between studies should be treated with caution because each has used different methods to identify the VLS.
3.2 Regional patterns of DMS variability
VLSDMS is generally small in the subtropical gyres, specifically the equatorial and subtropical South Pacific and South Atlantic (Fig. 4; see Table S2, Supplement, for the campaign-averaged VLSDMS of each sampling campaign, e.g. campaign numbers: 30, M10a, black; 31, M10b, dark red; and 32, M10c, cyan). The average VLSDMS from all transects in the three M10 low- to mid-latitude circumnavigation campaign datasets (mean = 6.34 km, GSD = 2.59) is consistently smaller than the global value (mean = 12.57 km, GSD = 2.33) (Fig. 4). The relative homogeneity of small VLSDMS in these oligotrophic domains is not replicated in the VLS of any other variables (Fig. S3, Supplement). The subtropical gyres of the Southern Hemisphere are permanently stratified biomes, bounded to the south by a band of seasonally stratified biomes (Fay and McKinley, 2014). At the boundary transitions from permanently to seasonally stratified conditions, there are some notable exceptions to the low VLSDMS, e.g. the Benguela upwelling (southeast Atlantic) and South Australia upwelling (Fig. 4).
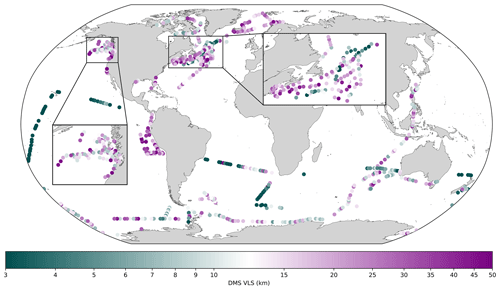
Figure 4Global distribution of 763 transects coloured by VLSDMS (km, log scale). The colour bar diverges at the global geometric mean VLSDMS (12.57 km). See Fig. S3 in the Supplement for equivalent VLS distribution maps of Chl, density, SSHA, salinity, and SST and Fig. S1 for the spatiotemporal distribution of VLSDMS.
In contrast, the average (mean = 22.06 km, GSD = 1.60) of VLSDMS in the Peruvian upwelling (eastern equatorial Pacific) is consistently larger than the global average (mean = 12.57 km, GSD = 2.33) (Fig. 4). Larger VLSDMS values are also found along parts of the Pacific and Atlantic coastlines of North America, with smaller VLSDMS values further offshore (Fig. 4, inset). The VLSDMS values in the Arctic, northeastern Pacific, northwestern Atlantic, and southeast Indian open ocean regions are highly variable. The Southern Ocean has VLSDMS generally below the global average and features some localised pockets with larger VLS (Fig. 4). The DMS concentration variability in mid- to high-latitude regions is seasonal (Hulswar et al., 2022), and VLSDMS could be influenced by the season/time of year.
3.3 Drivers of DMS variability
3.3.1 Transect and campaign-averaged VLS regressions
Simple linear regressions are used to explore the relationship between VLSDMS and VLS for SST, salinity, density, Chl, and SSHA. The possibility of a relationship with latitude (as discussed in Royer et al., 2015) is also investigated. Transect and campaign-average VLSDMS do not vary with latitude (R2 = 0.02, n = 35, p > 0.05; Table 1). No significant relationships are observed between transect VLSDMS and VLS for SST, SSS, density, Chl, and SSHA. Averaging transect VLS data into campaign averages reduces the noise and enables statistically significant relationships to be identified. The campaign-averaged VLSdensity explains 37 % of the variations in VLSDMS (Table 1; Fig. 5a); VLSSSHA (used as an indicator of the dynamic eddy field in the open ocean) and VLSChl each explain approximately half of the campaign-averaged VLSDMS (46 % and 47 %, respectively; Table 1; Fig. 5b and c).
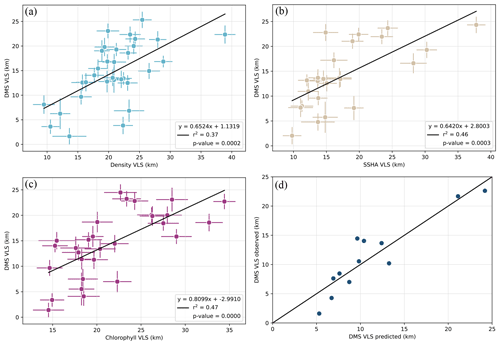
Figure 5Campaign geometric mean VLSDMS (km) plotted versus (a) VLSdensity, (b) VLSSSHA, and (c) VLSChl. Error bars indicate 1 GSD of the data within each campaign. (d) Campaign geometric mean VLSDMS predicted using coefficients from the VLSSSHA–Chl–density multiple linear regression model (Model 7, Table 1; Supplement, Table S4; Fig. S4) versus observed VLSDMS for the subset of 12 DMS campaigns included in the multiple linear regression model. The 1 : 1 line is shown.
3.3.2 Multiple linear regression of VLSDMS
Multiple linear regression (MLR) is used on the campaign-averaged VLS for SST, salinity, density, Chl, and SSHA to explore VLSDMS variance (Table 1; see Table S4, Supplement, for regression coefficients). Eleven MLR combinations were tested, and all results are significant (p < 0.01), except for the combination of VLSChl, VLSSSHA, and VLSSST (Model 17, Table 1). Note that the number of available datasets is reduced in the MLR models that have more input variables, which results in the contribution of fewer data (campaigns) to the result. The number of input data is substantially increased if campaign averages are calculated without filtering the data prior to correlation, so they only contain data where the two or more correlated variables are co-located. Relaxing the criteria such that the transects need not be coincident increases the number of campaigns that can be included in each MLR model. The “relaxed criterion” approach is less robust but gives similar results to those presented here (see Table S3, Supplement).
Individual VLSChl and/or VLSSSHA regressions with VLSDMS are outperformed (i.e. R2 > 0.47) by four MLR combinations (Models 7–10, Table 1). The combination of VLSdensity and VLSChl (Model 9, Table 1) substantially improves the regression with VLSDMS (adjusted R2 increases to 0.63). MLR Model 9 has the most campaigns (n = 26) of any model and the third highest number of available data transects (n = 224); VLSChl (54 %) and VLSdensity (46 %) make approximately equal contributions to the changes in VLSDMS described by Model 9.
The largest amount of VLSDMS variability explained by the MLR models uses the combination of VLSSSHA, VLSChl, and VLSdensity, improving the adjusted R2 to 0.77 (Model 7, Table 1; Fig. 5d). The dominant parameter in Model 7 is VLSSSHA (52 % of the explained variance), with VLSChl and VLSdensity accounting for 34 % and 14 %, respectively. Combining VLSChl and VLSSSHA (MLR Model 11) reduces the available input data (n = 20) and does not increase the explained variance in VLSDMS compared to using only one or other of the input parameters. When paired with one other variable, VLSSSHA and VLSChl dominate the explained variance in MLR models (Models 12–16, Table 1).
4.1 Global statistics
This is the first study of submesoscale seawater DMS variability from a global perspective. Spatial variability length scale (VLS) analysis is applied to every ocean basin and at different times of year using a consistent methodology. Characteristic spatial variability in all six variables (DMS, SST, salinity, density, Chl, SSHA) occurs at the low mesoscale (in the tens of kilometres) in all regions. The campaign-averaged VLSDMS ranges from 2–30 km (Table S2, Supplement); this is in general agreement with previous work (Royer et al., 2015; Nemcek et al., 2008; Asher et al., 2011; Tortell, 2005b; Tortell and Long, 2009; Tortell et al., 2011). There is no correlation between the campaign-averaged DMS concentration and VLSDMS (R2 = 0.01, p > 0.05), which suggests that understanding the variability may be a helpful and independent approach to understanding the processes that control surface ocean DMS.
4.2 Regional patterns of DMS variability
VLSDMS is generally above average at the edge of ocean basins, e.g. parts of northwestern Atlantic, northeastern Pacific, and the California coast (Fig. 4, inset). It may be possible that the longer length scales of coastal DMS spatial variability are driven by large phytoplankton blooms, which previous local and regional studies suggest can dominate coastal domains (Asher et al., 2011; Nemcek et al., 2008). This work does not investigate the detail of drivers of DMS variability in individual regions or domains.
Open ocean domains such as the subtropical gyres in the Southern Hemisphere have generally small VLSDMS, a feature not evident in the VLS of the other parameters (Figs. 4 and S2, Supplement). Short length scales of DMS variability in stable stratified biomes offer the opportunity for future work to re-examine these regions for as yet unidentified drivers of variability. Most low-latitude DMS data used in this study originate from a single sampling campaign (e.g. Malaspina Expedition 2010; Royer et al., 2015). To test if small VLSDMS is a persistent feature in undersampled subtropical open oceans, more high-resolution observations are needed.
Factors driving temporal DMS variability are not explored in this study. However, complex VLSDMS fluctuations at high latitudes (e.g. northwestern Atlantic, northeastern Pacific, Southern Ocean; Fig. 4) may be capturing variations in both space and time; VLSDMS in high-latitude dynamic regions could be related to the seasonality of biological productivity and eddy activity (see Asher et al., 2011; Behrenfeld et al., 2019; Bell et al., 2021; Fox et al., 2020; Gaube et al., 2019; Herr et al., 2019; Lana et al., 2011; McGillicuddy, 2016). Additionally, it is plausible that VLSDMS in the polar regions may be sensitive to the seasonal impact of sea ice on biogeochemical processes (see Galí et al., 2021; Lannuzel et al., 2020; Stefels et al., 2018). There are not enough repeat measurements made in high-latitude (high seasonal variability) regions to establish the impact of seasonality on VLSDMS. In this study, the only region sampled during different seasons is the northwestern Atlantic (four Atlantic NAAMES campaigns; Bell et al., 2021), and there is not yet compelling evidence of a temporal difference between the VLSDMS of these cruises/seasons. The VLSDMS values of the NAAMES1 transects (November; average = 11.93 km, GSD = 1.76) are significantly different (p < 0.01) from the transect VLSDMS of NAAMES3 (U = 99, p < 0.01; September; average = 20.89 km, GSD = 1.69) and NAAMES4 (U = 89, p < 0.01; March–April; average = 21.94 km, GSD = 1.57), but not from NAAMES2 (U = 108, p = 0.014; May–June; average = 18.4 km, GSD = 1.56). VLSDMS values of the NAAMES2, 3, and 4 transects are not significantly different from each other (all p > 0.2).
4.3 Drivers of DMS variability
The variance in campaign-averaged VLSDMS data explained by physical processes (represented by VLSSSHA) is as important as biogeochemical processes (represented by VLSChl), with each parameter able to explain just under half of the VLSDMS (Models 1 and 2, Table 1; Fig. 5). This conclusion contrasts with the findings of Royer et al. (2015), who find that the majority of VLSDMS (65 %) in the low to mid-latitudes is more similar to the VLS of biological variables that represent biomass and physiology (Chl and fluorescence) than to the VLS of physical variables. These contrasting conclusions potentially reflect the fact that length scales of physical oceanographic variability increase towards the Equator due to the effects of the Earth's rotation. The Coriolis parameter and therefore Rossby radius are intrinsically latitudinally dependent (Jacobs et al., 2001). The longer transects used by Royer et al. (2015) at low to mid-latitudes enable them to capture scales of variability that may be associated with large physical features. This point is discussed further in in Sect. 4.5.
A larger proportion of campaign-averaged VLSDMS variability (77 %) can be explained using VLSChl, VLSSSHA, and VLSdensity (Model 7, Table 1) compared to just VLSSSHA or VLSChl. The data included in the VLSSSHA–Chl–density MLR (Model 7, Table 1) are a subset but include at least one campaign from each major ocean basin (Fig. S4, Supplement) and thus represent a significant relationship with global applicability. VLSSSHA explains the majority of VLSDMS in the VLSSSHA–Chl–density MLR (52 %) (Model 7, Table 1) and improves the prediction of changes in VLSDMS compared to using just VLSChl and VLSdensity (Model 9, Table 1). The VLSSSHA–Chl–density MLR (Model 7, Table 1) includes measurements from the NAAMES4 (2018) cruise, which targeted a substantive eddy and observed a persistent high Chl feature coincident with elevated DMS levels (Bell et al., 2021). The water mass within an eddy tends to be retained by the circulation, such that plankton within the eddy are accumulated under relatively stable physics (upwelling or downwelling) and consistent biogeochemical conditions (Bell et al., 2021). Eddies may thus drive conditions where DMS variability is closely associated with biological activity and a clear covariation in VLS is observed, even if the relationship between DMS and Chl concentration is less obvious (della Penna and Gaube, 2019). The relationship between eddy structure, biogeochemistry, and DMS may explain the link between changes in VLSDMS, VLSSSHA, and VLSChl. The importance of VLSSSHA for predicting VLSDMS is consistent with results recently reported by McNabb and Tortell (2022), who apply two independent machine learning techniques to analyse DMS in the northeastern Pacific. McNabb and Tortell (2022) demonstrate the power of mesoscale eddies for predicting DMS variability (Spearman correlation coefficients = 0.35 and 0.42, depending on the machine learning method employed), using the same SSHA product used in this study (using only summertime measurements, 1997–2017). The VLSSSHA–Chl–density MLR model coefficients (Model 7, Table S4, Supplement) are used to predict VLSDMS for the target input data subset (Fig. 5d). The residuals of predicted VLSDMS are not systematically biased within the full range of the data (5–25 km).
4.4 Implications for global DMS parameterisation
Low-resolution measurements have previously been used to predict mean spatiotemporal patterns of DMS, both regionally and globally. Several studies have parameterised DMS as a function of surface mixed layer depth (MLD), light, and Chl (Vallina and Simó, 2007; Galí et al., 2018; Simó and Dachs, 2002; Aumont et al., 2002; Anderson et al., 2001; Belviso et al., 2004a; Aranami and Tsunogai, 2004). For example, Simó and Dachs (2002) use climatological MLD and remotely sensed Chl to estimate average DMS concentrations, while Vallina and Simó (2007) use climatological MLD, surface irradiance, and light attenuation to estimate surface DMS from the “solar radiation dose”. Galí et al. (2018) employ an algorithm driven by climatological Argo MLD and satellite-derived Chl, SST, and photosynthetically active radiation (PAR). Only the latter algorithm was additionally validated at finer resolution using non-climatological data to enable regional time series studies (Galí et al., 2019). SSHA reflects surface mixing and changes to the MLD (Gaube et al., 2019). This study supports the choice of key variables used in existing empirical parameterisations by demonstrating that, even on small scales, physical mixing (SSHA, density) and biological activity (Chl) explain a large portion of surface seawater DMS spatial variability in the global ocean.
The DMS parameterisations with global coverage that rely on remote and autonomous observations predict spatially and seasonally averaged surface seawater DMS reasonably well (e.g. Galí et al., 2018; Simó and Dachs, 2002; Vallina and Simó, 2007). However, some studies have questioned whether such parameterisations are overly reliant on spatial and/or temporal averaging, often to 1∘ and/or monthly resolution (e.g. Derevianko et al., 2009). The spatiotemporal averaging used to develop global parameterisations may lead to an overconfidence in current predictive capabilities because key parameters are not included. Statistically significant MLR relationships in this study are obtained once the transect data are averaged by campaign, and the average VLS for all six variables in our study is tens of kilometres. Using VLS analysis to assess the covariation of parameters at the submesoscale provides insights that can help to improve global parameterisations. Our results indicate that patterns of mesoscale and submesoscale DMS variability, particularly those associated with SSHA, will be obscured at the 1∘ resolution of most global parameterisations, highlighting the importance of modelling work at finer resolutions (e.g. Galí et al., 2019; McNabb and Tortell, 2022, 2023). Regional studies have tested empirical predictive relationships for DMS with varying degrees of success (Asher et al., 2011; Royer et al., 2015; Bell et al., 2006, 2021).
4.5 Study limitations and unidentified drivers of DMS variability
This work provides as comprehensive an assessment of DMS variability across the global ocean as existing data allow; however, many regions have not yet been sampled at high enough resolution to permit an assessment of VLSDMS. For example, only 7 of the 37 campaigns in this study have made high-resolution DMS measurements in low-latitude waters (30∘ N–30∘ S). There is a seasonal sampling bias within the DMS database, and the northwestern Atlantic is the only region to have been assessed for VLS throughout the seasonal cycle (Bell et al., 2021). More data are needed.
Satellite-derived VLSChl and VLSSSHA have been used to predict VLSDMS (e.g. Model 7, Table 1), but this relies on the assumption that the satellite-retrieved data are representative of phytoplankton productivity and eddy activity throughout the research cruise/campaign. Satellite retrievals for Chl with higher than monthly temporal resolution or, in the case of SSHA, higher than 0.17∘ spatial resolution may improve the ability to explain variance in VLSDMS.
Transect lengths between 100 and 199 km are used to ensure comparability between datasets/regions because VLS results from previous studies appear to be sensitive to the length of data transect (see Fig. S5, Supplement). However, by limiting the transect length, it is difficult to identify large eddies using VLSSSHA. Eddy length scales are typically larger at low latitudes due to the dependence of the Coriolis parameter on latitude (Chelton et al., 1998). The maximum VLS in this study is between 50 and 99.5 km (half the transect length), which is long enough to capture the eddy variability at latitudes where the eddy length scale is related to the Rossby radius of deformation, i.e. poleward of 30∘, where the deformation radius is < 30 km (Eden, 2007). Equatorward of 30∘, eddy length scales are not well predicted by the Rossby radius of deformation and can exceed 50 km (Tulloch et al., 2011; Scott and Wang, 2005; Klocker et al., 2016; Eden, 2007; Rhines, 1975). The VLSSSHA analysis approach used in this study is designed to identify the dominant scale of variability in physical features up to 50–99.5 km; therefore, it may not capture the full extent of variability associated with large eddies at low latitudes. Large eddies will, however, still be captured in the VLSSSHA analysis where a transect segments an eddy without passing through its centre. We also note that although SSHA is used to represent eddy features, at the Equator, stratification and strong westward currents tend to dominate SSHA variability rather than rotation and eddy transport (Williams and Follows, 2011).
In the subtropical gyres, VLSDMS is typically small (< 10 km; Fig. 4), which is qualitatively consistent with the short (days) response time of DMS to perturbations in the dynamic equilibrium of DMS production and consumption in these waters (Galí and Simó, 2015); VLSDMS in subtropical waters does not correspond well with the VLS of any of the other parameters (Fig. S3, Supplement). Cycling of reduced sulfur compounds in subtropical waters is well documented to be part of a different biogeochemical regime compared to productive, higher-latitude waters (e.g. Galí and Simó, 2015; Toole and Siegel, 2004). In stable oligotrophic regions where there is less variability in physical mixing and phytoplankton productivity, VLSDMS could thus be dominated by alternative parameters that drive variability in the biological cycling of DMS such as zooplankton grazing (Simó et al., 2018) and microbial organosulfur metabolism (Nowinski et al., 2019; Cui et al., 2015; Alcolombri et al., 2015).
The so-called “summer paradox” describes the seasonal misalignment between maximum concentrations of phytoplankton biomass and DMS in low-latitude waters, and it has been challenging to model (e.g. Galí and Simó, 2015; Polimene et al., 2012; Toole et al., 2008; Vallina et al., 2008). In these areas, characterised by low seasonal amplitude in phytoplankton biomass, changes in phytoplankton species succession and physiological stress control DMS production yields and rates and, ultimately, DMS seasonality. By contrast, aggregated loss processes exhibit low seasonal variability and are insufficient to explain large-scale DMS seasonality in summer paradox areas (Galí and Simó, 2015). Previous studies observed important short-term variations in the balance between DMS sources and sinks in oligotrophic waters, concomitant with meteorological forcing (Royer et al., 2016). Hence, it is plausible to hypothesise that subtle changes in this balance can explain some of the variance in VLSDMS. Light exposure in surface waters influences plankton physiological production and stress, photochemical reactions, and bacterial activity and thus has a significant impact on the cycling of reduced sulfur in oligotrophic regions (see Toole and Siegel, 2004; Vallina et al., 2008). These factors have not been included in the present study.
This study presents a comprehensive and objective analysis of DMS variability based on a large global dataset of high-frequency observations at the local/regional scale. The work shows that the variability length scale for DMS is typically small (< 30 km) and that a substantial proportion of the campaign-averaged variance can be explained by the VLS of key biological (Chl) and physical (density, SSHA) observations (Model 7, Table 1). The results improve confidence in the validity of the biological and physical parameters used to currently parameterise seawater DMS at large scales and used in many global climate models (e.g. Bock et al., 2021; Galí et al., 2018; Mulcahy et al., 2020; Simó and Dachs, 2002). However, there is substantial variability in VLSDMS when assessing individual transects, which suggests that unaccounted-for variables are also important (e.g. light, wind speed, microbial diversity and activity). Making high-frequency measurements of these parameters at the same time as high-frequency DMS measurements may help to elucidate their role in DMS cycling.
DMS and ancillary in situ data (SST and salinity) are sourced from the global surface seawater DMS database (GSSDD; https://saga.pmel.noaa.gov/dms/) and supplied by authors Rafel Simó, Martí Galí, Anoop S. Mahajan (Malaspina Expedition in 2010–2011, M10), Thomas G. Bell (North Atlantic Aerosol and Marine Ecosystem Study in 2015–2018, NAAMES; https://doi.org/10.5067/SeaBASS/NAAMES/DATA001, Behrenfeld et al., 2018), and George Manville (Southern oCean SeAsonaL Experiment in 2019, SCALE). Requests for access to M10 and SCALE DMS data can be sent to the corresponding authors (George Manville and Thomas G. Bell). Satellite data are available in online NASA repositories for chlorophyll a (https://doi.org/10.5067/AQUA/MODIS/L3M/CHL/2018, NASA Goddard Space Flight Center, 2018) and sea surface height anomalies (https://doi.org/10.5067/SLREF-CDRV2, Zlotnicki et al., 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/bg-20-1813-2023-supplement.
GM, PRH, TGB, and JPM devised the study. GM conducted the analysis and interpretation and wrote the paper, with input from PRH and TGB. JPM, MG, and RS provided insight and helped to improve the analysis and interpretation. All co-authors contributed to the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the UK Natural Environmental Research Council (through a PhD studentship for George Manville: NE/R007586/1). The contribution of Thomas G. Bell was via the NAAMES (a NASA Earth Venture Suborbital program, NNX#15AF31G) and CARES (NERC: NE/W009277/1) projects. Jane P. Mulcahy was supported by the Met Office Hadley Centre Climate Programme funded by BEIS and also received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 101003536. This research was supported by the Spanish National Plan for Scientific and Technical Research and Innovation through project BIOGAPS (CTM2016-81008-R) to Rafel Simó, through project DMS-Cons (202230I123) to Martí Galí, and through the Severo Ochoa Centre of Excellence grant (CEX2019-000928-S) to the ICM-CSIC. Rafel Simó is a holder of a European Research Council Advanced Grant (ERC-2018-ADG-834162) under the EU's Horizon H2020 research and innovation programme. The Indian Institute of Tropical Meteorology is funded by the Ministry of Earth Sciences, Government of India.
We thank the contributors of high-frequency DMS data (Stephen Archer, Alycia Herr, Tereza Jarníková, James Johnson, Christa Marandino, Sarah-Jeanne Royer, Eric Saltzman, Philippe Tortell, Miming Zhang) for making their DMS data available (see Table S2, Supplement for full details) via the Global Surface Seawater DMS Database. George Manville and Thomas G. Bell thank those involved in the 2019 SCALE (Southern oCean SeAsonaL Experiment) spring–summer campaign, including Thomas Ryan-Keogh and Marcello Vichi, Knowledge Bengu, and the crew of the SA Agulhas II. Special thanks go to Sandy Thomalla for facilitating George Manville and Thomas G. Bell's involvement in the SCALE project and to Tebatso Martin Moloto for assisting George Manville in the onboard measurement of DMS.
This research has been supported by the Natural Environment Research Council (grant nos. NE/R007586/1 and NE/W009277/1), Met Office Hadley Centre Climate Programme funded by BEIS, the Horizon 2020 (grant nos. 101003536 and ERC-2018-ADG-834162), the Spanish National Plan for Scientific and Technical Research and Innovation (grant nos. CTM2016-81008-R, 202230I123, and CEX2019-000928-S), and the Indian Institute of Tropical Meteorology (IITM).
This paper was edited by Peter Landschützer and reviewed by two anonymous referees.
Alcolombri, U., Ben-Dor, S., Feldmesser, E., Levin, Y., Tawfik, D. S., and Vardi, A.: Identification of the algal dimethyl sulfide-releasing enzyme: A missing link in the marine sulfur cycle, Science, 348, 1466–1469, https://doi.org/10.1126/SCIENCE.AAB1586, 2015.
Anderson, T. R., Spall, S. A., Yool, A., Cipollini, P., Challenor, P. G., and Fasham, M. J. R.: Global fields of sea surface dimethylsulfide predicted from chlorophyll, nutrients and light, J. Marine Syst., 30, 1–20, https://doi.org/10.1016/S0924-7963(01)00028-8, 2001.
Aranami, K. and Tsunogai, S.: Seasonal and regional comparison of oceanic and atmospheric dimethylsulfide in the northern North Pacific: Dilution effects on its concentration during winter, J. Geophys. Res.-Atmos., 109, 1–15, https://doi.org/10.1029/2003JD004288, 2004.
Asher, E. C., Merzouk, A., and Tortell, P. D.: Fine-scale spatial and temporal variability of surface water dimethylsufide (DMS) concentrations and sea-air fluxes in the NE Subarctic Pacific, Mar. Chem., 126, 63–75, https://doi.org/10.1016/j.marchem.2011.03.009, 2011.
Aumont, O., Belviso, S., and Monfray, P.: Dimethylsulfoniopropionate (DMSP) and dimethylsulfide (DMS) sea surface distributions simulated from a global three-dimensional ocean carbon cycle model, J. Geophys. Res., 107, 4-1–4-19, https://doi.org/10.1029/1999jc000111, 2002.
Azen, R. and Budescu, D. V.: The Dominance Analysis Approach for Comparing Predictors in Multiple Regression, Psychol. Methods, 8, 129–148, https://doi.org/10.1037/1082-989X.8.2.129, 2003.
Bates, T. S., Lamb, B. K., Guenther, A., Dignon, J., and Stoiber, R. E.: Sulfur emissions to the atmosphere from natural sources, J. Atmos. Chem., 14, 315–337, https://doi.org/10.1007/BF00115242, 1992.
Behrenfeld, M., Bidle, K., Boss, E., Carlson, C., Gaube, P., Giovannoni, S., Graff, J., Halsey, K., Kramer, S., Menden-Deuer, S., Nelson, N., Saltzman, E., Siegel, D., and Westberry, T.: North Atlantic Aerosol and Marine Ecosystem Study (NAAMES) 2015–2018, SeaWiFS Bio-optical Archive and Storage System (SeaBASS), NASA [data set], https://doi.org/10.5067/SeaBASS/NAAMES/DATA001, 2018.
Behrenfeld, M. J., Moore, R. H., Hostetler, C. A., Graff, J., Gaube, P., Russell, L. M., Chen, G., Doney, S. C., Giovannoni, S., Liu, H., Proctor, C., Bolaños, L. M., Baetge, N., Davie-Martin, C., Westberry, T. K., Bates, T. S., Bell, T. G., Bidle, K. D., Boss, E. S., Brooks, S. D., Cairns, B., Carlson, C., Halsey, K., Harvey, E. L., Hu, C., Karp-Boss, L., Kleb, M., Menden-Deuer, S., Morison, F., Quinn, P. K., Scarino, A. J., Anderson, B., Chowdhary, J., Crosbie, E., Ferrare, R., Hair, J. W., Hu, Y., Janz, S., Redemann, J., Saltzman, E., Shook, M., Siegel, D. A., Wisthaler, A., Martin, M. Y., and Ziemba, L.: The North Atlantic Aerosol and Marine Ecosystem Study (NAAMES): Science motive and mission overview, Front. Mar. Sci., 6, 122, https://doi.org/10.3389/FMARS.2019.00122, 2019.
Bell, T. G., Malin, G., McKee, C. M., and Liss, P. S.: A comparison of dimethylsulphide (DMS) data from the Atlantic Meridional Transect (AMT) programme with proposed algorithms for global surface DMS concentrations, Deep-Sea Res. Pt. 2, 53, 1720–1735, https://doi.org/10.1016/j.dsr2.2006.05.013, 2006.
Bell, T. G., Malin, G., Lee, G. A., Stefels, J., Archer, S., Steinke, M., and Matrai, P.: Global oceanic DMS data inter-comparability, Biogeochemistry, 110, 147–161, https://doi.org/10.1007/s10533-011-9662-3, 2012.
Bell, T. G., Porter, J. G., Wang, W. L., Lawler, M. J., Boss, E., Behrenfeld, M. J., and Saltzman, E. S.: Predictability of Seawater DMS During the North Atlantic Aerosol and Marine Ecosystem Study (NAAMES), Front. Mar. Sci., 7, 1200, https://doi.org/10.3389/FMARS.2020.596763, 2021.
Belviso, S., Moulin, C., Bopp, L., and Stefels, J.: Assessment of a global climatology of oceanic dimethylsulfide (DMS) concentrations based on SeaWiFS imagery (1998–2001), Can. J. Fish. Aquat. Sci., 61, 804–816, https://doi.org/10.1139/f04-001, 2004a.
Belviso, S., Bopp, L., Moulin, C., Orr, J. C., Anderson, T. R., Aumont, O., Chu, S., Elliott, S., Maltrud, M. E., and Simó, R.: Comparison of global climatological maps of sea surface dimethyl sulfide, Global Biogeochem. Cy., 18, GB3013, https://doi.org/10.1029/2003GB002193, 2004b.
Bock, J., Michou, M., Nabat, P., Abe, M., Mulcahy, J. P., Olivié, D. J. L., Schwinger, J., Suntharalingam, P., Tjiputra, J., van Hulten, M., Watanabe, M., Yool, A., and Séférian, R.: Evaluation of ocean dimethylsulfide concentration and emission in CMIP6 models, Biogeosciences, 18, 3823–3860, https://doi.org/10.5194/bg-18-3823-2021, 2021.
Boucher, O., Moulin, C., Belviso, S., Aumont, O., Bopp, L., Cosme, E., von Kuhlmann, R., Lawrence, M. G., Pham, M., Reddy, M. S., Sciare, J., and Venkataraman, C.: DMS atmospheric concentrations and sulphate aerosol indirect radiative forcing: a sensitivity study to the DMS source representation and oxidation, Atmos. Chem. Phys., 3, 49–65, https://doi.org/10.5194/acp-3-49-2003, 2003.
Carslaw, K. S., Lee, L. A., Reddington, C. L., Pringle, K. J., Rap, A., Forster, P. M., Mann, G. W., Spracklen, D. V., Woodhouse, M. T., Regayre, L. A., and Pierce, J. R.: Large contribution of natural aerosols to uncertainty in indirect forcing, Nature, 503, 67–71, https://doi.org/10.1038/nature12674, 2013.
Charlson, R. J., Lovelock, J. E., Andreae, M. O., and Warren, S. G.: Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate, Nature, 326, 655–661, https://doi.org/10.1038/326655a0, 1987.
Chelton, D. B., deSzoeke, R. A., Schlax, M. G., el Naggar, K., and Siwertz, N.: Geographical Variability of the First Baroclinic Rossby Radius of Deformation, J. Phys. Oceanogr., 28, 433–460, https://doi.org/10.1175/1520-0485(1998)028<0433:GVOTFB>2.0.CO;2, 1998.
Chu, S., Elliott, S., and Maltrud, M. E.: Global eddy permitting simulations of surface ocean nitrogen, iron, sulfur cycling, Chemosphere, 50, 223–235, https://doi.org/10.1016/S0045-6535(02)00162-5, 2003.
Cui, Y., Suzuki, S., Omori, Y., Wong, S. K., Ijichi, M., Kaneko, R., Kameyama, S., Tanimoto, H., and Hamasaki, K.: Abundance and distribution of dimethylsulfoniopropionate degradation genes and the corresponding bacterial community structure at dimethyl sulfide hot spots in the tropical and subtropical Pacific Ocean, Appl. Environ. Microbiol., 81, 4184–4194, https://doi.org/10.1128/AEM.03873-14, 2015.
della Penna, A. and Gaube, P.: Overview of (sub)mesoscale ocean dynamics for the NAAMES field program, Front. Mar. Sci., 6, 384, https://doi.org/10.3389/FMARS.2019.00384, 2019.
Derevianko, G. J., Deutsch, C., and Hall, A.: On the relationship between ocean DMS and solar radiation, Geophys. Res. Lett., 36, L17606, https://doi.org/10.1029/2009GL039412, 2009.
Eden, C.: Eddy length scales in the North Atlantic Ocean, J. Geophys. Res.-Oceans, 112, 6004, https://doi.org/10.1029/2006JC003901, 2007.
Fay, A. R. and McKinley, G. A.: Global open-ocean biomes: mean and temporal variability, Earth Syst. Sci. Data, 6, 273–284, https://doi.org/10.5194/essd-6-273-2014, 2014.
Fernandes: python-seawater v3.3.2, Zenodo [code], https://doi.org/10.5281/zenodo.11395, 2014.
Fox, J., Behrenfeld, M. J., Haëntjens, N., Chase, A., Kramer, S. J., Boss, E., Karp-Boss, L., Fisher, N. L., Penta, W. B., Westberry, T. K., and Halsey, K. H.: Phytoplankton Growth and Productivity in the Western North Atlantic: Observations of Regional Variability From the NAAMES Field Campaigns, Front. Mar. Sci., 7, 24, https://doi.org/10.3389/FMARS.2020.00024, 2020.
Galí, M. and Simó, R.: A meta-analysis of oceanic DMS and DMSP cycling processes: Disentangling the summer paradox, Global Biogeochem. Cy., 29, 496–515, https://doi.org/10.1002/2014GB004940, 2015.
Galí, M., Devred, E., Levasseur, M., Royer, S. J., and Babin, M.: A remote sensing algorithm for planktonic dimethylsulfoniopropionate (DMSP) and an analysis of global patterns, Remote Sens. Environ., 171, 171–184, https://doi.org/10.1016/j.rse.2015.10.012, 2015.
Galí, M., Levasseur, M., Devred, E., Simó, R., and Babin, M.: Sea-surface dimethylsulfide (DMS) concentration from satellite data at global and regional scales, Biogeosciences, 15, 3497–3519, https://doi.org/10.5194/bg-15-3497-2018, 2018.
Galí, M., Devred, E., Babin, M., and Levasseur, M.: Decadal increase in Arctic dimethylsulfide emission, P. Natl. Acad. Sci. USA, 116, 19311–19317, https://doi.org/10.1073/PNAS.1904378116, 2019.
Galí, M., Lizotte, M., Kieber, D. J., Randelhoff, A., Hussherr, R., Xue, L., Dinasquet, J., Babin, M., Rehm, E., and Levasseur, M.: DMS emissions from the Arctic marginal ice zone, Elem. Sci. Anthr., 9, 00113, https://doi.org/10.1525/ELEMENTA.2020.00113, 2021.
Gaube, P., J. McGillicuddy, D., and Moulin, A. J.: Mesoscale Eddies Modulate Mixed Layer Depth Globally, Geophys. Res. Lett., 46, 1505–1512, https://doi.org/10.1029/2018GL080006, 2019.
Hales, B. and Takahashi, T.: High-resolution biogeochemical investigation of the Ross Sea, Antarctica, during the AESOPS (U.S. JGOFS) Program, Global Biogeochem. Cy., 18, GB3006, https://doi.org/10.1029/2003GB002165, 2004.
Halloran, P. R., Bell, T. G., and Totterdell, I. J.: Can we trust empirical marine DMS parameterisations within projections of future climate?, Biogeosciences, 7, 1645–1656, https://doi.org/10.5194/bg-7-1645-2010, 2010.
Herr, A. E., Kiene, R. P., Dacey, J. W. H., and Tortell, P. D.: Patterns and drivers of dimethylsulfide concentration in the northeast subarctic Pacific across multiple spatial and temporal scales, Biogeosciences, 16, 1729–1754, https://doi.org/10.5194/bg-16-1729-2019, 2019.
Hulswar, S., Simó, R., Galí, M., Bell, T. G., Lana, A., Inamdar, S., Halloran, P. R., Manville, G., and Mahajan, A. S.: Third revision of the global surface seawater dimethyl sulfide climatology (DMS-Rev3), Earth Syst. Sci. Data, 14, 2963–2987, https://doi.org/10.5194/essd-14-2963-2022, 2022.
Humphries, G. R. W., Deal, C. J., Elliott, S., and Huettmann, F.: Spatial predictions of sea surface dimethylsulfide concentrations in the high arctic, Biogeochemistry, 110, 287–301, https://doi.org/10.1007/S10533-011-9683-Y, 2012.
Jacobs, G. A., Barron, C. N., and Rhodes, R. C.: Mesoscale characteristics, J. Geophys. Res., 106, 581–600, https://doi.org/10.1029/2000JC000669, 2001.
Kettle, A. J., Andreae, M. O., Amouroux, D., Andreae, T. W., Bates, T. S., Berresheim, H., Bingemer, H., Boniforti, R., Curran, M. A. J., DiTullio, G. R., Helas, G., Jones, G. B., Keller, M. D., Kiene, R. P., Leek, C., Levasseur, M., Malin, G., Maspero, M., Matrai, P., McTaggart, A. R., Mihalopoulos, N., Nguyen, B. C., Novo, A., Putaud, J. P., Rapsomanikis, S., Roberts, G., Schebeske, G., Sharma, S., Simó, R., Staubes, R., Turner, S., and Uher, G.: A global database of sea surface dimethylsulfide (DMS) measurements and a procedure to predict sea surface DMS as a function of latitude, longitude, and month, Global Biogeochem. Cy., 13, 399–444, https://doi.org/10.1029/1999GB900004, 1999.
Klocker, A., Marshall, D. P., Keating, S. R., and Read, P. L.: A regime diagram for ocean geostrophic turbulence, Q. J. Roy. Meteor. Soc, 142, 2411–2417, https://doi.org/10.1002/qj.2833, 2016.
Lana, A., Bell, T. G., Simó, R., Vallina, S. M., Ballabrera-Poy, J., Kettle, A. J., Dachs, J., Bopp, L., Saltzman, E. S., Stefels, J., Johnson, J. E., and Liss, P. S.: An updated climatology of surface dimethlysulfide concentrations and emission fluxes in the global ocean, Global Biogeochem. Cy., 25, 1–17, https://doi.org/10.1029/2010GB003850, 2011.
Lannuzel, D., Tedesco, L., van Leeuwe, M., Campbell, K., Flores, H., Delille, B., Miller, L., Stefels, J., Assmy, P., Bowman, J., Brown, K., Castellani, G., Chierici, M., Crabeck, O., Damm, E., Else, B., Fransson, A., Fripiat, F., Geilfus, N. X., Jacques, C., Jones, E., Kaartokallio, H., Kotovitch, M., Meiners, K., Moreau, S., Nomura, D., Peeken, I., Rintala, J. M., Steiner, N., Tison, J. L., Vancoppenolle, M., van der Linden, F., Vichi, M., and Wongpan, P.: The future of Arctic sea-ice biogeochemistry and ice-associated ecosystems, Nat. Clim. Change, 10, 983–992, https://doi.org/10.1038/s41558-020-00940-4, 2020.
Mahajan, A. S., Fadnavis, S., Thomas, M. A., Pozzoli, L., Gupta, S., Royer, S. J., Saiz-Lopez, A., and Simó, R.: Quantifying the impacts of an updated global dimethyl sulfide climatology on cloud microphysics and aerosol radiative forcing, J. Geophys. Res., 120, 2524–2536, https://doi.org/10.1002/2014JD022687, 2015.
Manville, G. and Bell, T.: Ship-based continuous underway surface seawater dimethylsulfide concentration timeseries collected in the southeast Atlantic sector of the Southern Ocean as part of the spring cruise of the SCALE project, October–November 2019, NERC EDS British Oceanographic Data Centre NOC [data set], https://doi.org/10.5285/f70248ef-cb60-77d0-e053-6c86abc0c75a, 2023.
McGillicuddy, D. J.: Mechanisms of Physical-Biological-Biogeochemical Interaction at the Oceanic Mesoscale, Annu. Rev. Mar. Sci., 8, 125–159, https://doi.org/10.1146/ANNUREV-MARINE-010814-015606, 2016.
McNabb, B. J. and Tortell, P. D.: Improved prediction of dimethyl sulfide (DMS) distributions in the northeast subarctic Pacific using machine-learning algorithms, Biogeosciences, 19, 1705–1721, https://doi.org/10.5194/bg-19-1705-2022, 2022.
McNabb, B. J. and Tortell, P. D.: Oceanographic controls on Southern Ocean dimethyl sulfide distributions revealed by machine learning algorithms, Limnol. Oceanogr., 68, 616–630, https://doi.org/10.1002/LNO.12298, 2023.
Miles, C. J., Bell, T. G., and Lenton, T. M.: Testing the relationship between the solar radiation dose and surface DMS concentrations using in situ data, Biogeosciences, 6, 1927–1934, https://doi.org/10.5194/bg-6-1927-2009, 2009.
Mulcahy, J. P., Johnson, C., Jones, C. G., Povey, A. C., Scott, C. E., Sellar, A., Turnock, S. T., Woodhouse, M. T., Abraham, N. L., Andrews, M. B., Bellouin, N., Browse, J., Carslaw, K. S., Dalvi, M., Folberth, G. A., Glover, M., Grosvenor, D. P., Hardacre, C., Hill, R., Johnson, B., Jones, A., Kipling, Z., Mann, G., Mollard, J., O'Connor, F. M., Palmiéri, J., Reddington, C., Rumbold, S. T., Richardson, M., Schutgens, N. A. J., Stier, P., Stringer, M., Tang, Y., Walton, J., Woodward, S., and Yool, A.: Description and evaluation of aerosol in UKESM1 and HadGEM3-GC3.1 CMIP6 historical simulations, Geosci. Model Dev., 13, 6383–6423, https://doi.org/10.5194/gmd-13-6383-2020, 2020.
NASA Goddard Space Flight Center, Ocean Ecology Laboratory, Ocean Biology Processing Group: Moderate-resolution Imaging Spectroradiometer (MODIS) Aqua Chlorophyll Data, 2018 Reprocessing, NASA OB.DAAC, Greenbelt, MD, USA [data set], https://doi.org/10.5067/AQUA/MODIS/L3M/CHL/2018, 2018.
Nemcek, N., Ianson, D., and Tortell, P. D.: A high-resolution survey of DMS, CO2, and O2/Ar distributions in productive coastal waters, Global Biogeochem. Cy., 22, GB2009, https://doi.org/10.1029/2006GB002879, 2008.
Nowinski, B., Motard-Côté, J., Landa, M., Preston, C. M., Scholin, C. A., Birch, J. M., Kiene, R. P., and Moran, M. A.: Microdiversity and temporal dynamics of marine bacterial dimethylsulfoniopropionate genes, Environ. Microbiol., 21, 1687–1701, https://doi.org/10.1111/1462-2920.14560, 2019.
Polimene, L., Archer, S. D., Butenschön, M., and Allen, J. I.: A mechanistic explanation of the Sargasso Sea DMS “summer paradox”, Biogeochemistry, 110, 243–255, https://doi.org/10.1007/s10533-011-9674-z, 2012.
Quinn, P. K., Coffman, D. J., Johnson, J. E., Upchurch, L. M., and Bates, T. S.: Small fraction of marine cloud condensation nuclei made up of sea spray aerosol, Nat. Geosci., 10, 674–679, https://doi.org/10.1038/ngeo3003, 2017.
Rhines, P. B.: Waves and turbulence on a beta-plane, J. Fluid Mech., 69, 417–443, https://doi.org/10.1017/S0022112075001504, 1975.
Royer, S. J., Mahajan, A. S., Galí, M., Saltzman, E., and Simõ, R.: Small-scale variability patterns of DMS and phytoplankton in surface waters of the tropical and subtropical Atlantic, Indian, and Pacific Oceans, Geophys. Res. Lett., 42, 475–483, https://doi.org/10.1002/2014GL062543, 2015.
Royer, S. J., Galí, M., Mahajan, A. S., Ross, O. N., Pérez, G. L., Saltzman, E. S., and Simó, R.: A high-resolution time-depth view of dimethylsulphide cycling in the surface sea, Sci. Rep., 6, 32325, https://doi.org/10.1038/srep32325, 2016.
Saltzman, E. S., De Bruyn, W. J., Lawler, M. J., Marandino, C. A., and McCormick, C. A.: A chemical ionization mass spectrometer for continuous underway shipboard analysis of dimethylsulfide in near-surface seawater, Ocean Sci., 5, 537–546, https://doi.org/10.5194/os-5-537-2009, 2009.
Sanchez, K. J., Chen, C. L., Russell, L. M., Betha, R., Liu, J., Price, D. J., Massoli, P., Ziemba, L. D., Crosbie, E. C., Moore, R. H., Müller, M., Schiller, S. A., Wisthaler, A., Lee, A. K. Y., Quinn, P. K., Bates, T. S., Porter, J., Bell, T. G., Saltzman, E. S., Vaillancourt, R. D., and Behrenfeld, M. J.: Substantial Seasonal Contribution of Observed Biogenic Sulfate Particles to Cloud Condensation Nuclei, Sci. Rep., 8, 1–14, https://doi.org/10.1038/s41598-018-21590-9, 2018.
Scott, R. B. and Wang, F.: Direct Evidence of an Oceanic Inverse Kinetic Energy Cascade from Satellite Altimetry, J. Phys. Oceanogr., 35, 1650–1666, https://doi.org/10.1175/JPO2771.1, 2005.
Simó, R.: Production of atmospheric sulfur by oceanic plankton: biogeochemical, ecological and evolutionary links, Trends Ecol. Evol., 16, 287–294, 2001.
Simó, R. and Dachs, J.: Global ocean emission of dimethylsulfide predicted from biogeophysical data, Global Biogeochem. Cy., 16, 26-1–26-10, https://doi.org/10.1029/2001GB001829, 2002.
Simó, R., Saló, V., Almeda, R., Movilla, J., Trepat, I., Saiz, E., and Calbet, A.: The quantitative role of microzooplankton grazing in dimethylsulfide (DMS) production in the NW Mediterranean, Biogeochemistry, 141, 125–142, https://doi.org/10.1007/S10533-018-0506-2, 2018.
Stefels, J., van Leeuwe, M. A., Jones, E. M., Meredith, M. P., Venables, H. J., Webb, A. L., and Henley, S. F.: Impact of sea-ice melt on dimethyl sulfide (sulfoniopropionate) inventories in surface waters of Marguerite Bay, West Antarctic Peninsula, Philos. T. Roy. Soc. A, 376, 20170169, https://doi.org/10.1098/RSTA.2017.0169, 2018.
Tesdal, J.-E., Christian, J. R., Monahan, A. H., and von Salzen, K.: Evaluation of diverse approaches for estimating sea-surface DMS concentration and air–sea exchange at global scale, Environ. Chem., 13, 390–412, https://doi.org/10.1071/EN14255, 2015.
Toole, D. A. and Siegel, D. A.: Light-driven cycling of dimethylsulfide (DMS) in the Sargasso Sea: Closing the loop, Geophys. Res. Lett., 31, L09308, https://doi.org/10.1029/2004GL019581, 2004.
Toole, D. A., Siegel, D. A., and Doney, S. C.: A light-driven, one-dimensional dimethylsulfide biogeochemical cycling model for the Sargasso Sea, J. Geophys. Res.-Biogeosci., 113, G02009, https://doi.org/10.1029/2007JG000426, 2008.
Tortell, P. D.: Dissolved gas measurements in oceanic waters made by membrane inlet mass spectrometry, Limnol. Oceanogr.-Meth., 3, 24–37, https://doi.org/10.4319/lom.2005.3.24, 2005a.
Tortell, P. D.: Small-scale heterogeneity of dissolved gas concentrations in marine continental shelf waters, Geochem. Geophy. Geosy., 6, Q11M04, https://doi.org/10.1029/2005GC000953, 2005b.
Tortell, P. D. and Long, M. C.: Spatial and temporal variability of biogenic gases during the Southern Ocean spring bloom, Geophys. Res. Lett., 36, L01603, https://doi.org/10.1029/2008GL035819, 2009.
Tortell, P. D., Guéguen, C., Long, M. C., Payne, C. D., Lee, P., and DiTullio, G. R.: Spatial variability and temporal dynamics of surface water pCO2, δO2/Ar and dimethylsulfide in the Ross Sea, Antarctica, Deep-Sea Res. Pt. 1, 58, 241–259, https://doi.org/10.1016/j.dsr.2010.12.006, 2011.
Tulloch, R., Marshall, J., Hill, C., and Smith, K. S.: Scales, Growth Rates, and Spectral Fluxes of Baroclinic Instability in the Ocean, J. Phys. Oceanogr., 41, 1057–1076, https://doi.org/10.1175/2011JPO4404.1, 2011.
Vallina, S. M. and Simó, R.: Strong Relationship Between DMS and the Solar Radiation Dose over the Global Surface Ocean, Science, 315, 506–508, https://doi.org/10.1126/science.281.5374.200, 2007.
Vallina, S. M., Simó, R., Anderson, T. R., Gabric, A., Cropp, R., and Pacheco, J. M.: A dynamic model of oceanic sulfur (DMOS) applied to the Sargasso Sea: Simulating the dimethylsulfide (DMS) summer paradox, J. Geophys. Res.-Biogeosci, 113, G01009, https://doi.org/10.1029/2007JG000415, 2008.
Wang, W.-L., Song, G., Primeau, F., Saltzman, E. S., Bell, T. G., and Moore, J. K.: Global ocean dimethyl sulfide climatology estimated from observations and an artificial neural network, Biogeosciences, 17, 5335–5354, https://doi.org/10.5194/bg-17-5335-2020, 2020.
Williams, R. G. and Follows, M. J.: Ocean eddies, in: Ocean Dynamics and the Carbon Cycle, Cambridge University Press, 211–235, https://doi.org/10.1017/CBO9780511977817.010, 2011.
Woodhouse, M. T., Carslaw, K. S., Mann, G. W., Vallina, S. M., Vogt, M., Halloran, P. R., and Boucher, O.: Low sensitivity of cloud condensation nuclei to changes in the sea-air flux of dimethyl-sulphide, Atmos. Chem. Phys., 10, 7545–7559, https://doi.org/10.5194/acp-10-7545-2010, 2010.
Woodhouse, M. T., Mann, G. W., Carslaw, K. S., and Boucher, O.: Sensitivity of cloud condensation nuclei to regional changes in dimethyl-sulphide emissions, Atmos. Chem. Phys., 13, 2723–2733, https://doi.org/10.5194/acp-13-2723-2013, 2013.
Zindler, C., Marandino, C. A., Bange, H. W., Schütte, F., and Saltzman, E. S.: Nutrient availability determines dimethyl sulfide and isoprene distribution in the eastern Atlantic Ocean, Geophys. Res. Lett., 41, 3181–3188, https://doi.org/10.1002/2014GL059547, 2014.
Zlotnicki, V., Qu, Z., and Willis, J.: SEA_SURFACE_HEIGHT_ ALT_GRIDS_L4_2SATS_5DAY_6THDEG_V_JPL1609. Ver. 1812, PO.DAAC, CA, USA [data set], https://doi.org/10.5067/SLREF-CDRV2, 2019.